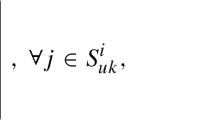Robust adaptive stabilization by high gain feedback for Markovian jump systems with partially unknown transition rates

Abstract

In this paper, a class of multi-input multi-output nonlinearly perturbed Markovian jump systems with partially unknown transition rates is considered. We assume that this class of systems is characterized only by some structural properties such as the system is strongly minimum phase, with a strict relative degree one set and positive definite high frequency gain matrices. For this class of systems, a universal adaptive high gain controller, which is not based on estimation algorithms or identification of parameters, is designed such that in the presence of certain nonlinear perturbations and external disturbances, the convergence and the boundedness of the closed-loop system signals in the mean square sense are ensured. A vertical take-off and landing (VTOL) helicopter example is provided to demonstrate the performance and effectiveness of the obtained results.

1 Introduction

In the past few decades, considerable attention has been devoted to Markovian jump systems (MJSs), due to their extensive applications in aerospace systems, manufacturing systems, power systems and networked control systems, etc. MJSs are systems made up of several subsystems or modes that can switch between them at random. Modeling abrupt phenomena such as random failures, component repairs, and sudden environmental changes has been done using such systems [1,2,3,4,5]. As a result, control researchers have devoted themselves to studying topics such as stability, stabilization, passivity analysis, sliding mode control and filtering problems (see, for instance, [6,7,8,9,10,11,12,13]).

Many MJSs results have been obtained so far based on the assumption that the transition rates (TRs) are fully known. In practice, however, we cannot always be sure that we will have complete information on the TRs, which means that incomplete TRs are common [6], and this is because obtaining adequate samples of the transitions may be time consuming or costly. Therefore, it is critical to investigate more general MJSs with partial information on transition probabilities.

On another research front line, significant improvement has been made in the field of high-gain adaptive control without identification for deterministic systems (see, for instance [14,15,16,17,18]). The primary issue under consideration is the construction of nonlinear measurement feedback controllers of simple structure, which are able to stabilize all systems in a specified class. The two distinguishing features of the approach of high-gain adaptive control without identification compared to other adaptive control approaches (see [15]) are: first, no attempt is made to identify systems dynamics (i.e., despite its efficiency in controlling the system, the controller remains totally ignorant of it) and second, the considered class of systems is not described by a specification of system parameters or state dimension but by a characterization of the system structure (e.g., minimum phase, known relative degree, known sign of the high frequency gain matrix).

The first attempt to solve the problem of high-gain adaptive stabilization for MJSs was done in [10]. The authors in [10] have shown that the simple time varying output feedback $u(t)=-k(t)y(t)$, adapted by $\dot{k}(t)=E\big \{\Vert y(t) \Vert ^{2}\big \}$ is a universal adaptive stabilizer in the sense that whenever it is applied to any multivariable MJLS with partially unknown TRs and satisfying the properties: strongly minimum phase, strict relative degree one set and positive definite high frequency gain matrices, the closed-loop non-linear system obtained will have the properties: finite escape time does not occur, all states are bounded and in particular, the state x(t) satisfies: $\int _{0}^{\infty }E\big \{\Vert x(t) \Vert ^{2}\big \}dt<\infty$,  $\sup _{0\le t< \infty }E\big \{\Vert x(t) \Vert ^{2}\big \}< \infty$ and $\lim _{t\rightarrow \infty }E\big \{\Vert x(t) \Vert ^{2}\big \}=0$. However, the problem of robustness of the universal adaptive controller with respect to nonlinear perturbations and external disturbances has not yet been investigated for this class of systems, which motivates this work. Furthermore, Many relevant studies have been conducted on vertical take-off and landing (VTOL) helicopters, which are capable of taking-off, landing within limited field, and stable hovering over target region (see, for instance, [19,20,21]). It is known that VTOL systems are characterized by strong nonlinearities compared to fixed wing designs. Also, due to their lightweight structure they are relatively sensitive to atmospheric disturbances (e.g., wind gusts) (see, [22]) which exist inevitably and can become strong especially in the case of the rapid flight maneuver. Thus, they should be considered in describing the system dynamics in the form of input disturbances and so the design of a robust stabilizing controller becomes an interesting problem for such practical systems.

The main contributions of the present paper are: first, to show that the high-gain universal adaptive controller presented in [10] is robust in the sense that the control objectives (bounded signals and convergence of the state of the system) are still met if the controller is applied to any MJS subjected to certain disturbances and satisfying the structural assumptions (strict relative degree one set, strongly minimum phase and positive definite high-frequency gain matrices). It will be shown that the designed stabilizer can cope with nonlinear time-varying perturbations, provided they are linearly bounded. Also, some arbitrary additive input disturbances $d(\cdot )$ which are bounded and square integrable are tolerated. And, second, to show that the desired closed-loop objectives are achieved by our control strategy for a VTOL helicopter system and that the effect of the perturbations and the external disturbances can be eliminated.

The rest of this paper is organized as follows: We describe our system and give some preliminaries in Sect. 2. In Sect. 3 some structural properties characterizing the considered class of perturbed systems are discussed. The design of a universal adaptive stabilizer for the class of strongly minimum phase nonlinearly perturbed MJSs is studied in Sect. 4 such that the effect of the perturbations is eliminated and the control objectives are guaranteed. A practical example which shows the applicability and the feasibility of our methods is given in Sect. 5. Finally, concluding remarks and future research directions are presented in Sect. 6.

2 Preliminaries

Fix the complete probability space $(\Omega ,\mathcal {F},\mathbb {P})$ and consider the m-input m-output MJS subjected to perturbations of the form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t)= A(r_{t})x(t)+B(r_{t})[u(t)+g(x(t),t)+d(t)],\\ y(t)= C(r_{t})x(t), \\ x(0)= x_{0},\; r_{0}\in \Upsilon , \end{array}\right. } \end{aligned}$$

(1)

where $x(t)\in \mathbb R^{n}$, $u(t)\in \mathbb R^{m}$ and $y(t)\in \mathbb R^{m}$ denote the state vector, control input and measured output, respectively. $\left\{ {r_{t},t\ge 0}\right\}$ is a time-homogeneous Markov process with right continuous trajectories which takes values in a finite space $\Upsilon =\left\{ {1,2,...,N}\right\}$ and has the following mode transition probabilities:

$$\begin{aligned} \mathbb {P}\{r_{t+h}=j/r_{t}=i\}={\left\{ \begin{array}{ll} \pi _{ij}h+o(h),\quad &{} i\ne j, \\ 1+\pi _{ii}h+o(h),\quad &{} i=j, \end{array}\right. }\end{aligned}$$

where $h>0$, $\lim _{h\longrightarrow 0} \frac{o(h)}{h}=0$ and $\pi _{ij}\ge 0$ ($i,j\in \Upsilon , j\ne i$) denotes the TR from mode i at time t to mode j at time $t+h$ with $\pi _{ii}=-\sum _{j=1, j\ne i}^{N} \pi _{ij}$ for each $i \in \Upsilon$. Hence, the TR matrix $\Pi$ is given by: $\Pi =\{\pi _{ij}\}_{N\times N}$.

The external disturbance vector $d(t) \in \mathbb R^{m}$ is an unknown bounded function which is assumed to be square-integrable, i.e.,

$$\begin{aligned} \int _{0}^{\infty }\Vert d(t) \Vert ^{2}dt<\hat{d}, \end{aligned}$$

where $\hat{d}$ is an unknown positive constant. The nonlinear perturbation $g(x, t)\in \mathbb R^{m}$ is assumed to be locally Lipschitz function for each fixed $t\in \mathbb R$, and $t \mapsto g(x, t)$ is measurable for each fixed x. In addition, this nonlinear function satisfies the following condition:

$$\begin{aligned} \Vert g(x,t)\Vert \le \hat{g}\Vert x\Vert , \end{aligned}$$

where $\hat{g}$ is an unknown constant. For each possible value $r_{t}=i$, $i \in \Upsilon$, the system matrices of the ith mode are denoted by $A_{i}$, $B_{i}$ and $C_{i}$, which are real valued constant matrices with appropriate dimensions. These matrices and the state space dimension $n \in \mathbb {N}$ need not to be known precisely.

In this paper, the TR matrix $\Pi$ is assumed to be partially unknown. This means that some elements in this matrix are unknown. Furthermore, we assume that a lower bound $\pi _{l}$ for the unknown diagonal elements of $\Pi$ is known. For example, if $N=4$, the TR matrix $\Pi$ can be considered as:

$$\begin{aligned} \begin{bmatrix} \pi _{11} &{} \hat{\pi }_{12} &{} \hat{\pi }_{13} &{} \pi _{14}\\ \hat{\pi }_{21} &{} \pi _{22} &{} \pi _{23} &{} \hat{\pi }_{24}\\ \hat{\pi }_{31} &{} \pi _{32} &{} \hat{\pi }_{33} &{} \pi _{34}\\ \pi _{41} &{} \hat{\pi }_{42} &{} \hat{\pi }_{43} &{} \hat{\pi }_{44}\\ \end{bmatrix}, \end{aligned}$$

where each unknown element is labeled with a hat “$\hat{\cdot }$”. For the sake of notational clarity, we denote the set $\Upsilon =\Upsilon _{\mathcal {K}}^{i} \cup \Upsilon _{\mathcal {UK}}^{i}$ ($\forall i \in \Upsilon$), with $\Upsilon _{\mathcal {K}}^{i} \triangleq \{j : \pi _{ij} \text { is known}\}$ and $\Upsilon _{\mathcal {UK}}^{i} \triangleq \{j : \pi _{ij} \text { is unknown}\}$. Also, the notation $\pi _{\mathcal {K}}^{i}\triangleq \sum _{j\in \Upsilon _{\mathcal {K}}^{i} }\pi _{ij}$ is used. The following definition is necessary in this paper.

Definition 1

[1] The stochastic system (1) with $u(t)\equiv 0$ is said to be stochastically stable, if for any initial condition $x_{0} \in \mathbb R^{n}$ and $r_{0} \in \Upsilon$, the following holds:

$$\begin{aligned} \int _{0}^{\infty }E\big \{\Vert x(t) \Vert ^{2}\big \}dt<\infty . \end{aligned}$$

3 Properties of the system class

The concepts of the relative degree set, (stochastically stable) zero dynamics and switched Byrnes-Isidori forms [23] play a key role in this paper. These concepts will be introduced and discussed in this section. The definition of the strict relative degree one set for the MJS (1) is given. Then, for this set of relative degrees and based on a change of coordinates, an equivalent MJS described by a set of switched Byrnes-Isidori forms is obtained. This new system will allow us to characterize the zero dynamics of system (1).

Definition 2

The perturbed MJS (1) is said to have strict relative degree one set, if the system corresponding to each mode $i\in \Upsilon$ is with a strict relative degree one. i.e.,

$$\begin{aligned} \det (C_{i}B_{i})\ne 0,\quad \forall i\in \Upsilon . \end{aligned}$$

$C_{i}B_{i}$ is the high frequency gain matrix corresponding to the mode $i\in \Upsilon$.

Remark 1

Note that Definition 2 can be regarded as a generalization of the definition of the strict relative degree one present in the deterministic case for time invariant linear systems (see, for example, [16]).

Assume from now on that system (1) has strict relative degree one set. In the following lemma, a state space transformation is used to produce a representation convenient for the analysis in this paper. Indeed, if $\det (C_{i}B_{i})\ne 0, \forall i\in \Upsilon$, then, we can decompose the state space, for each $i \in \Upsilon$, into the direct sum: $\mathbb {R}^n = Im B_{i} \oplus \ker C_{i}$, (see [14]) which leads to the following state space description of the MJS (1).

Lemma 1

Consider the perturbed MJS (1) and suppose that $\det (C_{i}B_{i})\ne 0, \forall i\in \Upsilon$. $\forall i \in \Upsilon$, let:

$$\begin{aligned} {\left\{ \begin{array}{ll} S_{i} \in \mathbb {R}^{n\times (n-m)}, \text {such that}\; Im S_{i}=\ker C_{i}\,,\\ R_{i}\triangleq \left( S_{i}^\top S_{i}\right) ^{-1} S_{i}^\top \left[ \mathbb {I}_{n}-B_{i}\left( C_{i}B_{i}\right) ^{-1} C_{i} \right] . \end{array}\right. } \end{aligned}$$

Then, $\forall i \in \Upsilon$, $T_{i} \triangleq \begin{bmatrix} C_{i}^\top&R_{i}^\top \end{bmatrix}^{\top }$, has the inverse $T_{i}^{-1}= \begin{bmatrix} B_{i} \left( C_{i}B_{i}\right) ^{-1}&S_{i} \end{bmatrix}$, and when $r_{t}=i$, the following state space transformation

$$\begin{aligned} \zeta ^{(i)}(t)=T_{i} x(t)= \begin{bmatrix} C_{i}x(t)\\ R_{i}x(t) \end{bmatrix} \end{aligned}$$

(2)

takes (1) into the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\zeta }^{(i)}(t)=\widetilde{A}_{i}\zeta ^{(i)}(t)+\widetilde{B}_{i}[u(t)+g(x(t),t)+d(t)], \\ y(t)=\widetilde{C}_{i}\zeta ^{(i)}(t), \end{array}\right. } \end{aligned}$$

(3)

where

$$\begin{aligned} \widetilde{A}_{i}=T_{i}A_{i}T_{i}^{-1}= \begin{bmatrix} A_{1i} &{} A_{2i} \\ A_{3i} &{} A_{4i} \end{bmatrix} ,\; \widetilde{B}_{i}=T_{i}B_{i}= \begin{bmatrix} C_{i}B_{i} \\ 0 \end{bmatrix} \end{aligned}$$

$$\begin{aligned} \widetilde{C}_{i}=C_{i}T_{i}^{-1}= \begin{bmatrix} \mathbb {I}_{m}&0 \end{bmatrix}, \end{aligned}$$

$A_{1i}\triangleq C_{i}A_{i}B_{i}\left( C_{i}B_{i}\right) ^{-1}\in \mathbb {R}^{m\times m}, A_{2i}\triangleq C_{i}A_{i}S_{i}\in \mathbb {R}^{m\times (n-m)}, A_{3i}\triangleq R_{i}A_{i}B_{i}\left( C_{i}B_{i}\right) ^{-1}\in \mathbb {R}^{(n-m)\times m}, A_{4i}\triangleq R_{i}A_{i}S_{i}\in \mathbb {R}^{(n-m)\times (n-m)}$.

Remark 2

Note that the set of the nonsingular matrices $T_{i}$, $\forall i \in \Upsilon$ in Lemma 1 is constructed by following the same line as for linear time-invariant deterministic systems, which leads to a set of Byrnes-Isidori forms for the N-modes of system (1) (see [15, 23]).

Remark 3

By using the following notation:

$$\begin{aligned} y(t)=C(r_{t})x(t)=y^{(r_{t})}(t), \end{aligned}$$

we can write, when $r_{t}=i$ :

$$\begin{aligned} \zeta ^{(i)}(t)= \begin{bmatrix} y^{(i)}(t) \\ \eta ^{(i)}(t) \end{bmatrix}, \end{aligned}$$

with $\eta ^{(i)}(t)\triangleq R_{i}x(t) \in \mathbb {R}^{n-m}$. Hence, Lemma 1 shows that the MJSs in (1) are transferred to the following switched Byrnes–Isidori forms:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{y}^{(r_{t})}(t)=A_{1}(r_{t}){y}^{(r_{t})}(t)+A_{2}(r_{t}){\eta }^{(r_{t})}(t)\\ \quad \quad \quad \quad \quad \quad +C(r_{t})B(r_{t})[u(t)+g(x(t),t)+d(t)], \\ \dot{\eta }^{(r_{t})}(t)=A_{3}(r_{t}){y}^{(r_{t})}(t)+A_{4}(r_{t}){\eta }^{(r_{t})}(t), \\ {y}^{(r_{0})}(0)=C(r_{0})x_{0},\; {\eta }^{(r_{0})}(0)=R(r_{0})x_{0}. \end{array}\right. } \end{aligned}$$

(4)

Remark 4

$\forall i,j\in \Upsilon$ we have :

$$\begin{aligned}\zeta ^{(j)}=T_{j}x=T_{j}T_{i}^{-1}\zeta ^{(i)},\end{aligned}$$

then, for every $i,j\in \Upsilon$, it follows that

$$\begin{aligned} {\left\{ \begin{array}{ll} {y}^{(j)}=C_{j}B_{i}\left( C_{i}B_{i}\right) ^{-1}{y}^{(i)}+C_{j}S_{i}{\eta }^{(i)}, \\ {\eta }^{(j)}=R_{j}B_{i}\left( C_{i}B_{i}\right) ^{-1}{y}^{(i)}+R_{j}S_{i}{\eta }^{(i)}. \end{array}\right. } \end{aligned}$$

(5)

The second equation in (4) represents the internal dynamics of system (1). If $y(\cdot )$ is equal to zero, then these dynamics are called zero dynamics. The latter are therefore described by the zero output system:

$$\begin{aligned} \dot{\eta }^{(r_{t})}(t)=A_{4}(r_{t}){\eta }^{(r_{t})}(t). \end{aligned}$$

(6)

In the following, we shall provide a characterization of the zero dynamics based on two important concepts which are the minimum phase and the strongly minimum phase properties.

Definition 3

The MJS (1) is said to be minimum phase, if the zero output system (6) is stochastically stable.

Definition 4

[10] The MJS (1) with partially unknown TRs is said to be strongly minimum phase, if for the zero output system (6) there exists a set of matrices $P_{i}=P_{i}^{\top }>0$, such that $\forall i\in \Upsilon$

$$\begin{aligned} \begin{aligned} \Gamma _{1}^{i}<\pi _{\mathcal {K}}^{i}(C_{j}S_{i})^{\top }(C_{j}S_{i})-\sum _{j\in \Upsilon _{\mathcal {K}}^{i} }\pi _{ij}(C_{j}S_{i})^{\top }(C_{j}S_{i}),\\ \forall j \in \Upsilon _{\mathcal {UK}}^{i},\quad if \, i \in \Upsilon _{\mathcal {K}}^{i}, \end{aligned} \end{aligned}$$

(7)

$$\begin{aligned} \begin{aligned} \Gamma _{2}^{i}<\pi _{\mathcal {K}}^{i}(C_{j}S_{i})^{\top }(C_{j}S_{i})-\sum _{j\in \Upsilon _{\mathcal {K}}^{i} }\pi _{ij}(C_{j}S_{i})^{\top }(C_{j}S_{i})\\ +\pi _{l}(C_{j}S_{i})^{\top }(C_{j}S_{i}),\\\forall j \in \Upsilon _{\mathcal {UK}}^{i},\quad if \, i \in \Upsilon _{\mathcal {UK}}^{i}, \end{aligned} \end{aligned}$$

(8)

where $\Gamma _{1}^{i}\triangleq A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\mathcal {P}_{\mathcal {K}}^{i}-\pi _{\mathcal {K}}^{i} S_{i}^{\top }R_{j}^{\top }P_{j}R_{j}S_{i}$, $\Gamma _{2}^{i}\triangleq A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\mathcal {P}_{\mathcal {K}}^{i}+\pi _{l}P_{i}-\pi _{l}S_{i}^{\top }R_{j}^{\top }P_{j}R_{j}S_{i} -\pi _{\mathcal {K}}^{i} S_{i}^{\top }R_{j}^{\top }P_{j}R_{j}S_{i}$ and $\mathcal {P}_{\mathcal {K}}^{i} \triangleq \sum _{j\in \Upsilon _{\mathcal {K}}^{i} }\pi _{ij}S_{i}^{\top }R_{j}^{\top }P_{j}R_{j}S_{i}$.

Remark 5

It is to be noted that if the MJS (1) is strongly minimum phase then it is minimum phase (see [10], Remark 3.5).

4 Universal adaptive controller design

In this section, we aim to show that the following adaptive control law introduced in [10]:

$$\begin{aligned} u(t)=-k(t)y(t), \quad \dot{k}(t)=E\big \{\Vert y(t) \Vert ^{2}\big \},\; k(0)\in \mathbb {R} \end{aligned}$$

(9)

is tolerant with respect to unknown nonlinear time-varying perturbations, provided they are linearly bounded and unknown additive input external disturbances which are bounded and square integrable. Let us consider the class of multi-input multi-output perturbed systems of the form of (1) which satisfy the assumptions: strict relative degree one set, strongly minimum phase and positive definite high frequency gain matrices (i.e., $C_{i}B_{i}+(C_{i}B_{i})^\top >0, \forall i\in \Upsilon$). Let

$$\begin{aligned} {\left\{ \begin{array}{ll} {\left\{ \begin{array}{ll} \dot{x}(t)= A(r_{t})x(t)+B(r_{t})[u(t)+g(x(t),t)+d(t)] \\ y(t)= C(r_{t})x(t),\\ x(0)= x_{0}, E\big \{\Vert x_{0}\Vert ^{2}\big \}<\infty , \; r_{0}\in \Upsilon ,\\ \end{array}\right. }\\ (A_{i}, B_{i}, C_{i}) \in \mathbb {R}^{n\times n}\times \mathbb {R}^{n\times m}\times \mathbb {R}^{m\times n}.\\ \Pi \text { partially unknown with known lower bound } \pi _{l} \\ \text { for the unknown diagonal elements}. \\ \text {Strict relative degree one set}.\\ \text {Strongly minimum phase}.\; n \; \text {arbitrary}.\\ C_{i}B_{i}+(C_{i}B_{i})^\top >0, \forall i\in \Upsilon . \end{array}\right. } \end{aligned}$$

(10)

We will show that the controller (9) is a universal adaptive stabilizer for the class (10). This means that whenever it is applied to any system in this class, the resulting closed-loop nonlinear system has the properties: finite escape time does not occur, all states are bounded and in particular, the state x(t) satisfies the second moment properties: $\int _{0}^{\infty }E\big \{\Vert x(t) \Vert ^{2}\big \}dt<\infty$,  $\sup _{0\le t< \infty }E\big \{\Vert x(t) \Vert ^{2}\big \}< \infty$ and $\lim _{t\rightarrow \infty }E\big \{\Vert x(t) \Vert ^{2}\big \}=0$.

Remark 6

It should be noted that in case the system has only one mode (i.e., $N = 1$), the feedback strategy (9) is reduced to the well-known universal adaptive stabilizer for minimum phase linear deterministic systems of strict relative degree one, which is the Willems-Byrnes controller: $u(t)=-k(t)y(t)$, $\dot{k}(t)=\Vert y(t) \Vert ^{2}$ (see [25]).

The following Lemma will be useful in proving the paper’s main result.

Lemma 2

Suppose the nonlinear perturbed MJS with partially unknown TRs

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{y}^{(r_{t})}(t)=A_{1}(r_{t}){y}^{(r_{t})}(t)+A_{2}(r_{t}){\eta }^{(r_{t})}(t)\\ \quad \quad \quad \quad \quad \quad +C(r_{t})B(r_{t})[u(t)+g(x(t),t)+d(t)], \\ \dot{\eta }^{(r_{t})}(t)=A_{3}(r_{t}){y}^{(r_{t})}(t)+A_{4}(r_{t}){\eta }^{(r_{t})}(t) \end{array}\right. } \end{aligned}$$

(11)

is strongly minimum phase with $C_{i}B_{i}+(C_{i}B_{i})^\top >0, \forall i\in \Upsilon$. Let $k:[0,t') \longrightarrow \mathbb {R}, t'\le \infty$, be a piecewise continuous function and suppose that there exists $t^{*}$ $\in [0,t')$ and $k^{*}>0$ such that $k(t)\ge k^{*},\forall t\ge t^{*}$. If feedback of the form $u(t)=-k(t)y(t)$ is applied to (11) and $k^{*}$ is sufficiently large, then there exist $\lambda _{1}>0$, $\lambda _{2}>0$ and $\beta >0$ such that the solution of the closed-loop system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{y}^{(r_{t})}(t)=\big [A_{1}(r_{t})-k(t)C(r_{t})B(r_{t})\big ] {y}^{(r_{t})}(t)\\ \quad \quad \quad \quad \quad \quad +A_{2}(r_{t}){\eta }^{(r_{t})}(t)+C(r_{t})B(r_{t})g(x(t),t)\\ \quad \quad \quad \quad \quad \quad +C(r_{t})B(r_{t})d(t),\\ \dot{\eta }^{(r_{t})}(t)=A_{3}(r_{t}){y}^{(r_{t})}(t)+A_{4}(r_{t}){\eta }^{(r_{t})}(t) \end{array}\right. } \end{aligned}$$

(12)

satisfies

$$\begin{aligned}&\quad E\Bigg \{\left\| \begin{pmatrix} {y}^{(r_{t})}\\ {\eta }^{(r_{t})} \end{pmatrix} \right\| ^{2}\Bigg \}\\&\le \Bigg [ \lambda _{1} E\Bigg \{\left\| \begin{pmatrix} {y}^{(r_{t_{0}})}\\ {\eta }^{(r_{t_{0}})} \end{pmatrix} \right\| ^{2}\Bigg \}+ \lambda _{2}\Bigg ] e^{-\beta (t-t_{0})} \end{aligned}$$

for all $t \in [t_{0},t'), t_{0} \in [0,t')$.

Proof

Consider the following set of positive-definite Lyapunov functions candidates defined by: $V(y^{(i)},\eta ^{(i)},i)=\frac{1}{2}\eta ^{(i)^{\top }}P_{i}\eta ^{(i)}+\frac{1}{2}y^{(i)^{\top }}y^{(i)}$, where $P_{i}=P_{i}^{\top }$, $i\in \Upsilon$ are the positive-definite solutions of the following inequalities:

$$\begin{aligned} \begin{aligned} \Gamma _{1}^{i}-\pi _{\mathcal {K}}^{i}(C_{j}S_{i})^{\top }(C_{j}S_{i})+\sum _{j\in \Upsilon _{\mathcal {K}}^{i} }\pi _{ij}(C_{j}S_{i})^{\top }(C_{j}S_{i})<0,\\ \forall j \in \Upsilon _{\mathcal {UK}}^{i},\quad if \, i \in \Upsilon _{\mathcal {K}}^{i}, \end{aligned} \end{aligned}$$

(13)

$$\begin{aligned} \begin{aligned} \Gamma _{2}^{i}-\pi _{\mathcal {K}}^{i}(C_{j}S_{i})^{\top }(C_{j}S_{i})+\sum _{j\in \Upsilon _{\mathcal {K}}^{i} }\pi _{ij}(C_{j}S_{i})^{\top }(C_{j}S_{i})\\pi_{l}(C_{j}S_{i})^{\top }(C_{j}S_{i})<0, \\ \forall j \in \Upsilon _{\mathcal {UK}}^{i},\quad if \, i \in \Upsilon _{\mathcal {UK}}^{i}, \end{aligned} \end{aligned}$$

(14)

where $\Gamma _{1}^{i}$ and $\Gamma _{2}^{i}$ are defined as in Definition 4.

Let $\mathcal {L}$ denote the infinitesimal generator of (11) [24]. By a straightforward calculation, one obtains

$$\begin{aligned}&\quad \mathcal {L}V(y^{(i)},\eta ^{(i)},i)\\&=y^{(i)^{\top }}A_{1i}y^{(i)}+y^{(i)^{\top }}[A_{2i}+A_{3i}^{\top }P_{i}]\eta ^{(i)}\\&\quad -\frac{1}{2}k(t)y^{(i)^{\top }}[C_{i}B_{i}+(C_{i}B_{i})^\top ]y^{(i)}\\&\quad +\frac{1}{2}\eta ^{(i)^{\top }}[A_{4i}^{\top }P_{i}+P_{i}A_{4i}]\eta ^{(i)}+ y^{(i)^{\top }}C_{i}B_{i}g(x,t)\\&\quad + y^{(i)^{\top }}C_{i}B_{i}d(t)+ y^{(i)^{\top }}\Theta _{1i}y^{(i)}\\&\quad +y^{(i)^{\top }}\Theta _{2i}\eta ^{(i)}+\frac{1}{2}\eta ^{(i)^{\top }}\Theta _{3i}\eta ^{(i)}, \end{aligned}$$

where $\Theta _{1i}\triangleq \frac{1}{2}\sum _{j=1}^{N}\pi _{ij}E_{ij}$, $\Theta _{2i}\triangleq \sum _{j=1}^{N}\pi _{ij}F_{ij}$ and $\Theta _{3i}\triangleq \sum _{j=1}^{N}\pi _{ij}G_{ij}$. $E_{ij}$, $F_{ij}$ and $G_{ij}$ are given as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} E_{ij}= E_{ij}^{\top }\triangleq (C_{i}B_{i})^{-\top }B_{i}^{\top } C_{j}^{\top }C_{j}B_{i}(C_{i}B_{i})^{-1}\\ \quad \quad \quad \quad \quad \quad +(C_{i}B_{i})^{-\top }B_{i}^{\top }R_{j}^{\top }P_{j}R_{j}B_{i}(C_{i}B_{i})^{-1},\\ F_{ij}\triangleq (C_{i}B_{i})^{-\top }B_{i}^{\top } C_{j}^{\top }C_{j}S_{i}+(C_{i}B_{i})^{-\top }B_{i}^{\top }R_{j}^{\top }P_{j}R_{j}S_{i}, \\ G_{ij}= G_{ij}^{\top }\triangleq S_{i}^{\top }C_{j}^{\top }C_{j}S_{i}+S_{i}^{\top }R_{j}^{\top }P_{j}R_{j}S_{i}. \end{array}\right. } \end{aligned}$$

(15)

We have

$$\begin{aligned}&\quad y^{(i)^{\top }}A_{1i}y^{(i)}+y^{(i)^{\top }}[A_{2i}+A_{3i}^{\top }P_{i}]\eta ^{(i)}+y^{(i)^{\top }}\Theta _{1i}y^{(i)}\\&\quad +y^{(i)^{\top }}\Theta _{2i}\eta ^{(i)}\\ {}&\le \Big (\Vert A_{1i}\Vert + \Vert A_{2i}\Vert +\Vert A_{3i}^{\top }P_{i}\Vert + \Vert \Theta _{1i}\Vert + \Vert \Theta _{2i}\Vert \Big )\times \Vert y^{(i)}\Vert ^{2}\\ {}&\quad +\frac{\sqrt{2}}{\sqrt{\alpha _{1}}}\times \Big (\Vert A_{1i}\Vert + \Vert A_{2i}\Vert +\Vert A_{3i}^{\top }P_{i}\Vert + \Vert \Theta _{1i}\Vert + \Vert \Theta _{2i}\Vert \Big )\\ {}&\quad \times \Vert y^{(i)}\Vert \frac{\sqrt{\alpha _{1}}}{\sqrt{2}}\Vert \eta ^{(i)}\Vert , \end{aligned}$$

where $\alpha _{1}>0$ is to be specified later.

Denote

$$\begin{aligned} H_{i}\triangleq \Vert A_{1i}\Vert + \Vert A_{2i}\Vert +\Vert A_{3i}^{\top }P_{i}\Vert + \Vert \Theta _{1i}\Vert + \Vert \Theta _{2i}\Vert , \end{aligned}$$

then

$$\begin{aligned}&\quad y^{(i)^{\top }}A_{1i}y^{(i)}+y^{(i)^{\top }}[A_{2i}+A_{3i}^{\top }P_{i}]\eta ^{(i)}+y^{(i)^{\top }}\Theta _{1i}y^{(i)}\\ {}&\quad +y^{(i)^{\top }}\Theta _{2i}\eta ^{(i)}\\&\le H_{i}\Vert y^{(i)}\Vert ^{2}+\frac{2}{\alpha _{1}}H_{i}^{2}\Vert y^{(i)}\Vert ^{2}+\frac{\alpha _{1}}{2}\Vert \eta ^{(i)}\Vert ^{2}. \end{aligned}$$

Also we have

$$\begin{aligned} y^{(i)^{\top }}C_{i}B_{i}d(t)&\le \Vert C_{i}B_{i}\Vert \Vert d(t)\Vert \Vert y^{(i)}\Vert \\&\le \Vert C_{i}B_{i}\Vert ^{2} \Vert d(t)\Vert ^{2} + \Vert y^{(i)}\Vert ^{2}, \end{aligned}$$

and for $\nu >0$ we have

$$\begin{aligned}&y^{(i)^{\top }}C_{i}B_{i}g(x,t)\\&\quad \le \Vert C_{i}B_{i}\Vert \Vert g(x,t)\Vert \Vert y^{(i)}\Vert \\&\quad \le \Vert C_{i}B_{i}\Vert \hat{g} \Vert x\Vert \Vert y^{(i)}\Vert \\&\quad \le \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2}\frac{1}{\nu ^{2}}\Vert x\Vert ^{2}+\nu ^{2}\Vert y^{(i)}\Vert ^{2} \\&\quad \le \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \frac{1}{\nu ^{2}}\Vert T_{i}^{-1}\Vert ^{2} \Big (\Vert y^{(i)}\Vert ^{2}+ \Vert \eta ^{(i)}\Vert ^{2}\Big )+ \nu ^{2}\Vert y^{(i)}\Vert ^{2}\\&\quad \le \Big ( \frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2} +\nu ^{2} \Big )\Vert y^{(i)}\Vert ^{2}\\&\qquad + \Big (\frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2} \Big ) \Vert \eta ^{(i)}\Vert ^{2}. \end{aligned}$$

Hence

$$\begin{aligned}&\quad \mathcal {L}V(y^{(i)},\eta ^{(i)},i)\\&\le \Big (H_{i}+\frac{2}{\alpha _{1}}H_{i}^{2}+ \frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2} +\nu ^{2}+1 \Big )\Vert y^{(i)}\Vert ^{2}\\ {}&\quad -\frac{1}{2}k(t)y^{(i)^{\top }}\Big [C_{i}B_{i}+(C_{i}B_{i})^{\top }\Big ]y^{(i)}\\ {}&\quad +\Big (\frac{\alpha _{1}}{2}+ \frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2}\Big )\Vert \eta ^{(i)}\Vert ^{2}\\ {}&\quad + \Vert C_{i}B_{i}\Vert ^{2} \Vert d(t)\Vert ^{2} + \frac{1}{2}\eta ^{(i)^{\top }}[A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\Theta _{3i}]\eta ^{(i)}. \end{aligned}$$

Now, in order to show that: $A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\Theta _{3i}<0$, $\forall i \in \Upsilon$, we consider two possible cases: $i \in \Upsilon _{\mathcal {K}}^{i}$ and $i \in \Upsilon _{\mathcal {UK}}^{i}$, respectively, that is, the diagonal element is known or unknown.

Case 1: $i \in \Upsilon _{\mathcal {K}}^{i}$. In this case, we have

$$\begin{aligned} \Theta _{3i}=\sum _{j=1}^{N}\pi _{ij}G_{ij}=&\sum _{j\in \Upsilon _{\mathcal {K}}^{i}}\pi _{ij}G_{ij}+\sum _{j\in \Upsilon _{\mathcal {UK}}^{i}}\hat{\pi }_{ij}G_{ij}\\ =&\sum _{j\in \Upsilon _{\mathcal {K}}^{i}}\pi _{ij}G_{ij}-\pi _{\mathcal {K}}^{i}\sum _{j\in \Upsilon _{\mathcal {UK}}^{i}}\dfrac{\hat{\pi }_{ij}}{-\pi _{\mathcal {K}}^{i}}G_{ij}. \end{aligned}$$

Since

$$\begin{aligned} 0\le \dfrac{\hat{\pi }_{ij}}{-\pi _{\mathcal {K}}^{i}}\le 1 , \sum _{j\in \Upsilon _{\mathcal {UK}}^{i}}\dfrac{\hat{\pi }_{ij}}{-\pi _{\mathcal {K}}^{i}}=1, \end{aligned}$$

it follows that

$$\begin{aligned}&\quad A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\Theta _{3i}\\&=\sum _{j\in \Upsilon _{\mathcal {UK}}^{i}}\dfrac{\hat{\pi }_{ij}}{-\pi _{\mathcal {K}}^{i}}\Big [A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\sum _{j\in \Upsilon _{\mathcal {K}}^{i} }\pi _{ij}G_{ij}-\pi _{\mathcal {K}}^{i}G_{ij}\Big ]. \end{aligned}$$

It is easily seen that $A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\Theta _{3i}<0$ is equivalent to

$$\begin{aligned} A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\sum _{j\in \Upsilon _{\mathcal {K}}^{i} }\pi _{ij}G_{ij}-\pi _{\mathcal {K}}^{i}G_{ij}<0, \quad \forall j \in \Upsilon _{\mathcal {UK}}^{i}. \end{aligned}$$

By the condition (13), it follows that $A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\Theta _{3i}<0$. This yields that

$$\begin{aligned} \frac{1}{2}\eta ^{(i)^{\top }}[A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\Theta _{3i}]\eta ^{(i)}\le -\alpha _{1}\Vert \eta ^{(i)}\Vert ^{2} \end{aligned}$$

where $\alpha _{1}\triangleq -\frac{1}{2}\max _{i\in \Upsilon }\Big \{\lambda _{max}(A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\Theta _{3i})\Big \}$. Hence, $\forall i \in \Upsilon _{\mathcal {K}}^{i}$:

$$\begin{aligned}&\quad \mathcal {L}V(y^{(i)},\eta ^{(i)},i)\\&\le \Big (H_{i}+\frac{2}{\alpha _{1}}H_{i}^{2}+ \frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2} +\nu ^{2}+1 \Big )\Vert y^{(i)}\Vert ^{2}\\ {}&\quad -\frac{1}{2}k(t)y^{(i)^{\top }}\Big [C_{i}B_{i}+(C_{i}B_{i})^{\top }\Big ]y^{(i)}\\ {}&\quad +\Big (\frac{\alpha _{1}}{2}-\alpha _{1}+ \frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2}\Big )\Vert \eta ^{(i)}\Vert ^{2}\\&\quad + \Vert C_{i}B_{i}\Vert ^{2} \Vert d(t)\Vert ^{2}\\&\le \Big (H_{i}+\frac{2}{\alpha _{1}}H_{i}^{2}+ \frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2} +\nu ^{2}+1 \Big )\Vert y^{(i)}\Vert ^{2}\\ {}&\quad -\frac{1}{2}k(t)y^{(i)^{\top }}\Big [C_{i}B_{i}+(C_{i}B_{i})^{\top }\Big ]y^{(i)}\\ {}&\quad +\Big (-\frac{\alpha _{1}}{2}+\frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2}\Big )\Vert \eta ^{(i)}\Vert ^{2}\\&\quad + \Vert C_{i}B_{i}\Vert ^{2} \Vert d(t)\Vert ^{2}. \end{aligned}$$

Case 2: $i \in \Upsilon _{\mathcal {UK}}^{i}$, that is, the diagonal element is unknown. In this case, we have

$$\begin{aligned} \Theta _{3i}\!=\!\sum _{j=1}^{N}\pi _{ij}G_{ij}\!=\!&\sum _{j\in \Upsilon _{\mathcal {K}}^{i}}\pi _{ij}G_{ij}\!+\!\hat{\pi }_{ii}P_{i}\!+\!\sum _{j\in \Upsilon _{\mathcal {UK}}^{i},j\ne i}\hat{\pi }_{ij}G_{ij}\\ =&\sum _{j\in \Upsilon _{\mathcal {K}}^{i}}\pi _{ij}G_{ij}+\hat{\pi }_{ii}P_{i}+(-\hat{\pi }_{ii}-\pi _{\mathcal {K}}^{i})\\&\quad \times \sum _{j\in \Upsilon _{\mathcal {UK}}^{i},j\ne i}\dfrac{\hat{\pi }_{ij}}{-\hat{\pi }_{ii}-\pi _{\mathcal {K}}^{i}}G_{ij}, \end{aligned}$$

and due to the fact that

$$\begin{aligned} 0\le \dfrac{\hat{\pi }_{ij}}{-\hat{\pi }_{ii}-\pi _{\mathcal {K}}^{i}}\le 1, \sum _{j\in \Upsilon _{\mathcal {UK}}^{i},j\ne i}\dfrac{\hat{\pi }_{ij}}{-\hat{\pi }_{ii}-\pi _{\mathcal {K}}^{i}}=1, \end{aligned}$$

we can write

$$\begin{aligned}&\quad A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\Theta _{3i}\\ {}&=\sum _{j\in \Upsilon _{\mathcal {UK}}^{i},j\ne i}\dfrac{\hat{\pi }_{ij}}{-\hat{\pi }_{ii}-\pi _{\mathcal {K}}^{i}}\Big [A_{4i}^{\top }P_{i}+P_{i}A_{4i}\\ {}&\quad \quad \quad \quad \quad +\sum _{j\in \Upsilon _{\mathcal {K}}^{i} }\pi _{ij}G_{ij}-\pi _{\mathcal {K}}^{i}G_{ij}+\hat{\pi }_{ii}P_{i}-\hat{\pi }_{ii}G_{ij}\Big ]. \end{aligned}$$

Thus, $A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\Theta _{3i}<0$ is equivalent to

$$\begin{aligned} A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\sum _{j\in \Upsilon _{\mathcal {K}}^{i} }\pi _{ij}G_{ij}-\pi _{\mathcal {K}}^{i}G_{ij}+\hat{\pi }_{ii}P_{i}-\hat{\pi }_{ii}G_{ij}<0\\ \forall j \in \Upsilon _{\mathcal {UK}}^{i}, j \ne i. \end{aligned}$$

(16)

By the similar arguments to Case 2 in the proof of Theorem 1 in [6] one obtains that (16) is equivalent to

$$\begin{aligned} A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\sum _{j\in \Upsilon _{\mathcal {K}}^{i} }\pi _{ij}G_{ij}-\pi _{\mathcal {K}}^{i}G_{ij}+\pi _{l}P_{i}-\pi _{l}G_{ij}<0, \\ \forall j \in \Upsilon _{\mathcal {UK}}^{i}. \end{aligned}$$

From (14), it may be concluded that $A_{4i}^{\top }P_{i}+P_{i}A_{4i}+\Theta _{3i}<0$. Thus, $\forall i \in \Upsilon _{\mathcal {UK}}^{i}$:

$$\begin{aligned}&\quad \mathcal {L}V(y^{(i)},\eta ^{(i)},i)\\ {}&\le \Big (H_{i}+\frac{2}{\alpha _{1}}H_{i}^{2}+ \frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2} +\nu ^{2}+1 \Big )\Vert y^{(i)}\Vert ^{2}\\ {}&\quad -\frac{1}{2}k(t)y^{(i)^{\top }}\Big [C_{i}B_{i}+(C_{i}B_{i})^{\top }\Big ]y^{(i)}\\ {}&\quad +\Big (-\frac{\alpha _{1}}{2}+\frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2}\Big )\Vert \eta ^{(i)}\Vert ^{2}\\ {}&\quad + \Vert C_{i}B_{i}\Vert ^{2} \Vert d(t)\Vert ^{2}. \end{aligned}$$

Consequently, by combining the results in case 1 and case 2, we get $\forall i \in \Upsilon$:

$$\begin{aligned}&\quad \mathcal {L}V(y^{(i)},\eta ^{(i)},i)\\ {}&\le \Big (H_{i}+\frac{2}{\alpha _{1}}H_{i}^{2}+ \frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2} +\nu ^{2}+1 \Big )\Vert y^{(i)}\Vert ^{2}\\ {}&\quad -\frac{1}{2}k(t)y^{(i)^{\top }}\Big [C_{i}B_{i}+(C_{i}B_{i})^{\top }\Big ]y^{(i)}\\ {}&\quad +\Big (-\frac{\alpha _{1}}{2}+\frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2}\Big )\Vert \eta ^{(i)}\Vert ^{2}\\ {}&\quad + \Vert C_{i}B_{i}\Vert ^{2} \Vert d(t)\Vert ^{2}. \end{aligned}$$

Denote $\alpha _{2}\triangleq \max _{i\in \Upsilon } \{\Vert C_{i}B_{i}\Vert ^{2}\}$ and $\alpha _{3}\triangleq \max _{i\in \Upsilon } \{\Vert C_{i}B_{i}\Vert ^{2}$$\Vert T_{i}^{-1}\Vert ^{2}\}$, then we have

$$\begin{aligned}&\quad \mathcal {L}V(y^{(i)},\eta ^{(i)},i)\\ {}&\le \Big (H_{i}+\frac{2}{\alpha _{1}}H_{i}^{2}+ \frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2} +\nu ^{2}+1 \Big )\Vert y^{(i)}\Vert ^{2}\\ {}&\quad -\frac{1}{2}k(t)y^{(i)^{\top }}\Big [C_{i}B_{i}+(C_{i}B_{i})^{\top }\Big ]y^{(i)}\\ {}&\quad +\Big (-\frac{\alpha _{1}}{2}+\dfrac{\alpha _{3}\hat{g}^{2}}{\nu ^{2}}\Big )\Vert \eta ^{(i)}\Vert ^{2}+ \alpha _{2} \Vert d(t)\Vert ^{2}, \end{aligned}$$

and since

$$\begin{aligned} C_{i}B_{i}+(C_{i}B_{i})^{\top }>0, \forall i\in \Upsilon , \end{aligned}$$

we get

$$\begin{aligned} -\frac{1}{2}y^{(i)^{\top }}(C_{i}B_{i}+(C_{i}B_{i})^{\top })y^{(i)}\le -\alpha _{4} \Vert y^{(i)}\Vert ^{2}, \end{aligned}$$

where $\alpha _{4}\triangleq \frac{1}{2}\min _{i\in \Upsilon }\lambda _{min}\big (C_{i}B_{i}+(C_{i}B_{i})^{\top }\big )$. Now, for $\nu$ sufficiently large so that

$$\begin{aligned} \bar{\alpha }\triangleq \frac{\alpha _{1}}{2}-\dfrac{\alpha _{3}\hat{g}^{2}}{\nu ^{2}}>0, \end{aligned}$$

and by choosing $k^{*}>0$ sufficiently large so that

$$\begin{aligned} k(t)\ge k^{*}\triangleq \frac{1}{\alpha _{4}}\max _{i\in \Upsilon }\Big (H_{i}+\frac{2}{\alpha _{1}}H_{i}^{2}+ \frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2} \\+\nu ^{2}+1 \Big )+\frac{\bar{\alpha }}{\alpha _{4}}, \quad \forall t\in [t^{*},t'). \end{aligned}$$

Then, $\forall t\in [t^{*},t')$ we have

$$\begin{aligned}&\quad \mathcal {L}V(y^{(i)},\eta ^{(i)},i)\\ \le&-(k(t)\alpha _{4}-H_{i}-\frac{2}{\alpha _{1}}H_{i}^{2} -\frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2} \\&\quad -\nu ^{2}-1 )\Vert y^{(i)}\Vert ^{2}-\bar{\alpha }\Vert \eta ^{(i)}\Vert ^{2} + \alpha _{2} \Vert d(t)\Vert ^{2}\\ \le&-\bar{\alpha }\Vert y^{(i)}\Vert ^{2}-\bar{\alpha }\Vert \eta ^{(i)}\Vert ^{2}+ \alpha _{2} \Vert d(t)\Vert ^{2}\\ \le&-\bar{\alpha }\Big (\Vert y^{(i)}\Vert ^{2}+\Vert \eta ^{(i)}\Vert ^{2}\Big )+ \alpha _{2} \Vert d(t)\Vert ^{2}. \end{aligned}$$

Moreover, we have

$$\begin{aligned}&\quad V(y^{(i)},\eta ^{(i)},i)\\&=\frac{1}{2}y^{(i)^{\top }}y^{(i)}+\frac{1}{2}\eta ^{(i)^{\top }}P_{i}\eta ^{(i)}\\&\le \frac{1}{2}\Big (\Vert y^{(i)}\Vert ^{2}+\Vert P_{i}\Vert \Vert \eta ^{(i)}\Vert ^{2}\Big )\\&\le \frac{1}{2} \max \{1,\Vert P_{i}\Vert \}\times \Big (\Vert y^{(i)}\Vert ^{2}+\Vert \eta ^{(i)}\Vert ^{2}\Big )\\&\le \frac{1}{2} \max _{i\in \Upsilon } \{1,\Vert P_{i}\Vert \}\times \Big (\Vert y^{(i)}\Vert ^{2}+\Vert \eta ^{(i)}\Vert ^{2}\Big ). \end{aligned}$$

Then

$$\begin{aligned}&\quad -\Big (\Vert y^{(i)}\Vert ^{2}+\Vert \eta ^{(i)}\Vert ^{2}\Big ) \\ {}&\le -\frac{2}{\max _{i\in \Upsilon } \{1,\Vert P_{i}\Vert \}} \times V(y^{(i)},\eta ^{(i)},i). \end{aligned}$$

Accordingly

$$\begin{aligned} \mathcal {L}V(y^{(i)},\eta ^{(i)},i)&\le -\bar{\alpha }\Big (\Vert y^{(i)}\Vert ^{2}+\Vert \eta ^{(i)}\Vert ^{2}\Big )+\alpha _{2} \Vert d(t)\Vert ^{2}\\&\le -\beta V(y^{(i)},\eta ^{(i)},i) + \alpha _{2} \Vert d(t)\Vert ^{2}, \end{aligned}$$

where $\beta \triangleq \frac{2\bar{\alpha }}{\max _{i\in \Upsilon } \{1,\Vert P_{i}\Vert \}}$.

Now, by Dynkin’s formula [26], we have $\forall t \in [t_{0}, t')$, $t_{0}\ge t^{*}$

$$\begin{aligned}&\quad E\Big \{V(y^{(r_{t})},\eta ^{(r_{t})},r_{t})\Big \}- E\Big \{V(y^{(r_{t_{0}})},\eta ^{(r_{t_{0}})},r_{t_{0}})\Big \}\\&=E\Big \{\int _{t_{0}}^{t}\mathcal {L}V(y^{(r_{s})},\eta ^{(r_{s})},r_{s})ds\Big \}\\ {}&\le -\beta \int _{t_{0}}^{t} E\Big \{V(y^{(r_{s})},\eta ^{(r_{s})},r_{s})\Big \}ds + \alpha _{2} \int _{t_{0}}^{t} \Vert d(s)\Vert ^{2}ds\\ {}&\le -\beta \int _{t_{0}}^{t} E\Big \{V(y^{(r_{s})},\eta ^{(r_{s})},r_{s})\Big \}ds + \hat{d}\alpha _{2}. \end{aligned}$$

Applying the Gronwall-Bellman lemma, we obtain

$$\begin{aligned}&\quad E\Big \{V(y^{(r_{t})},\eta ^{(r_{t})},r_{t})\Big \} \\ {}&\le \Big (\hat{d}\alpha _{2}+E\Big \{V(y^{(r_{t_{0}})},\eta ^{(r_{t_{0}})},r_{t_{0}})\Big \}\Big )e^{-\beta (t-t_{0})}, \\ {}&\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall t \in [t_{0}, t'), t_{0}\ge t^{*}, \end{aligned}$$

and since

$$\begin{aligned}&\quad E\Bigg \{\left\| \begin{pmatrix} {y}^{(r_{t})}\\ {\eta }^{(r_{t})} \end{pmatrix} \right\| ^{2}\Bigg \}\\&= E\Big \{\Vert y^{(r_{t})}\Vert ^{2}+\Vert \eta ^{(r_{t})}\Vert ^{2}\Big \} \le \frac{1}{\alpha _{5}}E\Big \{V(y^{(r_{t})},\eta ^{(r_{t})},r_{t})\Big \} \end{aligned}$$

with

$$\begin{aligned} \alpha _{5}\triangleq \frac{1}{2}\min _{i\in \Upsilon } \{1, \lambda _{min} (P_{i}) \} \end{aligned}$$

and

$$\begin{aligned}&\quad \hat{d}\alpha _{2}+ E\Big \{V(y^{(r_{t_{0}})},\eta ^{(r_{t_{0}})},r_{t_{0}})\Big \} \\ {}&\le \hat{d}\alpha _{2}+\alpha _{6} E\Big \{\Vert y^{(r_{t_{0}})}\Vert ^{2}+\Vert \eta ^{(r_{t_{0}})}\Vert ^{2}\Big \} \\ {}&\le \hat{d}\alpha _{2}+ \alpha _{6} E\Bigg \{\left\| \begin{pmatrix} y^{(r_{t_{0}})}\\ \eta ^{(r_{t_{0}})} \end{pmatrix}\right\| ^{2}\Bigg \} \end{aligned}$$

with

$$\begin{aligned} \alpha _{6} \triangleq max_{i \in \Upsilon }\{ 1, \lambda _{max}(P_{i}) \}, \end{aligned}$$

it may be concluded that

$$\begin{aligned}&\quad E\Bigg \{\left\| \begin{pmatrix} {y}^{(r_{t})}\\ {\eta }^{(r_{t})} \end{pmatrix} \right\| ^{2}\Bigg \}\\ {}&\le \Bigg [ \lambda _{1} E\Bigg \{\left\| \begin{pmatrix} {y}^{(r_{t_{0}})}\\ {\eta }^{(r_{t_{0}})} \end{pmatrix}\right\| ^{2}\Bigg \}+ \lambda _{2}\Bigg ] e^{-\beta (t-t_{0})}, \end{aligned}$$

for all $t\in [t_{0}, t'), t_{0}\ge 0$, where $\lambda _{1}=\frac{\alpha _{6}}{\alpha _{5}}>0$, $\lambda _{2}= \frac{\hat{d}\alpha _{2}}{\alpha _{5}}>0$ and $\beta >0.$ This completes the proof. $\square$

Now, consider any perturbed MJS in the class (10) and suppose that it is subject to the adaptive feedback controller (9). Then, the resulting nonlinear perturbed closed-loop MJS is given by:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t)= [A(r_{t})-k(t)B(r_{t})C(r_{t})]x(t)+B(r_{t})g(x(t),t)\\ \quad \quad \quad +B(r_{t})d(t), \; x_{0}\in \mathbb {R}^{n},\; r_{0}\in \Upsilon ,\\ \dot{k}(t)=E\big \{\Vert C(r_{t})x(t) \Vert ^{2}\big \}, \; k(0)\in \mathbb {R}. \\ \end{array}\right. } \end{aligned}$$

(17)

Since the right hand side of (17) is locally Lipschitz in $x(\cdot )$ and $k(\cdot )$ and measurable in t, it follows from the theory of stochastic differential equations (see [27]) that the initial value problem (17) has a solution $(x(\cdot ), k(\cdot )) :[0,\omega ) \longrightarrow \mathbb {R}^{n+1}$ on a maximal interval of existence $[0,\omega )$ for some $\omega \in (0,\infty ]$, and this solution is unique.

Theorem 1

Let $(x(\cdot ), k(\cdot )) :[0,\omega ) \longrightarrow \mathbb {R}^{n+1}$ be the maximal solution of the initial value problem (17). Then

• (i) $\omega =\infty$ almost surely.

• (ii) $\lim _{t\rightarrow \infty } k(t) \in \mathbb {R}$ exists.

• (iii) $\int _{0}^{\infty }E\big \{\Vert x(t) \Vert ^{2}\big \}dt<\infty$,  $\sup _{0\le t< \infty }E\big \{\Vert x(t) \Vert ^{2}\big \}< \infty$ and $\lim _{t\rightarrow \infty }E\big \{\Vert x(t) \Vert ^{2}\big \}=0$.

In other words, the controller (9) is a universal adaptive stabilizer for the class of multivariable perturbed MJSs (10).

Proof

By the transformations in Lemma 1, the closed-loop system (17) may be expressed in the form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{y}^{(r_{t})}(t)=\big [A_{1}(r_{t})-k(t)C(r_{t})B(r_{t})\big ] {y}^{(r_{t})}(t)\\ \quad \quad \quad \qquad +A_{2}(r_{t}){\eta }^{(r_{t})}(t))+C(r_{t})B(r_{t})g(x(t),t)\\ \quad \quad \quad \qquad +C(r_{t})B(r_{t})d(t),\\ \dot{\eta }^{(r_{t})}(t)=A_{3}(r_{t}){y}^{(r_{t})}(t)+A_{4}(r_{t}){\eta }^{(r_{t})}(t), \\ \dot{k}(t)=E\big \{\Vert y(t) \Vert ^{2}\big \}, \\ {y}^{(r_{0})}(0)\in \mathbb {R}^{m},\; {\eta }^{(r_{0})}(0)\in \mathbb {R}^{n-m}, \; k(0)\in \mathbb {R}. \end{array}\right. } \end{aligned}$$

(18)

Step 1: we show that $k(\cdot )$ is bounded on $[0, \omega )$, $\omega \le \infty$. i.e., $\sup _{0\le t< \omega }|k(t)|<\infty$.

By contradiction, we suppose that $k(\cdot )$ is unbounded on $[0,\omega )$. Since $\dot{k}(t)=E\big \{\Vert y(t) \Vert ^{2}\big \}\ge 0$, it follows that $k(\cdot )$ is a non-decreasing piecewise continuous function on $[0, \omega )$. In addition, since it is unbounded, this means that the assumptions on $k(\cdot )$ in Lemma 2 are met. Hence, we have

$$\begin{aligned} \quad E\big \{\Vert y(t) \Vert ^{2}\big \}\\\le E\Bigg \{\left\| \begin{pmatrix} {y}^{(r_{t})}\\ {\eta }^{(r_{t})} \end{pmatrix} \right\| ^{2}\Bigg \}\\\le \Bigg [ \lambda _{1} E\Bigg \{\left\| \begin{pmatrix} {y}^{(r_{0})}\\ {\eta }^{(r_{0})} \end{pmatrix} \right\| ^{2}\Bigg \}+ \lambda _{2}\Bigg ] e^{-\beta t},\quad \forall t \in [0,\omega ) \end{aligned}$$

(19)

for some $\lambda _{1}$, $\lambda _{2}$ and $\beta >0$. Furthermore, the adaptation law implies that

$$\begin{aligned} k(t) = \int _{0}^{t}E\big \{\Vert y(s) \Vert ^{2}\big \}ds+k(0), \quad t \in [0,\omega ). \end{aligned}$$

(20)

From the inequality (19), it is easily seen that (20) contradicts the assumption that $k(\cdot )$ is unbounded on $[0,\omega )$. Hence, $k(\cdot )$ is bounded on $[0,\omega )$.

Step 2: we show that the solution $(x(\cdot ), k(\cdot ))$ is global. i.e., $\omega =\infty$ almost surely.

By contradiction, assume that there exists some $\omega >0$ such that $\lim _{t\rightarrow \omega }\sup \Vert x(t) \Vert =\infty$. Since k(t) and d(t) are bounded, and g(x(t), t) is linearly bounded, we can easily show that the first equation in system (17) satisfies a linear growth condition, which implies (see [26]) that $\sup _{0\le t\le \omega }E\big \{\Vert x(t) \Vert ^{p}\big \} <\infty , \forall p>0$. Therefore, x(t) doesn’t have a finite escape time which contradicts $\lim _{t\rightarrow \omega }\sup \Vert x(t) \Vert =\infty$ and hence assertion (1) follows by the maximality of the solution on $[0,\omega )$.

Step 3: we show that $\lim _{t\rightarrow \infty } k(t)$ exists and is finite.

By putting $\omega =\infty$ in Step 1, it follows by the same arguments as in Step 1 that $\sup _{0\le t< \infty }|k(t)|<\infty$. Besides, due to the fact that k(t) is non-decreasing, we know that the limit $\lim _{t\rightarrow \infty } k(t)$ exists and is finite. This proves (1).

Step 4: we prove that $\lim _{t\rightarrow \infty }E\big \{\Vert \eta ^{(r_{t})}(t) \Vert ^{2}\big \}=0$.

Considering that system (17) (without the adaptation law) is strongly minimum phase (which yields that the homogeneous system $\dot{\eta }^{(r_{t})}(t)= A_{4}(r_{t}){\eta }^{(r_{t})}(t)$ is stochastically stable, see Remark 5), and the fact that from (1) and the adaptation law, we have $\int _{0}^{\infty }E\big \{\Vert y(t) \Vert ^{2}\big \}dt<\infty$, we can apply Theorem 3.27 in [4] to the second equation of system (18) to obtain: $\lim _{t\rightarrow \infty }E\big \{\Vert \eta ^{(r_{t})}(t) \Vert ^{2}\big \}=0$ and $\int _{0}^{\infty }E\big \{\Vert \eta ^{(r_{t})}(t) \Vert ^{2}\big \}dt<\infty$.

Step 5: we prove that $\lim _{t\rightarrow \infty }E\big \{\Vert x(t) \Vert ^{2}\big \}=0$.

We’ll start by demonstrating that $E\big \{\Vert x(t) \Vert ^{2}\big \}$ is bounded on $[0, \infty )$. In order to achieve this, let us consider system (18) without the adaptation law. The same set of Lyapunov functions candidates and the same techniques as in the proof of Lemma 2 may be used to get the following:

$$\begin{aligned}&\quad \mathcal {L}V(y^{(i)},\eta ^{(i)},i)\\&\le \Big (H_{i}+\frac{2}{\alpha _{1}}H_{i}^{2}+ \frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2} +\nu ^{2}+1 \Big )\Vert y^{(i)}\Vert ^{2}\\ {}&\quad -\frac{1}{2}k(t)y^{(i)^{\top }}\Big [C_{i}B_{i}+(C_{i}B_{i})^{\top }\Big ]y^{(i)}-\bar{\alpha }\Vert \eta ^{(i)}\Vert ^{2}\\ {}&\quad + \alpha _{2} \Vert d(t)\Vert ^{2}. \end{aligned}$$

Now, without loss of generality, assume that $k(0)>0$. Then, by the monotonicity of $k(\cdot )$ we have

$$\begin{aligned}&\quad \mathcal {L}V(y^{(i)},\eta ^{(i)},i)\\ {}&\le -(k(t)\alpha _{4}-H_{i}-\frac{2}{\alpha _{1}}H_{i}^{2}-\frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2}\\ {}&\quad -\nu ^{2}-1)\Vert y^{(i)}\Vert ^{2}-\bar{\alpha }\Vert \eta ^{(i)}\Vert ^{2} + \alpha _{2} \Vert d(t)\Vert ^{2}\\&\le -(k(t)\alpha _{4}-\alpha _{7})\Vert y^{(i)}\Vert ^{2}-\bar{\alpha }\Vert \eta ^{(i)}\Vert ^{2} + \alpha _{2} \Vert d(t)\Vert ^{2}, \end{aligned}$$

where $\alpha _{7}\triangleq \max _{i\in \Upsilon }\Big (H_{i}+\frac{2}{\alpha _{1}}H_{i}^{2}+ \frac{1}{\nu ^{2}} \Vert C_{i}B_{i}\Vert ^{2}\hat{g}^{2} \Vert T_{i}^{-1}\Vert ^{2} +\nu ^{2}+1\Big )$.

By using the Dynkin formula and the Fubini theorem, we get

$$\begin{aligned}&\quad E\Big \{V(y^{(r_{t})},\eta ^{(r_{t})},r_{t})\Big \}- E\Big \{V(y^{(r_{0})},\eta ^{(r_{0})},r_{0})\Big \}\\ {}&=E\Big \{\int _{0}^{t}\mathcal {L}V(y^{(r_{s})},\eta ^{(r_{s})},r_{s})ds\Big \}\\&\le E\Big \{\int _{0}^{t} \Big (-(k(s)\alpha _{4}-\alpha _{7})\Vert y^{(r_{s})}\Vert ^{2}-\bar{\alpha }\Vert \eta ^{(r_{s})}\Vert ^{2}\\ {}&\quad + \alpha _{2} \Vert d(s)\Vert ^{2}\Big )ds\Big \}\\&\le -\alpha _{4} E\Big \{\int _{0}^{t} k(s)\Vert y^{(r_{s})}\Vert ^{2}ds\Big \} + \alpha _{7} E\Big \{\int _{0}^{t}\Vert y^{(r_{s})}\Vert ^{2}ds\Big \} \\ {}&\quad -\bar{\alpha }E\Big \{\int _{0}^{t}\Vert \eta ^{(r_{s})}\Vert ^{2}ds\Big \}+\alpha _{2}\int _{0}^{t}\Vert d(s)\Vert ^{2}ds\\&\le -\alpha _{4} \int _{0}^{t}k(s) E\big \{\Vert y^{(r_{s})}\Vert ^{2}\big \}ds + \alpha _{7} \int _{0}^{t}E\big \{\Vert y^{(r_{s})}\Vert ^{2}\big \}ds \\ {}&\quad -\bar{\alpha }\int _{0}^{t}E\big \{\Vert \eta ^{(r_{s})}\Vert ^{2}\big \}ds+\alpha _{2}\int _{0}^{t}\Vert d(s)\Vert ^{2}ds. \end{aligned}$$

Due to the fact that $k(t)E\big \{\Vert y^{(r_{t})}(t)\Vert ^{2}\big \}=k(t)\dot{k}(t)= \frac{1}{2}\frac{d}{dt}\big (k^{2}(t)\big )$, we obtain the following

$$\begin{aligned}&\quad E\Big \{V(y^{(r_{t})},\eta ^{(r_{t})},r_{t})\Big \}-E\Big \{V(y^{(r_{0})},\eta ^{(r_{0})},r_{0})\Big \}\\ {}&\le -\frac{1}{2}\alpha _{4}\Big (k^{2}(t)-k^{2}(0)\Big )+ \alpha _{7} \int _{0}^{t}E\big \{\Vert y^{(r_{s})}\Vert ^{2}\big \}ds \\ {}&\quad -\bar{\alpha }\int _{0}^{t}E\big \{\Vert \eta ^{(r_{s})}\Vert ^{2}\big \}ds+\alpha _{2}\int _{0}^{t}\Vert d(s)\Vert ^{2}ds. \end{aligned}$$

Since we have

$$\begin{aligned} E\Bigg \{\left\| \begin{pmatrix} {y}^{(r_{t})}\\ {\eta }^{(r_{t})} \end{pmatrix}\right\| ^{2}\Bigg \}\le \frac{1}{\alpha _{5}}E\Big \{V(y^{(r_{t})},\eta ^{(r_{t})},r_{t})\Big \}, \end{aligned}$$

it follows that

$$\begin{aligned} 0 \le E\Bigg \{\left\| \begin{pmatrix} {y}^{(r_{t})}\\ {\eta }^{(r_{t})} \end{pmatrix} \right\| ^{2}\Bigg \}\le \frac{1}{\alpha _{5}}E\Big \{V(y^{(r_{0})},\eta ^{(r_{0})},r_{0})\Big \}\\ \quad -\frac{\alpha _{4}}{2\alpha _{5}}\Big (k^{2}(t)-k^{2}(0)\Big )+ \frac{\alpha _{7}}{\alpha _{5}} \int _{0}^{t}E\big \{\Vert y^{(r_{s})}\Vert ^{2}\big \}ds \\frac{\bar{\alpha }}{\alpha _{5}}\int _{0}^{t}E\big \{\Vert \eta ^{(r_{s})}\Vert ^{2}\big \}ds+\frac{\alpha _{2}}{\alpha _{5}}\int _{0}^{t}\Vert d(s)\Vert ^{2}ds. \end{aligned}$$

Now, letting t go to $\infty$ in the right hand side of the above inequality, we get

$$\begin{aligned} 0 \le E\Bigg \{\left\| \begin{pmatrix} {y}^{(r_{t})}\\ {\eta }^{(r_{t})} \end{pmatrix} \right\| ^{2}\Bigg \} \le \frac{1}{\alpha _{5}}E\Big \{V(y^{(r_{0})},\eta ^{(r_{0})},r_{0})\Big \}\\ -\frac{\alpha _{4}}{2\alpha _{5}}\Big (\lim _{t\rightarrow \infty }k^{2}(t)-k^{2}(0)\Big )+ \frac{\alpha _{7}}{\alpha _{5}} \int _{0}^{\infty }E\big \{\Vert y^{(r_{s})}\Vert ^{2}\big \}ds \\frac{\bar{\alpha }}{\alpha _{5}}\int _{0}^{\infty }E\big \{\Vert \eta ^{(r_{s})}\Vert ^{2}\big \}ds+\frac{\alpha _{2}}{\alpha _{5}}\int _{0}^{\infty }\Vert d(s)\Vert ^{2}ds < \infty . \end{aligned}$$

Therefore, $E\big \{\Vert x(t)\Vert ^{2}\big \}$ is bounded $\forall t \in [0,\infty )$.

Next, we will show that $E\big \{\Vert x(t)\Vert ^{2}\big \}$ is uniformly continuous on $[0,\infty )$. Let us consider system (17) without the adaptation law and let $V(x(t),r_{t})=\Vert x(t)\Vert ^{2}$. If $\mathcal {L}$ denotes the infinitesimal generator of the Markov process $(x(t),r_{t})$, then for any $0<s<t<\infty$, we have by the Dynkin formula:

$$\begin{aligned}&\quad E\Big \{V(x(t),r_{t})\Big \} - E\Big \{V(x(s),r_{s})\Big \}\\ {}&=E\Big \{\int _{s}^{t}\mathcal {L}V(x(\tau ),r_{\tau })d\tau \Big \}, \end{aligned}$$

The above equation implies that

$$\begin{aligned}&\quad E\big \{\Vert x(t)\Vert ^{2}\big \}-E\big \{\Vert x(s)\Vert ^{2}\big \}\\ {}&=E\Big \{\int _{s}^{t} 2x^{\top }(\tau ) \Big [\Big (A(r_{\tau })-k(\tau )B(r_{\tau })C(r_{\tau })\Big )x(\tau )\\ {}&\quad +B(r_{\tau })g(x(\tau ),\tau )+B(r_{\tau })d(\tau )\Big ]d\tau \Big \}. \end{aligned}$$

Using the Jensen inequality and the Fubini theorem, we obtain

$$\begin{aligned}&\quad \Big |E\big \{\Vert x(t)\Vert ^{2}\big \}-E\big \{\Vert x(s)\Vert ^{2}\big \}\Big |\\ {}&= \Big |E\Big \{\int _{s}^{t} 2x^{\top }(\tau ) \Big [\Big (A(r_{\tau })-k(\tau )B(r_{\tau })C(r_{\tau })\Big )x(\tau )\\ {}&\quad +B(r_{\tau })g(x(\tau ),\tau )+B(r_{\tau })d(\tau )\Big ]d\tau \Big \}\Big |\\&\le E\Big \{\int _{s}^{t} \Big |2x^{\top }(\tau ) \Big [\Big (A(r_{\tau })-k(\tau )B(r_{\tau })C(r_{\tau })\Big )x(\tau )\\ {}&\quad +B(r_{\tau })g(x(\tau ),\tau )+B(r_{\tau })d(\tau )\Big ]\Big |d\tau \Big \}\\&\le 2E\Big \{\int _{s}^{t} \Vert A(r_{\tau })-k(\tau )B(r_{\tau })C(r_{\tau })\Vert \times \Vert x(\tau )\Vert ^{2} d\tau \Big \}\\ {}&\quad +2E\Big \{\int _{s}^{t} \Vert B(r_{\tau })\Vert \hat{g} \times \Vert x(\tau )\Vert ^{2}d\tau \Big \}\\ {}&\quad +2E\Big \{\int _{s}^{t} \Vert B(r_{\tau })\Vert \times \Vert d(\tau )\Vert \times \Vert x(\tau )\Vert d\tau \Big \} \\&\le 2E\Big \{\int _{s}^{t} \Vert A(r_{\tau })\Vert \times \Vert x(\tau )\Vert ^{2} d\tau \Big \}+2\sup _{0\le \tau< \infty }|k(\tau )|\\ {}&\quad \times E\Big \{\int _{s}^{t}\Vert B(r_{\tau })C(r_{\tau })\Vert \times \Vert x(\tau )\Vert ^{2} d\tau \big \}\\ {}&\quad +2E\Big \{\int _{s}^{t} \Vert B(r_{\tau })\Vert \hat{g} \times \Vert x(\tau )\Vert ^{2}d\tau \Big \}\\ {}&\quad +2E\Big \{\int _{s}^{t} \Vert B(r_{\tau })\Vert \times \Vert d(\tau )\Vert \times \Vert x(\tau )\Vert d\tau \Big \} \\&\le \alpha _{8}E\Big \{\int _{s}^{t} \Vert x(\tau )\Vert ^{2} d\tau \Big \}+\alpha _{9}E\Big \{\int _{s}^{t} \Vert x(\tau )\Vert d\tau \Big \}\\&\le \alpha _{8}\int _{s}^{t} E\big \{\Vert x(\tau )\Vert ^{2}\big \} d\tau +\alpha _{9}\int _{s}^{t} E\big \{\Vert x(\tau )\Vert \big \} d\tau \\&\le \Big (\alpha _{8}\sup _{0\le \tau< \infty }E\big \{\Vert x(\tau ) \Vert ^{2}\big \}\\ {}&\quad +\alpha _{9}\sup _{0\le \tau < \infty }E\big \{\Vert x(\tau ) \Vert \big \}\Big )(t-s), \end{aligned}$$

where $\alpha _{8}$ and $\alpha _{9}$ are given by: $\alpha _{8}\triangleq 2\max _{i\in \Upsilon } \{\Vert A_{i} \Vert \}+2\sup _{0\le \tau < \infty }|k(\tau )|\times \max _{i\in \Upsilon } \{\Vert B_{i}C_{i} \Vert \}+ 2\hat{g}\max _{i\in \Upsilon } \{\Vert B_{i} \Vert \}$, and $\alpha _{9}\triangleq 2\sup _{0\le \tau < \infty }\Vert d(\tau )\Vert \times \max _{i\in \Upsilon } \{\Vert B_{i}\Vert \}$. Consequently, the above calculation shows that $E\big \{\Vert x(t)\Vert ^{2}\big \}$ is uniformly continuous on $[0,\infty )$. Now, since we have $\int _{0}^{\infty }E\big \{\Vert x(t) \Vert ^{2}\big \}dt<\infty$ and $E\big \{\Vert x(t) \Vert ^{2}\big \}$ is uniformly continuous on $[0,\infty )$, it yields by virtue of Barbalat’s lemma (see [28], Lemma A.6) that $\lim _{t\rightarrow \infty }E\big \{\Vert x(t) \Vert ^{2}\big \}=0$. This ends the proof of the theorem. $\square$

Remark 7

From the proof of Theorem 1, we can notice that the high gain property of the considered adaptive controller plays a key role in eliminating the effect of the considered uncertainties g(x(t), t). In addition, by the assumption that d(t) is bounded and square integrable, the desired control objectives were successfully achieved. It now remains to verify the effectiveness of the proposed techniques by a numerical example. This will be done in the next section.

Remark 8

It should be noted that unlike some other control methods, such as the sliding mode control ([9, 29]) which requires either knowledge or estimation of the unknown disturbances’ upper bounds, the proposed approach removes these requirements and reduces the control procedure.

5 Numerical example

In this section, we provide a practical example to show the effectiveness of the proposed methods. YALMIP and SeDuMi Matlab Toolboxes [30, 31] are used to solve LMI problems.

Example

Consider the following VTOL helicopter model with disturbances [13, 32]:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t)= A(r_{t})x(t)+B(r_{t})[u(t)+g(x(t),t)+d(t)],\\ y(t)= C(r_{t})x(t), \end{array}\right. } \end{aligned}$$

(21)

where $r_{t}$ indicates the airspeed and the state variables $x_{1}$, $x_{2}$, $x_{3}$ and $x_{4}$ are the horizontal velocity, the vertical velocity, the pitch rate and the pitch angle, respectively. The parameters $A({r_{t}})$ and $B({r_{t}})$ are given by:

$$\begin{aligned}A({r_{t}})=\begin{bmatrix} -0.0366&{}\quad 0.0271&{}\quad 0.0188&{}\quad -0.4555\\ 0.0482&{}\quad -1.01&{}\quad 0.0024&{}\quad -4.0208\\ 0.1002&{}\quad a_{32}(r_{t})&{}\quad -0.707&{}\quad a_{34}(r_{t})\\ 0&{}\quad 0&{}\quad 1&{}\quad 0 \end{bmatrix},\end{aligned}$$

$$\begin{aligned} B({r_{t}})=\begin{bmatrix} 0.4422&{}\quad 0.1761\\ b_{21}(r_{t})&{}\quad -7.5922\\ -5.5200&{}\quad 4.4900\\ 0 &{}\quad 0\end{bmatrix}.\end{aligned}$$

We also let:

$$\begin{aligned} C_{1}=\begin{bmatrix}2 &{}\quad 0 &{}\quad -1 &{}\quad 0\\ 1 &{}\quad -1 &{}\quad 0 &{}\quad 0\end{bmatrix}, \; C_{2}= \begin{bmatrix}0.5&{}\quad 0&{}\quad -0.5&{}\quad 0\\ 1&{}\quad -0.5&{}\quad 0&{}\quad 0\end{bmatrix}, \end{aligned}$$

$$\begin{aligned} C_{3}= \begin{bmatrix}-1&{}\quad 0&{} \quad -2&{}\quad -1\\ 0&{}\quad -2&{}\quad 0&{}\quad 1 \end{bmatrix}. \end{aligned}$$

The behavior of $r_{t}$ is modeled as a Markov chain with three states. The latter corresponds to three different airspeeds of 135 (nominal value), 60, and 170 knots. The values of parameters $a_{32}$, $a_{34}$, and $b_{21}$ are given as follows:

For airspeed 135 knots: $a_{32} =0.3681$, $a_{34}=1.4200$ and $b_{21}=3.5446$.

For airspeed 60 knots: $a_{32} =0.0664$, $a_{34}=0.1198$ and $b_{21}=0.9775$.

For airspeed 170 knots: $a_{32} =0.5047$, $a_{34}=2.5460$ and $b_{21}=5.1120$.

The nonlinear perturbation g(x, t) and the disturbance vector d(t) are assumed to be:

$$\begin{aligned} g(x,t)= \begin{bmatrix} 0.8\sin (20t)x_{2}(t) \\ 0.8\sin (20t)x_{4}(t) \end{bmatrix}, \end{aligned}$$

$$\begin{aligned} d(t)= \begin{bmatrix} \dfrac{t}{\big (1+t^{2}\big )} \\ 0.9\exp (-0.3t)\sin (0.6t) \end{bmatrix}. \end{aligned}$$

It can be easily verified that g(x, t) is linearly bounded and d(t) is bounded and square integrable.

We choose a TR matrix with a lower bound $\pi _{l}=-6$ for $\hat{\pi }_{11}$ and $\hat{\pi }_{22}$:

$$\begin{aligned}\Pi =\begin{bmatrix} \hat{\pi }_{11}&{} 3.8&{} \hat{\pi }_{13}\\ 3.8 &{}\hat{\pi }_{22} &{}\hat{\pi }_{23}\\ \hat{\pi }_{31} &{}\hat{\pi }_{32} &{}-2 \end{bmatrix}. \end{aligned}$$

Since we have

it follows that the system has strict relative degree one set. Hence, by Lemma 1, the following nonsingular matrices can be used:

to transform system (21) into the form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{y}^{(i)}(t)=A_{1i}{y}^{(i)}(t)+A_{2i}{\eta }^{(i)}(t)\\ \quad \quad \quad \quad +C_{i}B_{i}[u(t)+g(x(t),t)+d(t)], \\ \dot{\eta }^{(i)}(t)=A_{3i}{y}^{(i)}(t)+A_{4i}{\eta }^{(i)}(t), \end{array}\right. } \end{aligned}$$

(22)

where for mode 1 we have:

$$\begin{aligned} A_{11}= \begin{bmatrix} -0.6365 &{}\quad 0.3942\\ 0.0899 &{}\quad -0.9582 \end{bmatrix}, \; A_{21}= \begin{bmatrix} 1.0019 &{}\quad -2.3310\\ 0.9851 &{} \quad 3.5653 \end{bmatrix}, \end{aligned}$$

$$\begin{aligned} A_{31}= \begin{bmatrix} 0.0457 &{}\quad 0.0094\\ -0.7843 &{}\quad 0.1602 \end{bmatrix}, \; A_{41}= \begin{bmatrix} -0.1589 &{} \quad -0.4897\\ 2.0000 &{}\quad 0 \end{bmatrix}. \end{aligned}$$

For mode 2;

$$\begin{aligned} A_{12}= \begin{bmatrix} -0.6874 &{}\quad 0.0714\\ 0.1183 &{}\quad -0.9356 \end{bmatrix}, \; A_{22}= \begin{bmatrix} 0.2552 &{} -0.2877\\ 1.0211 &{} 1.5549 \end{bmatrix}, \end{aligned}$$

$$\begin{aligned} A_{32}= \begin{bmatrix} 0.0563 &{}\quad 0.0575\\ -1.8497 &{}\quad 0.1259 \end{bmatrix}, \; A_{42}= \begin{bmatrix} -0.1306 &{}\quad -0.6081\\ 1.0000 &{}\quad 0 \end{bmatrix}. \end{aligned}$$

And for mode 3;

$$\begin{aligned} A_{13}= \begin{bmatrix} -0.2433 &{}\quad 0.4865\\ -0.5727 &{}\quad -1.0622 \end{bmatrix}, \; A_{23}= \begin{bmatrix} -9.9819 &{}\quad 0.7228\\ 18.2960 &{}\quad 1.1880 \end{bmatrix}, \end{aligned}$$

$$\begin{aligned} A_{33}= \begin{bmatrix} -0.2816 &{}\quad -0.0220\\ 0.2487 &{}\quad 0.0149 \end{bmatrix}, \; A_{43}= \begin{bmatrix} 0.0000 &{}\quad 0.5000\\ 0.5779 &{}\quad -0.4481 \end{bmatrix}. \end{aligned}$$

By solving the LMI conditions in Definition 4, one can obtain the following feasible solutions for $P_{1}, P_{2}$ and $P_{3}$:

$$\begin{aligned} P_{1}= \begin{bmatrix} 830.3651 &{}\quad 52.3610\\ 52.3610 &{}\quad 303.6662 \end{bmatrix}, \; P_{2}= \begin{bmatrix} 769.7611 &{} \quad 9.2626\\ 9.2626 &{}\quad 308.1242 \end{bmatrix}, \end{aligned}$$

$$\begin{aligned} P_{3}= \begin{bmatrix} 1.9005 &{}\quad 1.1083\\ 1.1083 &{}\quad 1.0012 \end{bmatrix} \times 10^{3}. \end{aligned}$$

This means that the system (21) is strongly minimum phase. Also, it has positive definite high frequency gain matrices:

$$\begin{aligned}\lambda \big (C_{1}B_{1}+(C_{1}B_{1})^{\top }\big )=\lbrace {6.8052, 21.5402}\rbrace , \end{aligned}$$

$$\begin{aligned} \lambda \big (C_{2}B_{2}+(C_{2}B_{2})^{\top }\big )=\lbrace {4.5372, 9.3694}\rbrace , \end{aligned}$$

$$\begin{aligned} \lambda \big (C_{3}B_{3}+(C_{3}B_{3})^{\top }\big )=\lbrace {5.8667, 45.6977}\rbrace . \end{aligned}$$

where $\lambda (A)$ denotes the spectrum of the matrix A. Consequently, this perturbed system satisfies the three structural assumptions and hence it belongs to the class (10).

Now, by using the adaptive controller (9), we obtain the following simulation results: Fig. 1 shows the random jumping modes and Fig. 2 describes the trajectory of x(t) of the closed-loop system with the initial condition $x_{0}=\begin{bmatrix} 0.5&1.4&-1.8&2.1\end{bmatrix}^{\top }$. The trajectories of the adaptation gain k(t) with initial condition $k(0)=-1$ and the control input u(t) are illustrated, respectively, in Figs. 3 and 4. From Figs. 2 and 3, it is observed that a sufficiently large gain is found, which makes the trajectories of the closed loop system converge asymptotically to zero. Also, the bounded controller gain $k(\cdot )$ asymptotically converges to a value smaller than 2.5. Thus, the desired closed-loop objectives are achieved in the presence of the nonlinear perturbation g(x, t) and the external disturbance d(t). This confirms the results of Theorem 1.

Fig. 1

Markov switching signal ($r_{t}$)

Fig. 2

State responses of the closed-loop system

Fig. 3

Gain evolution for $u(t)=-k(t)y(t)$, $\dot{k}(t)=E\{\Vert y(t) \Vert ^{2}\}$

Fig. 4

Trajectories of the control input u(t)

6 Conclusion and future work

This paper has investigated the universal adaptive stabilization problem for a class of MJSs with nonlinear perturbations and external disturbances. The adaptive controller is designed such that the effect of the perturbations can be eliminated and the control objectives are guaranteed. Finally, a VTOL helicopter example has been presented which shows the effectiveness of the given methods. Future research will concentrate on the universal adaptive stabilization for MJSs with a strict relative degree two set and the case where the high frequency gain matrices are of unknown signs.