Generalized flip and strong resonances bifurcations of a predator–prey model

Abstract

In this paper, bifurcation analysis of a predator–prey discrete model equipped with Allee effect has been carried out both analytically and numerically. Stability circumstances of three fixed points of this model is represented briefly. In this study is shown that this model undergoes codimension one (codim-1) bifurcations such as the transcritical, fold, flip and Neimark–Sacker. Besides, codimension two (codim-2) bifurcations including the generalized flip, resonances 1:2, 1:3, 1:4 have been achieved. The non-degeneracy is one of the conditions to check for bifurcation analysis. Therefore the computing the critical normal form coefficients to verify the non-degeneracy of the listed bifurcations are needed. Using the critical normal form coefficients method to examine the bifurcation analysis makes it to avoid calculating the central manifold and converting the linear part of the map into Jordan form. This is one of the most effective methods in the bifurcation analysis that has not received much attention so far. So in this article our attention are turned to this method. For each bifurcation, normal form coefficients along with its scenario are investigated thoroughly. The bifurcation curves of fixed points under variation of one and two parameters and all codim-1,2 bifurcations curves are computed by using numerical methods in the numerical software matcontm. In the following, our represented analysis is proved by numerical simulation and displays more complex behaviours of model.

1 Introduction

The interaction between different species causes rivalry, understanding or consuming the other kinds (prey–predator). One of the most significant interplay between them, is the prey–predator relation which is a significant subject in ecology. Prey–predator models in both discrete and continuous time scales have been widely studied. Some studies about discrete-time models indicate that whenever populations include non-overlapping generations or the population density is low, these kinds of models described by difference equations, surpass continuous-time ones. Besides, dynamical phenomenon created in discrete-time models, is far richer than the dynamics of continuous-time models. See [3, 17, 26, 28, 29, 33].

The history of discrete prey–predator models dates back to at least [14] which is Lotka–Volterra classical model and has been investigated by many authors. As an example, for a genetic reproduction, a biological model is offered in [15] and is therefore proved that for specific values, there are constant curves on which quasi-periodic behaviors of model are seen. Some discrete ecosystem models have been studied in [16]. Also, bifurcation analysis of some of discrete prey–predator models is provided in [1, 2, 4, 18,19,20,21,22,23,24,25].

The Allee effect is the reduction of biological population growth rate of species with the density of smaller than a critical value. The Allee effect on a population, is an inevitable factor in the environment; specially with a low amount of population. This criterion was first introduced by Allee in 1931. Biological facts for deploying Allee effect requires the following assumptions [7]:

• No reproduction takes place without partners. From mathematical point of view, that is to say the Allee function is zero if the density is not high.

• The Allee effect reduces by increasing population density. Mathematically, it means that derivative of the Allee function calculated in population density values, are always positive.

• The Allee effect fades in high density which means Allee function come close to 1 when the population is large.

Many authors have studied stability analysis of prey–predator systems with and without Allee effect. See [8,9,10,11,12,13, 27, 30,31,32, 34] and existing resources as an example. In this paper, the following discrete prey–predator model equipped with Allee effect on prey kind is investigated. Neimark–Sacker codim-1 bifurcation of this model is studied in [5]. In this work, the all codim-1 and codim-2 bifurcations along with the normal form coefficients calculation and scenario for each bifurcation will be studied.

$$\begin{aligned} \left\{ \begin{array}{ll} x_{n+1}=rx_{n}(1-x_{n})-a x_{n}y_{n}\left( \frac{x_{n}}{m+x_{n}}\right) ,\\ y_{n+1}=bx_{n}y_{n}-dy_{n}. \end{array}\right. \end{aligned}$$

(1)

Here $x_{n}$ indicate the number of prey, $y_{n}$ is the number of predator, r is growth rate of prey, b display predation rates, d is per capita mortality rate of predators and m is Allee constant on the prey population.

This paper is organized as follows: In Sect. 2, stability of the fixed points of the model will be introduced. In Sect. 3, codim-1 bifurcations of the model such as transcritical, fold, flip and Neimark–Sacker, as well as the direction of the bifurcations will be given. In the following, in Sect. 4 the analysis of codim-2 bifurcations such as generalized flip, resonance 1:2, resonance 1:3 and resonance 1:4 along with the calculation of normal form coefficients of them will be represented. These coefficients are powerful tools to characterize the scenarios of bifurcations. The bifurcation curves and phase portraits diagrams of the system under variation of one or two parameters will be done numerically in Sect. 5. The conclusion will be represented in Sect. 6.

2 Existence and local stability of fixed points

The fixed points of (1) are the solutions $(x^{*},y^{ *})$ of the following equations

$$\begin{aligned} x^{*}&=rx^{*}(1-x^{*})-a x^{*}y^{*}\left( \frac{x^{*}}{m+x^{*}}\right) ,\\ y^{*}&=bx^{*}y^{*}-dy^{*}. \end{aligned}$$

The origin $E_{0}=(0,0)$ is always a fixed point of (1). Two further fixed points of the system are given by $E_{1}=(\frac{r-1}{r},0)$ which is biologically feasible for $r\ge 1$ and

$$\begin{aligned} E_{2}=\left( \frac{d+1}{b}, \frac{(bm+d+1)(rb-rd-r-b)}{ba(d+1)}\right) , \end{aligned}$$

which is biologically possible if $r>1$ and $b>\frac{r(d+1)}{r-1}$.

2.1 Stability of $E_{0}, E_{1}$ and $E_{2}$

The stability of the fixed points are given in [5], therefore we recall the following Proposition from [5].

Proposition 1

[5]

• 1. $E_{0}$ is locally asymptotically stable if $0<r<1$ and $0<d<1$.

• 2. $E_{0}$ is a non-hyperbolic if $r=1$ or $d=1$.

• 3. $E_{1}$ is locally asymptotically stable if $\max \{1,\frac{b}{b-d+1}\}<r<\min \{3,\frac{b}{b-d-1}\}$.

• 4. $E_{1}$ is a non-hyperbolic if $r=3$ or $d=\frac{b}{b-d\pm 1}$.

• 5. $E_{2}$ is a sink if $\frac{b}{b-d-1}<r<\min \lbrace r_{1}, r_{2}\rbrace$.

• 6. $E_{2}$ is a non-hyperbolic if $r=r_{2}$ and $\frac{4b+4bd+mb^{2}}{mb^{2}+(d+1)^{2}}<r<\frac{4b+4bd+5mb^{2}}{mb^{2}+(d+1)^{2}}$. where

  $$\begin{aligned} r_{1}{=}\frac{b(d{-}1)(mb{+}d{-}1){-}4b(mb{+}1)}{{-}d^{3}{-}d^{2}(5{-}b{+}bm){+}d(2b{-}7{+}b^{2}m{-}2bm){-}3{+}b{-}bm(b{+}1)}, \end{aligned}$$

  (2)

  and

  $$\begin{aligned} r_{2}{=}\frac{b(d{+}1)^{2}{+}mdb^{2}}{{-}d^{3}{-}d^{2}(4{-}b{+}bm){+}db(bm{+}2{-}2m){-}5d{+}b{-}2{-}bm}. \end{aligned}$$

  (3)

3 Bifurcation analysis

Let us consider model (1) as follows:

$$\begin{aligned} \begin{pmatrix} x\\ y \end{pmatrix}\mapsto N(x,y,\mu )=\begin{pmatrix} rx(1-x)-a xy\left( \frac{x}{m+x}\right) \\ bxy-dy. \end{pmatrix}, \end{aligned}$$

where $\mu =(r,a,m,b,d)$. The Jacobian matrix of model (1) is given by:

$$\begin{aligned} A(x,y,\mu )=\left( \begin{array}{cc} -2rx+r-\frac{2axy}{m+x}+\frac{ax^{2}y}{(m+x)^{2}} &{} \frac{-ax^{2}}{m+x}\\ by&{} bx-d \end{array} \right) , \end{aligned}$$

and the second, third, fourth and fifth multi-linear form of (1) are as follows:

$$\begin{aligned}&B(X,Y)=\begin{pmatrix} B_1(X,Y)\\ B_2(X,Y) \end{pmatrix}, \\&C(X,Y,Z)=\begin{pmatrix} C_1(X,Y,Z)\\ 0 \end{pmatrix},\\&D(X,Y,Z,U)=\begin{pmatrix} D_1(X,Y,Z,U)\\ 0 \end{pmatrix}, \\&E(X,Y,Z,U,W)=\begin{pmatrix} E_1(X,Y,Z,U,W)\\ 0 \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&B_{1}(X,Y)\\&\quad =\frac{-2(am^{2}y+m^{3}r+3m^{2}rx+3mrx^{2}+rx^{3})x_{1}y_{1}}{(m+x)^{3}}\\&\qquad -\frac{ax(2m+x)(x_{1}y_{2}+x_{2}y_{1})}{(m+x)^{2}},\\&B_{2}(X,Y) =b(x_{1}y_{2}+x_{2}y_{1}),\\&C_{1}(X,Y,Z) {=}\frac{6aym^{2}x_{1}y_{1}z_{1}}{(m{+}x)^{4}}\\&\quad -\frac{2am^{2}(x_{1}y_{1}z_{2}+x_{1}y_{2}z_{1}+x_{2}y_{1}z_{1})}{(m+x)^{3}},\\&D_{1}(X,Y,Z,U) =\frac{-24aym^{2}x_{1}y_{1}z_{1}u_{1}}{(m+x)^{5}}\\&\qquad {+}\frac{6am^{2}(x_{1}y_{1}z_{2}u_{1}+x_{1}y_{2}z_{1}u_{1} +x_{2}y_{1}z_{1}u_{1}+x_{1}y_{1}z_{1}u_{2}}{(m+x)^{4}},\\&E_{1}(X,Y,Z,U,W) =\frac{120aym^{2}x_{1}y_{1}z_{1}u_{1}w_{1}}{(m+x)^{6}}\\&\qquad {-}\frac{24am^{2}(x_{1}y_{1}z_{2}u_{1}w_{1}{+}x_{1}y_{2}z_{1}u_{1}w_{1} {+}x_{2}y_{1}z_{1}u_{1}w_{1}{+}x_{1}yz_{1}u_{1}w_{2}{+}x_{1}y_{1}z_{1}u_{2}w_{1})}{(m{+}x)^{5}},\\ \end{aligned} \end{aligned}$$

and

$$\begin{aligned} X&=(x_1,y_1)^T,\quad Y=(y_1,y_2)^T, \quad Z=(z_1,z_2)^T,\\ U&=(u_1,u_2)^T, \quad W=(w_1,w_2)^T. \end{aligned}$$

3.1 Codim 1 bifurcations

In this section consider a,  b, d and m as fixed and r is free parameter.

3.1.1 Transcritical bifurcation

Proposition 2

The fixed point $E_{0}$ is asymptotically stable for $0<r<1$ and $0<d<1$. It loses stability via branching for $r=1$ if $0<d<1$. i.e., at the point

$$\begin{aligned} t_{tsc}:~ (x,y,r)=(0,0,1), \end{aligned}$$

there is a transcritical bifurcation provided $d\ne 1$.

Proof

The multiplier of the fixed point (x, y) of (1) is $+1$ if

$$\begin{aligned} \left\{ \begin{array}{ll} N(x,y,\mu )=(x,y)^T,\\ \det (A(x,y,\mu )-I_2)=0, \end{array} \right. \end{aligned}$$

where $I_2=\left( {\begin{matrix} 1&{}0\\ 0&{}1 \end{matrix}}\right)$. It is clear that this system has only one solution $t_{tsc}$. The Jacobian matrix at the $t_{tsc}$ has two multipliers $\lambda _1= 1,\quad \lambda _2=-d$. The restriction of the map (1) to one dimensional centre manifold

$$\begin{aligned}&M(v)=qv+m_2v^2+{\mathcal {O}}(v^3),\\&M: {\mathbb {R}}\rightarrow {\mathbb {R}}^2, \quad m_2=(m_{21},m_{22})^T, \end{aligned}$$

which at the critical value has the form:

$$\begin{aligned} v \mapsto v+a_{fold}v^2+{\mathcal {O}}\left( v^3\right) , \end{aligned}$$

where

$$\begin{aligned} Aq=q,\quad A^Tp=p,\quad \left\langle p,q \right\rangle =1. \end{aligned}$$

Invariance property of the center manifold conclude that

$$\begin{aligned} \begin{pmatrix} 0&{}0\\ 0&{}-d-1 \end{pmatrix} \begin{pmatrix} m_{21}\\ m_{22} \end{pmatrix} =2a_{fold}q+\begin{pmatrix} 2\\ 0 \end{pmatrix}. \end{aligned}$$

Therefore we have

$$\begin{aligned} a_{fold}=-1. \end{aligned}$$

Note that the critical eigenvectors A and $A^T$ are $q=p=(1,0)^T$. Given that $E_0$ is always the fixed point and it will not be destroyed and $a_{fold}\ne 0$, It is concluded that the fixed point $E_0$ undergoes a transcritical bifurcation. $\square$

3.1.2 Period doubling bifurcation

Proposition 3

• (i) The fixed point $E_{1}$ is asymptotically stable for $\frac{b}{b-d+1}<r<\frac{b}{b-d-1}$. It loses stability via a supercritical flip for for $r=3$. i.e., there is a non-degenerate filp bifurcation of fixed point $E_1$ at $r=3$.

• (ii) There is a non-degenerate flip bifurcation of fixed point $E_1$ at $r=\frac{b}{b-d+1}$.

• (iii) There is a non-degenerate flip bifurcation of fixed point $E_2$ at $r={\frac{ \left( b \left( d-5 \right) m+ \left( d+1 \right) \left( d-3 \right) \right) b}{b \left( bd-{d}^{2}-b-2\,d-1 \right) m+ \left( d+ 1 \right) ^{2} \left( b-d-3 \right) }}$.

Proof

(i) It’s clear that at the point $(x,y,r)=(\frac{r-1}{r},0,3)$, the map (4) has a fixed point with multiplier 1, or on the other hand this point convinces the following equations

$$\begin{aligned} \left\{ \begin{array}{ll} N(x,y,\mu )-(x,y)^T=0,\\ \det (A(x,y,\mu )+I_2)=0. \end{array} \right. \end{aligned}$$

The restriction of the map (1) to one dimensional centre manifold

$$\begin{aligned}&M(v)=qv+m_2v^2+m_3v^3+{\mathcal {O}}(v^4),\\&M: {\mathbb {R}}\rightarrow {\mathbb {R}}^2, m_i=(m_{i1},m_{i2})^T,~i=2,3, \end{aligned}$$

which at $r=3$ becomes

$$\begin{aligned} w\mapsto -w+b_{PD}w^3+{\mathcal {O}}{(w^4)}, \end{aligned}$$

(4)

where

$$\begin{aligned} Aq=-q,\quad A^Tp=-p,\quad \left\langle p,q \right\rangle =1. \end{aligned}$$

As regard the fact that the center manifold is invariant the following linear equations are achieved

$$\begin{aligned} \left\{ \begin{array}{ll} \begin{pmatrix} -2&{} -4/3\,{\frac{a}{3\,m+2}}\\ 0&{}2/3\,b-d-1 \end{pmatrix} \begin{pmatrix} m_{21}\\ m_{22} \end{pmatrix} =\begin{pmatrix} 6\\ 0 \end{pmatrix},\\ \begin{pmatrix} -2&{}-4/3\,{\frac{a}{3\,m+2}}\\ 0&{}2/3\,b-d-1 \end{pmatrix} \begin{pmatrix} m_{31}\\ m_{32} \end{pmatrix} =6b_{PD}+\begin{pmatrix} 54\\ 0 \end{pmatrix}. \end{array} \right. \end{aligned}$$

(5)

By solving (5) we have

$$\begin{aligned} b_{PD}=9. \end{aligned}$$

Note that in his case we have used

$$\begin{aligned} q=\begin{pmatrix} 1\\ 0\end{pmatrix},\quad p=\begin{pmatrix} 1\\ {\frac{4a}{ \left( 3\,m+2 \right) \left( 2\,b-3\,d+3 \right) }} \end{pmatrix}. \end{aligned}$$

Given that $b_{PD}>0$, the flip bifurcation is super-critical and the double period cycle is stable.

(ii) Similar to (i) the critical normal form coefficient of the flip bifurcation is obtained as follows:

$$\begin{aligned} b_{PD}{=}{\frac{{-}6 \left( b{-}d{+}1 \right) ^{2} \left( d{-}1 \right) ^{2}{a}^{2} \left( b \left( bd-2\,{d}^{2}{+}3\,b-d+3 \right) m+ \left( d-1 \right) \left( bd-2\,{d}^{2}+b+2\,d \right) \right) }{ \left( bm+d-1 \right) ^{3} \left( 2\,b-3\,d+3 \right) ^{2}}}, \end{aligned}$$

by using

$$\begin{aligned} q=\begin{pmatrix} {\frac{ \left( b-d+1 \right) a \left( d-1 \right) ^{2}}{ \left( 2\,b- 3\,d+3 \right) b \left( mb+d-1 \right) }}\\ 1 \end{pmatrix}, \quad p=\begin{pmatrix} 0\\ 1 \end{pmatrix}. \end{aligned}$$

The flip bifurcation is non-degenerate provided $b_{PD}\ne 0$. If $b_{PD}$ is positive, the bifurcation is super-critical and the double period cycle is stable. For $b_{PD}$ negative, it is sub-critical and unstable.

(iii) Similar to (i) the critical normal form coefficient of the flip bifurcation is obtained as follows:

$$\begin{aligned} b_{PD}&=\frac{D_{1}}{D_{2}}, \end{aligned}$$

$$\begin{aligned} D_{1}&=6\, ( {b}^{2}dm-b{d}^{2}m-{b}^{2}m+b{d}^{2}-2\,bdm-{d}^{3}\\&\quad +\,2\,bd- bm-5\,{d}^{2}+b-7\,d-3 ) ^{2}{a}^{2} \\&\qquad ( b-2\,{d}^{6}-6\,{d}^{5}+4\,{d}^{4}+28\,{d}^{3}-2\,b{d}^{3}\\&\quad -\,5\,{b}^{3}{m}^{2}-5\,{b}^{2}{m}^{2}+b{d}^{5}+b{d}^{4}-2\,b{d}^{2}+4\,{b}^{2}m\\&\quad -\,11\,bm+bd-3\,b{d}^{4}m- 4\,b{d}^{5}m+32\,b{d}^{3}m\\&\quad +\,3\,{b}^{2}{d}^{3}{m}^{2}+7\,{b}^{3}d{m}^{2} +7\,{b}^{2}{d}^{2}{m}^{2}+4\,bdm\\&\quad +\,2\,{b}^{2}dm+46\,b{d}^{2}m-2\,{b}^{2} {m}^{2}{d}^{4}-3\,{b}^{2}d{m}^{2}\\&\quad -\,2\,{b}^{2}{d}^{3}m-6\,{b}^{2}{d}^{2} m+2\,{b}^{2}m{d}^{4}+{b}^{3}{m}^{2}{d}^{3}\\&\quad -\,3\,{b}^{3}{d}^{2}{m}^{2}+30 \,{d}^{2}+10\,d ),\\ D_{2}&= (4\,{b}^{2}dm-10\,bdm-5\,b{d}^{2}m-5\,bm+4\,b{d}^{2}\\&\quad +\,8\,bd+4\,b -23\,d-19\,{d}^{2}-5\,{d}^{3}-9 ) ( 2\,{b}^{2}m\\&\quad -\,3\,bdm-3\, bm+2\,b+2\,bd-3\,{d}^{2}-6\,d-3 ) ^{2}\\&\qquad ( bm+d+1 ) ^{3}. \end{aligned}$$

where we have used

$$\begin{aligned} q&= \left( \begin{array}{c} {\frac{ \left( {b}^{2}dm-b{d}^{2}m-{b}^{2}m +b{d}^{2}-2\,bdm-{d}^{3}+2\,bd-bm-5\,{d}^{2}+b-7\,d-3 \right) a \left( d+1 \right) }{ \left( 2\,{b}^{2}m-3\,bdm+2\,bd-3\,bm-3\,{d}^{2 }+2\,b-6\,d-3 \right) b \left( bm+d+1 \right) }}\\ 1 \end{array} \right) ,\\ p&= \left( \begin{array}{c} 2\,{\frac{ \left( 2\,{b}^{2}m-3\,bdm-3\,bm+ 2\,b+2\,bd-3\,{d}^{2}-6\,d-3 \right) b \left( bm+d+1 \right) }{ \left( 4\,{b}^{2}dm-10\,bdm-5\,b{d}^{2}m-5\,bm+4\,b{d}^{2}+8\,bd+4\,b -23\,d-19\,{d}^{2}-5\,{d}^{3}-9 \right) \left( d+1 \right) a}}\\ {\frac{ \left( d+1 \right) \left( 2\,{b}^{2}m-3 \,bdm-3\,bm+2\,b+2\,bd-3\,{d}^{2}-6\,d-3 \right) }{4\,{b}^{2}dm-10\,bd m-5\,b{d}^{2}m-5\,bm+4\,b{d}^{2}+8\,bd+4\,b-23\,d-19\,{d}^{2}-5\,{d}^{ 3}-9}}\end{array} \right) . \end{aligned}$$

The flip bifurcation is non-degenerate provided $b_{PD}\ne 0$. If $b_{PD}$ is positive, the bifurcation is super-critical and the double period cycle is stable. For $b_{PD}$ negative, it is sub-critical and unstable. $\square$

3.1.3 Neimark–Sacker bifurcation

Proposition 4

On the curve

$$\begin{aligned} t_{NS}:~(x,y,r), \end{aligned}$$

where

$$\begin{aligned} x&=\frac{d+1}{d},\quad y=\frac{br-dr-b-r}{a}\left( \frac{m}{d+1}+\frac{1}{b}\right) ,\\ r&={\frac{ \left( bdm+ \left( d+1 \right) ^{2} \right) b}{b \left( bd-{d }^{2}-2\,d-1 \right) m+ \left( d+1 \right) ^{2} \left( b-d-2 \right) } }, \end{aligned}$$

there is a non-degenerate Neimark–Sacker bifurcation.

Proof

The map (1) has a fixed point with a pair complex multiplier on the unit circle if

$$\begin{aligned} \left\{ \begin{array}{ll} N(x,y,\mu )=(x,y)^T,\\ \det (A(x,y,\mu ))=1. \end{array} \right. \end{aligned}$$

The exact solution to this system is as follows:

$$\begin{aligned} x&=\frac{d+1}{d},\quad y=\frac{br-dr-b-r}{a}\left( \frac{m}{d+1}+\frac{1}{b}\right) ,\\ r&={\frac{ \left( bdm+ \left( d+1 \right) ^{2} \right) b}{b \left( bd-{d }^{2}-2\,d-1 \right) m+ \left( d+1 \right) ^{2} \left( b-d-2 \right) } }, \end{aligned}$$

which implies the expansion for $t_{NS}$. To avoid the complexity of computation, in the following of the proof consider

$$\begin{aligned} a=3.5,\quad b=4.5,\quad , d=0.25,\quad m=0.23. \end{aligned}$$

In this case the fixed point $E_2$ has a simple multiplier

$$\begin{aligned} \lambda _{1,2}=e^{\pm i\theta _0}=0.417151311100000\pm .0908837050267683~i, \end{aligned}$$

this applies to non-resonances conditions. We consider

$$\begin{aligned} M(v,{\bar{v}})=\sum _{1\le k+l}\frac{1}{(k+l)!}m_{kl}(\beta )v^k{\bar{v}}^l, \quad v\in {\mathbb {C}}, \quad m_{kl}\in {\mathbb {C}}, \end{aligned}$$

is the center manifold at the parameter r. The restriction of the map (1) to two dimensional center manifold which at the critical value r has the form

$$\begin{aligned} v\mapsto e ^{i\theta _0}v+dv|v|^2+{\mathcal {O}}(v^4),\quad v\in {\mathbb {C}}, \end{aligned}$$

where d is a complex number. We have used the invariance property of the center manifold and have achieved

$$\begin{aligned} d=0.624653931607585644- 2.61138442528188186\,i \end{aligned}$$

therefore the first Lyapunov coefficient of the Neimark–Sacker bifurcation is obtain as follows:

$$\begin{aligned} c_{NS}=\mathfrak {R}\left( {e^{-i\theta _0}d}\right) =- 2.11274771163427921. \end{aligned}$$

Given that $c_{NS}<0$, the Neimark–Sacker bifurcation is super-critical and the closed invariant curve is stable. Note that

$$\begin{aligned} q&=\begin{pmatrix} - 0.238552358874129233+ 0.371975139178461423 \,i\\ 0.897065921718550596 \end{pmatrix},\\ p&=\begin{pmatrix} 0.0+ 1.34417585255314909\,i \\ 0.557372638652811059+ 0.357450118887474078\,i \end{pmatrix}, \end{aligned}$$

have been used, where

$$\begin{aligned} Aq=e^{i\theta _0}q,\quad A^Tp=e^{-i\theta _0}p,\quad \left\langle p,q\right\rangle =1. \end{aligned}$$

$\square$

4 Codim 2 bifurcations

In this section consider a,  b,  and d as fixed and r,  m are free parameters.

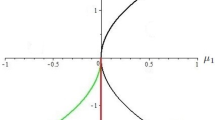
4.1 Generalized flip bifurcation

Proposition 5

There is a non-degenerate generalized flip bifurcation of the fixed point $E_2$ at $r=\frac{b}{b-d+1}$ and $m=-{\frac{ \left( d-1 \right) \left( d+1 \right) b-2\,d \left( d-1 \right) ^{2}}{b \left( \left( d+3 \right) b- \left( 2\,d+3 \right) \left( d-1 \right) \right) }}$.

Proof

If

$$\begin{aligned} r&=\frac{b}{b-d+1},\\ m&=-\frac{ \left( d-1 \right) \left( d+1 \right) b-2\,d \left( d-1 \right) ^{2}}{b \left( \left( d+3 \right) b- \left( 2\,d+3 \right) \left( d-1 \right) \right) }, \end{aligned}$$

the fixed point $E_1$ has a simple critical multiplier $\lambda _{1}=-1,$ and no other multiplier is not on the unit circle provided $\frac{b-2\,d+2}{b-d+1}\ne \pm 1$ and $b_{PD}=0$. The restriction of the map (1) to one dimensional centre manifold

$$\begin{aligned}&M(v)=qv+m_2v^2+m_3v^3+{\mathcal {O}}(v^4),\\&M: {\mathbb {R}}\rightarrow {\mathbb {R}}^2, m_i=(m_{i1},m_{i2})^T,~i=2,3, \end{aligned}$$

which at the critical value r and m has the form

$$\begin{aligned} v\mapsto -v+c_{GPD} v^5+{\mathcal {O}}(v^6), \end{aligned}$$

where

$$\begin{aligned} Aq=-q,\quad A^Tp=-p,\quad \left\langle p,q\right\rangle =1. \end{aligned}$$

The invariance property of the center manifold results in

$$\begin{aligned} c_{GPD}=\frac{c(a,b,d)}{\left( -3d+2b+3\right) ^9}, \end{aligned}$$

in which

$$\begin{aligned} c(a,b,d)&= ( b-d+1 ) ^{4}{a}^{4} ( bd-2\,{d}^{2}+3\,b-d+3) ^{4} \\&\quad ({b}^{2}+3\,{b}^{2}d+{b}^{2}{d}^{3}+3\,{b}^{2}{d}^ {2}+7\,b{d}^{2}\\&\quad -\,4\,b{d}^{4}+b-5\,{d}^{3}b+bd+7\,{d}^{2}-d\\&\quad -\,3\,{d}^{4}-7 \,{d}^{3}+4\,{d}^{5} ). \end{aligned}$$

The critical eigenvectors A and $A^T$ used here are as follows:

$$\begin{aligned} q&= \begin{pmatrix} {\frac{ \left( bd-2\,{d}^{2}+3\,b-d+3 \right) \left( d-1 \right) a \left( b-d+1 \right) }{b \left( -3\,d+2 \,b+3 \right) ^{2}}}\\ 1 \end{pmatrix},\quad p=\begin{pmatrix} 0\\ 1\end{pmatrix}. \end{aligned}$$

$\square$

4.2 Strong resonances bifurcations

Proposition 6

If

$$\begin{aligned} r&={\frac{b \left( d+5 \right) }{bd-{d}^{2}+b-2\,d-1}}, \\ m&=-{\frac{ \left( d+1 \right) \left( 4\,bd-5\,{d}^{2}+4\,b-14\,d-9 \right) }{b \left( 4\,bd-5\,{d}^{2}-10\,d-5 \right) }}, \end{aligned}$$

there is a non-degenerate 1 : 2 resonance bifurcation of the fixed point $E_2$.

Proof

The map (1) has a fixed point with two multipliers $-1$ if

$$\begin{aligned} \left\{ \begin{array}{ll} N(x,y,\mu )-(x,y)^T=(0,0)^T\\ \det (A(x,y,\mu ))-1=0,\\ \text{ trace }(A(x,y,\mu ))+2=0. \end{array} \right. \end{aligned}$$

The exact solution to this is as follows:

$$\begin{aligned} x&=\frac{d+1}{d}, \\ y&=\frac{br-dr-b-r}{a}\left( \frac{m}{d+1}+\frac{1}{b}\right) ,\\ r&={\frac{b \left( d+5 \right) }{bd-{d}^{2}+b-2\,d-1}}, \\ m&=-{\frac{ \left( d+1 \right) \left( 4\,bd-5\,{d}^{2}+4\,b-14\,d-9 \right) }{b \left( 4\,bd-5\,{d}^{2}-10\,d-5 \right) }}. \end{aligned}$$

The restriction of the map (1) to two dimensional centre manifold

$$\begin{aligned} M(v_1,v_2)=v_1q_0+v_2q_1+\sum _{2\le j+k \le 3} \frac{1}{j1k!}m_{jk}v_1^jv_2^k, \end{aligned}$$

where

$$\begin{aligned}&Aq_0=-q_0, \quad Aq_1=-q_1+q_0\\&A^Tp_0=-p_0, \quad A^Tp_1=-p_1+p_0,\\&\left\langle p_0,q_1\right\rangle =\left\langle p_1,q_0\right\rangle =1,\quad \left\langle p_0,q_0\right\rangle =\left\langle p_1,q_1\right\rangle =0, \end{aligned}$$

which at the critical value r and m has the form

$$\begin{aligned} \begin{pmatrix} v_1\\ v_2 \end{pmatrix} \mapsto \begin{pmatrix} -v_1+v_2\\ -v_2+C_{R2}v_1^3+D_{R2}v_1^2v_2 \end{pmatrix},\quad v=(v_1,v_2)\in {\mathbb {R}}^2. \end{aligned}$$

Due to the invarianr property of the center manifold we deduce that

$$\begin{aligned} C_{R2}=\frac{C_1(a,b,d)}{256(b-d-1)^4}, \quad D_{R2}=\frac{D_1(a,b,d)}{512(b-d-1)^6}, \end{aligned}$$

where

$$\begin{aligned} C_1(a,b,d)&= ( 112\,{b}^{3}{d}^{3}-428\,{b}^{2}{d}^{4}+548\,b\,{d}^{5}-235\,{ d}^{6}\\&\quad -\,32\,{b}^{3}{d}^{2}-736\,{b}^{2}{d}^{3}+2068\,b\,{d}^{4}\\&\quad -\,1380\,{d}^{5}-80\,{b}^{3}d+200\,{b}^{2}{d}^{2}+2232\,b\,{d}^{3}\\&\quad -\,3095\,{d}^{4} +480\,{b}^{2}d+152\,b\,{d}^{2}\\&\quad -\,3280\,{d}^{3}+100\,{b}^{2}-860\,b\,d- 1545\,{d}^{2}-\,300\,b\\&\quad -140\,d+75 ) ( 4\,b\,d-5\,{d}^{2} -\,10\,d-5 ) {a}^{2},\\ D_1(a,b,d)&= ( 3136\,{b}^{6}{d}^{4}-22048\,{b}^{5}{d}^{5}+64820\,{b}^{4}{d}^{ 6}\\&\quad -\,102048\,{b}^{3}{d}^{7}+90781\,{b}^{2}{d}^{8}-43290\,b\,{d}^{9}\\&\quad +\,8650\,{d}^{10}+1664\,{b}^{6}{d}^{3}-47232\,{b}^{5}{d}^{4}\\&\quad +\,245080\,{b}^{4}{ d}^{5}-556432\,{b}^{3}{d}^{6}+650350\,{b}^{2}{d}^{7}\\&\quad -\,386230\,b\,{d}^{8 }+92850\,{d}^{9}+832\,{b}^{6}{d}^{2}\\&\quad -\,27456\,{b}^{5}{d}^{3}+319948\,{b} ^{4}{d}^{4}-1176120\,{b}^{3}{d}^{5}\\&\quad +\,1929182\,{b}^{2}{d}^{6}-1489520\,b \,{d}^{7}+444200\,{d}^{8}\\&\quad -\,11008\,{b}^{5}{d}^{2}+183024\,{b}^{4}{d}^{3}\\&\quad -\,1217704\,{b}^{3}{d}^{4}+3055718\,{b}^{2}{d}^{5}-3246480\,b\,{d}^{6}\\&\quad +\, 1249000\,{d}^{7}-2080\,{b}^{5}d\\&\quad +\,60652\,{b}^{4}{d}^{2}-648016\,{b}^{3}{ d}^{3}+2762392\,{b}^{2}{d}^{4}\\&\quad -\,4373300\,b\,{d}^{5}+2288300\,{d}^{6}\\&\quad +\,14520\,{b}^{4}d-181728\,{b}^{3}{d}^{2}+1397514\,{b}^{2}{d}^{3}\\&\quad -\,3720940 \,b\,{d}^{4}+2856700\,{d}^{5}\\&\quad +\,1300\,{b}^{4}-33880\,{b}^{3}d+353122\,{b }^{2}{d}^{2}\\&\quad -\,1939680\,b\,{d}^{3}+2462600\,{d}^{4}\\&\quad -\,4200\,{b}^{3}+33570 \,{b}^{2}d-553120\,b\,{d}^{2}\\&\quad +\,1448200\,{d}^{3}+1675\,{b}^{2}-56930\,b \,d\\&\quad +\,556250\,{d}^{2}+4050\,b+126050\,d+12800 ) {a}^{2}. \end{aligned}$$

The critical generalised eigenvectors A and $A^T$ have been used are as follows:

$$\begin{aligned} q_0&=\begin{pmatrix} {\frac{ \left( d+1 \right) a\, \left( 4\,b\,d-5\,{d}^{2}-10\,d-5 \right) }{8b\, \left( b-d-1 \right) }} \\ 1 \end{pmatrix},\\ q_1&=\begin{pmatrix} -{\frac{a\, \left( 4\,b\,{d}^{2}-5\,{ d}^{3}+4\,b\,d-15\,{d}^{2}-15\,d-5 \right) }{16b\, \left( b-d-1 \right) }}\\ 0 \end{pmatrix},\\ p_0&=\begin{pmatrix} -{\frac{16b\, \left( b-d-1 \right) }{a\, \left( 4\,b\,{d}^{2}-5\,{d}^{3}+4\,b\,d-15\,{d}^{2}-15\,d-5 \right) } }\\ 2 \end{pmatrix},\\ p_1&=\begin{pmatrix} 0\\ 1 \end{pmatrix}. \end{aligned}$$

The non-degeneracy conditions of this bifurcation are $C_{1R2}=4C_{R2}\ne 0$ and $D_{1R2}=-2D_{R2}-6C_{R2}\ne 0$. The sign of $C_{1R2}$ specifies the type of the critical point. The bifurcation scenario is indicated by the coefficient $D_{R2}$. $\square$

Proposition 7

If

$$\begin{aligned} r&={\frac{b \left( d+2 \right) }{bd-{d}^{2}+b-2\,d-1}}, \\ m&=-{\frac{ \left( d+1 \right) \left( bd-2\,{d}^{2}+b-5\,d-3 \right) }{ b \left( bd-2\,{d}^{2}-4\,d-2 \right) }}, \end{aligned}$$

there is a non-degenerate 1 : 3 resonance bifurcation of the fixed point $E_2$.

Proof

The map (1) has a fixed point with a pair complex multiplier $e^{\pm i \frac{2\pi }{3}}$ if

$$\begin{aligned} \left\{ \begin{array}{ll} N(x,y,\mu )-(x,y)^T=(0,0)^T\\ \det (A(x,y,\mu ))-1=0,\\ \text{ trace }(A(x,y,\mu ))-1=0. \end{array} \right. \end{aligned}$$

The exact solution to this is as follows:

$$\begin{aligned} x&=\frac{d+1}{d}, \\ y&=\frac{br-dr-b-r}{a}\left( \frac{m}{d+1}+\frac{1}{b}\right) ,\\ r&={\frac{b \left( d+2 \right) }{bd-{d}^{2}+b-2\,d-1}}, \\ m&=-{\frac{ \left( d+1 \right) \left( bd-2\,{d}^{2}+b-5\,d-3 \right) }{ b \left( bd-2\,{d}^{2}-4\,d-2 \right) }}. \end{aligned}$$

The restriction of the map (1) to two dimensional centre manifold

$$\begin{aligned} M(v,{\bar{v}})=vq+{\bar{v}}{\bar{q}}+\sum _{2\le j+k } \frac{1}{j1k!}m_{jk}v^j{\bar{v}}^k, \end{aligned}$$

where

$$\begin{aligned} Aq=e^{\frac{2\pi }{3}i}q,\quad A^Tp=e^{\frac{-2\pi }{3}i}p,\quad \left\langle p,q\right\rangle =1, \end{aligned}$$

which at the critical value r and m has the form

$$\begin{aligned} v\mapsto e ^{\frac{2\pi }{3}i}v+B_{1}{\bar{v}}^2+C_{1}v|v|^2+{\mathcal {O}}(v^{4}),\quad v\in {\mathbb {C}}, \end{aligned}$$

Using the invariance property of the center manifold we have

$$\begin{aligned} B_{1}&={\frac{ ( 2-3/2\,b{d}^{2}+1/2\,{b}^{2}d+5\,{d}^{2}-2\,bd+11/2\,d +3/2\,{d}^{3} ) ( bd-2\,{d}^{2}-4\,d-2 ) a}{ ( b-d-1 ) ^{3}}}\\&\quad +\,i ( 2/3\,{b}^{2}\sqrt{3}+1/2\,\sqrt{3}{b}^{2}d+2\,\sqrt{3}-2\, b\sqrt{3}+13/3\,{d}^{2}\sqrt{3}-3/2\,b{d}^{2}\sqrt{3}\\&\quad +\,{\frac{31}{6 }}\,d\sqrt{3}+7/6\,{d}^{3}\sqrt{3}-11/3\,bd\sqrt{3} ) ( bd-2\,{d}^{2}-4\,d-2 ) a ( b-d-1 ) ^{-3}, \end{aligned}$$

and

$$\begin{aligned} C_{1}=\frac{C_{11}+iC_{12}}{24\,b \left( b-d-1 \right) ^{7}}, \end{aligned}$$

where

$$\begin{aligned} C_{11}&=- ( -168\,a-894\,b+180\,ab+2004\,{b}^{2}\\&\quad -\,15604\,b{d}^{2}+11700\,{ b}^{2}d+35630\,{b}^{2}{d}^{3}\\&\quad -\,19337\,{b}^{3}{d}^{2}-21230\,b{d}^{4}- 13048\,a{d}^{5}\\&\quad -\,5048\,a{d}^{2}-1384\,ad-14504\,a{d}^{4}-10696\,a{d}^{3 }\\&\quad -\,100\,a{b}^{2}-2968\,{d}^{7}a-656\,{d}^{8}a-64\,{d}^{9}a\\&\quad +\,28\,{b}^{3}a -4\,{b}^{4}a-5717\,bd-1784\,{b}^{3}+868\,{b}^{4}\\&\quad +\,28122\,{b}^{2}{d}^{2} -23555\,b{d}^{3}+5656\,ab{d}^{2}\\&\quad -\,836\,a{b}^{2}d-5426\,a{b}^{2}{d}^{3}+ 797\,a{b}^{3}{d}^{2}+14300\,ab{d}^{4}\\&\quad +\,1550\,abd-2905\,a{b}^{2}{d}^{2}+11498\,ab{d}^{3}\\&\quad +\,240\,a{b}^{3}d-5888\,a{b}^{2}{d}^{4}+1334\,a{b}^{3}{d }^{3}+11170\,ab{d}^{5}\\&\quad -\,1267\,{b}^{2}{d}^{6}a-3718\,{b}^{2}{d}^{5}a-115\,{b}^{4}{d}^{2}a\\&\quad -\,110\,{b}^{4}{d}^{4}a+8\,{b}^{5}{d}^{3}a+542\,{b}^{3} {d}^{5}a-166\,{b}^{4}{d}^{3}a\\&\quad +\,1193\,{b}^{3}{d}^{4}a-27\,{b}^{4}{d}^{5} a+3\,{b}^{5}{d}^{4}a+98\,{b}^{3}{d}^{6}a\\&\quad -\,180\,{b}^{2}{d}^{7}a-36\,{b}^ {4}ad+7\,{b}^{5}a{d}^{2}+1446\,b{d}^{7}a\\&\quad +\,5360\,b{d}^{6}a+168\,b{d}^{8} a+2\,{b}^{5}ad-218\,{b}^{5}\\&\quad +\,24\,{b}^{6}+3768\,{b}^{4}d-7784\,a{d}^{6}+ 25098\,{b}^{2}{d}^{4}\\&\quad -\,19522\,{b}^{3}{d}^{3}-11419\,b{d}^{5}+9318\,{d}^ {5}{b}^{2}-3392\,{d}^{6}b\\&\quad +\,4558\,{b}^{4}{d}^{3}-9643\,{b}^{3}{d}^{4}- 903\,{b}^{5}{d}^{2}\\&\quad +\,6277\,{b}^{4}{d}^{2}-705\,{b}^{5}d-429\,b{d}^{7}- 1864\,{d}^{5}{b}^{3}\\&\quad +\,1424\,{d}^{6}{b}^{2}-375\,{b}^{5}{d}^{3}+1199\,{b }^{4}{d}^{4}+45\,{b}^{6}{d}^{2}\\&\quad +\,44\,{b}^{6}d-9378\,{b}^{3}d) ( bd-2\,{d}^{2}-4\,d-2) ^{2}{a}^{2}, \end{aligned}$$

$$\begin{aligned} C_{12}&=\sqrt{3} ( -248\,a+98\,b+404\,ab-160\,{b}^{2}+2164\,b{d}^{2}\\&\quad -\, 1278\,{b}^{2}d-5898\,{b}^{2}{d}^{3}+2497\,{b}^{3}{d}^{2}\\&\quad +\,3650\,b{d}^{4 }-18928\,a{d}^{5}-7400\,a{d}^{2}-2036\,ad\\&\quad -\,21112\,a{d}^{4}-15624\,a{d}^ {3}-324\,a{b}^{2}\\&\quad -\,4280\,{d}^{7}a-944\,{d}^{8}a-92\,{d}^{9}a+124\,{b}^{ 3}a-20\,{b}^{4}a\\&\quad +\,707\,bd+132\,{b}^{4}-3870\,{b}^{2}{d}^{2}\\&\quad +\,3645\,b{d}^ {3}+10930\,ab{d}^{2}-2340\,a{b}^{2}d\\&\quad -\,12088\,a{b}^{2}{d}^{3}+2369\,a{b} ^{3}{d}^{2}+25130\,ab{d}^{4}\\&\quad +\,3198\,abd-7177\,a{b}^{2}{d}^{2}+21086\,ab {d}^{3}\\&\quad +\,856\,a{b}^{3}d-12056\,a{b}^{2}{d}^{4}+3404\,a{b}^{3}{d}^{3}\\&\quad +\,18954\,ab{d}^{5}-2299\,{b}^{2}{d}^{6}a-7114\,{b}^{2}{d}^{5}a\\&\quad -\,387\,{b}^ {4}{d}^{2}a-258\,{b}^{4}{d}^{4}a+22\,{b}^{5}{d}^{3}a\\&\quad +\,1112\,{b}^{3}{d}^{5}a-456\,{b}^{4}{d}^{3}a+2691\,{b}^{3}{d}^{4}a\\&\quad -\,57\,{b}^{4}{d}^{5}a+7 \,{b}^{5}{d}^{4}a+188\,{b}^{3}{d}^{6}a-314\,{b}^{2}{d}^{7}a\\&\quad -\,152\,{b}^{4}ad+25\,{b}^{5}a{d}^{2}+2330\,b{d}^{7}a+8838\,b{d}^{6}a\\&\quad +\,266\,b{d}^{8} a+10\,{b}^{5}ad-82\,{b}^{5}+12\,{b}^{6}\\&\quad +\,4\,{b}^{4}d-11256\,a{d}^{6}-4854\,{b}^{2}{d}^{4}+3534\,{b}^{3}{d}^{3}\\&\quad +\,2173\,b{d}^{5}-2064\,{d}^{5} {b}^{2}+712\,{d}^{6}b\\&\quad -\,1002\,{b}^{4}{d}^{3}+2195\,{b}^{3}{d}^{4}+159\,{b}^{5}{d}^{2}-781\,{b}^{4}{d}^{2}\\&\quad -\,57\,{b}^{5}d+99\,b{d}^{7}+504\,{d}^{5}{b}^{3}-356\,{d}^{6}{b}^{2}\\&\quad +\,121\,{b}^{5}{d}^{3}-351\,{b}^{4}{d}^{4}- 17\,{b}^{6}{d}^{2}+2\,{b}^{6}d\\&\quad +\,654\,{b}^{3}d )( bd-2\,{d}^{2}-4\,d-2) ^{2}{a}^{2}. \end{aligned}$$

The critical eigenvectors A and $A^T$ used here are as follows:

$$\begin{aligned} q&=\left( \begin{array}{c} {\frac{ \left( d+1 \right) a \left( bd-2\,{ d}^{2}-4\,d-2 \right) }{ \left( b-d-1 \right) b \left( 1/2+i/2\sqrt{3 } \right) }}\\ 1\end{array} \right) ,\\ p&= \left( \begin{array}{c} -4\,{\frac{ \left( b-d-1 \right) b}{ \left( i\sqrt{3}-3 \right) \left( d+1 \right) a \left( bd-2\,{d}^{2 }-4\,d-2 \right) \left( i\sqrt{3}-1 \right) }}\\ - 2\, \left( i\sqrt{3}-3 \right) ^{-1}\end{array} \right) . \end{aligned}$$

If $B_1\ne 0$, the stability of the bifurcating invariant closed curve is determined by

$$\begin{aligned} \mathfrak {R}\left( 3\left( 3e^{\frac{4\pi }{3}i}C_{1}-|B_{1}|^2 \right) \right) . \end{aligned}$$

$\square$

Proposition 8

If

$$\begin{aligned} r&={\frac{b \left( d+3 \right) }{bd-{d}^{2}+b-2\,d-1}}, \\ m&=-{\frac{ \left( d+1 \right) \left( 2\,bd-3\,{d}^{2}+2\,b-8\,d-5 \right) }{b \left( 2\,bd-3\,{d}^{2}-6\,d-3 \right) }}, \end{aligned}$$

there is a non-degenerate 1 : 4 resonance bifurcation of the fixed point $E_2$.

Proof

The map (1) has a fixed point with a pair complex multiplier ${\pm i}$ if

$$\begin{aligned} \left\{ \begin{array}{ll} N(x,y,\mu )-(x,y)^T=(0,0)^T\\ \det (A(x,y,\mu ))-1=0,\\ \text{ trace }(A(x,y,\mu ))=0. \end{array} \right. \end{aligned}$$

The exact solution to this is as follows:

$$\begin{aligned} x&=\frac{d+1}{d}, \\ y&=\frac{br-dr-b-r}{a}\left( \frac{m}{d+1}+\frac{1}{b}\right) ,\\ r&={\frac{b \left( d+3 \right) }{bd-{d}^{2}+b-2\,d-1}}, \\ m&=-{\frac{ \left( d+1 \right) \left( 2\,bd-3\,{d}^{2}+2\,b-8\,d-5 \right) }{b \left( 2\,bd-3\,{d}^{2}-6\,d-3 \right) }}, \end{aligned}$$

The restriction of the map (1) to two dimensional centre manifold

$$\begin{aligned} M(v,{\bar{v}})=vq+{\bar{v}}{\bar{q}}+\sum _{2\le j+k } \frac{1}{j1k!}m_{jk}v^j{\bar{v}}^k, \end{aligned}$$

where

$$\begin{aligned} Aq=iq,\quad A^Tp=-ip,\quad \left\langle p,q\right\rangle =1, \end{aligned}$$

which at the critical value r and m has the form

$$\begin{aligned} v\mapsto i~v+C_{1}v ^2{\bar{v}}+D_{1}{\bar{v}}^3+{\mathcal {O}}(v^5),\quad v\in {\mathbb {C}}. \end{aligned}$$

Using the invariance property of the center manifold we have

$$\begin{aligned} C_{1}&=\frac{C_{11}+iC_{12}}{32\, \left( b-d-1 \right) ^{6}},\\ D_{1}&=\frac{D_{11}+iD_{12}}{32\, \left( b-d-1 \right) ^{6}}, \end{aligned}$$

in which

$$\begin{aligned} C_{11}&=-( 255-303\,b+171\,{b}^{2}-3164\,b{d}^{2}\\&\quad +\,819\,{b}^{2}d+2776\,{d }^{2}-1603\,bd+1311\,d\\&\quad +\,3094\,{d}^{3}-2956\,b{d}^{3}+1405\,{b}^{2}{d}^{ 2}\\&\quad -\,192\,{b}^{3}d-1317\,b{d}^{4}+973\,{b}^{2}{d}^{3}-270\,{b}^{3}{d}^{2 }\\&\quad +\,16\,{b}^{4}d+232\,{b}^{2}{d}^{4}-225\,b{d}^{5}-106\,{b}^{3}{d}^{3}\\&\quad +\, 18\,{b}^{4}{d}^{2}+1911\,{d}^{4}+619\,{d}^{5}-48\,{b}^{3}\\&\quad +\,82\,{d}^{6}+ 6\,{b}^{4} ) {a}^{2}( 2\,bd-3\,{d}^{2}-6\,d-3) ^{2},\\ C_{12}&=- ( -180\,b+72\,{b}^{2}-2586\,b{d}^{2}+537\,{b}^{2}d\\&\quad +\,2308\,{d}^{2 }-1152\,bd+1043\,d+2702\,{d}^{3}\\&\quad -\,2682\,b{d}^{3}+1197\,{b}^{2}{d}^{2}- 116\,{b}^{3}d\\&\quad -\,1314\,b{d}^{4}+983\,{b}^{2}{d}^{3}-268\,{b}^{3}{d}^{2}+ 12\,{b}^{4}d\\&\quad +\,267\,{b}^{2}{d}^{4}-246\,b{d}^{5}-130\,{b}^{3}{d}^{3}+24 \,{b}^{4}{d}^{2}\\&\quad +\,1763\,{d}^{4}+607\,{d}^{5}-6\,{b}^{3}+86\,{d}^{6}\\&\quad +\,195 ) {a}^{2} ( 2\,bd-3\,{d}^{2}-6\,d-3 ) ^{2},\\ D_{11}&={a}^{2} ( 2\,bd-3\,{d}^{2}-6\,d-3 ) ^{2} ( 37+173\,b- 201\,{b}^{2}\\&\quad +\,280\,b{d}^{2}-543\,{b}^{2}d+524\,{d}^{2}\\&\quad +\,449\,bd+217\,d+ 666\,{d}^{3}-152\,b{d}^{3}\\&\quad -\,357\,{b}^{2}{d}^{2}+194\,{b}^{3}d-213\,b{d} ^{4}+15\,{b}^{2}{d}^{3}\\&\quad +\,64\,{b}^{3}{d}^{2}-20\,{b}^{4}d+46\,{b}^{2}{d} ^{4}-57\,b{d}^{5}\\&\quad -\,16\,{b}^{3}{d}^{3}+2\,{b}^{4}{d}^{2}+469\,{d}^{4}+ 173\,{d}^{5}\\&\quad +\,86\,{b}^{3}+26\,{d}^{6}-14\,{b}^{4} ),\\ D_{12}&={a}^{2} ( 2\,bd-3\,{d}^{2}-6\,d-3 ) ^{2} ( -396\,b+180 \,{b}^{2}\\&\quad -\,3878\,b{d}^{2}+987\,{b}^{2}d+3380\,{d}^{2}\\&\quad -\,2028\,bd+1625\,d+ 3690\,{d}^{3}+321-3502\,b{d}^{3}\\&\quad +\,1695\,{b}^{2}{d}^{2}-230\,{b}^{3}d- 1502\,b{d}^{4}\\&\quad +\,1125\,{b}^{2}{d}^{3}-326\,{b}^{3}{d}^{2}+24\,{b}^{4}d\\&\quad +\, 253\,{b}^{2}{d}^{4}-246\,b{d}^{5}-116\,{b}^{3}{d}^{3}+20\,{b}^{4}{d}^{ 2}\\&\quad +\,2225\,{d}^{4}+701\,{d}^{5}-24\,{b}^{3}+90\,{d}^{6}). \end{aligned}$$

Note that

$$\begin{aligned} q&= \left( \begin{array}{c} {\frac{ \left( \frac{1}{4}-\frac{1}{4}i \right) \left( d +1 \right) a \left( 2\,bd-3\,{d}^{2}-6\,d-3 \right) }{ \left( b-d-1 \right) b}}\\ 1\end{array} \right) ,\\ p&= \left( \begin{array}{c} {\frac{-2\,ib \left( b-d-1 \right) }{ \left( d+1 \right) a \left( 2\,bd-3\,{d}^{2}-6\,d-3 \right) }} \\ \frac{1}{2}+\frac{1}{2}i\end{array} \right) ,\\ \end{aligned}$$

are used in this case. If $D_1\ne 0$, the bifurcation scenario near the 1:4 point is determined by

$$\begin{aligned} A_{0}=-\frac{iC_{1}}{\vert D_{1}\vert }. \end{aligned}$$

$\square$

5 Numerical bifurcation analysis

In order to illustrate the bifurcation analysis of system (1) numerically, and validation of analytical results we carried out some simulations by using the matlab package matcontm.

5.1 Numerical bifurcation of $E_0$

We now perform a numerical continuation of the fixed point $E_0=(0,0)$ by using matcontm. By fixing $a=3.5,~b=4.5,~d=0.25,~m=0.23$ and r free, the matcontm report is

By Proposition 2, the fixed point $E_0$ has a transcritical bifurcation and we know that the transcritical point is a branch point so matcontm reports the transcritical point as a bp. The continuation of $E_0$ is shown in Fig. 1.

Fig. 1

Continuation of $E_{0}$ in $(x,r)-$ space

Fig. 2

Cascade of PD-points (iterates 1,2,4) visualized in the (x, r)-plane

Fig. 3

Bifurcation curves of starting from $E_2$. a Flip bifurcation curve. b Neimark–Sacker bifurcation curve

5.2 Numerical bifurcation of $E_1$

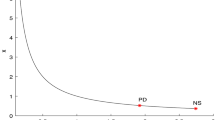
We now do a numerical continuation of $E_1$ . We fix $a=3.5,~b=4.5,~d=0.25,~m=0.23$ and vary r. matcontm reports the following:

The continuation of the 2-cycles emanating from the PD point $x=(0.666667 0.000000 3.000000)$ are as follows:

Continuation 2-cycle:

Continuation 4-cycle:

Fig. 4

Neutral saddle curve of the third iteration of (1)

Fig. 5

A curve of fold bifurcations of the second iterate, lp2, which emanates tangentially at a gpd point on a flip curve

Fig. 6

Phase portrait of the map (1) near the ns point . a Attracting fixed point for (1) that exists for $r=2.55$. b A phase portrait of the map (1) for $r=2.65$

The result is a fixed point curve of iteration 4, meaning we have calculated a curve of 4 cycles. The cascade of PD-points is visualized in Fig. 2.

5.3 Numerical bifurcation of $E_2$

We now do a numerical continuation of $E_2$ . We fix $a=3.5,~b=4.5,~d=0.25,~m=0.23$ and vary r. matcontm reports the following:

We select this ns, by assuming two control parameters r and m and keeping $a=3.5,~b=4.5,~d=0.25$, matcontm reports is as follows:

Fig. 7

Phase portrait of the map (1) near the ns point . a A phase portrait of (1) for $r=2.75$. b The breakdown of the closed invariant curve of (1) for $r=3.5$

We detect pd point and assume r and m as free parameters. matcontm report is as follows:

Fig. 8

Chaotic attractor for the map (1) for $r=3.7$

Flip and Neimark–Sacker bifurcations curves of starting from $E_2$ are shown in Fig. 3. Now we consider the gpd point computed on the flip curve. We compute a branch of fold points of the second iterate by switching at the gpd point. This curve emanates tangentially to the pd curve and forms the stability boundary of the 2-cycles which are born when crossing the pd curve. This curve is presented in Fig. 5.

5.3.1 Orbits of period 3

Let us consider the 1:3 resonance (R3) point. Because its normal form coefficient is negative, there is an area nearby the R3 point in which a stable close invariant curve coexists with an unstable fixed point, i.e., when parameter close to the R3 point, a saddle cycle of period three is appearing. Furthermore, a curve of Neutral Saddles of fixed points of the third iterate emanates. This curve have been computed by branch switching at the R3 point, see Fig. 4.

5.3.2 Numerical simulation

Qualitative dynamical behaviours of the map (1) near the computed ns point corresponding to $r=2.675849$ are determined by simulations (Fig. 5). Now we fix the parameters $a=3.5,~b=4.5,~d=0.25,~m=0.23$ and vary r. Figure 6a shows that $E_2$ is an stable attractor for $r=$. Figure 6b determine the behaviour of the map (1) before the ns point at $r=2.65$. The behaviour of the model after the ns point when $r=2.75$ is shown in Fig. 7a. From Figs. 6b and 7 a, we figure out the fixed point $E_2$ loses its stability via ns bifurcation if r varies from $r=2.65$ to $r=2.75$. Since the normal form coefficient of ns is negative, thus an stable closed invariant curve bifurcates from $E_2$, in which coexists with unstable fixed point $E_2$. Figure 7a confirms this phenomenon and Fig. 7b shows the breakdown of the closed curve for $r=3.5$. The strange attractor of the map (1) for $r=3.7$ is presented to Fig. 8, which exhibit a fractal structure.

6 Concluding remarks

A discrete time system of prey and predator with the Allee effect on prey population has been considered and the stability of fixed points is briefly discussed in this model. All of the codim-1 and codim-2 bifurcations of this model along with calculus of normal form coefficients and the direction of the bifurcations have been investigated. Bifurcations like transcritical, fold, flip and Neimark–Sacker, generalized flip, resonance 1:2, resonance 1:3 and resonance 1:4 have been gained and a numerical simulation has been done in order to support and verify the analysis results and to reveal more complicated dynamical behaviours of the model using numerical software matcontm.