1 Introduction

Controller design of a nonlinear system is in general difficult. One way to avoid such complexity is using a linearly approximated model so that a linear control technique can be easily applied. However, a certain degree of control error is inevitable when using the simplified model.

The objective of this work is to reduce this error using a neural network (NN)-based PID compensator. The controller structure of the system consists of two parts: base controller and NN-based PID. The base controller can be any classic linear controller that can perform stabilization and/or trajectory tracking. The error of the base controller, which may be induced by model simplifications, is compensated by the NN-based PID.

In this work, the full-state feedback linearization method is used on an approximated model for the design of the base controller. The neural network in the PID compensator takes state errors as input and generates PID gains as outputs. The PID compensator uses the updated gains and creates compensatory control input to the system. The neural network itself is also being updated online using the backpropagation learning algorithm. Finally, the two control inputs from the base linear controller and the NN-based PID compensator are added to generate the input to the system.

This control approach is implemented on the ball-on-plate system we built for this study and demonstrates improvement in stabilization and trajectory tracking control.

1.1 Literature review

The feedback linearization method which our proposed base controller is based on is a powerful tool in control design of nonlinear systems since a nonlinear system can be transformed to an equivalent linear system so that linear control techniques can be easily applied. Among numerous related studies, Ho et al. [1] used the aforementioned method to control a wheel that balances a ball on it. Ryu et al. [2] also used the feedback linearization method to balance a disk on a disk. In their work, the lower disk is attached to a DC motor and the upper disk which is free to roll is balanced on top of the lower disk.

However, this method is limited in that only a class of systems that satisfy necessary conditions is feedback linearizable. For those that do not satisfy the conditions, one possible solution would be simplification of the dynamic model so that feedback linearization becomes applicable with the approximate model. The ball-on-beam system is proven to be not feedback linearizable, so an approximated model approach is applied in [3], which we adopted in this study.

A typical approach to control the ball-on-plate system is to decouple the system into two independent ball-on-beam systems about each rotational axis of the plate through model simplification. A proven ball-on-beam controller can then be applied to each axis in order to finally control the ball-on-plate system.

Awtar et al. applied a double-loop control strategy where the outer loop calculates target angular positions of the plate while the inner loop uses PID control to achieve the target position [4]. Mochizuki and Ichihara proposed I–PD control, which is a variant of PID control, using the KYP (Kalman–Yakubovich–Popov) lemma [5]. Fuzzy logic has been also studied for the control of the ball-on-plate system in [6]. Ho et al. applied in [7] the approximate feedback linearization method which was first proposed in [3].

However, the simplification in controller design resulted from using an approximate model is often made at a cost of inferior performance of the control system. Therefore, we propose a compensation strategy to compensate for the effects of the ignored nonlinear terms as well as unmodeled dynamics. While a parallel control structure appears in fuzzy PID control [8, 9], we chose a neural network system as a compensator due to its high adaptivity to different system conditions. In addition, the error-based control method of the PID can be used for neural network training as it has shown reliable performance. For these collective reasons, the design of a NN-based PID controller is proposed in this work.

Controller design in the structure of neural network has been increasingly employed in a wide range of applications from vehicle vibration control [10] to robotic manipulators [11].

Jung et al. designed a neural network-based pre-filter for a conventional PID, based on the reference compensation technique (RCT) that can stabilize a two-dimensional inverted pendulum [12] as well as a wheeled inverted pendulum [13]. The neural network in these studies basically represents the inverse dynamics of the control system. A variant of PID controller which is also based on neural networks is presented in [11, 14] to improve the position control of a manipulator arm using pneumatic actuators. Similar to our proposed work, the backpropagation algorithm is used to update the neural network online. Cong and Liang [15] proposed a neural network controller that mimics a structure of PID using an activation and output feedback on three nodes in the hidden layer and implemented it on a single and a double inverted pendulum. In this work, the control performance is dependent on initial conditions of the states. Kang et al. presented an adaptive neural network controller that uses a PID structure in [16] where the particle swarm optimization (PSO) algorithm is adopted to choose better initial weights that prevent trapping in local minima. Another adaptive controller is proposed in [17] to control a Segway-type inverted pendulum. The controller is based on radial basis function neural networks (RBFNNs) and the same structure of controller is applied each for balancing and yaw control.

Neural networks also have been used as an estimator [18]. In the reference, the neural network is designed to estimate the system’s dynamic model and used with another neural network-based PI controller to control the speed of an induction motor under the presence of disturbances using the so-called projection algorithm. A high gain observer to estimate the state derivatives is also used in [19] with a neural network-based feedback controller that does not need offline training.

1.2 Paper outline

The rest of the paper is organized as follows. The dynamic model of the ball-on-plate system is derived in Sect. 2. Section 3 describes the design and structure of the proposed controller. The experimental setup we built for this study is explained in Sect. 4. Sections 5 and 6 present the simulation and experimental results, respectively, followed by concluding remarks in Sect. 7.

2 Dynamic model of the ball-on-plate system

In this section, we derive the equations of motion of the ball-on-plate system using the Euler–Lagrange equation. The derived model will later be simplified to two independent ball-on-beam systems such that the two rotational axis motions of the ball-on-plate system are controlled each by a ball-on-beam controller.

2.1 Dynamic model

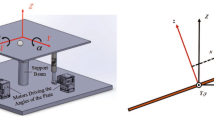
Figure 1 shows the 3D CAD model of the ball-on-plate system we developed for this study. While the derivation of the equations of motion is also available in [7], we present important steps in a slightly different manner to improve understanding.

Fig. 1
figure 1

Developed ball-on-plate system in CAD drawing

Full size image

The Euler–Lagrange equation is given by

$$\begin{aligned}&\frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q}}\right) - \frac{\partial L}{\partial q} = Q \end{aligned}$$
(1)

where Lagrangian \(L = T - V\). Here, T and V are the total kinetic and potential energies of the system, respectively. The generalized coordinate vector q for the system is given by \(q = [x, y, \theta _x, \theta _y]^T\) in which (x, y) is the ball position measured from the center of the plate. \(\theta _x\) and \(\theta _y\) are the plate tilting angles about x and y axes, respectively. The definitions of these state variables are visualized in Figs. 1 and 2. The generalized force vector Q represents the input torques about each axis, given by \(Q = [0, 0, \tau _x, \tau _y]^T\).

Fig. 2
figure 2

Global OXYZ and local oxyz coordinate systems

Full size image

First, between the local coordinate frame oxyz attached to the plate, denoted by ‘1’, and the global coordinate frame OXYZ, denoted by ‘0’, the rotation matrix is given by

$$\begin{aligned} R^0_1 = \begin{bmatrix} c_y&\quad 0&\quad s_y \\ s_x s_y&\quad c_x&\quad -s_x c_y\\ -c_x s_y&\quad s_x&\quad c_x c_y \end{bmatrix} \end{aligned}$$
(2)

where \(s_x\), \(c_x\), \(s_y\), and \(c_y\) denote \(\sin \theta _x\), \(\cos \theta _x\), \(\sin \theta _y\), and \(\cos \theta _y\), respectively.

The relationship of \(S(\omega ^0_p) = \dot{R}^0_1 (R^0_1)^T\) from [20, chap. 4] gives the angular velocity of the plate in the form of a skew symmetric matrix.

$$\begin{aligned} \begin{bmatrix} 0&\quad -\omega _{pz}&\quad \omega _{py} \\ \omega _{pz}&\quad 0&\quad -\omega _{px} \\ -\omega _{py}&\quad \omega _{px}&\quad 0 \end{bmatrix} = \begin{bmatrix} 0&\quad -{\dot{\theta }}_y s_x&\quad {\dot{\theta }}_y c_x \\ {\dot{\theta }}_y s_x&\quad 0&\quad -{\dot{\theta }}_x \\ -{\dot{\theta }}_y c_x&\quad {\dot{\theta }}_x&\quad 0 \end{bmatrix}\nonumber \\ \end{aligned}$$
(3)

From this relationship, the angular velocity of the plate in the global coordinate frame is obtained as

$$\begin{aligned} \omega ^0_p = [\omega _{px}, \omega _{py},\omega _{pz}]^T = [{\dot{\theta }}_x, {\dot{\theta }}_y c_x, {\dot{\theta }}_y s_x]^T \end{aligned}$$
(4)

It is more convenient to calculate the rotational kinetic energy with the angular velocity expressed in the local coordinate frame where the moments of inertia remain constant. Thus, we have

$$\begin{aligned} \omega ^1_p = (R^0_1)^T \omega ^0_p \end{aligned}$$
(5)

On the other hand, given the ball position in the local coordinate frame

$$\begin{aligned} p^1_b = [x, y, r]^T \end{aligned}$$
(6)

where r is the radius of the ball, the velocity of the ball can be obtained in the global coordinate frame such that

$$\begin{aligned} v^0_b = \frac{d p^0_b}{dt} = \frac{d\left( R^0_1 p^1_b\right) }{dt} \end{aligned}$$
(7)

Assuming no slip condition between the ball and the plate, the angular velocity of the ball relative to the plate is given by \(\left[ -\dfrac{\dot{y}}{r}, \dfrac{\dot{x}}{r}, 0\right] ^T\). Furthermore, since the plate is also rotating, adding the angular velocity of the plate of Eq. (5) yields the angular velocity of the ball, expressed in the local coordinate frame, as

$$\begin{aligned} \omega _b^1 = \left[ -\dfrac{\dot{y}}{r} + {\dot{\theta }}_x c_y,~ \dfrac{\dot{x}}{r} + {\dot{\theta }}_y,~ {\dot{\theta }}_x s_y \right] ^T \end{aligned}$$
(8)

Finally, the total kinetic and potential energies of the system are the sum of those of the plate and the ball, given by

$$\begin{aligned} T_{total}&= T_{plate} + T_{ball} \end{aligned}$$
(9)
$$\begin{aligned} V_{total}&= V_{plate} + V_{ball} \end{aligned}$$
(10)

where

$$\begin{aligned}&T_{plate} = \dfrac{1}{2}\left( \omega ^1_p\right) ^T \mathcal {I}_p \omega ^1_p \end{aligned}$$
(11)
$$\begin{aligned}&V_{plate} = 0 \end{aligned}$$
(12)
$$\begin{aligned}&T_{ball} = \dfrac{1}{2} m_b \left( v^0_b\right) ^T v^0_b + \dfrac{1}{2} I_b \left( \omega ^1_b\right) ^T \omega ^1_b \end{aligned}$$
(13)
$$\begin{aligned}&V_{ball} = m_b g[0 \quad 0 \quad 1] p^0_b \end{aligned}$$
(14)

Note that \(\mathcal {I}_p\) is the constant inertia tensor expressed in the body-attached frame given by

$$\begin{aligned} \mathcal {I}_p = \begin{bmatrix} I_{px}&\quad 0&\quad 0 \\ 0&\quad I_{py}&\quad 0 \\ 0&\quad 0&\quad I_{pz} \end{bmatrix} \end{aligned}$$
(15)

where \(I_{px}\), \(I_{py}\), and \(I_{pz}\) are the moment of inertia about x, y, and z axes, respectively and \(I_b\) is the moment of inertia of the ball (Table 1). Now by substituting \(L=T_{total}-V_{total}\) into Eq. (1), one can obtain the full dynamic model of the ball-on-plate system.

$$\begin{aligned} M\ddot{q} + C\dot{q} + G = Q \end{aligned}$$
(16)

Due to the length, the detailed expressions of the matrices of M, C, and G are not presented here, but one could easily derive with help of mathematical software such as Maple or Matlab.

Table 1 Description of the system parameters
Full size table

As mentioned earlier, the base controller in our proposed control structure is supposed to be designed with a simplified dynamic model. Ignoring coupling terms results in two independent, simplified ball-on-beam equations.

$$\begin{aligned}&\left( m_b + \frac{I_b}{r^2} \right) \ddot{x} - m_b x {\dot{\theta }}_y^2 - m_b g \sin \theta _y = 0 \end{aligned}$$
(17a)
$$\begin{aligned}&\begin{aligned}&\left( m_b x^2 + I_b + I_p\right) \ddot{\theta }_y + 2m_b x \dot{x} {\dot{\theta }}_y \\&\quad \quad \quad ~ - m_b g x \cos \theta _y - m_b g r \sin \theta _y = \tau _y \end{aligned} \end{aligned}$$
(17b)
$$\begin{aligned}&\left( m_b + \frac{I_b}{r^2} \right) \ddot{y} - m_b y {\dot{\theta }}_x^2 - m_b g \sin \theta _x = 0 \end{aligned}$$
(18a)
$$\begin{aligned}&\begin{aligned}&\left( m_b y^2 + I_b + I_p\right) \ddot{\theta }_x + 2m_b y \dot{y} {\dot{\theta }}_x \\&\quad \quad \quad ~ - m_b g y \cos \theta _x - m_b g r \sin \theta _x = \tau _x \end{aligned} \end{aligned}$$
(18b)

where \(I_p\) = \(I_{px}\) = \(I_{py}\) assuming the plate is square. Since these two sets of the equations in Eqs. (17) and (18) are basically identical for each axis of rotation, only Eq. (17) will be used in the controller design in the next section. Then, the same structure of the controller will be applied to the other rotational motion.

3 Controller design

The proposed controller consists of two subcontrollers: base linear controller and neural network (NN)-based PID compensator. When a simple controller design is chosen based on its approximated model, the NN-based PID compensator is designed such that it compensates for the errors that may have been caused by the simplification of the dynamic model with the base controller. This proposed controller works in a way that the control inputs from the two individual subcontrollers are added to finally generate torque input to the ball-on-plate system.

We use the approximate input-output feedback linearization method adopted from [3] to design the base controller. The method builds on the simplified model derived in Sect. 2.1 and further simplification is made during the controller design in Sect. 3.1. For the NN-based PID compensator, we design a neural network that takes state errors as input and updates the gains of the PID controller online to complement the base controller. The structure of proposed controller is shown in Fig. 3 and the detailed design of each subcontrollers are presented in this section.

Fig. 3
figure 3

Structure of the proposed controller (for one axis)

Full size image

3.1 Base controller design using approximate feedback linearization

The simplified dynamic model in Eq. (17) can be rewritten in an input-affine form as

$$\begin{aligned} \dot{X} = f(X) + g(X) \tau _y \end{aligned}$$
(19)

where \(X = [x, \dot{x}, \theta _y, {\dot{\theta }}_y]^T\). This system is said to be feedback linearizable if an output h(X) exists satisfying

$$\begin{aligned} \triangledown h~ \text {ad}^i_f g&= 0, \quad i = \{0, 1, 2\}, \end{aligned}$$
(20a)
$$\begin{aligned} \triangledown h~\text {ad}^3_f g&\ne 0, \end{aligned}$$
(20b)

where the Lie bracket is defined as \(\hbox {ad}_f g = \triangledown g f - \triangledown f g\) [21]. Then, by solving Eq. (20a), the output is obtained as \(h(X) = x\). Now to transform the nonlinear system to a linear one, we differentiate the output h with respect to time until the input appears.

$$\begin{aligned}&\zeta _1 = h(X) = x \end{aligned}$$
(21)
$$\begin{aligned}&\zeta _2 = \dfrac{d\zeta _1}{dt} = \dot{x} \end{aligned}$$
(22)
$$\begin{aligned}&\zeta _3 = \dfrac{d\zeta _2}{dt} = \dfrac{1}{m_b + \dfrac{I_b}{r^2}}\left( m_b x\dot{\theta }_y^2 + m_b g s_y \right) \end{aligned}$$
(23)
$$\begin{aligned}&\zeta _4 = \dfrac{d\zeta _3}{dt} = \dfrac{1}{m_b + \dfrac{I_b}{r^2}}\left( m_b\dot{x}\dot{\theta }_y^2 + m_b g\dot{\theta }_y c_y \right) \end{aligned}$$
(24)

in which the term \(2m_b x\dot{\theta }_y\ddot{\theta }_y/(m_b+I_b/r^2)\) is ignored in \(\zeta _4\). This approximation is necessary in order to make the system feedback linearizable. Then, we finally obtain, with \(\zeta \) = \([\zeta _1, \zeta _2, \zeta _3, \zeta _4]^T\),

$$\begin{aligned} {\dot{\zeta }} = \begin{bmatrix} 0&\quad 1&\quad 0&\quad 0 \\ 0&\quad 0&\quad 1&\quad 0 \\ 0&\quad 0&\quad 0&\quad 1 \\ 0&\quad 0&\quad 0&\quad 0 \end{bmatrix} \zeta + \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} v \end{aligned}$$
(25)

with the input transformation

$$\begin{aligned} v = \alpha (X) + \beta (X) \tau _y \end{aligned}$$
(26)

where \(\alpha (X)\) and \(\beta (X)\) are a function of the state variables and their expressions are provided in “Appendix”.

Since the transformed system in Eq. (25) is now linear, a linear control technique such as the pole placement method can be used to determine controller gains. The control input in Eq. (25) can be designed such that

$$\begin{aligned} v = (x^d)^{(4)} + K_4 \dddot{e} + K_3 \ddot{e} + K_2 \dot{e} + K_1 e \end{aligned}$$
(27)

where \(x^d\) is the desired ball trajectory and the error \(e = x^d - x\). The actual torque input \(\tau _y\) can then be obtained using the input transformation in Eq. (26).

3.2 NN-based PID controller

The combination of PID and neural network is used as a compensator in the form of

$$\begin{aligned} \tau _{NN} = K_p e + K_i \int _0^t e\,dt + K_d \dot{e} \end{aligned}$$
(28)

where the position error \(e = x^d - x\). The control gains \(K_p\), \(K_i\), and \(K_d\) are updated online through the neural network while adapting to different situations.

The structure of the neural network used in the controller is shown in Fig. 4. The designed neural network has three inputs, five neurons in the hidden layer, and three in the output layer in which all neurons of one layers are connected to all neurons of the next. The three inputs to the neural network are

$$\begin{aligned} S_1 = e, \quad S_2 = \int _0^t e\,dt, \quad S_3 = \dot{e} \end{aligned}$$
(29)

The outputs are three PID control gains.

$$\begin{aligned}&\phi _1 = K_p,\quad \phi _2 = K_i, \quad \phi _3 = K_d \end{aligned}$$
(30)
Fig. 4
figure 4

Designed neural network (biases, \(b_j\) and \(b_k\), are not shown)

Full size image

A tangent sigmoid and linear functions are used as transfer functions for the hidden and the output layers, respectively. Those functions are given by

$$\begin{aligned}&\phi _j(S_j) = \dfrac{2}{1+e^{-2 S_j}} - 1 \end{aligned}$$
(31)
$$\begin{aligned}&\phi _k(S_k) = S_k \end{aligned}$$
(32)

The final torque control input to the system is the sum of the base linear control \(\tau _{AFL}\) and the neural network control \(\tau _{NN}\) as shown in Fig. 3, such that

$$\begin{aligned} \tau = \tau _{\textit{AFL}} + \tau _{NN} \end{aligned}$$
(33)

To update the weights and biases of the neural network, the gradient descent learning algorithm [22] is applied with the following error function.

$$\begin{aligned} E = \dfrac{1}{2}(x^d - x)^2 \end{aligned}$$
(34)

Then, the update rules with an iterative index n are defined as

$$\begin{aligned} w_{kj}(n+1)= & {} w_{kj}(n) - \eta dw_{kj}(n) + \alpha dw_{kj}(n-1) \end{aligned}$$
(35)
$$\begin{aligned} b_k(n+1)= & {} b_k(n) - \eta db_k(n) + \alpha db_k(n-1) \end{aligned}$$
(36)
$$\begin{aligned} w_{ji}(n+1)= & {} w_{ji}(n) - \eta dw_{ji}(n) + \alpha dw_{ji}(n-1) \end{aligned}$$
(37)
$$\begin{aligned} b_j(n+1)= & {} b_j(n) - \eta db_j(n) + \alpha db_j(n-1) \end{aligned}$$
(38)

where

$$\begin{aligned} dw_{kj}(n)&= \dfrac{\partial E}{\partial w_{kj}}(n), \quad db_k(n) = \dfrac{\partial E}{\partial b_k}(n) \\ dw_{ji}(n)&= \dfrac{\partial E}{\partial w_{ji}}(n), \quad db_j(n) = \dfrac{\partial E}{\partial b_j}(n) \end{aligned}$$

and the learning rate \(\eta \) and momentum rate \(\alpha \) can be determined experimentally. Furthermore, we have the following equations using the chain rule.

$$\begin{aligned}&\frac{\partial E}{\partial w_{kj}} = \frac{\partial E}{\partial x}\frac{\partial x}{\partial \tau }\dfrac{\partial \tau }{\partial \tau _{NN}}\dfrac{\partial \tau _{NN}}{\partial \phi _k}\dfrac{\partial \phi _k}{\partial S_k}\dfrac{\partial S_k}{\partial w_{kj}} \end{aligned}$$
(39)
$$\begin{aligned}&\dfrac{\partial E}{\partial b_k} = \dfrac{\partial E}{\partial x}\dfrac{\partial x}{\partial \tau }\dfrac{\partial \tau }{\partial \tau _{NN}}\dfrac{\partial \tau _{NN}}{\partial \phi _k}\dfrac{\partial \phi _k}{\partial S_k}\dfrac{\partial S_k}{\partial b_k} \end{aligned}$$
(40)
$$\begin{aligned}&\begin{aligned} \dfrac{\partial E}{\partial w_{ji}}&= \dfrac{\partial E}{\partial x}\dfrac{\partial x}{\partial \tau }\dfrac{\partial \tau }{\partial \tau _{NN}}\left( \sum _{k=1}^3\dfrac{\partial \tau _{NN}}{\partial \phi _k}\dfrac{\partial \phi _k}{\partial S_k}\dfrac{\partial S_k}{\partial \phi _j}\right) \\&\qquad \times \dfrac{\partial \phi _j}{\partial S_j}\dfrac{\partial S_j}{\partial w_{ji}} \end{aligned} \end{aligned}$$
(41)
$$\begin{aligned}&\begin{aligned} \dfrac{\partial E}{\partial b_j}&= \dfrac{\partial E}{\partial x}\dfrac{\partial x}{\partial \tau }\dfrac{\partial \tau }{\partial \tau _{NN}} \left( \sum _{k=1}^3\dfrac{\partial \tau _{NN}}{\partial \phi _k}\dfrac{\partial \phi _k}{\partial S_k}\dfrac{\partial S_k}{\partial \phi _j}\right) \\&\qquad \times \dfrac{\partial \phi _j}{\partial S_j}\dfrac{\partial S_j}{\partial b_j} \end{aligned} \end{aligned}$$
(42)

For the calculation of each term in Eqs. (39)–(42), we obtain from Eq. (34)

$$\begin{aligned} \dfrac{\partial E}{\partial x} = -(x^d - x) \end{aligned}$$
(43)

Then, due to the nature of the gradient descent method, the direction of the term \(\dfrac{\partial x}{\partial \tau }\) is more important. Hence, using the finite difference method, one can simplify the term as follows.

$$\begin{aligned} \dfrac{\partial x}{\partial \tau }(n) = \text {sgn} \left( \frac{\Delta x}{\Delta \tau } \right) = \text {sgn}\left( \dfrac{x(n) - x(n-1)}{\tau (n) - \tau (n-1)}\right) \end{aligned}$$
(44)

where sgn(\(\cdot \)) denotes the sign function.

Also, from Eq. (33),

$$\begin{aligned} \dfrac{\partial \tau }{\partial \tau _{NN}} = 1 \end{aligned}$$
(45)

Since the neural network outputs are the gains of the PID controller, we have

$$\begin{aligned} \dfrac{\partial \tau _{NN}}{\partial \phi _1}&= x^d - x \end{aligned}$$
(46)
$$\begin{aligned} \dfrac{\partial \tau _{NN}}{\partial \phi _2}&= \int _0^t(x^d - x)dt \end{aligned}$$
(47)
$$\begin{aligned} \dfrac{\partial \tau _{NN}}{\partial \phi _3}&= \dot{x}^d - \dot{x} \end{aligned}$$
(48)

The neural network structure, as shown in Fig. 4, yields

$$\begin{aligned} \dfrac{\partial S_k}{\partial w_{kj}}&= \phi _j, \quad \dfrac{\partial S_k}{\partial b_k} = 1, \quad \dfrac{\partial S_k}{\partial \phi _j} = w_{kj}, \end{aligned}$$
(49)
$$\begin{aligned} \dfrac{\partial S_j}{\partial w_{ji}}&= \phi _i, \quad \dfrac{\partial S_j}{\partial b_j} = 1 \end{aligned}$$
(50)

Furthermore, from the transfer functions we selected in Eqs. (31) and (32),

$$\begin{aligned} \dfrac{\partial \phi _j}{\partial S_j}&= 1 - \phi _j^2 \end{aligned}$$
(51)
$$\begin{aligned} \dfrac{\partial \phi _k}{\partial S_k}&= 1 \end{aligned}$$
(52)

Finally, following the rules in Eqs. (35)–(38) will update the weights and biases of the neural network.

As it is often the case, the designed neural network requires offline training beforehand. This training is done by setting an acceptable set of PID gains, which can be first obtained experimentally, as desired outputs of the neural network.

4 Experimental setup

The experimental setup built for this study is shown in Fig. 5. It consists of three main components: mechanical system, vision system, and controller system.

Fig. 5
figure 5

Experimental setup

Full size image

4.1 Mechanical system

The experimental setup is designed such that a steel ball is free to roll on an acrylic plate that is placed on top of a center rod through a universal joint. The plate is controlled by two motors through a linkage mechanism. Each linkage is attached to the plate through a universal joint so that it can rotate around x and y axes at the same time. Dynamixel motors (XM430-W210-T) mounted on the bottom plate are used as actuators and the motor shaft is attached to the other end of each linkage.

Using geometry and small angle approximations, we have the following relationship between the plate angle \(\theta _y\) and the motor shaft angle \(\theta _m\).

$$\begin{aligned} \theta _y = \frac{d}{l}\theta _m \end{aligned}$$

and between the torque applied to the plate \(\tau \) and the motor output torque \(\tau _m\),

$$\begin{aligned} \tau = \frac{l}{d} \tau _m \cos \theta _m \cos \theta _x \end{aligned}$$

where d denotes the length of the lower link attached to the motor shaft and l denotes the distance from the center of the plate to the point where the upper (universal joint) link is attached.

Table 2 Values of the system parameters
Full size table

Table 2 shows the system parameters and their values of the actual system.

Fig. 6
figure 6

Simulation results for stabilizing the ball at \((0.1,-\,0.1\)). For clarity, only the y-axis rotational motion is plotted: a AFL alone and b AFLNN

Full size image
Fig. 7
figure 7

Simulation results for circular trajectory tracking (\(R = 0.06\) m and \(\omega = 6\) rad/s): a AFL alone and b AFLNN

Full size image

4.2 Vision system

A low-cost USB camera (Sony SLEH-00448) is used to track the ball on the plate. It runs at a frame rate of 120 Hz providing \(320\times 240\) pixel resolution. The OpenCV library is used for image processing. The camera is mounted at a height of 48 cm from the plate. Since the camera measures the ball’s position with respect to the global coordinate frame, the coordinates are transformed to the local frame using the rotation matrix in Eq. (2).

4.3 Control system

A 2.1 GHz laptop with Ubuntu Linux 16.04 LTS is used to control the entire system. The control code is written in C++ utilizing the OpenCV library for vision tracking and the Dynamixel library for motor control. While the Dynamixel motors can run at up to 330 Hz using low latency timer in Linux and the vision system at up to 120 Hz, the entire control loop is set to run at 100 Hz due to necessary computations such as neural network online update.

From the experimental torque–current relation data provided by the manufacturer under current mode, we adopted the following linear equation to control torque input of the actuators by sending corresponding current commands to the motors.

$$\begin{aligned} \tau = 1.3 i - 0.32 \end{aligned}$$
(53)

where i is in A and \(\tau \) is in N m.

5 Simulation results

This section presents simulation results of stabilization and trajectory tracking control by our controller designed in Sect. 3. The results are compared with those of the linear controller alone.

The control gain \(K_i\) of the base linear controller in Eq. (27) are chosen as \([K_1\), \(K_2\), \(K_3\), \(K_4]\) = [2401, 1372, 294, 28], which is the case when all the roots to the characteristic equation lie at \(-\,7\). The same gain matrix is used for control of the other axis as well as for experiments. As mentioned in Sect. 3.2, we first need a conventional PID controller working along with the base controller for offline training. For this training purpose, the PID control gains are chosen experimentally as \((K_p, K_i, K_d) = (1.0, 1.0, 0.1)\) which yields an acceptable control performance. For simulation study, the original nonlinear model in Eq. (16) is used to represent the physical system.

5.1 Stabilization

Figure 6 shows the simulation results for stabilizing the ball at \((x^d, y^d)\) = \((0.1,-\,0.1)\) m. To increase clarity, only the variables related to the y-axis rotational motion are shown since the other axis motion is analogous. Figure 6a shows the result of only using the base linear controller (AFL hereafter) for comparison purpose while Fig. 6b shows our proposed controller (AFLNN hereafter) in which the neural network-based PID compensator is used along with AFL. The initial conditions for all states were given zero in the simulations. Although a target point off the plate center was selected to see the performance difference between AFL and AFLNN, except for initial larger overshoots of AFLNN, both controllers resulted in the error of 0.001 m in both x and y axes. However, as it will be shown later in the experiment section, in practice AFL shows a fair amount of steady state error whereas AFLNN is capable of significantly reducing the errors which might be resulted from the model simplification.

Fig. 8
figure 8

PID control gains being updated through the neural network during trajectory tracking control

Full size image
Fig. 9
figure 9

Experimental results for stabilizing the ball at \((0.1,-\,0.1\)): a AFL alone and b AFLNN

Full size image
Fig. 10
figure 10

PID control gains being updated during the stabilization control experiment

Full size image

5.2 Trajectory tracking

To further demonstrate the performance of the proposed controller, a circular trajectory tracking control is conducted. The desired trajectory is chosen as

$$\begin{aligned}&x^d(t) = R\sin (\omega t) \end{aligned}$$
(54)
$$\begin{aligned}&y^d(t) = R\cos (\omega t) \end{aligned}$$
(55)

where R denotes the radius of the circle and \(\omega \) the angular velocity of the circular motion. Considering the size of the plate, it is selected that R = 0.06 m and \(\omega \) = 6 rad/s. Figure 7a shows the simulation results of AFL alone while Fig. 7b shows the result of the proposed controller. As it can be seen form the figure, the RMS deviation of the circular motions from the desired trajectory decreased from 8.4 mm to 0.6 mm in the steady state.

Figure 8 shows the adjustment of the PID gains by the neural network over time. It is seen that in this case the proportional gain, \(K_p\), plays an important role in reducing the steady state error as it rapidly increases in the beginning while the other gains are reasonably stable within a range.

6 Experimental results

It is worth mentioning that in the implementation of AFL, we need to measure higher time derivatives, \(\ddot{x}\) and \(\dddot{x}\), of the ball position apart from \(\dot{x}\) in the feedback control as seen in Eq. (27). These derivatives can be obtained from making use of the coordinate transformation in Eqs. (23) and (24), which are \(\ddot{x}\) = \(\zeta _3\) and \(\dddot{x}\) = \(\zeta _4\), to avoid impractical numerical differentiations for such high derivatives.

It also should be mentioned that in order to minimize unwanted instability of AFLNN in practice, the NN-based PID compensator is set to be activated after one second from start when the response is relatively settled with the base controller.

The learning rate of \(\eta = 0.3\) and momentum rate of \(\alpha = 0.6\) are used for the neural network in AFLNN for the experiments.

6.1 Stabilization

Figure 9 shows the experimental results of stabilization of the ball at \((0.1, -\,0.1)\) m. The ball was initially placed near the center of the plate when the control starts. As it can be seen in Fig. 9a, there is a steady state error in both x and y coordinates with AFL alone as the ball is stabilized at the averaged coordinates of \((0.073, -\,0.076)\) m. This error is caused by the simplifications and approximations that have been made on the system model in the design of the AFL base controller as explained in Sect. 3.1. As shown in Fig. 9b, the steady state error becomes almost eliminated when AFLNN is used as the ball is now stabilized at \((0.093, -\,0.093)\).

Figure 10 shows the changes in PID gains. Since the amount of additional torque input needed for the stabilization correction is relatively small, the PID gain updates occur within a small range. The error that AFL alone is not capable of eliminating is being gradually reduced as the PID gains are updated and the gains are also eventually stabilized within a small range as the ball is stabilized at the desired location.

6.2 Trajectory tracking

Fig. 11
figure 11

Experimental results for circular trajectory tracking (\(R = 0.08\) m and \(\omega = 2\) rad/s): a AFL alone and b AFLNN

Full size image
Fig. 12
figure 12

PID control gains being updated during the trajectory tracking control experiment

Full size image

Figure 11 shows the experimental results of the ball following a circular trajectory with \(R = 0.08\) m and \(\omega = 2\) rad/s. Figure 11a is with only AFL and Fig. 11b shows the improved result with AFLNN. It shows that in the steady state the deviation error decreases from 0.0115 to 0.0077 m in terms of the radius of the circular trajectory.

Figure 12 shows that the PID gains by AFLNN are being adjusted online successfully. It shows that the neural network tries to increase the system response by increasing \(K_p\) while the trajectory tracking accuracy becomes improved by increasing \(K_i\).

7 Conclusion

In order to avoid the difficulties of controller design of nonlinear systems, we proposed a controller consisting of a base linear controller and a neural network-based PID compensator. The controller is structured in a way that the outputs of the two subcontrollers are added together to generate a resultant control input to the system. We implemented the strategy on the ball-plate system and demonstrated the effectiveness of the proposed controller in stabilization and trajectory tracking control through simulations and experiments.

The suggested future research directions include the use of different training algorithms such as Levenberg–Marquardt for better convergence for the neural network’s online training and construction of a portable ball-on-plate system using a small single-board computer such as Raspberry PI.