1 Introduction

The van der Pol oscillator was first proposed by van der Pol [1] in 1920. The analytical solutions of periodic motions of such a self-excited oscillator have been of great interest for a century. The method of averaging was used by van der Pol [1] for determining periodic motions of circuits’ self-excited systems, and the presence of natural entrainment frequencies in such a system was observed in [2]. van der Pol [3] continued to study the nonlinear properties of the van der Pol oscillator. The approximate solutions of single degree of freedom and two-degree of freedom van der Pol oscillators were developed. The resonant and relaxation characteristics of the van der Pol oscillators were also discussed. In 1945, Cartwright and Littlewood [4] analyzed the dynamics of the forced van der Pol equation and proved the existence of periodic motions. In 1947, Littlewood [5] discussed the more general case about the dynamic flow of the van der Pol equation, and proved was that the periodic motions existed when new damping terms were added. In 1948, Levinson [6] used a piecewise linear model to describe the van der Pol equation and determined the existence of periodic motions. In 1949, Levinson [7] further developed the structures of periodic solutions in such a second order differential equation through the piecewise linear model, and discovered that infinite periodic solutions existed in such a piecewise linear model. In 1967, from the Levinson’s results, Smale [8] used the topological point to present the Smale horseshoe with discontinuous mappings to describe the existence of infinite periodic motions. Thus, one extensively used the concept of the Smale horseshoe to explain chaos in nonlinear dynamical systems. Herein, it should not be discussed any more. This paper will focus on the periodic motions in nonlinear dynamical systems.

In 1998, Buonomo [9] suggested a transformation of perturbation parameters for approximate solutions of the periodic solutions, and Buonomo [10] combined the perturbation method and harmonic balance method for improvement of the aforementioned approximate periodic solutions of the van der Pol equation. In 2001, Mickens [11] studied the periodic motion of the van der Pol equation through the backward Euler method. Mickens [12] also studied the computational time-step size effects on the period of the limit cycle of the van der Pol equations for such a numerical method. In 2006, Waluya and van Horssen [13] used the energy and phase variables to study the van der Pol dynamic system, and the asymptotic approximate solutions and the periods of periodic motions were determined. Andrianov and van Horssen [14] used the same ideas for a generalized van der Pol equation and analytically approximated the corresponding periodic motions.

The aforementioned improved methods were based on the perturbation and classic harmonic balance method. One tried to find the way to get the more accurate solutions of periodic motions in the van der Pol oscillator. To solve such problems in nonlinear dynamical systems, in 2012, Luo [15] developed a generalized harmonic balance method. Such an approach transformed the nonlinear dynamic system into the dynamic system of coefficients through the finite Fourier series transformation. The steady-state solutions of periodic motions can be achieved accurately with a prescribed precision. Luo and Lakeh [16] used the generalized harmonic balance method to investigate a periodically forced van der Pol oscillator, and the stable and unstable solutions of period-m motions were presented analytically and the symmetric period-1 to period-5 the motions were demonstrated. Luo and Lakeh [17] studied period-1 motion and limit cycle in the van der Pol equation. The parameter map of excitation frequency and amplitude for period-1 motions was obtained. Luo and Lakeh [18] used the generalized harmonic balance method to study the period-m motions of a van der Pol–Duffing oscillator, and the bifurcation trees of period-m motions to chaos in such a van der Pol–Duffing oscillator were presented.

Indeed, the generalized harmonic method provided good results of periodic motions in nonlinear dynamical systems with polynomial nonlinearity. For non-polynomial nonlinear dynamical systems, the generalized harmonic balance method should be very difficult to use. Thus, in 2015, Luo [19] systematically developed the discrete mapping method (semi-analytical method) for such a non-polynomial nonlinear systems, and the periodic solutions of such nonlinear dynamic systems can be predicted analytically and accurately. The detailed discussion and application were presented in Luo [20]. Luo and Guo [21] used such a discrete mapping method to determine the bifurcation trees of period-1 motions to chaos and the frequency–amplitude characteristics of periodic motions to chaos were presented, which were compared to the corresponding analytical solutions. The results given by the analytical and semi-analytical methods match very well. Guo and Luo [22] further studied the complex periodic motions of a periodically forced Duffing oscillator and the bifurcation trees of periodic solutions were analytically predicted, and the harmonic–amplitude characteristics of periodic motions were also presented (also see, Guo and Luo [23]). Because the discrete mapping method (semi-analytical method) can be used to non-polynomial nonlinear dynamical systems, in 2017, Guo and Luo [24] used such a discrete mapping method to study the periodic motion to chaos in a periodically forced pendulum oscillator, and the bifurcation trees varying with the excitation amplitude were presented. Luo and Xing [25] applied the discrete mapping method to a time-delayed, quadratic nonlinear system. Luo and Xing [26] used the discrete mapping method to investigate complex periodic motions in a periodically forced, time-delayed hardening Duffing oscillator. Xing and Luo [27] also presented the possible infinite bifurcation trees of period-3 motion to chaos in a time-delayed, twin-well Duffing oscillator. In 2018, Xu and Luo [28] studied a two-degree-of-freedom van der Pol–Duffing oscillator with the discrete mapping method. The series of periodic motion to chaos was presented in such an oscillator. From the aforementioned study, a similar sequent order of periodic motions in the van der Pol oscillator should exist. In this paper, periodic motions in the van der Pol oscillator will be studied first.

In this paper, the semi-analytical solutions of periodic motions in the periodically forced van der Pol oscillator will be developed from the discrete mapping method. The stability and bifurcations of periodic motions will be discussed. The harmonic frequency–amplitude characteristics of periodic motions in the van der Pol oscillator will also be presented. Numerical simulations will be completed for comparison of numerical and analytical results.

2 A semi-analytical method

Consider a periodically forced, van der Pol oscillator as

$$ \ddot{x} - (\alpha_{1} - \alpha_{2} x^{2} )\dot{x} + \beta x = Q_{0} \cos\Omega t $$
(1)

where α1 and α2 are linear and nonlinear damping coefficients. β is the linear stiffness coefficient; Q0 and Ω are excitation amplitude and frequency, respectively. In state space, Eq. (1) becomes

$$ \begin{aligned} \dot{x} & = y, \\ \dot{y} & = (\alpha_{1} - \alpha_{2} x^{2} )\dot{x} - \beta x + Q_{0} \cos\Omega t. \\ \end{aligned} $$
(2)

For t ∊ [tk−1, tk], Eq. (2) can be discretized with a midpoint scheme and a mapping Pk (k = 1, 2, 3, …) (e.g., Luo [19, 20]) is defined as

$$ P_{k} :{\mathbf{x}}_{k - 1} \to {\mathbf{x}}_{k} \Rightarrow {\mathbf{x}}_{k} = P_{k} {\mathbf{x}}_{k - 1} $$
(3)

where \( {\mathbf{x}}_{k} = (x_{k} ,y_{k} )^{\text{T}} \) is the node of motion in the van der Pol oscillator. The algebraic equations of discrete implicit mapping for Pk (k = 1, 2, …, N) are

$$ \begin{aligned} x_{k} & = x_{k - 1} + \tfrac{1}{2}h(y_{k} + y_{k - 1} ), \\ y_{k} & = y_{k - 1} + h\left\{ {\tfrac{1}{8}\left[ {4\alpha_{1} - \alpha_{2} (x_{k} + x_{k - 1} )^{2} } \right](y_{k} + y_{k - 1} )} \right. \\ & \quad \left. { - \,\tfrac{1}{2}\beta (x_{k} + x_{k - 1} ) + Q_{0} \cos\Omega \left( {t_{k - 1} + \tfrac{1}{2}h} \right)} \right\} \\ \end{aligned} $$
(4)

where h = tk − tk−1 is the discrete time step, and t0 is the initial time.

For periodic motions, the mapping structure can be defined as P = PN ∘ PN−1 ∘ ⋯ ∘ P1, i.e.,

$$ \begin{aligned} & P_{1} :{\mathbf{x}}_{0} \to {\mathbf{x}}_{1} \Rightarrow {\mathbf{x}}_{1} = P_{1} {\mathbf{x}}_{0} , \\ & P_{2} :{\mathbf{x}}_{1} \to {\mathbf{x}}_{2} \Rightarrow {\mathbf{x}}_{2} = P_{2} {\mathbf{x}}_{1} = P_{2} \circ P_{1} {\mathbf{x}}_{0} , \\ & \vdots \\ & P_{k} :{\mathbf{x}}_{k - 1} \to {\mathbf{x}}_{k} \Rightarrow \\ &\quad {\mathbf{x}}_{k} = P_{k} {\mathbf{x}}_{k - 1} = P_{k} \circ P_{k - 1} \circ \cdots \circ P_{2} \circ P_{1} {\mathbf{x}}_{0} , \\ & \vdots \\ & P_{N} :{\mathbf{x}}_{N - 1} \to {\mathbf{x}}_{N} \Rightarrow \\ &\quad {\mathbf{x}}_{N} = P_{N} {\mathbf{x}}_{N - 1} = P_{N} \circ P_{N - 1} \circ \cdots \circ P_{k} \circ \cdots \circ P_{2} \circ P_{1} {\mathbf{x}}_{0} . \\ \end{aligned} $$
(5)

The associated algebraic equations for the mapping structure are:

$$ \begin{aligned} & \left. \begin{array}{l} x_{1} = x_{0} + \tfrac{1}{2}h(y_{1} + y_{0} ), \hfill \\ y_{1} = y_{0} + h\{ \tfrac{1}{8}[4\alpha_{1} - \alpha_{2} (x_{1} + x_{0} )^{2} ](y_{1} + y_{0} )\\ \quad\quad - \tfrac{1}{2}\beta (x_{1} + x_{0} ) + Q_{0} \cos \varOmega (t_{0} + \tfrac{1}{2}h)\} \hfill \\ \end{array} \right\}\quad {\text{ for }}\,\, P_{1} \\ & \left. \begin{array}{l} x_{2} = x_{1} + \tfrac{1}{2}h(y_{2} + y_{1} ), \hfill \\ y_{2} = y_{1} + h\{ \tfrac{1}{8}[4\alpha_{1} - \alpha_{2} (x_{2} + x_{1} )^{2} ](y_{2} + y_{1} ) \\ \quad\quad - \tfrac{1}{2}\beta (x_{2} + x_{1} ) + Q_{0} \cos \varOmega (t_{1} + \tfrac{1}{2}h)\} \hfill \\ \end{array} \right\}\quad {\text{for}}\,\, P_{2} \\ & \, \quad \vdots \\ & \left. \begin{array}{l} x_{k} = x_{k - 1} + \tfrac{1}{2}h(y_{k} + y_{k - 1} ) \\ y_{k} = y_{k - 1} + h\{ \tfrac{1}{8}[4\alpha_{1} - \alpha_{2} (x_{k} + x_{k - 1} )^{2} ] \\ \quad\quad \times(y_{k} + y_{k - 1} )- \tfrac{1}{2}\beta (x_{k} + x_{k - 1} ) \\ \quad\quad + \,Q_{0} \cos \varOmega (t_{k - 1} + \tfrac{1}{2}h)\} \\ \end{array} \right\}\quad {\text{for}}\,\, P_{k} \\ & \quad \vdots \\ & \\ & \left. \begin{array}{l} x_{N} = x_{N - 1} + \tfrac{1}{2}h(y_{N} + y_{N - 1} ) \\ y_{N} = y_{N - 1} + h\{ \tfrac{1}{8}[4\alpha_{1} - \alpha_{2} (x_{N} + x_{N - 1} )^{2} ]\\ \quad\quad \times(y_{N} + y_{N - 1} )- \tfrac{1}{2}\beta (x_{N} + x_{N - 1} ) \\ \quad \quad+ \,Q_{0} \cos \varOmega (t_{N - 1} + \tfrac{1}{2}h)\} \\ \end{array} \right\}\quad {\text{for}}\,\, P_{N} . \\ \end{aligned} $$
(6)

The periodicity condition is

$$ {\mathbf{x}}_{N} = {\mathbf{x}}_{0} \, \Rightarrow \, (x_{N} ,y_{N} )^{\text{T}} = (x_{0} ,y_{0} )^{\text{T}} . $$
(7)

There are all 2(N + 1) algebraic equations in Eqs. (6) and (7) for nodes \( {\mathbf{x}}_{k}^{ * } \) (k = 0, 1, …, N). Once the nodes are computed, the semi-analytical solutions of periodic motions are obtained. Further, the corresponding stability and bifurcations of periodic motions in the van der Pol dynamic system can be determined through eigenvalue analysis.

For the mapping structure in Eq. (5), consider a small disturbance \( \Delta {\mathbf{x}}_{k - 1} \) in the neighborhood of \( {\mathbf{x}}_{k - 1}^{ * } \)(i.e., \( {\mathbf{x}}_{k - 1} = {\mathbf{x}}_{k - 1}^{ * } +\Delta {\mathbf{x}}_{k - 1} \), k = 1, 2, …, N). With the variation of \( \Delta {\mathbf{x}}_{k} \), Eq. (6) can be linearized by

$$ \frac{{\partial {\mathbf{f}}_{k} }}{{\partial {\mathbf{x}}_{k - 1} }}|_{{({\mathbf{x}}_{k}^{ * } ,{\mathbf{x}}_{k - 1}^{ * } )}}\Delta {\mathbf{x}}_{k - 1} + \frac{{\partial {\mathbf{f}}_{k} }}{{\partial {\mathbf{x}}_{k} }}|_{{({\mathbf{x}}_{k}^{ * } ,{\mathbf{x}}_{k - 1}^{ * } )}}\Delta {\mathbf{x}}_{k} = {\mathbf{0}} $$
(8)

where \( {\mathbf{f}}_{k} = (f_{1,k} ,f_{2,k} )^{\text{T}} \) with

$$ \begin{aligned} f_{1,k} & = x_{k} - x_{k - 1} - \tfrac{1}{2}h(y_{k} + y_{k - 1} ), \\ f_{2,k} & = y_{k} - y_{k - 1} - h\left\{ {\tfrac{1}{8}[4\alpha_{1} - \alpha_{2} (x_{k} + x_{k - 1} )^{2} ](y_{k} + y_{k - 1} )} \right. \\ & \quad \left. { - \,\tfrac{1}{2}\beta (x_{k} + x_{k - 1} ) + Q_{0} \cos \varOmega (t_{k - 1} + \tfrac{1}{2}h)} \right\}. \\ \end{aligned} $$
(9)

Equation (8) gives

$$ \Delta {\mathbf{x}}_{k} = - \left[ {\frac{{\partial {\mathbf{f}}_{k} }}{{\partial {\mathbf{x}}_{k} }}} \right]^{ - 1} \left[ {\frac{{\partial {\mathbf{f}}_{k} }}{{\partial {\mathbf{x}}_{k - 1} }}} \right]_{{({\mathbf{x}}_{k}^{ * } ,{\mathbf{x}}_{k - 1}^{ * } )}}\Delta {\mathbf{x}}_{k - 1} = DP_{k}\Delta {\mathbf{x}}_{k - 1} $$
(10)

where

$$\begin{aligned} DP_{k} &= \left[ {\frac{{\partial {\mathbf{x}}_{k} }}{{\partial {\mathbf{x}}_{k - 1} }}} \right]_{{({\mathbf{x}}_{k}^{ * } ,{\mathbf{x}}_{k - 1}^{ * } )}} \\ &= \left[ {\begin{array}{*{20}c} {\frac{{\partial x_{k} }}{{\partial x_{k - 1} }}} & {\frac{{\partial x_{k} }}{{\partial y_{k - 1} }}} \\ {\frac{{\partial y_{k} }}{{\partial x_{k - 1} }}} & {\frac{{\partial y_{k} }}{{\partial y_{k - 1} }}} \\ \end{array} } \right]_{{({\mathbf{x}}_{k}^{ * } ,{\mathbf{x}}_{k-1}^{ * } )}} \,\,{\text{for}}\,\,k = 1, 2, \ldots , N \end{aligned}$$
(11)

and

$$ \frac{{\partial x_{k} }}{{\partial x_{k - 1} }} = \frac{{8 - h^{2} (\alpha_{2}\Delta _{1} - 2\beta + 4h\beta ) +\Delta _{2} }}{{8 + h^{2} \alpha_{2}\Delta _{1} + 2h^{2} \beta +\Delta _{2} }}, $$
$$ \frac{{\partial x_{k} }}{{\partial y_{k - 1} }} = \frac{{\left[ {(16 +\Delta _{2} ) - (2\beta -\Delta _{2} )h^{2} } \right]h}}{{2\left( {8 + h^{2} \alpha_{2}\Delta _{1} + 2h^{2} \beta +\Delta _{2} } \right)}}, $$
$$ \frac{{\partial y_{k} }}{{\partial x_{k - 1} }} = - \frac{{4h(\alpha_{2}\Delta _{1} + 2h\beta )}}{{8 + h^{2} \alpha_{2}\Delta _{1} + 2h^{2} \beta +\Delta _{2} }}, $$
$$ \frac{{\partial y_{k} }}{{\partial y_{k - 1} }} = \frac{{8 - h^{2} (\alpha_{2}\Delta _{1} + 4\beta -\Delta _{2} )}}{{8 + h^{2} \alpha_{2}\Delta _{1} + 2h^{2} \beta +\Delta _{2} }}, $$
$$ \Delta _{1} = (x_{k} + x_{k - 1} )(y_{k} + y_{k - 1} ), $$
$$ \Delta _{2} = -\,4\alpha_{1} + \alpha_{2} (x_{k} + x_{k - 1} )^{2} . $$
(12)

Finally, the perturbed variation of node \( \Delta {\mathbf{x}}_{N} \) is computed by

$$ \Delta {\mathbf{x}}_{N} = DP\Delta {\mathbf{x}}_{0} = \underbrace {{DP_{N} \cdot DP_{N - 1} \cdot \cdots \cdot DP_{2} \cdot DP_{1} }}_{{N\text{-multiplication}}}\Delta {\mathbf{x}}_{0} $$
(13)

The resulting Jacobian matrix of the period-1 motion is

$$ \begin{aligned} DP & = \left[ {\frac{{\partial {\mathbf{x}}_{N} }}{{\partial {\mathbf{x}}_{0} }}} \right]_{{({\mathbf{x}}_{N}^{ * } ,{\mathbf{x}}_{N - 1}^{ * } , \ldots ,{\mathbf{x}}_{0}^{ * } )}} \\ &= DP_{N} \cdot DP_{N - 1} \cdot \cdots \cdot DP_{2} \cdot DP_{1} \\ & = \prod\limits_{k = N}^{1} {\left[ {\frac{{\partial {\mathbf{x}}_{k} }}{{\partial {\mathbf{x}}_{k - 1} }}} \right]_{{({\mathbf{x}}_{k}^{ * } ,{\mathbf{x}}_{k - 1}^{ * } )}} } \\ \end{aligned} $$
(14)

The stability and bifurcation of period-1 motion can be determined by the eigenvalues of the Jacobian matrix DP as

$$ \left| {DP - \lambda {\mathbf{I}}_{2 \times 2} } \right| = 0 $$
(15)

From Luo [19, 20], the stability of period-1 motion can be determined as follows.

  1. i.

    If the magnitudes of all eigenvalues of DP are within the unit cycle (i.e., |λi| < 1, i = {1, 2}), the periodic solution will be stable.

  2. ii.

    If at least one magnitude of the eigenvalues is out of the unit cycle (i.e., |λi| > 1, i ∊ {1, 2}), the periodic solution will be unstable.

  3. iii.

    The boundaries between stable and unstable periodic solutions whose eigenvalues have the magnitudes on the unit cycle will generate bifurcation and stability conditions with higher order singularity.

The bifurcation conditions are as follows.

  1. iv.

    If λi = 1 with |λj| < 1 (i, j ∊ {1, 2}, i ≠ j), the saddle-node bifurcation (SN) occurs.

  2. v.

    If λi = − 1 with |λj| < 1 (i, j ∊ {1, 2}, i ≠ j), the period-doubling bifurcation (PD) occurs.

  3. vi.

    If |λi,j| = 1 (i, j ∊ {1, 2}, \( \lambda_{i} = \bar{\lambda }_{j} \)), the Neimark bifurcation (NB) occurs.

For the semi-analytical solutions of period-m motions in the van der Pol oscillator, the mapping in Eq. (3) becomes

$$ \begin{aligned}& P_{k}^{(m)} :{\mathbf{x}}_{k - 1}^{(m)} \to {\mathbf{x}}_{k}^{(m)} \; \Rightarrow {\mathbf{x}}_{k}^{(m)} = P_{k}^{(m)} {\mathbf{x}}_{k-1}^{(m)} ,\\ &\quad (k = 1,2, \ldots ,mN). \end{aligned}$$
(16)

where \( {\mathbf{x}}_{k}^{(m)} = (x_{k}^{(m)} ,y_{k}^{(m)} )^{\text{T}} ,\;(k = 1,2, \ldots ,mN) \). Similarly, the mapping structures of period-m motions of the van der Pol oscillator can be obtained as:

$$ P^{(m)} :{\mathbf{x}}_{0}^{(m)} \to {\mathbf{x}}_{mN}^{(m)} \Rightarrow {\mathbf{x}}_{mN}^{(m)} = P^{(m)} {\mathbf{x}}_{0}^{(m)} $$
(17)

where P(m) = P(m)mN ∘ P(m)mN-1 ∘ ··· ∘ P(m)2 ∘ P(m)1(m = 1, 2, …). The corresponding algebraic equations for P(m)k (k = 1, 2, …, mN) are

$$ \begin{aligned} x_{k}^{(m)} & = x_{k - 1}^{(m)} + \tfrac{1}{2}h\left( {y_{k}^{(m)} + y_{k - 1}^{(m)} } \right), \\ y_{k}^{(m)} & = y_{k - 1}^{(m)} + h\left\{ \tfrac{1}{2}\left( {y_{1,k}^{(m)} + y_{1,k - 1}^{(m)} } \right) \right. \\ &\quad \times\left[ {\alpha_{11} - \tfrac{1}{4}\alpha_{12} \left( {x_{1,k}^{(m)} + x_{1,k - 1}^{(m)} } \right)^{2} } \right] \\ & \quad \left. { - \tfrac{1}{2}\beta_{11} \left( {x_{1,k}^{(m)} + x_{1,k - 1}^{(m)} } \right) + Q_{0} \cos \Omega \left( {t_{k - 1} + \tfrac{1}{2}h} \right)} \right\} .\\ \end{aligned} $$
(18)

The periodicity condition is

$$ x_{mN}^{(m)} = x_{0}^{(m)} ,\quad y_{mN}^{(m)} = y_{0}^{(m)} . $$
(19)

Based on Eqs. (18) and (19), the periodic solutions of a period-m motion in the van der Pol oscillator can be obtained by solving 2(mN + 1) equations. Thus, the nodes \( {\mathbf{x}}_{k}^{(m) * } \) (k = 0, 1, 2, …, mN) give the semi-analytical solution of the period-m motion. For the stability and bifurcations of the period-m motions, in the neighborhood of \( {\mathbf{x}}_{k}^{(m) * } \), \( {\mathbf{x}}_{k}^{(m)} = {\mathbf{x}}_{k}^{(m) * } + \Delta {\mathbf{x}}_{k}^{(m)} \) (k = 0, 1, 2, …, mN), the variation of \( {\mathbf{x}}_{mN}^{(m) * } \) can be determined by the linearized equation of the period-m motion as

$$ \begin{aligned}\Delta {\mathbf{x}}_{mN}^{(m)} &= DP^{(m)}\Delta {\mathbf{x}}_{0}^{(m)} \\ &= \underbrace {{DP_{mN}^{(m)} \cdot DP_{mN - 1}^{(m)} \cdot \cdots \cdot DP_{2}^{(m)} \cdot DP_{1}^{(m)} }}_{{mN\text{-multiplication}}}\Delta {\mathbf{x}}_{0}^{(m)} \end{aligned}$$
(20)

where \( \Delta {\mathbf{x}}_{k}^{(m)} = DP_{k}^{(m)}\Delta {\mathbf{x}}_{k - 1}^{(m)} \),

$$ DP_{k}^{(m)} = \left[ {\frac{{\partial {\mathbf{x}}_{k}^{(m)} }}{{\partial {\mathbf{x}}_{k - 1}^{(m)} }}} \right]_{{\left({\mathbf{x}}_{k}^{(m) * } ,{\mathbf{x}}_{k - 1}^{(m) * } \right)}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial x_{k}^{(m)} }}{{\partial x_{k - 1}^{(m)} }}} & {\frac{{\partial x_{k}^{(m)} }}{{\partial y_{k - 1}^{(m)} }}} \\ {\frac{{\partial y_{k}^{(m)} }}{{\partial x_{k - 1}^{(m)} }}} & {\frac{{\partial y_{k}^{(m)} }}{{\partial y_{k - 1}^{(m)} }}} \\ \end{array} } \right]_{{({\mathbf{x}}_{k}^{(m) * } ,{\mathbf{x}}_{k - 1}^{(m) * } )}} $$
(21)

for k = 1, 2, …, mN. The components of the Jacobian matrix DP(m)k in Eq. (21) are the same as in Eq. (11), which can be determined by Eq. (12). The stability and bifurcation of period-m motion are determined by the eigenvalues, i.e.,

$$ \left| {DP^{(m)} - \lambda {\mathbf{I}}_{2 \times 2} } \right| = 0 $$
(22)

where

$$ \begin{aligned} DP^{(m)} & = \left[ {\frac{{\partial {\mathbf{x}}_{mN}^{(m)} }}{{\partial {\mathbf{x}}_{0}^{(m)} }}} \right]_{{({\mathbf{x}}_{mN}^{(m) * } ,{\mathbf{x}}_{mN - 1}^{(m) * } , \ldots ,{\mathbf{x}}_{0}^{(m) * } )}} \\ & = DP_{mN}^{(m)} \cdot DP_{mN - 1}^{(m)} \cdot \cdots \cdot DP_{2}^{(m)} \cdot DP_{1}^{(m)} \\ & = \prod\limits_{k = mN}^{1} {\left[ {\frac{{\partial {\mathbf{x}}_{k}^{(m)} }}{{\partial {\mathbf{x}}_{k - 1}^{(m)} }}} \right]_{{({\mathbf{x}}_{k}^{(m) * } ,{\mathbf{x}}_{k - 1}^{(m) * } )}} } \\ \end{aligned} $$
(23)

The stability and bifurcation conditions for period-m motions are the same as for the period-1 motion.

3 Periodic motions

To keep periodic solutions with the accuracy of 10−11, the time step h = Δt < 10−3 and the number of periodic nodes should be 1000 or bigger per period. To avoid collecting all node nodes, a set of Poincare mapping section is introduced for a better illustration of the nonlinear properties of the van der Pol oscillator. For period-m motions, the node points relative to the initial point and starting points of each period are collected in the Poincare mapping section (m = 1, 2, 3, …). That is,

$$ \sum\limits_{m} { = \left\{ {\left( {x_{k}^{(m)} ,y_{k}^{(m)} } \right)\left| \begin{array}{l} t_{k} = t_{0} + {{kT} \mathord{\left/ {\vphantom {{kT} {N,t_{0} = 0,T = {{2\pi } \mathord{\left/ {\vphantom {{2\pi }\Omega }} \right. }\Omega }}}} \right. } {N,t_{0} = 0,T = {{2\pi } \mathord{\left/ {\vphantom {{2\pi }\Omega }} \right. }\Omega }}} \hfill \\ k = 0,1,2, \ldots mN,\bmod (k,N) = 0 \hfill \\ m = 1,2, \ldots \hfill \\ \end{array} \right.} \right\}} . $$
(24)

For periodic motions, consider a set of parameters as

$$ \alpha_{1} = 16,\quad \alpha_{2} = 1,\quad \beta = 5,\quad Q_{0} = 100. $$
(25)

3.1 Semi-analytical solutions

In this section, the semi-analytical solutions of symmetric period-m motions in the van der Pol oscillator are presented through node (x(m)k, y(m)k) with \( \bmod (k,N) = 0 \). In all the plots, the solid and dashed curves represent the stable and unstable solutions of periodic motions, respectively. The acronym “SN” is used for the saddle-node bifurcation.

In Fig. 1, the sequent, independent, symmetric periodic motions are presented for Ω ∊ (0, 21). Eleven independent periodic motions of symmetric period-1 to period-21 motion are presented in this frequency range. In Fig. 1(i) and (ii), a global view of displacement x(m)k and velocity y(m)k (\( \bmod (k,N) = 0 \)) of symmetric periodic solutions is presented. From the global view, the evolution process of the periodic motion series to chaos can be concluded as follows

$$ 1\left( S \right) \triangleleft 3\left( S \right) \triangleleft 5\left( S \right) \triangleleft \cdots \triangleleft \left( {2l - 1} \right)\left( S \right) \triangleleft \cdots (l = 1, 2, \ldots ) $$
(26)
Fig. 1
figure 1

Period-m motions varying with excitation frequency. Global view (Ω ∊ (0, 21)): i displacement x(m)k, ii velocity y(m)k. The first zoomed view (Ω ∊ (2.0, 13.1)): iii displacement x(m)k, iv zoomed view of velocity y(m)k. Second zoomed view (Ω ∊ (13.2, 21.2)): v displacement x(m)k, vi velocity y(m)k. α1 = 16, α2 = 1, β = 5, Q0 = 100. (\( \bmod (k,N) = 0, \)k = 0, 1, …, mN − 1, m = 1, 3, …, 21)

Full size image

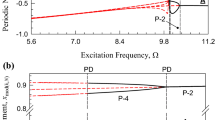
From the periodic motion sequence in Eq. (26), the symmetric period-1 motion appears first, which is represented by 1(S). The stable and unstable period-1 motions exist in Ω ∊ (0, + ∞). When the stable period-1 motion vanishes, with jumping or chaotic states, the symmetric period-3 motion exists (i.e., 3(S)). The symmetric period-3 motion only occurs in an independent, bounded frequency range. Three stable solutions are obtained. With another two stable branches adding, it turns to a symmetric period-5 motion (i.e., 5(S)). After symmetric period-5 motion, with two new branches of stable solutions adding, the symmetric period-5 motion becomes a symmetric period-7 motion. Such symmetric periodic motion evolution will continue to a symmetric period-(2l − 1) motion toward chaos when l → + ∞. The bifurcation points and frequency range of the symmetric period-(2l − 1) (i.e., (2l − 1)(S)) motions are shown in Table 1. As the symmetric periodic motion switches to another adjacent symmetric periodic motion, only saddle-node bifurcations exist. The jumping or chaotic transient motion exists between the two adjacent symmetric periodic motions. For the period-1 motion, the saddle-node bifurcation occurs at Ωcr ≈ 2.645. The period-1 motion is stable in Ω ∊ (0, 2.645) and unstable in Ω ∊ (2.645, + ∞). The symmetric period-3 motion exists within Ω ∊ (2.449, 4.462). Thus, from the period-1 to period-3 motion, the jumping phenomenon is observed. The symmetric period-5 motion exists in Ω ∊ (4.441, 6.205). The frequency ranges for the two periodic motions are overlapped. Thus, the jumping phenomenon will be observed. The symmetric period-7 motion is in Ω ∊ (6.333, 7.902). The frequency ranges between period-5 and period-7 motions are not overlapped. Thus, the switching between the period-5 and period-7 motions are chaotic in frequency range of Ω ∊ (6.205, 6.333). The symmetric period-9 to period-21 motions exist in the frequency range of Ω ∊ (8.248, 9.574), (10.229, 11.239), (12.219, 12.920), (14.190, 14.637), (16.136, 16.405), (18.063, 18.220), and (19.977, 20.069), respectively. The frequency ranges of the adjacent periodic motions are not overlapped. Thus the frequency gap exists for the two adjacent periodic motions in the motion sequence. The switching between the two adjacent periodic motions are chaotic. The saddle nodes occur on the boundaries of the frequency range of a symmetric periodic motion. In Fig. 1(iii) and (iv), the first zoomed window for the displacement x(m)k and velocity y(m)k is presented for a better view of periodic motions in such a sequence. The period-3 to period-13 motions are presented, and the branches of displacement and velocity are clearly presented for the slow varying portions in the periodic motion in the van der Pol oscillator. In Fig. 1(v) and (vi), the second zoomed window for period-15 to period-21 motions is presented. The period-15 and period-21 can be clearly observed.

Table 1 Saddle-node bifurcation points with jumping phenomenon of period-m motions (α1 = 16, α2 = 1, β = 5, Q0 = 100, Ω ∊ (0, 21), m = 1, 3, …, 21)
Full size table

3.2 Frequency-Amplitude analysis of periodic motions

Since the discrete node vectors \( {\mathbf{x}}^{(m)} {\mathbf{ = }}(x_{j}^{(m)} ,y_{j}^{(m)} ) \) (j = 1, 2, …, mN) of period-m motions are obtained, the period-m motions can be approximately expressed by the finite Fourier series as,

$$ {\mathbf{x}}^{(m)} (t) \approx {\mathbf{a}}_{0}^{(m)} + \sum\limits_{k = 1}^{M} {\left[ {{\mathbf{b}}_{{{k \mathord{\left/ {\vphantom {k m}} \right. } m}}} \cos \left( {\frac{k}{m}\Omega t} \right) + {\mathbf{c}}_{{{k \mathord{\left/ {\vphantom {k m}} \right. } m}}} \sin \left( {\frac{k}{m}\Omega t} \right)} \right]} . $$
(27)

In Eq. (27), there are 2(2 M + 1) unknown coefficients of \( {\mathbf{a}}_{0}^{(m)} ,{\mathbf{b}}_{{{k \mathord{\left/ {\vphantom {k m}} \right. } m}}} \) and \( {\mathbf{c}}_{{{k \mathord{\left/ {\vphantom {k m}} \right. } m}}} \). They can be determined from the analytically predicted node vectors \( {\mathbf{x}}_{j}^{(m)} \)(j = 1, 2, …, mN) with 2(mN + 1) ≥ 2(2 M + 1). Setting M = mN/2, the node vectors \( {\mathbf{x}}^{(m)} \) for the period-m motion are expressed with t ∊ [0, mT] as

$$ \begin{aligned} {\mathbf{x}}^{(m)} (t_{j} ) = {\mathbf{x}}_{j}^{(m)} & \approx {\mathbf{a}}_{0}^{(m)} + \sum\limits_{k = 1}^{{{{mN} \mathord{\left/ {\vphantom {{mN} 2}} \right. } 2}}} {\mathbf{b}}_{{{k \mathord{\left/ {\vphantom {k m}} \right. } m}}} \cos \left( {\frac{k}{m}\varOmega t_{j} } \right) \\ & \quad + {\mathbf{c}}_{k/m} \sin \left( {\frac{k}{m}\varOmega t_{j} } \right) \\ & \approx {\mathbf{a}}_{0}^{(m)} + \sum\limits_{k = 1}^{{{{mN} \mathord{\left/ {\vphantom {{mN} 2}} \right. } 2}}} {\mathbf{b}}_{{{k \mathord{\left/ {\vphantom {k m}} \right. } m}}} \cos \left( {\frac{k}{m}\frac{2\pi j}{N}} \right)\\ &\quad + {\mathbf{c}}_{{{k \mathord{\left/ {\vphantom {k m}} \right. } m}}} \sin \left( {\frac{k}{m}\frac{2\pi j}{N}} \right) \\ \end{aligned} $$
(28)

where Δt = T/N = 2π/(ΩN), tj = t0 + jΔt = 2πj/(ΩN) for (t0 = 0, j = 0, 1, …, mN). The coefficients of \( {\mathbf{a}}_{0}^{(m)} ,{\mathbf{b}}_{{{k \mathord{\left/ {\vphantom {k m}} \right. } m}}} \) and \( {\mathbf{c}}_{{{k \mathord{\left/ {\vphantom {k m}} \right. } m}}} \) can be achieved by the following formulas.

$$ \begin{aligned} {\mathbf{a}}_{0}^{(m)} & = \frac{1}{mN}\sum\limits_{j = 0}^{mN - 1} {{\mathbf{x}}_{j}^{(m)} } \\ {\mathbf{b}}_{{{k \mathord{\left/ {\vphantom {k m}} \right. } m}}} & = \frac{2}{mN}\sum\limits_{j = 0}^{mN - 1} {{\mathbf{x}}_{j}^{(m)} \cos \left( {\frac{k}{m}\frac{2\pi j}{N}} \right),} \\ {\mathbf{c}}_{{{k \mathord{\left/ {\vphantom {k m}} \right. } m}}} & = \frac{2}{mN}\sum\limits_{j = 0}^{mN - 1} {{\mathbf{x}}_{j}^{(m)} \sin \left( {\frac{k}{m}\frac{2\pi j}{N}} \right)} ,\\ &\quad (k = 1,2, \ldots ,{{mN} \mathord{\left/ {\vphantom {{mN} 2}} \right. } 2}) \\ \end{aligned} $$
(29)

where

$$ \begin{aligned} {\mathbf{a}}_{0}^{(m)} & = \left( {a_{1,0}^{(m)} ,a_{2,0}^{(m)} } \right)^{\text{T}} , \\ {\mathbf{b}}_{{{k \mathord{\left/ {\vphantom {k m}} \right. } m}}} & = \left( {b_{1,k/m} ,b_{2,k/m} } \right)^{\text{T}} , \\ {\mathbf{c}}_{k/m} & = \left( {c_{1,k/m} ,c_{2,k/m} } \right)^{\text{T}} . \\ \end{aligned} $$
(30)

The harmonic amplitudes and phases for a period-m motion in the van der Pol oscillator can be expressed as

$$ \begin{aligned} A_{1,k/m} & = \sqrt {(b_{1,k/m} )^{2} + (c_{1,k/m} )^{2} } ,\quad \varphi_{1,k/m} = \arctan \frac{{c_{1,k/m} }}{{b_{1,k/m} }}, \\ A_{2,k/m} & = \sqrt {(b_{2,k/m} )^{2} + (c_{2,k/m} )^{2} } ,\quad \varphi_{2,k/m} = \arctan \frac{{c_{2,k/m} }}{{b_{2,k/m} }}. \\ \end{aligned} $$
(31)

The periodic solutions of the period-m motion for the van der Pol oscillator in Eq. (27) can be rewritten as for j = 0, 1, …, mN

$$ \left\{ {\begin{array}{*{20}c} {x^{(m)} } \\ {y^{(m)} } \\ \end{array} } \right\} \approx \left\{ {\begin{array}{*{20}c} {a_{1,0}^{(m)} } \\ {a_{2,0}^{(m)} } \\ \end{array} } \right\} + \sum\limits_{k = 1}^{{{{mN} \mathord{\left/ {\vphantom {{mN} 2}} \right. } 2}}} {\left\{ {\begin{array}{*{20}c} {A_{1,k/m} \cos \left( {\frac{k}{m}\Omega t - \varphi_{1,k/m} } \right)} \\ {A_{2,k/m} \cos \left( {\frac{k}{m}\Omega t - \varphi_{2,k/m} } \right)} \\ \end{array} } \right\}} . $$
(32)

To avoid too much illustrations, only frequency-amplitude curves of displacement x(m)j for period-m motions will be presented. The displacements for the period-m motion are:

$$ x^{(m)} (t) \approx a_{0}^{(m)} + \sum\limits_{k = 1}^{{{{mN} \mathord{\left/ {\vphantom {{mN} 2}} \right. } 2}}} {b_{k/m} \cos \left( {\frac{k}{m}\Omega t} \right) + c_{k/m} \sin \left( {\frac{k}{m}\Omega t} \right)} $$
(33)

Thus,

$$ x^{(m)} (t) \approx a_{0}^{(m)} + \sum\limits_{k = 1}^{{{{mN} \mathord{\left/ {\vphantom {{mN} 2}} \right. } 2}}} {A_{k/m} \cos \left( {\frac{k}{m}\Omega t - \varphi_{k/m} } \right)} $$
(34)

where j = 0, 1, …, mN and

$$ A_{k/m} = \sqrt {(b_{k/m} )^{2} + (c_{k/m} )^{2} } ,\quad \varphi_{k/m} = \arctan \frac{{c_{k/m} }}{{b_{k/m} }}. $$
(35)

Based on the Fourier series expression of the periodic motions, the frequency–amplitude characteristics of period-m motion can be obtained. In all following plots, acronym “SN” means the saddle node. The stable and unstable solutions of period-m motions are respectively represented by the solid and dashed curves.

In Fig. 2, shown are the global views of the harmonic amplitudes of the symmetric period-m (m = 1, 3, …, 21) motions in the van der Pol oscillator with Ω ∊ (0, 21). For symmetric period-m motions, a(m)0 = 0 and A2l/m = 0 while A(2l-1)/m ≠ 0 (l = 1, 2, …). The harmonic amplitude Am/m = A1 versus with excitation frequency is presented in Fig. 2(i). The period-1 motion exist in all frequency range, but the period-m solutions (P-3, P-5, …, P-21) occur in a finite frequency range. All periodic motions consist of stable and unstable solutions, and the switching between the stable and unstable solutions is at saddle-node bifurcations. The quantity level of A1 is in Am/m ∊ (0.1, 10.0). The harmonic amplitude A3m/m = A3 varying with excitation frequency is shown in Fig. 2(ii). The saddle-node bifurcations are for the stability switching of periodic motion. The quantity level for harmonic amplitudes A3m/m = A3 are different from different period-m motions (m = 3, …, 21). A3 for period-1 motion has a quantity level of 10−6–101, but the quantity level of A3 = A3m/m (m = 3, …, 21) is 10−2–100. The harmonic amplitude A5m/m = A5 varying with excitation frequency is presented in Fig. 2(iii). The saddle-node bifurcations and stable and unstable branches of periodic solutions can be clearly illustrated. The quantity level for harmonic amplitude A5 is of 10−9–100, but the quantity level of A5m/m (m = 3, …, 21) is of 10−4–10−1. The harmonic amplitudes A7m/m, A9m/m and A11m/m are presented in Fig. 2(iv)–(vi), respectively. The quantity level of A7, A9 and A11 for period-1 motion is of 10−11–100. The quantity levels for A7m/m, A9m/m and A11m/m for period-m motion (m = 3, 5, …, 21) are of 10−5–10−1, 10−6–10−1 and 10−7–10−1, respectively. From the global view of harmonic amplitudes, the quantity level is high for the low frequency. With frequency increase, the quantity level of harmonic amplitudes drops.

Fig. 2
figure 2

A global view of the frequency–amplitude characteristics of period-m motion: i–viAk/m (k = 1, 3, …, 11). α1 = 16, α2 = 1, β = 5, Q0 = 100, (m = 1, 3, 5, …, 21)

Full size image

In Fig. 3, the harmonic amplitudes of the symmetric period-3 motion in the van der Pol oscillator are plotted for Ω ∊ (2.05, 4.75) as an example. For the symmetric period-3 motion, a(3)0 = 0 and A2j/3 = 0 but A(2j−1)/3 ≠ 0 (j = 1, 2, …). In Fig. 3(i), the harmonic amplitude A1/3 versus excitation frequency is presented. The saddle-node bifurcations and a closed loop formed by stable and unstable branch can be observed clearly. In Fig. 3(ii), the harmonic amplitude A3/3 = A1 is presented, which is a zoomed view of A1 for period-3 motion. Harmonic amplitude A3/3 has the quantity level of 100. In Fig. 3(iii), the harmonic amplitude A5/3 varying with excitation frequency is presented, and the quantity level of A5/3 is still 100. The harmonic amplitudes A7/3, A9/3 and A189/3 of the period-3 motion are presented in Fig. 3(iv)–(vi). The quantity levels of A7/3 and A9/3 are almost the same as 100. However, the quantity level of A189/3 is of 10−11–10−5. The harmonic amplitudes decay with increasing harmonic order. For a high accuracy of 10−11, at least harmonic 189 terms are required for the symmetric period-3 motion. The other period-m motion can be presented similarly.

Fig. 3
figure 3

Frequency–amplitude characteristics of period-3 motion: iA1/3, iiA3/3, iiiA5/3, ivA7/3, vA9/3, viA189/3. α1 = 16, α2 = 1, β = 5, Q0 = 100

Full size image

4 Numerical simulations

For verifying the semi-analytical solutions of periodic motions, numerical simulations of the periodic motions are completed by the midpoint integration method. The initial conditions for numerical solutions are obtained from the semi-analytical solutions. The time-responses of displacement and velocity, trajectories and harmonic amplitudes of the period-7 motion will be presented first, and the trajectories of other period-m motions will be presented. In all the following plots, circular symbols and solid curves represented analytical and numerical solutions, respectively. The acronym “I.C.” means the initial condition, which is denoted as a circular symbol. The shaded areas are for slowly varying segment of periodic motions.

In Fig. 4, the time-responses of displacement and velocity, trajectory and harmonic amplitude spectrum of the period-7 motion are presented with Ω = 7. The parameters are the same with Eq. (25). The corresponding initial conditions are \( x_{0} \approx -\,5. 0 5 8 8 7 , { }\dot{x}_{0} \approx 8. 2 2 3 8 9 \) from the semi-analytical prediction. In Fig. 4(i), the displacement response has two-segments for slowly varying zones and two fast varying spikes. In Fig. 4(ii), the velocity response has a slowly varying zone and two fast varying spikes. For each slowly varying segment zone, there are three waves (i.e., 3-W). The fast varying spike forms a wave to form 7-periods. The circular symbols are very dense for slowly varying segments, but very sparse for the fast varying spike. In Fig. 4(iii), the phase trajectory (x, y) of a stable period-7 motion in the van der Pol oscillator is presented. There are six slowly varying waves plus two-half, fast varying spikes.For harmonic amplitudes, a(7)0 = 0, A2l/7 = 0 and A(2l−1)/7 ≠ 0 (l = 1, 2, …). The main harmonic amplitudes are \( A_{1/7} \approx 8. 5 1 0 4 , \)\( A_{3/7} \approx 2. 6 1 9 1 , \)\( A_{5/7} \approx 1. 6 6 5 5 , \)\( A_{7/7} \approx 1. 2 4 6 9 , \)\( A_{9/7} \approx 0. 6 4 9 1 , \)\( A_{11/7} \approx 0. 5 0 2 7 , \)\( A_{13/7} \approx 0. 4 4 5 5 , \)\( A_{15/7} \approx 0. 3 4 5 1 , \)\( A_{17/7} \approx 0. 2 7 0 5 , \)\( A_{19/7} \approx 0. 2 2 1 2 , \)\( A_{21/7} \approx 0. 1 9 0 8 , \)\( A_{23/7} \approx 0. 1 6 1 5 , \)\( A_{25/7} \approx 0. 1 3 5 5 , \) and \( A_{27/7} \approx 0. 1 1 4 6. \)Ak/7 ∊ (10−14, 10−2) for k = 29, 31, …, 461 and \( A_{461/7} \approx 5. 1 6 2 0\times 1 0^{ - 13} \).

Fig. 4
figure 4

Period-7 motion in the van der Pol oscillator (Ω = 7): i displacement, ii velocity, iii trajectory, iv harmonic amplitudes. (I.e. \( x_{0} \approx -\,5. 0 5 8 8 7 , { }\dot{x}_{0} \approx 8. 2 2 3 8 9 \)) (α1 = 16, α2 = 1, β = 5, Q0 = 100). SV-slow varying, FV-fast varying. 3-W is three waves

Full size image

In Fig. 5, the phase trajectories of period-m motions (m = 1, 3, 5, 9, 11, …, 21) are presented. The trajectory of period-7 motion will not be presented because it was presented in Fig. 4(iii). All input data are presented in Table 2. The slowly-varying waves and fast varying spikes are listed. The numerical results match very well with the semi-analytical results. The slowly-varying zones are shaded. The initial conditions selected are \( {\mathbf{x}}_{0} \approx ( -\,3. 5 6 3 7, 1 9. 0 6 0 6 ) \) for period-1 motion. The corresponding trajectory is symmetric to (x, y) = (0, 0). The harmonic amplitudes are \( A_{1} \approx 1 0. 8 7 2 4 , \)\( A_{3} \approx 2. 8 1 8 6 , \)\( A_{5} \approx 1. 5 3 9 2 , \)\( A_{7} \approx 1. 0 1 8 6 , \) which can continue to \( A_{499} \approx 2. 7 2\times 1 0^{ - 13} . \) The period-1 motion needs 250 odd harmonic terms to be approximated with the accuracy of 10−13. In Fig. 5(ii), the phase trajectory of stable period-3 motion is presented with the initial condition of \( {\mathbf{x}}_{0} \approx ( -\,4. 9 3 6 8, 9. 3 6 7 9 ) \). There are two slowly varying waves. The harmonic amplitudes are \( A_{1/3} \approx 8. 5 0 3 5 , \)\( A_{3/3} \approx 3. 7 0 3 1 , \)\( A_{5/3} \approx 1. 3 9 4 6 , \)\( A_{7/3} \approx 1. 0 6 8 4 , \) up to \( A_{499/3} \approx 2. 1 3\times 1 0^{ - 13} . \) The period-3 motion needs 250 harmonic terms of A(2l−1)/3 to model such a period-3 motions. A trajectory of the stable period-5 motion is presented in Fig. 5(iii) with the initial condition of \( {\mathbf{x}}_{0} \approx ( -\,5. 0 3 9 2, 8. 6 7 9 0 ) \). There are 4 slowly varying waves in the slowly varying zone with two fast varying spikes. The harmonic amplitudes for the period-5 motion are \( A_{1/5} \approx 8. 4 9 4 3 , \)\( A_{3/5} \approx 2. 7 5 2 3 , \)\( A_{5/5} \approx 2. 0 6 4 2 , \)\( A_{7/5} \approx 0. 9 2 1 3 \) up to \( A_{499/5} \approx 6. 3 7\times 1 0^{ - 14} . \) The period-5 motion needs 250 harmonic terms to be approximated with the accuracy of 10−14. In Fig. 5(iv), the trajectory of period-9 motion is illustrated with the initial condition of \( {\mathbf{x}}_{0} \approx ( -\,5. 0 4 9 0, 7. 6 5 4 2 ) \). The eight slowing varying waves in the slowing varying zone are observed. The corresponding harmonic amplitudes are \( A_{1/9} \approx 8. 5 2 0 7 , \)\( A_{3/9} \approx 2. 5 8 2 6 , \)\( A_{5/9} \approx 1. 5 3 9 9 , \)\( A_{7/9} \approx 1. 1 4 4 5 , \)\( A_{9/9} \approx 0. 6 9 7 4 , \) up to \( A_{413/9} \approx 2. 0 9 6\times 1 0^{ - 12} . \) This period-9 motion needs 207 harmonic terms with accuracy of 10−12. The trajectory of a period-11 motion is presented in Fig. 5(v) with the initial condition of \( {\mathbf{x}}_{0} \approx ( -\,5. 0 3 6 3, 6. 9 1 3 2 ) \). The ten slowly varying waves in the slowing varying zone are observed in the trajectory. The harmonic amplitudes for such a period-11 motion are \( A_{1/11} \approx 8. 5 2 4 6 , \)\( A_{3/11} \approx 2. 5 6 3 2 , \)\( A_{5/11} \approx 1. 4 7 9 0 , \)\( A_{7/11} \approx 1. 0 3 4 7 , \) up to \( A_{405/11} \approx 7. 9 3 8\times 1 0^{ - 13} \). This period-11 motion needs 203 harmonic terms to keep the accuracy of 10−13. The trajectories of period-m motions (m = 13, 15, …, 21) are presented from Fig. 5(vi)–(x), respectively. The initial conditions are \( {\mathbf{x}}_{0} \approx ( -\,5. 0 2 9 0, 6. 2 1 1 2 ) \) for a period-13 motion, \( {\mathbf{x}}_{0} \approx ( -\,4. 7 8 2 6, 5. 7 6 5 0 ) \) for a period-15 motion, \( {\mathbf{x}}_{0} \approx ( -\,5. 5 3 5 2, 4. 8 5 9 6 ) \) for a period-17 motion, \( {\mathbf{x}}_{0} \approx ( -\,7. 4 9 1 3, 2. 9 7 0 1 ) \) for a period-19 motion and \( {\mathbf{x}}_{0} \approx ( -\,7. 2 8 2 4, 3. 0 4 3 7 ) \) for a period-21 motion. The (m − 1) slowly varying waves exist in the slowly varying zone. The harmonic amplitudes for period-m motions are Ak/m > 1 for k = 1, 3, …, 7 and \( A_{403/13} \approx 1. 5 1 2\times 1 0^{ - 12} \), \( A_{375/15} \approx 8. 2 4 9\times 1 0^{ - 12} , \)\( A_{339/17} \approx 1. 6 1\times 1 0^{ - 10} , \)\( A_{379/19} \approx 2. 2 2 4\times 1 0^{ - 11} , \)\( A_{377/21} \approx 3. 9 0\times 1 0^{ - 11} . \) The two fast varying spikes are observed.

Fig. 5
figure 5

Phase trajectories of period-m motions in the van der Pol oscillator (m = 1, 3, 5; 9, 11, …, 21). i P-1 motion (Ω = 1), ii P-3 motion (Ω = 3), iii P-5 motion (Ω = 5), iv P-9 motion (Ω = 9), v P-11 motion (Ω = 11), vi P-13 motion (Ω = 13), vii P-15 motion (Ω = 14.64), viii P-17 motion (Ω = 16.4), ix P-19 motion (Ω = 18.22), x P-21 motion (Ω = 20.07). α1 = 16, α2 = 1, β = 5, Q0 = 100

Full size image
Table 2 Input data for numerical simulations (α1 = 16, α2 = 1, β = 5, Q0 = 100)
Full size table

5 Conclusions

In this paper, the stable and unstable solutions of period-m motions in the periodically forced van der Pol oscillator were obtained. The sequence of symmetric period-1 to period-m motion is \( 1(S) \triangleleft 3(S) \triangleleft 5(S) \triangleleft \cdots \triangleleft ( 2l - 1)(S) \triangleleft \cdots \) (l → ∞). The chaotic motions or catastrophes between two adjacent periodic motions exist. The stability and bifurcations of period-m motions were determined through eigenvalue analysis. The frequency–amplitude characteristics of period-m motions are presented. Numerical simulations of period-m motions were carried out for illustration of the slowing varying waves and fast varying spikes in the van der Pol oscillator. The slowly and fast varying responses in the periodic motions of the van der Pol oscillator can be accurately determined.