1 Introduction

Tower cranes are used in the construction industry, due to their ability to easily hoist and transport massive loads to desired locations. Under normal practical conditions, the tower crane system operation results in significant dynamical stability control problems since its inherent nature of pendulum characteristics, i.e., the swaying effect [1], implying serious operational performance concerns, including fatal accidents and economical losses. The United States Department of Labor for Occupational Safety & Health Administration (OSHA) data indicates that an average of 71 crane related fatalities occur each year, with the significant risk of crane operator exposure to fatalities [2]. Over the years, crane manufacturers and engineers have attempted to reduce the number of motor-crane related fatalities by revising mechanical designs, motor load calculations, and electrical control components. However, minimal emphasis has been concentrated on the crane motor system operational dynamics, which is vital for the overall crane motor system stability under operational loads, external disturbances, and uncertain or varying component characteristics.

Dynamical control of most crane motor systems have mainly been based on the conventional Proportional, Integral, Derivative (PID) controllers, because of their simplicity for synthesis as well as implementations, and a few required, intuitive tuning parameters. However, practical crane motor system components typically exhibit uncertain or time-varying characteristics and significantly increase the complexity of the stability and performance problem, possibly exceeding the capabilities of PID controllers to handle under real-time practical conditions. In addition, the presence of plant uncertainties with unknown frequencies and external disturbances can even make the control of motor cranes too complex for a traditional PID controller to achieve reliable robust performance levels for all operational conditions. Thus, control approaches with potential to handle complex as well as nonlinear dynamical crane systems are proposed for superior operations. Overhead crane motor systems have been controlled by using Fuzzy logic [3, 4], with a need for an immense labor task to accurately define the fuzzy logic parameters, membership sets, and rules. Optimal control [5, 6] was also proposed, with a focus on system stability over the transient response performance levels. However, optimal control and associated stability margins are very much susceptible to model uncertainties as well as their magnitude and phase characteristics. Adaptive control approach [7, 8] was also proposed by mainly focusing on system performance levels with respect to the system stability perspectives under uncertainty. Furthermore, \(\hbox {H}_{{{\infty }}}\) control [9] was developed for overhead crane motor systems by considering the length of the hoist cable and angle of swing as the primary focal points and its implementation via the linear matrix inequality approach.

This research focuses on uncertain motor systems in crane operations, i.e., a crane motor inductor component-level uncertainty for the corresponding safety, stability, and performance levels, that illustrate significant variations under external influences during the real life motor crane applications. Fluctuating crane motor parameters such as armature coil resistance and inductance, with increasing temperature levels [10, 11] as the motor heats up during heavy operations, can considerably affect the stability and performance of motor crane systems. As generalized low-pass filters can be introduced in the design model to capture the parameter perturbation and also to suppress any disturbance that might affect the tracking of the motor speed, this study investigates a formal quantitative, low computational complexity modeling and optimization approaches, i.e., robust \(\hbox {H}_{{{\infty }}}\), \(\mu \), and linear parameter varying (LPV) modeling, control, and optimization frameworks, for guaranteed stability and performance levels during optimal crane motor operations under quantified as well as norm-bounded uncertainty terms. The proposed quantitative frameworks offer an effective numerical controller synthesis to handle component, dynamical, and exogenous component as well as signal uncertainties for worst-case conditions and to ensure safety, stability as well as desired performance levels of the corresponding crane system inherent dynamic stability conditions for accurate as well as safe real-time implementations. The study is organized as follows: the model development and derivation of the basic tower crane motor model is presented in Sect. 2. Section 3 describes the proposed \(\hbox {H}_{{{\infty }}}\) and \(\mu \) controller synthesis frameworks while Sect. 4 presents the Linear Parameter Varying (LPV) modeling and optimization framework with a candidate system motor inductor variations. As Sect. 5 discusses the proposed framework numerical implementation steps and simulation results, the conclusions are given in Sect. 6.

2 Basic crane motor modeling

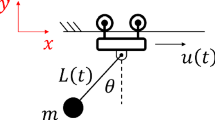
Motors in crane systems are accurately described by well-known mathematical models, with estimated parameters to adopt for the expected operating conditions. However, high performance, model-based closed-loop system performance is closely dependent to the accuracy of the estimated motor parameters, with inaccurate or varying parameters yielding unexpected stability and performance issues. As the consideration of all potential parameter variations most likely yields intractable problems, it is essential to identify the most critical parameters for stability and performance analysis. A permanent magnet DC motor implementation in a tower crane system, shown in Fig. 1, is considered in this research for clarity and easy extension to any type of motor dynamics in crane systems, to hoist payloads up and down to target locations; the horizontal jib or working arm of the crane carries the load on a trolley and moves it in and out of the crane center while the horizontal machinery arm contains the motor, other electronics and a large concrete counterweight. During the crane operations, the payload is hoist up/down by a steel cable rope that runs over a pulley which is connected to a DC motor gearbox system.

Fig. 1
figure 1

Single motor tower crane

Full size image
Fig. 2
figure 2

A DC motor armature circuit with the rotor connected load

Full size image

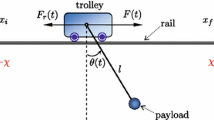
A DC motor system operating under a load, shown in Fig. 2, contains electrical and mechanical subsystems with the corresponding parameters given in Table 1 [12]. Using the physical laws for the corresponding electrical and mechanical subsystems yields the state-space model with inputs, outputs, and the governing system states.

Table 1 DC motor system parameters
Full size table

The DC motor generates an electromagnetic torque T that is proportional to the armature current i and the strength of the internal magnetic field. Assuming constant internal magnetic field, the motor electromagnetic torque is proportional to the armature current, given as \(T=k_{t}i\), where \(k_{t}\) denotes the motor structure-dependent torque constant. Also, the back emf e is proportional to the angular velocity \(\omega \) of the motor shaft as \(e=k_{b}\frac{d\theta }{dt}\), where \(k_{b}\) denotes the motor structure-dependent voltage constant and \(\omega =\frac{d\theta }{dt}\), \(\theta (t)\) being the angular position. Applying the Kirchhoff’s voltage law around the motor circuit in Fig. 2 yields

$$\begin{aligned} L_{o}\frac{di}{dt}+Ri+e=u \end{aligned}$$
(1)

Using the Newton’s 2nd law of rotational motion, the electromagnetic torque T causes a mechanical action that is governed by

$$\begin{aligned} J\frac{d^{2}\theta }{dt^{2}}+b\frac{d\theta }{dt}=T \end{aligned}$$
(2)

Rearranging (1) and (2), and substituting torque and back emf expressions yield (3), and (4), respectively.

$$\begin{aligned} \frac{di}{dt}= & {} -\frac{R}{L_{o}}i-\frac{k_{b}}{L_{o}}\omega +\frac{1}{L_{o}}u \end{aligned}$$
(3)
$$\begin{aligned} \frac{d\omega }{dt}= & {} -\frac{b}{J}\omega +\frac{k_{t}}{J}i \end{aligned}$$
(4)

Considering that \(x_{1}=i\), \(\dot{x}_{1}=\frac{di}{dt}\), \(x_{2}=\omega \), \(\dot{x}_{2}=\frac{d\omega }{dt}\), and the motor angular velocity as the system output, the motor system governing state-space representation can be given as

$$\begin{aligned}&\left[ \begin{array}{c} \dot{x}_{1}\\ \dot{x}_{2} \end{array}\right] =\left[ \begin{array}{cc} -\frac{R}{L_{0}} &{} -\frac{k_{b}}{L_{o}}\\ \frac{k_{t}}{J} &{} -\frac{b}{J} \end{array}\right] \left[ \begin{array}{c} x_{1}\\ x_{2} \end{array}\right] +\left[ \begin{array}{c} \frac{1}{L_{o}}\\ 0 \end{array}\right] u\nonumber \\&y=\left[ \begin{array}{cc} 0&1\end{array}\right] \left[ \begin{array}{c} x_{1}\\ x_{2} \end{array}\right] \end{aligned}$$
(5)

and the corresponding motor nominal system block diagram, for the Maxon RE Permanent Magnet DC motor (Catalog number 273753) [12] parameter data in Table 1, is given in Fig. 3. The state-space representation in (5) can be used to generate the nominal plant \(G_{o}(s)\) block diagram for controller design purposes as shown in Fig. 4, with the current i and the angular velocity \(\omega \) represent the system states \(x_{1}\) and \(x_{2}\), respectively.

Fig. 3
figure 3

The DC motor nominal plant block diagram

Full size image

3 Crane motor parametric uncertainty modeling, and \(\hbox {H}_{{{\infty }}}\) and \(\mu \) controller synthesis

For the crane system model parameter uncertainty modeling, control, and optimization considerations, the motor operating under load in Fig. 2 is considered to have the uncertain armature inductance \(L_{o}\) with significant perturbations. The same approach can easily be applied to other potentially important parameters, with higher level of problem complexity.

The main objective of the controller design is to achieve robust tracking performance while minimizing the effects of parameter or external perturbations associated with the real plant. Robust system theories synthesize controllers by using the linear, time-invariant (LTI) nominal models for norm-bounded uncertain plants to ensure robustness and stability, as robustness terms being manipulated as fictitious uncertainty components. For a stabilizing controller to exist under a common configuration, a necessary and sufficient condition must be achieved such that the closed-loop transfer matrix \(\left\| T_{wz} (s) \right\| _{{{\infty }}}\prec \gamma \) for the closed-loop system in Fig. 4, with the uncertain plant \(G(s)=G_{o}(s)(1+W(s)\triangle )\) in the multiplicative uncertainty case, where \(\gamma \) is a prescribed critical level for robustness, uncertainty \(\varDelta \), and uncertainty weighting function W(s). In Fig. 4, the inputs have been partitioned into exogenous disturbances w from the uncertainty, reference signal r(t) and control input u(t). Likewise, the outputs have been partitioned into the output z from a filter, i.e., an uncertainty weighting function, used to characterize the uncertainty as well as performance effects, and the plant output y(t) that is available to the controller C(s), through the error signal e(t).

Fig. 4
figure 4

The closed-loop control system with the plant multiplicative uncertainty

Full size image

Once the nominal plant \(G_{o}(s)\) is obtained from Fig. 3, a critical motor component is considered for parameter fluctuations as uncertainty. During the crane operations, the motor heats up and the change in temperature affects the armature coil inductance considerably by an increase of 10–20% perturbation [13] of the nominal armature coil inductance value. Thus, by utilizing the component-level multiplicative uncertainty description, the uncertain armature coil inductance component can be expressed as

$$\begin{aligned} L=L_{o}\left( 1+W_{L_{o}}\left( s\right) \varDelta _{L_{o}}\left( s\right) \right) \end{aligned}$$
(6)

where \(L_{o}\) is the nominal armature inductance value, \(W_{L_{o}}\left( s\right) \) is the armature inductance uncertainty weighting function covering all related uncertainty characteristics in the frequency domain, and \(\varDelta _{L_{o}}\left( s\right) \) is the corresponding bounded uncertainty term. Incorporating the uncertain armature inductance model into the nominal plant block diagram of the DC motor in Fig. 3 results in the uncertain crane motor model block diagram, as shown in Fig. 5.

Fig. 5
figure 5

The uncertain DC motor block diagram

Full size image

Using the diagram in Fig. 5 with two inputs and two outputs, the uncertain motor state-space model can also be written as

$$\begin{aligned} \left[ \begin{array}{c} \dot{x}_{1}\\ \dot{x}_{2} \end{array}\right]= & {} \left[ \begin{array}{cc} \frac{-R}{L_{o}} &{} \frac{k_{b}}{L_{o}}\\ \frac{k_{t}}{J} &{} \frac{-b}{J} \end{array}\right] \left[ \begin{array}{c} x_{1}\\ x_{2} \end{array}\right] +\left[ \begin{array}{cc} \frac{-1}{L_{o}} &{} \frac{1}{L_{o}}\\ 0 &{} 0 \end{array}\right] \left[ \begin{array}{c} d\\ u \end{array}\right] \nonumber \\ \left[ \begin{array}{c} z\\ \omega \end{array}\right]= & {} \left[ \begin{array}{cc} -R &{} -k_{b}\\ 0 &{} 1 \end{array}\right] \left[ \begin{array}{c} x_{1}\\ x_{2} \end{array}\right] +\left[ \begin{array}{cc} -1 &{} 1\\ 0 &{} 0 \end{array}\right] \left[ \begin{array}{c} d\\ u \end{array}\right] \end{aligned}$$
(7)

For a unity-feedback closed-loop control system having a multiplicative uncertainty description, as shown in Fig. 4, the system robust stability is achieved if and only if the corresponding controller (C(s)) satisfies

$$\begin{aligned} \left\| T(s)W(s)\right\| _{{{\infty }}}{{\prec }\, 1 \hbox { for all Re(s) } \ge 0} \end{aligned}$$
(8)

where W(s) is a given stable uncertainty weighting function and T(s) is the complementary sensitivity function, expressed as

$$\begin{aligned} T(s)=\frac{C(s)G_{o}(s)}{1+C(s)G_{o}(s)} \end{aligned}$$
(9)

Assuming that the robust tracking performance is characterized by a small sensitivity function S(s), given by

$$\begin{aligned} S(s)=\frac{1}{1+C(s)G_{o}(s)} \end{aligned}$$
(10)

then, the condition for nominal performance for the closed-loop system with multiplicative uncertainty becomes

$$\begin{aligned} \left\| S(s)W_{p}(s)\right\| _{{{\infty }}}{{\prec }\, 1 \hbox { for all Re(s) } }{{\ge } 0} \end{aligned}$$
(11)

where \(W_{p}(s)\) is the performance weighting function. To achieve the system performance under uncertainty, i.e., robust performance, the controller must satisfy both the robust stability and nominal performance conditions for all possible plant models, given as

$$\begin{aligned} \left\| \left| T(s)W(s)\right| +\left| S(s)W_{p}(s)\right| \right\| _{{{\infty }}}{{\prec } \,1 \hbox { for all Re(s) } \ge 0} \end{aligned}$$
(12)

A robust stability problem with two perturbations is equal to a robust performance problem with one perturbation, i.e., the main loop theorem [14], provided the \(\hbox {H}_{{{\infty }}}\) norm is used to quantify robust performance with the fictitious perturbation applied at the appropriate location in the feedback control system, as shown in Fig. 6 for the crane motor control system.

Fig. 6
figure 6

The feedback control system with the uncertainty and performance weighting functions

Full size image
Fig. 7
figure 7

The linear fractional transformation controller synthesis framework of the feedback control system

Full size image

A single motor with one uncertainty at the component level in a feedback control system in Fig. 6 can be considered for the robust performance criterion by using the common Linear Fractional Transformation (LFT) framework for the controller synthesis, as shown in Fig. 7, where \(\varDelta \) is the system uncertainty matrix that contains the bounded model uncertainty and the performance fictitious uncertainty terms, C(s) is the robust controller to be designed, and P(s) denotes the augmented plant of the closed-loop control system, shown in Fig. 6, including the nominal plant and performance as well as uncertainty weighting functions, given by

$$\begin{aligned} \left[ \begin{array}{c} \bar{e}\\ z\\ e \end{array}\right] =P(s)\left[ \begin{array}{c} \bar{r}\\ d\\ u \end{array}\right] \end{aligned}$$
(13)

where the augmented plant is obtained as

$$\begin{aligned} P(s)=\left[ \begin{array}{ccc} W_{p}(s) &{} -T_{d-y}(s)*W_{p}(s) &{} -T_{u-y}(s)*W_{p}(s)\\ 0 &{} T_{d-\bar{z}}(s)*W_{L_{o}}(s) &{} T_{u-\bar{z}}(s)*W_{L_{o}}(s)\\ 1 &{} -T_{d-y}(s) &{} -T_{u-y}(s) \end{array}\right] , \end{aligned}$$

where \(T_{a-b}(s)\) denotes the transfer function from the input a to the output b, and \(W_{L_{o}}(s)\) is the uncertainty weighting function that covers all inductance uncertainty behavior for different frequencies.

3.1 \(\hbox {H}_{{{\infty }}}\) controller

The \(\hbox {H}_{{{\infty }}}\) controller synthesis, for the given LFT representation in Fig. 7, can be stated as designing a controller C(s) such that

$$\begin{aligned} \left\| T_{\left| \begin{array}{c} \bar{r}\\ d \end{array}\right| \rightarrow \left| \begin{array}{c} \bar{e}\\ z \end{array}\right| }(s) \right\| _{{{\infty }}}{{\prec }\, 1} \end{aligned}$$
(14)

is satisfied for the performance and disturbance input–output transfer functions. The appropriate inductor uncertainty weighting function, \(W_{L_{o}}(s)\)

$$\begin{aligned} W_{L_{o}}(s)=(0.2)\left( \frac{s+10}{s+100}\right) \end{aligned}$$
(15)

is considered to cover all uncertainty around the nominal plant in the frequency domain, i.e., its steady-state value for low frequency range is more accurately known with respect to the instantaneous variations at relatively high frequencies, as shown in Fig. 8.

The control system aims for satisfactory steady-state tracking performance, i.e., minimize \(\left\| S(s)W_{p}(s)\right\| _{{{\infty }}}{{\prec }\, 1}\), where \(W_{p}(s)\) is the desired performance weighting function selected for the real plant. Using the performance weighting function selection guidelines and several iterations, the performance weighting function \(W_{p}(s)\)

$$\begin{aligned} W_{p}(s)=8100\left( \frac{\frac{s}{10}+1}{\frac{s}{0.001}+1}\right) \end{aligned}$$
(16)

was chosen to have a high gain value at low frequencies for superior steady-state performance while having relatively low gain at high frequencies for acceptable transient performance levels, whose frequency response is shown Fig. 8, comparatively with the uncertainty weighting function frequency response.

Fig. 8
figure 8

The uncertainty and performance weighting function frequency responses

Full size image

Although the \(\hbox {H}_{{{\infty }}}\) control framework is easy to handle, the corresponding controller synthesis results are mostly overly conservative due to the consideration of unstructured worst-case uncertainty description, including the stability and performance uncertainties, implying a need for the \(\mu \) control framework to potentially improve the results by exploiting particular uncertainty structures of each problem while significantly increasing the problem computational complexity.

3.2 \(\mu \) controller

The \(\mu \) control framework makes use of the structured uncertainty [15] description if the relationships between the individual plant and performance uncertainty terms are known. Assuming that the individual uncertainties are not interrelated, the simplest structured uncertainty description can be given as

$$\begin{aligned} {{\varDelta }}=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {{\varDelta }}_{1} &{} 0 &{} \cdots &{} 0\\ 0 &{} {{\varDelta }}_{2} &{} 0 &{} 0 \\ \vdots &{} 0 &{} \ddots &{} 0 \\ 0 &{} 0 &{} 0 &{} {{\varDelta }}_{n} \end{array}\right] \end{aligned}$$
(17)

The performance weighting function selection for the \(\mu \) controller design is expected to be more ambitious, compared to the \(\hbox {H}_{{{\infty }}}\) controller case, due to the fact that the \(\mu \) controller design assumed the simplest structured uncertainty description for the proposed crane motor problem. Using the design guidelines and several iterations, the performance weighting function for the real uncertain plant that provides satisfactory tracking performance was chosen to have a high gain at low frequencies. The quantification of the performance weighting function was accomplished by choosing the performance weighting function \(W_{p}(s)\)

$$\begin{aligned} W_{p}(s)=\left( 57300\right) \left( \frac{\frac{s}{10000}+1}{\frac{s}{0.1}+1}\right) \end{aligned}$$
(18)

such that \(W_{p}(s)^{-1}\) reflects the desired shape of the closed-loop sensitivity function S(s). Figure 9 shows the performance weighting function frequency response, selected for the \(\mu \) controller (new) design versus the one selected for the \(\hbox {H}_{{{\infty }}}\)controller (old) design.

Fig. 9
figure 9

The \(\mu \) and \(\hbox {H}_{{{\infty }}}\) controller performance weighting functions

Full size image

4 Crane motor linear parameter varying uncertainty modeling and controller synthesis

The linear parameter varying (LPV) control framework offers an effective advanced optimization approach for systems with time-varying parameter(s) \(\rho (t)\) for superior stability and performance outcomes. The time trajectory of \(\rho (t)\) is a-priori unknown, but the actual parameter values are considered to be measurable in future time points. The LPV control framework eliminates the repetitive task of manually tuning the control loop, i.e., varying the gain of the controller according to the time varying parameter \(\rho (t)\), by developing a gain scheduling [16] controller, i.e., switching among an array of linear time-invariant controllers for different operation points of a nonlinear system. However, the LPV design framework utilizes potential time-varying parameter(s) that are independent of the system states, ensuring linear dependence when compared to the gain-scheduling case of nonlinear relationship. For the sake of clarity, the crane system considers the motor armature inductance as the measurable time-varying parameter. Although additional plausible component fluctuations can also be taken into consideration for the time varying parameters for superior modeling and control performances, the corresponding computational complexity increases considerably, limiting the number of effective parameters.

Typical LPV system state space models [17] are given as

$$\begin{aligned} \left[ \begin{array}{c} \dot{x}(t)\\ y(t) \end{array}\right] =\left[ \begin{array}{cc} A(\rho (t)) &{} B(\rho (t))\\ C(\rho (t)) &{} D(\rho (t)) \end{array}\right] \left[ \begin{array}{c} x(t)\\ u(t) \end{array}\right] \end{aligned}$$
(19)

where \(\rho (t)\) is the time-varying parameter that takes on values in a known compact set P and has known bounds on \(\dot{\rho }(t)\), where \(P:\left\{ v\le \dot{\rho }(t)\le \bar{v}\right\} \), x(t) denotes the system states, y(t) denotes the system outputs, u(t) denotes the system inputs and \(A(\rho (t))\), \(B(\rho (t))\), \(C(\rho (t))\), and \(D(\rho (t))\) are the parameter dependent state space matrices that vary within a polytope, as shown in Fig. 10, dictated by the time-varying parameter \(\rho (t)\) variations. The LPV framework uses the Linear Fractional Transformation (LFT) during the controller synthesis, as shown in Fig. 11, where w indicates the reference and disturbance inputs, z denotes the weighted output of the performance objectives, u is the system input from the controller and y is the measured output to the controller. Then, the LPV controller framework is to synthesize an LPV controller \(K(\rho )\), described as

$$\begin{aligned} \begin{array}{l} \dot{x}_{k}(t)=A_{k}(\rho (t))x_{k}(t)+B_{k}(\rho (t))y(t)\\ u(t)=C_{k}(\rho (t))x_{k}(t) \end{array} \end{aligned}$$
(20)

such that the closed-loop system in Fig. 11 is stable and its \({||T_{w-z}(s)||}_\infty \) norm is bounded by \(\gamma \) such that \(1\succ \gamma \succ 0\) for all possible parameter trajectories.

Fig. 10
figure 10

Augmented LPV system

Full size image
Fig. 11
figure 11

LFT depiction of LPV synthesis

Full size image

The robust stability and performance for the closed-loop system in Fig. 11 can be ensured via the well-known Bounded Real Lemma, by utilizing (19) and (20) within the closed-loop diagram in Fig. 11 such that the \(L_{2}\) induced gain level \(\left( \gamma \succ 0\right) \) is achieved if there exists a matrix \(\left( X=X^{T}\succ 0\right) \) such that

$$\begin{aligned} \left[ \begin{array}{ccc} A_{cl}^{T}\left( \rho \right) X+XA_{cl}\left( \rho \right) &{} XB_{cl} &{} C_{cl}^{T}\left( \rho \right) \\ B_{cl}^{T}\left( \rho \right) X &{} -\gamma I &{} D_{cl}^{T}\left( \rho \right) \\ C_{cl}\left( \rho \right) &{} D_{cl}\left( \rho \right) &{} -\gamma I \end{array}\right] \prec 0 \end{aligned}$$
(21)

Thus, without loss of generality, the synthesis of the condition in (21) involves a search over the polytope, dictated by the time-varying parameter \(\left( \rho (t) \right) \) and corresponding LTI systems, by using a set of linear matrix inequalities (LMI). Assuming that the plant parameter dependence \(\left( G (\rho (t) ) \right) \) is affine, where \(\left( \rho (t) \right) \) is the time-varying parameter for the corresponding polytope, with vertices \(\rho _{j}\), \(j=1,2....,r\). Then, an LPV controller \(K\left( \rho \right) \) can be computed [18, 19] as follows:

(i) The vertex controller \(K_{j}=\left( A_{K_{j}},B_{K_{j}},C_{K_{j}},0\right) \), for \(\left( 1\le j\le r\right) \) can be computed by solving the set of linear matrix inequalities, given as

$$\begin{aligned} \left[ \begin{array}{cccc} XA_{j}+\hat{B}_{K_{j}}C_{2_{j}}+* &{} * &{} * &{} *\\ \hat{A_{K_{j}}^{T}+A_{j}} &{} A_{j}Y+B_{2_{j}}\hat{C}_{K_{j}}+* &{} * &{} *\\ \left( XB_{1_{j}}+\hat{B}_{K_{j}}D_{21_{j}}\right) ^{T} &{} B_{1_{j}}^{T} &{} -\gamma I &{} *\\ C_{1_{j}} &{} C_{1_{j}}Y+D_{12_{j}}\hat{C}_{K_{j}} &{} D_{11_{j}} &{} -\gamma I \end{array}\right] \prec 0 \end{aligned}$$
(22)

and

$$\begin{aligned} \left[ \begin{array}{cc} X &{} I\\ I &{} Y \end{array}\right] \succ 0 \end{aligned}$$
(23)

where \(\left( *\right) \) denotes the terms whose expressions follow the requirement that the matrix is self-adjoint. This step produces \(\left( \hat{A}_{K_{j}},\hat{B}_{K_{j}},\hat{C}_{K_{j}}\right) \) and the symmetric matrices X and Y.

Fig. 12
figure 12

The step response of the nominal crane motor plant with the controller

Full size image

(ii) \(A_{K_{k}}\), \(B_{K_{j}}\)and \(C_{K_{j}}\) can be computed as \(A_{K_{j}}=N^{-1}\left( \hat{A}_{K_{j}}-XA_{j}Y-\hat{B}_{K_{j}}C_{2_{j}}Y-XB_{2_{j}}\hat{C}_{K_{j}}\right) M^{-T}\), \(B_{K_{j}}=N^{-1}\hat{B}_{K_{j}}\), and \(C_{K_{j}}=\hat{C}_{K_{j}}M^{-T}\), where N and M are matrices to hold \(I-XY=NM^{T}\).The resulting state-space matrices of the LPV polytopic controller \(K\left( s\right) \) is a convex combination of the vertex controller given by

$$\begin{aligned} \left[ \begin{array}{cc} A_{K} &{} B_{K}\\ C_{K} &{} 0 \end{array}\right] \left( \rho \right) =\sum _{j=1}^{r}\alpha _{j}\left[ \begin{array}{cc} A_{K_{j}} &{} B_{K_{j}}\\ C_{K_{j}} &{} 0 \end{array}\right] \end{aligned}$$
(24)

5 Numerical results

5.1 \(\hbox {H}_{{{\infty }}}\) control

The robust control toolbox in Matlab was used to implement and obtain the \(\hbox {H}_{{{\infty }}}\) control simulation results that indicated the corresponding controller having an achievable gamma value of 0.9882, with the controller state-space matrices. The step response of the plant with the controller also shows perfect steady-state tracking of the nominal plant output, as shown in Fig. 12.

In order to verify that the \(\hbox {H}_{{{\infty }}}\) controller designed can minimize the tracking error in the motor with perturbed armature coil inductance, a perturbation of 40% was added to the nominal value of the armature coil inductance \(L_{o}\), i.e., \(L_\textit{perturbed}=\left[ (40\%*L_{o})+L_{o}\right] \), resulting in the perturbed plant step response with the same \(\hbox {H}_{{{\infty }}}\) controller, shown in Fig. 13. A comparison between the step responses of the nominal and the perturbed plants was made by taking the error difference for both plants, and was found to be very small.

Fig. 13
figure 13

The step response of a perturbed crane motor with the controller

Full size image

5.2 \(\mu \) control

The Matlab simulation results for the \(\mu \) controller resulted in the \(\mu \) value of 0.99, i.e., implying robust performance, after performing several D-K iteration steps for the corresponding controller state-space representation, with the step response of the nominal crane motor plant for the \(\hbox {H}_{{{\infty }}}\) control and \(\mu \) control cases, shown in Fig. 14.

Fig. 14
figure 14

The step responses of the nominal crane motor with the \(\hbox {H}_{{{\infty }}}\) and \(\mu \) controllers

Full size image

5.3 LPV control

This study constructs and simulates the crane motor LPV system via the LPVTools software tool, developed by MUSYN Inc. [17], implemented in Matlab. The LPVTools provides numerous LPV data structures as well as modeling, simulation, analysis, and synthesis tools in the LPV framework. The LPVTools software tool uses the command (tvreal) to scale the time-varying parameter \(\rho (t)\) and its rate bound \(\dot{\rho }(t)\) into their corresponding maximum and minimum values. For the crane motor system, the armature coil inductance, with its nominal value of \((6.2E-04H)\), is considered to be the time varying parameter \(\rho (t)\) that can be measured in future real-time using an inductive sensor. The (tvreal) command is used to scale the time-varying parameter and the rate bound into \((1E-04\le \rho (t)\le 6.2E-04)\) and \((-1E-04\le \dot{\rho }(t)\le 1E-04)\), respectively, with the corresponding LPV state-space matrices, shown as.

$$\begin{aligned} A=\left[ \begin{array}{c@{\quad }c} \frac{-R}{\rho } &{} \frac{k_{b}}{\rho }\\ \frac{k_{t}}{J} &{} \frac{-b}{J} \end{array}\right] ,B=\left[ \begin{array}{c} \frac{1}{\rho }\\ 0 \end{array}\right] ,C=\left[ \begin{array}{c@{\quad }c} 1&0\end{array}\right] ,D=\left[ 0\right] \end{aligned}$$
(25)

The performance weighting function \(W_\textit{per}(s)\)

$$\begin{aligned} W_\textit{per}(s)=(0.085)\left( \frac{\frac{s}{0.01}+1000}{\frac{s}{0.01}+0.1}\right) \end{aligned}$$
(26)

was chosen, as shown in Fig. 15, after several iterations to achieve the robust performance, to have a high gain at low frequencies for superior steady-state tracking performance while having relatively low gain at high frequencies for acceptable transient response performance by using the nominal plant frequency domain characteristics.

Fig. 15
figure 15

The linear parameter varying framework performance weighting function frequency response

Full size image

The LPV controller synthesis utilized the (lpvsyn) command to implement the corresponding LFT framework and required the closed-loop performance objective characterization in terms of the weighted interconnection of the system, shown in Fig. 16, where the interconnection is defined in Matlab as systemnames = ‘wperf sys’; inputvar = ‘[omega;u]’; outputvar = ‘[wperf;omega – sys]’; input_to_sys = ‘[u]’; and input_to_wperf = ‘[omega – sys]’.

Fig. 16
figure 16

The weighted interconnection for the linear parameter varying system controller synthesis

Full size image

The LPV controller synthesis of the crane motor system resulted in the \(\gamma \) value of 0.9961, i.e., implying robust performance achievement, and effectively minimized the step response tracking error of the closed-loop LPV crane motor plant, as shown in Fig. 17, for the illustrative time-varying parameter \(\rho (t)\) trajectory selection of \(\rho (t)=0.0006\cos (0.0005t)\), as shown in Fig. 18.

Fig. 17
figure 17

The closed-loop linear parameter varying crane motor system response for the selected parameter trajectory

Full size image
Fig. 18
figure 18

The assumed crane motor inductor linear time-varying parameter trajectory

Full size image

The LPV motor crane system time-varying nature closely depends on the time-varying trajectory. Thus, each plausible time-varying parameter can be tested with the proposed LPV framework for their implementation efficiency and operation conditions.

Also, the \(\hbox {H}_{{{\infty }}}\), \(\mu \), and LPV controller step responses are examined altogether for the best tracking system, as shown in Fig. 19, where the time-varying parameter trajectory and the performance weighting function for each case could potentially change the current performance levels.

Fig. 19
figure 19

The step responses of the nominal crane motor with the \(\hbox {H}_{{{\infty }}}\), \(\mu \), and linear parameter varying controllers

Full size image

6 Conclusions

Three different robust system modeling and control frameworks have successfully been proposed for the tower crane motor closed-loop steady-state tracking control systems, under bounded unstructured as well as structured uncertainty and time-varying parameter trajectory cases to reflect real-life considerations. The proposed three control frameworks allow performance, stability and robustness to be combined into a single control synthesis framework and present great flexibility that allows ease of adaption into areas of control interest in crane motor systems.

The proposed robust modeling and synthesis frameworks can be scaled further by considering multiple significant parameter, dynamical, or signal uncertainties for superior performance levels during practical crane operations while the complexity of the proposed problems is expected to increase, effectively limiting the number of uncertain components to be arbitrarily large. In addition, as the performance in terms of steady-state tracking error depends on the performance weighting function selection, future studies can further characterize real-life constraints and associated candidate performance weighting functions under practical controller frameworks.