Stabilization for distributed semilinear systems governed by optimal feedback control

Abstract

This paper focuses on the problem of polynomial and weak stabilization of abstract distributed semilinear systems in a real Hilbert space governed by an optimal multiplicative feedback control. A new proposed feedback control is constructed to achieves the two kinds of stabilization. Necessary and sufficient conditions for stabilization problems are investigated as well. Furthermore, the used feedback control is the unique solution of an appropriate minimization problem. Some examples of hyperbolic and parabolic partial differential equations are provided. Finally, simulations are given.

1 Introduction

The present paper deals the problem of feedback stabilization for a class of distributed semilinear systems with multiplicative feedback control of the form:

$$\begin{aligned} \frac{dy(t)}{dt}=Ay(t)+p(t)By(t)+Ny(t),\, t>0. \end{aligned}$$

(1)

Here the state space is a real Hilbert space H endowed with inner product $\langle .,.\rangle$ and its associated norm $\Vert .\Vert$ and A is linear operator (generally unbounded) which is an infinitesimal generator of a linear $C_0$ semigroup of contractions S(t),  so that A is dissipative, i.e., $\langle A\phi , \phi \rangle \le 0,\, \forall \phi \in \mathcal {D}(A)$ while B and N are two nonlinear operators from H into itself, whereas p(t) is a scalar function which represents the control. In this case in order to be in agreement with standard notations used in the existing literature, we rather write the Eq. (1) in the form:

$$\begin{aligned} \displaystyle \frac{dy(t)}{dt}=Ay(t)+F(y(t)),\, t>0, \end{aligned}$$

where $F(y(t))=p(t)By(t)+Ny(t).$ Then, the system (1) is expected to be dissipative if the nonlinearity F has “the good sign”. Along any solution of (1) (while it is well defined), the derivative with respect to time of the energy $E(t):=\displaystyle \frac{1}{2}\Vert y(t)\Vert ^2,$ we have, at least formally, $E'(t)\le -\langle F(y(t)),y(t) \rangle ,$ since A generates a semigroup of contractions. In the sequel, we will make appropriate assumptions on F ensuring that $E'(t)\le 0$ and therefore, the system (1) is dissipative. It is then expected that the unique solution is globally well defined and that it energy decays asymptotically to 0 as $t\rightarrow +\infty .$ We make the following assumptions $\langle F(y(t)),y(t) \rangle \le 0,$ for all y(t) solution of the system (1). This assumption implies that $E'(t)\le 0.$ In the case when $N=0,$ the system (1) may be expressed as:

$$\begin{aligned} \frac{dy(t)}{dt}=Ay(t)+p(t)By(t),\, t>0. \end{aligned}$$

(2)

The stabilization problem of the system (2) has been studied by several authors (see [1,2,3,4]). In the earlier papers [2, 4], it has been shown in the case $H= \mathbb {R}^n,$ that the condition

$$\begin{aligned} \langle BS(t)\phi ,S(t)\phi \rangle =0,\, \forall t\ge 0\Rightarrow \phi =0, \end{aligned}$$

(3)

is sufficient for the weak stabilizability of the system (2). This result has been generalized to the infinite-dimensional case, under the assumption that B is sequentially continuous from $H_w$ (H endowed with its weak topology) to H (i.e., $\psi _n\rightharpoonup \psi \Rightarrow B\psi _n\rightarrow B\psi$ as $n\rightarrow +\infty$) which is equivalent to assuming that B is compact for bilinear control problem. It has been shown that the quadratic feedback control $p_{_0}(t)=-\,\langle By(t),y(t)\rangle ,$ weakly stabilizes the system (2) provided that the condition (3) holds (see [1]). The strong stabilization result has been obtained using the same control $p_{_0}(t)$ for the systems (2) with the following optimal decay estimate of the stabilized state

$$\begin{aligned} \Vert y(t)\Vert =\mathcal {O}\left( \displaystyle \frac{1}{\sqrt{t}}\right) \,\, \hbox {as}\,\, t \rightarrow +\,\infty , \end{aligned}$$

(4)

i.e., $\Vert y(t)\Vert \le \displaystyle \frac{M}{\sqrt{t}},\, M>0,$ for t large enough, such that the following condition

$$\begin{aligned} \int _{0}^{T}|\langle BS(t)\phi ,S(t)\phi \rangle |dt\ge \delta _{T} \Vert \phi \Vert ^2,\,\ (T, \delta _{T} > 0), \end{aligned}$$

(5)

holds (see [3]). In [5], it has been shown that if the resolvent of A is compact, B is a bounded linear self-adjoint and monotone operator, then under the sufficient assumption (3), the feedback control law:

$$\begin{aligned} p_{_*}(t)= -\displaystyle \frac{\langle By(t),y(t)\rangle }{1+|\langle By(t), y(t)\rangle |}, \end{aligned}$$

(6)

strongly stabilizes the system (2). In [6], the strong stabilization of the system (2) has been obtained with the decay estimate (4) via the same feedback control (6). The main objective in this work is to makes the initial system (1) weakly and strongly stable with an explicit decay estimate of the stabilized state for a large class of semilinear systems under certain necessary and sufficient conditions by using a feedback control of a lower cost than that $p_{_*}(y(t))$ (see Remark 3.1). Moreover, we will show that this control minimizes an appropriate cost. The candidate feedback control that fulfills the control requirements is the following:

$$\begin{aligned} p_{_{\log }}^*(t)= & {} \rho \log (1+ p_{_*}(t))=\rho \log \left( 1-\frac{\langle By(t),y(t)\rangle }{1+|\langle By(t), y(t)\rangle |}\right) ,\, \nonumber \\&\rho >0. \end{aligned}$$

(7)

This feedback profits from the advantage of being applicable as a constrained control, i.e., one can choose the control gain so that the feedback never takes values beyond a fixed threshold. The rest of this paper after this one is organized as follows. In Sect. 2 we will present some preliminary known results on the background material on nonlinear semigroups and nonlinear evolution equations respectively. In Sect. 3 we will analyze the existence and the uniqueness of the global mild solution of the system (1). Moreover, we will establish the strong stability of the system (1) with an explicit decay estimate by using (7). In Sect. 4 we will show that the given feedback control (7) yields the weak stabilization of the system (1). Section 5 is devoted to the minimization problem of a nonlinear cost by the feedback control (7). Finally, in Sects. 6 and 7, we will give some applications and simulations respectively.

2 Preliminary results

In this section, we present some preliminary results on nonlinear evolution equations which will be used later in our analysis.

Definition 2.1

([1, 7, 8]) Let H be a real Hilbert space. A (general nonlinear) semigroup $\Gamma (t)$ on H is a continuous map $\Gamma (t): H\longrightarrow H,\, t\in \mathbb {R}^+,$ satisfying

• (i) $\Gamma (0)=I_H$ (the identity operator).

• (ii) $\Gamma (t+s)=\Gamma (t)\Gamma (s),\, \forall t, s\in \mathbb {R}^+$ (proprieties of superposition).

• (iii) $\displaystyle \lim _{t\rightarrow 0^+}\Vert \Gamma (t)\varphi -\varphi \Vert =0,\, \forall \varphi \in H$ (continuity of $\Gamma (t)$ to $0^+$).

• (iv) Moreover, the linear semigroup $\Gamma (t)$ (resp. nonlinear semigroup $\Gamma (t)$) is said to be a semigroup of contractions, if $\Vert \Gamma (t)\Vert \le 1,\ \forall t\in \mathbb {R}^+$ (resp. $\Vert \Gamma (t)\varphi -\Gamma (t)\psi \Vert \le \Vert \varphi -\psi \Vert ,\, \forall \varphi , \psi \in H,\ \forall t\in \mathbb {R}^+$).

Definition 2.2

([8]) The linear operator A defined by $\mathcal {D}(A)=\{x\in H|\, \displaystyle \lim _{t\rightarrow 0^+}\frac{S(t)x-x}{t}\,\ \hbox {exists}\}$ and $Ax=\displaystyle \lim _{t\rightarrow 0^+}\frac{S(t)x-x}{t},\, \forall x\in \mathcal {D}(A),$ is called the infinitesimal generator (or just the generator) of the semigroup S(t) and $\mathcal {D}(A)$ is the domain of the operator A.

The following definitions concerns the weak solution of the system (1).

Definition 2.3

([8]) Let $t_1 >t_0.$ A function $y \in C([t_0, t_1]; H)$ is a weak solution of (1) on the interval $[t_0, t_1],$ if $y(t_0)=y_0,\, f(.,y(. )) \in L^1([t_0, t_1]; H)$ and if for each $\varphi \in \mathcal {D}(A^*)$ the function $\langle y(t),\varphi \rangle$ is absolutely continuous on $[t_0, t_1]$ and satisfies

$$\begin{aligned} \displaystyle \frac{d}{dt}\langle y(t),\varphi \rangle =\langle y(t),A^* \varphi \rangle +\langle f(t,y(t)),\varphi \rangle ,\,\, \forall t\in [t_0, t_1], \end{aligned}$$

(8)

where $f(t,y(t))=p(t)By(t)+Ny(t).$

Definition 2.4

([8]) Let $t_1 >t_0.$ A function $y:[t_0, t_1]\longrightarrow H$ is a weak solution of (1) on $[t_0,t_1],$ if y satisfies the variation of constants formula

$$\begin{aligned} y(t)=S(t-t_0)y(t_0)+\int _{t_0}^{t}S(t-\tau )f(\tau ,y(\tau ))d\tau ,\,\ \forall t\in [t_0, t_1]. \end{aligned}$$

(9)

The function y satisfying the variation of constants formula (9) is often called mild solution of the system (1). Furthermore, if the function $y : \mathbb {R}^+ \longrightarrow H$ is continuously differentiable with $y(t) \in \mathcal {D}(A),\, \forall t\ge 0,$ and satisfies the system (1), we call it a classical solution.

We recall the following basic definition on $\omega$-limit sets.

Definition 2.5

• 1. The weak $\omega$-limit set of $\psi$ is (possibly empty) the set given by

  $$\begin{aligned} \omega _{w}(\psi )= & {} \{\varphi \in H :\, \exists t_n\rightarrow +\infty \,\ \hbox {as}\,\ n \rightarrow \\&+\,\infty \,\ \hbox {such that}\,\ \Gamma (t_n)\psi \rightharpoonup \varphi \,\ \hbox {as}\,\ n \rightarrow +\infty \}. \end{aligned}$$

• 2. A subset C of H is said to be invariant if $\Gamma (t)C = C$ for all $t \in \mathbb {R}^+.$

Let us recall the following definitions concerning the asymptotic behavior of the system (1).

Definition 2.6

• (i) The system (1) is weakly (resp. strongly) stabilizable if there exists a feedback control $p(t) = \varphi (y(t)),$ where $\varphi : H \longrightarrow \mathbb {R},$ such that the corresponding unique mild solution satisfies the properties:

  • 1. for each $y_0\in H,$ there exists a unique mild solution y(t),  defined for all $t \in \mathbb {R}^+$ of the system (1),

  • 2. $\{0\}$ is a an equilibrium of the system (1),

  • 3. $y(t)\rightharpoonup 0,$ weakly (resp. $y(t)\rightarrow 0,$ strongly), as $t \rightarrow +\infty$ for all $y_0 \in H.$

• (ii) Furthermore, in addition of 1 and 2,  the system (1) is said polynomially stable, if there exist two constants $\beta >0$ and $M>0$ (depending on $y_0$) such that $\Vert y(t)\Vert \le \displaystyle \frac{M}{t^{\beta }},\, \forall t > 0$ for all sufficiently smooth initial data.

Remarks 2.1

• 1. Remarking that $1+p_{_*}(t)>0,\, \forall t\ge 0,$ then $p_{_{\log }}^*(t)$ is well defined.

• 2. It is readily seen that $p_{_{\log }}^*(t)\langle By(t),y(t) \rangle \le 0,\,\, \forall t\ge 0.$

• 3. The strong stability $\Rightarrow$ weak stability. The converse is not true in general.

2.1 Assumptions

In this paper, we consider the nonlinear operators B and N satisfy the following hypotheses:

($\mathcal {H}_1$)::

$B(0)=N(0)=0,$ so that 0 remain an equilibrium state for the nominal semilinear system (1).

($\mathcal {H}_2$)::

The operators B and N are locally Lipschitz, i.e., $\forall R>0$ and $\forall y, z\in \mathcal {B}_R=\{ \phi \in H;\,\ \Vert \phi \Vert \le R\},$ we have $\Vert Bz-By\Vert \le L_{R}\Vert z-y\Vert$ and $\Vert Nz-Ny\Vert \le L_{R}\Vert z-y\Vert ,\,\ L_{R}>0.$

($\mathcal {H}_3$)::

$\langle N\varphi ,\varphi \rangle \le 0,\, \forall \varphi \in H.$

($\mathcal {H}_4$)::

$|\langle B\varphi ,\varphi \rangle |\ge \mu \Vert N \varphi \Vert ^2,\,\ \forall \varphi \in H,\, \mu >0.$

Remark 2.1

From $(\mathcal {H}_2),$ one can deduce that $L_{R}=\max \left\{ \displaystyle \sup _{y,z\in \mathcal {B}_R(0);\,z\ne y} \frac{\Vert N z{-}N y\Vert }{\Vert z-y\Vert },\displaystyle \sup _{y,z\in \mathcal {B}_R(0);\,z\ne y} \frac{\Vert B z{-}B y\Vert }{\Vert z-y\Vert }\right\} .$

3 Strong stabilisation and decay estimate

Before we state our main result in this section, the following lemma will be needed.

Lemma 3.1

Let $\varphi : \mathbb {R}^+\longmapsto \mathbb {R}^+$ be a nonincreasing function and satisfying

$$\begin{aligned} C\varphi ^{1+\gamma }(t)\le \varphi (t)-\varphi (t+T),\, \forall t\ge 0, \end{aligned}$$

(10)

where $C> 0,\, \gamma > 0$ and $T>0$ are three constants. Then, we have

$$\begin{aligned} \varphi (t)=\mathcal {O}(t^{-\frac{1}{\gamma }})\,\ \hbox {as}\,\ t \rightarrow +\infty . \end{aligned}$$

(11)

Proof

It follows from (10) by putting $\psi (t)=\varphi ^{-\gamma }(t),$ that

$$\begin{aligned}&\psi (t+T)-\psi (t) =\int _{0}^{T}\frac{d}{d \theta }\big (\frac{\theta }{T} \varphi (t+T)\\&\qquad +\,(1-\frac{\theta }{T})\varphi (t)\big )^{-\gamma } d \theta \\&\quad = \frac{\gamma }{T} \big (\varphi (t)-\varphi (t+T)\big )\int _{0}^{T}\big (\frac{\theta }{T} \varphi (t+T) \\&\qquad +\,(1-\frac{\theta }{T})\varphi (t)\big )^{-1-\gamma } d \theta \ge \gamma C. \end{aligned}$$

Then, for any $n\in \mathbb {N},$ one can deduce

$$\begin{aligned} \psi ((n+1)T)\ge \psi (0)+(n+1)\gamma C. \end{aligned}$$

This last inequality leads us to the following relation

$$\begin{aligned} \varphi ((n+1)T)\le \displaystyle \frac{1}{\big (\varphi ^{-\gamma }(0)+(n+1) \gamma C\big )^{\frac{1}{\gamma }}}. \end{aligned}$$

(12)

Let us now set $n = [\displaystyle \frac{t}{T} ],$ (where [x] designs the integer part of x). In view of (12) we infer that

$$\begin{aligned} \varphi (t)\le \displaystyle \frac{1}{\big (\varphi ^{-\gamma }(0)-\gamma C+\frac{\gamma C}{T}t\big )^{\frac{1}{\gamma }}},\, \forall t\ge T. \end{aligned}$$

This achieves the proof of the Lemma 3.1. $\square$

In what follows, we will analyze the existence and the uniqueness of the global mild solution of the semilinear system (1). Additionally, we will establish a useful estimate which will be crucial to establish the weak and the strong stability of the system (1).

Theorem 3.1

Let A generate a semigroup of contractions S(t) on H,  and let B and N two nonlinear operators verify the hypotheses $(\mathcal {H}_1)-(\mathcal {H}_4).$ Then, the system (1) possesses a unique mild solution $y\in C(\mathbb {R}^+; H)$ for each $y_0 \in H$ and satisfies the following estimate:

$$\begin{aligned}&\int _{0}^{T}|\langle BS(\tau )y(t),S(\tau )y(t)\rangle |d\tau = \mathcal {O}\Bigg (\Vert y(t)\Vert \bigg (\displaystyle \int _{t}^{t+T}|\log (1 \nonumber \\&\quad -\,\frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |})\langle By(\tau ), y(\tau )\rangle | d\tau \bigg )^{\frac{1}{4}}\Bigg )\,\ \nonumber \\&\quad \hbox {as}\,\ t\rightarrow +\infty , \end{aligned}$$

(13)

for each $T > 0.$

Proof

Let us consider the function $g=f+N,$ where f is defined by:

$$\begin{aligned} f(\varphi )=\rho \log (1-\frac{\langle B\varphi ,\varphi \rangle }{1+|\langle B\varphi ,\varphi \rangle |})B\varphi ,\,\ \forall \varphi \in H. \end{aligned}$$

In this case the semilinear system (1) can be written as follows:

$$\begin{aligned} \frac{dy(t)}{dt}=Ay(t)+f(y(t))+Ny(t)=Ay(t)+g(y(t)),\, t>0. \end{aligned}$$

(14)

In order to study the stabilization problem of the system (14) it may be shown first of all that (14) admits a global mild solution. For this end, we shall show that the function g is locally lipschitz. For this reason, it suffice to show that f is locally lipschitz since N is. For any $R>0$ and $\forall y, z\in \mathcal {B}_R(0)$ i.e., $\Vert y\Vert \le R$ and $\Vert z\Vert \le R,$ we have

$$\begin{aligned}&\Vert f(z)-f(y)\Vert =\rho \Vert \log \left( 1- \displaystyle \frac{\langle Bz,z \rangle }{1+|\langle Bz,z \rangle |}\right) Bz \nonumber \\&\qquad -\,\log \left( 1- \displaystyle \frac{\langle By,y\rangle }{1+|\langle By,y\rangle |}\right) By\Vert \nonumber \\&\quad \le \rho \Vert \log \left( 1- \displaystyle \frac{\langle Bz,z \rangle }{1+|\langle Bz,z \rangle |}\right) Bz\nonumber \\&\qquad - \log \left( 1- \displaystyle \frac{\langle Bz,z \rangle }{1+|\langle Bz,z \rangle |}\right) By\Vert \nonumber \\&\qquad +\,\rho \Vert \log \left( 1- \displaystyle \frac{\langle Bz,z \rangle }{1+|\langle Bz,z \rangle |}\right) By\nonumber \\&\qquad -\,\log \left( 1- \displaystyle \frac{\langle By,y\rangle }{1+|\langle By,y\rangle |}\right) By\Vert . \nonumber \\&\quad \le \rho L_{R}\left| \log \left( 1- \displaystyle \frac{\langle Bz,z \rangle }{1+|\langle Bz,z \rangle |}\right) \right| \Vert z-y\Vert \nonumber \\&\qquad +\,\rho L_{R}\Vert y\Vert \left| \log \left( 1-\frac{\langle Bz,z \rangle }{1+|\langle Bz,z \rangle |}\right) \right. \nonumber \\&\qquad \left. -\,\log \left( 1- \frac{\langle By,y \rangle }{1+|\langle By,y \rangle |}\right) \right| . \end{aligned}$$

(15)

To do this, two cases arise.

• Case 1$\langle Bz,z \rangle \ge 0.$ In this case, we have

  $$\begin{aligned}&\left| \log \left( 1- \displaystyle \frac{\langle Bz,z \rangle }{1+|\langle Bz,z \rangle |}\right) \right| \\&\quad =|\log (1+\langle Bz,z \rangle )|\le |\langle Bz,z \rangle |\\&\quad \le R^2L_{R},\,\, (\log (1+x)\le x,\, \forall x\in [0,+\infty [). \end{aligned}$$

• Case 2$\langle Bz,z \rangle \le 0.$ In particular, in this, it is easy to see that

  $$\begin{aligned}&\left| \log \left( 1- \displaystyle \frac{\langle Bz,z \rangle }{1+|\langle Bz,z \rangle |}\right) \right| \le \displaystyle \frac{|\langle Bz,z \rangle |}{1+|\langle Bz,z \rangle |}\le |\langle Bz,z \rangle | \\&\quad \le R^2 L_{R},\,\, (\log (1+x)\le x,\, \forall x\in [0,+\infty [). \end{aligned}$$

Then, in both cases, we have

$$\begin{aligned} \left| \log \left( 1- \displaystyle \frac{\langle Bz,z \rangle }{1+|\langle Bz,z \rangle |}\right) \right| \le |\langle Bz,z \rangle |,\, \forall z\in H. \end{aligned}$$

(16)

It yields, by (15) that

$$\begin{aligned}&\Vert f(z)-f(y)\Vert \le \rho R^2L_{R}^2\Vert z-y\Vert \nonumber \\&\quad +\,\rho R L_{R} \left| \log \left( 1-\displaystyle \frac{\langle Bz,z \rangle }{1+|\langle Bz,z\rangle |}\right) \right. \nonumber \\&\quad \left. -\,\log \left( 1- \displaystyle \frac{\langle By,y\rangle }{1+|\langle By,y \rangle |}\right) \right| . \end{aligned}$$

(17)

It remains to show that the map h defined by:

$$\begin{aligned} h(\varphi )=\log (1-\frac{\langle B\varphi ,\varphi \rangle }{1+|\langle B\varphi ,\varphi \rangle |})=(\log \,\circ \,k)(\varphi ),\,\, \forall \varphi \in H, \end{aligned}$$

is locally Lipschitz, where $k(\varphi )=1- \dfrac{\langle B\varphi ,\varphi \rangle }{1+|\langle B\varphi ,\varphi \rangle |}.$ Since the function $\log$ is of $C^1$ on the interval $\mathrm {Im}(k):=[\frac{1}{1+R^2 L_{R}}, 1+2R^2 L_{R}],$ it suffice to show that the function k is locally Lipschitz. Indeed, $\forall R>0$ and $\forall y, z\in \mathcal {B}_R(0)$ with the fact that $\forall a, b\in \mathbb {R},\, ||a|-|b||\le |a-b|,$ we infer that

$$\begin{aligned}&|k(z)-k(y)| \\&\quad =\Big |\displaystyle \frac{\langle Bz,z \rangle {+}\langle Bz,z \rangle |\langle By,y \rangle |{-}\langle By,y \rangle {-}\langle By,y \rangle |\langle Bz,z\rangle |}{(1+|\langle Bz,z \rangle |)(1+|\langle By,y \rangle |)}\Big | \\&\quad \le \Big |\langle Bz,z \rangle -\langle By,y \rangle \Big |+\Big |\langle Bz,z \rangle |\langle By,y \rangle |\\&\qquad -\,|\langle Bz,z\rangle |\langle By,y \rangle \Big | \\&\quad \le |\langle Bz,z-y \rangle +\langle Bz-By,y \rangle |\\&\qquad +\,\Big |\langle Bz,z \rangle |\langle By,y \rangle |-\langle Bz,z \rangle |\langle Bz,z \rangle |\\&\qquad +\,\langle Bz,z \rangle |\langle Bz,z \rangle |-|\langle Bz,z\rangle |\langle By,y \rangle \Big | \\&\quad \le 2R L_{R}\Vert z-y\Vert +2R^2 L_{R} |\langle Bz,z \rangle -\langle By,y \rangle | \\&\quad \le 2R L_{R}\Vert z-y\Vert +2R^2L_{R}\Big |\langle Bz,z-y \rangle +\langle Bz-By,y \rangle \Big |\\&\quad \le 2RL_{R}(1+2R^2L_{R})\Vert z-y\Vert . \end{aligned}$$

That means that the function k is locally Lipschitz, and then h is. Consequently, f is locally Lipschitz. Then, the system (14) admits a unique mild solution defined on a maximal interval $[0, t_{\max }[,$ by the variation of constant formula:

$$\begin{aligned}&y(t)=\Gamma (t)y_0 =S(t)y_0+\displaystyle \int _{0}^{t}S(t-\tau )g(y(\tau )) d\tau \nonumber \\&\quad =S(t)y_0+\displaystyle \int _{0}^{t}S(t-\tau )\Big (\rho \log \Big (1\nonumber \\&\qquad -\, \displaystyle \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\Big )By(\tau )+Ny(\tau )\Big ) d\tau , \end{aligned}$$

(18)

where $\Gamma (t)$ define a nonlinear semigroup (see [8]). Next we will show that this solution is globally defined. Indeed, if $y_0\in \mathcal {D}(A),$ the solution of the system (14) becomes a classical one (see [8]). It follows after multiplying (14) by y(t) and using the fact that S(t) is a semigroup of contractions together with $(\mathcal {H}_3)$ that

$$\begin{aligned}&\frac{d\Vert y(t)\Vert ^2}{dt}\le 2\rho \log \left( 1- \displaystyle \frac{\langle By(t),y(t) \rangle }{1+|\langle By(t),y(t) \rangle |}\right) \langle By(t),y(t)\rangle \nonumber \\&\quad +\,2\langle Ny(t),y(t)\rangle \le 0,\,\, \forall t\ge 0, \end{aligned}$$

(19)

which implies

$$\begin{aligned} \Vert y(t)\Vert \le \Vert y_0\Vert ,\,\ \forall t\in [0, t_{\max }[. \end{aligned}$$

(20)

To show that (20) holds for all initial states $y_0 \in H,$ we will establish the Lipschitz continuity of y(t) with respect to $y_0.$ To this end, let $t \in [0, t_{\max }[$ be fixed and let $y_0 \in H.$ For any initial state $w_0 \in H,$ the corresponding solution w(t) of the system (14) verifies

$$\begin{aligned} w(\tau )-y(\tau )= & {} S(\tau )(w_0-y_0)+\displaystyle \int _{0}^{\tau }S(\tau -s) \big (g(w(s))\\&-\, g(y(s))\big )ds,\,\ \forall \tau \in [0, t]. \end{aligned}$$

Hence, using the fact that g is locally Lipschitz function and S(t) is a semigroup of contractions, we obtain

$$\begin{aligned}&\Vert w(\tau )-y(\tau )\Vert \le \Vert w_0-y_0\Vert +L\displaystyle \int _{0}^{t}\Vert w(s)\\&\quad -\,y(s)\Vert ds,\,\ \forall \tau \in [0,t], \end{aligned}$$

where L is the Lipschitz constant of the function g. It follows from the Gronwall’s inequality, that

$$\begin{aligned} \Vert w(\tau )-y(\tau )\Vert \le \Vert w_0-y_0\Vert e^{L t},\,\ \forall \tau \in [0,t]. \end{aligned}$$

(21)

Thus the map $y_0 \longmapsto y(t)$ is Lipschitz from H to H,  which enables us, since $\mathcal {D}(A)$ is dense in H,  to extend (20) to $y_0 \in H,$ and hence y(t) is a global solution i.e., $t_{\max } = +\infty ,$ (see [8]). Next, we will prove the estimate (13). From (18) the solution of the system (14) can be represented as follows:

$$\begin{aligned}&y(t)=S(t)y_0+\rho \displaystyle \int _{0}^{t}S(t-\tau )\log \left( 1\right. \nonumber \\&\quad \left. -\,\displaystyle \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau )\rangle |}\right) By(\tau )d\tau \nonumber \\&\quad +\,\displaystyle \int _{0}^{t}S(t-\tau )Ny(\tau )d\tau . \end{aligned}$$

(22)

Combining the Schwartz’s and Hölder’s inequalities with the fact that S(t) is a semigroup of contractions and employing (16) and (20) we get for all $t\in [0, T],$ that

$$\begin{aligned}&\Vert y(t)-S(t)y_0\Vert \le \rho L_{\Vert y_0\Vert }\Vert y_0\Vert \nonumber \\&\quad \displaystyle \int _{0}^{t}\Big |\log \Big (1-\,\displaystyle \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\Big ) |d\tau \nonumber \\&\quad +\displaystyle \int _{0}^{t}\Vert N y(\tau )\Vert d\tau \le \rho L_{\Vert y_0\Vert }\Vert y_0\Vert \nonumber \\&\quad \displaystyle \int _{0}^{t}|\log \Big (1 -\,\displaystyle \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\Big )\langle By(\tau ),y(\tau ) \rangle |^{\frac{1}{2}} d\tau \nonumber \\&\quad +\,\displaystyle \int _{0}^{t}\Vert N y(\tau )\Vert d\tau \le \rho T^{\frac{1}{2}}L_{\Vert y_0\Vert }\Vert y_0\Vert \nonumber \\&\quad \Big (\displaystyle \int _{0}^{T}\big |\log \Big (1 -\, \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau )\rangle |}\Big )\langle By(\tau ), y(\tau )\rangle \big |d\tau \Big )^{\frac{1}{2}}\nonumber \\&\quad +\,T^{\frac{1}{2}}\bigg (\displaystyle \int _{0}^{T}\Vert N y(\tau )\Vert ^2 d\tau \bigg )^{\frac{1}{2}}. \end{aligned}$$

(23)

On the other hand, we have

$$\begin{aligned}&\langle BS(\tau )y_0,S(\tau )y_0\rangle =\langle BS(\tau )y_0-By(\tau ),S(\tau )y_0\rangle \nonumber \\&\quad -\,\langle By(\tau ),z(\tau )\rangle +\langle By(\tau ),y(\tau )\rangle , \end{aligned}$$

(24)

where $z(t)=\rho \displaystyle \int _{0}^{t}S(t-\tau )\log (1- \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |})By(\tau )d\tau +\displaystyle \int _{0}^{t}S(t-\tau )N y(\tau )d\tau .$ Then, from (24) it comes

$$\begin{aligned}&|\langle BS(\tau )y_0,S(\tau )y_0\rangle |\le 2L_{\Vert y_0\Vert }\Vert y(\tau )-S(\tau )y_0\Vert \Vert y_0\Vert \nonumber \\&\quad +\,|\langle By(\tau ),y(\tau )\rangle |. \end{aligned}$$

(25)

Replacing $y_0$ by y(t) in both (23) and (25) and using the semigroup property of the solution y(t) together with the hypothesis $(\mathcal {H}_4)$ and the fact that the function $t\longmapsto \Vert y(t)\Vert$ is decreases for all $t\ge 0,$ we find that

$$\begin{aligned}&|\langle BS(\tau )y(t),S(\tau )y(t)\rangle | \le 2\rho T^{\frac{1}{2}}L_{\Vert y_0\Vert }^2\Vert y(t)\Vert ^2\nonumber \\&\quad \bigg (\displaystyle \int _{0}^{T}|\log \bigg (1 -\, \displaystyle \frac{\langle By(t+\tau ),y(t+\tau ) \rangle }{1+|\langle By(t+\tau ),y(t+\tau ) \rangle |}\bigg )\nonumber \\&\quad \langle By(t+\tau ), y(t+\tau )\rangle \big | d\tau \bigg )^{\frac{1}{2}}\nonumber \\&\quad +\,2T^{\frac{1}{2}}L_{\Vert y_0\Vert }\Vert y(t)\Vert \bigg (\displaystyle \int _{0}^{T}\Vert N y(t+\tau )\Vert ^2 d\tau \bigg )^{\frac{1}{2}}\nonumber \\&\quad +\,|\langle By(t+\tau ),y(t+\tau )\rangle | \nonumber \\&\quad \le 2\rho T^{\frac{1}{2}}L_{\Vert y_0\Vert }^2\Vert y(t)\Vert ^2\bigg (\displaystyle \int _{t}^{t+T}|\log \bigg (1\nonumber \\&\quad -\, \displaystyle \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\bigg )\langle By(\tau ), y(\tau )\rangle \big | d\tau \bigg )^{\frac{1}{2}}\nonumber \\&\quad +\,\displaystyle \frac{2T^{\frac{1}{2}}L_{\Vert y_0\Vert }\Vert y(t)\Vert }{\mu ^{\frac{1}{2}}}\bigg (\displaystyle \int _{t}^{t+T}|\langle By(\tau ),y(\tau )\rangle |d\tau \bigg )^{\frac{1}{2}} \nonumber \\&\quad +\,|\langle By(t+\tau ),y(t+\tau )\rangle |. \end{aligned}$$

(26)

To show the estimate (13) two cases are distinguished.

• Case 1$\langle B y(\tau ),y(\tau )\rangle \le 0.$ In this case, using the following inequality $x-\displaystyle \frac{x^2}{2}\le \log (1+x),\ \forall x\in [0, +\infty [,$ we have

  $$\begin{aligned}&\left| \log \left( 1-\displaystyle \frac{\langle By(\tau ),y(\tau )\rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\right) \right| \\&\quad \ge \displaystyle \frac{|\langle By(\tau ),y(\tau ) \rangle |}{1+|\langle By(\tau ),y(\tau ) \rangle |}\Big (1-\frac{|\langle By(\tau ),y(\tau )\rangle |}{2(1+|\langle By(\tau ),y(\tau ) \rangle |)}\Big )\\&\quad \ge \displaystyle \frac{|\langle By(\tau ),y(\tau ) \rangle |}{2(1+|\langle By(\tau ),y(\tau ) \rangle |)}. \end{aligned}$$

• Case 2$\langle B y(\tau ),y(\tau )\rangle \ge 0.$ In this case, using the fact that $\log$ is nondecreasing function on $]0,+\infty [,$ we get

  $$\begin{aligned}&\left| \log \left( 1-\frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\right) \right| =|\log (1\\&\quad +\,\langle By(\tau ),y(\tau ) \rangle )| \ge \left| \log \left( 1+\frac{|\langle By(\tau ),y(\tau ) \rangle |}{1+|\langle By(\tau ),y(\tau ) \rangle |}\right) \right| . \end{aligned}$$

From the first case, we deduce that

$$\begin{aligned} \left| \log \left( 1-\frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\right) \right| \ge \frac{|\langle By(\tau ),y(\tau ) \rangle |}{2(1+|\langle By(\tau ),y(\tau ) \rangle |)}. \end{aligned}$$

Then, more precisely in the two cases, we have

$$\begin{aligned}&|\langle By(\tau ),y(\tau ) \rangle | \nonumber \\&\quad \le 2(1+|\langle By(\tau ),y(\tau ) \rangle |)\left| \log \left( 1-\dfrac{\langle By(\tau ),y(\tau )\rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\right) \right| \nonumber \\&\quad \le 2(1+L_{\Vert y_0\Vert }\Vert y(\tau )\Vert ^2)\left| \log \left( 1-\dfrac{\langle By(\tau ),y(\tau )\rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\right) \right| .\nonumber \\ \end{aligned}$$

(27)

It yields from (26) by using (27) and Schwartz’s inequality, that

$$\begin{aligned}&|\langle BS(\tau )y(t),S(\tau )y(t)\rangle | \le 2\rho T^{\frac{1}{2}}L_{\Vert y_0\Vert }^2\Vert y(t)\Vert ^2\\&\bigg (\displaystyle \int _{t}^{t+T}\bigg |\log \bigg (1\quad -\, \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\bigg )\langle By(\tau ), y(\tau )\rangle \bigg | d\tau \bigg )^{\frac{1}{2}}\\&\quad +\,\frac{2^{\frac{3}{2}}T^{\frac{3}{4}}L_{\Vert y_0\Vert }\Vert y(t)\Vert (1+L_{\Vert y_0\Vert }\Vert y_0\Vert ^2)^{\frac{1}{2}}}{\mu ^{\frac{1}{2}}}\\&\quad \bigg (\displaystyle \int _{t}^{t+T}\bigg |\log \bigg (1 -\, \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\bigg )\langle By(\tau ), y(\tau )\rangle \bigg | d\tau \bigg )^{\frac{1}{4}}\\&\quad +\,2^{\frac{1}{4}}L_{\Vert y_0\Vert }^{\frac{1}{2}}(1+L_{\Vert y_0\Vert }\Vert y_0\Vert ^2)^{\frac{1}{4}}\Vert y(t+\tau )\Vert \bigg |\\&\quad \log \bigg (1 -\,\frac{\langle By(t+\tau ),y(t+\tau ) \rangle }{1+|\langle By(t+\tau ),y(t+\tau ) \rangle |}\bigg )\langle By(t+\tau ),y(t+\tau )\rangle |^{\frac{1}{4}}. \end{aligned}$$

One can deduce by using (16) with Schwartz’s and Holder’s inequalities that

$$\begin{aligned}&|\langle BS(\tau )y(t),S(\tau )y(t)\rangle | \le 2\rho T^{\frac{3}{4}}L_{\Vert y_0\Vert }^{\frac{5}{2}}\Vert y(t)\Vert ^3\nonumber \\&\quad \bigg (\displaystyle \int _{t}^{t+T}\bigg |\log \bigg (1 -\, \displaystyle \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\bigg )\langle By(\tau ), y(\tau )\rangle \big | d\tau \bigg )^{\frac{1}{4}}\nonumber \\&\quad +\,\frac{2^{\frac{3}{2}}T^{\frac{3}{4}}L_{\Vert y_0\Vert }\Vert y(t)\Vert (1+L_{\Vert y_0\Vert }\Vert y_0\Vert ^2)^{\frac{1}{2}}}{\mu ^{\frac{1}{2}}} \nonumber \\&\quad \bigg (\displaystyle \int _{t}^{t+T}\bigg |\log \bigg (1 -\, \displaystyle \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\bigg )\langle By(\tau ), y(\tau )\rangle \big | d\tau \bigg )^{\frac{1}{4}}\nonumber \\&\quad +\,2^{\frac{1}{4}}L_{\Vert y_0\Vert }^{\frac{1}{2}}(1+L_{\Vert y_0\Vert }\Vert y_0\Vert ^2)^{\frac{1}{4}}\Vert y(t)\Vert \bigg |\nonumber \\&\quad \log \bigg (1 -\,\frac{\langle By(t+\tau ),y(t+\tau ) \rangle }{1+|\langle By(t+\tau ),y(t+\tau ) \rangle |}\bigg )\langle By(t+\tau ),y(t+\tau )\rangle |^{\frac{1}{4}}. \end{aligned}$$

(28)

Integrating the inequality (28) with respect $\tau$ over the interval [0, T] and using Schwartz’s inequality, we arrive at

$$\begin{aligned}&\displaystyle \int _{0}^{T}|\langle BS(\tau )y(t),S(\tau )y(t)\rangle |d\tau \le C \Vert y(t)\Vert \nonumber \\&\quad \bigg (\displaystyle \int _{t}^{t+T}\bigg |\log \bigg (1 -\, \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\bigg )\langle By(\tau ), y(\tau )\rangle \bigg | d\tau \bigg )^{\frac{1}{4}},\nonumber \\ \end{aligned}$$

(29)

where

$C{:=}T^{\frac{3}{4}}L_{\Vert y_0\Vert }^{\frac{1}{2}}\Big (1{+} 2\rho TL_{\Vert y_0\Vert }^{2}\Vert y_0\Vert ^2{+}\frac{2^{\frac{3}{2}}T L^{\frac{1}{2}}_{\Vert y_0\Vert }(1+L_{\Vert y_0\Vert }\Vert y_0\Vert ^2)^{\frac{1}{2}}}{\mu ^{\frac{1}{2}}}\Big ).$ Therefore, this complete the proof of the Theorem 3.1. $\square$

Based on the previous results, we are able to establish the polynomial stability of the system (1), which leads us to the following theorem.

Theorem 3.2

Let A generate a semigroup of contractions S(t) on H,  and let B and N are two nonlinear operators satisfy $(\mathcal {H}_1)-(\mathcal {H}_4).$ Then (7) strongly stabilizes the system (1) with the explicit decay estimate:

$$\begin{aligned} \Vert y(t)\Vert =\mathcal {O}(\frac{1}{\sqrt{t}}),\, \hbox {as}\,\ t\rightarrow +\infty , \end{aligned}$$

(30)

provided that (5) holds.

Proof

Multiplying (14) by y(t) and using the fact that A generates a semigroup of contractions together with the condition ($\mathcal {H}_3$), we obtain:

$$\begin{aligned}&\frac{d\Vert y(t)\Vert ^2}{dt}\le 2\rho \log \left( 1-\frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\right) \\&\quad \langle By(t),y(t)\rangle .\,\ \forall y_0\in \mathcal {D}(A). \end{aligned}$$

That is

$$\begin{aligned}&\Vert y(t+T)\Vert ^2-\Vert y(t)\Vert ^2 \le 2\rho \displaystyle \int _{t}^{t+T}\log \left( 1\right. \nonumber \\&\quad \left. -\,\frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\right) \langle By(\tau ),y(\tau )\rangle d\tau \le 0. \end{aligned}$$

(31)

The last inequality (31) holds by density argument for all $y_0\in H.$ It yields, by combining (5) with (29) that

$$\begin{aligned} K\Vert y(t)\Vert ^4\le \Vert y(t)\Vert ^{2}-\Vert y(t+T)\Vert ^{2},\, \forall t\ge 0, \end{aligned}$$

(32)

where $K:=\displaystyle \frac{2\rho \delta _T^4}{C^4}.$ If we set $\varphi (t)=\Vert y(t)\Vert ^{2},$ we obtain from (32) that $K\varphi ^{1+\gamma }(t)\le \varphi (t)-\varphi (t+T),\, \forall t\ge 0,$ where $\gamma =1.$ Then, the required estimate (30) follows easily from the Lemma 3.1. $\square$

Remark 3.1

• 1. We note that $\delta _{T}=\displaystyle \inf _{\Vert y\Vert =1}\int _{0}^{T}|\langle BS(t)y,S(t)y\rangle |dt.$

• 2. We have $|p_{_{\log }}^*(t)|\le |p_{_*}(t)|<1$ provided that $0<\rho \le \frac{1}{1+L_{\Vert y_0\Vert }\Vert y_0\Vert ^2}.$ In the rest of this paper we will choose $\rho \in (0, \frac{1}{1+L_{\Vert y_0\Vert }\Vert y_0\Vert ^2} \big ].$

• 3. Since $\Vert y(t)\Vert$ decreases, then $\exists t_{0}\ge 0,\, y(t_{0})=0\Leftrightarrow y(t)=0,\, \forall t\ge t_{0}.$

• 4. We have $\langle By(t),y(t)\rangle =0,\, \forall t\ge 0 \Rightarrow p^*_{_{\log }}(y(t))=0.$ This implies from $(\mathcal {H}_4)$ that $N=0.$ Then, the solution of the system (1) can be written as $y(t)=S(t)y_0.$ From (5) we get $y(t)=0,\, \forall t\ge 0.$

• 5. We have (5) implies (3) but the converse is not true in general.

• 6. In the finite dimensional case, we have (3) implies (5) (see [9]).

In the following next result we give a necessary condition for the strong stability of the system (1).

Proposition 3.1

If the system (1) is polynomially stable such that $(\mathcal {H}_1)-(\mathcal {H}_4)$ are satisfied. Then, for all $\varphi \in H,$ we have

$$\begin{aligned} BS(t)\varphi= & {} 0,\, \forall t\ge 0\Rightarrow \Vert S(t)\varphi \Vert = \mathcal {O}(t^{-\frac{1}{\gamma }}),\, \gamma \nonumber \\&\quad >0,\, \hbox {as}\,\ t\rightarrow +\infty . \end{aligned}$$

(33)

Proof

We suppose that the system (1) is strongly stable, and let $\varphi \in H$ be such that $BS(t)\varphi =0,\, \forall t\ge 0.$ Then, by using $(\mathcal {H}_4),$ we obtain $y (t) = S (t) \varphi$ is the unique mild solution of (1) starting at $y (0) =\varphi .$ Consequently, the strong stabilization hypothesis implies that $\Vert S(t)\varphi \Vert = \mathcal {O}(t^{-\frac{1}{\gamma }}),\, \gamma >0,\, \hbox {as}\,\ t\rightarrow +\infty .$$\square$

4 Weak stabilization

The exact observability condition (5) does not holds when the nonlinear operator B is sequentially continuous. In the following next result, we will show that if B is sequentially continuous, then the assumption (5) can be relaxed to the weaker assumption (3) and the control (7) ensures the weak stabilization of the system (1).

Theorem 4.1

Let A generate a semigroup S(t) of contractions on H,  and let B is sequentially continuous as well as $(\mathcal {H}_1)-(\mathcal {H}_4)$ hold. Then, the control (7) weakly stabilizes (1) provided that (3) holds.

Proof

We have

$$\begin{aligned}&\displaystyle \frac{d}{dt}\Vert y(t)\Vert ^2{\le }2\rho \log \left( 1{-}\frac{\langle By(t),y(t) \rangle }{1{+}|\langle By(t),y(t) \rangle |}\right) \langle By(t),y(t)\rangle \\&\quad +\,2\langle Ny(t),y(t)\rangle \le 0,\,\ \forall y_0\in \mathcal {D}(A). \end{aligned}$$

The last estimate implies by using ($\mathcal {H}_3$) that

$$\begin{aligned}&\rho \displaystyle \int _0^t\left| \log \left( 1-\displaystyle \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\right) \langle By(\tau ),y(\tau )\rangle \right| d\tau \nonumber \\&\quad \le \Vert y_0\Vert ^2,\,\ \forall t\ge 0. \end{aligned}$$

(34)

The inequality (34) holds, by density argument, for all $y_0\in H.$ It follows then, that the following integral

$$\begin{aligned} \displaystyle \int _0^t\left| \log \left( 1-\displaystyle \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\right) \langle By(\tau ),y(\tau )\rangle \right| d\tau \end{aligned}$$

converges for all $y\in H.$ So, from the Cauchy criterion, we deduce for any $T>0,$ that

$$\begin{aligned}&\displaystyle \int _{t}^{t+T}\left| \log \left( 1-\displaystyle \frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\right) \langle By(\tau ),y(\tau )\rangle \right| d\tau \nonumber \\&\quad \rightarrow 0 \,\ \hbox {as} \,\ t\rightarrow +\infty . \end{aligned}$$

(35)

Let us now show that $y(t) \rightharpoonup 0$ as $t \rightarrow +\infty ,$ (where $\rightharpoonup$ refers to weak convergence). Therefore, in view of (20) and the fact that the state space H is reflexive, we obtain $\omega _w(y_0)\ne \emptyset$ and invariant subset of H. Then, there exists a sequence $(t_n)$ and $\psi \in \omega _w(y_0)$ such that $t_n \rightarrow +\infty$ and $y(t_n) \rightharpoonup \psi$ as $n \rightarrow +\infty .$ Then, from (35) we have

$$\begin{aligned}&\displaystyle \int _{t_n}^{t_n+T}\left| \log \left( 1-\frac{\langle By(\tau ),y(\tau ) \rangle }{1+|\langle By(\tau ),y(\tau ) \rangle |}\right) \langle By(\tau ),y(\tau )\rangle \right| d\tau \nonumber \\&\quad \rightarrow 0 \,\ \hbox {as} \,\ n\rightarrow +\infty , \end{aligned}$$

(36)

which implies by (13) and the fact that $t\longmapsto \Vert y(t)\Vert$ decreases on $\mathbb {R}^+,$ that

$$\begin{aligned} \displaystyle \int _{0}^{T}| \langle BS(\tau )y(t_n),S(\tau )y(t_n)\rangle |d\tau \rightarrow 0 \,\ \hbox {as} \,\ n\rightarrow +\infty . \end{aligned}$$

(37)

In view of B is sequentially continuous and $S(\tau )$ is continuous $\forall \tau \ge 0,$ we infer that $S(\tau )y(t_n) \rightharpoonup S(\tau )\psi$ and $BS(\tau )y(t_n) \rightarrow BS(\tau )\psi$ as $n \rightarrow +\infty .$ Then $\displaystyle \lim _{n\rightarrow +\infty }\langle BS(\tau )y(t_n), S(\tau )y(t_n)\rangle =\langle BS(\tau )\psi , S(\tau )\psi \rangle .$ Hence, by the dominated convergence theorem, we have $\displaystyle \lim _{n\rightarrow +\infty }\displaystyle \int _0^T|\langle BS(\tau )y(t_n),S(\tau )y(t_n)\rangle |d\tau =\displaystyle \int _0^T|\langle BS(\tau )\psi ,S(\tau )\psi \rangle |d\tau .$ Moreover, it comes from (37) that $\displaystyle \int _0^T|\langle BS(\tau )\psi , S(\tau )\psi \rangle |d\tau =0.$ Since the map $\tau \longmapsto S(\tau )\psi$ is continuous on $[0,+\infty ),$ we deduce that $\langle BS(\tau )\psi , S(\tau )\psi \rangle = 0,\, \forall \tau \ge 0.$ By virtue of the weak observability condition (3) we get $\psi = 0.$ Hence $\omega _w(y_0)=\{0\},$ i.e., $y(t) \rightharpoonup 0$ as $t \rightarrow +\,\infty .$ Hence, the proof of Theorem 4.1 is completed.$\square$

In what follows we will give a necessary condition for the weak stability of the system (1).

Proposition 4.1

If the system (1) is weakly stable such that $(\mathcal {H}_1)-(\mathcal {H}_4)$ hold. Then for all $\varphi \in H,$ we have

$$\begin{aligned} BS(t)\varphi =0,\, \forall t\ge 0\Rightarrow S(t)\varphi \rightharpoonup 0\,\ \hbox {as}\,\ t\rightarrow +\infty . \end{aligned}$$

(38)

Proof

Suppose that the system (1) is weakly stabilizable, and let $\varphi \in H$ be such that $BS(t)\varphi =0,\, \forall t\ge 0.$ Then, it follows by using $(\mathcal {H}_4),$ that $y (t) = S (t) \varphi$ is the unique mild solution of (1) starting at $y (0) = \varphi .$ Consequently, the weak stabilization hypothesis implies that $S(t)\varphi \rightharpoonup 0\,\ \hbox {as}\,\ t\rightarrow +\infty .$

$\square$

Remark 4.1

• 1. Note that the sequential continuity notion coincides with the compactness condition, when the operator is linear.

• 2. The inequality (5) is not satisfied when the semigroup S(t) is compact. Indeed, if $(\varphi _{k})$ is an orthonormal basis of the Hilbert space H,  then applying (5) for $y = \varphi _{k}$ and using the fact that $\varphi _{k}\rightharpoonup 0,$ as $k\rightarrow +\infty ,$ we obtain the contradiction $\delta _T = 0.$ Hence, our exponential stabilization result here does not applied. However, the weak stabilization does.

• 3. If we replace the sequential continuous condition of B by the compactness condition of S(t),  we retrieve the same result of the Theorem 4.1.

5 Optimal control

In this section we are concerned with the following minimization problem:

(39)

where $h(\varphi )=\rho \log (1-\frac{\langle B\varphi ,\varphi \rangle }{1+|\langle B\varphi ,\varphi \rangle |}),\, \varphi \in H$ and $\mathcal {V}_{ad}$ is the set of all controls p which are bounded, i.e., $\exists p_{_{\max }}> 0,\, |p(t)| \le p_{_{\max }},\, \forall t \ge 0$ such that the corresponding solution y(.) to (1) exists on the interval $[0, +\infty [,$ and satisfies $\Vert y(t)\Vert \le M,\, \forall t\ge 0,$ where $M\ge 0$ and $Q(p) <+\infty .$

The following result provides significant information on the continuity of the state function with respect to the controls, and its stated as follows.

Theorem 5.1

Let A generates a semigroup S(t) of contractions on H and that B and N are two nonlinear operators satisfy $(\mathcal {H}_1)-(\mathcal {H}_4).$ Then, for all $y_0 \in H$ and $t > 0,$ the map $p \longmapsto y$ is continuous from $L^2([0, t]; \mathbb {R})$ to C([0, t], H).

Proof

Let $y_0 \in H$ and $t > 0$ be fixed. Let $p \in L^2([0, t]; \mathbb {R})$ and $(p_n) \subset L^2([0, t]; \mathbb {R})$ such that $p_n\rightarrow p$ in $L^2([0, t]; \mathbb {R})$ as $n\rightarrow +\infty$ and let y(t) and $y_{p_n}(t)$ are the solutions of the system (1) associated with control p(t) and $p_n(t)$ respectively. Then, the variation of constants formula gives:

$$\begin{aligned} \begin{array}{ll} y_{p_n}(t)-y(t) &{} =\displaystyle \int _{0}^{t} S(t-\tau )(p_n(\tau )-p(\tau ))By(\tau )d\tau \\ &{}\quad +\,\displaystyle \int _{0}^{t} S(t-\tau )p_n(\tau )(By_{p_n}(\tau )-By(\tau ))d\tau \\ &{}\quad +\,\displaystyle \int _{0}^{t} S(t-\tau )(Ny_{p_n}(\tau )-Ny(\tau ))d\tau . \end{array} \end{aligned}$$

Hence, using Schwartz’s inequality, we obtain $\Vert y_{p_n}(t)-y(t)\Vert \le \alpha _n+L_{M}\displaystyle \int _{0}^{t}(1+|p_n(\tau )|) \Vert y_{p_n}(\tau )-y(\tau )\Vert d\tau ,$ where $\alpha _n=L_{M}\Vert p_n-p\Vert _{L^2([0,t])}\Big (\displaystyle \int _{0}^{t}\Vert y(\tau )\Vert ^2 d\tau \Big )^{\frac{1}{2}}.$ It follows from the Gronwall’s inequality that

$$\begin{aligned} \Vert y_{p_n}(t)-y(t)\Vert \le \alpha _n e^{L_{M}(t+1)\displaystyle \int _{0}^{t}|p_n(\tau )|d\tau }. \end{aligned}$$

Then, using once again the Schwartz’s inequality, we get

$$\begin{aligned} \Vert y_{p_n}(t)-y(t)\Vert \le \alpha _n e^{L_{M}(t+1)\sqrt{t}\Big (\displaystyle \int _{0}^{t}|p_n(\tau )|^2 d\tau \Big )^{\frac{1}{2}}}, \end{aligned}$$

which tends to zero as $n\rightarrow +\infty$ and hence $y_{p_n}(t)\rightarrow y(t)$ in H and $y_{p_n}\rightarrow y$ in $L^2([0, t]; H)$ as $n\rightarrow +\infty .$$\square$

In what follows, we use the crucial following lemma to solve the optimal control problem (39).

Lemma 5.1

Let A generate a semigroup S(t) of contractions on H and let B and N are two nonlinear operators satisfy $(\mathcal {H}_1)-(\mathcal {H}_4).$ Then, for all $p \in \mathcal {V}_{ad},$ there exists $K = K(\rho , T, M, L_{M}, p_{_{\max }}) > 0$ such that

$$\begin{aligned}&\displaystyle \int _{0}^{T}|\langle BS(\tau )y(t), S(\tau )y(t)|d\tau \nonumber \\&\quad \le K (1+e^{(1+p_{_{\max }})TL_M}) \Vert y(t)\Vert \nonumber \\&\qquad \times \,\bigg \{\bigg (\displaystyle \int _{t}^{t+T}\frac{|\langle By(s),y(s)\rangle |}{|h(y(s))|}|p(s) |^2 ds\bigg )^{\frac{1}{2}} \nonumber \\&\qquad +\,\bigg (\displaystyle \int _{t}^{t+T}|h(y(s))\langle By(s),y(s)\rangle | d\tau \bigg )^{\frac{1}{4}} \bigg \}. \end{aligned}$$

(40)

Proof

In view of

$$\begin{aligned}&\displaystyle \frac{d}{dt}\Vert y(t)\Vert ^2\le 2\rho \log \left( 1-\frac{\langle By(t),y(t) \rangle }{1+|\langle By(t),y(t) \rangle |}\right) \\&\quad \times \langle By(t),y(t)\rangle +\,2\langle Ny(t),y(t)\rangle \le 0,\, \forall y_0\in \mathcal {D}(A), \end{aligned}$$

we deduce that (7) is an admissible control, so $\mathcal {V}_{ad}\ne \emptyset .$ Let $p \in \mathcal {V}_{ad},\, t \ge 0.$ The solution of the system (1) satisfies:

$$\begin{aligned} y(\tau )= & {} S(\tau -t)y(t)+\displaystyle \int _{t}^{\tau }S(\tau -s)p(s)By(s)ds\nonumber \\&+\,\displaystyle \int _{t}^{\tau }S(\tau -s)N y(s)ds,\, \tau \ge t. \end{aligned}$$

(41)

Applying the Gronwall’s inequality, we get

$$\begin{aligned} \Vert y(\tau )\Vert \le \Vert y(t)\Vert e^{(1+p_{_{\max }})TL_{M}},\,\ \forall \tau \in [t, t+T]. \end{aligned}$$

(42)

It follows by using Schwartz’s inequality and (42) from the expression:

$$\begin{aligned}&\langle BS(\tau -t)y(t), S(\tau -t)y(t)\rangle =\langle BS(\tau \nonumber \\&\quad -\,t)y(t) - By(\tau ), S(\tau -t)y(t)\rangle -\langle By(\tau ), z(\tau )\rangle \nonumber \\&\quad +\,\langle By(\tau ), y(\tau )\rangle \end{aligned}$$

(43)

where $z(\tau )=\displaystyle \int _{t}^{\tau }p(s)S(\tau -s)By(s)ds+\displaystyle \int _{t}^{\tau }S(\tau -s)Ny(s)ds,$ that

$$\begin{aligned}&|\langle BS(\tau -t)y(t),S(\tau -t)y(t)\rangle |\nonumber \\&\quad \le (1+e^{(1+p_{_{\max }})TL_{M}})L_{M}\Vert y(t)\Vert \Vert y(\tau )-S(\tau -t)y(t)\Vert \nonumber \\&\qquad +\,|\langle By(\tau ),y(\tau )\rangle |,\ \forall \tau \in [t, t+T]. \end{aligned}$$

(44)

From (41) by combining the Schwartz’s and Hölder’s inequalities with the fact that S(t) is a semigroup of contractions and employing the hypotheses ($\mathcal {H}_4$) and $\Vert y(t)\Vert \le M,\, \forall t\ge 0,$ we get for all $\tau \in [t, t + T ],$ that

$$\begin{aligned}&\Vert y(\tau )-S(\tau -t)y(t)\Vert \le ML_{M}\displaystyle \int _{t}^{t+T}|p(s)| ds\nonumber \\&\qquad +\displaystyle \int _{t}^{t+T}\Vert N y(s)\Vert ds \nonumber \\&\quad \le ML_{M}\displaystyle \int _{t}^{t+T}\frac{|\langle By(s),y(s)\rangle |^{\frac{1}{2}}}{|h(y(s))|^{\frac{1}{2}}}\times |p(s) |\times \frac{|h(y(s))|^{\frac{1}{2}}}{|\langle By(s),y(s)\rangle |^{\frac{1}{2}}}ds\nonumber \\&\qquad +\,\frac{\sqrt{T}}{\sqrt{\mu }} \bigg (\displaystyle \int _{t}^{t+T}|\langle By(s),y(s)\rangle |ds\bigg )^{\frac{1}{2}}\nonumber \\&\quad \le \sqrt{\rho T} ML_{M}\bigg (\displaystyle \int _{t}^{t+T}\frac{|\langle By(s),y(s)\rangle |}{|h(y(s))|} p^2(s)ds \bigg )^{\frac{1}{2}}\nonumber \\&\qquad +\,\dfrac{\sqrt{T}}{\sqrt{\mu }} \bigg (\displaystyle \int _{t}^{t+T}|h(y(s))\langle By(s),y(s)\rangle |^{\frac{1}{2}}\frac{|\langle By(s),y(s)\rangle |^{\frac{1}{2}}}{|h(y(s))|^{\frac{1}{2}}}ds\bigg )^{\frac{1}{2}}.\nonumber \\ \end{aligned}$$

(45)

In view of (44) by using the last inequality (45) we infer for all $\tau \in [t, t+T],$ that

$$\begin{aligned}&|\langle BS(\tau -t)y(t),S(\tau -t)y(t)\rangle | \nonumber \\&\quad \le \sqrt{\rho T} M L_{R}^2(1+e^{(1+p_{_{\max }})TL_{M}})\Vert y(t)\Vert \nonumber \\&\qquad \times \,\bigg (\displaystyle \int _{t}^{t+T}\frac{|\langle By(s),y(s)\rangle |}{|h(y(s))|} p^2(s)ds \bigg )^{\frac{1}{2}}\nonumber \\&\qquad +\,\frac{\sqrt{T}}{\sqrt{\mu }}(1+e^{(1+p_{_{\max }})TL_{M}})L_{M}\Vert y(t)\Vert \nonumber \\&\qquad \times \, \bigg (\displaystyle \int _{t}^{t+T}|h(y(s))\langle By(s),y(s)\rangle |^{\frac{1}{2}}\frac{|\langle By(s),y(s)\rangle |^{\frac{1}{2}}}{|h(y(s))|^{\frac{1}{2}}}ds\bigg )^{\frac{1}{2}}\nonumber \\&\qquad +\,|\langle By(\tau ), y(\tau ) \rangle |\nonumber \\&\quad \le \sqrt{\rho T} M L_{M}^2(1+e^{(1+p_{_{\max }})TL_{M}})\Vert y(t)\Vert \nonumber \\&\qquad \times \,\bigg (\displaystyle \int _{t}^{t+T}\frac{|\langle By(s),y(s)\rangle |}{|h(y(s))|} p^2(s)ds \bigg )^{\frac{1}{2}}\nonumber \\&\qquad +\,\frac{\sqrt{T}}{\sqrt{\mu }}(1+e^{(1+p_{_{\max }})TL_{M}})L_{M}\Vert y(t)\Vert \nonumber \\&\qquad \times \, \bigg (\displaystyle \int _{t}^{t+T}|h(y(s))\langle By(s),y(s)\rangle |^{\frac{1}{2}}\frac{|\langle By(s),y(s)\rangle |^{\frac{1}{2}}}{|h(y(s))|^{\frac{1}{2}}}ds\bigg )^{\frac{1}{2}}\nonumber \\&\qquad +\,L_{M}^{\frac{1}{2}}e^{(1+p_{_{\max }})TL_{M}} \Vert y(t)\Vert |h(y(s))\langle By(\tau ),y(\tau )\rangle |^{\frac{1}{4}}\nonumber \\&\qquad \times \,\displaystyle \frac{|\langle By(\tau ),y(\tau )\rangle |^{\frac{1}{4}}}{|h(y(\tau ))|^{\frac{1}{4}}}. \end{aligned}$$

(46)

It yields from (46) by using (27) and using still $\Vert y(t)\Vert \le M,\, \forall t\ge 0,$ with Schwartz’s inequality that

$$\begin{aligned}&|\langle BS(\tau -t)y(t),S(\tau -t)y(t)\rangle | \nonumber \\&\quad \le \sqrt{\rho T} M L_{M}^2(1+e^{(1+p_{_{\max }})TL_{M}})\Vert y(t)\Vert \nonumber \\&\qquad \times \,\bigg (\displaystyle \int _{t}^{t+T}\frac{|\langle By(s),y(s)\rangle |}{|h(y(s))|} p^2(s)ds \bigg )^{\frac{1}{2}}\nonumber \\&\qquad +\,\frac{(2\rho ^{-1}T^3(1{+}L_{M}M^2))^{\frac{1}{4}}}{\sqrt{\mu }}(1{+}e^{(1+p_{_{\max }})TL_{M}})L_{M}\Vert y(t)\Vert \nonumber \\&\qquad \times \,\bigg (\displaystyle \int _{t}^{t+T}|h(y(s))\langle By(s),y(s)\rangle |ds\bigg )^{\frac{1}{4}}\nonumber \\&\qquad +\,(2\rho ^{-1}(1+L_{M}M^2))^{\frac{1}{4}} L^{\frac{1}{2}}_{M}e^{(1+p_{_{\max }})TL_{M}}\nonumber \\&\qquad \times \,\Vert y(t)\Vert |h(y(\tau ))\langle By(\tau ),y(\tau )\rangle |^{\frac{1}{4}}. \end{aligned}$$

(47)

Integrating the last inequality with respect $\tau$ over $[t, t + T ],$ and using twice the Schwartz’s inequality, then yields the desired estimate (40) where $K :=\max \Big \{\sqrt{\rho }T^{\frac{3}{2}} M L_{M}T, (2\rho ^{-1} T^3L_{M})^{\frac{1}{4}}(1+\frac{L_{M}^{\frac{1}{2}}}{\mu ^{\frac{1}{2}}})\Big \}.$$\square$

Theorem 5.2

Let A generate a semigroup S(t) of isometries on H and let B and N are two nonlinear operators satisfy $(\mathcal {H}_1)-(\mathcal {H}_4)$ such that (5) holds. Then, any admissible control is a strongly stabilizing one and furthermore, the control (7) is the unique solution of (39).

Proof

Integrating the relation (19), we obtain

$$\begin{aligned}&2\displaystyle \int _{0}^{t}|\langle By(\tau ),y(\tau )\rangle h(y(\tau ))|d\tau \nonumber \\&\quad +\,2\displaystyle \int _{0}^{t}|\langle Ny(\tau ),y(\tau )\rangle |d\tau \le \Vert y_0\Vert ^ 2,\, \forall t\ge 0. \end{aligned}$$

(48)

This last inequality holds $\forall y_0 \in H,$ since by virtue of (21), the function $y_0 \longmapsto y(t)$ is continuous from H to $L^2(0, t;H).$ Then $p^*_{_{\log }} \in \mathcal {V}_{ad}$ and then $\mathcal {V}_{ad} \ne \emptyset .$ Let $t > 0,$$p \in C^1([0, t]),$ and let y(.) be the corresponding solution of the system (1). For $y_0 \in \mathcal {D}(A)$ and $s \in [0, t],$ we have $y(s) \in \mathcal {D}(A)$ and $s\longmapsto y(s)$ is differentiable. This assertion follows from [8]. So, for all $p\in \mathcal {V}_{ad}$ there exists a sequence $(p_n)\subset C^1([0, t])$ such that $p_n \rightarrow p$ in $L^2(0, t, H)$ as $n\rightarrow +\infty .$ Then, since A is skew-adjoint and the fact that $p_n\in C^1([0, t])$ then the corresponding solution $y_{p_n}(t)$ to $p_n(t)$ verifies

$$\begin{aligned}&\frac{d\Vert y_{p_n}(t)\Vert ^2}{dt}=\frac{|\langle By_{p_n}(t),y_{p_n}(t)\rangle |}{|h(y_{p_n}(t))|}\Big \{ h(y_{p_n}(t))-p_n(t)\Big \}^2\\&\quad -\,\frac{|\langle By_{p_n}(t),y_{p_n}(t)\rangle |}{|h(y_{p_n}(t))|}\Big \{ h^2(y_{p_n}(t))+p^2_n(t)\Big \}\\&\quad -\,2|\langle Ny_{p_n}(t),y_{p_n}(t)\rangle |. \end{aligned}$$

This means that

$$\begin{aligned}&\displaystyle \int _{0}^{t}\Big \{\frac{|\langle By_{p_n}(t),y_{p_n}(t)\rangle |}{|h(y_{p_n}(t))|}|p_n(t)|^2\nonumber \\&\qquad + |h(y_{p_n}(t))\langle By_{p_n}(t),y_{p_n}(t)\rangle |\Big \}d\tau \nonumber \\&\quad =\displaystyle \int _{0}^{t} \frac{|\langle By_{p_n}(t),y_{p_n}(t)\rangle |}{|h(y_{p_n}(t))|}|h(y_{p_n}(\tau ))-p_n(\tau )|^2 d\tau \nonumber \\&\qquad -\,2\displaystyle \int _{0}^{t}|\langle Ny_{p_n}(t),y_{p_n}(t)\rangle | d\tau +\Vert y_{p_n}(0)\Vert ^2-\Vert y_{p_n}(t)\Vert ^2.\nonumber \\ \end{aligned}$$

(49)

Letting $n \rightarrow +\infty ,$ and using the fact that the two maps $y_0\longmapsto y(t)$ and $p\longmapsto y(t)$ are continuous, we obtain

$$\begin{aligned}&\displaystyle \int _{0}^{t}\Big \{\frac{|\langle By(t),y(t)\rangle |}{|h(y(t))|}|p(t)|^2+ |h(y(t))\langle By(t),y(t)\rangle |\Big \}d\tau \nonumber \\&\quad =-\,2\displaystyle \int _{0}^{t}|\langle Ny(t),y(t)\rangle | d\tau +\Vert y_0\Vert ^2-\Vert y(t)\Vert ^2 \nonumber \\&\qquad +\,\displaystyle \int _{0}^{t} \frac{|\langle By(t),y(t)\rangle |}{|h(y(t))|}|h(y(\tau ))-p(\tau )|^2 d\tau . \end{aligned}$$

(50)

In view of (5) and (40) we deduce that

$$\begin{aligned}&\delta \Vert y(t)\Vert \le K (1+e^{(1+p_{_{\max }})TL_{M}})\nonumber \\&\quad \times \,\bigg \{\bigg (\displaystyle \int _{t}^{t+T}\frac{|\langle By(s),y(s)\rangle |}{|h(y(s))|}|p(s) |^2 ds\bigg )^{\frac{1}{2}}\nonumber \\&\quad +\,\bigg (\displaystyle \int _{t}^{t+T}|h(y(s))\langle By(s),y(s)\rangle | d\tau \bigg )^{\frac{1}{4}} \bigg \}. \end{aligned}$$

(51)

Since $Q(p) <+\infty ,$ by Cauchy criterion, we have

$$\begin{aligned}&\displaystyle \int _{t}^{t+T}\frac{|\langle By(\tau ),y(\tau )\rangle |}{|h(y(\tau ))|}|p(\tau )|^2 d\tau \rightarrow 0\,\ \hbox {and}\,\ \\&\quad \times \,\displaystyle \int _{t}^{t+T}|h(y(\tau ))\langle By(\tau ),y(\tau )\rangle | d\tau \rightarrow 0\,\ \hbox {as}\,\ t\rightarrow +\infty . \end{aligned}$$

Then, from (51) one can deduce that $\Vert y(t)\Vert \rightarrow 0$ as $t\rightarrow +\,\infty .$ In other words p is a strongly stabilizing control. Then, letting $t\rightarrow +\infty$ in (50), we get

$$\begin{aligned} Q(p)=\Vert y_{0}\Vert ^2+\displaystyle \int _{0}^{+\infty } \frac{|\langle By(t),y(t)\rangle |}{|h(y(t))|}|h(y(\tau ))-p(\tau )|^2 d\tau , \end{aligned}$$

(52)

which implies that $Q(p) \ge \Vert y_{0}\Vert ^2=Q(p^*_{_{\log }}),\,\ \forall p\in \mathcal {V}_{ad},$ so that (7) is an optimal control of the problem (39). Let $p_i(t),\, i = 1, 2,$ be two solutions of the problem (39). From (52) we deduce that $p_i(t) = h (y_i(t)),$ where $y_i(t)$ verifies

$$\begin{aligned} \frac{d y(t)}{dt}=Ay(t)+h(y(t))By(t)+Ny(t),\,\ y(0)=y_0, \end{aligned}$$

thus $y_1(t) = y_2(t)$ and hence $p_1(t) = p_2(t).$$\square$

6 Applications

The main goal of this section is to present same applications to illustrate the previous theoretical results.

6.1 Strong stabilization

Example 6.1

Applications to Liénard’s equations.

Let us consider the two-dimensional system:

$$\begin{aligned}&\ddot{y}(t)=-\,y(t)+p(t)f(y(t))\dot{y}(t)+g(y(t))\dot{y}(t),\, t>0;\,\ \nonumber \\&\quad (y(0), \dot{y}(0))=(y_0,y_1) \end{aligned}$$

(53)

where $f, g : \mathbb {R}\longmapsto \mathbb {R}$ are two locally Lipschitz functions such that $f(0)=g(0)=0$ and $g\le 0.$ Here the space $H = \mathbb {R}^2.$ The inner product is defined by:

$$\begin{aligned} \langle y,z\rangle =y_1z_1+y_2z_2,\,\ \forall y=(y_1,y_2),z=(z_1,z_2)\in \mathbb {R}^2. \end{aligned}$$

If we set $A=\left( \begin{array}{cc} 0 &{} 1 \\ -1 &{} 0 \\ \end{array} \right) ,$$B\left( \begin{array}{c} y_1 \\ y_2 \\ \end{array} \right) =\left( \begin{array}{c} 0 \\ y_2f(y_1) \\ \end{array} \right)$ and $N\left( \begin{array}{c} y_1 \\ y_2 \\ \end{array} \right) =\left( \begin{array}{c} 0 \\ y_2 g(y_1) \\ \end{array} \right) ,\, \forall (y_1, y_2)\in H,$ one can easy deduce that the system (53) has the same form as (1). The operator A is skew adjoint and $e^{t A}=\left( \begin{array}{cc} \cos (t) &{} \sin (t) \\ -\sin (t) &{} \cos (t) \\ \end{array} \right)$ (see e.g [10]). Moreover, we have

$$\begin{aligned}&\left\langle B e^{t A}\left( \begin{array}{c} y_1 \\ y_2 \\ \end{array} \right) ,e^{t A}\left( \begin{array}{c} y_1 \\ y_2 \\ \end{array} \right) \right\rangle =(y_2 \cos (t)\\&\quad -\,y_1 \sin (t))^2 f (y_1 \cos (t) + y_2 \sin (t)). \end{aligned}$$

If $f (y_1) > 0,\, \forall y_1\ne 0,$ then (3) holds, as well as (5) since $\dim (H)<+\infty$ (see [9]). Moreover, ($\mathcal {H}_4$) is verified if there exists $\gamma >0$ such that $|g(y_1)|\le \gamma \sqrt{|f(y_1)|},\, \forall y_1\in \mathbb {R}.$ Hence, based on the Theorem 3.2 results, the solution of the system (53) satisfies:

$$\begin{aligned}&y^2(t)+\dot{y}^2(t)=\mathcal {O}(\displaystyle \frac{1}{t})\,\ \hbox {as}\,\ t\rightarrow +\infty ,\,\ \hbox {if}\,\ (y(t),\\&\dot{y}(t)) \ne (0, 0) \end{aligned}$$

using the feedback control defined by:

$$\begin{aligned} p^*_{_{\log }}(t)=\left\{ \begin{array}{ll} \rho \log (1-\displaystyle \frac{\dot{y}^2(t) f(y(t))}{1+\dot{y}^2(t) |f(y(t))|)} &{} (y(t), \dot{y}(t)) \ne (0, 0) \\ 0, &{} (y(t),\dot{y}(t)) =( 0,0). \end{array} \right. \end{aligned}$$

The resulting stabilized semilinear system (53) constitutes a special class of Liénard equations which is more general than that treated in ([11, 12]) when they considered only the case $g = 0.$ Furthermore, the stabilizing feedback control $p^*_{_{\log }}(t)$ minimizes the following cost:

$$\begin{aligned} Q(p)= & {} \displaystyle \int _{0}^{+\infty } \Big \{ \Big (\frac{p^2(t)}{\rho \log (1+f(y(t))\dot{y}^2(t))} \\&+\,\rho \log (1+f(y(t))\dot{y}^2(t))\Big )f(y(t))\dot{y}^2(t)) \\&+\,2g(y(t))\dot{y}^2(t)\Big \} dt,\,\ \forall p\in \mathcal {V}_{ad}, \end{aligned}$$

more precisely, we have $Q(p^*_{_{\log }})=y^2(0)+\dot{y}^2(0).$

Example 6.2

The beam equation.

In this example we consider the monodimensional beam equation with Neumann boundary conditions, which is given by:

$$\begin{aligned} \left\{ \begin{array}{lll} \dfrac{\partial ^2 y}{\partial t^2}(x,t) =-\,\dfrac{\partial ^4 y(x,t)}{\partial x^4}+p(t)\dfrac{\partial y}{\partial t}(x,t) \\ -\dfrac{\dfrac{\partial y}{\partial t}(x,t)}{1+|\dfrac{\partial y}{\partial t}(x,t)|}\quad (x,t)\in (0,1)\times (0,+\infty ) \\ y(\xi ,t) =\dfrac{\partial ^2 y}{\partial x^2}(\xi ,t)=0\quad (\xi ,t)\in \{0,1\}\times [0,+\infty ). \end{array} \right. \end{aligned}$$

(54)

Let us note that $A_1=-\,\dfrac{\partial ^4 }{\partial x^4},$ we have $\mathcal{D}(A_1)=\{y\in L^2(0,1);\,\ A_1 y\in L^2(0,1),\, y(x,.) =\dfrac{\partial ^2 y}{\partial x^2}(x,.)=0,\,x\in \{0,1\}\};$ and $V=\mathcal{D}(A_1^\frac{1}{2})$ is a Hilbert space endowed with the inner product

$$\begin{aligned} \langle y_1,y_2\rangle _V=\langle A_1^\frac{1}{2}y_1,A_1^\frac{1}{2}y_2\rangle _{L^2(0,1)}=\displaystyle \int _{0}^{1}\frac{\partial ^2 y_1(t)}{\partial x^2}\frac{\partial ^2 y_2(t)}{\partial x^2}dx \end{aligned}$$

(see [1]). Let $\varphi _j=\sqrt{2}\sin {(j\pi x)},\, \forall j\in I\! N^*,$ denote the normalized eigenfunctions of $A_1$ and its spectrum is formed by an increasing positive sequence $(\lambda _j)_{j\in \mathbb {N}^*}$ of corresponding eigenvalues, where $\lambda _j=(j\pi )^4.$ Here the state space $H=(H^2(0,1)\cap H_0^1(0,1))\times L^2(0,1)$ endowed with the inner product:

$$\begin{aligned}&\langle y,z\rangle =\langle y_1,z_1\rangle _V+\langle y_2,z_2\rangle _{ L^2(0,1)}=\displaystyle \int _{0}^{1}\frac{\partial ^2 y_1(t)}{\partial x^2}\frac{\partial ^2 z_1(t)}{\partial x^2}dx\\&\quad +\,\displaystyle \int _{0}^{1}y_2(t)z_2(t)dx,\,\, \forall \, y=(y_1,y_2),\,z=(z_1,z_2)\in H. \end{aligned}$$

If we denote $A=\left( \begin{array}{cc} 0 &{} I \\ A_1 &{} 0 \\ \end{array} \right) ,$$B=\left( \begin{array}{cc} 0 &{} 0 \\ 0&{} I \\ \end{array} \right)$ and $N=\left( \begin{array}{cc} 0 &{} 0 \\ 0 &{} f\\ \end{array} \right)$ where $f(\phi )=-\,\displaystyle \frac{\phi }{1+|\phi |}.$ The system (54) can be rewritten to the abstract initial form (1). It is easy to see that $(\mathcal {H}_1)-(\mathcal {H}_4)$ are satisfied. Furthermore, the condition (5) is verified. Indeed, let $y=\displaystyle \sum _{j= 1}^{+\infty }\left( \begin{array}{c} \alpha _j\\ \sqrt{\lambda _j }\,\beta _j \\ \end{array} \right) \varphi _j\in H.$ Using separation of variables argument of the semigroup S(t) generated by the skew adjoint operator A,  we obtain

$$\begin{aligned}&S(t)y=\displaystyle \sum _{j= 1}^{+\infty }\left( \begin{array}{c} \alpha _j\cos {(\sqrt{\lambda _j}\,t)}+\beta _j\sin {(\sqrt{\lambda _j}\,t)}\\ -\alpha _j\sqrt{\lambda _j}\sin {(\sqrt{\lambda _j}\,t)}+\beta _j\sqrt{\lambda _j} \cos {(\sqrt{\lambda _j}\,t)} \\ \end{array} \right) \nonumber \\&\quad \varphi _j,\,\ \forall t\ge 0, \end{aligned}$$

(55)

which implies

$$\begin{aligned}&\langle BS(t)y,S(t)y\rangle {=}\displaystyle \sum _{j= 1}^{+\infty }\lambda _j\Big (\alpha _j\sin {(\sqrt{\lambda _j}\,t)}{-}\beta _j\cos {(\sqrt{\lambda _j}\,t)}\Big )^2 \\&\quad =\displaystyle \sum _{j= 1}^{+\infty }\lambda _j\Big (\alpha _j^2\sin ^2{(\sqrt{\lambda _j}\,t)}-\alpha _j\beta _j\sin {(2\sqrt{\lambda _j}\,t)}\\&\qquad +\,\beta _j^2\cos ^2{(\sqrt{\lambda _j}\,t)}\Big ). \end{aligned}$$

It yields by integrating the last equality from 0 to $\frac{1}{\pi },$ that

$$\begin{aligned} \displaystyle \int _0^{\frac{1}{\pi }}|\langle BS(t)y,S(t)y\rangle |dt{=}\frac{1}{2\pi }\displaystyle \sum _{j= 1}^{+\infty }\lambda _j(\alpha _j^2+\beta _j^2){=}\frac{1}{2\pi }\Vert y\Vert ^2. \end{aligned}$$

So, the inequality (5) is verified for $T=\frac{1}{\pi }$ and $\delta _{\frac{1}{\pi }}=\frac{1}{2\pi }.$ We conclude by using Theorem 3.2 that the control:

Fig. 1

The norm of the stabilized state

$$\begin{aligned} p^*_{_{\log }}(t)=\left\{ \begin{array}{ll} -\rho \log (1+\int _{0}^{1}\\ \big (\frac{\partial }{\partial t} y(x,t)\big )^2dx),&{} \text{ if } (y(.,t),\frac{\partial }{\partial t} y(.,t)) \ne (0,0)\\ 0, &{} \text{ otherwise }, \end{array}\right. \end{aligned}$$

(56)

satisfies:

$$\begin{aligned}&\displaystyle \int _{0}^{1}\big (\frac{\partial ^2}{\partial x^2} y(x,t)\big )^2dx+\displaystyle \int _{0}^{1}\big (\frac{\partial }{\partial t} y(x,t)\big )^2 dx\\&\quad = \mathcal {O}\big (\displaystyle \frac{1}{t}\big )\,\ \hbox {as}\,\ t\rightarrow +\infty , \end{aligned}$$

where $\rho >0.$ Moreover, the stabilizing feedback control $p^*_{_{\log }}(t)$ minimizes the following cost:

$$\begin{aligned}&Q(p) = \displaystyle \int _{0}^{+\infty } \bigg \{ \Big [\frac{p^2(t)+\rho ^2\log ^2(1+\int _{0}^{1}\big (\frac{\partial }{\partial t} y(x,t)\big )^2dx)}{\rho \log (1+\int _{0}^{1}\big (\frac{\partial }{\partial t} y(x,t)\big )^2dx)}\Big ]\\&\quad \times \,\int _{0}^{1}\big (\frac{\partial }{\partial t} y(x,t)\big )^2 dx +2\displaystyle \int _{0}^{1}\frac{\big (\frac{\partial }{\partial t} y(x,t)\big )^2 }{1+|\frac{\partial }{\partial t} y(x,t)|}dx\bigg \} dt,\, \forall p\in \mathcal {V}_{ad}. \end{aligned}$$

Example 6.3

Transport equation.

Consider the system defined on $H = L^2(0,+\infty )$ by the following equation

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial y}{\partial t}(x,t) =-\,\dfrac{\partial y(x,t)}{\partial x}\\ +p(t) a(x)y(x,t)\\ -\dfrac{y(x,t)}{1+\Vert y(t)\Vert _{_H}},&{}(x,t)\in (0,+\infty )\times (0,+\infty ) \\ y(x,0)=y_0(x),&{} x\in (0,+\infty ). \end{array} \right. \end{aligned}$$

(57)

In the sequel, we take $a \in L^{\infty }(0,+\infty )$ such that $a\ge c>0$ in $(2,+\infty )$ and

$$\begin{aligned} a(x)=\left\{ \begin{array}{ll} -3, &{} 0<x<1 \\ 3, &{} 1\le x \le 2. \end{array} \right. \end{aligned}$$

Here, we take $Ay{=}-\,\dfrac{\partial y}{\partial x},$$\forall y\in \mathcal {D}(A){=}\{ H^1(0,+\infty );y(0)=0\}.$ Furthermore, the inner product is defined by:

$$\begin{aligned} \langle y_1,y_2\rangle =\displaystyle \int _{0}^{+\infty }y_1(t)y_2(t)dt,\,\ \forall y_1, y_2\in L^2(0,+\infty ). \end{aligned}$$

The operator A generates the semigroup of contractions $S(t),\, t \ge 0$ defined, for all $y_0 \in H,$ by

$$\begin{aligned} S(t)y_0(x)=\left\{ \begin{array}{ll} y_0(x-t), &{} \hbox {if}\,\ x>t \\ 0, &{} \hbox {if}\,\ x\le t, \end{array} \right. \end{aligned}$$

(see e.g. [13]). Furthermore, it is evidently to see that $(\mathcal {H}_1)-(\mathcal {H}_4)$ are satisfy. We will establish (5)) for $T = 2.$ We have

$$\begin{aligned}&\displaystyle \int _{0}^{2}|\langle BS(t)y_0(x),S(t)y_0(x) \rangle |dt \\&\quad =\displaystyle \int _{0}^{2}\int _{t}^{+\infty }|a(x)|y^2_0(x-t)dxdt \\&\quad =\displaystyle \int _{0}^{+\infty }y^2_0(x)\displaystyle \int _{0}^{2}|a(x+t)|dtdx \\&\quad \ge 2\min \{3, c\}\Vert y_0\Vert _{_H}^2. \end{aligned}$$

This implies (5). Hence, the following control $p_{_{\log }}^*(t)=\log (1-\frac{\int _{0}^{+\infty }a(x)y(x)dx}{1+|\int _{0}^{+\infty }a(x)y(x)dx|})$ strongly stabilizes (57) with the decay estimate: $\displaystyle \int _{0}^{+\infty }y^2(x,t)dx=\mathcal {O}(\frac{1}{t})\,\ \hbox {as}\,\ t\rightarrow +\infty .$

6.2 Weak stabilization

Example 6.4

The heat equation.

Let us consider the semilinear heat equation with Neumann boundary conditions:

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial y}{\partial t}(x,t) =\dfrac{\partial ^2 y(x,t)}{\partial x^2}\\ +p(t) By(x,t)+N y(x,t),&{}(x,t)\in (0,1)\times (0,+\infty ) \\ \dfrac{\partial y}{\partial x}(0,t)=\dfrac{\partial y}{\partial x}(1,t)=0,&{} \forall t\ge 0, \end{array} \right. \end{aligned}$$

(58)

Here $H=L^2(0,1);$$A=\dfrac{\partial ^2 }{\partial x^2}$ and $\mathcal{D}(A)=\{y\in H^2(0,1);\, \dfrac{\partial y}{\partial x}(0,t)=\dfrac{\partial y}{\partial x}(1,t)=0\}.$ Moreover, the inner product is defined by:

$$\begin{aligned} \langle y_1,y_2\rangle =\displaystyle \int _{0}^{1}y_1(x)y_2(x)dx,\,\ \forall y_1, y_2\in L^2(0,1). \end{aligned}$$

The normalized eigenfunctions of A are given by $\varphi _1(x)=1$ and $\varphi _j(x)=\sqrt{2}\cos {((j-1)\pi x)},$ associated with its eigenvalues $\lambda _1=0$ and $\lambda _j=-\,(j-1)^2\pi ^2,\, \forall j\ge 2$ respectively. The operator A generates a semigroup of contractions S(t) such that $S(t)y=\displaystyle \sum _{j=1}^{+\infty }e^{\lambda _j t} \langle y,\varphi _j\rangle \varphi _j$ and we consider $By=\displaystyle \sum _{j=1}^{+\infty }\alpha _j\langle y,\varphi _j\rangle \varphi _j,$ where $\alpha _j> 0,\, \forall j\ge 1,$ such that $\displaystyle \sum _{j=1}^{+\infty }\alpha ^2_j <+\infty .$ Clearly B is compact. Moreover, we have $\langle BS(t)y,S(t)y\rangle =\displaystyle \sum _{j=1}^{+\infty }\alpha _j e^{2 \lambda _j t}|\langle y, \varphi _j\rangle |^2,\, \forall t\ge 0.$ Besides, we set $Ny=-\,\displaystyle \sum _{j=1}^{+\infty }\frac{\sqrt{\alpha _j}}{1+\Vert y\Vert }\langle y,\varphi _j\rangle \varphi _j,\, \forall y\in L^2(0,1).$ It is clear that (3) holds as well as all the hypotheses $(\mathcal {H}_1)-(\mathcal {H}_4).$ Consequently, by Theorem 4.1 result, the control:

$$\begin{aligned} p^*_{_{\log }}(t)=\left\{ \begin{array}{ll} -\rho \log (1+\sum _{j=1}^{+\infty }\alpha _j|\langle y,\varphi _j\rangle |^2)&{} \text{ if } y(.,t)\ne 0 \\ 0&{}\text{ otherwise }, \end{array} \right. \end{aligned}$$

weakly stabilizes (58).

Fig. 2

The norm of the free state

Fig. 3

The evolution of the stabilizing control

Fig. 4

The evolution of $\frac{p^*_{\log }(.)}{p_*(.)}$

Remark 6.1

With the usual homogeneous Dirichlet boundary conditions, the eigenvalues of the operator $\Delta$ are all $\lambda _j < 0,$ for any $j \ge 1.$ Then, using the hypothesis $(H_3),$ the system (58) is exponentially stable (taking $p(t) = 0$).

7 Simulations

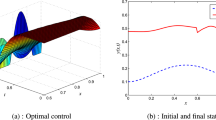
In this section, we give simulations of the system (53). Taking $\rho =0.2$ which satisfies the second point of the Remark 3.1. Furthermore, we take $f(y)=|y|,$$g(y)=10^{-3}y^2,$$y(0)=2$ and $\dot{y}(0)=0.$ Then, we obtain the results shown in the Figs. 1, 2, 3 and 4.

From Fig. 4, one can deduce that $|p^*_{\log }|=o(|p_*|)$ as $t\rightarrow +\infty .$

7.1 Conclusion

Under the exact observability inequality (5) we have established the polynomial stabilization for infinite dimensional semilinear systems with a new constrained multiplicative feedback control. The rate of polynomial convergence is explicitly expressed. We also have considered the question of weak stabilization by the same feedback control. Moreover, the stabilizing feedback is the unique minimizing control of an appropriate functional cost. Furthermore, some applications are given to illustrates our main results. Also, the simulations illustrate perfectly the established theoretical results.