1 Introduction

Over the last few decades, stabilization as well as tracking of an underactuated mechanical systems have drawn researchers’ attention. The underactuated mechanical systems (UMS) are having sets of nonlinear dynamical equations with lesser actuators than configuration variables. These systems are increasing demand day to day due to theoretical hindrance and practical implementation. The control of UMS requires a broad analysis because of its large applications in robot manipulators, underwater vehicles, aerospace engineering [1,2,3], etc. The lower numbers of control inputs in these class of systems have the perspectives of reducing weight and cost, increasing reliability and sustaining less energy. In order to design the controller, the class of systems play a crucial role because they fail to obey Brockett’s necessary condition [4]; these are the non-minimum phase systems and relative degrees of them are not properly defined [5]. The feedback linearization (FL) is not realizable due to nonlinear linked between actuated and unactuated degrees of freedom. Also, until and unless the zero dynamics [6] stabilization guarantees, the partial feedback linearization (PFL) [7] is not possible for these particulars.

The rotational pendulum falls under category of an underactuated mechanical systems, which yields above-mentioned structural difficulties due to underactuation. The RP system is also familiar as Furuta pendulum (FP) by its inventor name Katsuhisa Furuta. It composes of a driven arm which can rotate \(360^{\circ }\) angles in the horizontal plane, and a pendulum which is joined to the arm and spins vertically [8]. The actuator is right attached to the arm of the rotational pendulum system. There is no direct control signal for the pendulum, converting it underactuated. The research of the rotational pendulum was motivated by an essential of controller design to balance the rocket in a vertical steady position during the time that it escapes. The RP model is highly nonlinear, coupled, open-loop unstable, found to possess non-minimum phase structure, and is not feedback linearizable. Therefore, the original problem consists of stabilizing the pendulum around its upright position during rotation of arm. There are diverse control techniques for the rotational pendulum found in the literature. The energy based controls are formulated to swing-up the pendulum discussed in [9,10,11]. However, these are explicitly applicable to the problem of swinging-up. Furthermore, a nonlinear controller based on approximate linearization [12], a constructive procedure via the FL [13], a stabilizing controller through the PFL [14], the FL controller selecting position and velocity tracking errors as an output function [15], and a trajectory tracking controller derived from the input–output FL [16] are applied to the FP. Anyway, the closed loop analysis of the controllers developed through linearization techniques, for e.g., partial linearization, approximate linearization, and pseudo-linearization are inconvenient to obtain. In addition, the rotational pendulum system is highly uncertain in nature because of large nonlinear terms present in the model, unstructured dynamics, coupling between actuated and unactuated variables along with deviations in the model parameters and external disturbance interacting in it. The Kalman filtering based technique applied to a similar one of the rotational pendulum system is found in [17]. In [18], a flatness based approach is incorporated to design the controller for local stabilization of the FP. Only unmodeled perturbation affecting in arm is considered to validate the controller. In [19], an active disturbance rejection control (ADRC) is designed with two decoupled linear observers which are obtained by flatness of linearized model of FP. The number of observers in ADRC lead to design complexity in the controller. Nonetheless, the flatness property decomposes non-integral chain form of the RP into integral chain, the controller design meets challenge while the system is coupled, highly nonlinear, holds non-minimum phase characteristics and is not in phase variable form. Therefore, stabilization of the pendulum around its upright position against unavoidable nonlinearities existing in the model, large parametric uncertainty and external disturbance requires the robust controller.

The SMC, type of variable structure controllers (VSC), is very powerful design strategy in the control systems community due to its simple constructive procedure and robustness property against matching condition [20]. A comparative study of SMC strategies is found in [21]. In particular, there has been some research on SMC in the literature which is successfully applied to the RP system. In [22], a nonlinear SMC designed by the state-dependent Riccati equation (SDRE) is applied for swinging-up and stabilization of the FP. A coupled SMC forcing a coupled sliding surface to be reached in finite time is proposed in [23]. The adaptive PID with SMC for the RP is applied in which parameter gains of controller are obtained via adaptive law given in [24]. An optimal sliding mode cascade control is proposed in [25] for stabilization of the pendulum. In [26], an adaptive SMC is implemented for the FP. However, in presence of large parametric uncertainty arising in the model and a bounded time-varying external disturbance (with unknown upper bound) imposing in the model, the above-mentioned schemes may not give satisfactory performance. Therefore, the SMC design is fairly inspiring for the underactuated rotational pendulum system.

The variations in pendulum dynamics with gravitational change while it swings-up from its highly stable to most unstable vertical upright locus through rotation of an arm, is considered as an uncertainty. In addition, coupling coefficients between actuated and unactuated degrees of freedom always introduce some uncertainty in the model. The motivation of feedback control strategy, e.g. the SMC requires feedforward control in addition which can estimate the highly nonlinear terms (disturbance) in the model. The observer based techniques, such as a nonlinear disturbance observer has strong design structure to eliminate an adverse effects of large nonlinearities. By design, the NDO is placed in forward whereas the SMC is put in feedback as given in [27,28,29,30]. The estimations of nonlinearities are included in the design part of the SMC, so that it can stabilize the output variables in spite of extremely nonlinear terms present in the model, in addition large perturbations along with external disturbance. Besides, the conventional SMC has a significant disadvantage of high-frequency oscillations [31] due to discontinuous function in the control input. The oscillation is known as chattering which can yield instability and unwanted system response. One of the solutions is the higher-order SMC [32] which has replaced classical sliding mode approach due to its chattering avoidance properties [33]. But, the higher-order SMC has an implementation complexity for the particular. The simpler way to make control signal smooth is by introducing a saturation function in the switching control which is designed as a combination of power rate reaching law and proportional rate term. The chattering is reduced by predefined boundary layer in saturation function with some trade-off in control.

Fig. 1
figure 1

The rotational pendulum system

Full size image

The contributions are highlighted as follows:

  • A nonlinear disturbance observer based sliding mode control law is proposed of stabilizing the fourth order extremely nonlinear coupled rotational pendulum system.

  • The controller is developed to balance the pendulum around its vertical unstable equilibrium locus from different initial positions through rotation of an arm.

  • The design modification in the SMC is done by adding disturbance (massive nonlinear terms present in the model) estimation via a NDO, so that it can stabilize the output variables in presence of severe nonlinearities in the model with large parametric uncertainty and external disturbance.

  • As a result, the control strategy offers enlarged stability region of an arm (in horizontal half-plane) and a pendulum (over vertical half-plane) both for large initial conditions.

  • Also, the controller design ensures an asymptotic stability of the zero dynamics in the form of sliding mode dynamics via obtained sliding coefficients using the LQR technique.

  • Furthermore, the chattering is mitigated with the combination of power rate reaching law and proportional rate term in the switching control.

  • The asymptotic stability of the overall rotational pendulum system is proven using energy like Lyapunov function.

The rest of the paper is outlined as follows. In Sect. 2, the dynamic model of the RP is described. The NDO and its stability proof are formulated in Sect. 3. Section 4 explains development of the NDO based SMC scheme for stabilization of the pendulum together with stability analysis. The zero dynamics stabilization is narrated in Sect. 5. The simulation results with discussions are presented in Sect.  6. Concluding remarks are conveyed in Sect. 7, followed by acknowledgements and references.

2 Dynamic model of the rotational pendulum

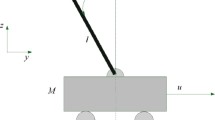
The equations of motion for the RP system shown in Fig. 1 is described by Euler–Lagrange method as [2]

$$\begin{aligned} \frac{d}{dt}\frac{\partial L(\mathbf q ,\dot{\mathbf{q }})}{\partial \dot{\mathbf{q }}}-\frac{\partial L(\mathbf q ,\dot{\mathbf{q }})}{\partial \mathbf q }=\mathbf F (\mathbf q )u \end{aligned}$$
(1)

where the kinetic and the potential energies are K and P, and the Lagrangian of the system is \(L=K-P\); the output variables (actuated and unactuated) and their velocities are \(\mathbf q =\left[ q_1,q_2 \right] ^T\in {\mathbb {R}}^2\) and \(\dot{\mathbf{q }}=\left[ \dot{q}_1,\dot{q}_2 \right] ^T\in {\mathbb {R}}^2\), respectively; \(\mathbf F (\mathbf q )=\left[ 1,0 \right] ^T\) is the input matrix; and \(u\in {\mathbb {R}}^1\) is the control signal.

Equation (1) is written alternatively as

$$\begin{aligned} \underbrace{\begin{bmatrix} d_{11}&\quad d_{12} \\ d_{21}&\quad d_{22} \end{bmatrix}}_\mathbf{D (\mathbf{q })} \begin{bmatrix} \ddot{q_1} \\ \ddot{q_2} \end{bmatrix} + \underbrace{\begin{bmatrix} c_{11}&\quad c_{12} \\ c_{21}&\quad c_{22} \end{bmatrix}}_\mathbf{C (\mathbf q ,\dot{\mathbf{q }})} \begin{bmatrix} \dot{q_1} \\ \dot{q_2} \end{bmatrix} + \underbrace{\begin{bmatrix} g_{1} \\ g_{2} \end{bmatrix}}_\mathbf{G (\mathbf{q })} = \begin{bmatrix} u \\ 0 \end{bmatrix} \end{aligned}$$
(2)

where the inertia matrix \(\mathbf D (\mathbf{q })\) is symmetric and positive-definite, coriolis and centrifugal force matrix is \(\mathbf C (\mathbf q ,\dot{\mathbf{q }})\), and gravitational force vector is \(\mathbf G (\mathbf{q })\).

(or),

$$\begin{aligned}&\begin{bmatrix} J_1+m_2(l^2_1+l^2_2\sin ^2\phi _2)&\quad m_2l_2l_1\cos \phi _2 \\ m_2l_2l_1\cos \phi _2&\quad J_2+m_2l^2_2 \end{bmatrix} \begin{bmatrix} \ddot{{\phi }_1} \\ \ddot{{\phi }_2} \end{bmatrix} \nonumber \\&\quad + \begin{bmatrix} \frac{1}{2}m_2l^2_2\sin (2\phi _2)\dot{\phi }_2&\quad -~m_2l_2l_1\sin (\phi _2)\dot{\phi }_2 \\&\quad +~\frac{1}{2}m_2l^2_2\sin (2\phi _2)\dot{\phi }_1 \\ -~\frac{1}{2}m_2l^2_2\sin (2\phi _1)\dot{\phi }_1&\quad 0 \end{bmatrix} \begin{bmatrix} \dot{{\phi }_1} \\ \dot{{\phi }_2} \end{bmatrix}\nonumber \\&\quad + \begin{bmatrix} 0 \\ -~m_2gl_2\sin \phi _2 \end{bmatrix} = \begin{bmatrix} u \\ 0 \end{bmatrix} \end{aligned}$$
(3)

where pendulum mass is \(m_2\); arm length and distance to the center of gravity (CG) of pendulum are \(l_1\) and \(l_2\); arm inertia and pendulum inertia around its CG are \(J_1\) and \(J_2\); rotational angles of arm and pendulum are \(\phi _1\) and \(\phi _2\), respectively.

Now, the following state space form of (3) obtained using the property of Legendre transformation in [3] is

$$\begin{aligned} \dot{z}_1&=z_2 \nonumber \\ \dot{z}_2&=a_1(z)+b_1(z)u \nonumber \\ \dot{z}_3&=z_4 \nonumber \\ \dot{z}_4&=a_2(z)+b_2(z)u \end{aligned}$$
(4)

where \(z_1=\phi _1\), \(z_2=\dot{\phi }_1\), \(\dot{z}_2=\ddot{\phi }_1\), and \(z_3=\phi _2\), \(z_4=\dot{\phi }_2\), \(\dot{z}_4=\ddot{\phi }_2\). Also, \(a_1(z)\), \(a_2(z)\), \(b_1(z)\), and \(b_2(z)\) are smooth functions obtained from (3). The disturbances \(d_{c1}\) and \(d_{c2}\) imposed through the control input channels of (4) are accounted as matched, respectively.

Remark 1

The SMC law based on NDO is designed for the 4th order coupled nonlinear rotational pendulum system in (4) where extremely nonlinear terms in the model are accurately estimated through a NDO explained in the next section.

3 Nonlinear disturbance observer

The full order observer in [27] applied to the 4th order highly nonlinear coupled RP model in (4) is in the form of

(5)
(6)

where \(\hat{d}_j\) is the estimation of disturbance \(d_j\) (represents severe nonlinearities in the model), \(\hat{z}_{j+1}\) and \(\hat{z}_{j+2}\) are the estimations of states \(z_{j+1}\) and \(z_{j+2}\), respectively, and the observer gains \(p_j,p_{j+1}\) (for \(j = 1\)) and \(p_{j+1},p_{j+2}\) (for \(j = 2\)) must be greater than zero.

3.1 Stability of NDO

Theorem 1

The NDO in (5)–(6) implemented for the 4th order rotational pendulum system is efficiently able to estimate severe nonlinearities existing in the model.

Proof

The Lyapunov function is selected as

$$\begin{aligned} V_{DO_1}=\frac{1}{2p_1}\tilde{d}^2_1+\frac{1}{2}\tilde{e}^2_2 \end{aligned}$$
(7)

where \(\tilde{d}_1(=d_1-\hat{d}_1)\) and \(\tilde{e}_2(=z_2-\hat{z}_2)\) are the estimation errors in disturbance \(d_1\) and state \(z_2\).

Now, we have

$$\begin{aligned} \dot{V}_{DO_1}&=\frac{1}{p_1}\tilde{d}_1\dot{\tilde{d}}_1+\tilde{e}_2\dot{\tilde{e}}_2 \nonumber \\&=\frac{1}{p_1}\tilde{d}_1\left( \dot{d}_1-\dot{\hat{d}}_1\right) +\tilde{e}_2\left( \dot{z}_2-\dot{\hat{z}}_2\right) \end{aligned}$$
(8)

Putting (4) and (5) into (8), we get

$$\begin{aligned} \dot{V}_{DO_1}&=\frac{1}{p_1}\tilde{d}_1\left( \dot{d}_1-\dot{\hat{d}}_1\right) \nonumber \\&\quad +~\tilde{e}_2 \left\{ \dot{z}_2-\left( a_1(z)+b_1(z)u - p_2\left( \hat{z}_2-z_2\right) -\hat{d}_1 \right) \right\} \nonumber \\&=\frac{1}{p_1}\tilde{d}_1 \dot{d}_1-\frac{1}{p_1}\tilde{d}_1 p_1\left( \hat{z}_2-z_2\right) +\tilde{e}_2 \left\{ a_1(z)+b_1(z)u - d_1 \right. \nonumber \\&\left. \quad -~\left( a_1(z)+b_1(z)u-p_2\left( \hat{z}_2-z_2\right) -\hat{d}_1\right) \right\} \nonumber \\&=\frac{1}{p_1}\tilde{d}_1 \dot{d}_1-\tilde{d}_1 \left( \hat{z}_2-z_2\right) +\tilde{e}_2\left( -~d_1+\hat{d}_1 + p_2\left( \hat{z}_2-z_2\right) \right) \nonumber \\&=\frac{1}{p_1}\tilde{d}_1\dot{d}_1+\tilde{d}_1\tilde{e}_2+\tilde{e}_2\left( -~\tilde{d}_1-p_2\tilde{e}_2\right) \nonumber \\&=\frac{1}{p_1}\tilde{d}_1\dot{d}_1 -p_2\tilde{e}^2_2 \le 0 \end{aligned}$$
(9)

Also, for disturbance \(d_2\), the Lyapunov candidate is

$$\begin{aligned} V_{DO_2}=\frac{1}{2p_3}\tilde{d}^2_2+\frac{1}{2}\tilde{e}^2_4 \end{aligned}$$
(10)

where, the estimation errors are \(\tilde{d}_2(=d_2-\hat{d}_2)\) and \(\tilde{e}_4(=z_4-\hat{z}_4)\).

In similar way of (9), it can be proven that

$$\begin{aligned} \dot{V}_{DO_2}=\frac{1}{p_3}\tilde{d}_2\dot{d}_2 -p_4\tilde{e}^2_4 \le 0 \end{aligned}$$
(11)

Remark 2

Since the estimations of disturbance and state compensate each other derived by (5) and (6), therefore, the errors in disturbance estimation as well as in state estimation are bounded in the sense of Lyapunov. Equations (9) and (11) strictly say that the errors in both the estimations converge to zero asymptotically.

4 Controller design

The linearized dynamics of (4) is defined as

$$\begin{aligned} \dot{z}(t)=Az(t)+Bu(t) \end{aligned}$$
(12)

The sliding surface is considered as

$$\begin{aligned} \sigma =Kz(t) \end{aligned}$$
(13)

Taking differentiation of (13) and then substituting (12), we obtain

$$\begin{aligned} \dot{\sigma }= KAz(t)+KBu(t) \end{aligned}$$
(14)

The equivalent control is designed by equating \(\dot{\sigma }=0\) in (14) as

$$\begin{aligned} u_{eq}=(KB)^{-1}\left\{ -~KAz(t)+\hat{d}_1+\hat{d}_2 \right\} \end{aligned}$$
(15)

and the switching control is defined as a combination of power rate reaching law (where \(0<\gamma <1\)) and proportional rate term i.e.

$$\begin{aligned} u_{sw}=(KB)^{-1}(-~c_1|\sigma |^{\gamma }sat(\sigma )-c_2\sigma ) \end{aligned}$$
(16)

where \(c_1\) and \(c_2\) are chosen larger than maximum bound of the errors in disturbance estimations \(\tilde{d}_1\) and \(\tilde{d}_2\) to ensure sliding.

Therefore, the sliding mode controller incorporates an equivalent control and the switching control, and we have

$$\begin{aligned} u(t)=u_{eq}+u_{sw} \end{aligned}$$
(17)

In order to mitigate chattering in the control signal, a saturation function \(sat(\sigma )\) is taken up instead of a signum function \(sgn(\sigma )\) and is written as

$$\begin{aligned} sat(\sigma )={\left\{ \begin{array}{ll} 1, \quad \sigma >\varOmega \nonumber \\ k\sigma , \quad |\sigma |\le \varOmega \quad \text{ and } \quad k=\frac{1}{\varOmega } \nonumber \\ -~1, \quad \sigma <-~\varOmega \end{array}\right. } \end{aligned}$$

where \(\varOmega \) is the boundary layer.

In \(sat(\sigma )\) function, the switching control takes action while states are beyond the boundary layer, otherwise, the feedback control is involved. Hence, chattering issue can be limited entirely.

4.1 Stability of SMC

Theorem 2

The designed control law in (17) is capable to bring the states into sliding manifold. Also, the controller forces the states to reach to the origin asymptotically once the errors in estimations converge to zero via the NDO in (5)–(6) and retains them there thereafter.

Proof

The chosen Lyapunov function is

$$\begin{aligned} V_{SMC}=\frac{1}{2}\sigma ^2 \end{aligned}$$
(18)

Taking derivative of (18), we have

$$\begin{aligned} \dot{V}_{SMC}&=\sigma \dot{\sigma } \nonumber \\&= \sigma \lbrace KAz(t)+KBu(t) \rbrace \nonumber \\&= \sigma \left\{ KAz(t)+\left( -~KAz(t)+\hat{d}_1+\hat{d}_2 - c_1|\sigma |^{\gamma }sat(\sigma )-c_2\sigma \right) \right\} \nonumber \\&= \sigma \left\{ \hat{d}_1 +\hat{d}_2 - c_1|\sigma |^{\gamma }sat(\sigma ) -c_2\sigma \right\} \nonumber \\&= \parallel \hat{d}_1\parallel \mid \sigma \mid + \parallel \hat{d}_2 \parallel \mid \sigma \mid - c_1|\sigma |^{\gamma }|\sigma | -c_2|\sigma |^2 \nonumber \\&\le 0 \end{aligned}$$
(19)

Now, for an entire closed loop system, the Lyapunov candidate is outlined from (7), (10), and (18) as

$$\begin{aligned} V_{total}&= V_{DO_1}+V_{DO_2}+V_{SMC} \\&= \frac{1}{2p_1}\tilde{d}_1+\frac{1}{2}\tilde{e}_2 + \frac{1}{2p_3}\tilde{d}_2+\frac{1}{2}\tilde{e}_4 + \frac{1}{2} \sigma ^2 \end{aligned}$$

It follows \(\dot{V}_{total}\le 0\). \(\square \)

Remark 3

The power rate reaching law including the proportional rate term in the switching control varies the reaching speed to retain states within switching manifold forever. Also, the selection of saturation function makes control signal smooth.

5 Zero dynamics

The study of zero dynamics for the RP system is explained in this section.

Theorem 3

The sliding surface in (13) is governed for developing an SMC law in (17) based on the NDO that actively estimates severe nonlinearities in the dynamic model of the RP in (4). With its robustness property, the SMC scheme is able to take the states into the sliding mode and keeps them to the origin forever. Therefore, the closed loop dynamics of (3) is formed as follows

$$\begin{aligned} \ddot{\phi }_1&= \mathbf D ^{-1}(\phi )\left[ -~d_{22}u+\left( -~\frac{d_{11}d_{22}v_{12}}{d_{12}}+d_{22}v_{11} -\frac{v_{21}D}{d_{12}}\right) \dot{\phi }_1 \right. \nonumber \\&\left. \quad +~ d_{22}v_{12}\dot{\phi }_2 - \left( \frac{D}{d_{12}}+\frac{d_{11}d_{22}}{d_{12}}\right) g_{2}\right] \nonumber \\ \ddot{\phi }_2&= \mathbf D ^{-1}(\phi )\left[ d_{12}u+(d_{11}v_{21}-d_{12}v_{11})\dot{\phi }_1 - d_{12}v_{12}\dot{\phi }_2 + d_{11}g_{2}\right] \nonumber \\ \end{aligned}$$
(20)

The calculating dynamics of (20) acts as the zero dynamics which can be represented like as the sliding mode dynamics

$$\begin{aligned} M(\phi )\ddot{\phi }+N(\phi )\dot{\phi }+P(\phi )=Q(t) \end{aligned}$$
(21)

Proof

The sliding surface is given by

$$\begin{aligned} K_1\phi _1+K_2\dot{\phi }_1+K_3\phi _2+K_4\dot{\phi }_2=0 \end{aligned}$$
(22)

which yields the sliding mode. Differentiation of (22) involves

$$\begin{aligned} K_1\dot{\phi }_1+K_2\ddot{\phi }_1+K_3\dot{\phi }_2+K_4\ddot{\phi }_2=0 \end{aligned}$$
(23)

\(\dot{\phi }_1\) and \(\ddot{\phi }_1\) are determined from (22) and (23) as

$$\begin{aligned} \dot{\phi }_1&= -\frac{K_1}{K_2}\phi _1 -\frac{K_3}{K_2}\phi _2-\frac{K_4}{K_2}\dot{\phi }_2 \nonumber \\&=\varTheta (\phi _1,\phi _2,\dot{\phi }_2) \end{aligned}$$
(24)
$$\begin{aligned} \ddot{\phi }_1&= \frac{K^2_1}{K^2_2}\phi _1+\frac{K_1K_3}{K^2_2}\phi _2 +\left( \frac{K_1K_4}{K^2_2}-\frac{K_3}{K_2}\right) \dot{\phi }_2-\frac{K_4}{K_2}\ddot{\phi }_2 \nonumber \\&= \varXi (\phi _1,\phi _2,\dot{\phi }_2,\ddot{\phi }_2) \end{aligned}$$
(25)

Now, putting \(\dot{\phi }_1\) in (24) and \(\ddot{\phi }_1\) in (25) into (3), and we have

$$\begin{aligned}&\begin{bmatrix} J_1+m_2\left( l^2_1+l^2_2\sin ^2\phi _2\right)&\quad m_2l_2l_1\cos \phi _2 \\ m_2l_2l_1\cos \phi _2&\quad J_2+m_2l^2_2 \end{bmatrix} \begin{bmatrix} \varXi (\phi _1,\phi _2,\dot{\phi }_2,\ddot{\phi }_2) \\ \ddot{\phi }_2 \end{bmatrix} \nonumber \\&\quad +~ \begin{bmatrix} \frac{1}{2}m_2l^2_2\sin (2\phi _2)\dot{\phi }_2&\quad -~m_2l_2l_1\sin \phi _2\dot{\phi }_2 \\&\quad +~\frac{1}{2}m_2l^2_2\sin (2\phi _2)\dot{\phi }_1 \\ -~\frac{1}{2}m_2l^2_2\sin (2\phi _2)\dot{\phi }_1&\quad 0 \end{bmatrix} \begin{bmatrix} \varTheta (\phi _1,\phi _2,\dot{\phi }_2) \\ \dot{\phi }_2 \end{bmatrix} \nonumber \\&\quad +~ \begin{bmatrix} 0 \\ -~m_2gl_2\sin \phi _2 \end{bmatrix} = \begin{bmatrix} u \\ 0 \end{bmatrix} \end{aligned}$$
(26)

The control strategy u in (17) forces (26) in getting the zero dynamics given by (21) in the structure of sliding mode dynamics

$$\begin{aligned}&(m_2l_2l_1\cos \phi _2) \varXi \left( \phi _1,\phi _2,\dot{\phi }_2,\ddot{\phi }_2\right) +\left( J_2+m_2l^2_2\right) \ddot{\phi }_2 \nonumber \\&\quad -~\left( \frac{1}{2}m_2l^2_2\sin (2\phi _2)\dot{\phi }_1\right) \varTheta \left( \phi _1,\phi _2,\dot{\phi }_2\right) -m_2gl_2\sin \phi _2=0 \end{aligned}$$
(27)

\(\square \)

In this fashion, Theorem 3 is proven completely for (27) in the frame of (21).

5.1 Asymptotic stability

The zero dynamics in (21) can be framed as

$$\begin{aligned} \ddot{\phi }+M^{-1}N\dot{\phi }+M^{-1}P=M^{-1}Q \end{aligned}$$
(28)

The sliding coefficients in (22) are obtained through the LQR technique. The obtained parameters satisfy \(K_1<K_3\) and \(K_2<K_4\). So that, the equilibrium of the zero dynamics is found to be stabilized asymptotically in (28) along with calculated gains.

Proof

Let a Lyapunov function

$$\begin{aligned} V=e^{-\varphi (t)}S\left( \phi ,\dot{\phi }\right) \end{aligned}$$
(29)

where the function \(\varphi (t)\) is continuous and exists for \(t\rightarrow \infty \) with the condition \(\varphi (t)\geqslant Q(t)\). Consider \(S(\phi ,\dot{\phi })=(1+M^{-1}N\dot{\phi }+M^{-1}P) \) that satisfies the boundary \(\varUpsilon (||\phi ||)\leqslant V \leqslant \varPsi (||\phi ||)\) for specified span of \(\phi \), in which \(\varUpsilon (||\phi ||)\) and \(\varPsi (||\phi ||)\) are the continuous functions, respectively. Now,

$$\begin{aligned} \dot{V}&= -\,\varphi (t) e^{-\varphi (t)}S+\dot{S}e^{-\varphi (t)} \nonumber \\&= -\,e^{-\varphi (t)}\left[ \varphi (t) S - M^{-1}N - \dot{M}^{-1}N \dot{\phi } - M^{-1}\dot{N}\dot{\phi } \right. \nonumber \\&\left. \quad -~\dot{M}^{-1}P - M^{-1}\dot{P}\right] \end{aligned}$$
(30)

With the condition \(\varphi (t)\geqslant Q(t)\), (30) turns

$$\begin{aligned} \dot{V}&\leqslant -e^{-\varphi (t)}\left[ \varphi (t)\left( 1+M^{-1}N\dot{\phi }+M^{-1}P\right) \right. \nonumber \\&\quad \left. -~M^{-1}N - \frac{M\dot{N} + N\dot{M}}{M^2} \dot{\phi } - \frac{M\dot{P} + P\dot{M}}{M^2}\right] \nonumber \\&\leqslant -e^{-\varphi (t)}\bar{S}(\phi , \dot{\phi }) \end{aligned}$$
(31)

where the continuous function \(e^{-\varphi (t)}\bar{S}(\phi ,\dot{\phi })\) is positive definite. The function \(\bar{S}(\phi ,\dot{\phi })\) is positive with the necessary conditions \(K_3>K_1\) and \(K_4>K_2\). Hence, it is observed from (29) and (31) that \(S(\phi ,\dot{\phi })\) is bounded by \(\phi _1\) in horizontal half-sector and \(\phi _2\) over upper half-region. It explains that the control law in (17) is enough to stabilize the zero dynamics of the RP system inside specified zone of \(\phi \). Furthermore, an asymptotic stability of the zero dynamics in (28) is constructed using the fact that Q(t) reaches towards 0 as \(t\rightarrow \infty \). \(\square \)

Fig. 2
figure 2

The building blocks of NDO based SMC for the rotational pendulum system

Full size image

6 Results and discussions

The rotational pendulum is a benchmark control problem which is investigated using the SMC based NDO in (17) with large parametric uncertainty and any bounded time-varying external disturbance in the input channels. The block diagram of closed loop control system for the RP via the NDO based SMC is shown in Fig.  2. The simulation is carried out in the environment of Matlab/Simulink with two different initial conditions (IC), such as IC-(1) ([\(\phi _1\), \(\dot{\phi }_1\), \(\phi _2\), \(\dot{\phi }_2\)] = [1.1, 0, 0.5, 0]) and IC-(2) ([\(\phi _1\), \(\dot{\phi }_1\), \(\phi _2\), \(\dot{\phi }_2\)] = [\(\pi \), 0, 1.1, 0]).

The linearized model of the RP in (4) is given as

$$\begin{aligned} A=\begin{bmatrix} 0&\quad 1&\quad 0&\quad 0 \\ 0&\quad 0&\quad -~4.8733&\quad 0 \\ 0&\quad 0&\quad 0&\quad 1 \\ 0&\quad 0&\quad 74.5197&\quad 0 \end{bmatrix}; B=\begin{bmatrix} 0 \\ 55.3820 \\ 0 \\ -~81.7971 \end{bmatrix} \end{aligned}$$
(32)
Fig. 3
figure 3

IC-(1) (\(\phi _1(0)=1.1\) rad, \(\dot{\phi }_1(0)=0\)  rad/sec, \(\phi _2(0)=0.5\) rad, \(\dot{\phi }_2(0)=0\) rad/sec): a arm angle, b pendulum angle, c control signal (N / m), and d sliding surface in presence of large parametric uncertainty and external disturbance

Full size image
Fig. 4
figure 4

IC-(2) (\(\phi _1(0)= \pi \) rad, \(\dot{\phi }_1(0)=0\)  rad/sec, \(\phi _2(0)=1.1\) rad, \(\dot{\phi }_2(0)=0\) rad/sec): a arm angle, b pendulum angle, c control signal (N / m), and d sliding surface along with huge perturbations and external disturbance

Full size image
Fig. 5
figure 5

States and their estimations: a, b for IC-(1): [\(\phi _1\), \(\dot{\phi }_1\), \(\phi _2\), \(\dot{\phi }_2\)] = [1.1, 0, 0.5, 0]; c, d for IC-(2): [\(\phi _1\), \(\dot{\phi }_1\), \(\phi _2\), \(\dot{\phi }_2\)] = [\(\pi \), 0, 1.1, 0]

Full size image
Fig. 6
figure 6

Phase portraits: a, b IC-(1): [\(\phi _1\), \(\dot{\phi }_1\), \(\phi _2\), \(\dot{\phi }_2\)] = [1.1, 0, 0.5, 0]; c, d IC-(2): [\(\phi _1\), \(\dot{\phi }_1\), \(\phi _2\), \(\dot{\phi }_2\)] = [\(\pi \), 0, 1.1, 0]

Full size image

The RP system is open-loop unstable since the eigenvalues of matrix A are locating at \(\lambda _{eigen} = 0, 0, 8.6325, -~8.6325\). The parameters of the RP are given in [2]. The controller gains \( [K_1, K_2, K_3, K_4 ] = [-~0.078, -~0.075, -~3.102, -~0.181] \) are obtained through the LQR method using of system matrix A, input matrix B, state weighted matrix \(Q = 10^{-2}*[10, 0, 0, 0; 0, 0.1, 0, 0; 0, 0, 1, 0; 0, 0, 0, 0.5]\), and control weighted matrix \(R = 12\). The constants for the controller design are chosen as \(c_1=15\), \(c_2=10\), and \(\gamma =0.5\). The time-varying external disturbances \(d_{c1}=\sin (0.3t)\) and \(d_{c2}=0.5\sin (\frac{\pi }{2}+0.3t)\) enter via the control input channels into the model, respectively. Furthermore, the parameter variations of \(50\%\), \(10\%\), \(10\%\), \(5\%\), and \(5\%\) in \(m_2\), \(l_1\), \(l_2\), \(J_1\), and \(J_2\), respectively are added in the model as numerical values. The nonlinear disturbance observer in (5)–(6) is applied to estimate highly nonlinear terms present in the model accurately. For this, the observer gains are selected as \(p_1=600\), \(p_2=28,000\), \(p_3=50\), and \(p_4=1500\). The SMC based NDO scheme in (17) is applied to the coupled nonlinear model in (4).

For comparison purpose, the coupled sliding mode controller is simulated for the same RP system with same initial conditions mentioned in above. The coupled SMC law in [23] is of the given form:

$$\begin{aligned} u_{total} = u_{{eq}_1} + u_{{sw}_2} \end{aligned}$$

where \( u_{{eq}_1} = (\lambda g_p u^{{eq}_1}_p + g_c u^{{eq}_1}_c)/(\lambda g_p + g_c) \), \( u_{{sw}_2} = (-\,k sgn (\sigma _{smc}))/(\lambda g_p + g_c) \), \( g_p = d_{22}/(d_{11}d_{22} - d^2_{12}) \), \( g_c = - d_{12}/(d_{11}d_{22} - d^2_{12}) \), \( u^{{eq}_1}_p = g^{-1}_p (-~f_p-c_p\dot{q}_1) \), \( u^{{eq}_1}_c = g^{-1}_c (-~f_c-c_c\dot{q}_2) \), \( f_p = -(c_{12}d_{22}\dot{q}_2-d_{12}g_2)/(d_{11}d_{22}-d^2_{12}) \), \( f_c = (c_{12}d_{12}\dot{q}_2-d_{11}g_2)/(d_{11}d_{22}-d^2_{12}) \), \( \sigma _{smc} = \lambda \sigma _p +\sigma _c \), \( \sigma _p = \dot{q}_1 + c_p q_1 \), \( \sigma _c = \dot{q}_2 + c_c q_2 \), \( c_p = 0.3 \), \( c_c = 3.1077 \), \( \lambda = 0.1 \), and \( k = 20 \).

Table 1 Quantitative measurements of arm and pendulum angles
Full size table

The comparison results of the designed NDO based SMC strategy and the coupled SMC method [23] are shown in Figs. 3, 4, 5 and 6. The proposed controller can withstand large parameter deviations and any bounded external disturbance in the input channels without producing considerable variations in the output variables. As a result, the stability region of an arm (in horizontal half-zone) and a pendulum (over upper half-zone) both are expanded for large initial conditions. Whereas, due to the extreme nonlinearities existing in the model, the coupled SMC is not able to handle even large deviations in parameters along with external disturbance. Therefore, stability zone using the coupled SMC is restricted.

In Fig. 3, two methods, the proposed one and the compared one are analyzed with their results for given IC-(1). The developed controller gives states regulation against severe nonlinearities in the model, large parametric uncertainty and external disturbance, whereas the coupled SMC fails to do that. Again, chattering occurred in the control signal via the coupled SMC is prominent, while the SMC based NDO offers chatter free control with optimum control energy. Figure 4 reveals that the proposed control is able to produce the satisfactory results with given IC-(2) against extremely nonlinear terms existing in the model, huge deviations in the model parameters including external disturbance, while the compared one stops simulation due to the singularity occurred. An addressed one exhibits excellent disturbance rejection capabilities while controlling the RP. Also, the estimated states exactly track to the actual states from an initial time shown in Fig. 5 for both IC-(1) and IC-(2) using of proposed law. It ensures that the estimation errors in disturbances converge to zero. The phase portrait represents the direction of vector fields as shown in Fig. 6a–d. This phase plane analysis defines that the trajectories achieve equilibrium by using the proposed NDO based SMC.

Lastly, the developed control law is compared to the existing law on the basis of quantitative analysis, such as IAE, ITAE, ISE, and ITSE given in Table 1. It can be observed that the proposed controller shows better quantitative performance compared to the existing method. In addition, an addressed method enlarges the stability region in presence of large nonlinearities in the model including huge parameter deviations and matched disturbance which is externally applied.

7 Conclusion

In this paper, the design of NDO based SMC for highly nonlinear coupled uncertain rotational pendulum system is presented. The developed method is then exploited of stabilizing the RP system. The nonlinearities existing in the model are accurately estimated via an NDO. Then, the controller is designed using linear model of the RP and disturbance estimation, and is applied to the nonlinear model in presence of severe nonlinearities in the model, huge parameter deviations and matched disturbance. An asymptotic stability of the zero dynamics can guarantee in the form of sliding mode dynamics through sliding coefficients obtained by the LQR method. The controller is capable of nullifying the chattering problem frequent in the control input. Furthermore, this control strategy expands stability zone of an arm and a pendulum both for significantly large initial conditions. The numerical simulations obtained with a developed controller are compared with an existing SMC and efficiency in performance is experienced.