1 Introduction

During human immunodeficiency virus (HIV) infection, a part of infected cells in eclipse stage returns to the uninfected state. In addition, Cytotoxic T Lymphocytes (CTL) cells play an important role in antiviral defense by killing the productive infected cells. Therefore, many mathematical models has been proposed to model the role of CTL immune response in HIV infection. One of the earliest of these models was proposed by Nowak and Bangham [1] in order to describe the interaction between susceptible cells, infected cells, viruses and CTL cells. Further, the model of [1] was improved by many researchers (see for example, [2–5]). All the above models have not considered the cure of infected cells in eclipse stage. For this reason, Rong et al. [6] constructed an HIV infection model with bilinear incidence rate and cure of infected cells in eclipse stage, but they not considered the CTL immune response and they only established the local stability of equilibria. The global stability was investigated by Buonomo and Vargas-De-L?on [7]. To improve the model [6], Hu et al. [8] replaced the bilinear incidence rate by a saturated incidence rate and they investigated the global stability of the improved model. In 2015, Wang et al. [9] replaced the saturated incidence rate by the Beddington–Deangelis functional response and they established the local and global stability of equilibria. In addition, Maziane et al. [10] replaced the saturated incidence rate by the Hattaf’s [11] incidence rate and they extended the ODE model to a system with partial differential equations in order to take into account the mobility of the virus. The global stability of both models is investigated by constructing suitable Lyapunov functionals. In [12], Lv et al. replaced the bilinear incidence rate by the Beddington–DeAngelis functional response and they included the CTL immune response into the model [6]. By constructing suitable Lyapunov functionals, they investigated the global stability of equilibria in the terms of the basic reproduction number and the immune response reproduction number.

To extend the model of Lv et al. [12] and improve the ODE models presented in [6–10] by considering the effect of CTL immune response, we propose the following model

$$\begin{aligned}&\displaystyle \frac{dT}{dt}=\lambda -\mu _{T}T(t)-f(T(t),V(t))V(t)+\rho E(t),\nonumber \\&\displaystyle \frac{dE}{dt}=f(T(t),V(t))V(t)-(\mu _{E}+\rho +\gamma )E(t),\nonumber \\&\displaystyle \frac{dI}{dt}=\gamma E(t)-\mu _{I}I(t)-pI(t)C(t),\\&\displaystyle \frac{dV}{dt}=kI(t)-\mu _{V}V(t),\nonumber \\&\displaystyle \frac{dC}{dt}=aI(t)C(t)-\mu _{C}C(t),\nonumber \end{aligned}$$
(1)

where T(t), E(t), I(t), V(t) and C(t) denote the densities of uninfected CD\(4^{+}\) T cells, infected cells in the eclipse stage (unproductive infected cells), productive infected cells, free virus particles and CTL cells at time t, respectively. The parameter \(\lambda \) is the production rate of the uninfected cells, \(\mu _{T}\) is their death rate and f(T, V) is the rate of uninfected cells to become infected by virus. The parameters \(\mu _{E}\), \(\mu _{I}\) and \(\mu _{V}\) denote the death rates of unproductive infected cells, productive infected cells and virus, respectively. The constant \(\rho \) is the rate at which the unproductive infected cells return to the uninfected cells. The constant \(\gamma \) is the rate at which infected cells in the eclipse stage become productive infected cells and k is the production rate of virions by infected cells. The productive infected cells are killed by CTL cells at rate p while a denotes the proliferation rate of CTL cells. Here, we consider the Hattaf’s [11] incidence rate of the form \(f(T,V)=\frac{\beta T}{1+\alpha _{1}T+\alpha _{2}V+\alpha _{3}TV}\), where \(\alpha _1\), \(\alpha _2\), \(\alpha _3\ge 0\) are the saturation factors measuring the psychological or inhibitory effect and \(\beta >0\) is the infection coefficient. We recall that this incidence rate includes the common types such as the bilinear incidence (or mass action incidence) when \(\alpha _1=\alpha _2=\alpha _3=0\), the saturated incidence rate when \(\alpha _1=\alpha _3=0\) or \(\alpha _2=\alpha _3=0\), the Beddington-DeAngelis functional response introduced in [13, 14] when \(\alpha _3=0\), and Crowley-Martin functional response presented in [15] and used in [16, 17] when \(\alpha _3=\alpha _1\alpha _2\). It is important to note that the model of Lv et al. [12] is a special case of system (1) when \(\alpha _3=0\). The first aim of this study is the generalization of the main results presented in [12].

System (1) assumes that cells and viruses are well mixed, and ignores the mobility of cells and viruses. Motivated by the works [18–21] and make the model more realistic by considering the mobility of cells and viruses, we propose the following diffusive HIV infection model

$$\begin{aligned} \displaystyle \frac{\partial T}{\partial t}= & {} \lambda -\mu _{T}T(x,t)-f(T(x,t),V(x,t))V(x,t)\nonumber \\&+\,\rho E(x,t),\nonumber \\ \displaystyle \frac{\partial E}{\partial t}= & {} f(T(x,t),V(x,t))V(x,t)\nonumber \\&-\,(\mu _{E}+\rho +\gamma )E(x,t),\\ \displaystyle \frac{\partial I}{\partial t}= & {} \gamma E(x,t)-\mu _{I}I(x,t)-pI(x,t)C(x,t),\nonumber \\ \displaystyle \frac{\partial V}{\partial t}= & {} d\triangle V(x,t)+kI(x,t)-\mu _{V}V(x,t),\nonumber \\ \displaystyle \frac{\partial C}{\partial t}= & {} a I(x,t)C(x,t)-\mu _{C}C(x,t),\nonumber \end{aligned}$$
(2)

where T(x, t), I(x, t), E(x, t), V(x, t) and C(x, t) are the densities of uninfected CD4\(^{+}\) T cells, infected cells in the eclipse stage, productive infected cells, free virus particles and CTL cells at location x and time t, respectively. The positive constant d is the diffusion coefficient of virus, and the other positive constant parameters have same meanings as in ODE model (1).

In this study, we consider our model (2) with homogenous Neumann boundary condition

$$\begin{aligned} \displaystyle \frac{\partial V}{\partial \nu }=0 \text { on } \partial \Omega \times (0,+\infty ), \end{aligned}$$
(3)

and initial conditions

$$\begin{aligned} \begin{array}{lll} T(x,0)=\phi _{1}(x)\ge 0, \quad E(x,0)=\phi _{2}(x)\ge 0,\\ I(x,0)=\phi _{3}(x)\ge 0,\quad V(x,0)=\phi _{4}(x)\ge 0,\\ C(x,0)=\phi _{5}(x)\ge 0,\quad x\in \bar{\Omega }, \end{array} \end{aligned}$$
(4)

where \(\Omega \) is a bounded domain in \(\hbox {I R}^{n}\) with smooth boundary \(\partial \Omega \), \(\Delta =\displaystyle {\sum \nolimits _{i=1}^{n}}\frac{\partial ^{2}}{\partial x_{i}^{2}}\) is the Laplacian operator and \(\frac{\partial V}{\partial \nu }\) is the outward normal derivative on \(\partial \Omega \). Biologically speaking, the Neumann boundary condition means that the free virus particles do not move across the boundary \(\partial \Omega \).

The organization of this paper is as follows. In the next section, we well first determine the equilibria of our ODE model and derive two threshold parameters for viral infection \(R_{0}\) and for CTL immune response \(R_{1}\). After, we establish the global stability of these equilibria that are the infection-free equilibrium, the immune-free infection equilibrium and the chronic infection equilibrium. Further, we focus on the global dynamics of our PDE model in Sect. 3. In order to validate our theoretical results, numerical simulations are presented in Sect. 4. Finally, a brief conclusion and discussion are given in Sect. 5.

2 Global stability of the ODE model

System (1) has always an infection-free equilibrium of the form \(Q_{0}(\displaystyle \frac{\lambda }{\mu _{T}},0,0,0,0)\).

Hence, the basic reproduction number of (1) is given by

$$\begin{aligned} R_{0}=\frac{\lambda \beta k\gamma }{\mu _{I}\mu _{V}(\lambda \alpha _{1}+\mu _{T})(\rho +\mu _{E}+\gamma )}. \end{aligned}$$
(5)

We recall that \(R_{0}\) represents the number of secondary infections produced by one productive infected cell during the period of infection when all cells are uninfected.

The other equilibria of system (1) are solutions of the following system

$$\begin{aligned}&\lambda -\mu _{T}T-f(T,V)V+\rho E= 0, \end{aligned}$$
(6)
$$\begin{aligned}&f(T,V)V-(\mu _{E}+\rho +\gamma )E = 0, \end{aligned}$$
(7)
$$\begin{aligned}&\gamma E-\mu _{I}I-pIC = 0, \end{aligned}$$
(8)
$$\begin{aligned}&kI-\mu _{V} V = 0, \end{aligned}$$
(9)
$$\begin{aligned}&aIC-\mu _{C}C = 0. \end{aligned}$$
(10)

By (5), we get \(C=0\) or \(I=\frac{\mu _{C}}{a}.\)

If \(C=0\), using (6)–(4), we obtain \(E=\frac{\lambda -\mu _{T}T}{\mu _{E}+\gamma }\), \(I=\frac{\gamma (\lambda -\mu _{T}T)}{\mu _{I}(\mu _{E}+\gamma )}\), \(V=\frac{k\gamma (\lambda -\mu _{T}T)}{\mu _{I}\mu _{V}(\mu _{E}+\gamma )}\) and

$$\begin{aligned} f\left( T,\displaystyle \frac{k\gamma (\lambda -\mu _{T}T)}{\mu _{I}\mu _{V}(\mu _{E}+\gamma )}\right) =\displaystyle \frac{(\rho +\mu _{E}+\gamma )\mu _{V}\mu _{I}}{k\gamma }. \end{aligned}$$

Since \(E=\frac{\lambda -\mu _{T}T}{\mu _{E}+\gamma }\ge 0\), we have \(T\le \frac{\lambda }{\mu _{T}}\). So, there is no biological equilibrium when \(T>\frac{\lambda }{\mu _{T}}\). Define the function \(g_{1}\) on the interval \(\big [0,\frac{\lambda }{\mu _{T}}\big ]\) by

$$\begin{aligned} g_{1}(T)=f\left( T,\displaystyle \frac{k\gamma (\lambda -\mu _{T}T)}{\mu _{I}\mu _{V}(\mu _{E}+\gamma )}\right) -\displaystyle \frac{(\rho +\mu _{E}+\gamma )\mu _{V}\mu _{I}}{k\gamma }. \end{aligned}$$

We have \(g_{1}(0)=-\frac{(\rho +\mu _{E}+\gamma )\mu _{V}\mu _{I}}{k\gamma }<0\), \(g_{1}(\frac{\lambda }{\mu _{T}})=\frac{(\rho +\mu _{E}+\gamma )\mu _{V}\mu _{I}}{k\gamma }(R_{0}-1)\) and

$$\begin{aligned} g_{1}'(T)=\frac{\partial f}{\partial T}-\frac{k\gamma \mu _{T}}{\mu _{I}\mu _{V}(\mu _{E}+\gamma )}\frac{\partial f}{\partial V}>0. \end{aligned}$$

If \(R_{0}>1\), there exist an other biological equilibrium \(Q_{1}(T_{1},E_{1},I_{1},V_{1},0)\) with \(T_{1}\in (0,\frac{\lambda }{\mu _{T}})\), \(E_{1}=\frac{\lambda -\mu _{T}T_{1}}{\mu _{E}+\gamma }\), \(I_{1}=\frac{\gamma (\lambda -\mu _{T}T_{1})}{\mu _{I}(\mu _{E}+\gamma )}\) and \(V_{1}=\frac{k\gamma (\lambda -\mu _{T}T_{1})}{\mu _{I}\mu _{V}(\mu _{E}+\gamma )}\). This equilibrium correspond to positive levels of healthy cells, unproductive infected cells, productive infected cells and virus, but no CTL immune response.

If \(C\ne 0\), then \(I=\frac{\mu _{C}}{a}\). Using (6)–(4), we deduce \(E=\frac{\lambda -\mu _{T}T}{\mu _{E}+\gamma }\), \(V=\frac{k\mu _{C}}{a\mu _{V}}\) and

$$\begin{aligned} f\left( T,\displaystyle \frac{k\mu _{C}}{a\mu _{V}}\right) =\displaystyle \frac{a\mu _{V}(\mu _{E}+\rho +\gamma )(\lambda -\mu _{T}T)}{k\mu _{C}(\mu _{E}+\gamma )}. \end{aligned}$$

Since \(C=\frac{a \gamma (\lambda -\mu _{T}T)-\mu _{I} \mu _{C} (\mu _{E}+\gamma )}{p\mu _{C}(\mu _{E}+\gamma )}\ge 0\), we have \(T\le \frac{\lambda }{\mu _{T}}-\frac{\mu _{I}\mu _{C}(\mu _{E} + \gamma )}{a \gamma \mu _{T}}\). Then there exists no equilibrium when \(T>\frac{\lambda }{\mu _{T}}-\frac{\mu _{I}\mu _{C}(\mu _{E} + \gamma )}{a \gamma \mu _{T}}\) or \(\frac{\lambda }{\mu _{T}}-\frac{\mu _{I}\mu _{C}(\mu _{E} + \gamma )}{a \gamma \mu _{T}}\le 0\).

Define the function \(g_{2}\) on the interval \(\big [0,\frac{\lambda }{\mu _{T}}-\frac{\mu _{I}\mu _{C}(\mu _{E} + \gamma )}{a \gamma \mu _{T}}]\) by

$$\begin{aligned} g_{2}(T)=f\left( T,\displaystyle \frac{k\mu _{C}}{a\mu _{V}}\right) -\displaystyle \frac{a\mu _{V}(\mu _{E}+\rho +\gamma )(\lambda -\mu _{T}T)}{k\mu _{C}(\mu _{E}+\gamma )}. \end{aligned}$$

We have \(g_{2}(0)=-\frac{\lambda a\mu _{V}(\mu _{E}+\rho +\gamma )}{k\mu _{C}(\mu _{E}+\gamma )}<0\) and \(g_{2}'(T)=\frac{\partial f}{\partial T}+\frac{\mu _{T}a\mu _{V}(\mu _{E}+\rho +\gamma )}{k\mu _{C}(\mu _{E}+\gamma )}>0.\)

In addition to \(R_{0}\), we define the CTL immune response reproduction number \(R_{1}\) of our ODE model by

$$\begin{aligned} R_{1}=\displaystyle \frac{aI_{1}}{\mu _{C}}, \end{aligned}$$
(11)

where \(\frac{1}{\mu _{C}}\) represents the average life expectancy of CTL cells, and \(I_{1}\) is the number of productive infected cells at \(Q_{1}\). Hence, \(R_{1}\) represents the average number of CTL cells activated by the productive infected cells when viral infection is successful.

If \(R_{1}<1\), then \(I_{1}<\frac{\mu _{C}}{a}\), \(T_{1}>\frac{\lambda }{\mu _{T}}-\frac{\mu _{I}\mu _{C}(\mu _{E} + \gamma )}{a \gamma \mu _{T}}\) and

$$\begin{aligned}&g_{2}\left( \frac{\lambda }{\mu _{T}}-\frac{\mu _{I}\mu _{C}(\mu _{E} + \gamma )}{a \gamma \mu _{T}}\right) = f\left( \frac{\lambda }{\mu _{T}}\right. \\&\qquad \left. -\frac{\mu _{I}\mu _{C}(\mu _{E} + \gamma )}{a \gamma \mu _{T}},\frac{k\mu _{C}}{a\mu _{V}}\right) -\frac{(\rho +\mu _{E}+\gamma )\mu _{V}\mu _{I}}{k\gamma }\\&\quad < f(T_{1},V_{1})-\frac{(\rho +\mu _{E}+\gamma )\mu _{V}\mu _{I}}{k\gamma }. \end{aligned}$$

Hence, \(g_{2}(\frac{\lambda }{\mu _{T}}-\frac{\mu _{I}\mu _{C}(\mu _{E} + \gamma )}{a \gamma \mu _{T}})<0\). Then there is no equilibrium when \(R_{1}<1\).

If \(R_{1}>1\), then \(I_{1}>\frac{\mu _{C}}{a}\), \(T_{1}<\frac{\lambda }{\mu _{T}}-\frac{\mu _{I}\mu _{C}(\mu _{E} + \gamma )}{a \gamma \mu _{T}}\) and \(g_{2}(\frac{\lambda }{\mu _{T}}-\frac{\mu _{I}\mu _{C}(\mu _{E} + \gamma )}{a \gamma \mu _{T}})>0\). Therefore, if \(R_{1}>1\), there exists an infection equilibrium \(Q_{2}(T_{2},E_{2},I_{2},V_{2},C_{2})\) with \(T_{2}\in (0,\frac{\lambda }{\mu _{T}}-\frac{\mu _{I}\mu _{C}(\mu _{E} + \gamma )}{a \gamma \mu _{T}})\), \(E_{2}=\frac{\lambda -\mu _{T}T_{2}}{\mu _{E}+\gamma }\), \(I_{2}=\frac{\mu _{C}}{a}\), \(V_{2}=\frac{k\mu _{C}}{a\mu _{V}}\) and \(C_{2}=\frac{a \gamma (\lambda -\mu _{T}T_{2})-\mu _{I} \mu _{C} (\mu _{E}+\gamma )}{p\mu _{C}(\mu _{E}+\gamma )}\). This equilibrium denotes the state in which both the virus and the CTL immune response are present.

Summarizing the above discussions in the following result.

Theorem 2.1

  1. (i)

    When \(R_0 \le 1\), the system (1) has always an infection-free equilibrium of the form \(Q_{0}(\displaystyle \frac{\lambda }{\mu _{T}},0,0,0,0)\).

  2. (ii)

    When \(R_0>1\), the system (1) has an immune-free infection equilibrium of the form \(Q_{1}(T_{1},E_{1},I_{1},V_{1},0)\) with \(T_{1}\in (0,\displaystyle \frac{\lambda }{\mu _{T}})\), \(E_{1}=\frac{\lambda -\mu _{T}T_{1}}{\mu _{E}+\gamma }\), \(I_{1}=\frac{\gamma (\lambda -\mu _{T}T_{1})}{\mu _{I}(\mu _{E}+\gamma )}\) and \(V_{1}=\frac{k\gamma (\lambda -\mu _{T}T_{1})}{\mu _{I}\mu _{V}(\mu _{E}+\gamma )}\).

  3. (iii)

    When \(R_1>1\), the system (1) has an infection equilibrium of the form \(Q_{2}(T_{2},E_{2},I_{2},V_{2},C_{2})\) with \(T_{2}\in (0,\frac{\lambda }{\mu _{T}}-\frac{\mu _{I}\mu _{C}(\mu _{E} + \gamma )}{a \gamma \mu _{T}})\), \(E_{2}=\frac{\lambda -\mu _{T}T_{2}}{\mu _{E}+\gamma }\), \(I_{2}=\frac{\mu _{C}}{a}\), \(V_{2}=\frac{k\mu _{C}}{a\mu _{V}}\) and \(C_{2}=\frac{a \gamma (\lambda -\mu _{T}T_{2})-\mu _{I} \mu _{C} (\mu _{E}+\gamma )}{p\mu _{C}(\mu _{E}+\gamma )}\).

Now, we focus on the global stability of the three equilibria of system (1). At first, we have

Theorem 2.2

If \(R_{0}\le 1\), then the infection-free equilibrium \(Q_{0}\) is globally asymptotically stable.

Proof

Consider the following Lyapunov functional

$$\begin{aligned}&W_{0}(T,E,I,V,C)= T-T_{0}-\int _{T_{0}}^{T}\displaystyle \frac{f(T_{0},0)}{f(S,0)}dS\\&\quad +\,\displaystyle \frac{\rho (T-T_{0}+E)^{2}}{2(1+\alpha _{1}T_{0})(\mu _{T}+\mu _{E}+\gamma )T_{0}}\\&\quad +\,\displaystyle \frac{\rho +\mu _{E}+\gamma }{\gamma }I+E+\displaystyle \frac{\mu _{I}(\rho +\mu _{E}+\gamma )}{k\gamma }V\\&\quad +\,\displaystyle \frac{p(\rho +\mu _{E}+\gamma )}{a\gamma }C, \end{aligned}$$

where \(T_{0}=\frac{\lambda }{\mu _{T}}\).

Calculating the time derivative of \(W_{0}\) along the positive solutions of system (1), we obtain

$$\begin{aligned}&\frac{dW_{0}}{dt} = \bigg (1-\displaystyle \frac{f(T_{0},0)}{f(T,0)}\bigg )\dot{T}\\&\quad +\,\displaystyle \frac{\rho }{(1+\alpha _{1}T_{0})(\mu _{T}+\mu _{E}+\gamma )T_{0}}(T-T_{0}+E)(\dot{T}+\dot{E})\\&\quad +\,\displaystyle \frac{\rho +\mu _{E}+\gamma }{\gamma }\dot{I}+\dot{E}+\displaystyle \frac{\mu _{I}(\rho +\mu _{E}+\gamma )}{k\gamma }\dot{V}\\&\quad +\,\displaystyle \frac{p(\rho +\mu _{E}+\gamma )}{a\gamma }\dot{C}.\\ \end{aligned}$$

Noting that \(\lambda =\mu _{T}T_{0}\), we get

$$\begin{aligned}&\frac{dW_{0}}{dt} =\bigg (1-\displaystyle \frac{f(T_{0},0)}{f(T,0)}\bigg )\mu _{T}(T_{0}-T)+\displaystyle \frac{f(T_{0},0)f(T,V)}{f(T,0)}V\\&\quad +\,\rho \bigg (1-\displaystyle \frac{f(T_{0},0)}{f(T,0)}\bigg )E -\displaystyle \frac{\rho \mu _{T}(T-T_{0})^{2}}{(1+\alpha _{1}T_{0})(\mu _{T}+\mu _{E}+\gamma )T_{0}}\\&\quad -\,\displaystyle \frac{\rho (\mu _{E} +\gamma )E^{2}}{(1+\alpha _{1}T_{0})(\mu _{T}+\mu _{E}+\gamma )T_{0}}\\&\quad +\,\displaystyle \frac{\rho E}{(1+\alpha _{1}T_{0})T_{0}}\big (T_{0}-T\big )-\displaystyle \frac{\mu _{I}\mu _{V}(\rho +\mu _{E}+\gamma )}{k\gamma }V\\&\quad -\,\displaystyle \frac{\mu _{C}p(\rho +\mu _{E}+\gamma )}{a\gamma }C\\&=-\left( \displaystyle \frac{1}{T}+\displaystyle \frac{\rho }{(\mu _{T}+\mu _{E}+\gamma )T_{0}}\right) \displaystyle \frac{\mu _{T}(T-T_{0})^{2}}{1+\alpha _{1}T_{0}}\\&\quad -\,\displaystyle \frac{\rho (\mu _{E}+\gamma )E^{2}}{(1+\alpha _{1}T_{0})(\mu _{T}+\mu _{E}+\gamma )T_{0}}\\&\quad -\,\displaystyle \frac{\rho (T-T_{0})^{2}E}{(1+\alpha _{1}T_{0})TT_{0}}+\displaystyle \frac{\mu _{I}\mu _{V}(\rho +\mu _{E}+\gamma )}{k\gamma }(R_{0}-1)V\\&\quad -\,\displaystyle \frac{(\alpha _{2}+\alpha _{3}T)V^{2}}{1+\alpha _{1}T+\alpha _{2}V+\alpha _{3}TV}f(T_{0},0)\\&\quad -\,\displaystyle \frac{\mu _{C}p(\rho +\mu _{E}+\gamma )}{a\gamma }C. \end{aligned}$$

Therefore, \(\frac{dW_{0}}{dt}\le 0\) if \(R_{0}\le 1\). Further, \(\frac{dW_{0}}{dt}=0\) if and only if \(T=\frac{\lambda }{\mu _{T}}\), \(E=0\), \(I=0\), \(V=0\) and \(C=0\). Hence, the largest compact invariant set in \(\{(T,E,I,V,C)|\frac{dW_{0}}{dt}=0\}\) is just the singleton \(\{Q_{0}\}\). Thus, the global stability of the infection-free equilibrium \(Q_{0}\) follows from LaSalle’s invariance principle [22]. \(\square \)

Theorem 2.3

The immune-free infection equilibrium \(Q_{1}\) of system (1) is globally asymptotically stable if \(R_{1}\le 1<R_{0}\) and

$$\begin{aligned}&R_{0}\le 1\nonumber \\&+\,\displaystyle \frac{[\mu _{T}\mu _{I}\mu _{V}(\mu _{E}+\gamma )+\alpha _{2}\mu _{T}\lambda k\gamma ](\mu _{E}+\rho +\gamma )+\rho \alpha _{3}k\gamma \lambda ^{2}}{\rho \mu _{I}\mu _{V}(\mu _{E}+\rho +\gamma )(\mu _{T}+\alpha _{1}\lambda )}.\nonumber \\ \end{aligned}$$
(12)

Proof

Construct a Lyapunov functional \(W_{1}\) as follows

$$\begin{aligned}&W_{1}(T,E,I,V,C)= T-T_{1}-\int _{T_{1}}^{T}\displaystyle \frac{f(T_{1},V_{1})}{f(S,V_{1})}dS\\&\quad +\,\displaystyle \frac{\rho (1+\alpha _{2}V_{1})(T-T_{1}+E-E_{1})^{2}}{2(1+\alpha _{1}T_{1}+\alpha _{2}V_{1}+\alpha _{3}T_{1}V_{1})(\mu _{T}+\mu _{E}+\gamma )T_{1}}\\&\quad +\,\displaystyle \frac{f(T_{1},V_{1})V_{1}}{\gamma E_{1}}I_{1}\Phi \left( \displaystyle \frac{I}{I_{1}}\right) +E_{1}\Phi \left( \displaystyle \frac{E}{E_{1}}\right) \\&\quad +\,\displaystyle \frac{\mu _{I}f(T_{1},V_{1})V_{1}}{k\gamma E_{1}}V_{1}\Phi \left( \displaystyle \frac{V}{V_{1}}\right) +\displaystyle \frac{p f(T_{1},V_{1})V_{1}}{a\gamma E_{1}}C, \end{aligned}$$

where \(\Phi (x)=x-1-\ln (x)\).

The time derivative of \(W_{0}\) along the positive solutions of system (1) satisfies

$$\begin{aligned} \displaystyle \frac{dW_{1}}{dt}= & {} \bigg (1-\displaystyle \frac{f(T_{1},V_{1})}{f(T,V_{1})}\bigg )\dot{T}\\&+\,\displaystyle \frac{\rho (1+\alpha _{2}V_{1})(T-T_{1}+E-E_{1})(\dot{T}+\dot{E})}{(1+\alpha _{1}T_{1} +\alpha _{2}V_{1}+\alpha _{3}T_{1}V_{1})(\mu _{T}+\mu _{E}+\gamma )T_{1}}\\&+\,\displaystyle \frac{f(T_{1},V_{1})V_{1}}{\gamma E_{1}}\left( 1-\displaystyle \frac{I_{1}}{I}\right) \dot{I}+ \left( 1-\displaystyle \frac{E_{1}}{E}\right) \dot{E}\\&+\,\displaystyle \frac{\mu _{I}f(T_{1},V_{1})V_{1}}{k\gamma E_{1}}\left( 1-\displaystyle \frac{V_{1}}{V}\right) \dot{V}\\&\times \,\displaystyle \frac{p f(T_{1},V_{1})V_{1}}{a\gamma E_{1}}\dot{C}. \end{aligned}$$

By \(\lambda =\mu _{T} T_{1}+f(T_{1},V_{1})V_{1}-\rho E_{1}\), we get

$$\begin{aligned} \displaystyle \frac{dW_{1}}{dt}= & {} -\displaystyle \frac{(1+\alpha _{2}V_{1})(T-T_{1})^{2}}{TT_{1}(1+\alpha _{1}T_{1}+\alpha _{2}V_{1}+\alpha _{3}T_{1}V_{1})}\bigg ((\mu _{T} T_{1}\\&-\,\rho E_{1})+\displaystyle \frac{\rho \mu _{T} T}{\mu _{T}+\mu _{E}+\gamma }+\rho E\bigg )\\&-\,\displaystyle \frac{\rho (E-E_{1})^{2}(1+\alpha _{2}V_{1})(\mu _{E}+\gamma )}{T_{1}(1+\alpha _{1}T_{1}+\alpha _{2}V_{1}+\alpha _{3}T_{1}V_{1})(\mu _{T}+\mu _{E}+\gamma )}\\&+\,f(T_{1},V_{1})V_{1}\bigg (5-\displaystyle \frac{f(T_{1},V_{1})}{f(T,V_{1})}-\displaystyle \frac{I_{1}E}{E_{1}I}\\&-\,\displaystyle \frac{f(T,V)}{f(T_{1},V_{1})}\displaystyle \frac{VE_{1}}{V_{1}E}-\displaystyle \frac{V_{1}I}{VI_{1}} -\displaystyle \frac{f(T,V_{1})}{f(T,V)}\bigg )\\&-\,\displaystyle \frac{f(T_{1},V_{1})(1+\alpha _{1}T)(\alpha _{2}+\alpha _{3}T)(V-V_{1})^{2}}{(1+\alpha _{1}T +\alpha _{2}V_{1}+\alpha _{3}TV_{1})(1+\alpha _{1}T+\alpha _{2}V+\alpha _{3}TV)}\\&+\,\displaystyle \frac{p\mu _{C} f(T_{1},V_{1})V_{1}}{a\gamma E_{1}}(R_{1}-1)C. \end{aligned}$$

Using the arithmetic-geometric inequality, we get

$$\begin{aligned}&5-\displaystyle \frac{f(T_{i},V_{i})}{f(T,V_{i})}-\displaystyle \frac{I_{i}E}{E_{i}I}-\displaystyle \frac{f(T,V)}{f(T_{i},V_{i})}\displaystyle \frac{VE_{i}}{V_{i}E}-\displaystyle \frac{V_{i}I}{VI_{i}}\nonumber \\&\quad -\,\displaystyle \frac{f(T,V_{i})}{f(T,V)}\le 0,\quad \text {for all } i=1,2. \end{aligned}$$
(13)

Therefore, \(\frac{dW_{1}}{dt}\le 0\) if \(R_{1}\le 1\) and \(\rho E_{1}\leqslant \mu _{T} T_{1}\).

Obviously, the condition \(\rho E_{1}\leqslant \mu _{T} T_{1}\) is equivalent to

$$\begin{aligned} R_{0}\le & {} 1\\&+\displaystyle \frac{[\mu _{T}\mu _{I}\mu _{V}(\mu _{E}+\gamma )+\alpha _{2}\mu _{T}\lambda k\gamma ](\mu _{E}+\rho +\gamma )+\rho \alpha _{3}k\gamma \lambda ^{2}}{\rho \mu _{I}\mu _{V}(\mu _{E}+\rho +\gamma )(\mu _{T}+\alpha _{1}\lambda )}. \end{aligned}$$

In addition, \(\frac{dW_{1}}{dt}=0\) if and only if \(T=T_{1}\), \(E=E_{1}\), \(I=I_{1}\), \(V=V_{1}\) and \(C=0\). Hence, the largest compact invariant set in \(\{(T,E,I,V,C)|\frac{dW_{1}}{dt}=0\}\) is the singleton \(\{Q_{1}\}\). This proves the global stability of \(Q_{1}\) by using LaSalle invariance principle. \(\square \)

Remark 2.4

If \(\alpha _{3}=0\), then the condition (12) becomes

$$\begin{aligned} R_{0}\le 1+\displaystyle \frac{[\mu _{T}\mu _{I}\mu _{V}(\mu _{E}+\gamma )+\alpha _{2}\mu _{T}\lambda k\gamma ](\mu _{E}+\rho +\gamma )}{\rho \mu _{I}\mu _{V}(\mu _{E}+\rho +\gamma )(\mu _{T}+\alpha _{1}\lambda )}, \end{aligned}$$

which is the condition given by Lv et al. [12] that ensures the global asymptotic stability of the immune-free infection equilibrium.

It is important to see that

$$\begin{aligned}&\lim _{\rho \rightarrow 0}\displaystyle \frac{[\mu _{T}\mu _{I}\mu _{V}(\mu _{E}+\gamma )+\alpha _{2}\mu _{T}\lambda k\gamma ](\mu _{E}+\rho +\gamma )+\rho \alpha _{3}k\gamma \lambda ^{2}}{\rho \mu _{I}\mu _{V}(\mu _{E}+\rho +\gamma )(\mu _{T}+\alpha _{1}\lambda )}\\&\quad =\infty ,\\&\lim _{\gamma \rightarrow \infty }\displaystyle \frac{[\mu _{T}\mu _{I}\mu _{V}(\mu _{E}+\gamma )+\alpha _{2}\mu _{T}\lambda k\gamma ](\mu _{E}+\rho +\gamma )+\rho \alpha _{3}k\gamma \lambda ^{2}}{\rho \mu _{I}\mu _{V}(\mu _{E}+\rho +\gamma )(\mu _{T}+\alpha _{1}\lambda )}\\&\quad =\infty . \end{aligned}$$

According to theorem 2.3, we get the following result

Corollary 2.5

  1. (i)

    The immune-free infection equilibrium \(Q_{1}\) is globally asymptotically stable if \(R_{1}\le 1<R_{0}\) and \(\rho \) sufficiently small.

  2. (ii)

    The immune-free infection equilibrium \(Q_{1}\) is globally asymptotically stable if \(R_{1}\le 1<R_{0}\) and \(\gamma \) sufficiently large.

Finally, we investigate the global stability of the third equilibrium \(Q_{2}\).

Theorem 2.6

The chronic infection equilibrium with immune response \(Q_{2}\) is globally asymptotically stable if \(R_{1}>1\) and

$$\begin{aligned} k\beta \mu _{C}\rho\le & {} \alpha _{1}\lambda \rho a\mu _{V}+\mu _{T}(\rho +\mu _{E}+\gamma )(\alpha _{2}k\mu _{C}+a\mu _{V})\nonumber \\&+\,\alpha _{3}\rho \lambda k\mu _{C}. \end{aligned}$$
(14)

Proof

Define a Lyapunov functional \(W_{2}\) as follows

$$\begin{aligned}&W_{2}(T,E,I,V,C)= T-T_{2}-\int _{T_{2}}^{T}\displaystyle \frac{f(T_{2},V_{2})}{f(S,V_{2})}dS\\&\quad +\,\displaystyle \frac{\rho (1+\alpha _{2}V_{2})(T-T_{2}+E-E_{1})^{2}}{2(1+\alpha _{1}T_{2}+\alpha _{2}V_{2}+\alpha _{3}T_{2}V_{2})(\mu _{T}+\mu _{E}+\gamma )T_{2}}\\&\quad +\,\displaystyle \frac{f(T_{2},V_{2})V_{2}}{\gamma E_{2}}I_{2}\Phi \left( \displaystyle \frac{I}{I_{2}}\right) +E_{2}\Phi \left( \displaystyle \frac{E}{E_{2}}\right) \\&\quad +\,\displaystyle \frac{(\mu _{I}+pC_{2})f(T_{2},V_{2})V_{2}}{k\gamma E_{2}}V_{2}\Phi \left( \displaystyle \frac{V}{V_{2}}\right) \\&\quad +\,\displaystyle \frac{p f(T_{2},V_{2})V_{2}}{a\gamma E_{2}}C_{2}\Phi \left( \displaystyle \frac{C}{C_{2}}\right) . \end{aligned}$$

Calculating the derivative of \(W_{2}\) along the positive solutions of the system (1), we have

$$\begin{aligned} \displaystyle \frac{dW_{2}}{dt}= & {} \bigg (1-\displaystyle \frac{f(T_{2},V_{2})}{f(T,V_{2})}\bigg )\dot{T}\\&+\,\displaystyle \frac{\rho (1+\alpha _{2}V_{2})(T-T_{2}+E-E_{2})}{(1+\alpha _{1}T_{2} +\alpha _{2}V_{2}+\alpha _{3}T_{2}V_{2})(\mu _{T}+\mu _{E}+\gamma )T_{2}}\left( \dot{T}+\dot{E}\right) \\&+\,\displaystyle \frac{f(T_{2},V_{2})V_{2}}{\gamma E_{2}}\left( 1-\displaystyle \frac{I_{2}}{I}\right) \dot{I}+\left( 1-\displaystyle \frac{E_{2}}{E}\right) \dot{E}\\&+\,\displaystyle \frac{f(T_{2},V_{2})V_{2}}{k\gamma E_{2}}(\mu _{I}+pC_{2})\\&\times \,\left( 1-\displaystyle \frac{V_{2}}{V}\right) \dot{V} \displaystyle \frac{p f(T_{2},V_{2})V_{2}}{a\gamma E_{2}}\left( 1-\displaystyle \frac{C_{2}}{C}\right) \dot{C}. \end{aligned}$$

Applying the equality \(\lambda =\mu _{T} T_{2}+f(T_{2},V_{2})V_{2}-\rho E_{2}\), we get

Fig. 1
figure 1

Stability of the infection-free equilibrium \(Q_{0}\) for system (1)

Full size image
$$\begin{aligned} \displaystyle \frac{dW_{2}}{dt}= & {} \bigg (1-\displaystyle \frac{f(T_{2},V_{2})}{f(T,V_{2})}\bigg )\mu _{T}(T_{2}-T)\\&+\,\displaystyle \frac{f(T_{2},V_{2})f(T,V)}{f(T,V_{2})}V\\&-\,\displaystyle \frac{\mu _{T}\rho (1+\alpha _{2}V_{2})}{(1+\alpha _{1}T_{2}+\alpha _{2}V_{2}+\alpha _{3}T_{2}V_{2})(\mu _{T}+\mu _{E}+\gamma )T_{2}}(T-T_{2})^{2}\\&-\,\displaystyle \frac{\rho (1+\alpha _{2}V_{2})(\mu _{E}+\gamma )}{(1+\alpha _{1}T_{2}+\alpha _{2}V_{2}+\alpha _{3}T_{2}V_{2})(\mu _{T}+\mu _{E}+\gamma )T_{2}}(E-E_{2})^{2}\\&-\,\displaystyle \frac{\rho (1+\alpha _{2}V_{2})(E-E_{2})(T-T_{2})}{(1+\alpha _{1}T_{2} +\alpha _{2}V_{2}+\alpha _{3}T_{2}V_{2})T_{2}}\\&+\,\bigg (1-\displaystyle \frac{f(T_{2},V_{2})}{f(T,V_{2})}\bigg )\big ((\mu _{E}+\gamma )E_{2}+\rho E\big )\\&+\,f(T_{2},V_{2})V_{2}\bigg [-\displaystyle \frac{I_{2}E}{IE_{2}}+\displaystyle \frac{\mu _{I}I_{2}}{\gamma E_{2}}\\&-\,\displaystyle \frac{\mu _{V}V(\mu _{I}+pC_{2})}{k\gamma E_{2}}-\displaystyle \frac{V_{2}I(\mu _{I}+pC_{2})}{V\gamma E_{2}}\\&+\,\displaystyle \frac{\mu _{V}V_{2}(\mu _{I}+pC_{2})}{k\gamma E_{2}}+\displaystyle \frac{p\mu _{C}C_{2}}{a\gamma E_{2}}\bigg ]\\&-\,\displaystyle \frac{f(T,V)E_{2}}{E}+f(T_{2},V_{2})V_{2},\\= & {} -\,\displaystyle \frac{(1+\alpha _{2}V_{2})(T-T_{2})^{2}}{TT_{2}(1+\alpha _{1}T_{2}+\alpha _{2}V_{2}+\alpha _{3}T_{2}V_{2})}\bigg ((\mu _{T} T_{2}-\rho E_{2})\\&+\,\displaystyle \frac{\rho \mu _{T} T}{\mu _{T}+\mu _{E}+\gamma }+\rho E\bigg )\\&-\,\displaystyle \frac{\rho (E-E_{2})^{2}(1+\alpha _{2}V_{2})(\mu _{E}+\gamma )}{T_{2}(1+\alpha _{1}T_{2}+\alpha _{2}V_{2}+\alpha _{3}T_{2}V_{2})(\mu _{T}+\mu _{E}+\gamma )}\\&+\,f(T_{2},V_{2})V_{2}\bigg (5-\displaystyle \frac{f(T_{2},V_{2})}{f(T,V_{2})}-\displaystyle \frac{I_{2}E}{E_{2}I}\\&-\,\displaystyle \frac{f(T,V)}{f(T_{2},V_{2})}\displaystyle \frac{VE_{2}}{V_{2}E}-\displaystyle \frac{V_{2}I}{VI_{2}} -\displaystyle \frac{f(T,V_{2})}{f(T,V)}\bigg )\\&-\,\displaystyle \frac{f(T_{2},V_{2})V_{2}(1+\alpha _{1}T)(\alpha _{2}+\alpha _{3}T)(V-V_{2})^{2}}{V_{2}(1+\alpha _{1}T +\alpha _{2}V_{2}+\alpha _{3}TV_{1})(1+\alpha _{1}T+\alpha _{2}V+\alpha _{3}TV)}. \end{aligned}$$

From (13), we deduce that \(\frac{dW_{2}}{dt}\le 0\) if \(R_{1}>1\) and \(\rho E_{2}\leqslant \mu _{T} T_{2}\).

However, this last condition is equivalent to

$$\begin{aligned} k\beta \mu _{C}\rho\le & {} \alpha _{1}\lambda \rho a\mu _{V}+\mu _{T}(\rho +\mu _{E}+\gamma )(\alpha _{2}k\mu _{C}+a\mu _{V})\\&+\,\alpha _{3}\rho \lambda k\mu _{C}. \end{aligned}$$

Note that \(\frac{dW_{1}}{dt}=0\) if and only if \(T=T_{2}\), \(E=E_{2}\), \(I=I_{2}\), \(V=V_{2}\) and \(C=C_{2}\). Hence, the largest compact invariant set in \(\{(T,E,I,V,C)|\frac{dW_{2}}{dt}=0\}\) is the singleton \(\{Q_{2}\}\). Based on the LaSalle invariance principle, we deduce that \(Q_{2}\) is globally asymptotically stable. This completes the proof. \(\square \)

We remark that the condition (14) holds for \(\rho \) sufficiently small, or \(\gamma \) sufficiently large. Hence, we have the following corollary.

Corollary 2.7

  1. (i)

    The chronic infection equilibrium \(Q_{2}\) is globally asymptotically stable if \(R_{1}>1\) and \(\rho \) sufficiently small.

  2. (ii)

    The chronic infection equilibrium \(Q_{2}\) is globally asymptotically stable if \(R_{1}>1\) and \(\gamma \) sufficiently large.

In addition, we have the following remark.

Remark 2.8

If \(\alpha _{3}=0\), then the condition (14) becomes

$$\begin{aligned} k\beta \mu _{C}\rho \le \alpha _{1}\lambda \rho a\mu _{V}+\mu _{T}(\rho +\mu _{E}+\gamma )(\alpha _{2}k\mu _{C}+a\mu _{V}), \end{aligned}$$

which is the condition given by Lv et al. [12] that ensures the global asymptotic stability of the chronic infection equilibrium.

Fig. 2
figure 2

Stability of the infection-free equilibrium \(Q_{0}\) for system (2)

Full size image
Fig. 3
figure 3

Stability of the immune-free infection equilibrium \(Q_{1}\) for system (1)

Full size image

3 Global stability of the PDE model

It is not hard to see that the PDE model (2) has the same three equilibria as the ODE model (1), namely, the infection-free equilibrium \(Q_{0}\), the immune-free infection equilibrium \(Q_{1}\) which exists whenever \(R_{0}>1 \)and the chronic infection equilibrium \(Q_{2}\) which exists if \(R_{1}>1\).

Now, we investigate the global stability of problem (2)–(4) by constructing appropriate Lyapunov functionals. The construction of these Lyapunov functionals is based on the method proposed by Hattaf and Yousfi [23].

Theorem 3.1

For all diffusion coefficients, we have

  1. (i)

    The infection-free equilibrium \(Q_{0}\) of problem (2)–(4) is globally asymptotically stable if \(R_{0}\le 1\).

  2. (ii)

    The immune-free infection equilibrium \(Q_{1}\) of problem (2)–(4) is globally asymptotically stable if \(R_{1}\le 1<R_{0}\) and the condition (12) holds .

  3. (iii)

    The chronic infection equilibrium \(Q_{2}\) of problem (2)–(4) is globally asymptotically stable if \(R_{1}>1\) and the condition (14) holds.

Proof

Let \(u(t,x)=\big (T(t,x),I(t,x),V(t,x),E(t,x),C(t,x)\big )\) be a solution of (2)–(4), and we put

$$\begin{aligned} L_{i}=\int _{\Omega }W_{i}\big (u(x,t))dx, \end{aligned}$$

where \(W_{i}\) is the Lyapunov functional for the ODE model (1) at \(Q_{i}\), \(i=0,1,2\).

It is easy to check that \(W_{i}\) satisfies the condition (15) given in [23], for all \(i=0,1,2\). From Proposition 2.1 given in Ref. [23], we deduce that \(L_{i}\) is a Lyapunov functional for problem (2)–(4) at \(Q_{i}\). This completes the proof. \(\square \)

Fig. 4
figure 4

Stability of the immune-free infection equilibrium \(Q_{1}\) for system (2)

Full size image
Fig. 5
figure 5

Stability of the chronic infection equilibrium \(Q_{2}\) for system (1)

Full size image

4 Numerical simulations

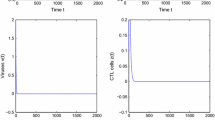
In this section, we present some numerical simulations to validate our theoretical results. Firstly, we consider parameter values \(\Lambda =10\) cells \(\mu l^{-1}\) day\(^{-1}\), \(\mu _{T}=0.0139\) day\(^{-1}\), \(\beta =2.4\times 10^{-5}\) \(\mu l\) virion\(^{-1}\) day\(^{-1}\), \(\alpha _{1}=0.1\), \(\alpha _{2}=0.01\), \(\alpha _{3}=0.00001\), \(\rho =0.01\) day\(^{-1}\), \(\gamma =0.01\) day\(^{-1}\), \(\mu _{I}=0.27\) day\(^{-1}\), \(\mu _{E}=0.0347\) day\(^{-1}\), \(p=0.001\) cell\(^{-1}\) \(\mu l\) day\(^{-1}\), \(k=1200\) virion cell\(^{-1}\) day\(^{-1}\), \(\mu _{V}=3\) day\(^{-1}\), \(a=0.002\) cell\(^{-1}\) \(\mu l\) day\(^{-1}\), \(\mu _{C}=0.1\) day\(^{-1}\) and \(d=0.1\). Here, the values p, a and \(\mu _{C}\) are taken from [1, 5], while the other parameter values are chosen from [10]. For these set of parameter values, we have \(R_{0}=0.1141<1\). Hence, systems (1) and (2) have an infection-free equilibrium \(Q_{0}(719,4245,0,0,0,0)\) which is globally asymptotically stable according to Theorems 2.2 and 3.1 (i). Figures 1 and 2 illustrate this result.

Secondly, we choose \(\beta =0.0012\) \(\mu l\) virion\(^{-1}\) day\(^{-1}\) and do not change the other parameter values. By calculation, we have \(R_{0}=3.2055>1\), \(R_{1}=0.1427<1\) and \(\frac{[\mu _{T}\mu _{I}\mu _{V}(\mu _{E}+\gamma )+\alpha _{2}\mu _{T}\lambda k\gamma ](\mu _{E}+\rho +\gamma )+\rho \alpha _{3}k\gamma \lambda ^{2}}{\rho \mu _{I}\mu _{V}(\mu _{E}+\rho +\gamma )(\mu _{T}+\alpha _{1}\lambda )}= 2.2725\). In this case, both systems have an immune-free equilibrium \(Q_{1}(138.53,183.16,6.80,2724.2,0)\). By Theorems 2.3 and 3.1 (ii), \(Q_{1}\) is globally asymptotically stable (see Figs. 3 and 4). We see that in the absence of CTL cells, the number of CD4\(^{+}\) T cells decreases to the value 138.53, which means that the patient enters in the phase AIDS (< 200 cell mm\(^{-3}\)).

Fig. 6
figure 6

Stability of the chronic infection equilibrium \(Q_{2}\) for system (2)

Full size image
Fig. 7
figure 7

Stability of the immune-free infection equilibrium \(Q_{1}\) with condition (12) not satisfied

Full size image

Thirdly, we change one parameter which is \(a=0.065\) cell\(^{-1}\) \(\mu l\) day\(^{-1}\). By calculation, we have \(R_{1}=4.6379>1\). Then systems (1) and (2) have a chronic infection equilibrium \(Q_{2}(370.56,106.97,1.57,629.65,409.12)\). Therefore, by Theorems 2.6 and 3.1 (iii), \(Q_{2}\) is globally asymptotically stable (see Figs. 5 and 6). In this case, we see that in the presence of CTL cells, the number of CD4\(^{+}\) T cells increases to the value \(252.0792>200\) cell mm\(^{-3}\), which means that the patient is no longer in the phase AIDS.

Finally, in Fig. 7, we see that the dynamics of HIV infection converges to steady state \(Q_{1}\) for all initial conditions. However, the condition (12) is not satisfied with \(R_{0}=4.1501>1\), \(R_{1}=0.0999<1\) and

$$\begin{aligned}&1+\displaystyle \frac{[\mu _{T}\mu _{I}\mu _{V}(\mu _{E}+\gamma )+\alpha _{2}\mu _{T}\lambda k\gamma ](\mu _{E}+\rho +\gamma )+\rho \alpha _{3}k\gamma \lambda ^{2}}{\rho \mu _{I}\mu _{V}(\mu _{E}+\rho +\gamma )(\mu _{T}+\alpha _{1}\lambda )}\\&\quad =2.3910. \end{aligned}$$

Similarly, in Fig. 8, we see that the dynamics of HIV infection converges to steady state \(Q_{2}\) for all initial conditions. However, the condition (14) is not satisfied with \(R_{1}=3.4338\) and \(\alpha _{1}\lambda \rho a\mu _{V}+\mu _{T}(\rho +\mu _{E}+\gamma )(\alpha _{2}k\mu _{C}+a\mu _{V})+\alpha _{3}\rho \lambda k\mu _{C}-k\beta \mu _{C}\rho =-0.0041<0\). Therefore, the conditions (12) and (14) are not necessary for the global stability of \(Q_{1}\) and \(Q_{2}\).

Fig. 8
figure 8

Stability of the chronic infection equilibrium \(Q_{2}\) with condition (14) not satisfied

Full size image

5 Conclusion and discussion

In this paper, we have proposed two HIV infection models. The first is an ODE model with cure of infected cells in eclipse stage, CTL immune response and Hattaf’s incidence rate which includes the traditional bilinear incidence rate, the saturated incidence rate, the Beddington–DeAngelis functional response and the Crowley-Martin functional response. The second is a PDE model that extends the first one by taking into account the diffusion of virus. The two models admits three equilibria, namely, the infection-free equilibrium \(Q_{0}\), the immune-free infection equilibrium \(Q_{1}\) which exists whenever \(R_{0}>1 \) and the chronic infection equilibrium \(Q_{2}\) which exists if \(R_{1}>1\). The global stability of these three equilibria have obtained in terms of the basic reproduction number \(R_{0}\) and the CTL immune response reproduction number \(R_{1}\). It is shown that \(Q_f\) is globally asymptotically stable when \(R_{0}\le 1\), \(Q_1\) is globally asymptotically stable when \(R_{1}\le 1<R_{0}\) and the condition (12) holds, and \(Q_{2}\) is globally asymptotically stable when \(R_{1}>1\) and the condition (14) holds.

In addition, we remark that if the cure rate \(\rho \) is sufficiently small or the value of \(\gamma \) is sufficiently large, the conditions (12) and (14) are satisfied. From the numerical simulations (Figs. 7 and 8), we see that both equilibria \(Q_{1}\) and \(Q_{2}\) remain globally asymptotically stable without the conditions (12) and (14) are satisfied.

Observing that the basic reproduction number \(R_{0}\) is independent of the CTL immune parameters. Further, by comparing the components of healthy cells, infected cells in the eclipse stage, productive infected cells and viral load before and after the activation of CTL response, we have \(T_{2}\)>\(T_{1}\), \(E_{2}<E_{1}\), \(I_{2}<I_{1}\) and \(V_{2}<V_{1}\) when \(R_{1}>1\). Therefore, we deduce that the activation of CTL immune response is unable to eliminate the virus in the host population, but plays an important role in HIV infection by reducing the viral load, increasing the healthy cells and decreasing the two classes of infected cells.