1 Introduction

Increased usage of fossil fuels leads to extreme CO2 emissions, climate change, and destabilization of global energy prices [1,2,3,4]. To mitigate this problem, renewable energy systems that are characterized by their reliability [5], efficiency [6], and sustainability [7] have found their usage. Hybrid and electric vehicles have become significantly important [8]. Presently, several countries around the world are investing in renewable energy systems either on a pilot scale or an industrial scale. Since early 1970s, significant progress has been made in the area of various renewable energy systems such as solar panels, wave energy converters, wind turbines, hydrokinetic turbines, and others [9, 10]. Among these, wind and hydro turbines have found their applications in off-grid power generation [11]. Usually, the wind turbines can be categorized into (a) horizontal-axis wind turbines (HAWTs) that rotates around a horizontal axis with the rotor positioned parallel to the flow direction and (b) vertical-axis wind turbine (VAWTs) that rotate about a vertical axis that is perpendicular to the flow direction [12, 13]. In general, the HAWTs are more efficient in harvesting wind energy; however, the materials and manufacturing methods have made them more expensive for small-scale power generation [14, 15]. Various types of VAWTs such as Darrius, Gorlov, and Savonius rotors [16,17,18,19,20] have found their applications in small-scale power generation. Among these, the drag-based Savonius rotor has become popular due to its simplicity, ease of fabrication, directional independence [10, 11], lower cost, and low noise level [21,22,23,24]. However, the Savonius rotor suffers from low efficiency [25], and this enables the researchers to investigate further to improve its performance [26].

A conventional two-bladed Savonius wind rotor is shown in Fig. 1. It works on the principle of drag force that arises between the concave and the convex sides of the blade. It is evident from the literature that the advancing blade experiences higher drag than the returning blade, thereby resulting in a net positive torque. This net positive torque further produces the rotational motion to the rotor. On the other side, the lift force also contributes to the net torque production, but it is not significant compared to the drag force [10]. However, the drag produced by the returning blade is significant enough to reduce the performance of the rotor blade. In view of this, the attention must be drawn to minimize the negative torque produced by the returning blade. In this regard, several researches have been made to enhance the power coefficient (Cp) by enhancing the design of parameters, such as arc angle of the blade and various others geometric parameters [27,28,29,30]. While the past two decades have witnessed various new blade profiles study, notable among them are as follows: Bach [31], Benesh [32], twisted [33], fish-ridge [34], new elliptical [35] spline [36], and other types (Table 1). It is evident that the blade profiles play a major role in minimizing the negative torque produced by the returning blade, and this can improve the Cp of the Savonius rotor. This happens due to fact that the wake formation on the concave side of the returning blade is found to be smaller. Furthermore, the flow separation also gets delayed due to higher curvature at the leading edge of the blade [32,33,34,35].

Fig. 1
figure 1

A typical two-bladed Savonius wind rotor

Full size image
Table 1 Selected investigations on various Savonius rotor blade profiles
Full size table

1.1 Present objective

Although the available Savonius rotor designs have showcased an enhancement in the Cp, there is always a scope to evolve newer blade profiles. In view of this, the present objective is to develop a new blade profile using a parabolic curve. This type of parabolic profile for the design of blades in a Savonius rotor has not been attempted till date. In this work, a 2D computational fluid dynamics (CFD) study is performed on the new parabolic blade profile using ANSYS Fluent software [40]. The torque and power coefficients (CT and Cp) values are studied at different tip speed ratios (TSRs) and Reynolds numbers (Re). In addition to this, drag and lift coefficients (CD and CL) are also studied. On the basis of all the above parameters, the performance of the parabolic profile is compared with that of a conventional semicircular profile under similar environment.

2 Parameters defined

2.1 Torque coefficient (CT)

The ratio of the torque (T) produced by the turbine shaft to the torque available in wind is termed as torque coefficient [41, 42]. It can be expressed by Eq. (1).

$$ C_{T} = \frac{T}{{\frac{1}{2}\rho AV^{2} R}} $$
(1)

where T = torque (Nm), ρ = air density (kg/m3), A = swept area (m2), V = wind velocity (m/s), R = effective turbine radius (m).

2.2 Power coefficient (C p)

The ratio of turbine shaft power (\(P_{{{\text{turbine}}}}\)) to the available wind power (\(P_{{{\text{available}}}}\)) is termed as power coefficient [41, 42]. It can be expressed by Eq. (2).

$$ C_{{\text{p}}} = \frac{{P_{{{\text{turbine}}}} }}{{P_{{{\text{available}}}} }} = \frac{T}{{\frac{1}{2}\rho AV^{3} }} $$
(2)

where T = torque (Nm), ω = angular velocity (rad/s), ρ = air density (kg/m3), A = swept area (m2), V = wind velocity (m/s).

2.3 Tip speed ratio (TSR)

The ratio of tangential speed of the rotor to the inlet wind speed is terms as tip speed ratio. It can be expressed by Eqs. (3) and (4).

$$ {\text{TSR}} = \frac{R\omega }{V} $$
(3)
$$ C_{{\text{p}}} = C_{{\text{T}}} \times {\text{TSR}} $$
(4)

3 Generation of the new profile

The present parabola can be drawn by following the equation \(x^{2} = 4ay\) as shown in Fig. 2. In the present study, only one parabola with focus (F = 0, 0) and the vertex point (O = 0, − 2) is chosen arbitrarily to generate the blade profile. However, there may be an infinite number of parabolas that can be optimized by using optimization algorithm. The present work deals with unfolding the potential of a new blade profile for which an arbitrary parabola with section cut angle (θ) is chosen.

Fig. 2
figure 2

The section cut angle (θ) on the parabola

Full size image

The standard parabolic equation with vertex (0, − 2) and directrix length (a = 2) is given by Eq. (5).

$$ \left( {x - h} \right)^{{2}} = { 4}a\left( {y - k} \right) $$
(5)

Thus, the present parabolic equation can be written as:

$$ x^{{2}} = {8}y + {16} $$
(6)

Beside this, the line AB can be expressed as

$$ y = - \tan \theta \cdot x + l - 2 $$
(7)

where \(l = 0.164D\).

Considering that points A and B meet both Eqs. (6) and (7), the arc AOB can be expressed as a function of θ, as given by Eq. (8).

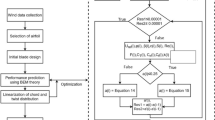
$$ x^{2} = 8y + 16\left( {\frac{{ - 8\tan \theta - \sqrt {64\tan^{2} \theta + 1049.6} }}{2} < x < \frac{{ - 8\tan \theta + \sqrt {64\tan^{2} \theta + 1049.6} }}{2}} \right) $$
(8)

The geometry of the blade profile is generated on SOLIDWORKS. The θ is made by the line AB with respect to the x axis on the parabola. The line AB dissects the parabola to create an arc AOB that gives one-half of the blade profile. The line AB intersects the y-axis at point C about which θ can be varied and optimized. The length OC thus becomes the depth of cut (l) on the parabola, and this is 0.164D from point O. The θ is dependent on l, i.e., for each θ, there is a fixed value of l to get the required chord length (L) of the blade profile. The flowchart adopted to get the optimum profile is shown in Fig. 3.

Fig. 3
figure 3

The flowchart adopted to get the optimum profile

Full size image

3.1 Geometric details of the tested profiles

The diameter (D) and thickness (t) of the blade profile is taken as 200 and 2 mm, respectively. The diameter of the semicircular profile is kept similar to that of the parabolic profile (Fig. 4). The overlap ratio (OR) is kept at 0.0 for both the profiles [43, 44].

Fig. 4
figure 4

Geometry of the test profiles

Full size image

4 Numerical Simulation Aspect

This section deals with the details of the computational domain, meshing, solver setup, grid and time independence tests followed by the validation of the 2D numerical model.

4.1 Computational domain

The computational domain (15D × 22.D) can be categorized as rotational and non-rotational zones. The rotational zone consists of the rotor blades that is coinciding with the origin. The overall diameter of the rotor blade is D, and the corresponding rotational zone is 2D [43, 44], while the non-rotational zone is surrounded by a rectangle (Fig. 5).

Fig. 5
figure 5

Domain and boundary conditions

Full size image

4.2 Meshing of the domain

The meshing of the domain is shown in Fig. 6. The ANSYS Fluent 20.2 software [40] meshing is used to discretize the computational domain. The domain is divided into small control volumes and discretized to solve the Reynolds averaged Navier–Stokes (RANS) equations. Due to subsonic flow, equal accuracy can be expected in both the structured and the non-structured meshes [45]. However, the unstructured mesh can be easily made in the case of a complex geometry. In addition, due to the faster generation of grids, the unstructured mesh with tri-elements is used to discretize the rotor domain [43, 44], while the outer stator domain is discretized by quadrilateral elements [9]. The sliding mesh option is chosen at the ‘Int’ between the rotational and the non-rotational zones. With a first layer thickness from the wall of 0.05 mm and a growth rate of 1.2, the inflation layer is provided for increased precision around the blade profile perimeter. The maximum number of inflation layers is 10 and the growth rate is 1.2 can be seen in Fig. 6. In the numerical model, the value of the dimensionless wall distance y + in the region of the cohesive sublayer is found to be less than unity [9, 41].

Fig. 6
figure 6

Meshing near the rotor

Full size image

4.3 Boundary conditions

For setting the boundary conditions, the upper and lower walls are equidistant from the center and are found to have symmetrical behavior. Both the walls are at a distance of 7.5D from the origin (Fig. 5) and are named as symmetry [43]. The vertical left edge (Inlet) is situated at 7.5D from the origin, and at the same time, the right vertical edge (Outlet) is situated at 15D from the origin as shown in Fig. 5. The inlet velocity (V) of 7.3 m/s is provided in the positive x axis direction with a maximum turbulence of 1% is given as the boundary condition [43]. The 'Pressure outlet' is taken as an output boundary condition with the same amount of turbulence intensity. In the solver setup, the air is taken as the working fluid, and hence, the standard atmospheric conditions are provided [44] (Fig. 6).

4.4 Turbulence model and solver setup

In the solver setup, the air is taken as the working fluid, and hence, the standard atmospheric conditions are provided. As the flow around the rotor blade is turbulent, it is important to choose a turbulence model accordingly. Previous numerical studies with various turbulence models suggest the use of the SST k–ω turbulence model for its good predictive power [46, 47]. The SST k–ω model is thus chosen to get the average properties of turbulence near the turbine wall region. This model incorporates the feature of calculating the averaged properties of the flow within and outside the boundary layer. The sliding mesh (reference frame motion) is chosen for all the numerical simulations. The time step size is found based on 1°/step rotation of the rotor blade at TSR = 0.8. The timestep size is assumed to be 0.0002988577 s and the total number of time steps is 1800 for 2D simulations. Numerical simulations are performed for 5 complete rotations of the rotor. Though the dynamic steady state is reached after the first rotation, still the last rotation is chosen for the study. A maximum of 20 iterations per time step with convergence criterion 10–4 (for stopping the solution) is chosen to stop the solution. The conservative and temporal terms are discretized using a second-order upwind scheme. The semi-implicit method for the pressure-linked equation is chosen for the pressure–velocity coupling to increase the stability of the solution.

4.5 Mesh and time dependency test

The mesh independence and the time step independence tests performed on the 2D study are shown in Figs. 7 and 8. The number of grid elements are varied from 71,790 to 203,372. While moving from grid elements 71,790 to 120,849, there is an increase in CT by 7.1%. This CT is not changing much (about 0.4%) while moving from grid elements 120,849 to 203,372. Thus, the number of grid elements of 120,849 is chosen for the 2D simulation. Similarly, the time independence test is done to check the temporal stability. It is seen that the higher the degree/step (1.5°/level and 2°/level), the lower is the average CT (Table 2). This happens due to the flow being not captured properly near the rotor wall. While the time step sizes of 0.5°/step and 1°/step are set to capture the flow correctly near the rotor wall, however, the step size of 1°/step is adopted for the ease the computational effort [35].

Fig. 7
figure 7

Grid independency test

Full size image
Fig. 8
figure 8

Time independency test

Full size image
Table 2 Averaged CT at different degrees of rotation
Full size table

4.6 Computational validation

The results of the numerical simulation obtained in this study are validated with the reported work of Alom et al. [35] as depicted in Fig. 9. The present test model is selected in such a way that it has the same AR (= 1.0) as that of the reported numerical model. Reynold's number considered in the validation study is taken as 0.89 × 105 to replicate the published work [35]. The numerical results are found to be consistent with published data (Fig. 9).

Fig. 9
figure 9

Variation of Cp with TSR

Full size image

5 Results and discussion

In this section, results of the new parabolic profile at different θ are reported. Results of the semicircular profile are also projected for a direct comparison. Thereafter, for the optimum profile, the effect of Re and TSR are studied besides evaluating the variation of CD and CL. This is followed by velocity magnitude, total pressure magnitude, and turbulence intensity contours.

5.1 Selection of the optimum parabolic blade profile

A series of 2D unsteady numerical simulations are performed to understand the aerodynamics of a parabolic profile to arrive at the optimum profile by CT and Cp analyses. Thus, eight different profiles are generated at different θ (ranges from 27.5° to 45°). The variation of CT with respect to the angle of attack (α) of the parabolic profiles is shown in Fig. 10. The TSR is kept 0.8 for the selection of optimum blade profile [35, 39, 43]. The parabolic profile at θ = 32.5° shows the maximum CT as compared to other values of θ besides the semicircular profile. However, the comparison of CT for all the eight profiles becomes overlapped. Therefore, a direct comparison (in terms of Cp) of the parabolic profile for various θ is shown in Fig. 11. The Cp of the parabolic profile at θ = 32.5° is found to be the maximum among all. This parabolic profile with θ = 32.5° is chosen for further analysis.

Fig. 10
figure 10

Variation of CT with α

Full size image
Fig. 11
figure 11

Variation of Cp with θ

Full size image

5.2 Effect of TSR

The effect of TSR on the performance of the optimum parabolic profile (θ = 32.5°) is studied in terms of CT and Cp at an inlet velocity of 6.7 m/s (Figs. 12, 13). The results of the semicircular profile are also shown for a direct comparison. The rotor speed (u) is found to be decreasing with the increase in load, and thereby CT decreases with the increase in TSR (Fig. 12). On the other side, Cp increases up to TSR = 0.8 and then decreases, indicating the optimum TSR to be 0.8. The parabolic profile shows a \(C_{{{\text{pmax}}}}\) of 0.319 at TSR = 0.8, while the semicircular profile shows the \(C_{{{\text{pmax}}}}\) of 0.266 at the same TSR (Fig. 13). Thus, the parabolic profile provides an improvement of Cp by 20% over the semicircular profile. Hence, TSR = 0.8 is taken for further analysis.

Fig. 12
figure 12

Variation of CT with TSR

Full size image
Fig. 13
figure 13

Variation of CP with TSR

Full size image

5.3 Lift and drag coefficient analysis

Figures 14 and 15 show the variations of CD and CL of the optimum parabolic and semicircular profiles. For the parabolic profile, the \(C_{{{\text{Dmax}}}}\) is found to be 2.34 at α = 184° and \(C_{{{\text{Dmin}}}}\) of 0.45 at α = 90°, while for the semicircular profile, the \(C_{Dmax}\) is found to be 1.98 at α = 182° and \(C_{{{\text{Dmin}}}}\) of 0.3 at α = 90° and 270°. Thus, the parabolic profile shows an increment of \(C_{{{\text{Dmax}}}}\) by 18.18% against the semicircular profile. On the other hand, the \(C_{{{\text{Lmax}}}}\) for the parabolic and semicircular profiles are found to be 2.4 (at α = 133°) and 2.13 (at α = 130°), respectively. This analysis demonstrates an improved performance of the parabolic profile against the semicircular profile in terms of CD and CL.

Fig. 14
figure 14

CD of the optimum parabolic and semicircular profiles at TSR = 0.8

Full size image
Fig. 15
figure 15

CL of the optimum parabolic and semicircular profiles at TSR = 0.8

Full size image

5.4 Effect of Reynolds number

In the present work, lower range of Reynolds number (Re) is taken to check its dependency on the Cp. The Re is calculated using formula, Re = \(\frac{\rho VD}{\mu }\), [35, 48, 49] where ρ is the density of air (kg/m3), V is the inlet velocity (m/s), μ is the dynamic viscosity of the air (kg/(m s). Numerical simulations at six different Reynolds numbers as shown in Table 3 have been carried out for the optimum parabolic (θ = 32.5°) and semicircular profiles at TSR = 0.8. The literature suggests that the Cp of the blade profile usually increases with an increase in Re [48, 49]. Therefore, the Re study is done on the parabolic profile along with the semicircular profile to arrive at the optimum Re. Thus, simulation results obtained in this regard are shown in Table 3. It can be seen that as Re increases, the Cp also increases in the range of tested Re. This happens because, for a constant rotor diameter, the increase in wind speed delays the flow separation around the rotor profile and it generally occurs on the lower side of the returning blade. The flow separation occurs earlier in the semicircular profile due to its sharp curvature which results in lesser Cp against the new parabolic profile. As a result, the lift force also contributes to the pressure recovery which further contributes to the enhancement of CT and Cp of the blade profile. Though there is a pressure recovery at higher wind speeds, still the Cp increases up to the optimum Re. Here in the present study, the optimum Re is different for both the profiles. The parabolic and semicircular profiles show an optimum Re of 0.97 × 105 and 0.93 × 105, respectively, with the corresponding Cp of 0.324 and 0.266. The optimum Re corresponding to the semicircular profile is chosen for further study. Hence, the corresponding inlet velocity of 6.7 m/s is taken for the TSR study.

Table 3 Cp of the test profiles at different Re
Full size table

5.5 Contours analysis

From the visualization of total pressure, and turbulent intensity contours, an attempt has been made to draw some meaningful inferences in this subsection.

5.5.1 Total pressure contours

The total pressure contours of the parabolic and semicircular profiles are shown in Figs. 16 and 17. The total pressure of the advancing side of the parabolic profile ranges between 21 and 56 N/m2, while the total pressure of the advancing side of the semicircular profile lies between 7 and 45 N/m2. The low-pressure region forming the recirculation behind the advancing side of the parabolic profile is lower than the semicircular profile. Moreover, the high-pressure region on the convex side of the returning side of the parabolic profile is smaller than the semicircular profile thereby improving the net torque. As the semicircular profile is characterized by a higher curvature, the flow separation is likely to occur earlier than in the parabolic profile. For the parabolic profile, the adverse pressure gradient is much lower than the semicircular profile. The parabolic profile thus has a higher CD and Cp.

Fig. 16
figure 16

Total pressure contours of the parabolic profiles at α = 0° and 90°

Full size image
Fig. 17
figure 17

The total pressure contours of the semicircular profile at α = 0° and 90°

Full size image

5.5.2 Turbulence intensity contours

Turbulence intensity is the property of turbulence that measures the degree of turbulence in the flow. The contours of turbulence intensity for the parabolic and semicircular profiles are shown in Figs. 18 and 19. The turbulence intensity is found to be low near the blade region in the parabolic profile ranging from 0.03 to 0.12%; however, it is found to range from 0.06 to 0.18% for the semicircular profile. As the magnitude of intensity is much lower in the parabolic profile, the vortex formation downstream of the profile is reduced. Further, a smoother flow field behind the returning side of the parabolic profile is observed as compared to its semicircular counterpart. This causes a higher Cp for the parabolic profile.

Fig. 18
figure 18

Turbulence intensity contours of the parabolic profile at α = 0° and 90°

Full size image
Fig. 19
figure 19

Turbulence intensity contours of the semicircular profile at α = 0° and 90°

Full size image

6 Conclusion

A series of 2D unsteady numerical simulations are carried out for a newly developed parabolic profile at different section cut angle (θ) using SST k–ω turbulence model. The results obtained in the present study show an optimum performance of the parabolic profile at θ = 32.5°. The effect of the Re study suggests that with the increase in Re, the Cp also increases. The newly developed parabolic profile is found to have a \(C_{{{\text{pmax}}}}\) of 0.324 at a Re = 0.97 × 105, while for the semicircular profile, it is 0.266. Moreover, the parabolic profile shows higher Cp values than the semicircular profile throughout the tested range of Re. On the other hand, TSR = 0.8 has shown the potential to harness more power than the other TSRs. Apart from this, the numerical results show that the optimum parabolic profile harnesses power with a peak Cp of 0.319 at TSR = 0.8 at velocity of 6.7 m/s, whereas the semicircular profile shows a peak Cp of 0.2663 at the same TSR and velocity. Thus, there is an improvement of \(C_{{{\text{pmax}}}}\) by around 20% in the 2-bladed parabolic profile in comparison to the semicircular profile. From the analysis of lift and drag coefficients, it is noted that the \(C_{{{\text{Dmax}}}}\) in the case of the parabolic profile is 2.34 which is 18.18% more than the semicircular profile (\(C_{{{\text{Dmax}}}}\) = 1.98). The \(C_{{{\text{Lmax}}}}\) for the parabolic and the semicircular profiles are found to be 2.4 and 2.13, respectively. The present study shows the superiority of the parabolic profile with θ = 32.5° as compared to the conventional semicircular profile. As the parabolic profile is characterized by a lower curvature, the flow separation on this profile is likely to get delayed as compared its semicircular counterpart. This enhances the pressure recovery thereby reducing the negative torque and improving the performance of the rotor. In order to find the feasibility of the new design, 3D numerical studies and wind tunnel experiments need to be conducted prior to the field tests and prototype development.