Abstract
Vibration signal processing is a crucial task in machine fault diagnosis. Several signal processing methods in the past relied on more conventional approaches to diagnose bearing defects. Recent advances in artificial intelligence have sparked the development of deep learning-based signal processing methods for bearing fault diagnosis. Many of the proposed methods do not apply to signals heavily polluted with noise. In this paper, a new method for bearing fault diagnosis is presented, which combines variational mode decomposition and wavelet thresholding to denoise vibration signal, time–frequency continuous wavelet transform to generate scalogram images, and deep learning structure to classify and diagnose bearing fault. The proposed method incorporates signal denoising, time–frequency transform, and deep learning to process and diagnose machine faults in the presence of background noise. Data collected from a bearing test rig are used to validate the accuracy of the proposed method, effectiveness, and robustness. The results show that the proposed method can extract “clean” vibration signals from noisy signals and accurately diagnose the fault.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Rolling element bearing (REB) is an important mechanical component widely used in various engineering components across many fields. Its health condition and proper functioning significantly impact the safety and stability of engineering equipment [1, 2] as well as the smooth functioning of many systems. The failure of REBs introduces dangerous and sometimes costly consequences [3, 4] to the process or system in which they are installed. The complex vibration transmission path of REBs makes it difficult to accurately diagnose REB faults [5]. As a result, advanced rolling bearing fault diagnosis methods are highly sought after to accurately diagnose and prevent catastrophic machinery failures [6].
Signal processing is a crucial task involved in machine fault diagnosis. Since the dawn of preventive maintenance and machine health monitoring, many vibration signal processing techniques have been developed to address the problem of bearing fault diagnosis. In general, signal processing techniques for machinery fault diagnosis can be classified into three broad categories: vibration analysis based on the direct manipulation of time series data, machine learning (ML) based, and deep learning (DL) based. Vibration analysis-based signal processing techniques can be further classified into time-domain, frequency-domain, and time–frequency domain analysis [7]. Traditional ML-based methods include artificial neural networks (ANN), principal component analysis (PCA), support vector machines (SVM), etc. Traditional DL-based algorithms for bearing fault diagnosis include a convolutional neural network (CNN), autoencoder, deep belief network (DBN), recurrent neural network (RNN), generative adversarial network (GAN), and deep learning-based transfer learning methods.
Time-domain analysis can be directly applied to vibration data since they are collected as time series data. Time-domain analysis is based on the use of statistical condition indicators such as mean, peak, peak-to-peak interval, and standard deviation, besides other higher order condition indicators such as probability density, kurtosis, crest factor, skewness and shape factor calculated from time-series signals to detect bearing faults [8, 9]. Time-domain vibration analysis is not limited to statistical condition indicators. Frequency-domain analysis is the most widely used technique for bearing fault diagnosis [10]. The advantages of frequency-domain analysis methods far surpass those of time-domain analysis because of their ability to easily isolate and identify important frequency components of a vibration signal as features. At the top of the list is fast Fourier transform (FFT), which can efficiently isolate narrow-band spectra. Vibration data from REBs contain valuable high and low ranges of frequency spectra components. Since REBs produce short-duration pulses during generation, these pulses generate high energy in specific ranges of the frequency band of the power spectrum in the frequency domain. The FFT technique has been applied to generate a power spectrum commonly used to extract bearing fault features and identify bearing faults [11,12,13]. Other efficient frequency-domain tools for bearing fault detection commonly used include envelope spectrum analysis [14], frequency filter sideband analysis, higher order spectra [15], and cepstrum analysis [16]. Time–frequency domain analysis is considered superior to time-domain analysis and frequency-domain analysis. It extends the capability of frequency-domain analysis on nonstationary waveform signals, such as waveforms obtained under variable speed conditions. Time–frequency analysis methods commonly used for machine fault diagnosis include short-term Fourier transfer (STFT) [17, 18], Wigner-Ville distribution (WVD) [19, 20], reduced interference distribution (RID), wavelet analysis such as wavelet transform methods (continuous wavelet transform, CWT, and discrete wavelet transform, DWT) and wavelet packet transform (WPT). These methods can process nonstationary signals for machine fault diagnosis. However, they present some shortcomings which limit their application in bearing fault diagnoses, such as the fixed temporal resolution of STFT controlled by choice of SFT window and limited by the uncertainty principle, the cross-term interface of Wigner-Ville distribution, and energy leakage issue and wavelet function selection of wavelet transform [21, 22]. Empirical mode decomposition (EMD) and, later variant, empirical ensemble mode decomposition EEMD) are powerful time–frequency analysis tools used to analyze vibration signals for machine fault diagnosis [23,24,25]. Also, the EMD of the Hilbert–Huang transform (HHT) is another powerful technique that is used to decompose vibration signals without the base function and can be applied to both stationary and nonstationary signals [26, 27]. Some drawbacks of EMD, EEMD, and related methods are centered around computational complexity, long execution time, and complicated results with changing working conditions. The techniques discussed so far have been used to successfully diagnose machine faults but heavily rely on manual feature extraction and, in some cases, visual inspection, which requires much human expertise and is generally susceptible to errors.
More advanced fault diagnosis techniques have been developed in recent years that combine the efficient feature extraction capability using time–frequency domain transform techniques with DL’s learning and classification capability to automate the machine fault diagnosis process. Using time–frequency domain techniques, 1-D vibration or acoustic emission signals can be converted to 2-D representation (image), characteristic of the corresponding fault type. The power of convolutional neural networks specializing mostly in image classification can then be exploited to efficiently and accurately classify the fault. Duong et al. [28] applied to envelop analysis to extract envelop signals from 1-D acoustic signals and then applied CWT with damage frequency band information to generate a defect signature wavelet image (DSWI). DSWI describes the acoustic emission signal in the time–frequency domain, reduces the nonstationary effect in the signal, and shows discriminate pattern visualization for different fault types associated with the defect signature. Classification results using deep CNN (DCNN) yielded 98.79% accuracy for the combined DSWI-DCNN approach. Verstraete et al. explored three time–frequency analysis techniques: STFT, WT, and HHT, to generate image representations of fault signals which are then fed into a CNN network for fault classification. This method resulted in the accurate prediction of the fault types. This method also explored noise scenarios but relied on the transform techniques to “see through” the noise. This could work in many cases. However, in others, low- or high-frequency noise could make it difficult for the CNN network to accurately distinguish the fault features from the noisy data. By far, the most common method for image generation in vibration signal analysis is CWT. The combined use of CWT and CNN for machine fault diagnosis has been widely explored in prior research [29,30,31,32,33,34]. Xiao et al. [33] developed the improved variational mode decomposition (IVMD) and CNN to process stationary vibration signals. The minimum average Pearson coefficient principle analyzes fault signals in time to determine the best signal decomposition mode. The signals are then transformed to the frequency domain using CWT for easy feature extraction. The extracted features are used to train CNN networks. IVMD-based CNN is more accurate than other methods, such as RNN, LSTM, and GRU. Despite the impressive results obtained using existing approaches, additional preprocessing techniques could be used to improve the accuracy of the results for real-world data. In real-world applications, vibration data is often mixed with noise which could make it difficult to accurately identify the faults. Advanced signal denoising techniques can reduce the noise components in vibration signals resulting in a reconstructed fault signal for fault identification. Denoising techniques such as empirical mode decomposition (EMD) [35], variational mode decomposition (VMD) [36], ensemble empirical mode decomposition (EEMD) [37], and WT have been used for time-series signal denoising. It is possible to leverage the power of these denoising techniques to preprocess real-world data before fault identification methods are applied. Even though existing DL-based fault diagnosis approaches have been accurately used to identify machine faults, these approaches still have some areas that require improvement. Most existing methods do not address a dedicated approach to dealing with very noisy vibration data often encountered in complex systems comprising many vibrations pruned subsystems. Given the fact that most existing methods use simulation data or data obtained from bearing test rigs (in the case of bearing fault diagnosis), these datasets are acquired in isolation from other equipment and components and do not represent a real-world setup. A close correlation between the noise frequency and that of the “clean” vibration signal poses a serious challenge for the DL models to accurately identify the fault features from the data.
This study proposes a novel method for bearing fault diagnosis that combines three crucial stages of signal processing: pre-processing, feature extraction, and fault classification. In the pre-processing stage, a VMD filtering method based on improved Bhattacharyya distance (VMD-IBD) with optimal parameters using the MIGA algorithm is prosed, which first uses VMD to decompose the input noise-added signal into intrinsic mode functions (IMFs). Then calculates the variance of each IMF and the original signal. Bhattacharyya distance is then used to calculate the similarity between the original signal and the IMFs to select the best IMFs for reconstructing of the filtered signal. The VMD-IBD filtering method removes low- and high-frequency noise components while l, leaving no effect on the intrinsic signal information. The next stage in pre-processing uses wavelet denoising through wavelet thresholding to remove any remaining same frequency noise from the signal. The effectiveness of the proposed denoising approach is demonstrated through comparative analysis of filtering performance metrics such as signal-to-noise ratio (SNR) and root mean square error (RMSE) against VMD and wavelet denoising. Feature extraction from the reconstructed vibration signal is achieved through 2D transform in the form of scalogram images and CNN deep neural network and classified using softmax classification at the output of the deep neural network. The performance of the proposed fault diagnosis method is compared with other DL-based approaches.
The rest of the paper is organized as follows. In Sect. 2, the proposed method for bearing fault diagnosis is discussed. Section 3 describes the experimental setup, conditions, and data acquisition methods. Section 4 presents the results and discussion of the proposed approach using bearing fault vibration signals from an experimental bearing fault test rig and other deep learning-based methods. Finally, Sect. 5 summarizes and concludes the paper with proposals for improvements to be explored in future work.
2 The proposed signal processing and fault diagnosis approach
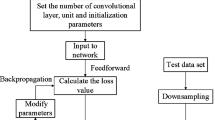
This section describes the bearing fault diagnosis method. Figure 1 is an overview of the proposed method. The implementation of the approach is divided into several steps. The first involves data preprocessing and preparation. Gaussian white noise is added to the signal to simulate real-world data. The raw time series vibration signals, \(x\left(t\right)\), are arbitrarily segmented into smaller segments of appropriate length denoted as \(f\left(t\right)\) and denoised to remove noise VMD and WT. The CWT method converts the denoised signals into scalogram images and groups them according to the fault types, which will later serve as classes during classification. The image data are appropriately sized for input to the CNN. The time–frequency graphs of certain defects are similar, so a basic wavelet transform cannot reliably detect the fault frequencies. A more efficient diagnosis strategy must be developed. Technology based on deep learning has shown promise for use in data analysis. The CNN structure can discern the broad outlines of information and the small distinctions unseen to the human eye. Since CNN models are adept at multivariable processing, a time–frequency graph may serve as the input for training. As a result, the third step involves model building, training, and fault classification using CNN with the data generated in the second step. Due to CNN’s excellent multivariate processing capability, it can be trained using scalogram images. The final step is testing and validation of the trained CNN model. The trained model is used to identify the bearing fault types based on the input data.
An overview of the proposed methodology
2.1 Sensor signal preprocessing
2.1.1 Additive white Gaussian noise (AWGN)
The vibration signals that validate signal processing methods are obtained from bearing test rigs. Bearing test rigs are designed for experimental investigation, often isolated from other larger systems. In real-world applications, the bearing subsystem is often part of a larger system that vibrates alongside the system under investigation. These “external” vibrations introduce noise to the bearing subsystem, which can often lead to data processing errors if not carefully dealt with. To simulate a bearing test rig observed as part of a larger vibrating system, noise is added to the vibration data from a bearing test rig in the form of an AWGN to mimic the process of many random processes occurring in the whole system, a technique typically used to simulate such scenarios of data acquisition. The noise is additive because it is added to any noise that might be intrinsic to the bearing subsystem. WGN has the same probability density function as a normal or Gaussian distribution, and its values are identically distributed and statistically independent at any two points in time. The noisy data with the AWGN demonstrates the quality and accuracy of the denoising technique to retrieve the original vibration signal generating the image data used for fault identification.
An AWGN discrete vibration data \({X}_{i}\) is the sum of input signal \({F}_{i}\) and noise \({Z}_{i}\) which is identically distributed and drawn from a nonzero normal distribution with variance \(N=\mathrm{var}\left({F}_{i}\right)\). The noise \({Z}_{i}\) has a uniform power spectral density across the system’s frequency band.
2.1.2 Time-series signal standardization
The measuring units for various variables are frequently varied in real-world situations. Before analysis, data are frequently standardized to remove the dimensional effect of variables and guarantee that each variable has the same expressive capacity. Equation (3) demonstrates how standardizing measured vibration signals rescales the signal distribution so that the mean observable value is closer to 0 and the standard deviation is closer to 1, reducing errors in signal acquisition while lowering computational complexity and calculation time. For a given sensor signal \(x\left( k \right)\), the standardized signal \(\tilde{y}\left( k \right)\) is defined by
where the mean \(\hat{x}_{\mu } \left( k \right)\) and standard deviation \(\sigma \left( {x\left( k \right)} \right)\) of the original signal are defined as follows
2.1.3 Time-series signal segmentation
To integrate the time–frequency wavelet transform into convolutional neural networks to process vibration signals and establish a bearing fault detection scheme, selecting an appropriate segment length to include at least one revolution of the shaft is crucial. The datasets collected from healthy and faulty bearings are segmented into smaller samples such that the vibration characteristics of each sample can be correctly and uniquely identified. Another advantage of segmenting the data is that the dataset can be zoomed in to capture hidden features buried deep within the wavelet transforms. An overlapping sliding window segmentation technique was applied to segment the data samples, as demonstrated in Fig. 2. The MATLAB implementation of the algorithm is presented in “Appendix A”. Arbitrary segment lengths were used in this study. The segment lengths of the sliding window used in this study were chosen based on an adaptation of the Nyquist-Shannon sampling theorem [38]. In the context of vibration data analysis, this theorem suggests that the segment length should be long enough to capture at least two cycles of the highest frequency component related to the fault. Define the ball-pass frequency of outer-race (BPFO) as \(f_{{{\text{BPFO}}}}\) and the ball-pass frequency of inner-race (BPFI) as \(f_{{{\text{BPFI}}}}\). According to the modified Nyquist-Shannon sampling theorem, the segment length \(L_{{\text{W}}}\) should satisfy the conditions: \(L_{{\text{W}}} \ge 2f_{{{\text{BPFO}}}}\) and \(L_{{\text{W}}} \ge 2f_{{{\text{BPFI}}}}\).
Schematic illustration of the overlapping sliding window segmentation algorithm
Deep neural networks generally require a large dataset for training. The larger the dataset, the more accurately the model can be trained for its intended purpose. The segmentation technique adopted here serves the crucial purpose of data augmentation.
2.1.4 Time-series signal denoising using variable mode decomposition (VMD) and wavelet thresholding (WT)
Bearing vibration signal captured using encoders carries useful information about the signal and any faults present. During operation, the signal is not steady but includes high- and low-frequency noise components. Vibration data used in this study were obtained in a variable speed environment which makes traditional signal analysis methods such as Fourier transform and other spectral analysis methods insufficient to denoise and detect the faults. In this research, we used VMD, which filters out the low- and high-frequency noise signals from the original vibration signal. WT is then carried out to filter the same frequency noise data.
2.1.4.1 VMD decomposition
A noisy time series vibration signal \({x}_{n}\left(t\right)\) can be decomposed into a finite number of intrinsic mode functions (IMFs) using VMD. The narrowband IMFs obtained using VMD is defined by
where \(u_{k}\) is an amplitude and frequency modulation signal defined as \({u}_{k}\left(t\right)={\sum }_{k=1}^{K}{A}_{k}\left(t\right)\mathrm{cos}\left({\mathrm{\varphi }}_{k}\left(t\right)\right)\) with K-orders, \({\mathrm{\varphi }}_{k}\left(t\right)\) is the phase of positive modes, and \({A}_{k}\left(t\right)\) is a slowly varying envelope signal for which each mode has an instantaneous slowly varying non-decreasing frequency, concentrated around a central value \(f_{k}\). The process of VMD simultaneously calculates all the mode waveforms and their central frequencies and consists of determining a set \(\left\langle {u_{k} \left( t \right),\,\,f_{k} \left( t \right)} \right\rangle\) that minimizes the constrained variation problem. The variational constraint problem can be defined as [36]
where \(\left\{ {u_{k} } \right\}: = \left\{ {u_{1} ,u_{2} , \ldots ,u_{K} } \right\}\) is the set of all modes, \(\left\{ {f_{k} } \right\}: = \left\{ {f_{1} ,f_{2} , \ldots ,f_{K} } \right\}\) is the set of all center frequencies, and \(\delta \left( t \right)\) is a unit pulse function. The constrained problem in its current state is very difficult to solve. To calculate the waveform modes and central frequencies, the constrained problem is transformed into an unconstrained problem by finding an optimal solution to the augmented Lagrange function defined by
where \(\alpha\) is the penalty factor that ensures the signal reconstruction accuracy in the presence of Gaussian noise, \(\lambda \left( t \right)\) is the Lagrange multiplier, the inner product \(\left\langle {f\left( t \right),g\left( t \right)} \right\rangle = \int\nolimits_{ - \infty }^{\infty } {f\left( t \right) * g\left( t \right){\text{d}}t}\), \(L_{2}\)-norm \(\left\| {f\left( t \right)} \right\|_{2}^{2} = \left\langle {f\left( t \right),f\left( t \right)} \right\rangle\) and * denotes signal convolution.
The augmented Lagrange function has three parts. The first part of Eq. (7) is the regularization term which involves using the Hilbert transform to calculate the analytical signal associated with each mode, demodulate the analytical signal by multiplying with a complex exponent, and estimate the bandwidth of the analytical signal through \(L_{2}\)-norm. The next two terms enforce the constraint \(x\left(t\right)-\sum_{k=1}^{K}{u}_{k}\left(t\right)\) by imposing a quadratic penalty and incorporating a Lagrange multiplier.
The above optimization problem defined by the augmented Lagrange function can be solved using the Alternate Direction Method of Multipliers (ADMM) algorithm proposed by Boyd et al. [39]. ADMM is a popular algorithm due to its remarkable effectiveness in minimizing objectives with linearly separable structures [40]. The complete optimization algorithm is shown in Table 1. A detailed development of the algorithm can be found in [36]. Only the final complete optimization algorithm is presented here. The saddle points of the Augmented Lagrange function are obtained by alternately updating \(u_{k}^{n + 1}\), \(f_{k}^{n + 1}\), and \(\lambda_{k}^{n + 1}\), which are the optimal solutions of Eq. (7).
The next section introduces the WT technique for enhanced noise reduction. WT is applied to the reconstructed signal from VMD.
2.1.4.2 Selection of optimum parameters for VMD using Multi-objective multi-island genetic algorithm (MIGA)
VMD decomposition requires that the penalty factor \(\alpha\), decomposition number \(K\), updating parameter of Lagrange multiplier \(\tau\), initialization of central frequencies \(f_{k}^{1}\), relative and absolute tolerances \(\varepsilon_{r}\) and \(\varepsilon_{a}\) respectively, be set. The decomposition result depends on the values of \(\alpha\) and \(K\). In this research, \(f_{k}^{1} = 0\), \(\tau = 0.01\), \(\varepsilon_{r} = 1 \times 10^{ - 7}\), \(\varepsilon_{a} = 1 \times 10^{ - 4}\) [36, 41, 42]. The bandwidth size of the IMF components depends on the penalty factor setting. The penalty factor \(\alpha\) and the bandwidth are directly proportional. The value of \(K\) should be carefully chosen since a large \(K\) leads to the generation of unnecessary components. Optimization is therefore a necessary tool to set the values of \(\alpha\) and \(K\). In this research, the choice range for \(\alpha\) is \((25, 4500)\) and that for \(K\) \(\left(2, 14\right)\). The MIGA algorithm is used to find the optimal values for \(\alpha\) and \(K\). MIGA algorithm I summarized in Table 2.
A key step in implementing the MIGA algorithm is selecting the appropriate fitness functions. The concept of envelope entropy \(E_{e}\) [43] and Renyi entropy \(R_{e}\) [44] are used to develop the fitness functions. The \(E_{e}\) value of each IMF component of a VMD decomposed signal can provide information about its sparsity. The larger the \(E_{e}\) value, the smaller the sparsity hence the noisier the IMF component. The larger the \(E_{e}\) value, the greater the sparsity of the IMF component, which indicates more periodic shocks in the signal. The fitness function can be written as
where \(E_{e}\) is defined by
\(a\left( j \right)\) is the Hilbert demodulation of the original signal. A sample simulation signal for bearing fault can be used to show why \(E_{e}\) is a suitable parameter for the fitness function. The signal is expressed as
where \(\tau = 0.02,0.04,0.06, \ldots ,\) \(y\left( t \right)\) is a single pulse response, \(n\left( t \right)\) is a Gaussian white noise whose noise intensity is determined by the standard deviation, and \(c\left( t \right)\) is the sum of the time-shifted noisy impulse response. For the simulation, \(y_{0} = 3\), \(f_{n} = 3000\,{\text{Hz}}\), \(\zeta = 0.09\), \(f_{s} = 200\,{\text{kHz}}\), the sampling number \(N_{s} = 2 \times 10^{6}\), and the simulation time is \(t = 10\,{\text{s}}\) to emulate that of the real signal from a bearing test rig.
Figure 3 shows a simulated vibration waveform with increasing noise intensity and corresponding \(E_{e}\) values. It can be observed by visual inspection of the charts that an increase in noise intensity reduces the sparsity of the signal; hence the \(E_{e}\) value increases. Thus, the objective is to minimize the \(E_{e}\) value of the signal to expose the fault impact.
Simulated time-domain waveform showing varying noise intensity as indicated by the Gaussian Noise Variance, and the variation in Envelope Entropy
Renyi entropy \(R_{e}\) is very sensitive to signal changes and can be used to easily identify small changes in a signal [45]. A small noise in a fault signal increases the concentration of the man frequency as explained by better aggregation energy, hence a smaller \(R_{e}\) value. Thus, the objective is to minimize the \(R_{e}\) value, thereby decreasing the noise. The fitness function can be written as
where \(R_{e}\) is defined by
\(\alpha \ge 0\) indicates the order of the \(R_{e}\). The use of \(R_{e}\) in the fitness function is justified by observing the frequency domain waveforms of the simulated signal with increasing noise intensity, shown in Fig. 4. An increased noise level gradually submerges the main frequency in the background noise. Better noise aggregation is observed when the intensity is reduced hence a smaller \(R_{e}\) value, and vice versa.
Simulated frequency-domain waveform showing varying noise intensity as indicated by the Gaussian Noise Variance, and the variation in Envelope Entropy
For a given vibration signal, each IMF has its unique values of \(E_{e}\) and \(R_{e}\) due to the influence of the values of \(K\) and \(\alpha\). The final fitness function is taken as the average of the two fitness functions and used to find the most suitable values for the parameters \(K\) and \(\alpha\). Therefore,
2.1.4.3 Selection criteria for Final IMF components from VMD using Improve Bhattacharyya Distance (IBD)
The Bhattacharyya distance (BD) is a measure of the sensitivity or similarity of two probability density functions developed by Aril Kumar Bhattacharyya in the 1930s at the Indian Statistical Institute [46]. According to the original formulation, for any two probability distributions P and Q obtained through kernel density estimation defined on the same domain \(\chi\), the BD is defined by
where
is the Bhattacharyya Coefficient (BC) for discrete probability distributions. IBD reformulates the BD based on variance rather than probability density and uses the new formulation to measure the distance between the two probability distributions. Since the new formulation implores variance, fewer number of computations are involved making the approach easier and computationally inexpensive.
In terms of variance, for any two discrete probability distributions X and Y, the variances are:
The BD for the two variances \(D\left( X \right)\) and \(D\left( Y \right)\) is defined by
where \(BC\left[ {D\left( X \right),D\left( Y \right)} \right]\) is the BC of the two distributions and
The IBD approach measures the similarity between the IMFs obtained by VMD decomposition and the original input noisy vibration signal to distinguish the effective from the non-effective IMF components. Through the experiments and tests on the vibration data used in this research, the VMD-IBD approach effectively removed low-frequency noise. The selected components are used to reconstruct the denoised through the principle of superposition. The steps involved in the VMD-IBD decomposition and reconstruction are summarized in the algorithm in Table 3 and illustrated in Fig. 5.
Flowchart of VMD decomposition and Improve Bhattacharyya distance criteria for IMF selection and signal reconstruction
2.1.5 Time-series signal denoising using wavelet thresholding
Raw vibration signals from a bearing test rig contain valuable information that is difficult to identify using time series data alone or other time-series processing methods. Advanced signal processing can identify crucial time–frequency domain information. Suppose \(\hat{f}\left( t \right) = \left[ {\hat{f}\left( {t_{1} } \right),\hat{f}\left( {t_{2} } \right), \ldots ,\hat{f}\left( {t_{M} } \right)} \right]\) is a “clean” vibration signal and \(f\left( t \right) = \left[ {f\left( {t_{1} } \right),f\left( {t_{2} } \right), \ldots ,f\left( {t_{M} } \right)} \right]\) is a “noisy” vibration signal, both of which are time-series signals, if σ is the noise level and \({z}_{i}\) are independent and identically distributed standard Gaussian random variables which constitute a Gaussian white noise denoted as\({z}_{i} \sim N(\mathrm{0,1})\). The raw vibration signal can be modeled by
where \(t_{i} = {i \mathord{\left/ {\vphantom {i M}} \right. \kern-0pt} M}\). Denoising the signal implies isolating \(f\left( t \right)\) to minimize the mean-squared error defined by
subject to the fact that \(\hat{f}\) is at least as smooth as \(f\), where \(\hat{f}\) is the reconstruction of \(f\) through wavelet analysis. Wavelet analysis can be defined using multiresolution analysis (MRA) approach first formulated by Mallat [47, pp. 674–693].
Orthogonal basis and local time–frequency analysis form the basis of diverse signal representations. Wavelet denoising involves using a thresholding algorithm in orthogonal decompositions such as multi-resolution analysis or wavelet packet transform. Wavelet thresholding requires that the proper threshold be selected to generate a better estimate of the denoised signal. Thresholding the wavelet coefficients of a signal keeps the local regularity of the signal and can be divided into three steps [48, 49]:
-
(1)
Decomposition This step involves sequentially dividing the data into different components at different resolutions. Each decomposition results in two signals called approximation and details. The approximation signal is further decomposed into a new approximation and detail signal. The number of decompositions refers to the level, which depends on the analysis, the frequencies of interest, and the selected filters or wavelet type. To compute the wavelet decomposition of the signal at a level \(N\) on an orthogonal basis, choose a wavelet type and level used to generate a filter bank of conjugate mirror filters.
-
(2)
Thresholding Decomposition is followed by selecting of a suitable threshold using a thresholding estimator on the orthogonal basis, applied on all coefficients, not including the lowest frequency energy components. Decomposition maintains the signal regularity.
-
(3)
Reconstruction The final step is wavelet reconstruction of the denoised signal using the approximation coefficients of level M and the modified detail coefficients of levels from 1 to M.
MRA uses discrete wavelet transform (DWT) to decompose a signal using a series of conjugate mirror filter pairs. DWT analysis is very efficient and suited for transient, time-varying signals and performs best in detecting discontinuities and minute changes. For a basic formulation of MRA for wavelet analysis, consider a time series function \(f\left( t \right) \in L^{2} \left( {\mathbb{R}} \right)\) with respect to the wavelet function \(\psi \left( t \right)\) and a scaling function \(\varphi \left( t \right)\). A wavelet series expansion of \(f\left( t \right)\) results in a series of coefficients called the DWT of \(f\left( t \right)\). The DWT pair is defined as
and
where \(M={2}^{j}\). The transform comprises of \(M\) coefficients. With a minimum and maximum scale of 0 and \(j-1\) respectively. The coefficients \({W}_{\varphi }\left({j}_{0},k\right)\) and \({W}_{\psi }\left(j,k\right)\) are the approximation and detail coefficients, respectively, computed through DWT. The required signal \(f\left(t\right)\) is reconstructed through DWT synthesis or inverse DWT. The process in Eqs. (27)–(29) is valid only for orthonormal basis and tight frames [50], and Eq. (29) is called the multiresolution expansion of \(f\left(t\right)\).
The MRA process consists of a sequence of successive approximation closed subspaces \({V}_{j}\) defined by \(V_{j} = \overline{{\mathop {{\text{span}}}\limits_{k} \left\{ {\varphi_{j,k} \left( t \right)} \right\}}}\) (where \({V}_{j}\) can be increased by increasing \(j\)), which satisfies the conditions \(\dots {V}_{2}\subset {V}_{1}\subset\) \({V}_{0}\subset\) \({V}_{-1}\subset\) \({V}_{-2}\dots\), \(\overline{{\bigcup }_{j\in {\mathbb{Z}}}{V}_{j}}={L}^{2}\left({\mathbb{R}}\right)\) where \(\bigcap_{j\in {\mathbb{Z}}}{V}_{j}\) denotes [51]. Each subspace \({V}_{j}\) is the scale space. First, the signal \(f\) is projected onto\({V}_{j}\). The space is then decomposed into a lower resolution space \({V}_{j+1}\) which satisfy \({V}_{j+1}\perp\) and \(V_{j + 1} = V_{j} \oplus W_{j}\) [51], where \(W_{j} = \overline{{\mathop {{\text{span}}}\limits_{k} \left\{ {\psi_{j,k} \left( t \right)} \right\}}}\). The scaling function is defined by
\(k\) determines the position of \({\varphi }_{{j}_{0},k}\left(t\right)\) along the time axis, \({j}_{0}\) determines its width, and \(2^{{{{j_{0} } \mathord{\left/ {\vphantom {{j_{0} } 2}} \right. \kern-0pt} 2}}}\) controls its amplitude. The wavelet function is defined by
\(\psi \left(t\right)\) is also called the mother wavelet. Both \({\varphi }_{{j}_{0},k}\left(t\right)\in B\) and \({\psi }_{j,k}\left(j,k\right)\in B\) where \(B=\left[\left\{{\psi }_{j,k}\left(j,k\right)\right\}, \left\{{\varphi }_{{j}_{0},k}\left(t\right)\right\}\right]\) is an orthogonal basis. The wavelet basis functions are obtained from a single mother wavelet by translation and scaling.
The basic concept of MRA is to find the approximate features and details of the signal through scalar products using scaling and wavelet functions. Vibration signals used in this study have sharp and gentle spikes observed where the faults occur. These fault spikes could be of high or low frequency, depending on the nature of the fault and the system parameters and functioning. The spikes observed, as well as other details of the signal, can be discriminated from the noise through MRA decomposition into different levels. The choice of the mother wavelet function and scaling function determines the final waveform shape of the denoised signal. Orthogonal basis wavelet is used to perform MRA, resulting in a unique reconstructed signal from the wavelet transform. MRA is optimal for extracting the useful signal and suppressing the noise. The method is characterized by high disturbance resistibility and accuracy. The decomposition is carried out on several levels. The maximum decomposition level depends on the size of the data, defined by the expression \(L_{\max } = \log_{2} \left( N \right)\), N = length of the signal. Depending on the data, the maximum decomposition level \(L_{\max }\) is rarely attained since “over decomposition” removes most of the useful components of the original signal. After performing several experiments, the decomposition level chosen for this study is 3 \(\left( {L_{\max } = {\text{ceil}}\left( {\log_{2} 15000} \right) = 14} \right)\), for a segment length of 15,000.
Figure 6 shows a flowchart of the thresholding procedure using MRA. The wavelet decomposition is done by filtering the input signal \(f\) by a pair of low- and high-pass mirror filters defined, respectively, by \(h\left[ k \right]\) and \(g\left[ k \right] = \left( { - 1} \right)^{1 - k} h\left[ {1 - k} \right]\). The filters \(h\left[ k \right]\) and \(g\left[ k \right]\) are used as filter banks at reconstruction. The decomposition results are approximates and detail coefficients evaluated using the filters \(\overline{h}\left[ k \right] = h\left[ { - k} \right]\) and \(\overline{g}\left[ k \right] = g\left[ { - k} \right]\). The relationship between the low- and high-pass filter and the scaler and wavelet functions can be expressed as
Thresholding procedure with MRA, where the lowest-frequency approximate \(W_{\varphi }^{3} \left( t \right)\) is kept (no processing using the thresholding function) a 3-level decomposition flowchart, b 3-level reconstruction flowchart
At the reconstruction stage,
The choice of wavelet function is not unique. However, it is chosen from several “already-built” wavelets based on the signal or image processing domain and is required to satisfy the multiresolution condition [50]. Many wavelet models have been developed over the years with different effects, such as Haar wavelet for rectangular-shaped signals and images, Daubechies wavelet for signal compression and solving fractal problems, Morlet wavelet for wavelet-based analysis, Meyer wavelet for image processing, image restoration, and biomedical signal compression, Symlet wavelet which is an asymmetrical Daubechies wavelet suitable for signal denoising, etc. Signal denoising within this study's context will use the eighth-order symlet wavelet (sym8). A flowchart of the WT denoising algorithm is shown in Fig. 7.
Wavelet thresholding denoising algorithm flowchart
Donoho and Johnstone [52] suggested that the significant wavelet coefficients could be extracted by thresholding. The thresholding shrinks the wavelet coefficients towards zero if their absolute value is below a certain threshold level \(\gamma \ge 0\). The simplest form of thresholding is hard thresholding which can be defined as
where \(\eta_{{\text{H}}} \left[ {\alpha_{m} \left( {j,k} \right),\gamma } \right]\) is the wavelet estimation coefficient after hard thresholding, \(\alpha_{m} \left( {j,k} \right)\) is the wavelet decomposition coefficient before thresholding, and \(\gamma\) is the threshold level. This approach is a keep-or-kill approach that results in discontinuities in the amplitude of the shrunk coefficients. Soft thresholding approach, however prevents discontinuity and can be expressed as [53]
where \(\eta_{{\text{S}}} \left[ {\alpha_{m} \left( {j,k} \right),\gamma } \right]\) are the wavelet coefficients after the soft thresholding process and \({\text{sgn}}\left( \cdot \right)\) is the signum function. This is the shrink-or-kill approach that prevents the discontinuities observed during hard thresholding. However, all other coefficients which represent the original signal are also shrunk, causing a decrease in the SNR of the denoised signal, which is highly undesirable.
Universal thresholding was chosen as the denoising method, which has been proven optimal for many applications, as stated in [54]. According to the universal thresholding method, the risk of the estimator with j-level threshold given by \({\text{Tr}}_{j} = \sigma \sqrt {2\ln \left( {n_{j} } \right)} ,\quad j = 1, \ldots ,N\) and \(N \ge 4\) is
where \(f_{B}\) is the projection of \(f\) on the basis \(B\), \(\sigma\) is the standard deviation of the noise signal, \(r_{{{\text{th}}}}\) is the threshold risk, and \(n_{j}\) is the number of j-level wavelet coefficients. In this application, \(n_{j}\) is kept constant at \(n_{j} = N\). Noise variance \(\sigma^{2}\) estimation is an important factor during thresholding estimation. The noise variance is unknown in practical applications and must be estimated during wavelet denoising. According to Mallat [55], the variance of the noise \(W\) is estimated from the median \(M_{x}\) of absolute wavelet coefficients \(\left| {\left\langle {W,\psi_{l,k} } \right\rangle } \right|\) by neglecting the influence of the piecewise smooth clean signal \(f\):
The noise variance estimation is carried out using hard thresholding for the data used in this study. Due to the nature of the signal noise and through various experiments, a level-dependent variance estimation was chosen. That is, the influence of Gaussian noises is spread to all the levels; thus the variance should be estimated level by level [56].
In summary, for this research, the Universal Threshold wavelet denoising was carried out through MRA with a symlet 8 (sym8) wavelet. Level-dependent noise estimation was used with hard thresholding. The number of denoising levels was set to \(L = 3\) for the best results, which retains the most information about the original signal (signal integrity) while removing as much noise as possible.
2.1.6 Performance metrics for evaluation of the denoising technique
For a given original vibration signal sequence \(f{\text{a}}\) and denoised vibration signal \(f_{{{\text{den}}}}\) both of length \(N\), the root mean square error (RMSE) and signal-to-noise ratio (SNR) performance metrics are used to evaluate the quality of the denoising process. The RMSE is defined as
According to [57], for any two samples \(x\) and \(y\), the correlation coefficient between the two samples is defined by
The correlation coefficient between \(f_{{{\text{orig}}}}\) and \(f_{{{\text{den}}}}\) is defined as
In terms of the samples of \(f_{{{\text{orig}}}}\) and \(f_{{{\text{den}}}}\), the correlation coefficient can be defined as
The correlation coefficient here represents the percentage of the signal in the noise-added waveform. The SNR in decibels (dB) can be defined in terms of \(\rho\) as
2.2 Continuous wavelet transform (CWT)
Wavelet transforms have widely been used as great mathematical tools in various areas of signal processing to decompose and process complex signals, often in multiple dimensions [58, 59]. CWT is a mathematical method used to decompose and analyze variable signals that need variable time–frequency localization of features throughout the signal train [60]. Fast Fourier transform (FFT) and inverse fast Fourier transform (IFFT) are widely used in signal processing to analyze varying time–frequency signals but lack the crucial capability of providing a time history of the signal being processed as well as when the frequencies occur [61]. Given that fault detection scenarios often require the analysis of time series vibration signals, the changing frequencies of the signal with time make FFT and IFFT viable choices for analysis. Another reasonable argument for using wave transforms in analyzing such signals is that the features of the signals are often very complex and hidden deep in the frequency domain, which makes sense as not much can be deduced by simply observing the time series data.
The Fourier transform \(F\left( f \right)\) of a signal is defined by
for a time \(t\) and frequency \(f\). Fourier transform is suitable for stationary signals and is ineffective in analyzing nonstationary signals [17, 62]. Consider a nonstationary time-varying signal \(x\left( t \right)\). Wavelet transforms are base functions formed through the dilations and translation of a base prototype function \(\psi \left( t \right)\). The CWT \(W\left( {a,b} \right)\) of a signal \(x\left( t \right)\) is defined by
The Morlet wavelet function can be used as the base prototype function for the construction of CWT, as defined by
Taking the Fourier transform of Eq. (32) gives
where \(a\) is the scale parameter, \(\sigma\) is the time width of the undilated Morlet base prototype function and \(s\left( t \right) = \exp \left( {2i\pi ft} \right)\). The frequency and scale are related by \(f = {{f_{0} } \mathord{\left/ {\vphantom {{f_{0} } a}} \right. \kern-0pt} a}\). CWT works by translating the base prototype function \(\psi \left( f \right)\) with modulation frequency \(f\) centered at integral multiples of \(f_{0}\) to form a set of frequency domain functions. For implementation, CWT expression can be written in discrete form using Riemann sum for an integral part, known as discrete wavelet transform DWT [63], as follows
where \(1 \le k \le M\), \(- \infty \le k \le \infty\), \(M\) denotes the product of the number of octaves and the voices in each octave, \(t = nT_{s}\), \(T_{s}\) is the sampling time in seconds, and \(f_{s}\) is the sampling frequency in Hertz. When computed, CWT displays the transformed signal amplitude and phase distribution in time and scale.
Another useful wavelet transform technique that could be used is the short-time Fourier Transform (STFT) which is generally characterized by a fixed duration window. CWT uses dilation operations to carry out wavelet transform by dividing the time–frequency plane into resolution cells with variable lengths depending on the scale parameter \(a\), which makes it suitable for variable frequency cases as opposed to STFT, where its resolution cells are of the fixed duration time window. Figure 8 shows sample wavelet transforms represented in two dimensions as scalogram images. The scalogram images resulting from CWT are resized to 224 × 224 × 3 to match the input of the CNN network.
a Flow diagram of proposed CWT wavelet transform. b Sample vibration signals with their corresponding CWT scalogram images, generated from time-series signal samples with 4500 datapoints into a 4500px by137px image resized to 780px by1080px for better visibility of the frequency peaks
2.3 Convolutional neural network (CNN)
Neural networks are a part of machine learning and are at the core of all deep learning algorithms. There are many classes of neural networks, but CNN is particularly interesting, which will be used in this research article [64, 65]. CNNs are a supervised learning method for image classification and computer vision tasks [66]. In comparison to other classification methods, CNNs provide a more scalable approach to image classification and object recognition applications by leveraging matrix multiplication to identify patterns in an image [67], with one drawback being the need for graphical processing units (GPUs) to handle the large complex computations in an optimized and reasonable time frame [68]. Another noticeable advantage of CNNs over other networks is their ability to adopt weight replications, receptive fields, and subsampling, low complexity, and anti-noise capability. The basic structure of a CNN has an input layer, convolution layers, pooling layers, fully-connected (FC) layers, and an output layer.
2.3.1 Convolution layer
The convolution layer distinguishes CNNs from other types of deep learning networks, and is where most of the computations and feature extraction occurs [69]. A typical input to the convolution layer is an RBG image. Part of the convolution layer is the feature detector, also called the filter or kernel, which “scans” across the receptive field of the image, searching for the presence of features in a process called convolution. The kernel is a 2D array of weights that may vary in size and represents part of the image. Applying the filter to a section of the image requires a dot product between the input pixels in that area and the filter matrix. The result is fed into an output array. The filter then shifts by a stride, and the process is repeated over the entire image. The output from the convolution layer is a feature or activation map. The weights of the feature map are adjusted by backpropagation and gradient descent during training. The hyperparameters in the convolution layer set initially before training commence include several filters, filter size, stride, and zero padding. The output from the output layer is activated by passing it through a Leaky Rectified Linear Unit (Leaky ReLU) to introduce nonlinearities.
Significant characteristics can be extracted by convolution, which is a special type of filtering method. There are multiple convolutional kernels in each convolutional layer under normal conditions. A convolution layer is created by convolutional filters and learnable kernels for nonlinear transformations. Convolutional filters and learnable kernels create a convolution layer for nonlinear transformations. The convolution process is expressed as
where \(y_{k}^{n}\) is the \(k{\text{th}}\) feature graph of the \(i{\text{th}}\) convolution layer, φ() is the activation function, \(M_{k}\) is the input graph set, β is the function Kernel and \(b_{k}^{n}\) is the corresponding bias.
2.3.2 Activation operation
After the convolution layer, the activation layer nonlinearly modifies the logit value of each convolution output and speeds up CNN convergence. When employing the back-propagation learning approach to update the parameters, the weights in the shallow layer become more trainable due to a leaky ReLU activation layer. The formula for the Leaky ReLU activation function is defined as follows:
where \(k_{i}\) is a fixed value in the interval (0, 1) inclusive and \(y_{ik}^{n}\) is the \(k{\text{th}}\) feature graph activation value of the convolution layer output \(y^{n}\).
2.3.3 Polling layer
Pooling layers are down-sampling layers for dimensionality reduction. It reduces the number of input parameters. The pooling layer has a weightless filter that sweeps across the entire input, applying an aggression function to values within the receptive field. The results are used to populate the output matrix [69]. Max pooling sweeps a filter across the input and chooses pixels with a maximum value in the receptive field. The pooling layer reduces the input graph by extracting the main features while decreasing the dimensional complexity of the output and sensitivity to the environment with minimal loss of invalid information in the input feature graph [70]. For example, if the input feature size is 6 × 6, a pooling operation with the size of 2 × 2 and the step size of 2, down-samples the input features to an output of 3 × 3. The max pooling transformation process can be expressed as
where \(a_{tk}^{n}\) is the activation value of the \(t{\text{th}}\) neuron in the \(n{\text{th}}\) layer of the \(k{\text{th}}\) frame and \(W\) is the width of the pooling area. No parameters are learned in the pooling layer.
2.3.4 Batch normalization
The batch normalization (BN) layer reduces the deep neural network's internal covariance shift, accelerates training, increases efficiency, and improves generalization. In the first step of the BN layer process, the mean value \(\mu_{{\text{B}}}\) of the mini-batch is subtracted from the input volume layer value and then divided by the standard deviation \(\sigma_{{\text{B}}}^{2}\). However, this will result in the input value being constrained to a narrow range. As a result, once the standardization process is complete, it requires multiplication by a scaling amount denoted by γ and an offset value denoted by β. The input of the batch normalization layer is denoted by \(y_{k}^{n} = \left[ {y_{1k}^{n} ,\,y_{2k}^{n} ,\, \ldots ,\,y_{ik}^{n} ,\, \ldots ,\,\,y_{Nk}^{n} } \right]\). The max-pooling transformation is described as follows:
where \(\gamma_{k}^{n}\) and \(\beta_{k}^{n}\) are the scaling factor and offset of the BN layer, respectively, \(z_{ik}^{n}\) is the output of the BN layer, and \(\varepsilon\) is a numerical stability constant.
2.3.5 Fully connected layer
Image classification and object recognition are performed in the fully connected (FC) layer based on the features extracted from previous layers. The FC is a finite number of neurons whose input and output are vectors [69]. It uses a softmax activation function to classify inputs accordingly. Let \(\left\{ {a^{i} } \right\}_{i = 1}^{n}\) be the input sample set of the data to the FC layer. If \(P\left( {a^{i} = k|x^{i} } \right)\) is the probability that the sample matches the correct label, then according to the softmax regression model, which constitutes the softmax activation function, the output is given by
where \(x^{i}\) is the input eigenvector of the \(i{\text{th}}\) sample, \(K\) the number of classes or sample labels, the parameters of the softmax classification model is \(\phi = \left[ {\phi_{1} ,\,\,\phi_{1} ,\,\,...,\,\,\phi_{K} } \right]^{T}\), and \(R\) is the output. A dropout layer can be added after the fully connected layer to limit overfitting [70]. The key goal of introducing the dropout layer is to remove nodes (input and hidden layer) in the neural network during training, thereby preventing overfitting. The dropout layer temporarily removes all forward and backward connections with the dropout nodes. This creates a new architecture from the existing parent network through a dropout probability. Overfitting happens when some neurons change in response to the mistakes of other neurons. This creates a complex co-adaptation between neurons, which in turn causes the overfitting problem. The dropout layer prevents co-adaptation between neurons, by randomly dropping out neurons thereby enhancing generalization.
For this study, the back-propagation (BP) algorithm and adaptive momentum estimation algorithm (Adam optimizer) [71] are used to train and optimize the training parameters of the CNN model. The training parameters are optimized by calculating the error between the real and predicted values. The weight and biases (trainable parameters) are rapidly updated and fine-tuned to minimize the estimated error. The training error is measured using Categorical Cross-Entropy (CCE) loss function \(F\left( \theta \right)\) is defined as follows
where \(n\) is the number of samples and \(m\) is the number of categories. Since the last layer is connected to the softmax layer for classification, CCE is used as the loss function such that the framework can optimize and calculate the gradients together.
The update rules for the Adam optimizer are defined as
where \(m_{ij}^{\left( t \right)}\) is the decay rate of the mean gradients, \(v_{ij}^{\left( t \right)}\) is the mean square of gradients, \(w_{ij}\), \(\beta_{1}\), and \(\beta_{2}\) are weights, and \(C\), the cost function that requires optimization. The normalized mean of gradients \(\hat{m}_{ij}^{\left( t \right)}\) and mean of square gradients \(\hat{v}_{ij}^{\left( t \right)}\) are defined as
The final update rule for each weight \(w_{ij}\) is defined as
where η is the learning rate and ε is a numerical stability constant. For this study, η = 0.00004, β1 = 0.9, β2 = 0.9, and ε = 1 × 10−8.
3 Experimental setup, data acquisition and data preparation
3.1 Experiment setup and data acquisition
The effectiveness of the proposed fault diagnosis approach is tested and validated using experimental vibration signal data. A full experimental setup of the bearing fault test used to simulate the various fault types in this study is shown in Fig. 9.
Experimental Setup showing drive units, bearing units, and measuring instruments (Image source: [72])
The fault simulation test rig used to simulate a variety of bearing fault types and acquisition of vibration and rotational speed data is the Spectra Quest machinery fault simulation (model MFS-PK5M) at Ottawa University lab [72]. ER16K bearings with 9 balls, each with a pitch diameter of 38.52 mm and ball diameter of 7.94 mm, were used for the test, mounted at the ends of a central drive shaft connected to an electric motor whose speed is controlled by an AC drive unit. One end of the drive shaft had a healthy bearing, while the other end had a test bearing. An ICP accelerometer, model 623C01, was used to collect vibration data, while an EPC model 775 incremental encoder set at 1024 CPR measures the rotational speed. Vibration signals for healthy bearings and four error types were recorded during the tests for four different speed conditions at different rotating frequencies: increasing rotating speed, decreasing rotational speed, increasing then decreasing rotational speed, and decreasing then increasing rotational speed. The tests were carried out under no load conditions.
3.2 Description of the dataset and computation environment
Experiments were conducted with data from a bearing test rig to validate the proposed signal processing method. The bearing test rig was operated under five operating conditions and varying rotational speeds. The vibration data for the tests were sampled at 200 kHz for 10 s per sample. Three trials are carried out for each operational speed setting resulting in 60 samples. Each sample has two channels: Channel 1 represents the accelerometer’s vibration data, while Channel 2 represents the encoder’s speed data. The bearing fault types in the University of Ottawa dataset [72] can be classified into: healthy (H), inner race fault (IF), outer race faults (OF), ball faults (BF), and combined fault (CF). The 60 samples are insufficient for any deep-learning model. Before converting into images, each sample was first divided into overlapping segments using the sliding window algorithm whose length could be chosen arbitrarily but sufficiently long enough to cover at least a complete revolution of the rotating shaft.
Three datasets were generated for this study: original dataset (data collected from the bearing test rig were not preprocessed before converting to images), noise added dataset (the data collected from the bearing test rig was supplemented with AWGN), and denoised dataset (data collected from the bearing test rig was supplemented with AWGN to simulate a scenario where the bearing subsystem is part of a larger system with vibration noise, and then denoised using the proposed denoising technique in this study). For each of the three datasets, six separate sub-datasets were generated using 2500, 5000, 7500, 10,000, 12,500 and 15,000 segment lengths that correspond to 59,940, 26,638, 17,100, 12,600, 9960 and 8220 scalogram images. According to the parameters detailed in [72], the rotational frequency \(f_{r}\) of the bearing shaft falls between the range \(9.8 \le f_{r} \le 29.0\) while the BPFO and BPFI falls between the range \(35.0 \le f_{{{\text{BPFO}}}} \le 103.5\) and \(53.2 \le f_{{{\text{BPFI}}}} \le 157.5\) respectively; thus the chosen segment lengths satisfy the conditions mentioned in Sect. 2.1.3. Each sub-dataset is grouped into five subsets corresponding to the respective fault types. Two separate sets of experiments were conducted in this study. The first set of experiments investigated the effects of denoising the vibration data instead of using unfiltered noisy data for signal processing. The second set of experiments investigates the effect of segment length and operating speed conditions on the model's overall performance. In all experiments, the same CNN architecture as previously described was used. For each experiment and image dataset, 70% of the randomized images were used to train, 20% to validate, and 10% to test the network. Each experiment was carried out 5 times, and the results averaged out to minimize the effect of randomness. This large dataset requires a large computation power made possible by GPU processors.
The computation was carried out with keras tensorflow 2.12.0 on a Dell Precision 7550 laptop with a Linux Operating system (Ubuntu 22.04.2 LTS distro): Intel Core i7 – 10875H CPU, 64 bits system from Intel corporation with 32 GB of RAM, equipped with an NVIDIA TU104GLM (Quadro RTX 4000 Mobile / Max Q) GPU graphics card and 1T SSD hard drive.
3.3 Description of the deep learning architecture
To evaluate the performance and accuracy of the proposed bearing fault diagnosis method, we apply it to vibration data from a bearing test rig under varying test conditions. Due to the complicated structure of deep learning models, it is difficult to choose appropriate parameters. However, based on prior research in the same field and experience, trial-and-error analysis was used to determine the structure and parameters of the CNN architecture in this research for fault classification and identification, as shown in Table 4, and the corresponding CNN structure is shown in Fig. 10.
CNN architecture
The CNN architecture used for image classification is a modified version of the well-refined AlexNet [73]. The neural net comprises eight weighted layers (five convolution and three fully connected layers). In this study, the last fully connected layer has five neurons. Its output is fed to a 5-way softmax layer, producing a probability distribution over the 5 classes representing the five faults. A maxpooling layer with filter size 5 × 5 and stride of 2 pixels, for which the number of filters corresponds to the outputs of the respective convolution layers (96 filters and 256 filters, respectively, after C1 and C2), were added after the first two convolution layers. The subsequent 3 successive convolution layers do not have a maxpooling layer. The ReLU activation function was applied to the output of all convolution and fully connected layers.
The first convolution layer, C1 filters the 224 × 224 × 3 input image using 96 filters of size 11 × 11 with a stride of 4 pixels. The output has a size of 54 × 54 × 96. After passing through the first maxpooling layer P1, the output becomes 26 × 26 × 96, fed into the second convolution layer. The second convolution layer accepts the maxpooled output from C1 as input and filters it using 256 filters of size 5 × 5, stride of 2 pixels and padding of 2 pixels. The response from this layer is maxpooled using the P2 layer with an output size of 12 × 12 × 256. The output is then passed through three consecutive convolution layers without any maxpooling. The third convolution layer C3 has 384 filters of size 3 × 3, padding of 1 pixel and stride of 1 pixel with an output size of 12 × 12 × 384. The fourth convolution layer C4 has 384 filters of size 3 × 3, padding of 1 pixel and stride of 1 pixel. The output from this layer has a size of 12 × 12 × 384. The fifth convolution layer C5 has 256 filters of size 3 × 3, the same stride and padding as C3 and C4. The output from C5 has a size of 12 × 12 × 256 which is passed through a maxpooling layer P3 with 256 filters of size 3 × 3 and stride of 2 pixels with an output of 5 × 5 × 256.
The output from P3 is flattened through a flatten layer (FL) to a linear output of 6400 neurons before passing the results through three successive fully connected layers D1, D2 and D3. Each D1 and D2 have 4096 neurons followed by a dropout layer with a dropout rate of 0.1. The last FL D3 has 5 neurons corresponding to the five fault classes with a softmax classification function.
To solve the problem of overfitting, a sequence of data augmentation steps was used. First, the input image was randomly rotated with a rotation factor of 0.2. The second step involves randomly flipping the image along the horizontal and vertical axis. The third data augmentation method applied random contrast of 0.1 to all the images before finally rescaling the image. Every input image has input pixels in the range [0, 255]. The rescaling layer transforms the image pixels to the range [0, 1] by multiplying by a \(\mathrm{scale}=1./255\). Also, a dropout layer with a dropout rate of 0.1 was applied after each of the first two FLs to reduce overfitting.
To train the network, an Adam optimizer with a CCE loss function was used with a minimum batch size of 32 at a learning rate of 0.0001. The maximum number of epochs for training was 100. The entire network has 46,767,493 trainable parameters.
4 Results and discussion
4.1 Performance analysis of the proposed vibration data denoising method
In this study, vibration signals from an experimental bearing test rig were used to evaluate the performance and accuracy of the proposed bearing fault diagnosis method. In order to observe the effects of noise when the bearing subsystem is treated as part of a larger system, the samples of the vibration data from a real bearing test rig were supplemented with AWGN. The proposed denoising method in the preprocessing stage was used to demonstrate how the added noise can be removed before further processing. The variance of the input noise-added signal was used as the variance of the AWGN. SNR and RMSE were used to evaluate the effectiveness of the proposed denoising technique and the results compared with VMD and wavelet denoising methods in isolation.
The first part of the denoising step implores the VMD denoising method, which is an effective way to decompose the vibration signal into IMFs. The MIGA algorithm was used to obtain optimal parameters for VMD decomposition. The optimal values for the penalty factor \(\alpha\) and the decomposition number \(K\) were 12 and 2500, respectively. VMD decomposition of a random normalized sample vibration signal with AWGN of segment length of 20,000 using the optimal parameters is shown in Fig. 11. It can be observed that most of the signal noise is distributed in the high-frequency IMF components of VMD as indicated by the central frequencies shown in Fig. 12.
Sample vibration signal decomposed using VMD with optimal parameters K = 12 and \(\alpha = 2500\), showing 12 IMFs
Power spectrum of VMD decomposed IMFs showing the location of the central frequencies
Using the IBD approach summarized in Algorithm 3 in Table 3, the maximum slope is \(\theta_{\max } = 0.15\) at index \(i_{\max } = 10\). Applying the technique depicted in Table 3 to select the IMFs for reconstruction, the first two IMFs (IMF1 and IMF2) will be eliminated, leaving IMF3 and IMF12 to reconstruct the VMD-IBD denoised signal. The reconstructed signal is further denoised using WT resulting in a better-quality signal. Figure 13 shows the results of denoising using various methods compared to the proposed method. It should be noted that most of the noise was removed during the WT stage, which is far superior to the VMD-IBD method. When the noise-added vibration signal was first processed with the VMD-IBD denoising method before WT denoising, the quality of denoising was better than directly processing it with WT. This shows that the proposed denoising method improved the quality of the denoised signal, as evident from the close similarity between the raw normalized vibration signal and that using the proposed method, as shown in Fig. 13.
a Comparison of various stages of signal pre-processing of a random inner race vibration signal. b Comparing the final denoised signal to the original normalized raw vibration signal sample with the highest SNR value and lowest RMSE value
To investigate the quality of denoising using the proposed scheme, 1000 random segments of length 15,000 for each of the five classes were used. After applying the proposed denoising method to these samples, the SNR and RMSE values were average. The results for the noise-added data, VMD denoised data, WT denoising data, and VMD-IBD+WT denoised data are shown in Fig. 14. Figure 14 shows the average RMSE of the denoising effects using various denoising methods. The noise-added data had the largest RMSE for each class, while the lowest RMSE was observed for samples processed with the proposed VMD-IBD+WT denoising method.
Average performance metrics of the denoising effects on 1000 random samples of each fault type a RMSE, b SNR
The smaller the RMSE, the better the performance of the method. For all 5 classes, WT performed better than the VMD approach, but both performed less than the proposed method. Figure 14 shows the average SNR values of the denoising effect, further confirming the observations with RMSE. The proposed denoising method shows the largest SNR values compared to the other methods showing the high quality of the denoised signal.
The quality of denoising is evident from the time–frequency transforms (CWT) shown in Fig. 15, whereby the noise recorded in the noise-added data in Fig. 15 and the remaining noise from the VMD denoising method is completely removed, as shown in Fig. 15. The denoised signal using the proposed method results in a signal that is very close to the original normalized raw vibration signal.
Denoising results using the proposed method on ball fault bearings vibration signals. a Noisy vibration signal. b Original vibration signal without added white. c Denoised vibration signal using the proposed method
4.2 Performance analysis of the proposed bearing fault diagnosis method
Several experiments were conducted to evaluate the performance of the proposed bearing fault diagnosis approach. Experiments were carried out on three separate groups of data generated from the same vibration dataset: original, noise-added, and denoised. Datasets with segments 2500, 5000, 7500, 10,000, 12,500 and 15,000 were generated for each category of datasets earlier mentioned. A total of five separate groups of experiments were carried out to evaluate the effectiveness of the method. Note that the fault classification results of each experiment were averaged over 5 runs to reduce the effects of randomness.
Experiments were conducted to evaluate how segment length affects classification results, using pre-defined lengths of 2500, 5000, 7500, 10,000, 12,500, and 15,000. The vibration samples were segmented, denoised, and converted into image data. Then, the deep learning model was used for fault classification. The results of the experiments are summarized in Table 5. More detailed results are presented in Tables 6, 7 and 8. The tables present the bearing fault classification results for different segment lengths using the original, denoised, and noise-added datasets. It provides performance metrics such as precision, recall, and F1 scores for each bearing fault class. The results demonstrate the impact of segment length on the accuracy of the deep neural network.
Analyzing the results from all three tables, it can be observed that longer segment lengths generally lead to higher accuracy. Table 6 presents the original dataset's bearing fault classification results for different segment lengths. The validation accuracy for the original data increases from 99.46% for the data with a segment length of 2500 to 99.85% for that with a segment length of 15,000. Table 7 shows the classification results of bearing faults for various segment lengths using the denoised dataset. The results reveal that the denoised dataset achieves higher accuracy across various segment lengths than the noise-added datasets. High accuracies ranging from 98.28% for data with a segment length of 2500 to 99.70% for a segment length of 15,000 were observed for the denoised data. The training and validation accuracy of the denoised data is comparable to those of the original vibration data, with a percentage training accuracy error of 0.49% and a percentage validation error of 0.93%. This low error between the model performance for the original vibration data and the denoised vibration data shows that the denoising method effectively separates the vibration signal from the added noise. This indicates that the proposed denoising method effectively improves the quality of the vibration data, resulting in better fault classification performance. The precision, recall and F1 scores consistently indicate superior performance for all the bearing fault classes. This confirms the effectiveness of the proposed denoising method in removing noise from the vibration data, enabling the deep neural network to accurately classify bearing faults.
Table 8 presents the bearing fault classification results for different segment lengths using the noise-added dataset. The results in Table 8 shows that the accuracy of the model decreases when the raw vibration data is supplemented with white Gaussian noise. The precision, recall, and F1 scores indicate a significant decline compared to the original and denoised datasets. This highlights the adverse effect of noise on fault diagnosis accuracy, further emphasizing the importance of the denoising step in the proposed method. The presence of AWGN reduces the model’s performance to accurately classify the faults. The worse performance was observed for the 2500 segment with a 31.23% validation accuracy compared to 95.56% for the 15,000 segment length. So, even though the model performs poorly with the noise-added data, the accuracy improves with increased segment length since the images become more distinguishable at higher segment lengths.
The performance metrics are evaluated using Eqs. (53), (54), (55), and (56).
Another significant observation is that the computational time drops significantly as the segment length increases. The number of segments directly equal to the sum of the number of training and validation images, decreases as the segment length increases. As a result, fewer iterations are required per epoch due to the reduced sample size, hence a decrease in computation time observed across all three tables.
Experiments with signals under different speed conditions were conducted to evaluate the robustness and adaptive learning and classification capability of the proposed method. Four shaft speed conditions were tested: increasing, decreasing, increasing then decreasing, and decreasing then increasing. The bearing fault classification results for different operating speed conditions using the denoised dataset are presented in Table 9. It reports the training and validation accuracies and the computation time for each speed profile. It is observed that the increasing speed conditions generally have a slightly higher accuracy in both training and validation phases. This trend is consistent across different segment lengths. The higher accuracies achieved under increasing speed conditions indicate that the deep neural network can better capture the fault patterns present in the vibration data when the speed increases. On the other hand, decreasing speed conditions show slightly lower accuracy than increasing speed conditions. However, the difference in accuracy is relatively small, indicating a certain level of robustness of the model against variations in speed conditions. This suggests the trained deep neural network can generalize well and perform reasonably even when tested under different speed conditions. This could be attributed to the efficient capability of CWT to isolate the distinctive frequency features of each signal under variable conditions. There is also no effect on the computation time since it is largely affected by the size of the dataset. This result shows that the proposed method does not depend on the speed of operation of the shaft and can be used in any speed condition.
The experimental training and validation progress for the original, denoised, and noise-added vibration data are, respectively, shown in Figs. 16, 17 and 20. The poor performance of the noise-added data can be further ascertained by observing the training and validation progress in Fig. 20. In contrast, the original and denoised data have closely similar results. The confusion matrices for all considered segment lengths for the original and denoised data are also shown in Figs. 18 and 19, respectively. The confusion matrices show that the model can effectively classify the test images as opposed to the poor results depicted in Fig. 21 for the noise-added data. The performance of the model for the noise-added vibration data, as observed in the confusion matrices, shows that the presence of the noise significantly affects the accuracy of the results, as seen by the increased number of false positives and false negatives due to confusion between scalogram images of different fault types especially at smaller segment lengths (Figs. 20, 21).
Results for denoised data a Training and Validation accuracy curves. b Training and validation loss
Results for original data a Training and Validation accuracy curves. b Training and validation loss
Confusion matrix for bearing fault detection results for different segment lengths for the original vibration signal a 2500, b 5000, c 7500, d 10,000, e 12,500
Confusion matrix for bearing fault detection results for different segment lengths for the denoised vibration signal a 2500, b 5000, c 7500, d 10,000, e 12,500
Results for noise added data a Training and Validation accuracy curves. b Training and validation loss
Confusion matrix for bearing fault detection results for different segment lengths for the noisy vibration signal a 2500, b 5000, c 7500, d 10,000, e 12,500
The adaptive learning capability, robustness, and ability of the deep neural network model to generalize were further investigated with signals under different operation conditions for training and testing. Given that there are four operating speed conditions, the model is trained with images generated from vibration data with one operating speed condition and tested with images obtained from vibration signals acquired under the other three for all six segment lengths. The experiments were performed using the vibration data that has been denoised using the proposed denoising method. The bearing fault classification accuracies obtained under these scenarios and averaged over 5 runs are presented in Table 10.
The results show that the choice of training and testing speed conditions has a slight impact on the testing accuracies. Matching the speed conditions between training and testing generally leads to higher accuracies, indicating that consistency in the speed profile contributes to improved fault classification performance. For a segment length of 2500, the highest testing accuracy of 97.44% is achieved when the model is trained with an increasing speed condition (Inc) and tested with a decreasing then increasing speed condition (DecTI). Similarly, for segment lengths of 5000, 7500, 10,000, 12,500, and 15,000, the highest testing accuracies are achieved with specific combinations of training and testing speed conditions. Interestingly, the testing accuracies are comparable across different conditions for some segment lengths. For example, for a segment length of 7500, the testing accuracies range from 99.22 to 99.88% across various training and testing speed conditions. This suggests that the model's performance is relatively robust to variations in speed conditions and capable of adapting and generalizing. It is important to note that while matching the speed conditions generally leads to higher accuracies, the models still exhibit reasonable accuracy even when tested under different speed conditions from that which they were trained. This indicates a certain level of adaptability and generalization capability of the deep neural network, enabling it to classify bearing faults effectively even in varying operational conditions.
4.3 Comparison with other popular deep learning and machine learning methods
Some popular deep-learning techniques for machinery fault diagnosis have been reported with very good performance. These techniques include CWT+CNN, deep neural networks (DNN), 1D convolutional neural networks (1D-CNN), and long short-term memory (LSTM). Experiments were carried out with these methods on the same dataset, and the results were compared with the proposed signal processing technique presented in this paper. Frequency spectra of the original raw vibration signal were used as input into the DNN and CNN networks, while the raw time series data was used as input to the LSTM network. The noise-added vibration data was directly converted to scalogram images using CWT, and the same CNN-based algorithm in the proposed framework was used. The structure of the DNN in each experiment contained an input layer, 4 hidden layers, and an output layer. The hyperparameters of the DNN network are shown in Table 11. Each CNN contained 3 convolutional-pooling layer units with ReLU activation functions. The convolutional kernel used in all CNNs is of dimension 5, and the max pooling stride of 2. A learning rate of 0.001 and a maximum epoch of 500 was set for both DNNs and CNNs training, while an 80–20% dataset split was used for training and validation datasets. The output layer of DNNs and CNNs has dimension 5, corresponding to the number of classes. Condition monitoring features such as peak value, crest factor, standard deviation, variance measure, kurtosis, skewness, shape factor, root mean square (RMS), entropy, impulse factor, margin factor, root mean square frequency (RMSF), and root variance frequency (RVF) calculated through spectral averaging method as described in [74, 75], were used for bearing fault diagnosis using support vector machine (SVM). The result using this manual feature extraction method is included in Table 11.
The comparison results presented in Table 11 show that the proposed bearing fault diagnosis method can more accurately identify bearing faults from noisy vibration signals than the DNN, 1D-CNN, LSTM, and SVM methods. This shows that the denoising technique makes it easier for the deep learning structure to accurately identify the faults since the frequency features of the vibration signals are not easily mixed up and confused with the noisy components. Compared to other signal processing methods carried out on the same dataset, the proposed method presented in this paper combines signal denoising techniques with deep learning based on CNN architecture for feature extraction and fault classification. By so doing, the proposed method presents several advantages over other methods:
-
(1)
It filters out low and high-frequency components and white noise from the data based on the optimized parameters, advanced denoising, and WT techniques. This method reduces the noise level in the acquired signal with little changes to the original features of the actual vibration signal profile of the healthy or faulty bearings. This significantly improves the fault diagnosis accuracy.
-
(2)
By using deep learning, the fault diagnosis is automated as opposed to other unreliable manual techniques as they depend on visual inspection or statistical analysis.
-
(3)
Due to the time-varying variable speed condition considered in this study, significant denoising and CWT technique decompose the input signal into a time–frequency representation, making it good for time and frequency localization. Combined with the power of deep learning, a powerful tool is developed to effectively identify subtle changes in the vibration signal due to existing faults.
-
(4)
The weights obtained during deep learning represent changes in pixel depth in the scalogram images, which corresponds to time–frequency characteristics of the vibration signal and can be correlated to the fault features of the bearings. By applying denoising techniques, the effects of identical noise levels that can create confusion in distinguishing the frequency peaks in the time–frequency representation are limited, thereby improving the accuracy of the results. This makes the proposed method effective for bearing fault diagnosis and bearing health monitoring.
LSTM is also based on deep learning but has the lowest accuracy in diagnosing the bearing faults from the raw time-series signals. This could be attributed to the fact that the network cannot accurately identify the distinguishing features from the signals. Also, the classification accuracies from SVM with the manually extracted features through spectral average-based method is significantly lower than that of the proposed method and other deep learning methods, indicating that the proposed framework is more efficient for bearing diagnosis than the regular machine learning methods such as SVM on manually extracted features.
5 Conclusion
This paper presented a time-series signal processing method for denoising and bearing fault diagnosis using vibration signals. The proposed method combines several advanced time-series signal processing and denoising techniques with a deep learning structure for effective and efficient automatic vibration signal processing, feature extraction, and bearing fault diagnosis. The presented method was divided into three crucial steps. First, the time series vibration signals are preprocessed and prepared. In this stage, the time series vibration signals are supplemented with AWGN to simulate the bearing subsystem as part of a larger industrial system whose vibration signals are considered the source of heavy noise. Then the noise-added signal is standardized and split into smaller segments of arbitrary length using an overlapping sliding window approach. Next, the noised added vibration signals are denoised using two successive denoising techniques: VMD-IBD with optimized parameters to remove low and high-frequency noise signals and then wavelet denoising to remove the same frequency noise signal to obtain a reconstructed vibration signal with less noise that resembles the original vibration signal as closely as possible. The final denoised vibration signal was processed using CWT to generate 2D time–frequency domain scalogram images. Finally, the generated image dataset was used to train a CNN deep neural network with a softmax classification layer to automatically identify the bearing fault.
The proposed method was validated using the Ottawa University vibration dataset from a bearing test rig. The validation results showed that the proposed method could diagnose bearing faults using vibration signals mixed with heavy noise signals through unsupervised learning with high accuracy and robustness. The results also showed that segment length and operating speed conditions have little or no significant effect on the accuracy of the results. It was established that the speed conditions for training and testing do not significantly affect the accuracy of the method. As a result, the model can be trained in one-speed conditions and used to identify faults under other speed conditions. By denoising, the noise-added vibration signal, the performance of the deep neural network to accurately identify the fault was significantly improved.
The proposed bearing fault diagnosis method was more accurate than other deep learning and traditional machine learning methods. The proposed bearing fault diagnosis method had the highest accuracy over other deep learning and traditional machine learning methods. It was able to remove the added white noise and traces of noise in the original vibration signal from the bearing test rig. The time–frequency transform of the denoised signal revealed important aspects of the faults, making it easier for the CNN to accurately classify the faults. The method proposed in the paper demonstrated its capability to extract “clean” vibration signals even in the presence of background noise and accurately classify and automatically diagnose the bearing faults. This method could be used to diagnose bearing faults in variable speed conditions and the presence of heavy background noise.
In future work, we will explore the effects of different parameter selections for the denoising stage on the accuracy of diagnosis. Optimizing the parameter selection process is key to improving the denoising process for better performance and robustness. One crucial limitation of this work is that it involves three crucial computationally intensive stages (denoising, time–frequency transformation, and deep learning model training). This limitation makes it difficult to use the proposed method for on-the-fly bearing fault diagnosis in real-time applications. Despite these limitations, the proposed method has proven its effectiveness, accuracy, and robustness in many applicable scenarios.
References
Li J, Wang H, Wang X, Zhang Y (2020) Rolling bearing fault diagnosis based on improved adaptive parameterless empirical wavelet transform and sparse denoising. Measurement 152:107392. https://doi.org/10.1016/j.measurement.2019.107392
Jin Z, He D, Wei Z (2022) Intelligent fault diagnosis of train axle box bearing based on parameter optimization VMD and improved DBN. Eng Appl Artif Intell 110:104713. https://doi.org/10.1016/j.engappai.2022.104713
Qian W, Li S, Lu J (2022) Adaptive nearest neighbor reconstruction with deep contractive sparse filtering for fault diagnosis of roller bearings. Eng Appl Artif Intell 111:104749. https://doi.org/10.1016/j.engappai.2022.104749
Cheng Y, Hu K, Wu J, Zhu H, Shao X (2021) A convolutional neural network based degradation indicator construction and health prognosis using bidirectional long short-term memory network for rolling bearings. Adv Eng Inform 48:101247. https://doi.org/10.1016/j.aei.2021.101247
Wei J, Huang H, Yao L, Hu Y, Fan Q, Huang D (2020) New imbalanced fault diagnosis framework based on cluster-MWMOTE and MFO-optimized LS-SVM using limited and complex bearing data. Eng Appl Artif Intell 96:103966. https://doi.org/10.1016/j.engappai.2020.103966
Schwendemann S, Amjad Z, Sikora A (2021) Bearing fault diagnosis with intermediate domain based layered maximum mean discrepancy: a new transfer learning approach. Eng Appl Artif Intell 105:104415. https://doi.org/10.1016/j.engappai.2021.104415
Jardine AKS, Lin D, Banjevic D (2006) A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech Syst Signal Process 20(7):1483–1510. https://doi.org/10.1016/j.ymssp.2005.09.012
Dyer D, Stewart RM (1978) Detection of rolling element bearing damage by statistical vibration analysis. J Mech Des 100(2):229–235. https://doi.org/10.1115/1.3453905
Collacott RA (1977) Mechanical fault diagnosis and condition monitoring. Springer, Dordrecht. https://doi.org/10.1007/978-94-009-5723-7
Tandon N, Choudhury A (1999) A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings. Tribol Int 32(8):469–480. https://doi.org/10.1016/S0301-679X(99)00077-8
Rai VK, Mohanty AR (2007) Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert-Huang transform. Mech Syst Signal Process 21(6):2607–2615. https://doi.org/10.1016/j.ymssp.2006.12.004
Lin H, Ye Y-C, Huang B-J, Su J-L (2016) Bearing vibration detection and analysis using enhanced fast Fourier transform algorithm. Adv Mech Eng. https://doi.org/10.1177/1687814016675080
Lin H-C, Ye Y-C (2019) Reviews of bearing vibration measurement using fast Fourier transform and enhanced fast Fourier transform algorithms. Adv Mech Eng 11(1):1687814018816751. https://doi.org/10.1177/1687814018816751
Randall RB (2021) Some special signal processing techniques. In: Vibration–based condition monitoring. Wiley, New York, pp 147–198. https://doi.org/10.1002/9781119477631.ch5
Saidi L, Ben Ali J, Fnaiech F (2014) Application of higher order spectral features and support vector machines for bearing faults classification. ISA Trans. https://doi.org/10.1016/j.isatra.2014.08.007
Randall RB (2021) Cepstrum analysis applied to machine diagnostics. In: Vibration–based condition monitoring. Wiley, New York, pp 199–229. https://doi.org/10.1002/9781119477631.ch6
Gao R, Yan R (2006) Non-stationary signal processing for bearing health monitoring. IJMR 1:18–40. https://doi.org/10.1504/IJMR.2006.010701
Wang WJ, McFadden PD (1993) Early detection of gear failure by vibration analysis I. Calculation of the time-frequency distribution. Mech Syst Signal Process 7(3):193–203. https://doi.org/10.1006/mssp.1993.1008
Quinde IR, Sumba JC, Ochoa LE, Guevara Jr. AV, Morales-Menendez R (2019) Bearing fault diagnosis based on optimal time-frequency representation method. IFAC-Pap 52(11):194–199. https://doi.org/10.1016/j.ifacol.2019.09.140
Zhou Y, Chen J, Dong GM, Xiao WB, Wang ZY (2011) Wigner–Ville distribution based on cyclic spectral density and the application in rolling element bearings diagnosis. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 225(12):2831–2847. https://doi.org/10.1177/0954406211413215
Yan R, Gao RX, Chen X (2014) Wavelets for fault diagnosis of rotary machines: a review with applications. Signal Process 96:1–15. https://doi.org/10.1016/j.sigpro.2013.04.015
Peng ZK, Chu FL (2004) Application of the wavelet transform in machine condition monitoring and fault diagnostics: a review with bibliography. Mech Syst Signal Process 18(2):199–221. https://doi.org/10.1016/S0888-3270(03)00075-X
Gao Q, Duan C, Fan H, Meng Q (2008) Rotating machine fault diagnosis using empirical mode decomposition. Mech Syst Signal Process 22(5):1072–1081. https://doi.org/10.1016/j.ymssp.2007.10.003
Han H, Cho S, Kwon S, Cho S-B (2018) Fault diagnosis using improved complete ensemble empirical mode decomposition with adaptive noise and power-based intrinsic mode function selection algorithm. Electronics 7(2):2. https://doi.org/10.3390/electronics7020016
Chen X, Ge D, Liu X, Liu M (2019) Roller bearing fault diagnosis based on empirical mode decomposition and targeting feature selection. IOP Conf. Ser. Mater. Sci. Eng. 630(1):012023. https://doi.org/10.1088/1757-899X/630/1/012023
Xuan Z, Ge M (2012) Application of the Hilbert–Huang transform for machine fault diagnostics. Appl Mech Mater 182–183:1484–1488. https://doi.org/10.4028/www.scientific.net/AMM.182-183.1484
Thakker HT, Dave V, Vakharia V, Singh S (2020) Fault diagnosis of ball bearing using Hilbert Huang transform and LASSO feature ranking technique. IOP Conf Ser Mater Sci Eng 841(1):012006. https://doi.org/10.1088/1757-899X/841/1/012006
Duong BP, Kim JY, Jeong I, Im K, Kim CH, Kim JM (2020) A deep-learning-based bearing fault diagnosis using defect signature wavelet image visualization. Appl Sci 10(24):24. https://doi.org/10.3390/app10248800
Gou L, Li H, Zheng H, Li H, Pei X (2020) Aeroengine control system sensor fault diagnosis based on CWT and CNN. Math Probl Eng 2020:e5357146. https://doi.org/10.1155/2020/5357146
Gao D, Zhu Y, Wang X, Yan K, Hong J (2018) A fault diagnosis method of rolling bearing based on complex Morlet CWT and CNN. In: 2018 Prognostics and system health management conference (PHM-Chongqing), pp 1101–1105. https://doi.org/10.1109/PHM-Chongqing.2018.00194
Xu Y, Li Z, Wang S, Li W, Sarkodie-Gyan T, Feng S (2021) A hybrid deep-learning model for fault diagnosis of rolling bearings. Measurement 169:108502. https://doi.org/10.1016/j.measurement.2020.108502
Neupane D, Kim Y, Seok J (2021) Bearing fault detection using scalogram and switchable normalization-based CNN (SN-CNN). IEEE Access 9:88151–88166. https://doi.org/10.1109/ACCESS.2021.3089698
Xiao Q, Li S, Zhou L, Shi W (2022) Improved variational mode decomposition and CNN for intelligent rotating machinery fault diagnosis. Entropy 24(7):908. https://doi.org/10.3390/e24070908
Zhang X, Wang H, Wu B, Zhou Q, Hu Y (2022) A novel data-driven method based on sample reliability assessment and improved CNN for machinery fault diagnosis with non-ideal data. J Intell Manuf. https://doi.org/10.1007/s10845-022-01944-x
Huang NE et al (1998) The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc R Soc Lond Ser Math Phys Eng Sci 454(1971):903–995. https://doi.org/10.1098/rspa.1998.0193
Dragomiretskiy K, Zosso D (2014) Variational mode decomposition. IEEE Trans Signal Process 62(3):531–544. https://doi.org/10.1109/TSP.2013.2288675
Wu Z, Huang NE (2011) Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv Adapt Data Anal. https://doi.org/10.1142/S1793536909000047
Shannon CE (1949) Communication in the presence of noise. Proc IRE 37(1):10–21. https://doi.org/10.1109/JRPROC.1949.232969
Boyd S, Parikh N, Chu E, Peleato B, Eckstein J (2011) Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn 3:1–122. https://doi.org/10.1561/2200000016
Bertsekas DP (1995) Nonlinear programming. Athena Scientific, Belmont
Variational mode decomposition - MATLAB vmd. https://www.mathworks.com/help/wavelet/ref/vmd.html. Accessed 04 Apr 2023
Chen Q, Chen J, Lang X, Xie L, ur Rehman N, Su H (2021) Self-tuning variational mode decomposition. J Frankl Inst 358(15):7825–7862. https://doi.org/10.1016/j.jfranklin.2021.07.021
Tang G, Wang X (2015) Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing. J Xi’an Jiaotong Univ 49:73–81. https://doi.org/10.7652/xjtuxb201505012
Dou D, Li L, Zhao Y (2011) Fault diagnosis of rolling bearings using EEMD-Renyi entropy and PCA-PNN. J Southeast Uni Nat Sci Edit 41:107–111. https://doi.org/10.3969/j.issn.1001-0505.2011.S1.023
Zhang L, Song C, Wang C, Xu T, Yi J (2019) Bearing performance degradation assessment based on a combination of multi-scale entropy and K-medoids clustering, pp 1–6. https://doi.org/10.1109/PHM-Qingdao46334.2019.8943049
Sen PK (1996) Anil Kumar Bhattacharyya (1915–1996): a reverent remembrance. Calcutta Stat Assoc Bull 46(3–4):151–158. https://doi.org/10.1177/0008068319960301
Mallat S (1989) A theory of multiresolution signal decomposition: the wavelet representation. IEEE Trans Pattern Anal Machine Intell 11:674–693. https://doi.org/10.1109/34.192463
Luo G, Zhang D (2012) Wavelet denoising. https://doi.org/10.5772/37424
Meyer Y (2002) Matlab help file. The Mathwork inc
Gonzalez R, Faisal Z (2019) Digital image processing second edition
Daubechies I (1992) Ten lectures on wavelets. Soc Ind Appl Math. https://doi.org/10.1137/1.9781611970104
Donoho DL, Johnstone IM (1994) Ideal spatial adaptation by wavelet shrinkage. Biometrika 81(3):425–455. https://doi.org/10.1093/biomet/81.3.425
Coifman RR, Donoho DL (1995) Translation-Invariant De-Noising. In: Antoniadis A, Oppenheim G (eds) Wavelets and statistics. Lecture notes in statistics. Springer, New York, pp 125–150. https://doi.org/10.1007/978-1-4612-2544-7_9
Donoho DL, Johnstone IM (1994) Ideal denoising in an orthonormal basis chosen from a library of bases. C R Acad Sci Sér I Math 319:1317–1322
Stéphane M (2009) Chapter 7—Wavelet bases. In: Stéphane M (ed) A wavelet tour of signal processing, 3rd edn. Academic Press, Boston, pp 263–376. https://doi.org/10.1016/B978-0-12-374370-1.00011-2
Johnstone IM, Silverman BW (1997) Wavelet threshold estimators for data with correlated noise. J R Stat Soc Ser B Methodol 59(2):319–351. https://doi.org/10.1111/1467-9868.00071
Johnson DH, Dudgeon DE (1992) Array signal processing: concepts and techniques. Simon & Schuster Inc, New York
Wang Y, He Z, Zi Y (2010) Enhancement of signal denoising and multiple fault signatures detecting in rotating machinery using dual-tree complex wavelet transform. Mech Syst Signal Process 24(1):119–137. https://doi.org/10.1016/j.ymssp.2009.06.015
Ng C-T (2014) On the selection of advanced signal processing techniques for guided wave damage identification using a statistical approach. Eng Struct 67:50–60. https://doi.org/10.1016/j.engstruct.2014.02.019
Tary JB, Herrera RH, van der Baan M (2018) Analysis of time-varying signals using continuous wavelet and synchrosqueezed transforms. Philos Trans R Soc Math Phys Eng Sci 376(2126):20170254. https://doi.org/10.1098/rsta.2017.0254
Fast Fourier Transform—an overview | ScienceDirect Topics. https://www.sciencedirect.com/topics/engineering/fast-fourier-transform. Accessed 10 Sep 2022
Zhou S, Tang B, Chen R (2009) Comparison between non-stationary signals fast Fourier transform and wavelet analysis. In: 2009 International Asia symposium on intelligent interaction and affective computing, pp 128–129.https://doi.org/10.1109/ASIA.2009.31
Wavelets and wavelet transform systems and their applications. https://doi.org/10.1007/978-3-030-87528-2. Accessed 12 Sep 2022
Lu C, Wang Z, Zhou B (2017) Intelligent fault diagnosis of rolling bearing using hierarchical convolutional network based health state classification. Adv Eng Inform 32:139–151. https://doi.org/10.1016/j.aei.2017.02.005
Gu J, Peng Y, Lu H, Chang X, Chen G (2022) A novel fault diagnosis method of rotating machinery via VMD, CWT and improved CNN. Measurement 200:111635. https://doi.org/10.1016/j.measurement.2022.111635
Girshick R, Donahue J, Darrell T, Malik J (2014) Rich feature hierarchies for accurate object detection and semantic segmentation. In: 2014 IEEE conference on computer vision and pattern recognition, pp 580–587.https://doi.org/10.1109/CVPR.2014.81
Turay T, Vladimirova T (2022) Toward performing image classification and object detection with convolutional neural networks in autonomous driving systems: a survey. IEEE Access 10:14076–14119. https://doi.org/10.1109/ACCESS.2022.3147495
Alzubaidi L et al (2021) Review of deep learning: concepts, CNN architectures, challenges, applications, future directions. J Big Data 8(1):53. https://doi.org/10.1186/s40537-021-00444-8
IBM Cloud Education (2021) What are convolutional neural networks? Convolutional neural networks. https://www.ibm.com/cloud/learn/convolutional-neural-networks. Accessed 12 Oct 2022
Jin X, Xu C, Feng J, Wei Y, Xiong J, Yan S (2016) Deep learning with S-shaped rectified linear activation units. Proc AAAI Conf Artif Intell 30(1):1. https://doi.org/10.1609/aaai.v30i1.10287
Srivastava N, Hinton GE, Krizhevsky A, Sutskever I, Salakhutdinov R (2014) Dropout: a simple way to prevent neural networks from overfitting. J Mach Learn Res 15:1929–1958
Huang H, Baddour N (2018) Bearing vibration data collected under time-varying rotational speed conditions. Data Brief 21:1745–1749. https://doi.org/10.1016/j.dib.2018.11.019
Krizhevsky A, Sutskever I, Hinton GE (2017) ImageNet classification with deep convolutional neural networks. Commun ACM 60(6):84–90. https://doi.org/10.1145/3065386
Magar R, Ghule L, Li J, Zhao Y, Farimani AB (2021) FaultNet: a deep convolutional neural network for bearing fault classification. IEEE Access 9:25189–25199. https://doi.org/10.48550/arXiv.2010.02146
Van Hecke B, He D, Qu Y (2014) On the use of spectral averaging of acoustic emission signals for bearing fault diagnostics. J Vib Acoust 136(6):061009. https://doi.org/10.1115/1.4028322
Acknowledgements
National Natural Science Foundation of China No. (51875266).
Author information
Authors and Affiliations
Contributions
HH: Conceptualization, Methodology, Software, Validation, Writing—original draft, Writing—review and editing, Visualization. LAN: Supervision, Data collection, Software, Conceptualization, Analysis, Writing—review and editing. ST: Supervision, Conceptualization, Review. JG: Supervision.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Technical Editor: Jarir Mahfoud.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A
Appendix A
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Hamdaoui, H., Ngiejungbwen, L.A., Gu, J. et al. Improved signal processing for bearing fault diagnosis in noisy environments using signal denoising, time–frequency transform, and deep learning. J Braz. Soc. Mech. Sci. Eng. 45, 576 (2023). https://doi.org/10.1007/s40430-023-04471-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40430-023-04471-9