1 Introduction

Robotic manipulators are employed in the current industrial environment to enhance product quality as well as productivity, accuracy, speed, and flexibility in the workplace. Robotic manipulators are rapidly being used in risky, tedious, or repetitive industrial processes, despite the complicated and tough requirements of industrial applications. Material picking and placing is one of the essential uses of mechanical robotic manipulators. These manipulators can also be used for welding, assembling, manufacturing, painting, and other operations in the car industry, as well as for handling radioactive and biohazardous materials during robotically assisted surgery. Manufacturing needs to be more effective and high-quality, and this requirement has motivated the development of more robust and sophisticated robotic manipulators [1,2,3,4].

The adoption of flexible link manipulators (FLMs) and flexible joint manipulators (FJMs) have witnessed a notable surge in recent times, attributed to their extensive applicability across domains encompassing industry, medicine, aerospace, instrumentation, satellites, and industrial automation. These manipulators are progressively replacing rigid links characterized by larger dimensions and greater mass within diverse industrial sectors [5]. Furthermore, the design of flexible and lightweight manipulators offers advantages such as enhanced maneuverability and reduced power consumption. Nonetheless, these systems pose challenges in terms of modeling, measurement, stabilization, and control, primarily attributed to the oscillations exhibited by flexible links [6].

The importance of mathematical modeling for multi-DOF manipulators is necessary in any practical control process; the mathematical model of the manipulator is normally developed using the Lagrangian approach [7,8,9,10]. In general, mathematical modeling is really challenging and time-consuming, especially for strongly coupled multi-input multi-output systems; Recent research offers a thorough and comprehensive critical analysis of mathematical modeling methods [2]. Using a numerical modeling method, the powerful MATLAB Simulink and Simscape toolboxes were utilized to create SimMechanics models of robotic manipulators from CAD assemblies [1, 9, 10]. Simscape multibody models are favored because they are simple to get, and they can be simulated and controlled [1, 5, 11,12,13,14]. Using simulation software has several advantages, including understanding of how the multi-DOF robotic manipulator systems work in a simulated environment and avoiding the complexity of mathematical formulations.

Sliding mode control (SMC) is a widely utilized nonlinear control strategy employed to guide state trajectories toward predetermined sliding surfaces through the application of discontinuous control inputs [10, 15,16,17,18,19]. Nevertheless, the SMC law’s discontinuity can lead to the manifestation of the chattering effect, characterized by the occurrence of high-frequency oscillations in the controlled variable. This phenomenon has the potential to disrupt the stability of the controlled system or substantially reduce the actuators’ operational lifespan [10, 15].

Numerous strategies have been proposed in the literature to address the chattering phenomenon [20]. One of the approaches involves approximating the SMC’s discontinuous control with a continuous counterpart. Although this technique effectively reduces tracking error, it comes at the cost of compromising the overall efficiency of SMC by generating a pseudo-sliding mode instead of the desired ideal sliding mode [20]. An alternative solution to mitigate chattering entails employing the higher-order sliding mode control approach. This method confines the discontinuity to a derivative of the control variable, incorporating these derivatives with respect to time up to a specified order in addition to the sliding variable. Notably, this approach exhibits favorable suitability for application in electromagnetic or mechanical systems due to its continuous nature of control action [20].

The existing literature encompasses various studies exploring the sliding mode controller and its diverse applications. For instance, a comparative investigation conducted by prior researchers [21] evaluated the performance of the SMC controller in comparison to the PID controller. The outcomes indicated that the SMC exhibited a faster and more robust response, albeit with a relatively larger control signal than the PID controller.

Geng et al. [22] explored three distinct types of non-singular terminal sliding mode controllers implemented on a robotic arm subject to external disturbances. Through simulation results, they demonstrated the efficacy of the proposed modifications in enhancing the controller’s convergence rate while reducing the magnitude of the control input signal.

In a study conducted by Mohammad-Reza Moghanni-Bavil-Olyaei et al. [23], a comparative analysis was performed between the sliding mode control (SMC) with proportional-derivative (PD) surface and the block back-stepping control approach. The aim of this comparison was to evaluate the trajectory tracking performance of a single-link flexible-link flexible-joint manipulator (SFLFJM).

An additional research endeavor focused on an integrated second-order SMC controller and the application of an algorithm for designing the control scheme for manipulator robots. This study aimed to evaluate the practicability of the proposed controller and confirm its effectiveness in terms of convergence and robustness. Satisfactory results were obtained through experiments conducted on a real industrial robot, validating the algorithm’s practicality and effectiveness [10, 20].

Numerous studies have investigated the concept of adaptive sliding mode control [24,25,26]. Additionally, there have been several studies that explore the integration of fuzzy logic with sliding mode control (SMC) [27,28,29]. To enhance the performance of SMC control, Genetic Algorithms (GA) were utilized to determine optimal parameters for a conventional SMC controller [30, 31]. Vijay and Jena devised a Particle Swarm Optimization (PSO)-based backstepping sliding mode controller and observer for robot manipulators [32]. PSO was employed to tune sliding surface parameters of SMC combined with an Artificial Neuro Fuzzy Inference System (ANFIS) and adjust the membership functions of Takagi Sugeno fuzzy SMC, respectively [33, 34]. A novel approach in [35] introduced the combination of a PSO algorithm with super-twisting SMC to eliminate chattering. Medjghou et al. introduced an optimized extended Kalman filter with integral type 2 fuzzy SMC using Biogeography-based optimization (BBO) [36]. Oliveira et al. proposed using gray wolf optimization (GWO) with a chaotic basis to tune robust higher-order SMC for the position control of a robot manipulator [37]. To find the best control parameters for the fuzzy controller in APIDFSMC and control uncertain systems, the GA-based adaptive PID fuzzy sliding mode control strategy (APIDFSMC-GA) is introduced [38]. With a proportional-integral-derivative-type nonsingular fast terminal sliding mode control, an adaptive robust controller for uncertain nonlinear systems is designed to provide the essential attributes of rapid transient response, finite-time convergence, negligible steady-state error, and chattering cancellation [39]. Different optimization techniques, such as the Antlion Optimization Algorithm (ALO), Sine Cosine Algorithm (SCA), gray wolf optimizer (GWO), and Whale Optimizer Algorithm (WOA), are used to control the nonlinear 2-DOF system in a sliding mode controller (SMC) with PID surface [15].

In the context of scientific research and technical applications, the use of evolutionary algorithms (EAs), a type of efficient and effective optimization approach, has recently grown in popularity. Modern practical optimization issues are usually non-convex, discontinuous, or even non-differentiable, which makes it difficult for traditional optimization techniques, like gradient-based approaches, to handle these types of problems [40,41,42].

Natural processes are used by swarm-based optimization algorithms (SOAs) to drive a search toward the optimal solution. Instead of using just one solution for each iteration, SOAs use a population of solutions, in contrast to simple optimization algorithms like stochastic process and hill climbing. The difference between SOAs and these algorithms in this regard is substantial. A population of solutions is processed at each iteration, and a population of solutions is also created each iteration [41, 42].

The gray wolf optimizer (GWO) is a new developed metaheuristic algorithm inspired by nature, characterized by a small number of parameters for tuning [40]. However, the original GWO and its variants may encounter challenges such as lack of population diversity, premature convergence, and difficulty in achieving a balance between exploration and exploitation. To address these limitations, a new variant called Memory Enhanced Linear Population Size Reduction GWO (MELGWO) is proposed [41]. This variant incorporates memory to retain better solutions, evolutionary operators to enhance exploration, and a stochastic local search technique. Additionally, a linear population size reduction strategy is employed to maintain a diverse population and prevent premature convergence. As iterations progress, the swarm size is gradually reduced to minimize redundant exploration. The local search component significantly improves the exploitation capability of GWO, resulting in the generation of more wolves near the best solutions in the memory swarm [41]. Through the integration of these features, the MELGWO algorithm demonstrates superior performance compared to the original GWO algorithm, effectively addressing the limitations and achieving enhanced optimization results.

This study encompasses the utilization of the Lagrangian method and the Simscape Multibody toolbox within MATLAB to construct a comprehensive model of a 3-DOF RLM. To validate the fidelity of this model, the investigation commences with an analysis of open-loop system responses for both the mathematical and Simscape representations, elucidated in Sect. 2. In Sect. 3, the formulation of a Sliding Mode Controller (SMC) with a PID sliding surface is elaborated. Section 4 expounds on the employment of the memory enhanced linear population size reduction gray wolf optimizer (MELGWO) metaheuristic optimization technique, designed to confer overall robustness, stability, and exceptional tracking performance to the closed-loop three-link maneuver system. A meticulous examination of the proposed controller’s efficacy in mitigating disturbances and noise, along with its resilience against variations in payload mass, is undertaken in Sect. 5. Furthermore, the adaptability of the controller to the maneuver’s joint flexibility is discussed. Finally, Sect. 6 encapsulates the study’s key findings and concluding remarks.

In the entire study, all vectors are written with bold lowercase letters and all matrices are written with uppercase letters.

2 Modeling the three DOF rigid-link robotic manipulator

The model of the 3-DOF rigid-link manipulator derived from the Lagrangian method depends on the kinetic and potential energies of the links. The more complex the problem, the more variables, assumptions, and iterations we might need to make, and this takes long derivation time. On the other side, the powerful tool Simscape Multibody that is fully integrated with MATLAB and Simulink, enables rapid modeling, simulation, and analysis of systems.

The Simscape modeling and validation of the Lagrange’s model with Simscape model are included in the following subsections.

2.1 Lagrange mathematical modeling

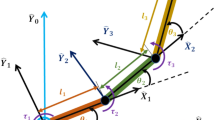
By considering the kinetic and potential properties of the mechanical system, the Lagrange’s equations of motion can be obtained. Figure 1 illustrates a system comprising three linkages and three joints, denoted as \({J}_{1}\), \({J}_{2}\), and \({J}_{3}\). The lengths of the links are represented as \({l}_{1}\), \({l}_{2}\), and \({l}_{3}\), while their masses are indicated by m1, m2, and m3, respectively. A comprehensive listing of these properties is provided in Table 1.

Fig. 1
figure 1

Representation of the three-link robotic model

Full size image
Table 1 The physical parameters of the three-link robotic manipulator
Full size table

In the context of the manipulator, the dynamic model can be expressed as follows:

$$B\left({\varvec{\theta}}\right)\ddot{{\varvec{\theta}}}+\mathbf{f}\left({\varvec{\theta}}, \dot{{\varvec{\theta}}}\right)+\mathbf{g}\left({\varvec{\theta}}\right)+{\varvec{D}}={\varvec{\tau}}$$
(1)

where \({\varvec{\theta}}\left({\varvec{t}}\right),\dot{{\varvec{\theta}}}({\varvec{t}}),\ddot{{\varvec{\theta}}}({\varvec{t}})\) denote the vectors of joints angles, joints velocities and joints accelerations, \(B\left({\varvec{\theta}}\right)\) is the inertia matrix, \(\mathbf{f}\left({\varvec{\theta}}, \dot{{\varvec{\theta}}}\right)\) is the vector of centrifugal and Coriolis forces, g \(\left({\varvec{\theta}}\right)\) is the gravitational force vector, \({\varvec{\tau}}\) is the vector of input torques and \({\varvec{D}}\) is the vector of external disturbances which is assumed to be bounded with \(\Vert {\varvec{D}}\Vert \le d\), where d is a positive constant.

Using the information given in Table 1, the entries of the inertia matrix are as follows:

$$\begin{aligned} B_{11} =\, & 0.1306 + 0.12 m_{L} + 0.04\left( {1 + 2m_{L} } \right){\text{ cos}}\left( {\theta_{2} + \theta_{3} } \right) \\ & + 0.08\left( {1.125 + m_{L} } \right) {\text{cos}}\left( {\theta_{2} } \right) + 0.04\left( {1 + 2m_{L} } \right) {\text{cos}}\left( {\theta_{3} } \right) \\ \end{aligned}$$
(2)
$$\begin{aligned} B_{12} =\, & 0.0571 + 0.08 m_{L} + 0.02\left( {1 + 2m_{L} } \right) {\text{cos}}\left( {\theta_{2} + \theta_{3} } \right) \\ & + 0.04\left( {1.125 + m_{L} } \right) {\text{cos}}\left( {\theta_{2} } \right) + 0.04\left( {1 + 2m_{L} } \right) {\text{cos}}\left( {\theta_{3} } \right) \\ \end{aligned}$$
(3)
$$\begin{aligned} B_{13} & = D_{31} = 0.0135 + 0.04 m_{L} \\ &\quad+ 0.02\left( {1 + 2m_{L} } \right) {\text{cos}}\left( {\theta_{2} + \theta_{3} } \right) \\ &\quad+ 0.02\left( {1 + 2m_{L} } \right) {\text{cos}}\left( {\theta_{3} } \right) \end{aligned}$$
(4)
$$B_{22} = 0.0135 + 0.04 m_{L} + 0.02\left( {1 + 2m_{L} } \right) {\text{cos}}\left( {\theta_{3} } \right)$$
(5)
$$B_{23} = B_{32} = 0.0571 + 0.08 m_{L} + 0.04\left( {1 + 2m_{L} } \right) {\text{cos}}\left( {\theta_{3} } \right)$$
(6)
$$B_{33} = 0.0135 + 0.04m_{L}$$
(7)

where \({m}_{L}\) is the payload mass.

The elements of the centrifugal and Coriolis force vector are defined by:

$$\begin{aligned} f_{1} = & - \left[ {0.04\left( {1.125 + m_{L} } \right) {\text{sin}}\left( {\theta_{2} } \right) + 0.02\left( {1 + 2m_{L} } \right) {\text{sin}}\left( {\theta_{2} + \theta_{3} } \right) } \right] \dot{\theta }_{2}^{2} \\ & - \left[ {0.02\left( {1 + 2m_{L} } \right) {\text{sin}}\left( {\theta_{3} } \right) + 0.02\left( {1 + 2m_{L} } \right) {\text{sin}}\left( {\theta_{2} + \theta_{3} } \right)} \right] \dot{\theta }_{3}^{2} \\ & - \left[ {0.08\left( {0.125 + m_{L} } \right) {\text{sin}}\left( {\theta_{2} } \right) + 0.04\left( {1 + 2m_{L} } \right){\text{sin}}\left( {\theta_{2} + \theta_{3} } \right)} \right] \dot{\theta }_{1} \dot{\theta }_{2} \\ & - \left[ {0.04\left( {1 + 2m_{L} } \right) {\text{sin}}\left( {\theta_{3} } \right) + 0.04\left( {1 + 2m_{L} } \right) {\text{sin}}\left( {\theta_{2} + \theta_{3} } \right)} \right]\dot{\theta }_{2} \dot{\theta }_{3} \\ & - \left[ {0.04\left( {1 + 2m_{L} } \right) {\text{sin}}\left( {\theta_{3} } \right) + 0.04\left( {1 + 2m_{L} } \right){\text{sin}}\left( {\theta_{2} + \theta_{3} } \right)} \right] \dot{\theta }_{1} \dot{\theta }_{3} \\ \end{aligned}$$
(8)
$$\begin{aligned} f_{2} = & \left[ { 0.04\left( {0.125 + m_{L} } \right) {\text{sin}}\left( {\theta_{2} } \right) + 0.02\left( {1 + 2m_{L} } \right) {\text{sin}}\left( {\theta_{2} + \theta_{3} } \right)} \right] \dot{\theta }_{1}^{2} \\ & - \left[ {0.02\left( {1 + 2m_{L} } \right) {\text{sin}}\left( {\theta_{3} } \right)} \right]\dot{\theta }_{3}^{2} - \left[ {0.04\left( {1 + 2m_{L} } \right) {\text{sin}}\left( {\theta_{3} } \right)} \right]\dot{\theta }_{1} \dot{\theta }_{3} \\ & - \left[ {0.04\left( {1 + 2m_{L} } \right) {\text{sin}}\left( {\theta_{3} } \right)} \right]\dot{\theta }_{2} \dot{\theta }_{3} \\ \end{aligned}$$
(9)
$$\begin{aligned} f_{3} &= 0.2\left( {1 + 2m_{L} } \right)\left[ {{\text{sin}}\left( {\theta_{3} } \right) + {\text{sin}}\left( {\theta_{2} + \theta_{3} } \right)} \right]\dot{\theta }_{1}^{2}\\ &\quad + 0.2\left( {1 + 2m_{L} } \right){\text{sin}}\left( {\theta_{3} } \right) \dot{\theta }_{2}^{2} \\ & \quad+ 0.4\left( {1 + 2m_{L} } \right)\;{\text{sin}}\left( {\theta_{3} } \right)\dot{\theta }_{1} \dot{\theta }_{2} \\ \end{aligned}$$
(10)

The components of the gravity force vector are as follows:

$$\begin{aligned} {\text{g}}_{1} & = 0.1{\text{g }}\left[ {\left( {5 + 2m_{L} } \right) {\text{cos}}\left( {\theta_{1} } \right) }\right. \\ &\quad \left. {+ \left( {1 + 2m_{L} } \right){\text{cos}}\left( {\theta_{1} + \theta_{2} + \theta_{3} } \right)}\right. \\ &\quad \left. {+ \left( {3 + 2m_{L} } \right) {\text{cos}}\left( {\theta_{1} + \theta_{2} } \right)} \right] \end{aligned}$$
(11)
$${\text{g}}_{2} = 0.1{\text{g }}\left[ {\left( {1 + 2m_{L} } \right){\text{cos}}\left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) + \left( {3 + 2m_{L} } \right) {\text{cos}}\left( {\theta_{1} + \theta_{2} } \right)} \right]$$
(12)
$${\text{g}}_{3} = 0.1{\text{g }}\left[ {\left( {1 + 2m_{L} } \right){\text{cos}}\left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) } \right]$$
(13)

where \(\mathrm{g}\) is acceleration of gravity.

2.2 MATLAB Simscape multibody model

The use of Simscape add-on products grants access to more sophisticated parts and analysis tools, which aid in the design and analysis of control systems. The created model can be parameterized using MATLAB variables and expressions, while Simulink is employed to develop control schemes for our physical system. The process of developing the Simscape model encompasses several sequential stages, as outlined below:

  1. I.

    System Solver In this phase, the comprehensive configuration of mechanical and simulation parameters for the entire system is undertaken. Factors such as acceleration, the gravity vector, linearization delta, and the global frame are defined. Furthermore, the specification of the solver configuration, utilizing the Runge–Kutta method, is executed.

  2. II.

    Link Creation Within the framework of the Simscape toolbox, the "Brick Solid" block is employed. This block functions as a representation of a solid structure, integrating geometry, inertia, mass, graphics elements, and associated frames. Notably, it serves as the fundamental unit for constructing rigid bodies. During this stage, the intrinsic attributes of the links, encompassing geometric dimensions and mass properties, are meticulously defined.

  3. III.

    Creation of Joints Within the Simscape toolbox, the "Revolute Joint" block is utilized to establish a revolute joint connecting two frames. This specific joint configuration enables rotational motion along a singular degree of freedom.

  4. IV.

    Frame Transformations The integration of rigid transformations assumes a pivotal role in defining fixed 3D transformations between frames. These transformations encompass both translational and rotational components, thereby accommodating diverse combinations of translational shifts and rotational adjustments.

The MATLAB Simscape model, which represents the entire rigid link manipulator (RLM) system is shown in Fig. 2.

Fig. 2
figure 2

MATLAB Simscape model of the robotic manipulator

Full size image

To validate the accuracy of the mathematical model, a comparative analysis is conducted between the open-loop behaviors of the mathematical model and the MATLAB Simscape model. This evaluation is performed under varying input torque conditions of \(0.5 \mathrm{N} \mathrm{m}\), \(1 \mathrm{N} \mathrm{m}\), and \(1.5 \mathrm{N} \mathrm{m}\) for each joint, as depicted in Fig. 3. The responses of the Lagrange model are compared with those of the Simscape model in Fig. 4. Evidently, a significant congruence between the two responses is observed, substantiating the suitability of the Simscape model for subsequent investigations.

Fig. 3
figure 3

System configuration during validation of the Lagrange’s model and the Simscape model of the 3-link robot manipulator

Full size image
Fig. 4
figure 4

Validation results a The measured angles of both modeling techniques and b The measured angular velocities of both modeling techniques

Full size image

3 Sliding mode controller with linear PID sliding surface

Selecting the sliding surface function is a necessary step before designing a sliding mode controller. Then, an equivalent controller and switching mode controller should be constructed depending on the states of the dynamical system. The basic principle behind this kind of control is to place, regardless of the initial conditions, the representative point of the system’s evolution on a hypersurface of the phase space, representing a set of static relationships between the state variables. There are two components in the sliding mode control as described in Eq. (14).

$${\varvec{\tau}}\left({\varvec{t}}\right)={{\varvec{\tau}}}_{\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{t}}\left({\varvec{t}}\right)+{{\varvec{\tau}}}_{\mathbf{d}\mathbf{i}\mathbf{s}\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{t}}\left({\varvec{t}}\right)$$
(14)

where \({{\varvec{\tau}}}_{\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{t}}\left({\varvec{t}}\right)\) is the continuous part of the controller (called the equivalent controller) and \({{\varvec{\tau}}}_{\mathbf{d}\mathbf{i}\mathbf{s}\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{t}}\left({\varvec{t}}\right)\) is the discontinuous part (called the switching mode controller).

The PID sliding surface for the existing SMC can be specified with Eq. (15).

$${\varvec{\sigma}}\left({\varvec{t}}\right)={K}_{p}{\varvec{e}}\left({\varvec{t}}\right)+{K}_{i}{\int }_{0}^{t}{\varvec{e}}\left({\varvec{t}}\right)dt+{K}_{d}\dot{{\varvec{e}}}\left({\varvec{t}}\right)$$
(15)

where \({K}_{p},{K}_{i} and {K}_{d}\) are positive definite diagonal matrices. Furthermore, \({\varvec{e}}\left({\varvec{t}}\right)={{\varvec{\theta}}}_{{\varvec{d}}}\left({\varvec{t}}\right)-{{\varvec{\theta}}}_{m}\left({\varvec{t}}\right)\) is the tracking error vector with \({{\varvec{\theta}}}_{{\varvec{d}}}\left({\varvec{t}}\right)\), \({{\varvec{\theta}}}_{{\varvec{m}}}\left({\varvec{t}}\right)\) denote the desired and the measured angular position vectors.

To find the continuous equivalent controller \({{\varvec{\tau}}}_{\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{t}}\left({\varvec{t}}\right)\), it is necessary that \(\dot{{\varvec{\sigma}}}\left({\varvec{t}}\right)=0\). Applying this, we arrive at the following equation:

$${{\varvec{\tau}}}_{\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{t}}\left({\varvec{t}}\right)=B\left({\varvec{\theta}}\right)\left[{\ddot{{\varvec{\theta}}}}_{{\varvec{d}}}\left({\varvec{t}}\right)+{K}_{d}^{-1}\left({K}_{p}\dot{{\varvec{e}}}\left({\varvec{t}}\right)+{K}_{i}{\varvec{e}}\left({\varvec{t}}\right)\right)\right]+{\varvec{f}}\left({\varvec{\theta}},\dot{{\varvec{\theta}}}\right)+\mathbf{g}\left({\varvec{\theta}}\right)$$
(16)

where we have used Eqs. (1) and (15).

The switching mode control law \({{\varvec{\tau}}}_{\mathbf{d}\mathbf{i}\mathbf{s}\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{t}}\left({\varvec{t}}\right)\) is chosen to be of the following form [43,44,45]

$${{\varvec{\tau}}}_{\mathbf{d}\mathbf{i}\mathbf{s}\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{t}}\left({\varvec{t}}\right)=B\left({\varvec{\theta}}\right) \lambda\, \mathbf{s}\mathbf{i}\mathbf{g}\mathbf{n}\,({\varvec{\sigma}}({\varvec{t}}))$$
(17)

where \(\lambda\) is a positive definite diagonal matrix and \(\mathbf{s}\mathbf{i}\mathbf{g}\mathbf{n}(\bullet )\) is the signum vector function.

To find the minimum values of the controller gains that ensures the system stability we consider the following positive definite Lyapunov function candidate:

$$V=0.5 {{\varvec{\sigma}}}^{{\varvec{T}}}B\left({\varvec{\theta}}\right)\boldsymbol{ }{\varvec{\sigma}}$$
(18)

Using Eqs. (1), (15), (16) and (17), the time derivative of \(V\) is upper bounded as follows

$$\dot{V}\le -\left({\rho }_{\mathrm{min}}\left\{{K}_{d}B\left({\varvec{\theta}}\right)\lambda \right\}-d\right)\Vert {\varvec{\sigma}}\Vert$$
(19)

where \({\rho }_{\mathrm{min}}\left\{\bullet \right\}\) is the minimum eigen value of the matrix \(\left\{\bullet \right\}\).

The structure of Eq. (19) proves that the system is globally exponentially stable, and the system reaches the sliding surface in a finite time provided that \({\rho }_{\mathrm{min}}\left\{{K}_{d}B\left({\varvec{\theta}}\right)\lambda \right\}-d>0.\)


Since the signum function causes chattering in practice, it will be replaced here with the saturated vector function \(\mathbf{tanh}\left({\varvec{\sigma}}\left({\varvec{t}}\right)/\delta \right)\), where \(\delta\) is a very small positive constant. This replacement changes the state of the system stability, and the system becomes globally ultimately bounded stable. The later causes the system states converge to the sphere defined by\(\Vert \sigma \Vert \le \delta\). Since the sliding surface is a stable system, the ultimate bound of the tracking error will be \(\Vert e\Vert \le \frac{\delta }{{\rho }_{\mathrm{min}}\left\{{K}_{p}\right\}}\). Due to the later and to improve the system performance, the elements of the diagonal matrices\({k}_{{p}_{ii}}\),\({k}_{{I}_{ii}}\),\({{k}_{d}}_{ii}\), \({\lambda }_{ii}\) and the value of \(\delta\) are to be optimized with the metaheuristic optimization algorithms.

4 The MELGWO algorithm

The gray wolf optimizer (GWO) algorithm [40] suffers from slow convergence and being trapped in local optima when applied to multi-modal optimization problems. To address these limitations, a modified version of GWO called MELGWO was proposed [41]. The modifications include a memory swarm to store the best solutions found during iterations, evolutionary operators to enhance search efficiency, stochastic local search, and Linear population size reduction technique (LPSR) into the basic GWO algorithm to improve its capabilities for both exploitation and exploration, and to maintain a better balance between the two. The following subsections describe the procedures of exploration and exploitation of the proposed algorithm, also the pseudocode is described in Algorithm (\(1\)).

4.1 Initialization and fitness evaluation

Initially, the algorithm identifies the three wolves with the lowest cost function values in the population, denoted as \({X}_{\alpha }\), \({X}_{\beta }\) and \({X}_{\delta }\), corresponding to the alpha, beta, and delta wolves, respectively. During each iteration, these three wolves are regarded as the leaders and are assumed to contain the optimal solution. All wolves randomly move toward these leaders to explore the region for the optimum. The position of each wolf (i.e., \(i=\mathrm{1,2},...,{N}_{P}\)) is updated in every iteration using Eqs. (\(20\))–(\(23\)) [40, 41], where \({N}_{\mathrm{P}}\) represents the population size.

$$X{1}_{j}={X}_{\alpha ,j}-\left[2\times \theta \times r\mathrm{and}-\theta \right]\left|2\times r\mathrm{and}\times {X}_{\alpha ,J}-{X}_{i,j}\right|$$
(20)
$$X{2}_{j}={X}_{\beta ,j}-\left[2\times \theta \times r\mathrm{and}-\theta \right]\left|2\times r\mathrm{and}\times {X}_{\beta ,J}-{X}_{i,j}\right|$$
(21)
$$X{3}_{j}={X}_{\delta ,j}-\left[2\times \theta \times r\mathrm{and}-\theta \right]\left|2\times r\mathrm{and}\times {X}_{\delta ,J}-{X}_{i,j}\right|$$
(22)
$$\theta =2\left(1-\frac{It}{I{t}_{\mathrm{max}}}\right)$$
(23)

where \(j\) represents the index for the dimensions of the problem and ranges from \(1\) to \(D\). \(\theta\) denotes a coefficient that gradually decreases from \(2\) to \(0\) as the iterations progress. The term \(rand\) represents a random number generated from a uniform distribution between \(0\) and \(1\). The calculated positions of the \(i\mathrm{th}\) wolf, \({X}_{1}\), \({X}_{2}\), and \({X}_{3}\), correspond to the directions toward the alpha, beta, and delta leaders, respectively, during the random movement. Since the \(ith\) wolf can only occupy one position, its position after the iteration is determined by taking the average of \({X}_{1}\), \({X}_{2}\), and \({X}_{3}\) [40, 41] as follows.

$${X}_{i,j}=\frac{X{1}_{j}+X{2}_{j}+X{3}_{j}}{3}$$
(24)

The value of \({X}_{i,j}\), representing the position of the ith wolf in the \(jth\) dimension, is compared with the lower and upper bounds of the \(jth\) variable. If \({X}_{i,j}\) is outside the range defined by these bounds, it is set to the corresponding limit.

4.2 Memory swarm modification

The memory swarm of wolves is designed to store the present position and corresponding cost function value of the explorer swarm wolves, including the initial best solutions (alpha, beta, and delta). The memory swarm is updated with better wolves from the explorer swarm after performing evolutionary operations.

4.3 Evolutionary operators

The incorporation of evolutionary operators into the gray wolf optimizer (GWO) algorithm’s explorer swarm can improve its search efficiency. Among the evolution-based algorithms, Differential Evolution (DE) has simple principles, few parameters, and is widely used. DE consists of three primary processes: mutation, crossover, and selection. After selecting an individual (target vector, \({X}_{j}\)), two weight variances are applied to the population to provide variation. The mutation operator is defined as listed in Eq. (\(25\)) [41]

$${V}_{j}^{(t+1)} = {X}_{j}+ F \times \left({X}_{\mathrm{alpha}} - {X}_{j}\right)$$
(25)

where \({X}_{\mathrm{alpha}}\) and \({X}_{j}\) represent the position of the best wolf and a random wolf. To ensure that wolves can evolve in a way that benefits their development, an optimal variation factor must be created. A dynamic scaling factor listed in Eq. (\(26\)) [41] is developed to increase the algorithm’s exploration ability during the initial search process, allowing it to escape local optima and strengthen the local search in later iterations.

$$F={f}_{\mathrm{min}}+\left({f}_{\mathrm{max}}-{f}_{\mathrm{min}}\right)\times \frac{I{t}_{\mathrm{max}}-\left(It-1\right)}{I{t}_{\mathrm{max}}}$$
(26)

where \({f}_{\mathrm{max}}\), \({f}_{\mathrm{min}}\), \(I{t}_{\mathrm{max}}\) and \(It\) represents the maximum and minimum values of \(F\), maximum number of iterations and current iteration number, respectively.

The target vector, \({X}_{j}\), is then crossed over with the corresponding variation vector \({V}_{j}^{(t+1)}\) to generate a test individual, \({U}_{j}^{(t+1)}\) as listed in Eq. (\(27\)) [41] where a stochastic technique is employed to ensure that at least one bit of \({U}_{j}^{(t+1)}\) is different from the variation vector, \({V}_{j}^{(t+1)}\).

$${U}_{j}^{(t+1)} =\left\{\begin{array}{cc} {V}_{j}^{(t+1)}& \mathrm{if}\, r\mathrm{and}\,(j)\le {P}_{c}\\ {X}_{j}& \mathrm{otherwise}\end{array}\right\} \mathrm{for} j=\mathrm{1,2},\dots \dots D$$
(27)

where \({V}_{j}\), \({U}_{j}\) and \({X}_{j}\) represent the variation, trial, and target vectors and \({P}_{\mathrm{c}}\) is the probability of crossover. The process of selecting between trial and target vectors involves the implementation of a greedy strategy. Once mutation and crossover have been performed, the resulting trial vector, \({U}_{j}^{(t+1)}\), is compared with the target vector, \({X}_{j}^{t}\). The superior vector is then chosen as the new solution, as illustrated in Eq. (\(28\)) [41].

$$X_{j}^{{(t + 1)}} = \left\{ {\begin{array}{*{20}c} {U_{j}^{{(t + 1)}} } & {{\text{if}}\;U_{j}^{{(t + 1)}} } & {lt;f\left( {X_{j}^{t} } \right)} \\ {X_{j}^{{(t + 1)}} = X_{j}^{t} } & {{\text{otherwise}}} & {} \\ \end{array} } \right\}{\text{for}}\; j = {\text{1}},{\text{2}}, \ldots \ldots D$$
(28)

4.4 Stochastic local search

The implementation of stochastic local search is executed in proximity to half of the wolves that have been randomly selected. For the ith wolf within the memory swarm, the local search process entails several steps. Initially, the nearest neighboring wolf is identified among all the wolves within the memory swarm, based on the Euclidean distance between their respective positions within the search space. The corresponding position of the nearest neighbor is denoted by\({X}_{n,j}\), where\(j = 1, 2, . . . , D\).

During step \(2\) of the process, a local or temporary wolf (referred to as\({X}_{t,j}\), where\(j = 1, 2, . . . , D\)) is stochastically generated based on the cost function of the nearest neighbor. If the cost function of the nearest neighbor is less than or equal to that of the current \(ith\) wolf, the temporary wolf is generated using Eq. (\(29\)) [41], which generates a new neighbor that lies between the \({i}^{th}\) wolf and its neighbor. Conversely, if the cost function of the nearest neighbor is higher than that of the \(ith\) wolf, the temporary wolf is generated using Eq. (\(30\)) [41], which generates a new neighbor that is situated away from the nearest neighbor.

$${X}_{t,j}={X}_{i,j}+{c}_{1}\times r\;\mathrm{and}\times \left({X}_{n,j}-{X}_{i,j}\right)$$
(29)
$${X}_{t,j}={X}_{i,j}+{c}_{1}\times r\;\mathrm{and}\times \left({X}_{i,j}-{X}_{n,j}\right)$$
(30)

In this study, the acceleration coefficient, denoted as \({c}_{1}\), has a fixed value of \(2\). The position of the particle, \({X}_{t,j}\), is assessed for satisfaction of the specified bounds. If any of the bounds are violated, the corresponding value of \({X}_{t,j}\) is adjusted to the violated bound.

4.5 Linear population size reduction technique

LPSR involves removing members of the wolf population by utilizing a linear equation. At iteration \(1\), the wolf population size is \({P}_{\mathrm{int}}\), while the final wolf population size is represented as \({P}_{\mathrm{min}}\). The wolf population size for the succeeding generation, \({N}_{G+1}\), is calculated using Eq. (\(31\)) [41].

$${N}_{G+1} = \mathrm{round}\left[\frac{{P}_{\mathrm{min}}-{P}_{\mathrm{int}} }{\mathrm{Max NFEs}}\right] \times \mathrm{NFE}+{P}_{\mathrm{int}}$$
(31)

In this study, \({P}_{\mathrm{min}}\) is defined as the minimum number of wolves, which is determined by the algorithm’s parameters or can be specified by the user. For this research, \({P}_{\mathrm{min}}\) is set to \(10\). The current number of function evaluations is represented by \(\mathrm{NFE}\), while the maximum number of function evaluations is denoted as \(\mathrm{Max NFEs}\).

figure a

5 Enhancing the controller performance through optimization

All of the simulations provided in this study have been run in MATLAB/SIMULINK with the ODE45 solver,listed in Eq and the simulation time is taken to be 5 s. Equations (32), (33) and (34), list the desired trajectories of the links. The integral time absolute error (ITAE) is listed in Eq. (35) served as the objective function of the tuning process. A representation of the SMC–PID optimization process is shown in Fig. 5. Table 2 lists the various parameters of the MELGWO and the other algorithms in literature have been utilized to optimize controller gains. The curves of objective function values versus iteration for MELGWO and other optimization techniques from literature study such as Particle Swarm Optimization (PSO), Golden Jackal Optimizer (GJO), Enhanced Artificial Bee Colony with Multi-elite Guidance (MELGWO), Genetic Algorithm (GA), Artificial Bee Colony (ABC), Sine Cosine Algorithm (SCA), Jellyfish Search Optimizer (JSO), Arithmetic Optimization Algorithm (AOA), Whale Optimizer Algorithm (WOA), Differential Evolution (DE), and gray wolf optimizer (GWO) are depicted in Fig. 6.

Fig. 5
figure 5

Schematic representation of the optimization process

Full size image
Table 2 The design parameters of MELGWO and the algorithms in literature
Full size table
Fig. 6
figure 6

Convergence history of the optimization process versus iteration

Full size image
$${\theta }_{d1}=\mathrm{sin}\left(2t\right)-0.1$$
(32)
$${\theta }_{d2}=\mathrm{cos}\left(2t\right)-0.1$$
(33)
$${\theta }_{d3}=\mathrm{cos}\left(2t\right)-0.1$$
(34)
$$\mathrm{ITAE }={\int }_{0}^{t}t\left|{\varvec{e}}({\varvec{t}})\right|\mathrm{d}t$$
(35)

Table 3 displays the parameters of the robotic system model’s upper and lower search spaces, together with the MELGWO optimized values. The lower bound values for the sliding surface and switching mode gains in the controller have been specifically chosen to ensure the system stability. The process of selecting these values incorporated several factors, including the physical properties of the system such as inertia and weight of each link, as well as the system dynamics, desired performance, and stability criteria. These considerations were crucial in determining the lower bounds that would guarantee the stability of the system and ensure its proper functioning.

Table 3 The search space and best parameters of the controller using MELGWO algorithm
Full size table

On the other hand, the upper bound values were selected in a more approximate manner. While these values have not been derived through a rigorous optimization process, they were carefully chosen to establish a reasonable range for the parameters without violating any operational constraints. The intent behind this selection was to encompass a broad range of feasible values that could be explored for experimentation and analysis purposes.

Table 4 presents the best, average, and worst objective function values obtained by the MELGWO optimizer in comparison to other meta-heuristic algorithms in the literature where ten separate runs of each algorithm have been performed. It is notable that the MELGWO algorithm has produced the minimum results overall runs with the lowest standard deviation with the lowest objective function values. The later finding illustrates how the MELGWO method outperforms other algorithms in the literature in terms of result superiority and robustness. Figure 7a, b, c demonstrates the trajectory tracking of each link and Fig. 7d shows the X–Y plot of end-effector. As it can be seen, the desired and actual trajectories are nearly identical. The controller exhibits superior tracking performance, as evidenced by the objective function values of links 1, 2, and 3. Which are 0.002709, 0.005522 and 0.000042, respectively.

Table 4 Objective function of MELGWO Algorithm compared with other algorithms
Full size table
Fig. 7
figure 7

Tracking trajectory curves for a link 1, b link 2, c link 3 and d \({\varvec{X}}-{\varvec{Y}}\) plot of the end-effector

Full size image

6 Comprehensive performance assessment

A robust controller must eliminate measured and unmeasured noise and disturbance and be adaptable to any uncertainties in the system [3]. Therefore, disturbance and noise rejection and adaptability to mass uncertainty in the payload have been investigated and provided in this section. Furthermore, the effect of the joint’s flexibility is also investigated.

6.1 Disturbance and noise rejection

The dynamic disturbance signal and noise, listed in Eqs. (36) and (37), are injected at the output of each controller and sensor of joint at the same time as shown in Fig. 8.

$${D}_{i}=\mathrm{per}\times {\tau }_{i}$$
(36)
$${N}_{i}=\mathrm{per}\times ({\theta }_{mi})$$
(37)

where \(i\)=1:3 and \({\tau }_{i}\), \({\theta }_{i}\) correspond to the applied torques and measured angles, respectively.

Fig. 8
figure 8

The optimized manipulator subjected to disturbance at controller output and noise at sensors

Full size image

The systems performance is checked for varying percentage \((\mathrm{per})\) values from \(\text{1\%}\) to severe conditions of \(\text{5\%}\) percentage of disturbance and noise. The corresponding objective function values of the optimized controller with MELGWO to the variation in percentage of disturbance and noise are listed in Table 5.

Table 5 OBJF variation against the percentage of disturbance and noise
Full size table

The controller has been designed to minimize the error-based OBJF, and its effectiveness is evident from the observed percentage of increase in OBJF values. This increase ranges from \(0.829\%\) under conditions of low disturbance and noise to \(43.108\%\) under conditions of severe disturbance and noise.

6.2 Adaptability to the variation in mass of payload

The primary objective of a maneuvering system is to perform the task of gripping and manipulating objects with diverse masses using its end-effector. When there is a change in the mass of the end-effector, it introduces a new configuration to the system, necessitating the need for a robust controller. The robust controller is essential to mitigate the impact of variations in the end-effector mass and ensure stable and reliable performance [3]. The mass of the payload has been incrementally increased by 0.1 kg, ranging from 0.1 to 0.5 kg, in order to evaluate the robustness of the controllers. Table provides a comprehensive list of the obtained OBJF values corresponding to the increasing payload mass (Table 6).

Table 6 OBJF variation against increasing the mass of payload
Full size table

The optimized controller utilizing the MELGWO algorithm demonstrates resilience in the face of payload mass variations. Through analysis, it is observed that the OBJF values exhibit an inflation ranging from \(1.903\%\) under low uncertainty conditions to \(27.7028\%\) under severe uncertainty conditions. This indicates that the controller maintains its performance and robustness even in challenging situations with significant uncertainties.

6.3 Effect of joint flexibility

In this section, we will examine the effectiveness of the optimized controller approach in dealing with the impact of joint flexibility. To simulate the system, we utilize the Simscape Multibody toolbox, which allows us to model the three joints as flexible elements. These joints exhibit internal mechanics characterized as listed in Table 7. This configuration enables us to analyze how the controller responds when joint flexibility is present and assess its ability to adapt to such conditions. Figure 9a, b, c shows the error in the trajectories of link 1,2 and 3, respectively, and Fig. 9d shows the X–Y plot of end-effector. It can be observed that the proposed controller demonstrates exceptional tracking performance with 0.0068, 0.0192 and 0.2162 objective function value for each link, respectively. This indicates the controller’s capability to effectively handle flexible joint manipulator (FJM), ensuring precise and smooth trajectory tracking.

Table 7 The internal mechanical properties of the FJM configuration
Full size table
Fig. 9
figure 9

The trajectory tracking curves of the FJM system: a Link 1, b Link 2, c Link 3, and d the \({\varvec{X}}-{\varvec{Y}}\) plot of the end-effector

Full size image

7 Conclusion

The optimization of a sliding mode controller with a proportional integral derivative (PID) surface has been achieved by employing an enhanced gray wolf optimizer algorithm (MELGWO). The selection of the optimal parameters of the sliding surface poses a challenge due to the vast search space, leading many existing optimization algorithms to become trapped in local optima and fail to identify the optimal parameters for the sliding surface and switching mode controller gain. The MELGWO algorithm is chosen for its exceptional exploratory and exploitative techniques, enabling it to find the best solution. The convergence analysis conducted in this study provides evidence of the MELGWO algorithm’s exceptional capability to overcome local minima through its proficient exploration and exploitation techniques. This algorithm demonstrates superiority over other algorithms mentioned in the existing literature in terms of its ability to navigate and escape from local minima solutions. The investigation focuses on disturbance and noise rejection, as well as robustness against uncertainty in payload mass. The proposed controller demonstrates the ability to mitigate the effects of disturbances and noises, maintaining the objective function (OBJF) at a minimum even in highly noisy and disturbed systems. The controller effectively minimizes the OBJF, with the percentage increase in OBJF values ranging from 0.829% under conditions of low disturbance and noise to 43.108% under conditions of severe disturbance and noise. Additionally, the optimized controller exhibits resilience to variations in payload mass analysis, with the percentage increase in OBJF values ranging from 1.903% under low uncertainty conditions to 27.7028% under severe uncertainty conditions. Furthermore, the adaptability of the controller to joint flexibility is evaluated, demonstrating superior tracking performance with minimal vibration in the movement of the end effector.