Analyses of energy loss characteristics of a low-specific speed centrifugal pump as turbines (PATs) based on entropy generation analysis model

Abstract

Low-specific speed centrifugal pump as turbines (PATs) are widely applied in fields with high head and small flow rate inlet conditions to recover excess hydraulic energy of chemical and mining industries because they are easy to produce, install, operate, and maintain. However, given their low efficiency, the energy recovery system is unsatisfactory compared with the traditional hydraulic turbine in terms of economics. To deeply reveal the energy loss characteristics of PATs, the entropy generation analysis model is adopted to visualize the high energy loss regions and quantify the energy loss in the key domains of PATs. The relationship between entropy generation and local flow characteristic is established using the regularized helical method, flow section diagnosis method, and outflow condition of impeller analysis method. Results show that the wall entropy generation rate has the greatest contribution to the irreversible hydraulic loss at the domains except for the outlet duct, and the proportion of direct entropy generation rate is remarkably smaller than those of the other components of entropy generation rate and can be ignored. The leakage flow of the front chamber wear ring greatly influences the wall entropy generation rate of the outlet duct, and the local wall entropy generation of the chamber and impeller is proportional to the velocity of its upstream inlet. In the volute, the entropy generation is primarily caused by large-scale vortices induced by the backflow, impact between fluids, and high-velocity gradients. The high values of the turbulent entropy generation rate distribution in the impeller are mainly concentrated at the inlet of the flow channel, trailing edge of the blade, mid-posterior of the pressure side, and throat of the blade. The vortex-breaking baffle could improve the uniformity of axial velocity effectively and decline the divergent flow angle to stabilize the flow in the outlet duct of PATs. The results of this study indicate that the proposed approach can improve the efficiency and stabilize the operation of PATs.

1 Introduction

Electrical energy has dramatically improved the level and quality of people’s lives in the past few decades. For example, in China, the city’s night transforms from a sea of darkness into a kingdom of colorful light. However, because of hot weather-induced water scarcity and fossil energy strain due to the Russia–Ukraine war, widespread power outages occurred in the summer of 2022 in Sichuan Province, China, and Toronto, Canada. Hence, improving energy efficiency and conservation can reduce carbon emissions and enhance the living environment of mankind [1, 2]. Excess hydraulic energy with the flow state of high head and small flow rate is prevalent in chemical and mining industries. Its pressure is decreased by pressure reducing valves for convenience in actual production, causing massive energy waste [3, 4]. The use of PATs to recover this energy could be beneficial to improve the profits of enterprises and environmental protection. However, although the low-specific speed PATs are small in size and are low cost, they have low efficiency. Therefore, many investigators attempt to reveal the reasons for the complicated inner flow characteristics and the low efficiency of PATs from various aspects in recent years.

The inner flow characteristic of PATs is closely related to their ability to recover energy, especially in negative phenomena, such as flow shock, flow deviation, backflow, and vortices, that lead to decline in hydraulic efficiency [5,6,7]. David et al. [8] adopted velocity vector analysis and CFD methods to analyze the flow behavior at the impeller inlet and outlet and then determine the energy characteristic under the best efficiency point (BEP) of PATs. They found that the outlet blade angle of the runner under the BEP is shaped. The hydraulic efficiency and operation stability of PATs are deteriorated by the larger-scale vortices of the inner flow channel. Wang et al. [9] studied the characteristics of the structure and evolution of the axial vortex in the S-blade impeller. They concluded that the hydraulic losses in the impeller were mainly caused by the large axial vortices and were much more serious in the part-load conditions. Cao et al. [10] used the synergy field analysis methods to evaluate the energy transfer performance of PATs and investigated the inherent correlation degree between pressure and velocity and the field synergy degree. The results indicated that the energy loss regions of PATs were distributed in the blade leading edge, trailing edge, and volute tongue, where the disorder synergy field distribution is strong at these locations. Compared with the traditional hydraulic turbine, the outlet duct of PATs is incapable of energy recovery. However, as the only downstream component of the impeller, the hydraulic loss in the outlet duct could reflect the flow characteristic in the impeller to a certain extent. Ghorani et al. [5] indicated that the hydraulic loss of the outlet duct increases with the increase in flow rate and is concentrated at its front due to the backflow of the impeller outlet.

Many scholars have attempted to improve the hydraulic pressure energy recovery of PATs given that their structure parameters directly affect their inner flow characteristics [11,12,13]. The cutwater geometry affects the hydraulic performance and radial force of the PATs due to the asymmetric structure of volute [14, 15]. Morabito et al. [16] designed a novel cutwater by the surrogate mode and CFD method to improve the flow characteristic near the cutwater and reduce the hydraulic loss of volute. The results showed that the new cutwater improves the turbulence kinetic energy distribution stability because of the 3.9% increase in the hydraulic efficiency of PATs under BEP and indicated that the length and the cutwater angle are the key variables that affect the inlet condition of the impeller. The impeller is the key component of PATs for energy conversion, and the relationship between the main parameters and flow characteristic of PATs should be determined. Yang et al. [17,18,19] investigated the blade numbers, impeller diameter, blade thickness, and impeller clearance effects on the hydraulic characteristic of PATs systematically. The results indicated that determining the appropriate impeller parameter according to the specific speed of PATs could achieve the optimum hydraulic performance. Wang et al. [20, 21] designed a special impeller with forward-curved blades to remarkably improve the performance of PAT compared with the conventional backward-curved blade centrifugal impellers. To reduce the flow loss in the non-flow zone, Doshi et al. [22] proposed an filling of cavity technology to reduce disk friction loss in the chamber, and results showed that the efficiency of PATs enhanced in the range of 1.3–3.6%.

The entropy generation analysis model is effective for the analysis of hydraulic loss visualization and quantification and is widely applied in the research fields of pumps, turbines, and hydrofoils, etc. [23,24,25]. Ghorani et al. [6] adopted the entropy generation theory and the Kriging surrogate model to optimize the impeller of PATs. The results showed that the optimal models can effectively prevent the negative phenomenon of blade inlet shock, vortices at the blade passage, and outlet deviation at the blade trailing edge. Xin et al. [26] conducted numerical research on the hydraulic loss of PATs under different flow rate conditions and found that the turbulence and wall entropy generation rate remarkably contributed to the energy losses. Wang et al. [27] studied the entropy production of PATs under the BEP and over-load operation conditions, and the results showed that the entropy losses in the impeller are much more than in the volute and outlet pipe. In our previous study, the feasibility of applying the PATs to the marine desulfurization system was studied, and the energy loss mechanism was revealed by the entropy production theory [28]. We found that the entropy production method can reliably calculate the irreversible energy loss of PATs, and the impeller losses account for 68.6% to 81.74% of the total energy losses with various flow rates.

Although the above references have made major progress in the research of the flow characteristic, performance improvement, and hydraulic loss characteristics of PATs. The energy loss mechanism and its relation to local flow characteristics in the low-specific speed centrifugal PATs are still not clear. And few researchers have devoted to revealing the reasons for the low effectiveness of the low-specific speed centrifugal PATs. Therefore, the energy loss characteristics of low-specific speed centrifugal PATs are quantification and visualization analyzed by the entropy generation analysis model, and the reasons for flow dissipation are revealed by local flow characteristics. The results can be given referred to improve the efficiency and stabilize the operation of PATs. The main content of this paper has been organized as follows: Sect. 2 describes the physical model and numerical methodology, Sect. 3 introduces the entropy generation analysis model, and Sect. 4 quantitative analyzes the entropy generation and presents the entropy generation rate distribution of PATs. Finally, Sect. 5 excerpts several valuable conclusions of this study.

2 Numerical method

2.1 Physical model

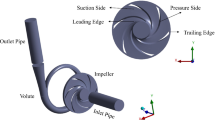
Specific speed (ns) is defined in Eq. (1); it is a dimensionless parameter used to classify the type of pumps [29]. The low-specific speed centrifugal pump has an ns from 8.33 to 66.66, and the inner flow type of the impeller is radial flow. The medium-specific speed centrifugal pump has an ns from 66.66 to 166.66, and the inner flow type of the impeller is mixed flow. The medium-specific speed centrifugal pump has an ns from 166.66 to 266.66, and the inner flow type of the impeller is axial flow [30]. The model applied in the present study is a low-specific speed centrifugal pump with an ns of 10.56. The designed flow, head, and rotating speed under the best efficiency point (BEP) of the pump are 73.8 m³/h, 138 m, and 2970 r/min, respectively. The calculated model presented in Fig. 1 comprises the inlet duct, volute, impeller, impeller clearance, front chamber, back chamber, and outlet duct. The balance hole at the impeller and the vortex-breaking baffle at the outlet duct were constructed to accurately capture the actual flow in the PATs. The main cross sections of the outlet duct and volute are drawn in Fig. 2.

Fig. 1

Calculate model of the PATs

Fig. 2

(a) Main cross sections of outlet duct and (b) Main cross sections of volute

The detailed geometric model parameters of the volute and impeller are shown in Fig. 3. The figure shows that the volute’s structure is asymmetrical from section XI–XI' to IX–IX'. Otherwise, the impeller is characterized by a relatively large diameter and narrow inlet, and the dimension ratio of D1/D2 is 3.35. Table 1 presents the main geometric parameters of the PAT.

$$ n_s = \frac{{n\sqrt {Q} }}{{H^{3/4} }} $$

(1)

where n, Q, and H are rotating speed, flow rate, and head under the BEP of pump or turbine, respectively.

Fig. 3

Geometric model of the impeller and volute: (a) geometric model of the volute and (b) geometric model of the impeller blade

Table 1 Main geometric parameters of the PATs

2.2 Governing equations and turbulence model

The mass and momentum conservation equations were used to determine the velocity and pressure distribution in the PATs and regardless of the temperature and density variation of the flow medium in the simulations. The Reynolds-averaged method is applied to the governing equations in the present study, mass conservation, and conservation of momentum are written as follows [31, 32].

Mass conservation:

$$ \frac{{\partial \overline{u}_i }}{\partial x_i } = 0 $$

(2)

Conservation of momentum:

$$ \frac{{\partial \bar{u}_i }}{{\partial t}} + \frac{\partial }{{\partial x_j }}\left( {\bar{u}_i \bar{u}_j } \right) = - \frac{1}{\rho }\frac{{\partial \bar{p}}}{{\partial x_i }} + \frac{1}{\rho }\frac{\partial }{{\partial x_j }}\left( {\mu \frac{{\partial \bar{u}_i }}{{\partial x_j }} - \rho \overline{{u^{\prime}_j u^{\prime}_j }}} \right) + f_i $$

(3)

where $x_i$ and $x_j$ are coordinate components, $f_i$ is the body force component, $\overline{u}_i$ and $\overline{u}_j$ are time-averaged velocity components in Cartesian coordinate, and $\rho$, $\overline{p}$, and $\rho \overline{u_i^{\prime} u_j^{\prime} }$ are density of flow medium, time-averaged pressure, and Reynolds stress tensor, respectively.

The flow characteristics are extremely complicated due to the high rotating speed of the impeller domain and distortion in flow channels. To better predict the precision flow characteristics and hydraulic performance of PATs, the shear stress transport (SST) k-ω turbulence model was selected to close the Reynolds-averaged governing equations under the steady calculation [33,34,35]. The SST k-ω turbulence model equations are shown in the following:

Turbulent kinetic energy equation:

$$ \frac{{\partial \left( {\rho k} \right)}}{\partial t} + \frac{{\partial \left( {\rho ku_j } \right)}}{\partial x_j } = P_k + \frac{\partial }{\partial x_j }\left[ {\left( {\mu + \frac{\mu_t }{{\sigma_{k3} }}} \right)\frac{\partial k}{{\partial x_j }}} \right] - \frac{{\rho k^{3/2} }}{{l{\,}_{k - \omega }}} $$

(4)

Turbulent frequency equation:

$$ \frac{{\partial \left( {\rho \omega } \right)}}{\partial t} + \frac{\partial }{\partial x_j }\left[ {\rho \omega u_j - \left( {\mu + \frac{\mu_t }{{\sigma_{\omega 3} }}} \right)\frac{\partial \omega }{{\partial x_j }}} \right] = \alpha_3 \frac{\omega }{k}P_k - \beta_3 \rho \omega^2 + 2\rho \left( {1 - F_1 } \right)\frac{1}{{\omega \sigma_{\omega 2} }}\frac{\partial k}{{\partial x_j }}\frac{\partial \omega }{{\partial x_j }} $$

(5)

where P_k is production term of equations, F₁ is blending functions used to switch the turbulence model between k-ω and k-ε based on the distance of a node to the nearest wall, µ is the dynamic viscosity, µ_t is the turbulence viscosity, and $\sigma_{k3}$, $\sigma_{\omega 3}$, $\alpha_3$, $\beta_3$, $\sigma_{\omega 2}$ are the model constants. $l{\,}_{k - \omega }$ in the second term on the right side of Eq. (4) is the turbulence scale, which is defined as

$$ l{\,}_{k - \omega} = k^{1/2} \omega \beta_k $$

Due to the blade with the distortion structure, for truly reflect the details of the flow inner the impeller, the correction coefficient f_r proposed by Spalart and Shur [36] considering the effects of curvature is used to modify production term the SST k-ω models.

$$ P_t = f_r \cdot P_t $$

(6)

where $f_r = \frac{2r^* }{{1 + r^* }}\left( {1 + c_{r1} } \right)\left[ {1 - c_{r3} \tan^{ - 1} \left( {c_{r2} \tilde{r}} \right)} \right] - c_{r1}$. c_r1, c_r2, c_r3 are constant which is equal to 1, 2, 1, respectively, and $\tilde{r}$ and $r^\ast$ are functions of the strain rate and system rotation.

2.3 Numerical schemes and boundary conditions

The 3D steady-state incompressible simulation of PATs under the flow rates from 60 m³/h to 200 m³/h conditions is performed in the ANSYS CFX 2022 R2. The grid frame change models of the static domain connecting to the static domain and rotating domain are set to none and froze frozen rotor with the General Grid Interface (GGI) mesh connection method, respectively. All the walls are set to adiabatic and no-slip walls with the sand grain roughness being 50 μm. All the flow domains are set to stationary domains except the impeller. The rotating speed of the impeller is 2985 rpm, and multiple frames of reference are adopted in the simulation. The fluid energy transport medium is pure water with a density and temperature which are 998.2 kg/m³ and 25 °C, respectively. The high-resolution advection scheme and implicit second-order backward Euler scheme are applied to the discretization of convective terms and time discretization of the momentum equations, respectively. Mass flow rate condition lies in the position of the inlet with a medium turbulence intensity of 5%, the total pressure boundary set as the outlet with the values of 101,325 Pa. By changing the mass flow rate of the inlet, the flow characteristics and hydraulic performance of PATs under different operation conditions will be obtained. The convergence criterion of continuity and momentum equations is the root mean square (RMS) below 10^–5.

2.4 Mesh generation and sensitivity analysis

Figure 4 shows the calculation mesh information of PATs main flow domains. Due to the complex model having the special asymmetrical structure of volute and distorted flow channel of the impeller, the volume of the domain is dissected by the unstructured type of mesh as its better grid adaptability [28, 37]. For precious capture of the detailed flow characteristics near the wall and to meet the values of the y + requirement of the turbulence model, the methodology of local mesh refinement is adopted to build the boundary layer. Nine different numbers of grids were created through an identical meshing method and the node number increased from 1.63 × 10⁶ to 7.01 × 10⁶. Select the head of PATs under the BEP condition as the criterion of grid independence, Fig. 5 plots the variation curves of the head with the number of grid nodes increased. It is indicated that when the grid number is larger than 5.31 × 10⁶, the head fluctuation of the PATs is not more than 0.5%. Considering the numerical accuracy and the ability of computational resources, the grid number of 6.14 × 10⁶ is preliminarily selected.

Fig. 4

Mesh detailed information: (a) Front chamber (b) Back chamber (c) Outlet duct (d) Volute (e) Impeller

Fig. 5

Grid independence verification

To further verify the grid independence, the grid convergence index (GCI) method is based on the Richardson extrapolation method, which was proposed by Roache [38] and recommended by the Fluids Engineering Division of the American Society of Mechanical Engineers [39]. Three groups of mesh (N₁, N₂, N₃) were used to check the grid independence, and the number of nodes is 6.35 × 10⁶, 3.84 × 10⁶, and 1.63 × 10⁶, respectively. The head and torque of PATs under the BEP condition are chosen to evaluate the grid error parameters. Table 2 presents the discretization errors of mesh cases. The discretization error of the mesh shows that the approximate relative error ($e_a^{21}$), extrapolated relative error ($e_{{\text{ext}}}^{21}$), and fine-grid convergence index (${\text{GCI}}_{{\text{fine}}}^{21}$) of head and torque are below 1%, which indicated that the mesh group of N₁ could ensure the accuracy of the calculation. Finally, the mesh group with 6.14 × 10⁶ nodes is selected for the simulation research in the present study. The mesh information for each domain is shown in Table 3.

Table 2 Computed discretization errors in head and torque

Table 3 Mesh information for each domain

2.5 Validation of numerical results

The hydraulic performance test of PATs is conducted at Ebara Great Pumps Co., Ltd., to verify the accuracy of the head and efficiency predicted by numerical methods. Figure 6a shows the hydraulic performance test system of PATs, which comprises the water tank, control valve, feed pump, data acquisition, processing system, pressure transducer, electromagnetic flowmeter, electric eddy current dynamometer (ECD), PATs, and connecting pipe. Figure 6b presents the physical model of PATs. The feed pump provides the hydraulic energy to drive PATs to work, and the ECD consumes the mechanical energy produced from the PATs. The ECD is directly connected to the PATs by the flexible coupling with the coaxiality error below 0.1 mm, and the real-time data of rotating speed and torque are stored in its supporting software. Through coordinated regulation of the ECD, control valve at the mainstream, and bypass pipe, the hydraulic performance of PATs under the different operating conditions is obtained. The uncertainty of the pressure transducer, electromagnetic flowmeter, torque, and rotating speed sensor is ± 0.2%, ± 0.1%, and ± 0.05%, respectively. The head and efficiency of PATs are calculated as follows [40].

$$ H = \left( {z_1 + \frac{p_1 }{{\rho g}} + \frac{v_1^2 }{{2g}}} \right) - \left( {z_2 + \frac{p_2 }{{\rho g}} + \frac{v_2^2 }{{2g}}} \right) $$

(7)

$$ \eta = \frac{\pi nT}{{30\rho gQH}} \times 100\% $$

(8)

where T is the torque of PATs, and z, p, and v are the vertical height, manometer pressure, and average velocity of cross section, respectively. The subscripts 1 and 2 represent inlet and outlet.

Fig. 6

Performance test of the PATs: (a) Hydraulic performance test system and (b) PATs

Figure 7 depicts the comparison between the head and efficiency and flow rate curve of PATs using CFD and experiment method. The variation of head and efficiency with the flow rate is consistent in these methods. As the flow rate increases, the head continually increases, whereas the efficiency increases initially and then decreased. The highest efficiency of PATs is reached at the flow rate of 160 m³/h. Under this operating condition, the head and efficiency predicted by the CFD method are 298.05 m and 70.47%, respectively. The maximum prediction error of the head is 5.05%, and the minimum error is 1.80%. The maximum and minimum prediction errors of efficiency are 5.58 and 2.88%, respectively. The maximum prediction error is located at the small flow condition (60 m³/h), and the minimum prediction error appears near the BEP. The finding indicates that the accuracy of the numerical calculation is closely related to the inner flow characteristics of PATs. Instability flow characteristics indicate poor prediction accuracy. However, the CFD prediction results are within the 6% error bar of the experiment data under all operating conditions. Therefore, the numerical simulation strategies adopted in the present study are dependable.

Fig. 7

Hydraulic performance characteristics comparison between CFD and experiment

3 Entropy generation analysis model

Compared to the traditional hydraulic turbines, the limitation of low-specific speed centrifugal pump as turbines is low efficiency thanks to their lack of inlet guide devices. Large irreversible hydraulic loss is the primary reason for the low efficiency of PATs, which comes from the flow dissipation and frictional effects of the wall. To deeply despite the energy loss mechanisms of PATs, the entropy generation method is applied to quantitative and visualization analysis of the high energy loss regions within key components in the present research. Specific entropy as a kind of state parameter, its transportation equation in Cartesian coordinates without regard to the heat transfer and compressible effect as follows [23].

$$ \rho \left( {\frac{\partial s}{{\partial t}} + u\frac{\partial s}{{\partial x}} + v\frac{\partial s}{{\partial y}} + w\frac{\partial s}{{\partial z}}} \right) = div\left( {\frac{{\mathop{q}\limits^{\rightharpoonup} }}{T}} \right) + \frac{\Phi }{T} + \frac{\Phi_\Theta }{{T^2 }} $$

(9)

where s, T, and $\mathop{q}\limits^{\rightharpoonup}$ are the specific entropy, temperature, and heat flow density vector, respectively.

The second term on the right side of Eq. (9) expresses as the specific entropy generation rate, which is caused by viscous dissipation and always positive, and it can be expressed as follows.

$$ \frac{\Phi }{T} = \frac{2\mu }{T}\left[ {\left( {\frac{\partial u}{{\partial x}}} \right)^2 + \left( {\frac{\partial v}{{\partial y}}} \right)^2 + \left( {\frac{\partial w}{{\partial z}}} \right)^2 } \right] + \frac{\mu }{T}\left[ {\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)^2 + \left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}}} \right)^2 + \left( {\frac{\partial v}{{\partial z}} + \frac{\partial w}{{\partial y}}} \right)^2 } \right] $$

(10)

The third term on the right side of Eq. (9) is caused by a heat transfer with finite temperature gradient, and it can be expressed as follows.

$$ \frac{\Phi_\Theta }{{T^2 }} = \frac{\lambda }{T^2 }\left[ {\left( {\frac{\partial T}{{\partial x}}} \right)^2 + \left( {\frac{\partial T}{{\partial y}}} \right)^2 + \left( {\frac{\partial T}{{\partial z}}} \right)^2 } \right] $$

(11)

Because the variation of temperature is not considered in the simulation, the dissipation caused by Eq. (11) can be ignored. Therefore, Eq. (9) can be simplified as follows.

$$ \rho \left( {\frac{\partial s}{{\partial t}} + u\frac{\partial s}{{\partial x}} + v\frac{\partial s}{{\partial y}} + w\frac{\partial s}{{\partial z}}} \right) = div\left( {\frac{{\mathop{q}\limits^{\rightharpoonup} }}{T}} \right) + \frac{\Phi }{T} $$

(12)

The flow inner the PATs are highly turbulent, thus the local entropy generation rate (LEGR) can be separated into two parts: One is direct entropy generation rate (DEGR) caused by time-averaged movement dissipation, and the other is turbulent entropy generation rate (TEGR) induced by velocity fluctuation.

LEGR can be defined as follows.

$$ \dot{s}_D = \dot{s}_{\overline{D}} + \dot{s}_{D^{\prime}} $$

(13)

in which

$$ \dot{s}_{\overline{D}} = \frac{2\mu }{T}\left[ {\left( {\frac{{\partial \overline{u}}}{\partial x}} \right)^2 + \left( {\frac{{\partial \overline{v}}}{\partial y}} \right)^2 + \left( {\frac{{\partial \overline{w}}}{\partial z}} \right)^2 } \right] + \frac{\mu }{T}\left[ {\left( {\frac{{\partial \overline{u}}}{\partial y} + \frac{{\partial \overline{v}}}{\partial x}} \right)^2 + \left( {\frac{{\partial \overline{u}}}{\partial z} + \frac{{\partial \overline{w}}}{\partial x}} \right)^2 + \left( {\frac{{\partial \overline{v}}}{\partial z} + \frac{{\partial \overline{w}}}{\partial y}} \right)^2 } \right] $$

(14)

$$ \dot{s}_{D^{\prime}} = \frac{{2\mu_{{\text{eff}}} }}{T}\left[ {\left( {\frac{{\partial u^{\prime}}}{\partial x}} \right)^2 + \left( {\frac{{\partial v^{\prime}}}{\partial y}} \right)^2 + \left( {\frac{{\partial w^{\prime}}}{\partial z}} \right)^2 } \right] + \frac{{\mu_{{\text{eff}}} }}{T}\left[ {\left( {\frac{{\partial u^{\prime}}}{\partial y} + \frac{{\partial v^{\prime}}}{\partial x}} \right)^2 + \left( {\frac{{\partial u^{\prime}}}{\partial z} + \frac{{\partial w^{\prime}}}{\partial x}} \right)^2 + \left( {\frac{{\partial v^{\prime}}}{\partial z} + \frac{{\partial w^{\prime}}}{\partial y}} \right)^2 } \right] $$

(15)

where $\dot{s}_D$,$\dot{s}_{\overline{D}}$, and $\dot{s}_{D^{\prime} }$ are local entropy generation rate, direct entropy generation rate, and turbulent entropy generation rate, respectively.$\mu$ is the dynamic viscosity, and $\mu_{{\text{eff}}}$ is effective dynamic viscosity.

Because the component of velocity fluctuation cannot be obtained by the Reynolds-averaged method, it is closely related to the turbulence model. Therefore, Kock et al. [41] and Mathieu et al. [42] proposed that the turbulent entropy generation rate is proportional to the turbulent eddy frequency(ω) and turbulent kinetic energy(k) but inversely proportional to the mean temperature(T) in the SST k-ω turbulence model.

Thus, the $\dot{s}_{D^{\prime} }$ can be calculated in the present study as follows.

$$ \dot{s}_{D^{\prime}} = \frac{0.09\rho \omega k}{T} $$

(16)

In addition, to the large velocity gradient and pressure gradient near the wall, the frictional effects between fluid and wall cannot be ignored in the irreversible flow loss evaluation of PATs. The wall entropy generation rate (WEGR) is proposed to quantitative analysis of the energy loss of PATs and diagnosis of its area distribution.

WEGR can be described as follows.

$$ \dot{s}_W = \frac{{\vec{\tau } \cdot \vec{v}}}{T} $$

(17)

where $\vec{\tau }$ is the shear stress of wall, and $\vec{v}$ is the velocity at the center of first grid node to the wall.

The total entropy generation $s_D$ can be calculated as follows.

$$ s_D = s_{\overline{D}} + s_{D^{\prime}} + s_W $$

(18)

in which

$$ s_{\overline{D}} = \int_V {\frac{2\mu }{T}\left[ {\left( {\frac{{\partial \overline{u}}}{\partial x}} \right)^2 + \left( {\frac{{\partial \overline{v}}}{\partial y}} \right)^2 + \left( {\frac{{\partial \overline{w}}}{\partial z}} \right)^2 } \right] + \frac{\mu }{T}\left[ {\left( {\frac{{\partial \overline{u}}}{\partial y} + \frac{{\partial \overline{v}}}{\partial x}} \right)^2 + \left( {\frac{{\partial \overline{u}}}{\partial z} + \frac{{\partial \overline{w}}}{\partial x}} \right)^2 + \left( {\frac{{\partial \overline{v}}}{\partial z} + \frac{{\partial \overline{w}}}{\partial y}} \right)^2 } \right]} dV $$

(19)

$$ s_{D^{\prime}} = \int_V {\frac{0.09\rho \omega k}{T}} dV $$

(20)

$$ s_W = \int_A {\frac{{\vec{\tau } \cdot \vec{v}}}{T}dA} $$

(21)

where $s_{\overline{D}}$, $s_{D^{\prime} },$ and $s_W$ are the direct entropy generation (SDEG), turbulent entropy generation (STEG), and wall entropy generation (SWEG), respectively.

4 Results and discussion

4.1 Entropy generation quantitative analysis in PATs

Figure 8a presents the total entropy generation of the main flow domain. As shown in Fig. 8a, the entropy generation is concentrated in the volute, mainly at the back and front chambers. As the flow rate increases, the total entropy generation of all domains of PATs is increased. However, when the flow rate is larger than 0.825 Q_b, the volute becomes the largest proportion of entropy generation in the PATs. Under the Q_b, the total entropy proportion of the domains in the PATs, from largest to smallest, is as follows: volute, front chamber, back chamber, impeller, outlet duct, impeller clearance, and inlet duct. Therefore, in the non-flow zones (such as front chamber and back chamber), the flow energy dissipation in the chamber should be considered, especially in the study of hydraulic energy loss and performance improvement of low-specific speed PATs.

Fig. 8

Entropy generation quantitative analysis: (a) Total entropy generation of main flow domain versus flow rates, (b) The proportion of entropy generation in domains of PAT under BEP, (c) Proportion of entropy generation for each component under different flow rate

The proportion of entropy generation in PAT domains under BEP is shown in Fig. 8b. Two conclusions could be drawn from the distribution of entropy generation components. First, the SWEG has the greatest contribution to the irreversible hydraulic loss in all PAT domains except the outlet duct. Second, the proportion of SDEG is remarkably smaller than the other components and can be ignored. The proportion of SWEG in the inlet duct, volute, impeller clearance, and back and front chamber is more than 80%. By contrast, the proportion of SWEG in the impeller and outlet duct declines, whereas the proportional of STEG is increased. Therefore, the proportion of entropy generation component is directly related to the local inner flow characteristic of PAT domain. When the flow in the channel is more stable, the proportion of SWEG is high and that of STEG is low.

Figure 8c illustrates the proportion of entropy generation for each component of PATs under different flow rates. The figure shows that the proportion of entropy generation of PATs is more than 77% under the all operation conditions. The proportion of entropy generation almost has no changes with the increase in flow rate, and the SWEG with relatively low values appears near the BEP. Compared with traditional hydraulic turbines or middle and high-specific speed pump, the high proportion of SWEG is the primary factor that reduces the inefficiency of specific speed PATs.

4.2 Wall entropy generation distribution in PATs

The entropy generation quantitative analysis results indicated that the proportion of SWEG contributes most to the irreversible flow dissipation in the low-specific speed PATs. The comparison of WEGR on the walls of PATs under different operation conditions is presented in Fig. 9, thereby revealing the reasons for the high proportion of SWEG and visualization on the wall of the main domains of PATs. The distribution of WEGR on the wall of different domains does not change with the variation of flow rate. The values of WEGR increased with the increase in flow rate. The high WEGR is evident in five locations: the partial outer diameters of the back and front chamber, the flow channel of the impeller approaching the tongue of the volute, the asymmetrical position and small area flow section of the volute, and the outlet duct wall near the inlet. The leakage flow of the front chamber wear ring greatly influences the WEGR of the outlet duct.

Fig. 9

WEGR on the walls of PATs main domain under different operation conditions

The average velocity on the interface of the main domains of PATs is plotted in Fig. 10 inspired by Eq. (17), further revealing the formation mechanism of WEGR. As shown in Fig. 10, the angle of circumferential direction is 0°, which indicates the position that coincides with the x-axis of the global coordinates; 90° represents the y-axis of the global coordinates. Overall, the variation rules of the average velocity on the interface of the present attention are essentially consistent, and the average velocity increases with increasing flow rate. For the inlet of the back and front chamber, the average velocity with certain fluctuations on the circumferential direction and the number of wave peaks is equal to the number of the blade. The peak values of the average velocity are between section IX-IX' and plane 7, and the lowest values are located near the tongue of the volute. Figures 9 and 10a, b indicate that the local EWGR of the chamber is proportional to the velocity of its upstream inlet. For the outlet of the volute, when the sectional area of flow declines, the fluctuation magnitude and peak values of the average velocity decrease. As shown in Fig. 10d, the average velocity of the inlet flow channel near the tongue of the volute and its adjacent channel counterclockwise are larger than those of the others. The thickness of the blade leading edge reached approximately 6° in the circumference direction. With the block effect of the leading edge of the blade, the average velocity decreased sharply. Figure 10a, b and d shows that in the tongue position (the angle of circumferential direction is approximately 95° to 120°), the minimum velocity appears in front, and the back chamber inlet does not appear on the impeller inlet. Thus, the effect of tongue position on the average velocity of the interface is large for the inlet of the front and back chamber but relatively small for the inlet of impeller.

Fig. 10

Average velocity on the interface of domains: (a) Front chamber inlet, (b) Back chamber inlet, (c) Volute outlet, (d) Impeller inlet

4.3 Entropy generation rate distribution in volute

Compared with the STEG, the SDEG slightly contributes to the hydraulic energy loss in low-specific speed PATs and can be omitted. Therefore, only the STEG can be selected to visualize the distribution of local entropy generation in the domains. Figure 11 shows the TEGR distribution and streamline diagrams of the volute section under different flow rates. The high values of TEGR are mainly concentrated near the volute wall due to the high-velocity gradients and viscosity. With the increase in flow rates, the velocity gradient near the wall further increased the STEG. The distribution of TEGR is asymmetrical from Plane 3 to Plane 7, especially under the BEP condition, which may be caused by the asymmetric structure of volute sections from XI–XI' to IX–IX'. Figures 9 and 11 indicate that although the magnitude of WEGR is lower than that of the TEGR, its high value distribution is more than that of TEGR. As a result, SWEG becomes the largest contribution to flow energy dissipation in the PATs.

Fig. 11

TEGR distribution and streamline inner the volute section

From the views of the distribution of streamlines in the volute section, the asymmetric of the vortex with different scales appeared from Plane 3 to Plane 7. With the increase in flow rate, the asymmetric of the vortex worsened especially inner Plane 7. The outlet backflow appears from Plane 3 to Plane 6, leading to the formation of a vortex. Furthermore, the asymmetric structure of the volute may intensify the form asymmetric of the vortex. Although the backflow occurs at the outlet of Plane 1, the vortex fails to form given the space limitation of the section.

To deeply research the vortex pattern and rotational characteristics inner the volute, the regularized helical method is adopted to extract the vortex core by regularized helical (Hn). The regularized helical method was proposed by Levy [43], and it can describe the motion and distribution of primary vortex and secondary flow accurately. The regularized helical is defined as follows:

$$ {\rm H}{\text{n = }}\frac{v \cdot \omega }{{\left| v \right|\left| \omega \right|}} $$

(22)

where the v and ω are the vector of velocity and vorticity, respectively. At the vortex core, the direction of velocity and vorticity is parallel, so the value of Hn tends to ± 1.

Q_b operation condition is selected to study the motion and distribution characteristic of the vortex given that the vortex pattern in the volute under different flow rates is consistent. Figure 12 shows the Hn diagrams of the volute section under BEP. The judgment method of vortex rotation direction is presented in Fig. 11. The method consists of the following steps: first, the flow direction is set as the positive direction; second, the values of Hn are calculated. When the value is negative the direction vortex rotation is clockwise; otherwise, the direction of the vortex rotation is counterclockwise. Based on the distribution of Hn, the streamlined schematic is drawn in each section of the volute. Figures 11b and 12 show that the main vortex characteristics depicted by the streamlines are the same as that extracted by CFX-POST. In addition, the outlet backflow characteristic at the partial sections of the volute is clearly reflected. Therefore, the regularized helical method can effectively describe the motion of a vortex and reflect the main flow characteristic of the vortex.

Fig. 12

Hn distribution and streamlines schematic diagram of the volute section under Q_b operation condition

The TEGR distribution on the x–y plane of the volute and vortex structures under different flow rates is shown in Fig. 13, exhibiting the relationship between the spatial structure of vortex and entropy generation. The distribution of high values of TEGR on the x–y plane of the volute is concentrated near the tongue and its downstream. With the increase in flow rate, the TEGR values of the small area in the inner flow cross section increase. The vortex identification method of Q criteria is applied to extract the large-scale vortex. In general, the vortex pattern and distribution position are the same as the flow rate increased. The vortex in the volute is mainly located downstream of the tongue, the surface of Plane 7 to Plane 1, and the surface of IX-IX' to Plane 8. In the downstream of the tongue, the vortex pattern is a horseshoe vortex, which is generated by the intersection between the circulation flow of the volute and the main flow from the inlet. The asymmetric structure of the volute sections induces the vortex to appear on its surface and which type is attached vortex. Figures 12 and 13 show that the wall shear vortex near Plane 7 to Plane 1 is the result of comprehensive effects from backflow, high-velocity gradients, and viscous effect. Therefore, the large-scale vortices induced by backflow, impact between fluids, and high-velocity gradients are the primary contribution to entropy generation in the volute.

Fig. 13

TEGR distribution and vortex structures inner the volute

4.4 Entropy generation rate distribution in impeller

The impeller is the unique component to output the recovered energy, and the entropy generation and flow characteristics are worthy of an in depth research. Figure 14 shows the TEGR distribution in the different spans of the impeller under different flow rates. The high values of TEGR are concentrated at the inlet of the flow channel, trailing edge of the blade, mid-posterior of the pressure side, and throat of the blade. As the flow rate increases, the distribution of TEGR in the different spans exhibits no significant changes. The leakage flow from the balance holes shocks the main flow in the impeller flow channel and significantly increases the local TEGR. The influence of leakage flow to the TEGR declines with the span away from the impeller hub. Compared with the different flow channels of the impeller, the distribution of TEGR is different even though the structure of the impeller is axial symmetry. The TEGR intensity becomes greater when the flow channel of the impeller is closer to the position of the tongue. Figures 12 and 13 show that the generation mechanism of TEGR may be inferred as follows: The inlet backflow induced the TEGR generation at the inlet of the impeller, the high-velocity gradients near the blade increased the local TGER, and the flow shock and confluence led to the high values at the trailing edge of the blade.

Fig. 14

TEGR distribution in the different span of impeller

To reveals the mechanism for energy conversion of the impeller, the flow section diagnosis method is applied in the present research to depict the process of energy variation in the impeller flow channel. The flow section diagnosis method is from the perspective of vortex dynamics to evaluate the pros and cons of flow characteristics [44]. The method of flow section diagnoses as follows.

Integral form of fluid momentum equation is

$$ \int_V {\rho t\frac{Du}{{Dt}}d} V = \int_V {\rho tfd} V + \oint {\tau dS} $$

(23)

where V is the control volume, u is the vector of velocity, f is body force, S is the area of control volume, and τ is the function of spatial variable, time variation (t), and direction of face element (n), that is, $\tau = \tau \left( {x,y,z} \right)$.

According to the Gauss’s law and point multiplication the vector of velocity at the two sides of Eq. (23), Eq. (23) is written as follows.

$$ \rho \frac{D}{Dt}\left( {\frac{1}{2}\left\| u \right\|^2 } \right) = \rho tf \cdot u + p\nabla \cdot u + \Delta \cdot \left( {T \cdot u} \right) - \Phi $$

(24)

where T is the second-order tensor, and $\Phi$ is the entropy generation rate.

Considering the symmetry of T and the inertia force is much larger than viscous force in the impeller under high Re condition, according to the Reynolds transport theorem, Eq. (24) is simplified as follows.

$$ \Omega M_z = \frac{\partial K}{{\partial t}} + G + P + D $$

(25)

where $\Omega M_z$ is the axial power applied by fluid to impeller, K is the total kinetic energy, and P and D are the compression power and dissipation power of whole control volume, respectively. G represents the process of energy decline after the fluid flow through the impeller channel.

in which

$$ P = \int_V {p\Delta \cdot udV} $$

(26)

$$ D = \mu \int_V {\Phi dV} $$

(27)

$$ G = \int_W {p^* } u_l dS - p_\infty^* US_{out} $$

(28)

where W is the flow section, $u_l$ is the velocity follow with the direction of streamline, U is the axial velocity, and $S_{out}$ is the outlet section area of impeller. $p^*$ and $p_\infty^*$ are defined as follows:

$$ p^* = p + \frac{1}{2}t\left\| u \right\|^2 $$

(29)

$$ p_\infty^* = p_\infty + \frac{1}{2}t\left\| u \right\|^2 $$

(30)

where $p_\infty$ represents the static pressure and defines the $P_{\text{u}} = \int_W {p^* } u_l dS$.

Figure 15 shows the P_u and distribution of $p^* u_l$ in a different streamwise location of the impeller versus the flow rate. Locations 1 to 4 represent the streamwise position of 0, 0.25, 0.5, and 0.82, respectively. The high values of $p^* u_l$ are concentrated near the suction side of the blade on the inlet section, with the flow section location away from the inlet of the impeller, and the values of $p^* u_l$ appeared close to the pressure side of the blade. The variation rules of the distribution of $p^* u_l$ on the different flow sections are unchanged contrary to the flow rate. Compared with part-load and over-load operation conditions, the variation of $p^* u_l$ on the flow section is relatively gentle under the BEP. Therefore, the key region of recovering hydraulic energy in the impeller channel is close to the suction side when the range of inlet to streamwise is 0.25, and near the pressure side when the range of streamwise to the outlet is 0.25. The variation of P_u from the inlet to the outlet of the flow channel of the impeller is plotted in Fig. 15d. The value of P_u is large with the increase in the flow rate. With the section located away from the inlet of the impeller, the total energy of the fluid declines monotonically, reflecting the process of hydraulic energy transformation to mechanical energy and irreversible energy dissipation.

Fig. 15

P_u and distribution of $p^* u_l$ in different streamwise locations of impeller

4.5 Entropy generation rate distribution in outlet duct

The outlet duct of PATs with the gradual contractile structure is not beneficial to energy recovery compared with the traditional turbine draft tube, which has a gradual expansion structure. In addition, the vortex-breaking baffle in the outlet duct prevents cavitation under the pump’s condition, and the effect on the energy dissipation and flow characteristic under the PATs condition should also be considered. Figure 16 shows the TEGR distribution in the different section planes under different flow rates. The position of the section plane is illustrated in Fig. 2b. Plane A is located at the impeller outlet, and Planes B and C are situated at the upstream and downstream of the baffle, respectively. As shown in Fig. 16, the high values of TEGR in Plane A are mainly concentrated at the outlet of the impeller channels under the part-load and BEP conditions, but are near the wall of the hub and shroud of the impeller under the over-load condition. In the upstream and downstream planes of the baffle, the peak regions of the TEGR distribution are near the wall of the outlet duct and the right-hand side of the baffle, respectively. The dissipation of TEGR in the different planes indicated that the baffle slightly affects the entropy generation of its upstream but greatly influences its downstream. The influence of the baffle on entropy generation in the plane decreases as the distance of the plane from the baffle increases.

Fig. 16

TEGR distribution in the different section plane

To investigate the relationship between TEGR and the local flow characteristic, the distribution of circumferential velocity and velocity vector in the different section planes under different flow rates is studied, and the results are shown in Fig. 17. The vortex with counterclockwise generated by the backflow of the impeller outlet appears in the Plane A, and its number is equal to the blade under the part-load condition. As the flow rate increases, the vortex in Plane A disappears, and the direction of circumferential velocity changes contrary to the rotation of the impeller. A similar phenomenon was observed in references [8] and [45]. Affected by the leakage flow which has high circumferential velocity from the front chamber, the direction near the wall velocity vector of Plane B and its downstream are consistent. The baffle effectively restricts the further development of circumferential velocity in the outlet duct and generated a large-scale vortex near the wall of the baffle. Figures 16 and 17 show that the leakage flow from the front chamber shocks the main flow in the outlet duct, and the high-velocity gradient near the wall and boundary of large-scale vortices and the vortex-breaking effect of the baffle mainly increase the local TEGR. As the baffle could effectively decline the TEGR at its downstream, its position and structure are worthy of an in depth research in the future to stabilize the flow in the outlet duct and improve the efficiency of PATs.

Fig. 17

Distribution of circumferential velocity and velocity vector in the different section plane

The velocity distribution in the outlet duct is non-uniform and with the high-velocity component of circumferential, which causes to generate the large-scales vortex and hydraulic loss. In order to further understand the flow characteristic at the downstream of the impeller, the velocity distribution uniformity ($\overline{\eta }$) and velocity-weighted average swirl angle ($\overline{\theta }$) are adopted for quantitative analysis of the velocity characteristic in different section planes. The velocity distribution uniformity could reflect the outflow condition of the impeller. The values of $\overline{\eta }$ are higher, and the velocity distribution in the section is more uniform. The $\overline{\eta }$ is defined as follows [37].

$$ \overline{\eta } = \left[ {1 - \frac{1}{{\overline{v}_a }}\sqrt {{\sum_{i = 1}^n {\left( {v_{ai} - \overline{v}_a } \right)^2 /n} }} } \right] \times 100 $$

(31)

where $\overline{v}_a$, $v_{ai}$, and n are the arithmetic average of axial velocity in the section plane, the axial velocity on each compute element, and the number of compute elements in the section plane.

Figure 18a plots the axial velocity uniformity in the different section planes versus the flow rate. With the plane away from the impeller outlet, the values of $\overline{\eta }$ are closer to 100. According to the definition of $\overline{\eta }$ and its negative value in Plane A indicated that the backflow flow occupied large areas on the impeller outlet, especially under the 0.71Q_b with the value is -148.16%. The vortex-breaking baffle in the outlet duct could improve the uniform of axial velocity effectively under all operating conditions of PATs. The axial velocity uniformity in the section of baffle downstream without a significant difference as the flow rate increases. The values of $\overline{\eta }$ in plane D under the 0.71Q_b, Q_b, and 1.25Q_b are 79.79%, 73.41%, and 64.64%, respectively.

Fig. 18

Axial velocity uniformity and velocity-weighted average swirl angle in the different section plane

The definition of divergent flow angle θ is the angle between axial velocity with the actual flow, which represents the influence of traverse velocity on the outflow condition of the impeller [46]. The smaller the values of θ, the better flow characteristic of the impeller outlet. The velocity weighted average divergent flow angle $\overline{\theta }$ is defined as follows.

$$ \overline{\theta } = \left( {\sum_{i = 1}^n {v_{ai} \arctan \frac{{v_{ti} }}{{v_{ai} }}} } \right)/\sum_{i = 1}^n {v_{ai} } $$

(32)

where $v_{ti}$ represents the traverse velocity on each compute element.

The velocity-weighted average swirl angle in the different section planes versus the flow rate is illustrated in Fig. 18b. In the Plane A, the values of $\overline{\theta }$ under all operation conditions of PATs are negative, which indicated that the velocity component of clockwise circumferential is occupied most of plane. With the plane position away from the impeller outlet, the values of $\overline{\theta }$ increase firstly and then decline. The values of $\overline{\theta }$ in the section of impeller downstream are negative under the 1.25Q_b, and the minimum values of it appear in Plane C. Similar results are also illustrated in Fig. 17 that the clockwise velocity vector is dominant in different planes. Under the Q_b, the $\overline{\theta }$ in the plane section of the outlet duct is relatively small with the values of 6.84%, 3.49%, and −4.39% in Plane B, Plane C, and Plane D, respectively. From the variation of $\overline{\theta }$ in different planes, it can be concluded that the vortex-breaking baffle could decline the divergent flow angle to stabilize the flow in the outlet duct of PATs.

5 Conclusion

The hydraulic energy loss characteristics of a low-specific speed centrifugal PAT have been investigated based on the entropy generation approaches by the numerical method. The total entropy generation of the main flow domains and the proportion of entropy generation in the PATs versus flow rates have been quantitatively analyzed. The regularized helical method, flow section diagnose method, and outflow condition of the impeller analysis method can effectively reveal the relationship between entropy generation and local flow characteristics in detail. The major conclusions can be summarized as follows:

• (1) In the low-specific speed centrifugal PATs, the SWEG has the greatest contribution to the irreversible hydraulic loss at the domains except for the outlet duct. The proportion of SDEG is remarkably smaller than the other components of entropy generation rate and can be ignored.

• (2) The local EWGR of the chamber and impeller is proportional to the velocity of its upstream inlet. The tongue position effect on the average velocity of the interface is large for the inlet of the front and back chamber but relatively small for the inlet of the impeller.

• (3) The regularized helical method can effectively describe the motion of the vortex and reflect the main flow characteristic of the vortex in the volute of PATs. The large-scale vortices induced by backflow, impact between fluids, and high-velocity gradients are the primary contributions to entropy generation in the volute.

• (4) The key region of recovering hydraulic energy in the impeller channel of low-specific speed PATs is close to the suction side when the range of inlet to streamwise is 0.25, and near the pressure side when the range of streamwise to the outlet is 0.25.

In summary, this study fills the gap of investigating the energy loss and flow characteristics of a low-specific speed centrifugal PAT with the features of the asymmetric volute structure, large volume chambers, and vortex-breaking baffle in the outlet duct. The reasons for the low efficiency of low-specific speed PATs have been revealed in this study, and the following research fields are recommend for further study to improve the efficiency and operation stability of PATs: (i) application of the filling technology or flow guide device to control the flow rate of the non-flow zone (such as the back chamber and front chamber); (ii) determination of the position and the structure of the vortex-breaking baffle in the outlet duct.

This study only considered one PAT model with low specific speed, and the conclusions might only be applicable to this type of PAT. Whether the conclusions drawn in the study accord with the middle or high-specific speed PATs should be investigated in the future.