1 Introduction

The mechanical and thermal properties of functionally graded materials (FGMs) are variable, unlike the usual materials [1]. This characteristic is causal to use in applications like aerospace [2], aeronautical [3], medical [4], and sensors [5] industry. One of these most significant applications is pressure vessels. Because of specific thermal and pressure conditions they should be designed carefully. In these vessels, inner pressure makes tensile circumferential stress and radial pressure stress that they cause to make large shear stress inside of the vessel. Under this condition, the vessel quickly will arrive to yield stress. The best way to improve this is to use FGMs [6]. Eslami et al. [7] have investigated on the analytical solution of elastic–plastic stress distribution in a nonhomogeneous anisotropic FGM spherical vessels. In their paper, assuming axial symmetry, the material mechanical property variation was considered as an exponential function of the radius of the sphere. Chen and Lin [8] have studied elastic behaviours of block wall FGMs sphere and cylinder. They assumed exponential in the radial direction for mechanical behaviours.

You et al. [9] have investigated the fabrication of a 3-layer homogenous-FGM-homogenous vessel. They derive a method for achieving constant circumferential stress in fully FGM vessels. Parvizi et al. [10] surveyed the elastic–plastic behaviour of FGM cylindrical vessels. They studied the effect of pressure and temperature gradient on elastic–plastic behaviour by considering Al-SiC as FGM. Elastic–plastic behaviour of thick-walled FGM spherical vessels has been investigated by Sadeghian and Toussi [11]. They assumed full elastic–plastic and Von Mises criterion for behaviour. They also studied the effect of the fabrication of FGM on temperature and stress distribution. Atashipour et al. [12] have studied the elastic–plastic behaviour of thick-walled spherical vessels with FGM coat. They assumed linear and nonlinear behaviour for FGMs. Yang et al. [13] used FGMs for increasing the adhesion between copper and tungsten layers. In their research, they have simulated the variance of stresses for FGM coatings by assuming constant heat flux during with finite element analysis for achieving optimal coefficient. Wang et al. [14] have presented thermo-elastic analysis of FGM cylindrical vessels with hemispherical caps. The study of piezoelectric-coated spheres has been established by Atashipour and Sburlati [15]. In their research, they have investigated stress and electrical potential distribution in a radial direction on spheres with piezoelectric coating. They have compared FGM spheres with a piezoelectric coat with homogenous spheres and concluded that using of FGMs can reduce stress. Kind of FGM coat effect on thick-walled FGM coat sphere yield at internal pressure and temperature gradient has been studied by Dehnavi and Parvizi [16]. In another paper, they [17] used a new material tailoring method to solve FGM spherical and cylindrical vessels.

More recently, Hashemi et al. [18] presented an optimum design of an FGM cylindrical and spherical vessels by using the material tailoring equation. They had investigated how the whole thickness of vessels could participate to contribute to the load bearing.

As observed in the literature review, few researches present the effect of pressure and temperature gradient in FGM spherical pressure vessels. The present work attempts to solve this problem, that is, to provide an analytical solution of pressure and temperature gradient for spherical pressure vessels that inside of the vessel covered with FGMs. The analytical solution was compared with the finite elements method (FEM) solution. The elastic property of FGM in inner and external radius was modelled by the Mori–Tanaka method. Also, properties change based on exponential function in a radius direction. Also, internal pressure and temperature gradient effective are investigated on the elastic–plastic behaviour of FG-homogenous thick spherical vessels.

2 FGM behaviour modelling

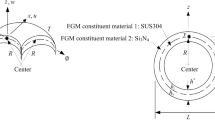
Figure 1 is the profile of the spherical vessel with an FGM coating. The superscript symbols H and FG refer to the homogeneous part and the functional calibrated material coating, respectively. \( E^{\text{H}},\alpha^{\text{H}}, K^{\text{H}} \) and \( Y^{\text{H}} \) denote elastic modulus, thermal expansion, heat transfer coefficient and the yield stress of the homogeneous component, respectively. The mechanical and thermal properties of the FGM shell are assumed to be changed only along the radius direction, and it varies continuously through the radial direction according to the exponential function, which is as follows:

Fig. 1
figure 1

2D schematic of the FG spherical vessel

Full size image
$$ \begin{aligned} E^{\text{FG}} \left(r \right) & = E_{0} r^{{n_{1}}} \quad \alpha^{\text{FG}} \left(r \right) = \alpha_{0} r^{{n_{3}}} \\ Y^{\text{FG}} \left(r \right) & = Y_{0} r^{{n_{2}}} \quad K^{\text{FG}} \left(r \right) = K_{0} r^{{n_{4}}} \\ \end{aligned} $$
(1)

Considering the spherical coordinate, \( r \) is the radial coordinate. Superscript \( n_{1},n_{2},n_{3} \) and \( n_{4} \) are the scaling indices, and \( E_{0}, \alpha_{0}, K_{0} \) and \( Y_{0} \) are the constants of gradation relations.

3 Equations of the problem

In order to solve the problem, the heat transfer equation and then equilibrium equation are solved in the radial direction. As a contract, the H-E, FG-P, FG-E superscripts are related to the homogeneous elastic part, the FG plastic part and the FG elastic part, respectively. Furthermore, according to axisymmetric conditions, only the equilibrium equation in the radial direction is used in this, and circumferential displacement, shear strain and stress are zero.

3.1 Temperature field

The heat transfer equation in the radial direction in spherical coordinates is equal to [7]:

$$ \frac{1}{{r^{2}}}\frac{d}{dr}\left({r^{2} K\frac{dT}{dr}} \right) = 0 $$
(2)

and the boundary conditions in this case are:

$$ \begin{aligned} T^{\text{FG}} \left(a \right) & = T_{a},\,T^{\text{H}} \left(c \right) = T_{c},\,T^{\text{FG}} \left(b \right) = T^{\text{H}} \left(b \right), \\ K^{\text{H}} \frac{{dT^{\text{H}}}}{dr}|_{r = b} & = K_{0} b^{{n_{4}}} \frac{{dT^{\text{FG}}}}{dr}|_{r = b} \\ \end{aligned} $$
(3)

By solving Eq. (2), for the homogeneous part and FGM, the temperature in these two parts is obtained as follows:

$$ \begin{aligned} T^{\text{FG}} \left(r \right) & = C_{1} r^{{- n_{4} - 1}} + C_{2} \\ T^{\text{H}} \left(r \right) & = C_{3} r^{- 1} + C_{4} \\ \end{aligned} $$
(4)

After applying the boundary conditions, \( C_{1},C_{2},C_{3} {\text{and}}C_{4} \) are obtained as follows:

$$ \begin{aligned} C_{1} & = K^{\text{H}} c\left({T_{a} - T_{c}} \right)/D \\ C_{2} & = T_{a} \left[{K_{0} \left({n_{4} + 1} \right)\left({c - b} \right)b^{{n_{4}}} - K^{\text{H}} c} \right]b^{{- n_{4} - 1}}/D + cT_{c} K^{\text{H}} a^{{- n_{4} - 1}}/D \\ C_{3} & = cK_{0} \left({n_{4} + 1} \right)\left({T_{a} - T_{c}} \right)/D \\ C_{4} & = \left[{K_{0} b^{{n_{4}}} \left({n_{4} + 1} \right)\left({cT_{c} - bT_{a}} \right) - cT_{c} K^{\text{H}}} \right]b^{{- n_{4} - 1}}/D + cT_{c} K^{\text{H}} a^{{- n_{4} - 1}}/D \\ D & = \left[{K_{0} b^{{n_{4}}} \left({n_{4} + 1} \right)\left({c - b} \right) - cK^{\text{H}}} \right]b^{{- n_{4} - 1}} + K^{\text{H}} a^{{- n_{4} - 1}} \\ \end{aligned} $$
(5)

3.2 Elastic solution on a sphere with FGM

The equilibrium equation for an element in spherical coordinates is as follows [19]:

$$ \frac{{d\sigma_{r}}}{dr} + 2\frac{{\sigma_{r} - \sigma_{\theta}}}{r} = 0 $$
(6)

where \( \sigma_{r} \) and \( \sigma_{\theta} \) are radial and peripheral stresses, respectively. The equation between strain and radial displacement is as follows:

$$ \varepsilon_{r} = \frac{du}{dr}, \varepsilon_{\theta} = \varepsilon_{\varphi} = \frac{u}{r} $$
(7)

The equation between stress and strain is as follows [19]:

$$ \begin{aligned} \sigma_{r} & = \lambda \left({\varepsilon_{r} + 2\varepsilon_{\theta}} \right) + 2\mu \varepsilon_{r} - \left({3\lambda + 2\mu} \right)\alpha T \\ \sigma_{\theta} & = \lambda \left({\varepsilon_{r} + 2\varepsilon_{\theta}} \right) + 2\mu \varepsilon_{r\theta} - \left({3\lambda + 2\mu} \right)\alpha T \\ \end{aligned} $$
(8)

where \( \mu \) and \( \lambda \) are Lamé’s constants and are defined as follows:

$$ \lambda = \frac{vE}{{\left({1 + v} \right)\left({1 - 2v} \right)}}, \mu = \frac{E}{{2\left({1 + v} \right)}} $$
(9)

Thus, after combining Eqs. (6–9), an ordinary differential equation of the second order is obtained in terms of radial displacement as follows:

$$ \begin{aligned} & \frac{{d^{2} u^{{{\text{FG}} - {\text{E}}}}}}{{dr^{2}}} + \frac{{n_{1} + 2}}{r}\frac{{du^{{{\text{FG}} - {\text{E}}}}}}{dr} + \frac{{2v\left({n_{1} + 1} \right) - 2}}{{r^{2} \left({1 - v} \right)}}u^{{{\text{FG}} - {\text{E}}}} \\ & \quad = \frac{{\alpha_{0} \left({v + 1} \right)}}{{\left({1 - v} \right)}} \times \left[{\left({n_{1} + n_{3} - n_{4} - 1} \right)C_{1} r^{{- n_{4} + n_{3} - 2}} + \left({n_{1} + n_{3}} \right) C_{2} r^{{n_{3} - 1}}} \right] \\ \end{aligned} $$
(10)

The general solution of Eq. (10) can be written as:

$$ \begin{aligned} u_{g}^{{{\text{FG}} - {\text{E}}}} & = S_{1} r^{{\xi_{1}}} + S_{2} r^{{\xi_{2}}} \\ \xi_{1,2} & = \frac{{- (n_{1} + 1) \pm \sqrt {n_{1}^{2} + \frac{{2n_{1} \left({1 - 5v} \right) + 9\left({1 - v} \right)}}{1 - v}}}}{2} \\ \end{aligned} $$
(11)

\( S_{1} \) and \( S_{2} \) are integral constants and are determined by applying boundary conditions. The particular solutions of Eq. (12) are assumed as:

$$ \begin{aligned} u_{p}^{{{\text{FG}} - {\text{E}}}} & = Z_{1} r^{{n_{3} + 1}} + Z_{2} r^{{n_{3} - n_{4}}} \\ Z_{1} & = \frac{{\left({1 + v} \right)\alpha_{0} \left({n_{1} + n_{3}} \right)C_{2}}}{{\left({1 - v} \right)\left[{n_{3}^{2} + \left({3 + n_{1}} \right)n_{3}} \right] + n_{1} \left({1 + v} \right)}} \\ Z_{2} & = \frac{{\left({1 + v} \right)\alpha_{0} \left({n_{1} + n_{3} - n_{4} - 1} \right)C_{1}}}{{\left({1 - v} \right)\left[{\left({n_{3} - n_{4}} \right)\left({n_{3} - n_{4} + n_{1} + 2} \right)} \right] + 2v\left({1 + n_{1}} \right) - 2}} \\ \end{aligned} $$
(12)

Using Eq. (7), find the radial and circumferential strains as follows:

$$ \begin{aligned} \varepsilon_{r}^{{{\text{FG}} - {\text{E}}}} & = S_{1} \xi_{1} r^{{\xi_{1} - 1}} + S_{2} \xi_{2} r^{{\xi_{2} - 1}} + Z_{1} \left({n_{3} + 1} \right)r^{{n_{3}}} + Z_{2} \left({n_{3} - n_{4}} \right)r^{{n_{3} - n_{4} - 1}} \\ \varepsilon_{\theta}^{{{\text{FG}} - {\text{E}}}} & = S_{1} r^{{\xi_{1} - 1}} + S_{2} r^{{\xi_{2} - 1}} + Z_{1} r^{{n_{3}}} + Z_{2} r^{{n_{3} - n_{4} - 1}} \\ \end{aligned} $$
(13)

Radial and circumferential stresses are also obtained by placing strains in Eq. (7):

$$ \sigma_{r}^{{{\text{FG}} - {\text{E}}}} = \frac{{- E_{0}}}{{\left({1 + v} \right)\left({1 - 2v} \right)}} \times \left\{{S_{1} r^{{\xi_{1} + n_{1} - 1}} \left[{\left({v - 1} \right)\xi_{1} - 2v} \right] + S_{2} r^{{\xi_{2} + n_{1} - 1}} \times \left[{\left({v - 1} \right)\xi_{2} - 2v} \right] + r^{{n_{3} + n_{1}}} \times \left[{Z_{1} n_{3} \left({v - 1} \right) - \left({v + 1} \right) + C_{2} \alpha_{0} \left({1 + v} \right)} \right] + r^{{n_{3} - n_{4} + n_{1} - 1}} \left[{Z_{2} ((n_{3} - n_{4})\left({v - 1} \right) - 2v)} \right] + C_{1} \alpha_{0} \left({1 + v} \right)} \right\} $$
(14)
$$ \sigma_{\theta}^{FG - E} = \frac{{E_{0}}}{{\left({1 + v} \right)\left({1 - 2v} \right)}}\left\{{S_{1} r^{{\xi_{1} + n_{1} - 1}} \left({\xi_{1} v + 1} \right) + S_{2} r^{{\xi_{2} + n_{1} - 1}} \left({\xi_{2} v + 1} \right) + r^{{n_{3} + n_{1}}} \left[{Z_{1} \left({v\left({n_{3} + 1} \right) + 1} \right) - C_{2} \alpha_{0} \left({1 + v} \right)} \right] + r^{{n_{3} - n_{4} + n_{1} - 1}} \left[{Z_{2} (v(n_{3} - n_{4}) + 1) - C_{1} \alpha_{0} \left({1 + v} \right)} \right]} \right\} $$
(15)

3.3 Elastic solution on a sphere with homogeneous material

As before, the equation of displacement in the homogeneous sphere can be obtained as follows:

$$ \frac{{d^{2} u^{{{\text{H}} - {\text{E}}}}}}{{dr^{2}}} + \frac{2}{r}\frac{{du^{{{\text{H}} - {\text{E}}}}}}{dt} - \frac{2}{{r^{2}}}u^{{{\text{H}} - {\text{E}}}} = \frac{{- \alpha^{\text{H}} \left({v + 1} \right)C_{3}}}{{\left({1 - v} \right)r^{2}}} $$
(16)

The general solution as follows:

$$ u^{{{\text{H}} - {\text{E}}}} = S_{3} r + \frac{{S_{4}}}{{r^{2}}} + \frac{{\alpha^{\text{H}} \left({v + 1} \right)C_{3}}}{{2\left({1 - v} \right)}} $$
(17)

Similar to the previous section, the radial and circumferential stresses and strains in the homogeneous section are obtained as follows:

$$ \begin{aligned} \varepsilon_{r}^{{{\text{H}} - {\text{E}}}} & = S_{3} - \frac{{2S_{4}}}{{r^{3}}} \\ \varepsilon_{\theta}^{{{\text{H}} - {\text{E}}}} & = S_{3} + \frac{{S_{4}}}{{r^{3}}} + \frac{{\alpha^{H} \left({v + 1} \right)C_{3}}}{{2r\left({1 - v} \right)}} \\ \end{aligned} $$
(18)
$$ \begin{aligned} \sigma_{r}^{{{\text{H}} - {\text{E}}}} & = \frac{{E^{\text{H}}}}{{\left({1 + v} \right)\left({1 - 2v} \right)}}[S_{3} \left({1 + v} \right) - \frac{{2S_{4} \left({1 - 2v} \right)}}{{r^{3}}} + \frac{{v\alpha^{\text{H}} \left({v + 1} \right)C_{3}}}{{r\left({1 - v} \right)}} - \left({1 - v} \right)\alpha^{\text{H}} \left({\frac{{C_{3}}}{r} + C_{4}} \right)] \\ \sigma_{\theta}^{{{\text{H}} - {\text{E}}}} & = \frac{{E^{\text{H}}}}{{\left({1 + v} \right)\left({1 - 2v} \right)}}[S_{3} \left({1 + v} \right) + \frac{{S_{4} \left({1 - 2v} \right)}}{{r^{3}}} + \frac{{\alpha^{\text{H}} \left({v + 1} \right)C_{3}}}{{2r\left({1 - v} \right)}} - \left({1 - v} \right)\alpha^{\text{H}} \left({\frac{{C_{3}}}{r} + C_{4}} \right)] \\ \end{aligned} $$
(19)

\( {\text{S}}_{3} \) and \( S_{4} \) are integral constants and are determined by applying boundary conditions.

3.4 Plastic solution on a sphere with FGM

As the pressure or temperature increases, the deformation reaches the plastic area. To start the submission in this study, the criterion of submission of Tresca has been used, although in a sphere, due to \( \sigma_{\varphi} = \sigma_{\theta} \), the two criteria of Tresca and Von Mises are the same. Given that circumferential stress in a sphere is usually greater than radial stress, the following equation is obtained [11]:

$$ \sigma_{\theta} - \sigma_{r} = Y $$
(20)

Assuming the elastic–plastic behaviour is complete and by placing Eq. (20) in Eq. (6), the radial and circumferential stresses in the plastic state are obtained as follows:

$$ \begin{aligned} \frac{{d\sigma_{r}}}{dr} & = 2\frac{{ Y_{0} r^{{n_{2}}}}}{r} \\ \sigma_{r}^{FG - p} & = \frac{{2r^{{n_{2}}} Y_{0}}}{{n_{2}}} + S_{5} \\ \sigma_{\theta}^{FG - p} & = \frac{{\left({2 + n_{2}} \right)r^{{n_{2}}} Y_{0}}}{{n_{2}}} + S_{5} \\ \end{aligned} $$
(21)

\( S_{5} \) is integral constants and are determined by applying boundary conditions. Assuming very small deformations, the elastic–plastic strain is obtained as follows [19]:

$$ \begin{aligned} \varepsilon_{r} & = \frac{1}{E}\left({\sigma_{r} - 2v\sigma_{\theta}} \right) + \varepsilon_{r}^{P} + \alpha T \\ \varepsilon_{\theta} & = \frac{1}{E}\left({- v\sigma_{r} + (1 - v)\sigma_{\theta}} \right) + \varepsilon_{\theta}^{P} + \alpha T \\ \end{aligned} $$
(22)

According to the principle of incompressibility in plastic deformation, i.e.\( \varepsilon_{r}^{P} + \varepsilon_{\theta}^{P} + \varepsilon_{\varphi}^{P} = 0 \), it can be written:

$$ \varepsilon_{r} + 2\varepsilon_{\theta} = \frac{du}{dr} + \frac{2u}{r} = \frac{{\left({1 - 2v} \right)}}{E}\left({\sigma_{r} + 2\sigma_{\theta}} \right) + 3\alpha T $$
(23)

By placing the stresses of Eq. (21) in the above equation, the following result is obtained:

$$ \frac{{du^{{{\text{FG}} - {\text{P}}}}}}{dr} + \frac{{2u^{{{\text{FG}} - {\text{P}}}}}}{r} = \frac{{2\left({1 - 2v} \right)\left({3 + n_{2}} \right)Y_{0}}}{{n_{2} E_{0}}}r^{{n_{2} - n_{1}}} + \frac{{3\left({1 - 2v} \right)S_{5}}}{{E_{0}}}r^{{- n_{1}}} + 3\alpha_{0} C_{2} r^{{n_{3}}} + 3\alpha_{0} C_{1} r^{{n_{3} - n_{4} - 1}} $$
(24)

where

$$ u^{{{\text{FG}} - {\text{P}}}} = \frac{{s_{6}}}{{r^{2}}} + \frac{{3\alpha_{0} C_{1}}}{{n_{3} - n_{4} + 2}}r^{{n_{3} - n_{4}}} + \frac{{3\alpha_{0} C_{2}}}{{n_{3} + 3}}r^{{n_{3} + 1}} + \frac{{2\left({1 - 2v} \right)\left({3 + n_{2}} \right)Y_{0}}}{{n_{2} E_{0} (n_{2} - n_{1} + 3)}}r^{{n_{2} - n_{1} + 1}} \frac{{3S_{5} \left({1 - 2v} \right)}}{{E_{0} \left({3 - n_{1}} \right)}}r^{{1 - n_{1}}} $$
(25)

\( S_{6} \) is integral constants and are determined by applying boundary conditions (Fig. 2).

Fig. 2
figure 2

Partial yield in an FGM coating

Full size image

The following boundary conditions apply to any condition, including elastic and plastic, in the internal radius, the regular season of the veneer and the homogeneous part and the external radius of the sphere, respectively:

$$ \begin{aligned} \sigma_{r}^{\text{FG}} \left(a \right) & = - P_{a} \\ \sigma_{r}^{\text{FG}} \left(b \right) & = \sigma_{r}^{h} \left(b \right) \\ u^{\text{FG}} \left(b \right) & = u^{\text{H}} \left(b \right) \\ \sigma_{r}^{\text{H}} \left(c \right) & = - P_{c} \\ \end{aligned} $$
(26)

Also, on the border between elastic and plastic of coating area, the following boundary conditions apply:

$$ \begin{aligned} \sigma_{r}^{{{\text{FG}} - {\text{E}}}} \left({r_{p}} \right) & = \sigma_{r}^{{{\text{FG}} - {\text{P}}}} \left({r_{p}} \right) \\ \sigma_{\theta}^{{{\text{FG}} - {\text{E}}}} \left({r_{p}} \right) & = \sigma_{\theta}^{{{\text{FG}} - {\text{P}}}} \left({r_{p}} \right) \\ u^{{{\text{FG}} - {\text{E}}}} \left({r_{p}} \right) & = u^{{{\text{FG}} - {\text{P}}}} \left({r_{p}} \right) \\ \end{aligned} $$
(27)

According to the relations (26–27), the integral constants of A–B as well as the radius of the r plastic area can be obtained which have been solved numerically using MATLAB software.

4 Properties of homogeneous material and coating

Since the sudden change of properties in the common joint of the coating and the homogeneous part causes a discontinuity in the circumferential stress, this discontinuity in the stress can cause the coating to separate from the homogeneous part. This study assumes that the materials in the coating are graded in such a way that in the common joint between the FGM and the homogeneous part, both materials have the same properties and are equal to the properties of the homogeneous material. With this assumption, the coefficients \( n_{1},n_{2},n_{3},n_{4} \) and the constants \( K_{0}, \alpha_{0}, E_{0} \), \( Y_{0} \) are obtained as follows:

$$ \begin{aligned} n_{1} & = \ln \left({\frac{{E_{a}}}{{E^{H}}}} \right)/\ln \left({\frac{a}{b}} \right) \\ n_{2} & = \ln \left({\frac{{Y_{a}}}{{Y^{H}}}} \right)/\ln \left({\frac{a}{b}} \right) \\ n_{3} & = \ln \left({\frac{{\alpha_{a}}}{{\alpha^{H}}}} \right)/\ln \left({\frac{a}{b}} \right) \\ n_{4} & = \ln \left({\frac{{K_{a}}}{{K^{H}}}} \right)/\ln \left({\frac{a}{b}} \right) \\ \end{aligned} $$
(28)

And

$$ \begin{aligned} E_{0} & = E_{a}/a^{{n_{1}}} \quad Y_{0} = Y_{a}/a^{{n_{2}}} \\ \alpha_{0} & = \alpha_{a}/a^{{n_{3}}} \quad K_{0} = K_{a}/a^{{n_{4}}} \\ \end{aligned} $$
(29)

In the above equations, subtitle \( a \) is related to the property of matter in a radius a.

In this research, Al-SiC composite has been used as a material of homogeneous material and functional calibrated coating. It is assumed that in the homogeneous part, the distribution of SiC particles is constant and equal to 10%.

In the FGMs, three types of coating are considered. In the first type of coating, the percentage of SiC in the radius is considered to be \( a \) as 0% (a-Al-0%SiC), in the second case it is 10% (a-Al-10% SiC), and in the third case, it is 20% (a-Al-20%SiC). Then, considering that the mechanical properties in the internal radius and the middle radius b (in the middle radius of the material must be homogeneous) are clear, using relations (28) and (29), the way of the grading in the coating is specified. It is clear that in the second case of the coating, the percentage of SiC in the coating is constant and equal to 10%, and therefore the whole sphere is made of homogeneous material. Mori–Tanaka’s method is a method for obtaining the effective properties of two-phase composites. Assuming the particles are spherical, the effective volumetric modulus \( K_e \) and the effective shear modulus \( G_e \) for the Al-x%SiC composite are defined as follows (x percentage volumetric phase SiC) [20]:

$$ \begin{aligned} \tilde{K}_{\text{e}} & = \frac{{x\left({3\tilde{K}_{\text{Al}} + 4G_{\text{Al}}} \right)\left({\tilde{K}_{\text{SiC}} - \tilde{K}_{\text{Al}}} \right)}}{{3\tilde{K}_{\text{Al}} + 4G_{\text{m}} + 3\left({1 - x} \right)\left({\tilde{K}_{\text{SiC}} - \tilde{K}_{\text{Al}}} \right)}} + \tilde{K}_{\text{Al}} \\ G_{\text{e}} & = 5xG_{\text{Al}} \left({3\tilde{K}_{\text{Al}} + 4G_{\text{Al}}} \right)\left({G_{\text{SiC}} - G_{\text{Al}}} \right)/ \left[{5G_{\text{Al}} (3K_{\text{Al}} + 6\left({1 - x} \right)\left({G_{\text{SiC}} - G_{\text{Al}}} \right)\left({\tilde{K}_{\text{Al}} + 2G_{\text{Al}}} \right)} \right] + G_{\text{Al}} \\ \end{aligned} $$
(30)

In the above relations,\( G \),\( \tilde{K} \) are the shear modulus and the volumetric modulus of each phase, respectively. \( x \) is also the volume percentage of the SiC phase and the effective elastic modulus is equal to:

$$ E_{\text{e}} = 9G_{\text{e}} \tilde{K}_{\text{e}}/\left({G_{\text{e}} + 3\tilde{K}_{\text{e}}} \right) $$
(31)

The effective heat transfer coefficient and the effective thermal expansion coefficient based on the Mori–Tanaka method are:

$$ \begin{aligned} K_{\text{e}} & = \frac{{x(K_{\text{SiC}} - K_{\text{Al}})K_{\text{Al}}}}{{K_{\text{Al}} + \left({1 - x} \right)(K_{\text{SiC}} - K_{\text{Al}})}} + K_{\text{Al}} \\ \alpha_{\text{e}} & = \frac{{\left({K_{\text{Al}} - K_{\text{e}}} \right)K_{\text{SiC}} \left({\alpha_{\text{SiC}} - \alpha_{\text{Al}}} \right)}}{{\left({K_{\text{Al}} - K_{\text{SiC}}} \right)K_{\text{e}}}} + \alpha_{\text{Al}} \\ \end{aligned} $$
(32)

The following weight percentage rule is used to obtain the yield strength:

$$ Y_{\text{e}} = (Y_{\text{SiC}} - Y_{\text{Al}})x + Y_{\text{Al}} $$
(33)

Table 1 shows the properties of Al and SiC, and Table 2 shows the effective properties of Al-10% SiC (homogeneous part material) calculated using Eqs. (31–33). Since SiC particles are ceramic and behave brittle, as an approximation, tensile strength is considered for these particles instead of yield strength.

Table 1 Properties of Al [21] and SiC [10]
Full size table
Table 2 Properties of Al-10%SiC
Full size table

Using Eqs. (31–33) to obtain effective properties in a radius for three types of coatings and also using Eqs. (27–28), how to grade in coatings is specified. Table 3 shows the constants and exponents for grading of three coatings types, taking into account a = 1 m and b = 1.2 m of FGM. It should be noted that in all examples of this study, the Poisson ratio for the homogeneous and function graded part is considered to be 0.3.

Table 3 Grading index and constants for three FGM coating
Full size table

5 Results and discussion

5.1 Comparison of results with FEM

To compare the results obtained using the presented equations, a simulation of the FEM of the model has been performed. Abaqus finite element software is used for this purpose. Figure 3 shows the finite symmetric finite element model (three-dimensional view) of the problem in this software. Due to the symmetry conditions in the direction of the two axes and to save on calculations, the problem is modelled in two dimensions and symmetric with a 90-degree segment. Because there is no standard model in this software to define the behaviour of an FGM, using a Python code, the FGM is divided into 40 parts along the radius and the properties of each part are based on Eq. (1) and the middle radius of each part allocated. The models for spherical vessels consist of 4500 CAX4T elements for static analysis. Also, by making the mesh smaller, the independence of the answer on the size of the mesh has been investigated. In this case, a = 1 m, b = 1.2 m and c = 1.4 m are considered. Properties for the homogeneous part are selected according to Table 1. Also, the properties for coating are selected according to a-Al-0% SiC (Table 3). Loading conditions are also considered as follows:

Fig. 3
figure 3

Axisymmetric finite element model (FGM coating has been divided into 40 part in the radial direction)

Full size image
$$ P_{a} = 50 {\text{MPa }},P_{c} = 0, T_{a} = - 30 ^\circ {\text{C}}, T_{c} = 0 ^\circ {\text{C}} $$

As shown in Fig. 4, the results of the finite element and analytical solution presented in this study are well consistent. The presence of fluctuations in the finite element results in the FG section is a function of the step-by-step property change in this section. Figure 4a shows the environmental stress along with the thickness of the sphere. With the right choice of how the coating is graded, this stress is joined in the common season of the coating and the homogeneous part. Radial stress in the thickness direction of the sphere wall is also shown in Fig. 4b. In this figure, the fracture point in the diagram is the boundary between the elastic and the plastic area in the FGM cover.

Fig. 4
figure 4

Comparison between analytical and FEM results: a radial stress and b circumferential stress

Full size image

5.2 The effect of internal pressure

Figure 5 shows the effect of internal pressure on the distribution of radial stress, circumferential stress, the dimensionless of yield \( \left({\sigma_{\theta} - \sigma_{r}} \right)/Y \) and radial displacement. The internal, middle and external radius of the sphere are chosen to be equal to \( a = 1{\text{m}} \), \( b = 1.2 {\text{m}}, \) and \( c = 1.4 {\text{m}} \), respectively. The material properties for the homogeneous part are selected according to Table 2, and the coating properties are selected according to a-Al-0% SiC (Table 3). The external pressure of the sphere is equal to Pc = 0, and the internal and external temperatures are considered to be \( T_{a} \) = − 30 °C and \( T_{c} \) = 0 °C, respectively, as shown in Fig. 5a. The radial stress in the internal radius of the sphere is equal to the internal pressure, and by moving towards the external radius, its value reaches the external pressure, i.e. zero (Fig. 5a). Circumferential stresses for different internal pressures are shown in Fig. 4b. As can be seen, in FGM coating and homogenous part area stresses are continuum due to material properties equality. Stress continuity can reduce the delamination of FGM layer risk. For each amount of internal pressure, circumferential stress is positive and the magnitude of this stress increases from FGM internal boundary condition to a maximum and after that, it decreases continuously to external boundary condition. In these curves, the external point between elastic and plastic area borders is in the FGM coating side. As shown in Fig. 5b, the maximum circumferential stress moved to external diameter, while internal pressure increased. The dimensionless yield criterion is shown in Fig. 5c, while this parameter equal to 1 states that there is plastic deformation. By yield from inside in boundary condition considering, the plastic area radius in each amount of pressure is confirmed until the last point that the dimensionless yield criterion is equal to 1. As was shown, at 39 MPa pressure plastic area radius is almost zero and at 79 MPa all part of the coat yielded. The dimensionless radial displacement is shown in Fig. 5d. The radial displacement increased as an increase in internal pressure as expected.

Fig. 5
figure 5

a Radial stress, b circumferential stress, c the dimensionless parameter of yield and d the radial dimensionless displacement for the variant amount of internal temperatures (Pc = 0, Ta = − 30 °C and Tc = 0 °C)

Full size image

5.3 Effect of temperature gradient

In this section the effect of temperature gradient in elastic–plastic behaviour of spheres with FGM coat by considering a sphere with the same dimensions and behaviours of the last part. Pc = 0, Pa = 40 MPa and Tc = 0 °C is assumed in this instance.

Radial stress distribution for a different amount of internal temperature of Ta is shown in Fig. 6a. For the internal temperature of − 40 °C radial stress is compressive in entire sphere thickness based on this figure. The temperature reduction causes that the radial stress near the internal radius still remains compressive, while the radial stress of external areas in the homogenous part converts to tensional. This point shows that the stresses caused by temperature have more effect on the external radius in lower temperatures. The distribution of circumferential stress in the sphere thickness is shown in Fig. 6b. Unlike the previous part that circumferential stress changed with the increase in pressure, in this instance stress increased initially in a constant ramp line and then decreased to an external radius in each temperature. This constant ramp line regards the plastic radial stress, and since this stress is independent of temperature, this mentioned line is constant in each temperature. The maximum stress is in the plastic area radius that increases with the reduction of temperature. The other point for circumferential stress is that circumferential stress changes its direction in homogenous part for below 40◦ C temperatures and the location of this change is almost constant. The dimensionless yield criterion is shown in Fig. 6c. It is obvious that the magnitude of radial stress will be greater than circumferential stress with the reduction of temperature in the near external radius area. The radial displacement for a different amount of temperature is shown in Fig. 6d. The sphere tends to shrink and negative displacement with decreasing temperature as expected. At higher temperatures, there is positive displacement because the effect of pressure is more than temperature. Also, at very low temperatures due to the effect of pressure in a thin area near the internal radius, there is a positive displacement.

Fig. 6
figure 6

a Radial stress, b circumferential stress, c the dimensionless parameter of yield and d the radial dimensionless displacement for the variant amount of internal temperatures (Pa = 40 MPa, Pc = 0 °C and Tc = 0 °C)

Full size image

5.4 The effect of the coating type

For a sphere with the same dimensions as the last part and 3 kinds of the coat as Fig. 3 and pressure and temperature condition as follows:

$$ P_{\text{a}} = 60\,{\text{MPa}},\,P_{\text{c}} = 0\,{\text{MPa}},\,T_{\text{a}} = - 70\,^{\circ} {\text{C}},\,T_{\text{c}} = 0^{\circ} {\text{C}} $$

The dimensionless yield criterion is shown in Fig. 7. As mentioned before, in a sphere with a-Al-20%SiC coat all of the spheres are homogenous. Also in a-Al-0%SiC and a-Al-20%SiC the FGM coat is softer and harder than the homogenous part, respectively. According to the picture, it is obvious that the plastic area radius in the sphere with the soft coat is smaller, and in the sphere with the hard coat, this mentioned radius is bigger than the elastic area radius in the homogenous sphere. It is also clear that the dimensionless yield criteria for 3 kinds of the coat are verge together by the approach to the external radius. Due to this point, it turns out that the kind of applying FGM coat can effect stresses that develop on the sphere, so with choosing the right kind of FGM coat it is possible to reach an optimized design for vessels under pressure and temperature gradient.

Fig. 7
figure 7

The dimensionless parameter for three types of coatings

Full size image

6 Conclusion

The issue of a spherical pressure vessel with a coating of functional graduated materials was investigated in this study. In this case, analytical equations were obtained for the elastic–plastic deformation in the sphere’s wall under pressure and temperature gradient. In this study, it was assumed that the temperature and pressure conditions were such that the yield would start from the internal radius of the sphere and expand in the vector towards the external radius, while the homogeneous part remained elastic. To prevent the discontinuity of the stress at the common boundary between the homogeneous part and the functional graduated coating, it was considered that the coating is graduated in such a way that in the common boundary area, its properties are the same as the properties of the homogeneous part. The effect of internal pressure, temperature gradient, as well as the type of coating on the sphere’s elastic–plastic behaviour, was also investigated. The obtained results showed that in large internal pressures, radial stresses are compressive and circumferential stresses are tensile, and as the internal pressure increases, the plastic region moves from the internal to the external radius. By lowering the internal temperature of the sphere, in the area close to the internal radius, the radial stresses are the compressive and, in the area, close to the external radius is the tensile. The opposite is true for circumferential stress. Also, with the lowering of the temperature, the yield of the sphere was beginning from the external radius.