1 Introduction

Nowadays, increasing the safety of structures is an important goal and many researchers investigate in this field. For this purpose, one of the best options is using energy absorbers. So far, structures have been analyzed by different materials like energy absorption that in most of them, two factors decrease in capital and keep occupants alive [1,2,3,4].

The behavior of thin-walled structures with different cross sections under the axial loading has been studied for many years. Ha et al. [5] by using a new tubular corrugated configuration mimicked the coconut tree profile. In an attempt to enhance the energy absorption, they minimized the initial peak crushing force and stabilized the crushing process. They used two parameters of the tapered angle and the wavelength, and they reported their results of the energy absorption. Firouzi et al. [6] worked on the energy absorption capability of a type of thin-walled profiles with H-shaped cross sections during the quasi-static flattening process. They used two different material models of rigid–linear work hardening and power hardening. Their results showed the specific energy absorption by the optimum H-shaped section is higher than the corresponding value of square, rectangular and circular tubes. Two multi-cell tubes with triangular and Kagome lattices were designed and manufactured by Hong et al. [7]. According to the research, lattice tubes have mean crushing forces compared to single-cell tubes. Lattice tubes have better energy-absorbing abilities. Song et al. [8] analyzed the light-weight thin-walled structures with patterned windows under the axial crushing. The finite element method has been used to investigate the effect of the size of windows on the tubes’ collapse parameters. According to the results, the initial peak decreases with the increase in the aspect ratio and the energy absorption decreases with the increase in the aspect ratio when the aspect ratio is small enough to be away from the extensional region. Energy absorption capability of different tapered tubes under the axial impact loading was reported by Nagel and Thambiratnam [9]. They varied the number of the tapered sides and the wall thickness. Ming et al. [10] studied the cylindrical curvature effects and implemented the energy method. They used a theoretical model for the study of the behavior of energy absorbers. In another study, crash parameters of the conventional square tubes were conducted using numerical analyses, through which the finite element models were well validated [11]. Bigdeli and Nouri [12] introduced two geometries for thin-walled cylinders and perused behaviors under the quasi-static axial loadings. Increasing the specific energy absorption, reducing the peak energy and improving the crushing were the main aims of their work. Baroutaji et al. [13] used the response surface method and the finite element modeling to design the experiments and explore the effects of the geometrical factors. They modeled the specific energy absorption and the collapse load of the circular tube. They reported that the specific energy absorption (SEA) of the circular tubes increases after an increase in the thickness and a decrease in the diameter. Also, the tubes with smaller width and diameter are more suitable to be used as the energy-absorbing components. Thin-walled tubes are among the best structures to absorb which leads to various energy absorption responses. Fang et al. [14] employed finite element method to demonstrate the dynamic crashing behavior of multi-cell tubes. Also, they used multi-objective particle swarm optimization algorithm to optimize the sectional parameters. Axial crushing [15,16,17,18], axial compression [19,20,21], oblique impact loading [22,23,24,25] and axial dynamic loading [26, 27] are different models to achieve this target. Montazeri et al. [28] researched on two types of thin-walled structures by the crushing mechanism. They introduced a holed tube, and the crushing behavior was compared with the grooved tube. This structure is crushed faster than the holed tube, and the maximum crushing force in former is lower. The effect of adding the silica nanoparticle to the epoxy, silica weight percent, particle size and various combinations of epoxy/silica on the energy absorption capability of thin-walled square columns was investigated by Shariati et al. [29]. Their results showed that when silica content was increased, the energy absorption capability of columns decreased and the specimens collapsed under the unstable and dangerous mode. Alavi Nia et al. [30] studied the normal collapse of thin-wall structures in Euler buckling exposed to the inclined loads. In this study, the effect of the collapse initiators on the energy absorption specifications of square tubes under the inclined quasi-static loads in experimental and numerical conditions has been investigated. Yang et al. [31] used two different origami patterns to investigate the energy absorption capacity and the deformation mechanism of the tubes under the uniaxial loading.

In this paper, the energy absorption characteristics of the thin-walled square structures have been evaluated by commercial software Abaqus/Explicit according to two design variables, the shell aspect ratio and the diameter ratio of the cutout. The numerical results were modeled using artificial neural network (ANN) and response surface method (RSM) and optimized by the genetic algorithm. Finally, numerical results were verified by means of empirical experiments.

2 Materials and method

2.1 Energy absorption indices

In general, several indices were employed to quantify the energy absorption characteristic of the thin-walled structures. Among them, energy absorption (EA), specific energy absorption (SEA), mean crushing load (MCL) and peak crushing load (PCL) are widely used. These indices are defined as below:

$$ {\text{EA}} = \int\limits_{0}^{L} {P(x)d(x)} $$
(1)
$$ {\text{SEA}} = \frac{\text{EA}}{m} $$
(2)
$$ {\text{MCL}} = \frac{\text{EA}}{L} $$
(3)

where P(x), L and M represent the exerted force during crashing, crashing length and absorbent mass, respectively. PCL is the initial peak force in the load–displacement diagram.

2.2 Design of experiment (DOE)

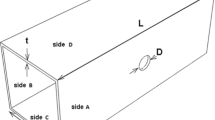
In this study, Minitab software version 17 was used to DOE. This DOE was carried out using the surface response method based on the central composite algorithm. The structures are thin-walled columns with rectangular cross sections which have an elliptical cutout in the center of the larger side. The aspect ratio of samples varies, but the sectional area of all of them is constant and equal to 900 mm2. Also, all samples have an elliptical cutout with a constant cross section of 200 mm2. Therefore, for this DOE, the effect of two parameters on the energy absorption of the samples was investigated: the absorbent aspect ratio (C = a/b) and the diameter ratio of the cutout (D = d1/d2). It should be noted that the range of changes for these parameters was considered as follows: \( 1 \le C \le 3 \) and \( 0.5 \le D \le 1.3 \). Furthermore, the height and the thickness of the shells were considered 100 mm and 1 mm, respectively. The schematic of the absorbent and its parameters are shown in Fig. 1.

Fig. 1
figure 1

Schematic of absorbent and its geometrical parameters

Full size image

Accordingly, the performed DOE is shown in Table 1.

Table 1 Design of experiment based on the central composite algorithm
Full size table

2.3 Finite element model (FEM)

The commercial finite element software Abaqus/Explicit is used to model the crushing problem. Steel alloy was used, and its mechanical properties were extracted according to the ASTM E8 standard [32] using an Instron 5500R apparatus. The stress–strain curve obtained from one of the samples and used for FE analysis is shown in Fig. 2. The density of the steel is 7800 kg/m3, the Young’s modulus 210 MPa, the yield stress 292 MPa and the Poisson ratio υ = 0.33.

Fig. 2
figure 2

Stress–strain curve of the used steel alloy

Full size image

To apply boundary conditions, two rigid plates were attached to the top and bottom of the samples. All degrees of freedom of the lower and upper plates were closed, and only the upper plate was allowed to be displaced in the direction of the sample’s height. Samples were compressed in the height direction through the top plate at a constant speed of 5 mm/min. In all analyses, the amount of the energy absorption was measured over 70% collapse of the initial height.

After defining the geometry and applying the boundary conditions and loading, the sample must be meshed for analysis. For this purpose, S4R element was used that is suitable for large strain analyses and allows the transverse shear deformation. The S4R is a four-node element that is a strong element in the analysis of thin-walled shells with a general application. Also, by this element, the reduced integration was used to calculate the element hardness matrix. As mentioned earlier, all samples have cutouts and applying an appropriate mesh around the cutout is important due to the stress concentration and high variation in stress. Figure 3 shows a general overview of the meshed sample and the mesh around the cutout. It should be noted that such problems have many deformations and also there are contacts on the wall surface. Hence, a self-contact algorithm was used to prevent the interpenetration during the folding of the walls.

Fig. 3
figure 3

A meshed sample and meshing around the cutout

Full size image

The mesh convergence with the number of 456, 1080, 3200 and 7200 elements is shown in Fig. 4. Based on this figure, the meshed sample with 3200 elements was selected.

Fig. 4
figure 4

Study of the mesh convergence and selection of 3200 elements

Full size image

2.4 Validation of the numerical result

The energy absorption behavior of numerical results is validated against the experimental results. Figure 5 shows the experimental and numerical deformation modes in different collapse lengths (L) for DOE1. Also, the force–displacement diagram of this sample is presented in Fig. 6. It can be seen that the numerical results are in good agreement with the experimental results.

Fig. 5
figure 5

Deformation modes in different collapse lengths for DOE1 a numerical, b experimental

Full size image
Fig. 6
figure 6

Force–displacement diagram for DOE1

Full size image

3 Results and discussion

3.1 Numerical results

As mentioned, several indices were employed to quantify the energy absorption characteristic of the thin-walled structures. For this study, energy absorption (EA), specific energy absorption (SEA), mean crushing load (MCL) and peak crushing load (PCL) were considered. An ideal energy absorber is the line parallel to the horizontal axis in the load–displacement diagram which has a minimum peak load and maximum energy absorption. Figure 7 shows the load–displacement behavior of some samples. The first peak represents the first wrinkle that is referred to as the peak load. Also, energy absorption parameters of all analyzed samples are reported in Table 2.

Fig. 7
figure 7

Load–displacement diagram of DOE1 to DOE9

Full size image
Table 2 Energy absorption parameters of all analyzed samples
Full size table

It can be seen that the lowest PCL and the highest SEA, with values 32.72 kN and 15.265 kJ/kg, are related to sample DOE1 with the aspect ratio 1 and the diameter ratio 0.9. According to Table 2, DOE4 has the highest EA which is equal to 1471 J. Also, the maximum value of MCL is related to DOE4 with the aspect ratio 2 and the diameter ratio 0.5. In order to have the proper absorbent, it is better to have the low initial peak and the high energy absorption. Therefore, DOE1 has a better fit. For a better comparison, energy absorption parameters of all samples are shown in Fig. 8.

Fig. 8
figure 8

Energy absorption parameters of all samples

Full size image

For example, the collapse behavior of DOE1 under quasi-static tests is represented in Fig. 9. As expected, the first wrinkling started from the cutout, and then the two edges of the cutout were placed on each other and then the strength of this section increased. Then, the shell wrinkled from another area and entered the plastic zone and a new peak was formed in the load–displacement chart. This process was repeated until the sample was completely crushed. This behavior of thin-walled structures increases the crashworthiness. For a better understanding, Fig. 10 shows the collapse behavior of DOE2–DOE9 under quasi-static loading.

Fig. 9
figure 9

Collapse behavior of DOE1 under quasi-static loading

Full size image
Fig. 10
figure 10

Collapse behavior of a DOE2, b DOE3, c DOE4, d DOE5, e DOE6, f DOE7, g DOE8 and h DOE9 under quasi-static loading

Full size image

3.2 Modeling results

In this section, in order to model the energy absorption characteristics, three methods of the response surface (linear and quadratic) and the artificial neural network were used.

3.2.1 Response surface method (RSM)

RSM is generally defined as a statistical regression method employing mathematical relations [33,34,35]. The first step in RSM is finding a formula between the response and independent variables. The mathematical expression of the linear and quadratic response surface method is as Eqs. 4 and 5, respectively [36,37,38,39]:

$$ \bar{Y}(X) = B_{0} + \sum {B_{i} X_{i} + \sum {B_{j} X_{j} } } $$
(4)
$$ \begin{aligned} \bar{Y}(X) & = B_{0} + \sum {B_{i} X_{i} + \sum {B_{j} X_{j} + \sum {B_{ii} X_{i}^{2} + \sum {B_{ij} X_{i} X_{j} + \sum {B_{jj} X_{j}^{2} + \cdots } } } } } \\ X & = X_{i,j, \ldots } \\ \end{aligned} $$
(5)

where Xi and Xj are inputs or predictors and B coefficients show the weight of each input in the output. For quadratic from Eq. 5, Bij coefficients show the two inputs interaction effect on the output.

3.2.2 Artificial neural network (ANN)

ANN model has been described by several researches in detail [40,41,42]. ANN is a nonlinear model which is composed of a large neuron collection. Neurons are connected to each other by links known as synapses, and there is a weight factor associated with each synapse [43,44,45]. A linear function can be calculated as follows:

$$ \eta_{l} = f(\beta_{l} ) = \theta_{l} + \sum\limits_{k = 1}^{p} {w_{lk} y_{k} } $$
(6)

where \( \eta_{l} \) is the response of the output layer, \( f(\beta_{l} ) \) is the transfer function associated with neuron l in the output layer, \( \beta_{l} \) is the sum of weighted input of neuron l, \( \theta_{l} \) is the bias, \( W_{lk} \) is the weight connection of neuron \( k \) and neuron l, and \( y_{k} \) is the input to the neuron l.

There are a lot of relations to evaluate the models; mean square error (MSE) is one of the most common relations

$$ {\text{MSE}} = \frac{{\sum\nolimits_{i = 1}^{M} {(y_{i} - \bar{y}_{i} )^{2} } }}{M} $$
(7)

In all three methods, 60% of the data was used for train and 40% for test. Figure 11a shows the PCL quantities extracted from three modeling methods in comparison with numerical results for train data. The error percent of each sample is shown in Fig. 11b for a better analysis. Figure 12a and b shows the results of the three methods of modeling compared with numerical results and their errors in test data, respectively.

Fig. 11
figure 11

a Comparison of PCL quantities extracted from three modeling methods with numerical results for train data, b error percent of each modeling method

Full size image
Fig. 12
figure 12

a Comparison of PCL quantities extracted from three modeling methods with numerical results for test data, b error percent of each modeling method

Full size image

The best model should be able to predict the minimum error in both train and test data. Hence, quadratic RSM was the best choice considering the least mean square error. The equation obtained for PCL from quadratic RSM is as follows:

$$ {\text{PCL}}(x_{1} ,x_{2} ) = 36.9928 - 3.0356x_{1} + 0.0221x_{2} + 1.6931x_{1}^{2} - 1.563x_{2}^{2} - 0.3932x_{1} x_{2} $$
(8)

where x1 represents \( C = \left( {\frac{a}{b}} \right) \) and x2 represents \( D = \left( {\frac{{d_{1} }}{{d_{2} }}} \right) \) in a direct manner. Related to Eq. 8, the effect of C is negative for the first order and is positive for D and, of course, negligible (see coefficients of x1 and x2); but the effect of C is positive in the second order and D is negative for this time. It is obvious that the effect of the shell aspect ratio is more than the diameter ratio of the cutout for PCL.

Figure 13a compares the results of the numerical analysis of MCL and modeling methods in training data. Also, the error percentage of each model is shown in Fig. 13b. Similarly, Fig. 14a and b shows the results of comparison between the modeling and numerical analysis of MCL and also their error in testing data, respectively. By checking the errors in both training and testing data, it can be seen that the least mean square error is related to quadratic RSM. Hence, like PCL, the quadratic RSM is the selected model for MCL. The equation obtained through the quadratic RSM for MCL is as follows:

$$ {\text{MCL}}(x_{1} ,x_{2} ) = 20.5727 - 2.4818x_{1} + 0.7092x_{1}^{2} - 1.3239x_{2}^{2} + 0.6313x_{1} x_{2} $$
(9)
Fig. 13
figure 13

Comparison of MCL results extracted from RSMs and ANN methods with numerical results for train data, b error percent of each modeling method

Full size image
Fig. 14
figure 14

Comparison of MCL results extracted from RSMs and ANN methods with numerical results for test data, b error percent of each modeling method

Full size image

Similar to PCL formula, x1 and x2 represent the C and D, respectively. As it is obvious in Eq. 9, the effect of C is negative for the first order and it is positive for the second order. Also, the effect of D is zero for the first order and negative for second order. It could be concluded that the behavior of MCL is mostly affected by the shell aspect ratio.

Based on the explanations in the previous part, the RSMs and ANN methods are used for modeling the SEA index, too. Figures 15 and 16 show the comparison of numerical data and the outcomes of the mentioned models and their relative errors for train and test data, respectively. The error analysis indicates that the least mean square error belongs to quadratic RSM. Therefore, similar to the PCL and MCL indices, quadratic RSM is more accurate for modeling SEA. The equation obtained through the quadratic RSM is shown in Eq. 10. Like before, x1 and x2 represent C and D, respectively. It is clear that the effect of both variables is positive for the first order, but the effect of D is negligible in comparison with C. Also, the effect of both variables is negative for the second order and it is obvious that the effect of C is more than D.

$$ {\text{SEA}}(x_{1} ,x_{2} ) = 12.212 + 3.4549x_{1} + 0.0426x_{2} - 1.0685x_{1}^{2} - 0.9269x_{2}^{2} + 0.4367x_{1} x_{2} $$
(10)
Fig. 15
figure 15

a Comparing SEA quantities extracted from three modeling methods with numerical results for train data, b error percent of each modeling method

Full size image
Fig. 16
figure 16

a Comparing SEA quantities extracted from three modeling methods with numerical results for test data, b error percent of each modeling method

Full size image

For a better comparison, the FEM results of the energy absorption characteristics and the selected model (quadratic RSM) results are presented in Table 3. The results indicate that the predictions of the selected model are clearly close to numerical results.

Table 3 Comparing the energy absorption characteristics in FEM and RSM
Full size table

Pearson correlation coefficient or the bivariate correlation (Pearson’s R), in statistics, is a measure of the linear correlation between two variables. It provides a measure of how well-observed experiments are predicted by the model. It has a value between +1 and − 1, where 1 is the total positive linear correlation, 0 is no linear correlation, and − 1 is the total negative linear correlation. The closer the value is to 1, the model provides a more accurate estimation of the results. Train and test regression plots for the mentioned energy absorption indices are shown in Figs. 17 and 18, respectively. It shows that the training R value for PCL, MCL and SEA is 0.99, 0.98 and 0.99 (Fig. 17), and the testing R values are 0.96, 0.99 and 0.93 (Fig. 18), respectively. Basically, the R value shows how much close the target values are to the output values. So, it can be said that quadratic RSM is well suited for predicting the energy absorption parameters.

Fig. 17
figure 17

The training R value for a PCL, b MCL and c SEA

Full size image
Fig. 18
figure 18

The testing R value for a PCL, b MCL and c SEA

Full size image

Based on the results obtained from the selected model, the behavior of each of the energy absorption parameters can be plotted as 3D graphs. Figures 19, 20 and 21 show the response surface of the PCL, MCL and SEA with design variables, C and D, respectively.

Fig. 19
figure 19

3D graph of PCL via different ratios of a/b and d1/d2

Full size image
Fig. 20
figure 20

3D graph of MCL via different ratios of a/b and d1/d2

Full size image
Fig. 21
figure 21

3D graph of SEA via different ratios of a/b and d1/d2

Full size image

3.3 Optimization results

Genetic algorithm (GA) was used to optimize the energy absorption parameters. A genetic algorithm is usually used to make high-quality solutions to optimize and search problems using bio-inspired operators. In genetic algorithm (GA), genes are expressed as a combination of binary 0 and 1. GA uses the independent variables. The binary type of GA was used in this work. In this type, each variable had a peculiar length based on its resolution.

As mentioned above, the ideal energy absorber should have low PCL and high SEA. Thus, in order to have an accurate optimization, a multi-objective optimization algorithm should be applied. This algorithm is derived from the multiple index decision making that is concerned with mathematical optimization problems including more than one objective function to be optimized simultaneously. Since the PCL and SEA are the most important crashworthiness indices, they were set as the goals of the multi-objective optimization. The optimized parameters were C and D. The multi-objective optimization is as follows:

$$ \left\{ {\begin{array}{*{20}l} {\text{Max}} \hfill & {{\text{SEA}} = f(C,D);} \hfill \\ {\text{Min}} \hfill & {{\text{PCL}} = f(C,D);} \hfill \\ {{\text{S}} . {\text{t}}} \hfill & {1 \le C \le 3} \hfill \\ {} \hfill & {0.5 \le D \le 1.3} \hfill \\ \end{array} } \right. $$
(11)

Based on this optimization, the best absorbent is a structure with C = 1 and D = 0.7.

4 Conclusion

In this paper, the effect of different aspect ratios and the elliptical cutout on crashworthiness of thin-walled structures with rectangular cross sections was proposed experimentally, numerically and mathematically. After implementing a DOE, the response surface method (quadratic and linear RSM) and artificial neural network (ANN) for FEM’s results were used to explore the effect of the geometrical factors on SEA, MCL and PCL. By comparing the mean squared error of each method, it was found that the quadratic RSM had the least error and was reported as the selected model. Regarding the relations extracted by quadratic RSM and the coefficients analysis, it was observed that the effect of the aspect ratio is greater than the diameter ratio on the absorption parameters. Finally, taking the aspect ratio and the diameter ratio as optimization parameters, the multi-objective optimization study was carried out using the genetic algorithm. Based on this optimization, the structure with C = 1 and D = 0.7 was introduced as the best absorbent. Compatible with these points, the optimum amounts of SEA and PCL were 14.48 kJ/kg and 34.62 kN, respectively.