1 Introduction

As an important component of rotating machinery, the health of bearing has an important impact on the reliability and safety of rotating machinery [1]. Hence, the effective and reliable remaining useful life (RUL) prediction of bearing is essential to formulate a timely maintenance schedule and improve the reliability of rotating machinery.

To date, most of the prediction methods can be generally divided into either model-based or data-driven methods. Compared with model-based methods [2, 3], the data-driven methods do not need to construct a complicated physical model and have been extensively applied in the RUL prediction of bearings. For example, Bastami et al. [4] utilized the artificial neural network and wavelet packet features to estimate the RUL of bearing. Zhu et al. [5] predicted the RUL of bearing by using the multi-scale convolutional neural network. Ren et al. [6] proposed a prediction framework for bearing based on auto-encoder and deep neural networks. However, instead of using direct monitoring signals, the above-mentioned data-driven prediction methods all need to utilize the indirect indicators to reflect the health status of bearing. Therefore, how to develop effective health indicators (HI) is crucial to simplify the data-driven-based prediction models and improve the accuracy of prediction [7].

The HI can be divided into physics HI (PHI) and virtual HI (VHI) according to their construction strategies [8]. The VHI only describes the degradation trend of machinery and has no clear physical significance. In contrast, the PHI is constructed by statistical methods or signal processing methods and is related to the physics of failures. In the existing literature of RUL prediction of bearing, a variety of PHIs have been applied to reflect the change of degradation trend and identify the physical failures. Among these PHIs, the root mean square (RMS) is the most widely used [2, 9,10,11,12]. For instance, Malhi et al. [13] utilized the peak value and RMS of the wavelet coefficients for the competitive learning-based preprocessing to predict the RUL of bearing. Gebraeel et al. [14] and Elwany et al. [15] constructed the PHI based on the average amplitude of the defective frequency and the first six harmonics. In addition, other HIs based on the statistical characteristics of time-domain signals were also constructed for bearing RUL prediction. For example, the correlation coefficient between two vibration signals was used to predict the RUL of bearing by Medjaher et al. [16]. Li et al. [17] extracted the degradation features based on mathematical morphology and proposed the general mathematical morphology particle for indicating the performance degradation of bearing. Singleton et al. [18] utilized the entropy of Cohen’s class of bilinear time–frequency distribution to construct the HI of bearing. Ali et al. [19] constructed the HI based on the energy entropy of the different intrinsic mode functions. Weibull distribution of the RMS entropy estimator was used as HI by Ali et al. [20]. Loutas et al. [21] utilized the Wiener entropy or spectral flatness as the HI for the RUL estimation of bearing. Qian et al. [22] extracted the recurrence plot entropy from the vibration signal for reflecting the degradation of bearing.

However, the vibration signals of bearings are often disturbed by ambient noise since the bearings are usually operated in complex environments. In addition, the amplitude of the impact will decrease due to the smoothing process which will occur on the surface of bearing failure when the bearing begins to degrade [23]. Therefore, although all the above-mentioned HIs can reflect the trend of bearing degradation, they also have some shortcomings in monotonicity and robustness, which will further affect the complexity and accuracy of the prediction models. Nevertheless, the development of PHIs with high monotonicity and robustness is in critical need to simplify the prediction models and improve the prediction accuracy.

To overcome the above-mentioned problem, this paper proposes a new HI based on the Wasserstein distance (WD) and the cumulative sum (CUSUM). First, a signal following the standard normal distribution is simulated as the reference signal. Then the WD between the reference signal and the monitoring signals of bearing is obtained after the frequency distribution histogram of the reference signal, and monitoring signals of the bearing are calculated. Finally, the CUSUM is used to amplify the fluctuation of the WD. The novelty (contribution) of this study includes (1) the distance between the distributions of vibration signals measured by WD is used to reflect the health status of bearings; and (2) the new HI constructed by WD and CUSUM significantly reduces the complexity of the model for predicting the RUL of bearings.

The rest of this paper is organized as follows. Section 2 introduces the theory of WD and CUSUM. In Sect. 3, the new health indicator is proposed. The effectiveness of the health indicator is evaluated by testing with three run-to-failure datasets in Sect. 4. In Sect. 5, the conclusion of this paper is drawn.

2 Theory Background

2.1 The theory of Wasserstein distance

The Wasserstein distance (WD) is a similarity measurement method of the distance between two distributions, and its essence is to measure the distance for weighted point sets. The WD is also known as Earth Mover’s distance [24]. In addition, it is the discrete version of the well-known Monge–Kantorovich mass transportation distance proposed by Mumford in 1991 [25]. To date, the WD has been widely applied in the color-based image retrieval [26], shape matching [27] and machine learning [28]. For two vibration signals of bearings \(X{ = }\left\{ {x_{1} ,x_{2} , \ldots x_{n} } \right\}\) and \(Y{ = }\left\{ {y_{1} ,y_{2} , \ldots y_{n} } \right\}\), the WD can be obtained as follows [29,30,31]:

Step 1: Calculate the frequency distribution histogram of the vibration signals. The histogram of the two vibration signals can be described as \(H_{X} = \left\{ {\left( {h_{X1} ,p_{X1} } \right),\left( {h_{X2} ,p_{X2} } \right), \ldots ,\left( {h_{Xm} ,p_{Xm} } \right)} \right\}\) and \(H_{Y} = \left\{ {\left( {h_{Y1} ,p_{Y1} } \right),\left( {h_{Y2} ,p_{Y2} } \right), \ldots ,\left( {h_{Yn} ,p_{Yn} } \right)} \right\}\), where \(h\) is the horizontal ordinate of the frequency distribution histogram, \(p\) is the ordinate of the frequency distribution histogram.

Step 2: Obtain the optimal flow. The WD is defined in terms of an optimal flow \(F = \left( {f_{ij} } \right)\), which minimizes

$$ {\text{WD}}\left( {H_{X} ,H_{Y} ,F} \right) = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {f_{ij} \cdot d_{ij} } } $$
(1)

where \(d_{ij}\) is the cost parameter which is some measure of dissimilarity between \(h_{Xi}\) and \(h_{Yj}\); \(d_{ij}\) is obtained by Euclidean distance in the following calculation, the \({\text{WD}}\left( {H_{X} ,H_{Y} ,F} \right)\) is the work required to move the earth from one histogram to another. The flow \(\left( {f_{ij} } \right)\) is subject to the following constraints:

$$ s.t.\left\{ {\begin{array}{*{20}l} {f_{ij} \ge 0{\kern 1pt} ,} \hfill & {1 \le i \le m,1 \le j \le n} \hfill \\ {\sum\limits_{j = 1}^{n} {f_{ij} \le p_{Xi} } ,} \hfill & {1 \le i \le m} \hfill \\ {\sum\limits_{i = 1}^{m} {f_{ij} \le p_{Yj} } ,} \hfill & {1 \le j \le n} \hfill \\ {\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {f_{ij} = \min \left( {\sum\limits_{i = 1}^{m} {p_{Xi} } ,\sum\limits_{j = 1}^{n} {p_{Yj} } } \right)} } } \hfill & {} \hfill \\ \end{array} } \right. $$
(2)

Step 3: Calculate the WD. Once the optimal flow \(f_{ij}^{ * }\) is found, the WD between the vibration signals of bearings \(X\) and \(Y\) can be calculated as

$$ {\text{WD}}\left( {X,Y} \right) = \frac{{\sum\nolimits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {f_{ij}^{ * } d_{ij} } } }}{{\sum\limits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {f_{ij}^{ * } } } }} $$
(3)

2.2 The theory of cumulative sum

The cumulative sum (CUSUM) is a control chart model which is proposed by Page [32] based on the likelihood ratio. The CUSUM can magnify the fluctuation of data by accumulating the difference between the measured value and the standard value. Therefore, the CUSUM has been widely used for monitoring the variability of the process. For a signal \(X{ = }\left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}\), the CUSUM can be obtained as follows [33, 34]:

Step 1: Select the reference samples. Select the first \(l\) samples from \(X\) as the reference samples, where \(l{ = }{n \mathord{\left/ {\vphantom {n 3}} \right. \kern-\nulldelimiterspace} 3}\) in the following calculation.

Step 2: Calculate the standard deviation of the reference samples. The standard deviation of the reference samples can be obtained as follows:

$$ \sigma { = }\sqrt {\frac{{\sum\nolimits_{i = 1}^{l} {\left( {x_{i} - \overline{x}} \right)^{2} } }}{l - 1}} $$
(4)

where \(\overline{x}\) is the mean of the reference samples.

Step 3: Obtain the CUSUM. The CUSUM calculates the upward and downward deviations from the target value as follows:

$$ {\text{CUH}}_{j}^{ + } = \max \left( {0,x_{j} - \left( {\delta_{0} + k} \right) + {\text{CUH}}_{j - 1}^{ + } } \right) $$
(5)
$$ {\text{CUH}}_{j}^{ - } = \max \left( {0,\left( {\delta_{0} - k} \right) - x_{j} + {\text{CUH}}_{j - 1}^{ - } } \right) $$
(6)

where \({\text{CUH}}_{j}^{ + }\) and \({\text{CUH}}_{j}^{ - }\) are the upward and downward CUSUM, respectively, \(\delta_{0}\) is the target value and \(\delta_{0} = \overline{x}\), \(k\) is the slack value and \(k = {\sigma \mathord{\left/ {\vphantom {\sigma 2}} \right. \kern-\nulldelimiterspace} 2}\).

3 The proposed health indicator

In general, the degradation process of the equipment is irreversible without being repaired or replaced, so the degradation trend of equipment tends to be monotonous upward or downward. Therefore, the HI with monotonicity is conducive to reflect the degradation of equipment. However, the degradation trend of equipment is often affected by environmental noise. The HI with robustness is conducive to improve the prediction result of the equipment. Therefore, a new WD- and CUSUM-dependent HI with monotonicity and robustness is proposed in this paper.

3.1 The effect of WD and CUSUM on the construction of proposed HI

In practice, the bearing signals without faults usually follow the Gaussian probability distribution. However, the bearing signals with faults always show the non-Gaussian characteristics when the bearing is under various fault conditions [35]. Figure 1 shows the life cycle of bearing and corresponding frequency distributions of bearing signals at different stages. As shown in Fig. 1, the (I), (II) and (III) are the monitoring signals of the normal condition, initial failure and serious failure of bearing, respectively. For normal condition (I), the probability density curve of the bearing signal is close to the normal distribution function which is estimated by the mean and variance of the signal (Fig. 1a).

Fig. 1
figure 1

The vibration signal of bearing. a The frequency distribution of (I); b the frequency distribution of (II); c the frequency distribution of (III)

Full size image

Therefore, the frequency distribution histogram of the bearing signal is the Gaussian distribution when the bearing is in good condition. However, for faulty conditions (II) and (III), the heavy tails are found in the frequency distribution histogram as shown in Fig. 1b, c. The probability density curves of the bearing signal (II) and (III) are far away from the normal distribution function which is estimated by the mean and variance of signal (II) and (III), respectively. In addition, the dominant tails of the frequency distribution histogram are dependent on fault degrees. The more fault degrees are, the heavier the tails of frequency distribution histogram will be. Accordingly, the corresponding frequency distribution histogram is farther away from the Gaussian distribution [36]. Therefore, the health status of bearings can be determined by the distance between the probability distributions of the vibration signals.

The WD has been used to effectively measure the distance between different distributions. Compared with Kullback–Leibler divergence (K–L divergence) and Jensen-Shannon divergence (JS divergence), the WD can still reflect the distance of two distributions even if the supporting sets of two distributions do not overlap or the overlap is little [37]. Therefore, the distance between different probability density distributions of bearings in different statuses can be effectively reflected by WD. Furthermore, the degradation process of bearings can be measured by WD.

In addition, the CUSUM can amplify the fluctuation of the signal by accumulating the difference between the value to be measured and the standard value even for small changes of signals. Hence, the fluctuation of the signal can be significantly reduced by CUSUM, which in turn improves the robustness of WD.

Therefore, the WD coupled with CUSUM can be used to construct the HI to reflect the health status of bearings and predict the RUL of bearings.

3.2 The framework of the proposed HI

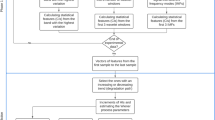
Through the above analysis, the degradation information of bearings can be effectively reflected by WD, while the monotonicity and robustness of WD can be effectively improved by CUSUM. Therefore, the WD-CUSUM can be used to predict the RUL of bearings. For the life-cycle monitoring signals of bearing \(X{ = }\left\{ {X_{1} ,X_{2} , \ldots X_{n} } \right\}\), where the \(X_{i} = \left\{ {x_{i1} ,x_{i2} , \ldots ,x_{im} } \right\}\) is the monitoring signal at the ith sampling point, \(n\) is the number of the monitoring signal, \(m\) is the length of a monitoring signal, the WD-CUSUM can be obtained as follows:

Step 1: Simulate a standard normal signal \(N\). Then calculate the frequency distribution histogram of \(N\).

Step 2: Calculate the frequency distribution histogram of \(X_{i}\). Then calculate the WD between the \(X_{i}\) and \(N\) according to the description in Sect. 2.1.

Step 3: Repeat Step 2 until the monitoring signals \(X\) are completely covered.

Step 4: Calculate the CUSUM of the WD between the monitoring signals \(X\) and standard normal signal \(N\). Then the WD-CUSUM of the life-cycle monitoring signals of bearing is obtained.

The calculation process is shown in Fig. 2.

Fig. 2
figure 2

The calculation process of the proposed method

Full size image

4 Result and discussion

To evaluate the performance of our proposed HI, three different run-to-failure datasets of the bearing are tested.

4.1 The description of datasets

The detailed information of these three datasets is described and also shown in Table 1.

Table 1 The detailed information of the three datasets
Full size table

Dataset 1 (IMS) This dataset is from the Center for Intelligent Maintenance Systems, University of Cincinnati (IMS) [38]. The four test bearings of type Rexnord ZA-2115 are installed on the same shaft which is rotating at a constant speed of 2000 RPM driven by an AC motor. 6000 lbs load is applied onto the shaft and bearing by a spring mechanism. A sampling frequency of 20 kHz is used. Each data record consists of 20,480 points. Two sets of life-cycle data (IMS #1 and IMS #2) are included in this dataset.

Dataset 2 (FEMTO-ST) This dataset is from the FEMTO-ST Institute [39]. The test bearings are driven by an asynchronous motor at the speed of 1800 RPM. 4000 N is applied onto the bearing by a force actuator, which consists of a pneumatic jack, where the supply pressure is delivered by a digital electro-pneumatic regulator. The sampling frequency is set to 25.6 kHz, and the vibration data are collected every 1 s. Each data record consists of 2560 points. Seven sets of life-cycle data are included in this dataset and named as bearing 1_1, bearing 1_2, bearing 1_3, bearing 1_4, bearing 1_5, bearing 1_6 and bearing 1_7, respectively.

Dataset 3 (HZ) This dataset is from Hangzhou Bearing Test and Research Center. The bearing test rig and installation position of bearing and sensor are shown in Fig. 3. The accelerometer is 1A110E of DONGHUA. The sensitivity of the sensor is ~ 5 mV/m s−2, and the range of the sensor is 1000 m s−2. The four test bearings of type HRB 6211 are installed on the same shaft which is rotating at a constant speed of 3000 RPM driven by an AC motor. A radial load of 15.97 kN is applied onto the bearing seat of bearing 2 and bearing 3. The details of the bearing are shown in Table 2. The sampling frequency is 20 kHz. Each data record which consists of 20,480 points is collected every 5 s. Four sets of life-cycle data are included in this dataset and named as HZ #1, HZ #2, HZ #3 and HZ #4, respectively.

Fig. 3
figure 3

Test rig and bearing installation information of HZ dataset. a bearing test rig, b installation position of sensor and bearing

Full size image
Table 2 Parameter information of 6211
Full size table

As shown in Table 1, although the fault locations of the bearing in FEMTO-ST are unknown, the three datasets can also represent different fault locations and operating conditions. Therefore, the three datasets are, respectively, used to evaluate the effect of the proposed HI.

4.2 Evaluation metrics for HIs

The complexity of prediction models and the prediction accuracy is greatly influenced by the performance of the HI. As mentioned above, the degradation process of the equipment is irreversible without being repaired or replaced, which is reflected by the monotonous upward or downward degradation trend. In addition, the monitoring signals of bearings are strongly influenced by environmental noise, which affects the robustness of HI. In this section, the monotonicity and robustness are used to evaluate the performance of the HI.

4.2.1 Monotonicity

In general, the monotonicity is considered as an inherent property of HI. The monotonicity metric based on the derivatives of the HI sequence is described as follows [40, 41]:

$$ {\text{Mon}}\left( {{\text{HI}}} \right) = \frac{1}{K - 1}\left| {{\text{No}}{.}{\kern 1pt} \,{\text{PD}} - {\text{No}}{.}{\kern 1pt} {\text{ND}}} \right| $$
(7)

where \(HI = \left\{ {hi_{1} ,hi_{2} , \ldots hi_{K} } \right\}\) is the HI sequence, \(K\) is the length of \(HI\), \({\text{No}}{.}\,{\kern 1pt} {\text{PD}}\) and \({\text{No}}{.}{\kern 1pt} \,{\text{ND}}\) are the number of the positive differences and negative differences, respectively. In this part, the positive differences and negative differences are defined as follows:

$$ {\text{PD:}}\,hi_{i + 1} - hi_{i} \ge 0 $$
(8)
$$ {\text{ND:}}\,hi_{i + 1} - hi_{i} < 0 $$
(9)

The value of monotonicity changes from 0 to 1. The higher the value obtained, the better performance of HI in monotonicity is.

4.2.2 Robustness

Smoothing method-dependent robustness can be used to describe how the HI responds to the environmental interferences. The smoother the degradation curve is, the more stable results can be obtained. The robustness metric is described as follows [41]:

$$ {\text{Rob}}\left( {{\text{HI}}} \right) = \frac{1}{K}\sum\nolimits_{i = 1}^{K} {\exp \left( { - \left| {\frac{{z_{i} - z_{i}^{S} }}{{z_{i} }}} \right|} \right)} $$
(10)

where \({\text{HI}} = \left\{ {hi_{1} ,hi_{2} , \ldots hi_{K} } \right\}\) is the HI sequence, \(K\) is the length of \({\text{HI}}\). In order to make the metric applied to the case that \(hi_{i} = 0\), the \({\text{HI}} = \left\{ {hi_{1} ,hi_{2} , \ldots ,hi_{K} } \right\}\) is transformed to \(Z = \left\{ {z_{1} ,z_{2} , \ldots ,z_{K} } \right\}\) by defining \(z_{i} = hi_{i} + \varepsilon\). \(\varepsilon\) is a small quantity. \(z_{i}^{S}\) is the mean trend value of HI at time \(t_{i}\) and can be determined by different smoothing methods. In this part, \(z_{i}^{S}\) is obtained by the cubical smoothing algorithm with five-point approximation [42]. The cubical smoothing algorithm with five-point approximation uses polynomial least square approximation to smooth the sampling points. The algorithm is simple and can obtain a good effect [43]. The \(z_{i}^{S}\) can be obtained as follows:

$$ \left\{ {\begin{array}{*{20}c} {z_{1}^{S} = \frac{1}{70}\left[ {69z_{1} + 4\left( {z_{2} + z_{4} } \right) - 6z_{3} - z_{5} } \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \\ {z_{2}^{S} = \frac{1}{35}\left[ {2\left( {z_{1} + z_{5} } \right) + 27z_{2} + 12z_{3} - 8z_{4} } \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \\ { \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \\ {z_{i}^{S} = \frac{1}{35}\left[ { - 3\left( {z_{i - 2} + z_{i + 2} } \right) + 12\left( {z_{i - 1} + z_{i + 1} } \right) + 17z_{i} } \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \\ { \vdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \\ {z_{K - 1}^{S} = \frac{1}{35}\left[ {2\left( {z_{K - 4} + z_{K} } \right) - 8z_{K - 3} + 12z_{K - 2} + 27z_{K - 1} } \right]} \\ {z_{K}^{S} = \frac{1}{70}\left[ { - z_{K - 4} + 4\left( {z_{K - 3} + z_{K - 1} } \right) - 6z_{K - 2} + 69z_{K} } \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \\ \end{array} } \right. $$
(11)

where \(i = 3,4, \ldots ,K - 2\).

4.3 The comparison of monotonicity and robustness of the three HIs

According to the steps described above, the monotonicity and robustness of WD-CUSUM-based HI of the three life-cycle datasets are calculated as shown in Figs. 4, 5 and 6. In addition, these results are also compared with the monotonicity and robustness of the RMS and kurtosis which are the two most common HI to reflect the degradation of bearings.

Fig. 4
figure 4

The evaluation metrics of the three indicators of IMS datasets

Full size image
Fig. 5
figure 5

The evaluation metrics of the three indicators of the FEMTO-ST Institute datasets

Full size image
Fig. 6
figure 6

The evaluation metrics of the three indicators of the Hangzhou datasets

Full size image

As shown in Figs. 4, 5 and 6, for the three datasets, the monotonicity of WD-CUSUM is the highest. Compared with the kurtosis, the RMS and WD-CUSUM all have higher robustness. Meanwhile, for most of the data, the robustness of the WD-CUSUM is the highest. It means that the WD-CUSUM has a better monotonic trend and smooth curve. However, for different datasets, there may be some differences in the monotonicity and robustness of the datasets due to the different test environments. For example, as shown in Fig. 5, for the FEMTO-ST Institute datasets, although the monotonicity of WD-CUSUM is the highest among the three indicators, some bearings are not as high as that of IMS datasets. The reasons should be as follows. On the one hand, the vibration signal of bearings can be affected by loading. The amplitude and distribution of vibration signals may change when the bearing is loaded. On the other hand, the recorded points of each data are too few to fully reflect the distribution of vibration signals in normal and fault situations. Therefore, the monotonicity of WD-CUSUM of these datasets may be lower than that of IMS datasets. However, the monotonicity and robustness of WD-CUSUM of these datasets are also the highest among the three indicators. Meanwhile, the monotonicity of the seven bearings varies greatly. To illustrate this phenomenon, the simple vibration waveforms of the seven bearings are given as Fig. 7, where only 2000 points are used for each sampling data. The red line is the vibration range of the initial vibration signal.

Fig. 7
figure 7

The vibration signals of the seven bearings

Full size image

As shown in Fig. 7, there are two main reasons for the different monotonicity of the seven bearings. (1) The influence of environmental noise is on the vibration signal. Like bearing 1_2 and bearing 1_6, there are a lot of obvious burrs in vibration signals due to the interference of environmental noise. (2) The stability of vibration signals is in the normal stage of bearing. The vibration signal in the normal stage of bearing should be stable when the bearing is under normal conditions. However, for bearing 1_5 and bearing 1_7, the vibration signal in the normal stage of bearing is sometimes lower than the red line. Therefore, at this time, the non-fault amplitude fluctuation of bearing vibration signal occurs. However, for bearing 1_1, bearing 1_3 and bearing 1_4, there are no obvious burrs in the vibration signal and the vibration signal in the normal stage of bearing is stable. Therefore, the monotonicity of bearing 1_1, bearing 1_3 and bearing 1_4 is higher than that of the other bearings.

In addition, for the Hangzhou datasets, as shown in Fig. 6, the monotonicity of WD-CUSUM is the highest among the three indicators and is basically the same as that of IMS datasets except the HZ #4. The reason is that the initial load affects the monotonicity of the WD-CUSUM. Meanwhile, for the HZ #1 and HZ #3, the robustness of WD-CUSUM is not the highest because the test environment has less interference. However, consistent with the above two datasets, the WD-CUSUM of these datasets also has good robustness.

Altogether, for the datasets with different fault locations in different test environments, although there are some differences in the monotonicity and robustness due to the different test environments, the monotonicity of the WD-CUSUM is the highest among the three indicators. In addition, the WD-CUSUM also has good robustness. Hence, compared with RMS and kurtosis, the WD-CUSUM has better monotonicity and robustness on the whole. Therefore, the WD-CUSUM can be effectively used for the RUL prediction of bearings.

4.4 The comparison of predicted results of the three HIs

In this part, the RUL of bearings is predicted according to the three HIs mentioned above to illustrate the performance of the three indicators in the prediction. The effective HI can simplify the prediction models. Besides, the regression model as the simplest trend prediction model is widely used in trend prediction [44, 45]. Therefore, in this part, the regression model is simply used to illustrate the performance of WD-CUSUM in the RUL prediction. Specifically, the \(\alpha { - }\lambda\) performance metric [46, 47] is also widely used to evaluate the performance of prediction. Therefore, the prediction results of the three indicators (RMS, kurtosis, and WD-CUSUM) are evaluated by \(\alpha { - }\lambda\) performance metric, where the \(\alpha\) is the upper and lower bounds of prediction error and the \(\lambda\) is the relative time distance between a given point and the end of bearing life [44]. For the IMS datasets, the two bearings (IMS #1 and IMS #2) are all used to illustrate the performance of prediction. However, for the FEMTO-ST Institute datasets, as the above analysis, not all the bearings can be used for prediction due to the monotonicity which is influenced by the test environment and recorded points. Hence, the three bearings (bearing 1_1, bearing 1_3 and bearing 1_4) which have good monotonicity are selected to illustrate the performance of prediction. In addition, for the Hangzhou datasets, as there are few data points in the degradation stage of HZ #2 and HZ #3, the HZ #1 and HZ #4 are selected to illustrate the performance of prediction. The waveforms of the three indicators of the selected bearings are, respectively, shown in Figs. 8, 9 and 10. The \(\alpha { - }\lambda\) performance metrics of them are, respectively, shown in Figs. 11, 12 and 13.

Fig. 8
figure 8

The HI of IMS datasets

Full size image
Fig. 9
figure 9

The HI of FEMTO-ST Institute datasets

Full size image
Fig. 10
figure 10

The HI of the Hangzhou datasets

Full size image
Fig. 11
figure 11

The \(\alpha { - }\lambda\) performance metric of IMS datasets

Full size image
Fig. 12
figure 12

The \(\alpha { - }\lambda\) performance metric of FEMTO-ST Institute datasets

Full size image
Fig. 13
figure 13

The \(\alpha { - }\lambda\) performance metric of the Hangzhou datasets

Full size image

As shown in Figs. 8, 9 and 10, the WD-CUSUM has better monotonic trend and smooth curve than RMS and kurtosis. These further prove the above calculation results in Sect. 4.3. In addition, compared with RMS and kurtosis, although the initial point of the degradation stage of WD-CUSUM is not the earliest, this is the easiest to be detected. And it is not necessary to be detected by other additional methods.

As shown in Figs. 11, 12 and 13, for the three datasets, the predicted RULs by WD-CUSUM all lie within the acceptable error bounds even if the simplest prediction model is used. And the predicted RULs are all closer to the actual RULs. However, for the RMS, only the predicted RUL of bearing 1_1 lies within the acceptable error bounds. The parts of the predicted RUL of IMS #2 and bearing 1_4 lie within the acceptable error bounds. The other predicted RULs are all not within the acceptable error bounds. In addition, the predicted RUL of HZ #1 is not convergent. For the kurtosis, all the predicted RULs are not convergent because there are no obvious trends in the degradation stage. Therefore, the WD-CUSUM can be effectively used to predict the RUL even though the prediction model is the simplest. To summarize, for the three datasets, the WD-CUSUM all have a better monotonic trend and smooth curve than RMS and kurtosis and can be effectively used to predict the RUL even though the prediction model is the simplest.

Altogether, through the comprehensive analysis of the above three run-to-failure datasets, the WD-CUSUM has strong applicability for the three datasets. The performance of WD-CUSUM is well whatever operating conditions and fault locations. Besides, the monotonicity and robustness of WD-CUSUM are the best among the three indicators. In addition, the initial point of the degradation stage of the WD-CUSUM can be detected more easily. And it is unnecessary to be detected by other additional methods. Meanwhile, predicted RULs by WD-CUSUM are all closer to the actual RULs even if the simplest prediction model is used. Therefore, the WD-CUSUM cannot only be effectively used as the HI to reflect the degradation of bearings, but also can be effectively used to predict the RUL of bearings.

5 Conclusions

To improve the prediction accuracy and simplify the prediction model, this paper proposes a new HI for RUL prediction of bearing. The conclusions drawn from this study are summarized as follows:

  1. 1.

    The degradation trend of bearing can be reflected by the change of the distribution of vibration signal. And the WD can effectively reflect the change of distribution of vibration signal in numerical form and further reflect the degradation state of bearing from the perspective of the distribution of vibration signal.

  2. 2.

    Through the verification of the run-to-failure dataset of the IMS, the FEMTO-ST Institute and the Hangzhou Bearing Test and Research Center, it is proved that the proposed HI has better monotonicity and robustness than RMS and kurtosis for the datasets with different fault locations under different operating conditions.

  3. 3.

    And the initial point of the degradation stage of the WD-CUSUM can be detected more easily.

  4. 4.

    In addition, the WD-CUSUM can also be used to predict the RUL of bearing by a simple prediction model effectively.

In conclusion, the proposed HI can be effectively applied to the RUL prediction of bearing. Although some important problems associated with the proposed HI have been investigated in this paper, there are still a few questions worthy of further consideration. The WD-CUSUM only pays attention to the change of vibration signal distribution in the degradation process of bearings, and the HI considering the multi-degradation information of bearings deserves further study.