1 Introduction

In the manufacturing field, most challenges faced by the technologists and engineers are with the development of technology. A lot of new engineering materials have been developed, in recent years. These materials have many new engineering potential applications. Because of the high machining cost, applications of these materials are limited. A cost-effective advance machining process is required for these materials. The ultrasonic machine with rotation is one of the advanced machining process. A rotary ultrasonic machine is a hybrid machine. Rotary ultrasonic machine combines the mechanism of the ultrasonic machine (USM) and diamond grinding for the material removal. Ultrasonic machine and diamond grinding have the low material removal rate as compared to the rotary ultrasonic machine [1]. This machine can be useful for machining of these materials.

Percy Legge invented the rotary ultrasonic machine in 1964. In RUSM, the slurry was released and a rotating workpiece had been replaced by the vibrating impregnated tool. At the United Kingdom Atomic Energy Authority (UKAEA), further improvement has been done. Close tolerances are achieved by the rotating ultrasonic transducer head, and it is required to build it practicable for stationary workpieces. For different shapes of tools, range of the operations could extend to tee slotting, end milling, and internal–external grinding [1]. The sting of the abrasive particles is progressively depredated, during the machining operation. Fresh supply of abrasive slurry is required, which is supplied in machining zone. Machined chips and grains of the work piece are flushed out at the same time [2, 3]. The method of ultrasonic depends on the abrasion phenomenon. Blows from the grains of the harder abrasion, brittle materials are removed [4,5,6]. Abrasion phenomenon is under curb of the tool, which regularly vibrates with low amplitude (5–75 µm) and feed [1]. The abrasives also cause wear in the tool, but this is minimized by making the tool of a ductile material. The particles of abrasive are themselves cleaved in the process and so must be gradually replaced by running a liquid carrying fresh abrasive into the working area, which also serves to flush away the product. The material is cut away as very small particles, but these are produced by many abrasive grains and the tool which vibrates at a high frequency (20–25 kHz), so total rate is sufficient for practical purposes [7].

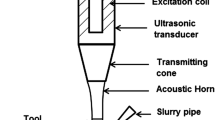
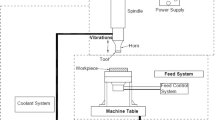
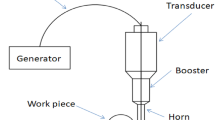
Figure 1 shows the set-up of rotary ultrasonic machine. In this figure, the electrical energy received from the pulse generator is converted into mechanical vibration, and then, the vibrator or resonance transducer acts as the base of mechanical oscillations. For the realization of cutting process, the amplitude is insufficient in rotary ultrasonic machine. To manage this insufficiency, horn is used. Horn (tool holder or concentrator) is fitted at the end of transducer. Horn cross-sectional area decreases from upper to lower end. At the input end transducer is there, and at the output end the tool. Horn amplifies the amplitude at input (transducer) end of horn, so at output (tool) end amplitude is sufficiently high for the machining. For making a hole in the workpiece, the tool is attached at the horn end. The system of vibration is formed by a tool, horn, and transducer mounted on a stand, with the help of a special clamping system.

Fig. 1
figure 1

Set-up of rotary ultrasonic machine

Full size image

Rozenberg et al. [1] have suggested that the current techniques for the mechanical working of ordinary materials have been highly developed and also improved in recent years. Ultrasonic cutting has the ability to solve complex and varied problems raised by the rapid advancement in the technology. Seah et al. [8] have suggested the three methods of the simulation for obtaining the frequencies in the modal analysis. Results are correlated with experimentally measured frequency. They investigated the design of efficient concentrators for the conventional ultrasonic machining process by employing the finite element analysis. Because of the low stresses generated in the conical horn, they suggested that the chances of failure by the fatigue loading are negligible. They also suggested that the stepped horn faces stress concentration if the radius of curvature of corners is small. This stress concentration leads to overheating and formation of crack. Amin et al. [9] have suggested horn design for the ultrasonic machine using FEA. They have also studied the amplification and the stresses in the horn. In the design of a double conical horn profile, at the lower part, cylindrical portion has been suggested. For obtaining the maximum magnification factor, optimization procedure has been used. After the safe working stresses for higher MRR, the concentrator material has been suggested. They also show that the concentrator profile should be cylindrical in shape at the lower (tool) end and conical shape at the upper (transducer) end. Thoe et al. [10] have suggested that the rotary ultrasonic machine has better performance as compared to the conventional ultrasonic machine. It is proposed the combined effect of the indentation of the workpiece surface, rolling contacts between the workpiece and free abrasive grains and sliding contact between the workpiece and embedded grains. They also show that the design of the tool and tool holder plays an important role in providing the resonant ultrasonic machining system to maximize MRR. Ya et al. [11] have suggested the movement of the abrasive particles in the tooltip of the RUSM, and the movement of abrasive particles is taken into consideration. They also developed a theoretical model for MRR of the machining process of RUSM. They show a model of MRR for RUSM combined with CNC technology. They also show that the MRR is affected by the concentration of abrasives, static load, grid, feed rate of a workpiece, the material of tool, and mechanical properties of the machined surface and rotational speed of the tool. Yadava and Deoghare [12] have analysed and designed the concentrator by employing the finite element method for the rotary ultrasonic machine with the same working condition as of the conventional ultrasonic machine. They also show that for the same boundary conditions and material properties the amplification factor is more for the RUSM as compared to the conventional ultrasonic machine. They also show that the stresses obtained for the other conditions are more than the stresses obtained for the resonance. Wang et al. [13] have suggested the new horn with a high magnification factor. A design procedure using FEA and multi-objective optimization algorithm has been developed to optimize the magnification factor. The frequency of the designed horn has been compared with the fabricated horn and found in good agreement. Rosca et al. [14] have suggested the horn design, which is used in mechanical manufacturing processes. The high amplification waves have been injected on the workpiece. In establishing the resonance condition, the dimensions of both the ultrasound transducer and tool are important. Roy et al. [15] have suggested the design of circular hollow horn for ultrasonic machine and use of FEA for determining the resonance frequency, the amplitude of vibration, and the stress components over the horn. This work attempts to establish a new design of ultrasonic horn, which is able to generate a higher amplitude of vibration at the tool end and simultaneously, experiencing the least equivalent stress compared to other designs. Naseri et al. [16] have suggested that the purpose of this investigation is to design a horn suitable for the application of UV on the ECAP process. To achieve maximum required load reduction, the whole system must be vibrated in one of the natural frequencies. Therefore, the natural frequency of the horn as the main part of the vibration set-up has been numerically and experimentally obtained using the modal analysis. Kumar et al. [17] have attempted to carry out a detailed design analysis of simple and complex horns in order to minimize the failure of horn attachments and maximize ultrasonic energy utilization. Razavi et al. [18] have suggested that for the calculation of the natural frequency and amplification factor the numerical analysis and analysis of free vibrations have initially performed with simple geometry for a five-element horn. Then, the numerical modal analysis of an ultrasonic-assisted surface rolling has been performed both assembled and individually in a complete ultrasonic-assisted surface rolling system. Wang et al. [19] have suggested that from the ultrasonic radiator configuration point of view a new design method is present in this study, which applies a stepped-plate to the horn end. For designing a stepped-plate radiator, the combination of mapping the acoustic field with arc-acoustic interaction using welding experimental measurements provides directive evidence. Firstly, to evaluate the ultrasonic action on the welding arc, the arc characteristic measurements were investigated in ultrasonic wave-assisted gas tungsten arc welding (U-GTAW).

In the above literature review, to get the low value of stresses and maximum amplitude of vibration for the resonance condition, horn design of different shape has been done. During the process, it is observed that the design of the horn of conical, exponential, cylindrical, stepped and some other shapes for the RUSM and the conventional ultrasonic machine have been done. The work has been done experimentally and theoretically for the RUSM and conventional ultrasonic machine for finding the MRR. The literature review shows that the theoretical model for the RUSM by using optimization procedure and FEA for the design of horn with quadratic and cubic Bezier profiles have not been done. Also, the effect of frequencies on the stress distribution for horn with Bezier profiles of the RUSM has been rarely studied. In this paper, the main aim is to design of quadratic and cubic Bezier horn for the RUSM. Firstly, multiobjective optimization techniques have been used for optimizing the control points of cubic and quadratic Bezier profiles. In this paper, the FEA-based MATLAB code has been developed to find the stress components, axial amplitude, and resonance frequency over the domain of different horn with Bezier profiles for the RUSM. For validation, the results are compared with available literature. The effect of frequencies on the stress distribution for horn with Bezier profiles of the RUSM has also been studied.

2 Horn design

The design of horn with Bezier profile for high amplification is based on the optimization procedure where the profile of the horn has been optimized by parameters of cubic and quadratic curve to meet the requirement of magnification. The quadratic Bezier curve is determined by a three point Bezier polygene L0, L1, L2 as shown in Fig. 2. The cubic Bezier curve is determined by a four point Bezier polygene L0, L1, L2, L3 as shown in Fig. 3. As described by Ibrahim Zeid [20], the last and first points, L2 and L0, respectively, on the curve are coincident with the last and first points of defining polygon for quadratic Bezier profile. Similarly also as described by Ibrahim Zeid [20], the last and first points, L3 and L0, respectively, on the curve are coincident with last and first points of defining polygon for cubic Bezier profile.

Fig. 2
figure 2

Quadratic Bezier profile and its three control points L0, L1 and L2

Full size image
Fig. 3
figure 3

Cubic Bezier profile and its four control points L0, L1, L2 and L3

Full size image

At the ends of the curve, the tangent vectors have the same directions as the last and first polygon spans, respectively. The parametric quadratic and cubic Bezier curves are given by Eqs. (1) and (2) [20]

$$P(u) = \left[ {\begin{array}{*{20}c} {(1 - u)^{2} } & {2u(1 - u)} & {u^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {P_{{L_{0} }} } \\ {P_{{L_{1} }} } \\ {P_{{L_{2} }} } \\ \end{array} } \right]\quad 0 \, \le u \le \, 1$$
(1)
$$P(u) = \left[ {\begin{array}{*{20}c} {(1 - u)^{3} } & {3u(1 - u)^{2} } & {3u^{2} (1 - u)} & {u^{3} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {P_{{L_{0} }} } \\ {P_{{L_{1} }} } \\ {P_{{L_{2} }} } \\ {P_{{L_{3} }} } \\ \end{array} } \right]\quad 0 \, \le u \le \, 1$$
(2)

where u is the parameter, and PLi is the position vector of the point Li.

The profile of the horn is optimized by allowing points L1 for quadratic Bezier and L1, L2 for cubic Bezier to move in the design space enclosed by the dashed rectangle in Figs. 2 and 3, respectively. The positions of the cubic Bezier points L0 and L3 are fixed by the specified back and front radii of horn, R1 and R2, and also that for quadratic Bezier L0 and L2 are fixed by the specified back and front radii of horn, R1 and R2, and length of the horn Z. The horn is assumed to be axisymmetric. An optimization flow chart has been shown in Fig. 4. For optimization of cubic and quadratic Bezier horn profile, the non-dominated sorting genetic algorithm [21] is applied. The Similar multiobjective optimization approach has been adopted by Wang et al. [13]. In each generation of genetic algorithm, the following are performed.

Fig. 4
figure 4

Optimization flowchart

Full size image

  • Select the parents which are fit for reproduction; parents are selected for reproduction to generate off spring. In the binary tournament selection process, two individuals are selected at random and their fitness is compared. The crowded comparison operator guides the selection process at the various stages of the algorithm towards a uniformly spread-out Pareto-optimal front [21].

  • Perform mutation and crossover operator on the selected parents. The algorithm uses simulated polynomial mutation and binary crossover [21].

  • Once the population is sorted based on the non-dominated sorting algorithm, perform selection from parents and offspring; only best solution is selected.

  • To maintain a constant population size, replace the unfit individuals with fit individuals.

The optimization process is shown in Fig. 4, initially the working frequency f and the geometry parameters R1, R2 and Z are specified. The objective functions of the optimization problem are

$$\begin{aligned} & {\text{Min}}(f \, {-} \, f_{0} )_{{}} \\ & {\text{Max}}\quad M = \frac{{u_{{L_{3} }} }}{{u_{{L_{0} }} }} \\ \end{aligned}$$
(3)

where f0 is the first longitudinal modal frequency of the population of each generation of the horn. M is the amplification defined by the ratio of the longitudinal displacement at lower end to upper end of the horn. To solve the two objective optimization problems, the fast non-dominated sorting approach [21] is used. In the sorting procedure, the concept of Pareto dominance [22] is utilized to evaluate fitness or assigning selection probability to solution. Table 1 is showing the merits and demerits aspects of several commonly used horn profiles.

Table 1 Merits and demerits aspects of several commonly used horn profiles
Full size table

3 Mathematical modelling and finite element formulation

The main purpose of the horn is to amplify the displacement (amplitude) produced by transducer and transmit to tool. The shape of the horn with decreasing cross-sectional area is shown in Fig. 2. Assumptions made in this theory are as follows:

  1. 1.

    Horn material is homogeneous isotropic and material property along the length of the horn is constant.

  2. 2.

    Vibration of the rod is harmonic.

  3. 3.

    In the cutting operation, transverse compression of the horn is neglected.

  4. 4.

    For the workpiece, tool, and horn, the slurry acts as the coolant, removes the debris from cutting zone, and at cutting zone supplies fresh abrasive.

3.1 Governing equations of axisymmetric horn

For the calculation of stresses in the axisymmetric horn, the equation of equilibrium [23,24,25] is given by (4),

$$\begin{aligned} & \frac{{\partial \sigma_{RR} }}{\partial R} + \frac{{\partial \sigma_{RZ} }}{\partial Z} + \frac{{ \sigma_{RR} - \sigma_{\theta \theta } }}{R} + b_{R} = 0 \\ & \frac{{\partial \sigma_{RZ} }}{\partial R} + \frac{{\partial \sigma_{ZZ} }}{\partial Z} + \frac{{ \sigma_{RZ} }}{R} + b_{Z} = 0 \\ \end{aligned}$$
(4)

where σRR, σZZ and σθθ are the radial, axial, and circumferential stress in the R, Z, and θ directions, respectively, σRZ is the shear stress in RZ plane, bZ, bR are the body forces in the Z and R directions, respectively.

If the radius of the horn is higher in comparison with thickness, tangential and radial stresses over the thickness can be neglected. If the radius of the horn is smaller than thickness, then the body forces are equal to inertia forces. [23,24,25] then,

$$b_{Z} = \, 0 \,\, {\text{and}}\,\, b_{R} = \rho \omega^{2} R$$

So Eq. (4) becomes

$$\begin{aligned} & \frac{{\partial \sigma _{{RR}} }}{{\partial R}} + \frac{{\partial \sigma _{{RZ}} }}{{\partial Z}} + \frac{{\partial \sigma _{{RR}} - \partial \sigma _{{\theta \theta }} }}{R} - \rho \omega ^{2} R = 0 \\ & \frac{{\partial \sigma _{{RZ}} }}{{\partial R}} + \frac{{\partial \sigma _{{ZZ}} }}{{\partial Z}} + \frac{{\sigma _{{RZ}} }}{R} = 0 \\ \end{aligned}$$
(5)

The longitudinal compression and extension takes place, due to the vibration of rod [26,27,28]. Hence Eq. (5) becomes

$$\begin{aligned} & \frac{{\partial \sigma_{RR} }}{\partial R} + \frac{{\partial \sigma_{RZ} }}{\partial Z} + \frac{{ \sigma_{RR} - \partial_{\theta \theta } }}{R} + \rho \omega^{2} R = \rho \frac{{\partial^{2} u_{R} }}{{\partial t^{2} }} \\ & \frac{{\partial \sigma_{RZ} }}{\partial R} + \frac{{\partial \sigma_{ZZ} }}{\partial Z} + \frac{{ \sigma_{RZ} }}{R} = \rho \frac{{\partial^{2} u_{Z} }}{{\partial t^{2} }} \\ \end{aligned}$$
(6)

where \(\rho \frac{{\partial^{2} u_{Z} }}{{\partial t^{2} }}\) and \(\rho \frac{{\partial^{2} u_{R} }}{{\partial t^{2} }}\) are the inertia forces in Z and R directions, respectively, so Eq. (6) is the governing equation of any shape of rotating horn (such as, stepped, conical, exponential, and cylindrical).

3.2 Boundary conditions of axisymmetric horn

At the transducer end, the initial amplitude is given; essential boundary condition (EBC) is given as.

$$u_{R} = u_{R}^{* } \;\; u_{Z} = u_{Z}^{* } \; \left( {{\text{At }}\,{\text{the}}\,{\text{ end}}\,{\text{ of}}\,{\text{ the}}\,{\text{ transducer}}} \right)\,{\text{ on }}\,B_{u}$$

where u*R is displacement in radial direction and the value is 0 and u*Z is the displacement in longitudinal direction and the value is 15 µm at the end of the transducer CD as shown in Fig. 5. Equation (7) shows the natural boundary condition.

$$\begin{array}{*{20}c} {\sigma_{RR} n_{R} + \sigma_{RZ} n_{Z} = t_{R} } \\ {\sigma_{RZ} n_{R} + \sigma_{ZZ} n_{Z} = t_{Z} } \\ \end{array} \quad B_{q} \;\left( {{\text{DABC}}} \right)\;{\text{on}}\;{\text{traction}}\;{\text{boundary}}$$
(7)

where tR and tZ are the traction forces and nR and nZ are the unit vectors.

Fig. 5
figure 5

Domain of Bezier profile horn with a cubic, b quadratic

Full size image

3.3 Finite element formulation of the axisymmetric horn

The linear and bilinear elemental equation is given in the matrix form related to the nodal value at the given nodes,

$$(\left[ K \right]^{e} - \omega^{2} \left[ M \right]^{e} )\left\{ u \right\}^{e} = \left\{ {f_{b} } \right\}^{e} + \left\{ {f_{t} } \right\}^{e}$$
(8)

where

$$\begin{aligned} \left[ K \right]^{e} & = \int\limits_{D} {\left[ B \right]}^{eT} \left[ D \right]\left[ B \right]^{e} R{\text{d}}R{\text{d}}Z \\ \left[ B \right]^{e} & = \left[ {\begin{array}{*{20}c} {\frac{{\partial N^{e}_{1} }}{\partial R}} & 0 & {\frac{{\partial N^{e}_{2} }}{\partial R}} & 0 & . & . & . & . & {\frac{{\partial N^{e}_{nne} }}{\partial R}} & 0 \\ {\frac{{N^{e}_{1} }}{R}} & 0 & {\frac{{N^{e}_{2} }}{R}} & 0 & . & . & . & . & {\frac{{N^{e}_{nne} }}{R}} & 0 \\ 0 & {\frac{{\partial N^{e}_{1} }}{\partial Z}} & 0 & {\frac{{\partial N^{e}_{2} }}{\partial Z}} & . & . & . & . & 0 & {\frac{{\partial N^{e}_{nne} }}{\partial Z}} \\ {\frac{{\partial N^{e}_{1} }}{\partial Z}} & {\frac{{\partial N^{e}_{1} }}{\partial R}} & {\frac{{\partial N^{e}_{2} }}{\partial Z}} & {\frac{{\partial N^{e}_{2} }}{\partial R}} & . & . & . & . & {\frac{{\partial N^{e}_{nne} }}{\partial Z}} & {\frac{{\partial N^{e}_{nne} }}{\partial R}} \\ \end{array} } \right] \\ \left[ D \right] & = \frac{E}{(1 + \mu )(1 - 2\mu )}\left[ {\begin{array}{*{20}c} {1 - \mu } & \mu & \mu & 0 \\ \mu & {1 - \mu } & \mu & 0 \\ \mu & \mu & {1 - \mu } & 0 \\ 0 & 0 & 0 & {\frac{1 - 2\mu }{2}} \\ \end{array} } \right] \\ \left[ M \right]^{e} & = \int\limits_{D} { \rho \left[ N \right]}^{eT} \left[ N \right]^{e} u \cdot R{\text{d}}R{\text{d}}Z \\ \left\{ {f_{b} } \right\}^{e} & = \int\limits_{{B_{q} }} {\left[ N \right]}^{eT} \rho n^{2} R \cdot {\text{d}}B_{q} \\ \left\{ {f_{t} } \right\}^{e} & = \int\limits_{{B_{q} }} {\left[ N \right]}^{eT} t_{Z} {\text{d}}B_{q} \\ \left\{ \sigma \right\}^{e} & = \left\{ {\begin{array}{*{20}c} {\sigma_{RR} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{ZZ} } \\ {\sigma_{RZ} } \\ \end{array} } \right\}^{e} \\ \end{aligned}$$
(9)

One-dimensional quadrature formulae are following

$$\begin{aligned} \int {F(\varepsilon ,\eta ){\text{d}}\varepsilon {\text{d}}\eta } & \approx \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {F(} \varepsilon_{i} ,\eta_{j} ) \cdot w_{i} w_{j} } \\ & \approx \int\limits_{ - 1}^{1} {\left[ {\sum\limits_{j = 1}^{n} {F(\varepsilon_{i} ,\eta_{j} )w_{j} } } \right]} {\text{d}}\varepsilon \\ & \approx \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {F(} \varepsilon_{i} ,\eta_{j} ) \cdot w_{i} w_{j} } \\ \end{aligned}$$
(10)

3.4 Assembly

The Assembly of the elemental equation is given by equation

$$([GK]_{nnm \times nnm} - \omega^{2} \left[ {GM} \right]_{nnm \times nnm} )\left\{ u \right\}_{nnm \times 1} = \left\{ {GF} \right\}_{nnm \times 1}$$
(11)

Where

$$\begin{aligned} \left[ {GK} \right]_{nnm \times nnm} & = \sum\limits_{e = 1}^{nem} {[K]^{e}_{nne \times nne} } \\ \left[ {GM} \right]_{nnm \times nnm} & = \sum\limits_{e = 1}^{nem} {[M]^{e}_{nne \times nne} } \\ \left\{ {GF} \right\}_{nnm \times 1} & = \sum\limits_{e = 1}^{nem} {\left\{ f \right\}^{e}_{nnb \times 1} } \\ \end{aligned}$$
(12)

3.5 Application of the essential boundary condition (EBC)

After application of EBC, the modified global equation of the form is

$$\left( {\left[ {\widehat{GK}} \right]_{nnm \times 2 \times nnm \times 2} - \omega^{2} \left[ {\widehat{GM}} \right]_{nnm \times 2 \times nnm \times 2} } \right)\left\{ u \right\}_{nnm \times 2 \times 1} = \left\{ {\widehat{GF}} \right\}_{nnm \times 2 \times 1}$$
(13)

3.6 Calculation of stress of an axisymmetric horn

Displacement–strain relationship is presented by the [26, 27]

$$\left\{ \in \right\}^{e} = \left\{ {\begin{array}{*{20}c} { \in_{RR} } \\ { \in_{\theta \theta } } \\ { \in_{ZZ} } \\ { \in_{RZ} } \\ \end{array} } \right\}^{e} = \left\{ {\begin{array}{*{20}c} {\frac{\partial u}{\partial R}} \\ {\frac{u}{R}} \\ {\frac{\partial v}{\partial Z}} \\ {\frac{\partial u}{\partial Z} + \frac{\partial v}{\partial R}} \\ \end{array} } \right\}^{e} = \left[ B \right]^{e} \left\{ u \right\}^{e}$$
(14)

Stress–Strain relationship becomes,

$$\left\{ { \sigma } \right\} = \left[ D \right]\left\{ \in \right\}$$
(15)

where \(\left\{ \sigma \right\}\) is the stress vector and given as,

$$\left\{ \sigma \right\} = \left\{ {\begin{array}{*{20}c} {\sigma_{RR} } & {\sigma_{\theta \theta } } & {\sigma_{ZZ} } & {\sigma_{RZ} } \\ \end{array} } \right\}^{\text{T}}$$

4 Results and discussion

In this work, the design of horn with Bezier profile for high amplification is based on the optimization procedure where the profile of the horn is optimized by parameters of cubic and quadratic curve to meet the requirement of magnification. For calculation of the stress components, displacement amplification, and natural frequency, the finite element method-based MATLAB code has been developed. For meshing, the horn domain ANSYS APDL is used as a pre-processor. The output of ANSYS software is the coordinates of the nodes and connectivity of the elements, and these data are used as the input of MATLAB code. For presenting the results in the graphical form, MS ORIGIN software is used. For the calculation of stress components, input obtained by the present MATLAB code nodal displacements has been used. The result is validated by the results available in the literature [12]. Then the stresses, displacement amplification, and natural frequency are calculated for the quadratic and cubic Bezier profiles of the horn. Table 2 is showing the specifications of the horns using steel AISI (4063) for RUSM.

Table 2 Specifications of the horns using steel AISI (4063) for RUSM
Full size table

4.1 Convergence test

Convergence test has been done for the accuracy of the solution by using finite element analysis. If an analytical solution to the problem is known, the accuracy of the problem is easy to determine. The convergence test has been done to find the exact number of an element; depending upon the many factors, these include the type of differential equation, element order, and solution quantity desired. The domain is taken as a quadratic and cubic Bezier profile of horn. Eight noded serendipity element is used for discretizing the domain of horn in the longitudinal direction. In the radial direction, one element is taken and the number of elements increases from 5 to 40. Take all procedures the same as previously, and the number of elements is increased from 1 to 5 in the radial direction as previously. The domain of quadratic and cubic Bezier profile of horns is axisymmetric in nature. A double number of nodes equal a single number of frequencies. Fundamental frequency of vibration is the lowest nonzero wi. The resonant frequencies vary with number of elements. When the less number of elements are used, the significant errors occur. When we take more or 75 elements, the variation in the natural frequency is negligible. The 75 elements are the optimum elements for further calculation in the domain of horn.

4.2 Model validation

The present MATLAB code has been validated by comparing the results of the axisymmetric stress problem of Kwon et al. [28], and also the displacement and stresses have been validated by taking all conditions the same as given in the literature [12]. The domain is axisymmetric about Z-axis as shown in Fig. 5. The initial displacement given on top-end CD is 15 µm. The problem has been solved using the developed FEA-based code by considering all the given boundary conditions. Eight noded serendipity element is selected for the discretization of the domain. The axial displacement along the axial length is calculated and compared with the result given in Yadava et al. [12] as shown in Fig. 6. The nature of variation of the curve of the quadratic and cubic Bezier horn is similar to Yadava et al. [12]. The average error in this comparison is 2.4% and 3.7% for quadratic and cubic Bezier horn, respectively. The result of the magnification factor and stress obtained for the quadratic Bezier horn from the present FEA model and corresponding value given in Yadava et al. [12] are very close to each other. The corresponding errors of this comparison are 2.94% and 0.2%, respectively, which shows the accuracy of the present FEA model.

Fig. 6
figure 6

Validation of FEM model for axial displacement (uZ)

Full size image

4.3 Axial displacement of the horn with different Bezier profile

Figure 7 shows a variation of the axial stress and value of axial stress is maximum for the cubic Bezier horn, but the stress is within the allowable endurance limit and the horn is safe. Figure 8 shows the maximum circumferential stress for the cubic Bezier horn and also the minimum value for the quadratic Bezier horn. Similar curve is obtained as explained in Ref. [12]. Figure 9 shows variation of radial stress along axis of horn. It also shows that the radial stress is maximum for the cubic Bezier horn and minimum for the quadratic Bezier horn.

Fig. 7
figure 7

Effect of axial stress along the horn axis for the cubic and quadratic Bezier profiles

Full size image
Fig. 8
figure 8

Effect of circumferential stress along the horn axis for the cubic and quadratic Bezier profiles

Full size image
Fig. 9
figure 9

Effect of radial stress along the horn axis for the cubic and quadratic Bezier profiles

Full size image

Figure 10 shows the variation of shear stress along the axis of the horn. The value of the shear stress is maximum for the cubic Bezier horn and the horn is safe. Due to the low value of shear stress, there is no distortion within the horn. Figure 11 shows the variation of equivalent stress along the axis of the horn. The maximum equivalent stress value for the cubic Bezier horn and its value is 192 MPa, but it is much lower than the allowable endurance limit. Quadratic Bezier horn has the equivalent stress 172 MPa, also it is much lower than the allowable endurance limit. Therefore, the horns with cubic and quadratic Bezier profiles are safe.

Fig. 10
figure 10

Effect of shear stress along the horn axis for the cubic and quadratic Bezier profiles

Full size image
Fig. 11
figure 11

Effect of equivalent stress along the horn axis for the cubic and quadratic Bezier profiles

Full size image

4.4 Stresses with rotation (250 RPM) in the horn with quadratic Bezier profile

Figure 12 shows the variation of axial, radial, shear, circumferential and equivalent stresses along the axis of the horn at R = 0 mm. The value of the maximum equivalent stress is 172 MPa. At the middle, equivalent, stress is maximum and towards the other two ends, the equivalent stress is near to zero. The allowable stress for selected material is more than the equivalent stress. Similar curve is obtained as explained in the Seah et al. [8]. In Fig. 12, it has been evaluated that the value of the shear stress is nearly zero along the axis of horn. In the horn, there is no distortion.

Fig. 12
figure 12

Variation of stress components along axis of the quadratic Bezier profile horn at R = 0 mm

Full size image

Figure 13 shows the variation of stress along the radial length of the horn at Z = 0 mm. Stress distribution along radial length is almost zero, because this end is free to move. Figure 14 shows a variation of the axial, radial, shear, circumferential, and equivalent stresses along the radial length of the horn at Z = 77.56 mm. Value of the maximum equivalent stress is 137 MPa. The allowable stress for selected material is more than the equivalent stress. Also maximum axial stress is 134 MPa. The allowable stress for selected material is more than the axial stress. It is observed that the variation of the stresses in this section is linear. From Fig. 14, it has also become clear that value of the radial, hoop, and shear stresses are zero in this section. Figure 15 shows the variation of stress along the radial length of the horn at Z = 124.44 mm. The variations of stresses is nearly linear at this section, and values of stresses are almost zero because this end is free to move.

Fig. 13
figure 13

Variation of stress components along axis of the quadratic Bezier profile horn at Z = 0

Full size image
Fig. 14
figure 14

Variation of stress components along axis of the quadratic Bezier profile horn at Z = 77.56 mm

Full size image
Fig. 15
figure 15

Variation of stress components along axis of the quadratic Bezier profile horn at Z = 124.44 mm

Full size image

4.5 Stresses with rotation (250 RPM) in the horn with cubic Bezier profile

Figure 16 shows variation of axial, radial, shear, circumferential, and equivalent stresses along the axis of the horn at R = 0 mm. The value of the maximum equivalent stress is 192 MPa. At the middle equivalent, stress is maximum, and towards the other two ends, the equivalent stress is near to zero. The allowable stress for selected material is more than the equivalent stress. A similar curve is obtained as explained in Seah et al. [8]. In Fig. 16, it has been evaluated that the value of the shear stress is nearly zero along the axis of horn. In the horn, there is no distortion takes place.

Fig. 16
figure 16

Variation of stress components along axis of the cubic Bezier profile horn at R = 0 mm

Full size image

Figure 17 shows the variations of stresses along the radial length of the horn at Z = 0 mm. Stress distribution along the radial length is almost zero because this end is free to move. Figure 18 shows a variation of the axial, radial, shear, circumferential, and equivalent stresses along the radial length of the horn at Z = 77.56 mm. The value of the maximum equivalent stress is 139.5 MPa. The allowable stress for selected material is more than the equivalent stress. Also, the maximum axial stress is 139 MPa. The allowable stress for selected material is more than the axial stress. It is observed that the variation of the stresses in this section is linear. From Fig. 18, it has also become clear that the value of radial, hoop, and shear stresses are zero in this section. Figure 19 shows the variation of stresses along the radial length of the horn at Z = 124.44 mm. The variation of stresses is nearly linear at this section, and the value of stresses is almost zero because this end is free to move.

Fig. 17
figure 17

Variation of stress components along axis of the cubic Bezier profile horn at Z = 0

Full size image
Fig. 18
figure 18

Variation of stress components along axis of the cubic Bezier profile horn at Z = 77.56 mm

Full size image
Fig. 19
figure 19

Variation of stress components along axis of the cubic Bezier profile horn at Z = 124.44 mm

Full size image

4.6 Effect of various frequencies on the components of stress for quadratic horn with Bezier profile

Figure 20 shows the plot between the component of axial stress and the axis of the horn for the various frequencies. In this figure, the value of the axial stress increases with the increase in the frequency and the variation of stresses over the horn also increases, but the value of stress is much lower at the resonance frequency (23.6 kHz) as compared to other frequencies. Figures 18, 19, and 20 show the variation of the components of the circumferential, radial, and shear stresses and the axis of horn for the various frequencies. Also in Figs. 21, 22, and 23, the radial, circumferential, and the values shear stress increase with the increase in the frequency, and the variation of stresses over the horn also increases, but the value of the circumferential, radial, and shear stresses are much lower at the resonance frequency (23.6 kHz) as compared to other frequencies. Similar results are obtained as explained in Ref. [12].

Fig. 20
figure 20

Effect of frequency on axial stress for quadratic Bezier profile horn

Full size image
Fig. 21
figure 21

Effect of frequency on circumferential stress for quadratic Bezier profile horn

Full size image
Fig. 22
figure 22

Effect of frequency on radial stress for quadratic Bezier profile horn

Full size image
Fig. 23
figure 23

Effect of frequency on shear stress for quadratic Bezier profile horn

Full size image

4.7 Effect of various frequencies on the components of stresses for the horn with cubic Bezier profile

Figure 24 shows the plot between the components of axial stress and the axis of the horn for the various frequencies. In this figure, the value of the axial stress increases with the increase in the frequency and the values of stresses over the domain of horn also increase, but the value of stress is much lower at the resonance frequency (23.8 kHz) as compared to other frequencies. Figures 21, 22, 23, and 24 show the variation of the components of the circumferential, radial, and shear stresses with the axis of horn for the various frequencies. Also in Figs. 25, 26, and 27, the radial, circumferential, and values of the shear stress increase with increase in the frequency and stresses over the domain of horn also increases, but the value of the circumferential, radial, and shear stresses are much lower at the resonance frequency (23.8 kHz) as compared to other frequencies. Similar results are obtained as explained in Ref. [12].

Fig. 24
figure 24

Effect of frequency on axial stress for cubic Bezier profile horn

Full size image
Fig. 25
figure 25

Effect of frequency on circumferential stress for cubic Bezier profile horn

Full size image
Fig. 26
figure 26

Effect of frequency on radial stress for cubic Bezier profile horn

Full size image
Fig. 27
figure 27

Effect of frequency on shear stress for cubic Bezier profile horn

Full size image

4.8 Experimental verification

Experimental verification has been done by Fig. 28. For comparison, the input parameter has been taken the same as Wang et al. [13]. It is found that the present cubic Bezier horn has 57.4% more amplitude as compared to Wang et al. [13] and also quadratic Bezier horn has 51% more as compared to Wang et al. [13]. Figure 28 shows a similar trend of the present result as given in the literature [13], and the magnification factor has been found more in the present cubic and quadratic Bezier horns. Through the experimental investigation, researchers have found that for high amplification the material removal rate is high as given in Rozenberg et al. [1]. In the present work, amplification has been found more so the material removal rate would be high for the designed cubic and quadratic Bezier horn profiles.

Fig. 28
figure 28

Experimental validation of amplitude

Full size image

5 Conclusions

In the present work, the design of horns with quadratic and cubic Bezier profiles has been done for RUSM by using the optimization and FEA. The stress components, natural frequency, and displacement amplification induced within the horn with quadratic and cubic Bezier profiles are calculated. The effect of frequencies on the stress distribution for horns with Bezier profiles for RUSM has also been studied and some main conclusions have been listed below:

  • Finite element analysis and multiobjective optimization algorithm have been developed to optimize displacement amplification of the horns with cubic and quadratic Bezier profile.

  • For the determination of displacement, a mathematical model has been developed within the horns with cubic and quadratic Bezier profiles, and also the components of stresses are found to be within the allowable limit.

  • The amplification for the horn with cubic and quadratic Bezier profiles proposed is 23.8% and 19% higher than the traditional conical horn with the same length and diameters of the end.

  • For the same boundary condition and material properties, the amplified displacement is found more for the horn with a cubic Bezier profile as compared to the quadratic Bezier profile.

  • The major responsible stress is the axial stress for a major part of horn, and the value is maximum and the generated induced stress is within the allowable limit. For the same boundary conditions and material properties, the amplitude is more with rotation as compared to without rotation.

  • The maximum equivalent stresses for quadratic and cubic Bezier profiles are 172 MPa and 192 MPa in the middle of the horn towards the lower end. The maximum equivalent stresses are lower than the allowable endurance limit (520 MPa). Designed horns with quadratic and cubic Bezier profiles have not failed by fatigue.

  • The components of stress generated at the lower end of the horn are almost zero because it is free to move. The induced shear stress is almost zero, so no distortion takes place within the horns with quadratic, and cubic Bezier profiles and stresses are the linear over radial length.

  • At the resonance frequency for the horn with quadratic and cubic Bezier profile, the value of the radial, axial, circumferential, and shear stresses are much lower as compared to the other obtained frequencies.

  • It is concluded that the present cubic and quadratic Bezier horns have 57.4% and 51% more amplitude as compared to experimental horn data found in the literature.