1 Introduction

The use of robots in industry has been become very widespread and is rapidly increasing. Robots with special applications are also increasing, and multifunctional robots are progressing and being industrialized. An important type of multifunctional robot is the biped robot with a humanlike appearance moving on two legs. Biped robots are likely to be able to do most of the daily tasks of humans and undertake different missions in the future with low limitations. However, due to high degrees of freedom and hybrid dynamics biped robots are one of the most complex systems in terms of locomotion and control.

Locomotion is the ability of moving from one place to another and includes various forms such as swimming, flying, walking and running. Legged locomotion is the most efficient form of natural locomotion on land; birds and amphibian having wings and fins are also equipped with legs to walk and run. For legged robots, the design and analysis of efficient gaits are still a challenging problem because fundamental principles of this type of locomotion are not completely understood. Humans and animals, for instance, can intrinsically distinguish proper gait specifications such as body trajectory or stride length to adapt terrain condition. This has motivated many attempts to design comprehensive mechanisms of legged locomotion [1, 2]. Legged robots possess a better mobility compared to wheeled vehicles. For instance, wheeled robots cannot pass through stairs or uneven terrain or complicated paths. Furthermore, similarities of biped robots to human kind make them ready to help people in many tasks of modern life. Another important aspect of legged robots is that they can have high degrees of freedom (DOF) making them able to cover a larger workspace [3,4,5,6]. These characteristics lead to a wide spectrum of applications such as hazardous inspection, giving service in crowded hospitals, companion and entertainment jobs at home.

The gait dynamics in various biped robot structures have already been investigated by researchers [4,5,6,7]. Raibert [3] designed and built spring-loaded inverted pendulum (SLIP)-like one-legged robots for 2D and 3D hopping gaits. The robots used pneumatic actuators, and their hopping motion was stabilized by controlling forward speed, hopping height, and body angle independently. McGeer introduced passive walking [8] and running [9] gaits and proved their stability for biped models with arc feet. Cherouvim et al. [10] investigated energy transfer between the single actuated DOF and other unactuated DOFs of a monopod model to get stable hopping motion. Hyon et al. [11] proposed an energy-preserving control method for planar running of a springy telescopic leg biped model with torso. Hu et al. [12] studied generating passive running gaits for a telescopic springy leg biped model with three point masses and then designed an event-based controller to stabilize it. Dadashzadeh et al. [4] generalized this control method to active running gaits of telescopic and kneed biped models on even and sloped terrains. The controller was a discrete state feedback controller on Poincare map.

Another control approach is to use continuous time controllers over running gait. Tzafestas et al. [13] designed a sliding mode controller (SMC) to stabilize the running gait without flight phase for a 5-link biped model. SMC method also has been used for tracking control of manipulators [14] and to stabilize biped walking gaits during double-support [15] and single-support phases [16]. Finite-time controller (FTC) is an extension of SMC that was introduced by Haimo [17] and generalized by Bhat [18]. Hong et al. [14] designed an FTC using state feedback and output feedback for a manipulator. Guo et al. [5] successfully applied FTC method to stance phase of a three-link hopper with foot and obtained stable hopping gaits. They also used an LQR controller for the flight phase due to its underactuation. The lack of applying FTC method to bipedal running is noticeable in the previous works. Convergence time is very important in controller design for bipedal running because of limited time intervals of running phases.

In this research, a finite-time sliding mode controller is designed for a biped robot which contains two telescopic legs. The biped model consists of two springy legs with feet and is fully actuated in stance phase. The contributions of this work consist of showing the effectiveness of finite-time control strategy to stabilize bipedal running, and comparing the results with an event-based controller. This work differs from the previous work [5] by the way that it controlled hopping of a one-legged hopper with three rigid links, but this work is about bipedal running with telescopic springy legs that needs also swing leg control. Biped robots with telescopic springy legs have passive-based running gaits and can be more efficient than kneed mechanism. The other difference is that in Ref [5], a LQR controller was used in flight phase but in this work fight phase is passive and the running gait is stabilized only by FTC in stance phase. The passive flight phase is advantageous for the gait efficiency and minimal control effort. In addition, we have optimized controller parameters to achieve smaller foot length to reject disturbance.

2 Dynamic modeling

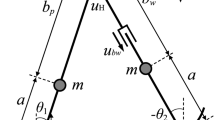
The biped robot model of this paper contains two prismatic springy legs with flat feet, a point mass \(m_{h}\) on the hip and two same point masses \(m\) on the middles of thighs. Each prismatic joint of the legs contains a massless spring \(k\) and a force actuator parallel to the spring. A torque actuator is located in hip joint between two legs, and two torque actuators are located in ankle joints. According to schematic structure of the robot shown in Fig. 1, it is clear that all joints are active and the system is fully actuated in stance phase provided that stance foot is in static equilibrium on the ground. It is assumed that shanks and feet are massless. Rest length of the spring is \(b_{0}\), while \(b\) represents its current length. Running gait dynamics is divided to two continuous time phases called stance phase and flight phase and two instantaneous transition phases called takeoff and touchdown. In Fig. 1, \(q_{1}\) is the angle between stance leg and horizontal and \(q_{2}\) is the angle between two legs. Counterclockwise rotation is positive, and clockwise is negative. The position of center of mass (CoM) is shown by \(\left( {X_{cm} ,Y_{cm} } \right) \in {\mathbb{R}}^{2}\). The values of parameters applied in the model are listed in Table 1. In the following subsections, derivation of dynamic equations of the system is explained.

Fig. 1
figure 1

Schematics of the robot in stance phase

Full size image
Table 1 Kinematic and mass properties of the robot
Full size table

2.1 Stance phase model

In the stance phase, one leg is on the ground and the other leg swings around the hip. During this phase, it is assumed that the foot of swing leg is parallel to the ground and length of swing leg is constant (equal to a + b0) so the system has three DOF. Also it is assumed that a mechanism shortens the massless part of the swing leg to clear it from ground with zero energy assumption. To derive the dynamic equation, we use Lagrange method. Stance phase-generalized coordinates vector is denoted by \(q_{s} = \left[ {q_{1} ,q_{2} ,b} \right]^{T}\) in which b the length of stance leg is. The Lagrangian function is

$$L\left( {q_{s} ,\dot{q}_{s} } \right) = T\left( {q_{s} ,\dot{q}_{s} } \right) - V\left( {q_{s} } \right)$$
(1)

where T is the total kinetic energy and V is the total potential energy. Using Lagrange equation,

$$\frac{\text{d}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \dot{q}_{{s_{i} }} }}} \right) - \frac{\partial L}{{\partial q_{{s_{i} }} }} = Q_{i} ,\quad i = 1,2,3$$
(2)

the dynamic model of the stance phase is summarized as

$$\left[ {M_{s} \left( {q_{s} } \right)} \right]_{3 \times 3} \left\{ {\ddot{q}_{s} } \right\} + \left[ {h_{s} \left( {q_{s} ,\dot{q}_{s} } \right)} \right]_{3 \times 3} \left\{ {\dot{q}_{s} } \right\} + \left[ {G_{s} \left( {q_{s} } \right)} \right]_{3 \times 1} = \left[ {B_{s} } \right]_{3 \times 3} \left\{ {u_{s} } \right\}_{3 \times 1}$$
(3)

in which, \(M_{s} \left( {q_{s} } \right)\) is inertia matrix, \(h_{s} \left( {q_{s} ,\dot{q}_{s} } \right)\) is Coriolis and centrifugal matrix, \(G_{s} \left( {q_{s} } \right)\) is a vector related to potential energy, \(u_{s} = \left[ {\tau_{1} ,\tau_{2} ,F_{1} } \right]^{T}\) is the control input vector containing torques of the ankle and hip actuators and force of the prismatic actuator of the stance leg, respectively.

It can be proven that \(M_{s}\) and \(h_{s}\) have the below properties [19]:

  1. 1.

    \(M_{s}\) is positive definite and \(d_{ \hbox{min} } I_{n \times n} \le M_{s} \le d_{ \hbox{max} } I_{n \times n}\), in which \(d_{ \hbox{min} }\) is the minimum eigenvalue and \(d_{ \hbox{max} }\) is the maximum eigenvalue of matrix \(M_{s}\).

  2. 2.

    \(h_{s}\) will be chosen such that \(\dot{M}_{s} - 2h_{s}\) is a skew-symmetric matrix.

2.2 Flight phase model

The flight phase starts when the support foot loses contact with ground in stance phase, and the whole robot starts to go a ballistic motion. During flight phase, the lengths of both legs are constant (equal to a + b0) and the feet are assumed to be kept parallel to the ground surface. The system is of 4 DOF with generalized coordinates vector of \(\varvec{q}_{f} = \left[ {q_{1} ,q_{2} ,x_{cm} ,y_{cm} } \right]^{T}\). \(q_{1}\), \(q_{2}\) are legs angles as defined above and \(x_{cm}\), \(y_{cm}\) are COM position components. Again, using Lagrangian function of the flight phase and Lagrange equation for the flight phase as

$$\frac{\text{d}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \dot{q}_{{f_{i} }} }}} \right) - \frac{\partial L}{{\partial q_{{f_{i} }} }} = Q_{i} ,\quad i = 1,2,3,4,$$
(4)

The dynamic model of the flight phase is written as

$$\left[ {M_{f} \left( {q_{f} } \right)} \right]_{4 \times 4} \left\{ {\ddot{q}_{f} } \right\} + \left[ {h_{f} \left( {q_{f} ,\dot{q}_{f} } \right)} \right]_{4 \times 4} \left\{ {\dot{q}_{f} } \right\} + \left[ {G_{f} \left( {q_{f} } \right)} \right]_{4 \times 1} = \left[ {B_{f} } \right]_{4 \times 1} \left\{ {u_{f} } \right\}_{1 \times 1}$$
(5)

where \(u_{f} = \tau_{2}\) is the control input that has only one element of hip actuator torque, \(G_{f} \left( {q_{f} } \right)\) is a vector related to total potential energy, \(M_{f} \left( {q_{f} } \right)\) and \(h_{f} \left( {q_{f} ,\dot{q}_{f} } \right)\) are inertia and Coriolis matrices, respectively.

2.3 Takeoff model

The transition phase from stance to flight phase is called takeoff. Because of massless foot and shank, takeoff occurs when the length of the spring in the stance leg reaches its free length, i.e., \(b = b_{0}\). Due to having no impact in this event, energy, angular and linear momentum are conserved before and after the takeoff. This keeps all positions and velocities of the robot components continuous. Therefore, the takeoff model is just a kinematic conversion of pre-event stance phase final state to post-event flight phase initial condition as

$$\left[ {q_{f}^{ + } ,\dot{q}_{f}^{ + } } \right] = {}_{s}^{f} \Delta \left( {q_{s}^{ - } ,\dot{q}_{s}^{ - } } \right)$$
(6)

where superscript “+” indicates the moment just after takeoff and superscript “-” shows the moment just before takeoff and \({}_{s}^{f} \Delta\) specifies the stance to flight transition map.

2.4 Touchdown model

Touchdown occurs at the end of flight phase and is followed by the next stance phase. At this instantaneous phase, an impulse is exerted to the robot leg from the ground. In the touchdown modeling, we assume that the collision is completely inelastic; there is no rebound and no slippage during foot landing. Touchdown does not affect the generalized coordinates instead causes an instantaneous change in velocities. In addition, because the stance leg in post-touchdown step is the swing leg in pre-touchdown step, there is a change in legs labeling.

$$q_{1s}^{ + } = q_{1f}^{ - } + q_{2f}^{ - }$$
(7)
$$q_{2s}^{ + } = - q_{2f}^{ - }$$
(8)
$$q_{3s}^{ + } = b_{0}$$
(9)

To calculate the generalized velocities after impact, we use linear and angular momentum conservation laws. The leg “FH” is the contact leg, and point F is assumed to behave as an ideal pivot after contact. Due to springy massless shank, there is an impulse acting on foot “F” perpendicular to the axis of “FH.” Therefore, the angular momentum of all parts around point “F” is conserved, the linear momentum of all parts is conserved in the direction of “FH” and the angular momentum of the leg “AH” is conserved around point “H,” i.e.,

$$H_{F}^{AHF} \left( {\dot{q}_{f}^{ - } } \right) = H_{F}^{AHF} \left( {\dot{q}_{s}^{ + } } \right)$$
(10)
$$L_{FH}^{AHF} \left( {\dot{q}_{f}^{ - } } \right) = L_{FH}^{AHF} \left( {\dot{q}_{s}^{ + } } \right)$$
(11)
$$H_{H}^{AH} \left( {\dot{q}_{f}^{ - } } \right) = H_{H}^{AH} \left( {\dot{q}_{s}^{ + } } \right)$$
(12)

where L shows the linear momentum and H shows angular momentum. By solving this system of three equations in three unknowns, the post-touchdown velocities \(\dot{\varvec{q}}_{s}^{ + }\) can be found.

3 Control algorithm

In this section, a finite-time control architecture is formulated for stable running of the considered biped model. To design a finite-time controller, a desired trajectory is needed for the generalized coordinates. It has been shown that, for any arbitrary forward speed, the considered biped model has passive periodic running gaits which are unstable [4]. These gaits can be stabilized using some linear event-based controllers [4]. In this research, we synthetize a finite-time controller to generate stable running gaits around the passive gaits.

3.1 Stance phase

The basic sliding mode controller has problems such as chattering and not reaching the desired trajectory before takeoff event. In fact, a finite-time robust control term can be added to the smooth terminal sliding mode controller in order to guarantee the desired trajectory to be reached in a finite time and to prevent chattering [5].

To design the controller for stance phase, we first define the tracking error of stance phase as

$$\tilde{q}_{s} = q_{s} - q_{d}$$
(13)

where \(q_{d}\) is the desired trajectory. The sliding surface is then defined as

$$s = \dot{\tilde{q}}_{s} + A\tilde{q}_{s} - \dot{v}\left( t \right) - Av\left( t \right) = \dot{w}\left( t \right) + Aw\left( t \right) = \dot{q} - \dot{q}_{r}$$
(14)

where \(A = {\text{diag}}\left( {\lambda_{1} ,\lambda_{2} ,\lambda_{3} } \right)\),\(\lambda_{i} > 0\), \(v\left( t \right)\) is the desired tracking error, \(w\left( t \right)\) is the difference between real and desired error

$$w\left( t \right) = \tilde{q}_{s} - v,$$
(15)

and reference trajectory \(q_{r}\) is defined as

$$\dot{q}_{r} = \dot{q}_{d} - A\tilde{q}_{s} + \dot{v} + Av.$$
(16)

To obtain a smooth trajectory for the system, the desired tracking error is defined as a third-order polynomial during time of convergence \(\left( {T_{\text{cs}} } \right)\). It is equal to zero after \(T_{\text{cs}}\). Hence

$$v\left( t \right) = \left\{ {\begin{array}{*{20}c} {p_{0} + p_{1} t + p_{2} t^{2} + p_{3} t^{3} } & {t \in \left[ {0,T_{\text{cs}} } \right]} \\ 0 & {t \in \left[ {T_{\text{cs}} ,\infty } \right]} \\ \end{array} } \right.$$
(17)

In order to start from the deviated position with slope zero and reach the desired position with slope zero, the coefficients of polynomial \(v\) are chosen as follows

$$\left\{ {\begin{array}{*{20}c} {p_{0} = \tilde{q}_{s} \left( 0 \right)} \\ {p_{1} = \dot{\tilde{q}}_{s } \left( 0 \right)} \\ {p_{2} = - \frac{3}{{\left( {T_{\text{cs}} } \right)^{2} }}\tilde{q}_{s} \left( 0 \right) - \frac{2}{{T_{\text{cs}} }}\dot{\tilde{q}}_{s } \left( 0 \right)} \\ {p_{3} = \frac{2}{{\left( {T_{\text{cs}} } \right)^{3} }}\tilde{q}_{s } \left( 0 \right) + \frac{1}{{\left( {T_{\text{cs}} } \right)^{2} }}\dot{\tilde{q}}\left( 0 \right)} \\ \end{array} } \right.$$
(18)

It is evident that

$$v\left( 0 \right) = \tilde{q}\left( 0 \right) , \dot{v}\left( 0 \right) = \dot{\tilde{q}}\left( 0 \right) , s\left( 0 \right) = 0 , w\left( 0 \right) = 0$$
(19)

By differentiating Eq. (16), we will have

$$\ddot{q}_{r} = \ddot{q}_{d} - A\dot{\tilde{q}}_{s} + \ddot{v} + A\dot{v}$$
(20)

Replacing Eqs. (14) and (18) into Eq. (3), the dynamic equations of stance phase are rewritten as

$$M_{s} \dot{s} + h_{s} s = B_{s} u - M_{s} \ddot{q}_{r} - h_{s} \dot{q}_{r} .$$
(21)

Theorem 2-1 proved by Guo et al. [5] can now be restated here as follows:

For the system “Eq. (3),” consider the following control rule

$$u = B_{s}^{\# } \left( {M_{s} \ddot{q}_{r} + h_{s} \dot{q}_{r} + G_{s} - M_{s} K_{1} s - M_{s} K_{2} sig^{\gamma } \left( s \right)} \right)$$
(22)

where \(B_{s}^{\# }\) is pseudo-inverse of matrix \(B_{s}\), \(K_{1} = diag\left( {k_{11} , k_{12} ,k_{13} } \right)\), \(K_{2} = diag\left( {k_{21} ,k_{22} ,k_{23} } \right)\) with \(k_{ij} > 0\), and function \(sig^{\gamma } \left( s \right)\) is

$$sig^{\gamma } \left( s \right) = \left[ {\begin{array}{*{20}c} {\left| {s_{1} } \right|^{\gamma } sign\left( {s_{1} } \right)} \\ {\left| {s_{2} } \right|^{\gamma } sign\left( {s_{2} } \right)} \\ {\left| {s_{3} } \right|^{\gamma } sign\left( {s_{3} } \right)} \\ \end{array} } \right] , 0 < \gamma < 1 .$$
(23)

Then, trajectory of the system is bounded for \(t > 0\) and sliding surface will be bounded by \(s \le s_{*}\) , where \(s_{*}\) is the unique solution of equation of

$$k_{1\hbox{min} } s + k_{2\hbox{min} } s^{\gamma } = 0$$
(24)

where \(k_{1\hbox{min} } = { \hbox{min} }\left( {k_{11} ,k_{12} ,k_{13} } \right)\) and \(k_{2\hbox{min} } = \hbox{min} \left( {k_{21} ,k_{22} ,k_{23} } \right)\).

Therefore, applying the control law of “Eq. (22)” to the system of “Eq. (3)” generates the state trajectory convergent in a finite time. The last term of the control law in “Eq. (22)” is a finite-time robust control term which prevents torque and force from chattering. The time of convergence \(T_{\text{cs}}\) should be chosen to be less than the stance phase interval to guarantee the convergence before the takeoff event.

3.2 Flight phase

Since the system is underactuated in flight phase, the finite-time controller “Eq. (22)” is not applicable in this phase. Stance phase controller has a vital role in rejecting disturbances and stabilizing the running gait. It brings back the state vector to the desired trajectory before touchdown and generates flight initial condition coincident to the desired condition. Therefore, we assume the robot moves passively in flight phase with no actuators. The only external force acting on the system during this phase is gravity. If the initial condition of the system in the flight phase is the same as the desired initial condition, the robot follows the desired trajectory [4].All disturbances in the flight phase can be considered as an initial condition deviation of the next stance phase.

4 Simulation results

In this section, we apply the control law introduced in Sect. 3 on the dynamic model of the robot and present the simulation results for both phases of running. Running gait starts with the stance phase, and we test the controller convergence by taking 1%, 4% and 8% deviation of the norm of initial conditions from the desired condition. The results are then compared to the results obtained from a similar system with linear control strategy introduced in Dadashzadeh et al. [4].

4.1 Finite-time control strategy

The biped model with massless springy feet possesses passive periodic running gaits which are unstable [4]. The gait is found by calculating fixed point of Poincare map of one complete running step. The fixed point is in fact a stance phase initial state vector which starts a passive running step from that condition that results in the same state vector at the beginning of the next stance phase. This gait needs a stabilizing controller to produce a stable running motion. We find a passive running gait with a forward speed of 10 m/s for our biped model and use its initial state vector as the desired initial condition for our finite-time controller simulations. Table 2 shows fixed parameters values of our finite-time controller. These values have been selected in a way to satisfy the required condition defined in Sect. 3. The time of convergence (\(T_{\text{cs}}\)) is selected about 30 percent of time duration of the stance phase. Controller coefficients \(K_{1} = {\text{diag}}\left( {k_{11} , k_{12} ,k_{13} } \right)\), \(K_{2} = {\text{diag}}\left( {k_{21} ,k_{22} ,k_{23} } \right)\) are obtained using an optimization problem to minimize the needed foot length \(\left( {L_{\text{foot}} } \right)\) or maximum deviation of \({\text{ZMP}}\) to stabilize a gait with 4% initial deviation.

Table 2 Values of the controller-fixed parameters
Full size table
$$\mathop {\hbox{min} }\limits_{{K_{1} , K_{2} }} \left( {{\text{ZMP}}_{ \hbox{max} } - {\text{ZMP}}_{ \hbox{min} } } \right)$$
(25)

Because the dynamic model of the closed loop gait is highly nonlinear with large amount of numerical calculations and optimization parameters number is relatively high, it is not claimed that we have found global minimum of this problem. Instead, we use a search algorithm that runs the model by varying the six parameters within a reasonable range. The ranges for each parameter are defined by trial and error. Considering three values for each parameter, 729 times executing the program is needed. After several successive runs of the search algorithm, the following optimal values of the controller coefficients were found that generate \(L_{\text{foot}} = 0.162\; {\text{m}}\). These values will be used in simulations of the next subsections.

$$k_{11} = 190,\; k_{12} = 150,\;k_{13} = 90,\; k_{21} = 40,\; k_{22} = 150,\; k_{23} = 210$$
(26)

Figure 2 shows variation of foot length versus controller coefficients around the found minimum point. In each subplot, only one parameter is varied and the others are constant. There was a rough search with resolution of 30 and then a finer search around min point with resolution of 5.

Fig. 2
figure 2

Variation of foot length versus controller coefficients

Full size image

4.1.1 One percent deviation of initial conditions

We first simulate the designed finite-time controller with 1% deviation in the norm of initial condition from the desired condition. Figure 3 shows that the position error of the system converges to zero within the defined time of convergence, and Fig. 4 shows that the major amount of velocity error subsides within the time of convergence. Small oscillations around zero in velocity error diagram after the time of convergence are due to lack of a positive definite matrix \(A\) in the definition of sliding surface. It means that the prior aim of the controller is lowering position error rather than velocity error. The results imply that this error does not affect the stability of system.

Fig. 3
figure 3

Position error using finite-time controller with 1% initial error

Full size image
Fig. 4
figure 4

Velocity error using finite-time controller with 1% initial error

Full size image

Figure 5 shows the ZMP value during the stance phase. The greater the difference between the maximum and the minimum value of ZMP, the longer the foot is needed to keep the gait stable. Figure 5 shows a difference of 15.1 cm between max and min value of ZMP which is a reasonable value for the foot length. Choosing a foot length greater than this value can guarantee stability of the stance foot on the ground during stance phase.

Fig. 5
figure 5

ZMP location during stance phase with 1% initial error

Full size image

Figure 6 illustrates the control inputs of the robot during the stance phase. The maximum torque of motors is 35 N m, and the maximum force of prismatic actuator is 20 N, which are small values relative to the robot weight 196 N. The very small control inputs are justified because we stabilize the robot running around an unstable passive periodic gait.

Fig. 6
figure 6

Control inputs of the robot during stance phase with 1% initial error

Full size image

4.1.2 Four percent deviation of initial conditions

We repeat the simulations with 4% deviation of the initial condition. The simulation results show that the finite-time controller can reject the initial disturbances and bring the state of system back to the desired trajectory within the specified convergence time (see Figs. 7 and 8). According to these figures, the controller makes position and velocity errors confined within an acceptable vicinity of zero at the end of the stance phase. These errors also remain close to zero in the passive flight phase with no control action and cause a small error for initial condition of the next stance phase which can be treated then by the stance phase controller. According to ZMP trajectory in Fig. 9, the required foot length to stabilize 4% initial deviations is 16.2 cm which is acceptable for a robot with the height of 1.3 m. Figure 10 depicts that the maximum torque and force control efforts are 80 N m and 20 N which is almost half of static load of the robot.

Fig. 7
figure 7

Position error using finite-time controller with 4% initial error

Full size image
Fig. 8
figure 8

Velocity error using finite-time controller with 4% initial error

Full size image
Fig. 9
figure 9

ZMP location during stance phase with 4% initial error

Full size image
Fig. 10
figure 10

Control inputs of the robot during stance phase with 4% initial error

Full size image

4.1.3 Eight percent deviation in norm of initial conditions

Finally, we deviate the stance initial condition from the desired path by 8% in the norm and apply the finite-time controller in stance phase. Figures 11 and 12 show the convergence of general coordinates of systems to the desired path before convergence time. As is seen in Fig. 13, the difference between minimum and maximum value of ZMP becomes very large so that the minimum length of foot should be 58.9 cm which is too long. This is due to the large deviation of the initial condition from the nominal gait. The larger the initial condition is deviated, the larger is the control torque (needed in ankle joint) to return the robot to the desired path. A larger ankle torque needs a longer foot to keep the stability. Figure 14 shows the joints input torques and force. The maximum torque and force are less than 30 N m and 150 N which are again less than the static loads of robot and are acceptable.

Fig. 11
figure 11

Position error using finite-time controller with 8% initial error

Full size image
Fig. 12
figure 12

Velocity error using finite-time controller with 8% initial error

Full size image
Fig. 13
figure 13

ZMP location during stance phase with 8% initial error

Full size image
Fig. 14
figure 14

Control inputs of the robot during stance phase with 8% initial error

Full size image

4.2 Comparison of the finite-time controller with a linear controller

To evaluate the performance of the presented finite-time controller of this paper, we compare the results with an event-based discrete LQR controller introduced by Dadashzadeh et al. [4]. This controller takes feedback only at touchdown event and generates control command for entire of the next step using state feedback controller for Poincare map. It has been proved to generate stable running gaits for both prismatic and kneed biped robots. We apply this controller for the same system of this paper with point feet. The simulation results show that this controller fails to stabilize the robot running in all cases of 1%, 4% and 8% initial errors, although it can stabilize the system with initial deviations lower than 0.5%. Figure 15 shows the divergence of the phase diagram of leg 1 for each of the tested initial deviation cases using discrete LQR controller. This comparison proves higher performance of the finite-time controller proposed in this work to the event-based LQR controller. However, actuator in ankle joint is essential for the finite-time controller and optional for LQR controller.

Fig. 15
figure 15

Phase diagram of leg 1 for running using LQR controller with a 1%, b 4% and c 8% initial error

Full size image

4.3 Remarks on the performance of the finite-time controller

Regarding simulation results in Sect. 4.1, it is shown that control law (22) is suitable for system (3) and converges it to the desired trajectory. Due to intrinsic oscillations of sliding mode controllers, there is a small deviation from the desired trajectory at the end of stance phase that can become larger during passive flight phase. Nonetheless, deviation value at the end of each flight phase is less than its relevant value at the beginning of stance phase. So, if the robot’s state converges to the desired trajectory at the first stance phase, stability of the next steps is guaranteed.

Considering foot length of the robot to be 30 cm, the maximum allowable ZMP interval should be equal to this value. By simulating the controller with various amounts of initial deviations according to Table 3 and by spline interpolation of the results, we found that the controller with optimized coefficients (26) is robust to stance initial deviations up to 5.39%. Initial deviations can be generated by external disturbances, friction or tracking errors. So, we consider the accumulated errors at the beginning of stance phase that are compensated during this phase and the passive flight phase starts with very small errors.

Table 3 Required foot length versus initial deviation
Full size table

5 Conclusion

A finite-time sliding mode controller with optimized gains was designed and applied to the running of a biped robot with telescopic legs, in this paper. It was shown that the tuned finite-time controller acting only in stance phase (with passive flight phase) stabilizes the whole cycle of the running gait. Results showed that, in contrast to the linear control strategy (reported in the previous works); the finite-time method could reject big disturbances and compensate large initial deviations from the desired path in the stance phase. For the chosen dynamics and optimized control parameters, if the norm of deviation from the desired initial condition was less than 5.39 percent, the control system could return the system to the desired gait having an acceptable foot length. For larger deviations, however, an unreasonably large foot was needed to keep the gait stable. Nonetheless, the controller could stabilize the gait using larger motor torques in these cases as well.