Determining biaxial tensile stresses by fracture cruciform specimen at different temperatures and strain rates for Ti–6Al–4V alloy

Abstract

Fracture loci of a ductile sheet metal, in some stress subspaces, can be predicted by determining the fracture stress points in the same subspace. This paper deals with determining the fracture stress points for Ti–6Al–4V alloy, under biaxial tension loading, at different temperatures and strain rates. For this purpose, biaxial tension of a fracture cruciform specimen was numerically simulated, using the ABAQUS software. In order to validate the finite element simulations, biaxial tensile fracture of an AA5083 cruciform specimen was numerically and experimentally studied. The material properties of AA5083 needed as the input data for simulations, were determined by performing experimental tests. Moreover, a dependent biaxial tensile mechanism was designed, manufactured and installed on an INSTRON-1343 uniaxial testing machine, to conduct the biaxial experimental tests. The numerical predictions for the location of fracture initiation, the path of fracture evolution and the force diagram in each of the specimen arms were compared with the experimental results. A good correlation was observed which confirms the validity of the finite element simulations. Then, the simulations were repeated for Ti–6Al–4V specimen. Hill1948 criterion was used to model the anisotropic plasticity, while Johnson–Cook damage model was incorporated to predict the fracture initiation and evolution path for different temperatures and strain rates. The results showed that the biaxial fracture stress points, corresponding to different displacement ratios, are mainly accumulated in the vicinity of equi-biaxial stress state. It can be concluded that, regardless of the anisotropy model, the fracture cruciform specimen cannot reveal a wide range of biaxial tension stress points.

1 Introduction

It is very important to know the fracture limit of ductile sheet metals in order to design the forming processes of various industrial parts. It is possible to predict the fracture behavior of ductile metal sheets via the forming limit stress diagram (FLSD) or the fracture loci of material and to propose suitable criterion for material behavior or to improve current criteria. The empirical data of biaxial fracture stress are needed in order to suggest and develop some of the phenomenological behavioral criteria in ductile metals. In this research work, the general purpose is to obtain biaxial fracture stress points for Ti–6Al–4V anisotropic alloy at different temperatures and strain rates via fracture cruciform specimen. Since measuring stress at a point in the body is a huge challenge, there is no alternative but to use computational methods and numerical analyses such as finite element method, in order to achieve the goal of this research. Therefore, this study was carried out using the finite element method as well as the experimental tests of fracture cruciform specimen.

The cruciform specimens are a combination of uniaxial tensile tests in two directions perpendicular to each other. The biaxial tensile test using the cruciform specimen is an appropriate test for understanding the behavior of materials under biaxial tensile in different states. The displacements or forces are applied at the two ends of the cruciform specimen in two directions of the sheet metal surface and with different ratios in order to create different states of tension [1].

The design of the cruciform specimen is one of the most controversial concepts in the biaxial tensile tests. The biaxial test specimens can be formed from a simple cylinder or a disk, which are hydrostatically pressurized from inside or on the surface, respectively, and from the cruciform specimens with different designs, as well. The cruciform specimens used by the researchers have different dimensions and shapes. The main purpose of the researchers is to create a net biaxial tensile within the effective tensile zone of cruciform specimen. One of the most important details within the effective tension region is to set the shear stress gradient to the least amount in order to create a purely biaxial stress state. Boehler et al. [2] showed that, in case the gradient of shear stresses emerge, however small, the principal stress axes could not be identified and the extraction of the behavior equation of the material would be invalid from the test results. The researchers have been looking for creating a biaxial stress in the middle of the specimen, without the stress in other parts of the specimen exceeding the amount found in the middle of the specimen. This is due to the fact that the specimen formability capacity and fracture strain in a uniaxial stress state are much less than that of the biaxial stress. Therefore, preventing any rupture in the cruciform specimen arms is attempted before the effective tension region in the middle of the specimen tears apart [3].

Among other experiments introduced to create biaxial stresses, one can name hydrostatic, punch and die, as well as Marciniak tests [4,5,6]. The loading is done out of the plane in these tests type. For this reason, the bending was created in metal sheets. Thus, determining the properties of the metal sheets was found to be error-prone. Therefore, the researchers focused on experiments in which they can load the specimen in plane and eliminate the effects of bending.

Using the finite element simulation, the researchers determined the cruciform specimen dimensions according to the type of tensile device, sheet thickness, sheet material, material yield/fracture status, etc. Boehler et al. [2] optimized the dimensions of the cruciform specimen for a metal sheet with two different thicknesses. Abu-Farha [7] also provided an optimal dimension for the cruciform specimen, which is more general than the one provided by Demmerle and Boehler. It is possible to study the biaxial fracture behavior of the ductile sheet metals using the fracture-optimized cruciform specimen [6, 8]. The Deng et al. [9] standardized cruciform specimen is used in the yield behavior of metal sheets.

Unlike a uniaxial tensile specimen which is standardized, the cruciform specimen does not have a specific standard in fracture conditions for biaxial tensile test [1]. However, ISO-16842 standard can be used for the yield state.

The anisotropy effects appear in a thin sheet, when the rolling operation is performed on it [10]. An anisotropic metal sheet is damaged faster in the weaker directions under a simultaneous biaxial loading [5, 11]. One issue that needs consideration in anisotropic materials is the mismatch between the exerted strain axes and the principal strain axes [2]. This causes the shear stress gradient to appear in the specimen. To overcome this problem, the researchers have deployed “off-axes” loading for uniaxial stresses. Boehler et al. [2] pointed out that by using an optimized specimen for an isotropic material and loading a specimen in which the arms are tightly attached to the tensile device, the reasonable results can also be made for anisotropic materials. Leotoing et al. [6] presented other distinctive dimensions for the fracture cruciform specimen. They also used this specimen to test the anisotropic materials and pointed out that these dimensions could create all strain paths and maintain maximum stress in the middle of the specimen without the arms bearing breakage. In this research, the Leotoing’s fracture specimen was used to examine the fracture in the AA5083 and Ti–6Al–4V alloys.

The researchers have designed different devices for carrying out biaxial experiments. Such devices can be divided into two parts: (1) independent biaxial tensile devices and (2) dependent biaxial tensile devices. The forces and displacements are applied independently to the arms of the cruciform specimen, alongside the two perpendicular axes in the independent biaxial tensile devices. Makinde et al. [12] devised a device for this purpose. It is possible to refer to the devices invented by Boehler et al. [2], Deng et al. [9] and Kuwabara et al. [11]. The key issue in designing these devices is how to apply the forces of each arm to the cruciform specimen. Researchers attempted to prevent the application of bending forces, from the arms, to the cruciform specimen in their designs. One of the important differences between these designs is in the way the cruciform specimen is placed on the device. The devices that load the specimen vertically, such as the device designed by Boehler et al., have advantages over other devices, since in these devices, it is easier to study the strain field in a cruciform specimen and apply the heat.

In general, independent biaxial tensile devices do not differ significantly from each other. The cost of such devices is very high. The high price of these devices incited the researchers to design a dependent biaxial tensile device. In these devices, the movement and force in one direction are relevant to the movement and force in other direction. In order to create different strain paths in the cruciform specimen, during the relationship between force and displacement in one direction to another, transformations are made by changing the length of the links, so that a movement in one direction would be a multiple of motion in another direction. In order to create motion in two directions, the cruciform specimen of the biaxial tensile mechanism is located in a tension–compression device. This will reduce the cost for making these devices, but the problem is that the number of created strain paths is limited. Ferron and Makinde [13] presented a plan with eight bar links. Fraunhofer [14], Brieu et al. [15], Vezer and Major [16], Abu-Farha [7] and Quaak [5] designed different dependent biaxial tensile devices.

In this research, a biaxial tensile mechanism was designed and fabricated to reduce the manufacturing costs and biaxial loading tests using Leotoing’s cruciform specimen. This device is slightly different from the designed devices so far, and it is created using the uniaxial tension–compression device of INSTRON-1343. The uniaxial tests for aluminum alloy 5083 were performed using uniaxial SANTAM-250 machine. The specimens were made in accordance with an ASTM-E8/E8M-13a standard in three directions, i.e., 0, 45° and 90°, compared to the rolling direction, and also were tested under different strain rates and temperatures. After the uniaxial and biaxial tests, for the aluminum alloy 5083, the simulations were carried out using the finite element method with ABAQUS software. The accuracy of simulations was also compared with experimental results.

Finally, by applying the different displacement ratios on the cruciform specimen arms, in the finite element software, biaxial tensile stresses at fracture points were calculated at the test section and in the moment before the fracture. The biaxial stress points are very practical for proposing a suitable behavior criterion or for modifying various fracture criteria. The fracture locus of the material can be obtained using these computational values in the first quarter of the stress plane. The numerical solution of the finite element method for Ti–6Al–4V alloy was repeated at different temperatures and strain rates, and biaxial stresses were obtained for each temperature and strain rate with different displacement ratios on the cruciform specimen arms. Unlike what is presented in the conditions of yielding by the standard cruciform specimen in the work of Deng et al. [9], the biaxial stresses do not follow a smooth and regular profile for the fracture behavior of the Ti–6Al–4V alloy. The biaxial stress points were gathered at most temperatures and strain rates for Ti–6Al–4V alloy in the vicinity of the equi-biaxial stress point in stress plane. On the other hand, in the vicinity of the uniaxial stress axes, the cruciform specimen is not capable of showing the points of the biaxial stresses. This phenomenon relates to the configuration of the Leotoing’s cruciform specimen. In spite of the unique features of the Leotoing’s cruciform specimen in comparison with the punch die and older specimens, this specimen solitarily cannot provide a wide range of biaxial tensile stress points in the fracture conditions.

The simulation made by the finite element method in this study was based on Hill1948 anisotropy criterion. This criterion is not able to predict the aluminum alloys behavior to a certain extent; however, it predicts the behavior of Ti–6Al–4V alloy very well. In principle, the actual loci of the material must be between the upper bound (quadratic) and the lower bound (like of Tresca loci) [17]. The predicted biaxial stress points for Ti–6Al–4V alloy using the Hill1948 anisotropy criterion are the upper bound of the biaxial stresses. In order to increase the precision of the calculated biaxial fracture stress points, one has to propose a method for measuring stress in the material fracture place for obtaining the actual value of the biaxial fracture stress and improving the predictive criteria of material fracture behavior. On the other hand, it is possible to repeat the finite element simulations using the other criteria and choose the most precise criterion by user’s considerations. ABAQUS software has limitations in this regard. However, it can be performed in a systematic and long-term work via coding methods.

2 Experimental works

2.1 Test specimens

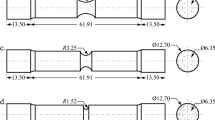
Figure 1 shows the Leotoing’s fracture cruciform specimen, which is designed to examine the fracture behavior in ductile sheet metals. ‏One of the features of this specimen is that it is optimized for the biaxial fracture tension tests. The cruciform specimen configuration is in a way that the gradient of stress is toward the center of the specimen, that is, the center of the test section, and the fracture occurs in the test section area with each loading ratio. If the material yield state is to be considered in the biaxial tensile test, the Deng or Kuwabara’s cruciform specimen should be used [9, 11]. The configuration of this cruciform specimen for the yield state is completely different from the configuration of the Leotoing’s fracture cruciform specimen.

Fig. 1

The drawing of the Leotoing’s cruciform specimen for considering the biaxial fracture behavior of ductile sheet metals (the unit is mm) [6, 8]

The Leotoing’s specimen was cut off from a sheet of AA5083 alloy with 4 mm thickness by a water jet machine. Then, the test section area was machined by CNC milling machine. After that, the grooves of the arms were created by CNC wire cut machine. In the end, the operation of creating the grid on a flat surface of the specimen was carried out using electrochemical etching. The grid was made up of circles with 5 mm diameter.

For measuring anisotropy properties, the uniaxial tensile tests were performed in 0°, 45° and 90° orientations, relative to the rolling direction of AA5083 alloy sheet. The uniaxial specimens were fabricated based on their standard ASTM-E8/E8M-13a. The specimens were first cut using water jet device and then wire cut machine.

2.2 Equipment and experimental setup

The SANTAM-250 machine has been used in the uniaxial tensile tests. Before doing the tests, the extensometer was calibrated by an extensometer calibrator for accurate measuring of gage length on the uniaxial specimen. A biaxial tensile-dependent mechanism is designed and fabricated in accordance with Fig. 2, to perform biaxial tests using the yield/fracture cruciform specimens. The mechanism is placed on an INSTRON-1343 uniaxial tension–compression machine.

Fig. 2

The dependent mechanism of the biaxial tensile installed on the uniaxial tension compression test machine of INSTRON-1343; (1) Dino-Lite microscope, (2) link, (3) heater, (4) INSTRON-1343 machine, (5) load cell, (6) counterweigh, (7) control unit, (8) laser thermocouple, (9) cruciform specimen

The test setup equipment include: INSTRON-1343 tension–compression machine with loading capacity of 50 tons and minimum grips speed up to 0.5 mm/min, the cruciform specimen according to Leotoing’s fracture model, the S-shaped load cells of the ZEMIC company (Code: H3-C3-10t-6B-D55) with loading capacity of 10 tons, DinoLite microscope type: AM 7013 MZI(R4), electrical heater with heat generation capacity up to 600 °C and a laser thermometer for measuring the specimen temperature when it is warming up. All of the mentioned components are shown in Fig. 2.

The sunken area in the Leotoing’s cruciform specimen is placed downward and in front of the heater. The other side which is smooth and gridded is upward, and the microscope is placed in front of it. In this way, the strain and strain rates are easily measured. The grid size on the flat surface of the cruciform specimen, in the test section area, is a circle with a diameter of 5 mm. Figure 2b shows how the Leotoing’s cruciform specimen is placed in the biaxial tensile mechanism. The load cells of the mechanism were calibrated by INSTRON-1343 tension–compression machine before performing biaxial tensile tests. In low loading amounts, the accuracy of the load cells was higher. Based on this loading, the software and the codes related to the load cells were calibrated.

The dependent mechanism of the biaxial tensile has some constraints, i.e., the difficulty in installing on the uniaxial tension–compression test machine of the INSTRON-1343, setting up links, the removal of the clearances and initial movement of the device until the loading initiation on the specimen, the specimen installation on grippers, high weight, needing a long time to prepare, the installation of camera or microscope. However, in spite of these, it is relatively cheap. The links length of the mechanism can be changed. That is, the displacements can be created with a little difference in two directions of rolling and transverse (RD and TD). This is a control option for the biaxial mechanism. This mechanism is not that user-friendly.

The part number 5 is load cell in Fig. 2. The two similar load cells are used in the mechanism. A load cell in the rolling direction and other load cell in the transverse direction are mounted in along the specimen arms. A demo piece to the form of load cell is applied on the other side of each load cell. Of course, the forth load cells can be used to increase the precision. The nominal load capacity of each load cell is 10 tons. The load cells are based on electrical strain gages technology and have a sensitivity of 2 mV/V. A signal conditioning module of ADAM-3016 was used for signal conditioning and collecting data. The signal conditioning module has 2.4 kHz band width that is suitable for dynamic measurements. A data acquisition card, ADVANTECH-4716 model, was used, which has AtD-16 bit and data acquisition rate of 250 KSample/S. The load cells were calibrated using the INSTRON-1343 device. The calibration was performed in the range of 3 tons. The LabVIEW 2017 (64 bit) software was used for collecting data, and then, the empirical force–time diagrams were drawn. Generally, the force measurement system output consists of the graph and the Excel file.

2.3 Experimental observations and measurements

2.3.1 Uniaxial tests

It is necessary to perform uniaxial tests in 0°, 45° and 90° orientations, relative to the rolling direction in order to consider the anisotropy of the sheet metals. The 0° and 90° orientations are rolling direction (RD) and transverse direction (TD), respectively. Therefore, according to the ASTM-E8/E8M-13a standard, these tests are performed for AA5083 alloy by the SANTAM-250 tension–compression machine and the experimental results are presented as the diagrams in Fig. 3.

Fig. 3

The experimental diagrams of engineering stress–strain for Al5083-H321 alloy

There was a flow discontinuity in Fig. 3. The flow discontinuities in aluminum alloys are commonly associated with phenomena of dynamics aging mechanisms. These include the formation of deformation bands at the specimen surface, or the negativity of the macroscopic strain sensitivity coefficient, which is a characteristic of the Portevin–Le Chatelier (PLC) effect. The creation of each tooth in the stress–strain curve is due to the creation of a deformation band along the specimen. Indeed, the flow discontinuity is caused by the sudden loss of specimen toughness and its surface roughness [18, 19]. The effect of PLC has not been investigated for AA5083 alloy in this study. There is no PLC in Ti–6Al–4V alloy behavior, and there is no need to study this alloy.

Figure 3 diagrams should be converted into true stress–plastic strain diagram for numerical applications of large deformations. Therefore, the true stress–plastic strain graphs are indicated in Fig. 4 in the three above-mentioned orientations. The yield stresses are obtained using 0.2% assumption of the center outside by simple uniaxial tensile specimens for each orientation. Hence, the yield stresses amounts for AA5083 alloy are: $\sigma_{{0{^\circ }}} = \sigma_{\text{RD}} = 225$, $\sigma_{{45{^\circ }}} = 220$, and $\sigma_{{90{^\circ }}} = \sigma_{\text{TD}} = 215$ MPa. It is worth noting that there is some error in the problem due to the global agreement of the method for determining the yield stress, as well as the slight curvature at the beginning of the elastic region of the stress–strain engineering diagrams.

Fig. 4

The true stress–plastic strain diagrams for AA5083 alloy

The biaxial fracture stress points for Ti–6Al–4V alloy at various temperatures and strain rates by the finite element method are considered in this paper. Therefore, the uniaxial stress–strain data are required at different temperatures and strain rates. Thus, the uniaxial experimental data in the work of Li et al. [20] are employed in this paper. The true stress–plastic strain diagrams for Ti–6Al–4V alloy in different temperature and strain rate states are shown in Fig. 5. The Ti–6Al–4V alloy finds the softening behavior with increasing temperature and decreasing strain rate as shown in Fig. 5. As the temperature decreases and the strain rate increases, the behavior of this alloy is reduced to hardening. This is very important in choosing the constitutive equations.

Fig. 5

True stress–plastic strain experimental curves of Ti–6Al–4V alloy at different temperatures and strain rates [20]

2.3.2 Biaxial tests

The biaxial experimental tests were done only for AA5083 alloy in an equi-biaxial state according to the test setup in Fig. 2. That is, the lengths of alike links were equal. This means that the cruciform specimen arms were placed under the same displacements. The test was carried out at ambient temperature, and the grips speed was set at 1 mm/min. The arms force of the cruciform specimen has been measured by two load cells in the biaxial tensile mechanism as described in Sect. 2.2. Figure 6 shows the force experimental curves in the load cells of the biaxial mechanism, i.e., the components of No. 5 in Fig. 2. The maximum difference between the two graphs of depicted in Fig. 6 is about 15.67%, and in the region near the summit, these two graphs match one another. The experimental graphs in Fig. 6 are very valuable.

Fig. 6

The force diagrams on the Leotoing’s cruciform specimen in the rolling (RD) and transverse (TD) directions

These graphs show the biaxial tensile behavior in the equi-biaxial tensile state, which are somewhat different from the uniaxial tensile behavior in Fig. 3, from the perspective of the appearance. The interesting point is the effect of anisotropic behavior on the force curve of the cruciform specimen arms in Fig. 6. Figure 6 shows that during the loading, the transverse direction tolerates less force than the rolling direction. However, at the end of the loading and the onset moment of fracture, the two will fit in with each other. Therefore, it can be stated from Fig. 6 that:

• 1. Stage I indicates the movement of the biaxial tensile mechanism at the start of loading onto the cruciform specimen. The biaxial tensile mechanism has a slight displacement down in its horizontal links before loading.

• 2. Stage II can be considered as a biaxial elastic region. The material is yielded at points Y_R and Y_T.

• 3. Stage III shows the material plastic behavior till the damage onset, as well as, the complete fracture of the material. It seems that at point F_o the damage is started, and the complete fracture occurs at point F_e.

Figure 7 shows the Leotoing’s broken specimen of AA5083 alloy and its section on the biaxial tensile mechanism, under equi-biaxial displacement. As shown in Fig. 7, the break section in the test section thickness has the angle of 45° relative to plane RD–TD. The angle also occurs in the uniaxial specimen for the ductile metal materials.

Fig. 7

The fracture of the cruciform specimen of Al5083 alloy, a the gridded surface, b the pit surface

The test section center area, that is, the uniform thickness circle at the center of the test section with a diameter of 2 mm, tends toward the intersection of the loading axes in Z direction, since the Leotoing’s cruciform specimen is not symmetric in the thickness or normal direction (ND). This may be a flaw and error factor in the experimental and numerical results. Figure 8 also shows how to fracture the cruciform specimen under the equi-biaxial tensile. The cruciform specimen is indicated before loading in Fig. 8a. The plastic deformation in forming ×  occurs at the corner directions of the test section, and it can be seen that the deformations are very slight in areas close to the arms, as well as on the axis of symmetry of the cruciform specimen in Fig. 8b, c. On the other hand, Fig. 8c shows the fracture outset in the test section area. The fracture begins at a place where the test section has a variable thickness. According to Fig. 1, there is an area of 2 mm in diameter with a thickness of 0.75 mm in the middle of the cruciform specimen test section. The test section has a thickness variation up to 2 mm in 12.5 mm radius as nonlinear. It is expected that in the experimental tests and in numerical analyses of finite elements, the fracture occurs in this region of the test section and not in the center of test section. In the present test, this hypothesis became a definite fact. Of course, experimental tests have been repeated and the result is the same for all of them. Figure 8d also explains the growth of damage and the way the cruciform specimen fractures. It is important to note that, in Fig. 8, the horizontal and vertical directions from the observer’s perspective are the rolling and the transverse directions, respectively.

Fig. 8

The fracture images in the cruciform specimen of AA5083 alloy by a Dino-Lite microscope; a before the loading, b the necking path, c the fracture beginning and d the fracture evolution

3 Numerical simulations of cruciform specimen

The ABAQUS finite element software was used in numerical analysis of the plastic deformation and the fracture of the cruciform specimen. The cruciform specimen was not modeled axi-symmetrically, because in the specimen corners directions, the damage or ruptures occur at one point, inside the test section. The simulations were initially carried out for aluminum alloy, because the experimental tests were done for the cruciform specimen of this material. The simulations of the cruciform specimen of Ti–6Al–4V alloy were done for variety states of temperatures and strain rates after assuring the accuracy of the solving method. The authors considered concepts such as the location of fracture at the test section, the fracture evolution and the forces of the specimen arms in comparing the simulation results, with regard to laboratory and data acquisition facilities.

3.1 Modeling and boundary conditions

The partitioning in the test section is very important for meshing the finite element model, because the test section has non-uniform thickness and also the failure occurs in this part. Thereupon, the element type C3D8R is selected. The whole finite element model has an elements number of 134,112. Based on Fig. 1, the partitioning and the meshing are shown in Fig. 9.

Fig. 9

The finite element model of the Leotoing’s cruciform specimen in ABAQUS software, the x-axis is rolling direction (RD), the y-axis is transverse direction (TD), and the z-axis is normal (thickness) direction (ND)

The loading is in the form of displacement and with different displacement ratios on the cruciform specimen arms. If it is assumed that U1 and U2 are the displacements in rolling (x) and transverse (y) directions, respectively, the displacements will be applied to the cruciform specimen arms with a ratio of U1/U2 for different states of 4:1, 4:2, 4:3, 4:4(1:1), 3:4, 2:4 and 1:4. Figure 10 shows the boundary and loading conditions. For instance, the boundary and loading conditions are expressed in Table 1 for the displacement ratio of U1/U2 = 4:1. Unregistered values for ABAQUS are also shown with the * mark in Table 1. It is worth noting that the displacement ratios 1:0 and 0:1 are for uniaxial states in rolling and transverse directions, respectively. The numerical solution of the cruciform specimen was performed only in the load ratio 1:1 according to the experimental test for AA5083 alloy. The conditions for a cruciform specimen of Ti–6Al–4V alloy include 7 displacement ratios, 3 temperatures and 5 strain rates.

Fig. 10

The boundary and loading conditions of Leotoing’s cruciform specimen in ABAQUS

Table 1 The boundary and loading conditions of Leotoing’s cruciform specimen for the displacement ratio of U1/U2 = 4:1

3.2 Behavior criteria

The Hill1948 criterion has been used to express the anisotropy behavior of both AA5083 and Ti–6Al–4V alloys. The Hill1948 criterion is considered as a reference criterion [21], and its anisotropic constants are easily determined through uniaxial experimental tests. This criterion is slightly weak in expressing the anisotropic behavior of AA5083 alloy. However, it predicts the anisotropic behavior of Ti–6Al–4V alloy very well. Hence, the performed simulations in this study are based on the Hill1948 criterion.

It is necessary to observe the onset, the place and the fracture path in the test section of the cruciform specimen in the finite element analysis. Therefore, one of the damage criteria should be used in this regard. In so doing, the ductile damage criterion has been selected for the finite element analysis of AA5083 alloy, and the Johnson–Cook model has been selected for the finite element analysis of Ti–6Al–4V alloy. The reason behind this choice is the relatively easy access to the models coefficients in these alloys and the finite element method responses.

The ductile criterion is a phenomenological model for predicting the damage onset due to nucleation, growth and coalescence of voids. The model assumes that the equivalent plastic strain at the onset of damage, $\bar{\varepsilon }_{D}^{pl}$, is a function of stress triaxiality and strain rate [22]:

$$\bar{\varepsilon }_{D}^{pl} = \bar{\varepsilon }_{D}^{pl} \left( {\eta ,\dot{\bar{\varepsilon }}^{pl} } \right)$$

(1)

where η = − p/q is the stress triaxiality, p is the pressure (hydrostatic) stress, q is the Mises equivalent stress, and $\dot{\bar{\varepsilon }}^{pl}$ is the equivalent plastic strain rate [23,24,25]. The criterion for damage initiation is met when the following condition is satisfied:

$$\omega_{D} = \int {\frac{{d\bar{\varepsilon }^{pl} }}{{\bar{\varepsilon }_{D}^{pl} \left( {\eta ,\dot{\bar{\varepsilon }}^{pl} } \right)}}} = 1$$

(2)

where ω_D is a state variable that increases monotonically with plastic deformation. At each increment and during the analysis, the incremental increase in ω_D is computed via:

$$\Delta \omega_{D} = \frac{{\Delta \bar{\varepsilon }^{pl} }}{{\bar{\varepsilon }_{D}^{pl} \left( {\eta ,\dot{\bar{\varepsilon }}^{pl} } \right)}} \ge 0$$

(3)

The Johnson–Cook dynamic failure model is based on the value of the equivalent plastic strain at element integration points; failure is assumed to occur when the damage parameter exceeds 1. The damage parameter, ω, is defined as [26]:

$$\omega = \sum {\left( {\frac{{\Delta \bar{\varepsilon }^{pl} }}{{\bar{\varepsilon }_{f}^{pl} }}} \right)}$$

(4)

where the increment of the equivalent plastic strain is $\Delta \bar{\varepsilon }^{pl}$, the strain at failure is $\bar{\varepsilon }_{f}^{pl}$, and the summation is performed over all increments in the analysis. The strain at failure, $\bar{\varepsilon }_{f}^{pl}$, is assumed to be dependent on a non-dimensional plastic strain rate, $\dot{\bar{\varepsilon }}^{pl} /\dot{\varepsilon }_{0}$; a dimensionless pressure/deviatoric stress ratio, p/q (where p is the pressure stress and q is the Mises stress); and the non-dimensional temperature, $\hat{\theta }$, defined earlier in the Johnson–Cook hardening model. The dependencies are assumed to be separable and are in the form of [27]:

$$\bar{\varepsilon }^{pl} = \left[ {d_{1} + d_{2} \exp \left( {d_{3} \frac{p}{q}} \right)} \right]\left[ {1 + d_{4} \ln \left( {\frac{{\dot{\bar{\varepsilon }}^{pl} }}{{\dot{\varepsilon }_{0} }}} \right)} \right]\left( {1 + d_{5} \hat{\theta }} \right)$$

(5)

where d₁–d₅ are failure parameters measured at or below the transition temperature, θ_transition, and $\dot{\varepsilon }_{0}$ is the reference strain rate. The constants values of $d_{1} - d_{5}$ are provided when the Johnson–Cook dynamic failure model is defined. This expression for $\bar{\varepsilon }_{f}^{pl}$ differs from the original formula published by Johnson and Cook [28] in the sign of the parameter d₃. This difference is motivated by the fact that most materials experience an increase in $\bar{\varepsilon }_{f}^{pl}$ with increasing pressure/deviatoric stress ratio; therefore, d₃ in the above expression will usually take positive values [29].

3.3 Material properties

The properties and the anisotropic parameters of the two alloys discussed above are presented in Table 2. These properties are used for numerical solutions. The ASTM517-00 international standard is applicable with respect to the anisotropy properties of the material used [30,31,32]. The anisotropy relationships include:

$$\begin{aligned} r_{{(x)^{0} }} & = {{\varepsilon_{{w(x)^{0} }} } \mathord{\left/ {\vphantom {{\varepsilon_{{w(x)^{0} }} } {\varepsilon_{{t(x)^{0} }} }}} \right. \kern-0pt} {\varepsilon_{{t(x)^{0} }} }} \\ R & = {{\left( {r_{{0{^\circ }}} + 2r_{{45{^\circ }}} + r_{{90{^\circ }}} } \right)} \mathord{\left/ {\vphantom {{\left( {r_{{0{^\circ }}} + 2r_{{45{^\circ }}} + r_{{90{^\circ }}} } \right)} 4}} \right. \kern-0pt} 4} \\ \Delta R & = {{\left( {r_{{0{^\circ }}} + r_{{90{^\circ }}} - 2r_{{45{^\circ }}} } \right)} \mathord{\left/ {\vphantom {{\left( {r_{{0{^\circ }}} + r_{{90{^\circ }}} - 2r_{{45{^\circ }}} } \right)} 4}} \right. \kern-0pt} 4} \\ \end{aligned}$$

(6)

Table 2 Some mechanical properties of AA5083 and Ti–6Al–4V alloy [27, 30, 34]

The strain ratio in the x direction is $r_{{(x)^{0} }}$. The strains in the width and thickness directions of the uniaxial specimen are ɛ_w and ɛ_t, respectively. The normal and planar anisotropy are explained by R and ΔR, respectively. The ratio of the width strain per thickness strain is expressed by r, but ɛ_t is not measurable due to thinness of the sheet, and therefore, the longitudinal and width strains are measured. Using the conservation principle of volume in the plastic deformation, the strain is obtained along the thickness. This means:

$$\begin{aligned} & \varepsilon_{l} + \varepsilon_{w} + \varepsilon_{t} = 0 \\ & \varepsilon_{t} = - (\varepsilon_{l} + \varepsilon_{w} ) \\ \end{aligned}$$

(7)

Generally, ɛ_l is the longitudinal strain in the longitudinal direction of the uniaxial specimen. It is necessary to calculate the anisotropy stress ratios as relation (8), which are calculated using the above relations in order to express anisotropy in ABAQUS software.

$$\begin{aligned} R_{11} & = R_{13} = R_{23} = 1 \\ R_{22} & = \left( {\frac{{r_{90} (r_{0} + 1)}}{{r_{0} (r_{90} + 1)}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \\ R_{33} & = \left( {\frac{{r_{90} (r_{0} + 1)}}{{r_{0} + r_{90} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \\ R_{12} & = \left( {\frac{{3r_{90} (r_{0} + 1)}}{{(2r_{45} + 1)(r_{0} + r_{90} )}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \\ \end{aligned}$$

(8)

These coefficients for AA5083 alloy are calculated from empirical tests in this paper and are listed in Table 2. The anisotropy coefficients for Ti–6Al–4V alloy are derived from references.

The used values for the ductile damage and the Johnson–Cook damage criteria coefficients of both alloys are presented in Table 3. The stress triaxiality parameter value was obtained 0.33 from the finite element analysis of the uniaxial specimen for AA5083 alloy. The equivalent plastic strain rate is 0.0003 in the uniaxial tensile experimental test of the AA5083 alloy.

Table 3 The parameters of the ductile and the Johnson–Cook damage models for AA5083 and Ti–6Al–4V alloys, respectively [24, 27, 33, 34]

The Johnson–Cook material constants and some other properties are used from Sun et al. and Polyzois’s research works for Ti–6Al–4V alloy [27, 33, 34].

The Johnson–Cook d₁–d₅ coefficients should be used in ABAQUS software. The transition temperature is the same room temperature according to Ref. [27]. The reference strain rate reduces the strain rate effect term to unity in the Johnson–Cook model. The biaxial tensile stress has been considered at a moment before fracture, in the place of fracture on the specimen. In order to show the fracture evolution of the finite element model, it is necessary to define the fracture (damage) evolution properties in the software. For this purpose, the fracture energy was considered 300 and for AA5083 alloy and 1000 for Ti–6Al–4V alloy. These values do not affect the results achieved from the current article.

The Johnson–Cook d₁–d₅ coefficients should be used in ABAQUS software. The transition temperature is the same room temperature according to Ref. [27]. The reference strain rate reduces the strain rate effect term to unity in the Johnson–Cook model. The biaxial tensile stress has been considered at a moment before fracture, in the place of fracture on the specimen. In order to show the fracture evolution of the finite element model, it is necessary to define the fracture (damage) evolution properties in the software. For this purpose, the fracture energy was considered 300 and for AA5083 alloy and 1000 for Ti–6Al–4V alloy. These values do not affect the results achieved from the current article.

3.4 Solver

The quasi-static solution has been used for simulating the cruciform specimen because the velocity and acceleration values are very low. The ABAQUS/Standard solver requires a long time period for solving the cruciform specimen and displays a variety of errors. Therefore, for more convenience, the ABAQUS/Explicit solver was used as well as the load rating and the mass scaling techniques. The contribution of inertial forces and kinetic energy is reduced for this kind of solution. A large part of the work done on the deformable piece increases the internal energy and contributes a little to kinetic energy. In this case, the kinetic energy level is at least or near zero. In the solution, the condition of the kinetic energy and the internal energy of the deformed material must be checked.

4 Results and discussion

The prepared CAE files (model database file) were implemented for each state of material, temperature, strain rate and displacement ratio based on the assumptions in Sect. 3 for the Leotoing’s cruciform specimen. In general, 7 and 105 runs were made for AA5083 and Ti–6Al–4V alloys, respectively. All of the CAE implementations required a high-performance computing (HPC) system for saving cost and time. The numerical results obtained for each of the alloys are presented below. On the other hand, it was necessary to apply a validation for alloys used. So, the materials validation was done by the uniaxial specimen and finite element method before the simulation of the Leotoing’s cruciform specimen.

4.1 Materials validation

The uniaxial tensile specimen according to ASTM-E8/E8M-13a was modeled in the FEM software, and the properties of the material are defined in Table 2 data. One side of the uniaxial specimen was fixed, and the other side was under stretching. An element was identified in the middle of the uniaxial specimen for each simulation in 0°, 45° and 90° orientations, and the true stress–plastic strain diagram was plotted for the specimen longitudinal direction in each state. Figure 11 shows the comparison of experimental and numerical results for each orientations of the AA5083 alloy. It can be seen from Fig. 11 that there is a good correlation between experimental and numerical results. This validation has been done solely for the plastic anisotropy, and the concepts of damage are not included.

Fig. 11

The comparison of experimental and simulation results for each direction of the AA5083 alloy, a the rolling, b the 45° and c the transverse directions

The true stress–plastic strain diagrams of Ti–6Al–4V alloy were obtained by the finite element method and via data of Fig. 5 and also Table 2 at 0°, 45° and 90° orientations. Due to the lack of experimental stress–strain data in two directions of 45° and 90° for Ti–6Al–4V alloy, the comparisons cannot be made between experimental and finite element results. The anisotropy coefficients used in this simulation are obtained from the work of Kotkunde et al. [34] at 400 °C, which are reliable. It is worth noting that the increasing temperature reduces the effect of anisotropy. For example, the true stress–plastic strain diagrams of Ti–6Al–4V alloy are shown in Fig. 12 at the temperature of 700 °C for three states of hardening (0.05 s⁻¹), perfectly plastic (0.005 s⁻¹) and softening (0.0005 s⁻¹). The apparent shape of the graphs obtained in Fig. 12 is similar to that found in Khan and Yu [35] experimental work for Ti–6Al–4V alloy at different temperatures and strain rates.

Fig. 12

The comparison of experimental and simulation results for each direction of the Ti–6Al–4V alloy, a the rolling, b the 45° and c the transverse directions at 700 °C and 0.05, 0.005 and 0.0005 s⁻¹

4.2 Numerical results of AA5083 alloy

Figure 13 shows the calculated forces diagram of the Leotoing’s cruciform specimen in rolling and transverse directions in terms of time.

Fig. 13

The force–time diagrams obtained from the numerical analysis at the rolling and transverse directions for the Leotoing’s cruciform specimen of AA5083 alloy

Considering that the results of finite element analysis are based on the uniaxial data, it is seen from Fig. 13 that:

• 1. There is not stage I in Fig. 13 similar to Fig. 6. The material is yielded in area Y_R,T in Fig. 13.

• 2. Zone II is the plastic deformation region.

• 3. The onset of damage occurred at point F_o. The material has been necking and relaxing before F_o.

• 4. The fracture is completed in F_e.

• 5. Figure 13 is very similar in appearance to Fig. 3.

It is worth noting that the two curves in Fig. 13 (and also Fig. 6) are interdependent, since they are simultaneously formed and affected by each other. Therefore, the presented interpretations are based on the biaxial fracture behavior of the material at the moment of the overlap of these two curves (at the fracture initiation and evolution locations). According to the above explanation, the error value for the fracture force of the two graphs of Figs. 6 and 13 is about 8.6%.

Figure 14 shows the distribution of the ductile damage criterion for the damage initiation and propagation conditions. The stress gradient is directed to the test section center at the cruciform specimen, and the specimen is sensitive to stress in its test section, on the way from the center to the corners. As the loading (displacements in the cruciform specimen arms) increases, this sensitivity increases and damage propagates at the test section as shown in Fig. 14b. The damage progresses to the specimen corners from the damaged onset point by increasing the load.

Fig. 14

The ductile damage criterion contour for the cruciform specimen fracture process of the Al5083 alloy using quasi-static finite element method compared with Fig. 8; a the damage initiation and b the damage evolution

Figure 8d shows the path of the damage propagation along the corner to the corner of the cruciform specimen test section. This is evident in Fig. 14b. Externally, there is an excellent correlation between the experimental and numerical results of Figs. 8 and 14. One of the attractive consequences for comparison in this research is to determine the location of damage onset in the test section of the specimen. Figure 8c shows the location of damage onset on a straight line (trigonometry) of 224.88° relative to the rolling direction and in radius of 8.2 mm. In Fig. 14a, this location is at an angle of 228.2° and in radius 3.2 mm. These results are very close to each other and desirable.

The curves of the kinetic energy and total strain energy obtained in the quasi-static solution of finite element analysis are shown in Fig. 15. In a quasi-static analysis, the amount of kinetic energy should not be increased by a small fraction of strain energy. This issue is realized in Fig. 15.

Fig. 15

The total internal and total kinetic energy (ALLIE and ALLKE) curves obtained from quasi-static analysis of the finite element method of AA5083 alloy for displacement ratio 1:1

A very practical result for the finite element analysis is the extraction of stress values at the location of damage detection in two directions of rolling and transverse of the sheet metal. It is known that a relatively accurate measurement of the fracture stress, at the point of the damaged piece, is currently very difficult and very challenging. Determining stress in such situations is performed first by measuring deformations or strains and then calculating them. Accordingly, in the AA5083 cruciform specimen, the stress values were obtained in an increment time before damage initiation to the rolling and transverse directions, respectively. The stress values are σ₁₁ = σ_RD = 477.5 MPa and σ₂₂ = σ_TD = 405 MPa. By repeating the analysis carried out in this study, the fracture loci of the material can be obtained for the different load ratios. The fracture loci is the same as the forming limit stress diagram (FLSD), which is very important and practical for designers as a fracture criterion. The accuracy of many criteria for the fracture behavior of different materials can also be verified by the FLSD, and/or a new criterion for material behavior can be suggested. The distribution of the damage criterion for the AA5083 cruciform specimen under the different displacement ratios is shown in Fig. 16. In all cases, the loading conditions are such that the displacement is applied on both pairs of arm, simultaneously.

Fig. 16

The ductile damage contour of the Leotoing’s cruciform specimen under different displacement ratios (DR) for AA5083 alloy

4.3 Numerical Results of Ti–6Al–4V Alloy

Numerical simulations of the cruciform specimen of Ti–6Al–4V alloy were performed based on the assumptions presented in Sect. 3 at different temperatures, strain rates and under different displacement ratios. The biaxial fracture stress points are calculated in each case and are also shown in Fig. 17. Generally, Fig. 17 shows the fracture loci of the Ti–6Al–4V alloy based on the finite element simulation, the uniaxial data and the Hill1948 anisotropy criterion. The fracture stress points on axes σ₁ and σ₂ are the uniaxial stresses in the rolling and transverse directions, respectively, which in turn are determined from the uniaxial experimental tests of Fig. 5. Each radial line that connects a bunch of stress points represents a displacement ratio in Fig. 18. One of the reasons behind the straightness of the radial lines in Fig. 18 is that the biaxial stress points are related to the fracture behavior of the material. Another reason is that the softening and the strain-hardening behaviors occur in the material by increasing the temperature and decreasing the strain rate and also by decreasing the temperature and increasing the strain rate, respectively. On the other hand, there is no control over the displacement impression on the cruciform specimen in this work. Therefore, the radial lines such as the work of the Deng et al. [9] for the yield state of material are not obtained. As can be seen from Fig. 17, in each case of temperature and strain rate, the biaxial stress points accumulate in the vicinity of the equi-biaxial stress point. This can be one of the characteristics of the Leotoing’s cruciform specimen to indicate fracture behavior.

Fig. 17

The calculated biaxial stress points in stress plane σ₁ − σ₂ for Ti–6Al–4V alloy and by different load ratios on the Leotoing’s cruciform specimen at different temperatures and strain rates

Fig. 18

The fracture radial paths of the displacement ratios in stress plane σ₁ − σ₂ for the Leotoing’s cruciform specimen of Ti–6Al–4V alloy at different temperatures and strain rates

The minimum kinetic energy and maximum internal energy required were also checked for each simulation. For instance, Fig. 19 shows this condition for solving at the temperature 650 °C, the strain rate 0.001 s⁻¹ and the displacement ratio 1:1.

Fig. 19

The total internal and total kinetic energy (ALLIE and ALLKE) curves obtained from quasi-static analysis of the finite element method of Ti–6Al–4V alloy at the temperature 650 °C, the strain rate 0.001 s⁻¹ and the displacement ratio 1:1

From the uniaxial tensile diagrams, the experimental simultaneous biaxial forces and the obtained forces of the finite element method, it can be seen that the biaxial large deformation behavior of the ductile sheet metals is essentially different from the uniaxial behavior of them. In the material behavior model (Hill1948) which has been implemented in the finite element software, all of the material constants are taken from uniaxial experimental tests. In other words, the anisotropy coefficients, the plastic behavior, the damage criteria constants, etc., are determined by the theories based on the uniaxial behaviors. Therefore, the outputs of the biaxial finite element analyses can be different with what is obtained in reality. It seems that in the line of this study, the efforts should be made to drive the biaxial fracture behaviors and properties, to standardize them, as well as to improve the method of the biaxial numerical analysis. The authors hope that they will be able to do this in their future researches. Hence, the result obtained in this study is only “Determination of the biaxial fracture stress points by the Leotoing’s cruciform specimen for Ti–6Al–4V alloy using finite element method and also the Hill1948 anisotropic criterion.”

5 Conclusion

In the previously published references, such as [1,2,3], only three stress points of the fracture have been used to propose an equation for the fracture loci of material. These points include uniaxial tension in 1- and 2-directions and also equi-biaxial state of stress. Therefore, the main limitation in the proposed fracture loci is the lack of number of the points which have been used. The main purpose in this paper is to determine the fracture stress points for Ti–6Al–4V alloy in stress subspace for different temperatures and strain rates. Such points will help in proposing more realistic fracture loci. For this purpose, the ABAQUS software was employed to simulate the biaxial tension of a specific fracture cruciform specimen, proposed by Leotoing [4, 5]. In order to achieve a proper dispersion of stress points, the simulation was repeated for different ratios of loadings. However, the results showed that despite a relatively wide range of loading ratios which were applied in the simulations, the resulted fracture stress points mainly lie in the vicinity of equi-biaxial stress state. Therefore, it seems that the Leotoing’s cruciform specimen is not suitable for this purpose. In other words, the Leotoing’s cruciform specimen is not suitable for studying the fracture behavior in practice. It is therefore an interesting subject to focus on improving the geometry of fracture cruciform specimen, in a manner that a proper dispersion of fracture stress points can be obtained for different loading ratios. Also, the other experimental test methods for biaxial stress states, such as Nakazima, Marciniak, Keeler [6] which are based on deep drawing of a blank sheet, can be used to obtain such stress points of fracture.