Multiple cracks analysis in a FG orthotropic layer with FGPM coating under anti-plane loading

Abstract

An analytical solution to the fracture analysis of a functionally graded (FG) orthotropic substrate with FG piezoelectric coating weakened by a screw dislocation is carried out. The material properties are assumed to vary exponentially through the thickness of the layers. The problem is solved under various types of anti-plane shear and in-plane electric loadings. At first, by considering a single-screw dislocation at crack location, an analytical solution is developed. Next, by using the Fourier transform, the problem is reduced to a system of singular integral equations with Cauchy-type singularities. Then, by computing the dislocation densities, both the stress intensity factors and the stress fields at the crack tips under different electromechanical loadings are determined. In this investigation, various examples are solved to show the applicability of the proposed solution by studying the effects of the cracks configurations, material properties, and non-homogeneity parameter on the stress intensity factors.

1 Introduction

Smart structures like piezoelectric materials have been manipulated in some advanced applications which necessitate the analysis of their behavior in different positions. Piezoelectric materials have various behaviors, so they are usually susceptible to cracking. Therefore, these materials have drawn a great attention of many researches in fracture mechanics. It is known that when piezoelectric materials deformed, they produce an electric field and undergo deformation when subjected to an electric field. Piezoelectric materials, due to this intrinsic coupling phenomenon, are used extensively in technologies such as aerospace, power generation and flow monitoring, and industrial equipment. A case in point is the application of such materials in airplanes wing with smart flexible flaps which are skeptical to cracking. Hence, the study of the fracture mechanics of piezoelectric materials plays an important role in the fracture problem.

To achieve advanced performance, piezoelectric components are often made as layered structures. For enhancing mechanical performance, the simplest structure is merely the composition of a piezoelectric layer and an orthotropic substrate which are used commonly [1].

Some investigations are done for weakened piezoelectric materials. For instance, Mousavi and Paavola [2] investigated the problem of cracked layer under anti-plane mechanical and in-plane electrical loading. The distributed dislocation technique was used to calculate the stress intensity factors (SIFs). Wang and Xu [3] by utilizing the Green’s function method studied the fracture problem of the interaction between a piezoelectric screw dislocation and a finite crack in a hexagonal piezoelectric solid. Huang and Kuang [4] considered piezoelectric material with respect to the first-order perturbation analysis of a non-ideal crack. The results showed the stress and electric intensity factors at the vicinity of cracks tips.

Besides, there have been some studies for the layered structures containing cracks. As an illustration, Lee et al. [5] considered the problem of Yoffe crack between a piezoelectric and two orthotropic layers under anti-plane loading. The results showed that the dynamic stress intensity factors depend on items such as crack length, the ratios of stiffness, and thickness. Narita and Shindo [6] studied the effect of the electroelastic interactions on the SIFs for the interface crack problem between piezoelectric and orthotropic materials. The SIFs and the effect of electroelastic interactions on the energy release rate were obtained. Kah Soh et al. [7] analyzed the interfacial crack problem subjected to anti-plane shear and in-plane electric loading. The effects of thickness and material constants on SIFs were shown to be significant. Li [8] presented a closed-form solution of two collinear crack normal to the piezoelectric strip boundaries. The SIFs and the energy release rate at the inner and outer crack tips were obtained. Li and Tang [9] investigated the interfacial crack problem between two dissimilar piezoelectric layer under the permeable crack assumption. Bayat et al. [10] investigated the problem of a cracked orthotropic layer with imperfect piezoelectric coating. SIFs and hoop stress on the imperfect bonding coefficient were calculated. Bagheri et al. [11] investigated cracked piezoelectric substrate with imperfect orthotropic coating. By using the dislocation densities, the field of stress intensity factors was determined. Feng et al. [12] considered the problem of interface crack between orthotropic substrate and a piezoelectric layer. Different material and geometrical parameters were considered to calculate SIFs. Kwon and Meguid [13] studied the fracture problem of Griffith crack between rectangular piezoelectric and two orthotropic layer. Ding and Li [14] considered and discussed the effects of periodic cracks in an FG piezoelectric strip bonded to a piezoelectric half-plane. Ueda [15] studied the crack problem in functionally graded piezoelectric (FGPM) layer bonded between two elastic coats under electromechanical loading. Numerical calculations are accomplished to compute the energy density factors.

Baghestani et al. [16] studied the problem of cracked orthotropic layer. The stress analysis of an orthotropic layer under in-plane point loads were carried out. Monfared et al. [17] investigated elastodynamic analysis of a cracked orthotropic layer under anti-plane loading using the distributed dislocation method. And in another investigation, Monfared and Ayatollahi [18] studied the cracked FG orthotropic half-plane containing multiple cracks under time-harmonic loading.

In the present study, a cracked FG orthotropic layer that is bonded to an FGP coating under different types of electromechanical loading is investigated. The problem is solved utilizing the Fourier transformation and disturbed dislocation technique to determinate the SIFs as well as the stress fields at cracks tips. Eventually, several examples are solved numerically to show the effect of various parameters such as cracks configuration, non-homogeneity parameter, various materials, and the type of loadings on the stress intensity factors.

In Sect. 2, the constitutive equations are presented, the displacement and stress fields for the FG orthotropic layer weakened by a single-screw-type dislocation bonded to the FGP coating are obtained. Next, in Sect. 3, the stress fields, without the dislocation, for different types of loadings applied to the boundaries are calculated. Then, the method to solve the system of integral equations for any cracks pattern is presented in Sect. 4. Finally, several examples are solved to show the influence of the aforementioned parameters on the stress intensity factors.

2 Formulation of the problem

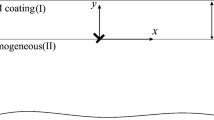
We consider an FG orthotropic layer with thickness $h_{2}$ bonded to an FGP layer with thickness $h_{1}$ that were polled in the $z$ direction (shown in Fig. 1). The single dislocation is chosen at point $(\zeta ,\eta )$ to analyze the stress fields which results in determination of the SIFs at crack tips.

Fig. 1

Schematic view of the FG orthotropic substrate with screw dislocation

2.1 Constitutive equations for the functionally graded piezoelectric coating

For the anti-plane deformation, the only nonzero displacement component is $w$, so other two elastic displacements $u$ and $v$ oriented in $x$ and $y$ axes disappear.

The displacement components are $u,v,w$ and the electric components are $E_{x} ,E_{y} ,E_{z}$, so we have

$$\begin{aligned} & u = 0,\quad E_{x} = E_{x} (x,y), \\ & v = 0,\quad E_{y} = E_{y} (x,y), \\ & w = w(x,y),\quad E_{z} = 0. \\ \end{aligned}$$

(1)

For the electric fields with respect to the electrical potential $\varphi (x,y)$ are

$$E_{x} = - \frac{\partial \varphi (x,y)}{\partial x},\quad E_{y} = - \frac{\partial \varphi (x,y)}{\partial y},$$

(2)

and the constitutive equations for the FGP layer in the region $0 < y < h_{1}$ are achieved by

$$\begin{aligned} \sigma_{zx1} (x,y) & = c_{44} (y)\frac{{\partial w_{1} (x,y)}}{\partial x} + e_{15} (y)\frac{\partial \varphi (x,y)}{\partial x},\quad D_{x1} (x,y) = e_{15} (y)\frac{{\partial w_{1} (x,y)}}{\partial x} - d_{11} (y)\frac{\partial \varphi (x,y)}{\partial x}, \\ \sigma_{zy1} (x,y) & = c_{44} (y)\frac{{\partial w_{1} (x,y)}}{\partial y} + e_{15} (y)\frac{\partial \varphi (x,y)}{\partial y},\quad D_{y1} (x,y) = e_{15} (y)\frac{{\partial w_{1} (x,y)}}{\partial y} - d_{11} (y)\frac{\partial \varphi (x,y)}{\partial y}, \\ \end{aligned}$$

(3)

in which $D_{x1} (x,y),\,\,D_{y1} (x,y)$ are the components of electric displacements. Furthermore, the shear modulus measured in a constant electric field is $c_{44} (y)$, dielectric constant measured at a constant strain is shown with $d_{11} (y)$, and the piezoelectric constant is depicted as $e_{15} (y)$. The equilibrium equation and the Maxwell equation are written for the stress and the electric displacement components, respectively, as follows:

$$\begin{aligned} \frac{{\partial \sigma_{xz1} (x,y)}}{\partial x} + \frac{{\partial \sigma_{yz1} (x,y)}}{\partial y} & = 0, \\ \frac{{\partial D_{x1} (x,y)}}{\partial x} + \frac{{\partial D_{y1} (x,y)}}{\partial y} & = 0. \\ \end{aligned}$$

(4)

By applying Eq. (3) into Eq. (4) we have

$$\begin{aligned} c_{44} (y)\Delta w_{1} + e_{15} (y)\Delta \varphi + \frac{{\partial c_{44} (y)}}{\partial y}\frac{{\partial w_{1} }}{\partial y} + \frac{{\partial e_{15} (y)}}{\partial y}\frac{\partial \varphi }{\partial y} & = 0, \\ e_{15} (y)\Delta w_{1} - d_{11} (y)\Delta \varphi + \frac{{\partial e_{15} (y)}}{\partial y}\frac{{\partial w_{1} }}{\partial y} - \frac{{\partial d_{11} (y)}}{\partial y}\frac{\partial \varphi }{\partial y} & = 0, \\ \end{aligned}$$

(5)

where $\Delta = \left( {\frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}} \right)$ is two-dimensional Laplacian operator. In this problem, for the sake of simplification, the FGP layer properties are assumed to vary exponentially in $y$ direction similarly which is described as follow

$$[c_{44} (y),e_{15} (y),d_{11} (y)] = {\text{e}}^{2\kappa y} \left[ {c_{44}^{0} ,e_{15}^{0} ,d_{11}^{0} } \right]$$

(6)

in which $c_{44}^{0} ,e_{15}^{0}$ and $d_{11}^{0}$ are material properties at $y = 0$. And $\kappa$ is FG constant with dimension $\frac{1}{\text{length}}$. By substituting Eq. (6) into Eq. (5), we have

$$\begin{aligned} c_{44}^{0} \Delta w_{1} + e_{15}^{0} \Delta \varphi + 2\kappa c_{44}^{0} \frac{{\partial w_{1} }}{\partial y} + 2\kappa e_{15}^{0} \frac{\partial \varphi }{\partial y} & = 0, \\ e_{15}^{0} \Delta w_{1} - d_{11}^{0} \Delta \varphi + 2\kappa e_{15}^{0} \frac{{\partial w_{1} }}{\partial y} - 2\kappa d_{11}^{0} \frac{\partial \varphi }{\partial y} & = 0. \\ \end{aligned}$$

(7)

It can be seen that Eq. (7) is coupled so the Bleustein function [19] is introduced to decouple the above-mentioned equations as

$$\psi (x,y) = \varphi - \alpha w_{1} ,\quad \alpha = e_{15}^{0} /d_{11}^{0}$$

(8)

By utilizing Eqs. (8), (7) could be separated as fallow

$$\Delta w_{1} + 2\kappa \frac{{\partial w_{1} }}{\partial y} = 0,\quad \Delta \psi + 2\kappa \frac{\partial \psi }{\partial y} = 0,$$

(9)

therefore, in terms of $(\psi ,w_{1} )$, the constitutive Eq. (3) is expressed as

$$\begin{aligned} \sigma_{zx1} & = [c_{44} (y) + \alpha e_{15} (y)]\frac{{\partial w_{1} }}{\partial x} + e_{15} (y)\frac{\partial \psi }{\partial x},\quad D_{x1} = - d_{11} (y)\frac{\partial \psi }{\partial x}, \\ \sigma_{zy1} & = [c_{44} (y) + \alpha e_{15} (y)]\frac{{\partial w_{1} }}{\partial y} + e_{15} (y)\frac{\partial \psi }{\partial y},\quad D_{y1} = - d_{11} (y)\frac{\partial \psi }{\partial y}. \\ \end{aligned}$$

(10)

2.2 Constitutive equations for the functionally graded orthotropic substrate

The constitutive equations for the anti-plane deformation of an FG orthotropic layer in the region $- \,h_{2} < y < 0$ are

$$\sigma_{zxi} (x,y) = G_{x} (y)\frac{{\partial w_{i} (x,y)}}{\partial x},\quad \sigma_{zyi} (x,y) = G_{y} (y)\frac{{\partial w_{i} (x,y)}}{\partial y},\quad i = 2,3,$$

(11)

where $G_{x} (y)$ and $G_{y} (y)$ are the FG orthotropic substrate constants in the $x$ and $y$ directions, respectively. The equilibrium equation for an FG orthotropic layer could be written as follows:

$$G_{x} (y)\frac{{\partial^{2} w_{i} }}{{\partial x^{2} }} + G_{y} (y)2\lambda \frac{{\partial w_{i} }}{\partial y} + G_{y} (y)\frac{{\partial^{2} w_{i} }}{{\partial y^{2} }} = 0,\quad i = 2,3,$$

(12)

and the shear moduli of an FG orthotropic layer, $G_{x} (y),G_{y} (y)$ are considered as

$$[G_{y} (y),G_{x} (y)] = e^{2\lambda y} \left[ {G_{y}^{0} ,G_{x}^{0} } \right]$$

(13)

so we could write

$$g^{2} \frac{{\partial^{2} w_{i} }}{{\partial x^{2} }} + \frac{{\partial^{2} w_{i} }}{{\partial y^{2} }} + 2\lambda \frac{{\partial w_{i} }}{\partial y} = 0,\quad g = \sqrt {G_{x} /G_{y} } \quad i = 2,3.$$

(14)

The self-equilibrium of stress and the continuity conditions taking into account the screw dislocation with the Burgers vector $b_{z}$ must be satisfied when there is no traction applied on the boundaries

$$\begin{aligned} & \sigma_{zy1} (x,h_{1} ) = 0,\quad \sigma_{zy2} (x,\eta^{ + } ) = \sigma_{zy3} (x,\eta^{ - } ), \\ & \sigma_{zy3} (x, - \,h_{2} ) = 0,\quad \sigma_{zy1} (x,0^{ + } ) = \sigma_{zy2} (x,0^{ - } ), \\ & D_{y} (x,0) = 0,\quad w_{1} (x,0^{ + } ) = w_{2} (x,0^{ - } ), \\ & D_{y} (x,h_{1} ) = 0,\quad w_{2} (x,\eta^{ + } ) - w_{3} (x,\eta^{ - } ) = b_{z} H(x - \zeta ). \\ \end{aligned}$$

(15)

in which $H(.)$ is the Heaviside step-function. The complex Fourier transform is utilized to solve the above-mentioned conditions which is defined by

$$f^{ * } (s) = \int\limits_{ - \infty }^{ + \infty } {f(x)} {\text{e}}^{isx} {\text{d}}x,\quad f(x) = \frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {f^{ * } (s)} {\text{e}}^{ - isx} {\text{d}}s.$$

(16)

By solving the Eq. (14) using the Fourier transform and applying the boundary conditions (15), the displacement components are obtained which leads to the determination of the stress fields in an FG orthotropic layer. The stress components have singular behavior at the vicinity of the crack tips, so by investigating the asymptotic meaning, $s \to \infty$ the singular terms can be separated. So the stress amounts can be shown as follows:

$$\begin{aligned} \sigma_{zx2} (x,y) & = - \frac{{b_{z} G_{x} }}{\pi }\left[ {\int\limits_{0}^{ + \infty } {\left\{ {\frac{{T_{11} }}{E}[T_{12} - T_{13} ] + \frac{{{\text{e}}^{sg (\eta - y )} }}{2}} \right\}} } \right.\cos [s(x - \zeta )]{\text{d}}s - \left. {\frac{g(y - \eta )}{{2[(x - \zeta )^{2} + g^{2} (y - \eta )^{2} ]}}} \right], \\ \sigma_{zy2} (x,y) & = - \frac{{b_{z} g^{2} G_{y} }}{\pi }\left[ {\int\limits_{0}^{ + \infty } {\left\{ {\frac{{T_{21} }}{E}[T_{22} - T_{23} ] - \frac{{{\text{e}}^{sg (\eta - y )} }}{2}} \right\}} } \right.\sin [s(x - \zeta )]{\text{d}}s + \left. {\frac{(x - \zeta )}{{2[(x - \zeta )^{2} + g^{2} (y - \eta )^{2} ]}}} \right]. \\ \end{aligned}$$

(17a)

for region $\eta < y < 0$ and

$$\begin{aligned} \sigma_{zx3} (x,y) & = \frac{{b_{z} G_{x} }}{\pi }\left[ {\int\limits_{0}^{ + \infty } {\left\{ {\frac{{T_{31} }}{E}[T_{32} - T_{33} ] - \frac{{{\text{e}}^{sg(y - \eta )} }}{2}} \right\}} } \right.\cos [s(x - \zeta )]{\text{d}}s + \left. {\frac{g(\eta - y)}{{2[(x - \zeta )^{2} + g^{2} (y - \eta )^{2} ]}}} \right], \\ \sigma_{zy3} (x,y) & = - \frac{{b_{z} g^{2} G_{y} }}{\pi }\left[ {\int\limits_{0}^{ + \infty } {\left\{ {\frac{{T_{41} }}{E}[T_{42} - T_{43} ] - \frac{{{\text{e}}^{sg(y - \eta )} }}{2}} \right\}} } \right.\sin [s(x - \zeta )]{\text{d}}s + \left. {\frac{(x - \zeta )}{{2[(x - \zeta )^{2} + g^{2} (y - \eta )^{2} ]}}} \right]. \\ \end{aligned}$$

(17b)

for region $- \,h_{2} < y < \eta$, in which the functions $T_{ij}$ are given in “Appendix A” and the parameters $E,\chi_{1} ,\chi_{2}$ and $\alpha_{1}$ read as follows

$$\begin{aligned} E & = \alpha_{1} \chi_{1}^{2} \cosh (h_{2} \chi_{1} )\sinh (h_{1} \chi_{2} ) + \chi_{1} \sinh (h_{2} \chi_{1} )\left[ {g^{2} G_{y} \chi_{2} \cosh (h_{1} \chi_{2} ) + \left( {\alpha_{1} \lambda - \kappa g^{2} G_{y} } \right)\chi_{1} \sinh (h_{1} \chi_{2} )} \right] \\ \chi_{1} & = \sqrt {s^{2} g^{2} + \lambda^{2} } ,\quad \chi_{2} = \sqrt {s^{2} + \kappa^{2} } ,\quad \alpha_{1} = (c_{44} + e_{15} \alpha ), \\ \end{aligned}$$

(18)

3 FG orthotropic layer bonded to FGP strip under various tractions

In this part, the FG orthotropic substrate and the FG piezoelectric coating without dislocation are considered to be under an anti-plane mechanical and in-plane electrical point load as well as two different types of shear tractions which are explained in Sects. 3.1 and 3.2 respectively.

3.1 Anti-plane mechanical and in-plane electrical point load

The boundary condition for the FG orthotropic substrate and the FGP coating under an anti-plane pure mechanical and in-plane electrical point loads with the magnitude $\tau_{0}$ and $D_{0}$ are defined as

$$\begin{aligned} & \sigma_{zy3} (x, - h_{2} ) = \tau_{0} \delta (x),\quad D_{y} (x,h_{1} ) = D_{0} \delta (x), \\ & \sigma_{zy1} (x,h_{1} ) = \tau_{0} \delta (x),\quad D_{y} (x,0^{ + } ) = D_{0} \delta (x), \\ \end{aligned}$$

(19)

where $\delta (x)$ is the Dirac delta function. Now, with respect to the Fourier transform Eq. (16), and the mention boundary conditions (19), similarly to the dislocation solution, the stress components can be obtained as follows:

$$\sigma_{zx2} (x,y) = - \int\limits_{0}^{ + \infty } {\left[ {\frac{x}{F}(d_{11} (A_{1} + A_{2} - A_{3} + A_{4} - A_{5} )\tau_{0} - A_{6} A_{7} ) + \left. {\frac{{G_{x} D_{0} e_{15\,} }}{{d_{11} \pi (\alpha_{1} + gG_{y} \,)}}{\text{e}}^{s\gamma y} } \right]} \right.} \sin (sx){\text{d}}s - \frac{{G_{x} D_{0} e_{15\,} }}{{d_{11} \pi (\alpha_{1} + gG_{y} )}}\left( {\frac{x}{{x^{2} + (yg)^{2} }}} \right)$$

$$\sigma_{zy2} (x,y) = \int\limits_{0}^{ + \infty } {\left[ {\frac{1}{F}(d_{11} (C_{1} - C_{2} + C_{3} + C_{4} + C_{5} )\tau_{0} - C_{6} C_{7} ) - \frac{{gG_{y} D_{0} e_{15} }}{{d_{11} \pi (\alpha_{1} + gG_{y} )}}{\text{e}}^{s\gamma y} } \right]} \cos (sx){\text{d}}s + \frac{{gG_{y} D_{0} e_{15} }}{{d_{11} \pi (\alpha_{1} + gG_{y} )}}\left( {\frac{yg}{{x^{2} + (yg)^{2} }}} \right)$$

(20)

in which the functions $F$ and $A_{i} ,\,\,C_{i} i = 1,2, \ldots ,7$ are given in “Appendix B” and parameters $\chi_{1} ,\chi_{2}$ and $\alpha_{1}$ are the same ones defined in Eq. (18).

3.2 Layers under uniform shear tractions

Two different types of loading are considered on the boundaries. At first, Case I, illustrates the constant shear traction on the boundaries defined by pure mechanical loading $\tau_{0}$ and dielectric displacement $D_{0}$ [5] and then Case II, explains the stresses for the uniform traction defined by pure mechanical loading $\tau_{0}$ without the effect of dielectric displacement on the crack opening which is considered in many investigations mentioned in the literature. The boundary condition can be shown as follows:

$$\begin{aligned} & \sigma_{zy3} (x, - h_{2} ) = \tau_{\text{eq}} ,\quad D_{y} (x,h_{1} ) = D_{0} , \\ & \sigma_{zy1} (x,h_{1} ) = \tau_{\text{eq}} ,\quad D_{y} (x,0^{ + } ) = D_{0} . \\ \end{aligned}$$

$$\tau_{\text{eq}} = \left\{ {\begin{array}{*{20}l} {\frac{{\alpha_{1} }}{{c_{44} }}\tau_{0} - \frac{{e_{15} }}{{d_{11} }}D_{0} ({\text{Case}}\,\,{\text{I}})} \hfill \\ {\tau_{0} \quad ({\text{Case}}\,\,{\text{II}})} \hfill \\ \end{array} } \right.$$

(21)

4 Multiple straight and curved cracks formulations

The dislocation method is capable of solving and analyzing layers weakened by multiple straight and curved cracks. So in this section, this method is employed to analyze the stress in the vicinity of the cracks tips. Therefore, the multiple cracks configurations with coordinates $(x_{i} ,y_{i} )$ may be explained in parametric form as fallow

$$x_{i} = x_{0i} + x_{i} (\omega ),\quad y_{i} = y_{0i} + y_{i} (\omega ),\quad - \,1 \le \omega \le 1,\quad i = 1,2, \ldots ,N.$$

(22)

The stress amounts on the surface of the $i$th crack in the local coordinates could be written as fallow, in which $\theta_{i}$ is the angel between x and tangent axes s

$$\sigma_{nz} (x_{i} ,y_{i} ) = \sigma_{yz} \cos \theta_{i} - \sigma_{xz} \sin \theta_{i} ,\quad i = 1,2, \ldots ,N$$

(23)

At this section, we consider dislocation with unknown dislocation density as $B_{zj} (p),\,\, - \,1 \le p \le 1.$ that is distributed on the very small segment $da_{j}$ located on the surface of the $j$th crack. The anti-plane traction components on the $i$th crack surface due to the presence of the distributed dislocations on the face of all $N$ cracks yield

$$\sigma_{nz} (x_{i} (\omega ),y_{i} (\omega )) = \sum\limits_{j = 1}^{N} {\int\limits_{ - 1}^{1} {k_{ij} (\omega ,p)a_{j} B_{zj} (p){\text{d}}p} } ,\quad i = 1,2, \ldots ,N.$$

(24)

With considering the Buckner’s principle [20], the left-hand side of Eq. (24) gives the stress components after changing the sign, which are obtained in Sect. 3. Besides, the kernels $k_{ij} (\omega ,p)$ appeared in Eq. (24) are the coefficients of $b_{z}$ in Eq. (18) for each region determined in Sect. 2 which are given in “Appendix C”.

The crack opening displacement across the $j$th crack using the definition of dislocation can be written as

$$w_{j}^{ - } (\omega ) - w_{j}^{ + } (\omega ) = \int\limits_{ - 1}^{\omega } {B_{zj} (p)\sqrt {(x^{\prime}_{j} (p))^{2} + (y^{\prime}_{j} (p))^{2} } {\text{d}}p} ,\quad j = 1,2, \ldots ,N.$$

(25)

The displacement fields must be single-valued, and as a consequence, the following closure conditions for embedded cracks should be employed

$$\int\limits_{ - 1}^{1} {B_{zj} (p)\sqrt {(x^{\prime}_{j} (p))^{2} + (y^{\prime}_{j} (p))^{2} } {\text{d}}p} = 0,\quad j = 1,2, \ldots ,N.$$

(26)

By calculating the unknown dislocation density $B_{zj} (p)$, it is feasible to determine the stress intensity factors. So, the system of integral Eqs. (24) and (26) is determined to find the dislocation density functions $B_{zj} (p)$. It should be mentioned that the stress fields behave as $1/\sqrt r$ in the vicinity of the crack tips where $r$ is the distance from the crack tip. The dislocation density can be expressed as

$$B_{zj} (p) = \frac{{q_{zj} (p)}}{{\sqrt {1 - p^{2} } }},\quad - \,1 \le p \le 1,\quad j = 1,2, \ldots ,N.$$

(27)

Parameters $q_{zj} (p)$ can be calculated by substituting Eq. (27) into Eqs. (24) and (26) and solving the resultant system of integral equations. So, by means of the crack opening displacement given in Eq. (25), the SIFs can be written for the vicinity of $i$th crack tip as follows:

$$\begin{aligned} K_{{{\rm I}{\rm I}{\rm I}L_{i} }} & = \frac{\sqrt 2 }{4}gG_{y} (y)\mathop {\lim }\limits_{{r_{{L_{i} }} \to 0}} \frac{{w_{i}^{ - } (\omega ) - w_{i}^{ + } (\omega )}}{{\sqrt {r_{{L_{i} }} } }}, \\ K_{{{\rm I}{\rm I}{\rm I}R_{i} }} & = \frac{\sqrt 2 }{4}gG_{y} (y)\mathop {\lim }\limits_{{r_{{R_{i} }} \to 0}} \frac{{w_{i}^{ - } (\omega ) - w_{i}^{ + } (\omega )}}{{\sqrt {r_{{R_{i} }} } }}. \\ \end{aligned}$$

(28)

in which subscripts $L$ and $R$ are the left and right tips of a crack, respectively, and

$$\begin{aligned} r_{{L_{i} }} & = \left[ {(x_{i} (\omega ) - x_{i} ( - \,1)^{2} + (y_{i} (\omega ) - y_{i} ( - \,1)^{2} } \right]^{{\frac{1}{2}}} , \\ r_{{R_{i} }} & = \left[ {(x_{i} (\omega ) - x_{i} (1)^{2} + (y_{i} (\omega ) - y_{i} (1)^{2} } \right]^{{\frac{1}{2}}} . \\ \end{aligned}$$

(29)

Consequently, the mode III stress intensity factors for embedded cracks are

$$\begin{aligned} k_{{{\rm I}{\rm I}{\rm I}L_{i} }} & = \frac{{gG_{y} (y)}}{2}\left[ {\left( {x_{i}^{{\prime }} ( - \,1)} \right)^{2} + \left( {y_{i}^{{\prime }} ( - \,1)} \right)^{2} } \right]^{{\frac{1}{4}}} q_{zi} ( - \,1), \\ k_{{{\rm I}{\rm I}{\rm I}R_{i} }} & = - \frac{{gG_{y} (y)}}{2}\left[ {\left( {x_{i}^{{\prime }} ( - \,1)} \right)^{2} + \left( {y_{i}^{{\prime }} ( - \,1)} \right)^{2} } \right]^{{\frac{1}{4}}} q_{zi} (1),\quad i = 1,2, \ldots ,N. \\ \end{aligned}$$

(30)

To determine stress intensity factors, the results for $q_{zi} ( \pm \,1)$ should be calculated utilizing the technique developed by Erdogan et al. [21].

Also, for some specific examples, elliptical cracks are investigated. The parametric form for these cracks is as follows:

$$x_{i} = a_{i} \sin (\phi p),\quad y_{i} = b_{i} \cos (\phi p),\quad - \,1 \le p \le 1,\quad i = 1,2, \ldots N$$

(31)

where a and b are the half length of major and minor axes of ellipse, respectively, and $\phi$ is the angle between crack tips and the vertical axis.

5 Result and discussion

At this section, some examples are solved to demonstrate the applicability of the distributed dislocation technique by solving and calculating the SIFs for multiple straight and curved cracks in the FG orthotropic substrate bonded to the FGP coating. The influence of different types and numbers of cracks on SIFs is considered. In the numerical results, PZT4 and PZT5 are used for piezoelectric layer and two different orthotropic properties are considered that are given in Tables 1 and 2, respectively.

Table 1 Material properties for piezoelectric coating.

Table 2 Material properties for orthotropic layer.

The thickness of the FG orthotropic substrate and FG piezoelectric coating will be assumed $h_{2} = 0.1\,{\text{m}}$ and $h_{1} = 0.1h_{2}$, respectively. The dimensionless crack length is considered to be $a/h_{2} = 0.5$ unless it is stated for a specific example. Three different types of loadings are applied to the boundaries in the following examples. In this study layers are investigated under electromechanical point load, constant shear stress defined by pure mechanical load $\tau_{0}$ and dielectric displacement $D_{0}$, and uniform shear stress $\tau_{0}$ which are explained in Sect. 3. The SIFs are normalized by $K_{0} = \tau_{0} \sqrt a$ unless otherwise stated for the specific examples. Also, in the majority of the examples, PZT4 is considered as the piezoelectric coating material unless it is expressed for the specific example.

Table 3 provides the results for various normalized dielectric constant and its effect on the stress intensity factors. The results are compared with those of [5], they have indicated that the effect of the second orthotropic layer is negligible on the SIFs. Besides, for this comparison, the crack is located in the vicinity of the interface of two layers. It can be seen that the dielectric constant has significant effect on the SIFs and can make them to be zero when $D^{*} = 1$.

Table 3 Stress intensity factor comparisons under dielectric effect $D^{*} = D_{0} (c_{44}^{0} e_{15}^{0} )/(\alpha_{1} d_{11}^{0} \tau_{0} )$

In Fig. 2 the stress distribution of a straight crack along its axis is depicted. As expected the stresses have singular behavior at the vicinity of the crack tips. The stress values drops rapidly and tends to be equal to the external load that applied on the boundaries when we are far away from the crack tips.

Fig. 2

Stress distribution along the crack tips (Uniform loading Case II, $g = 1.25$, $\kappa h_{2} = 0$, $\lambda h_{2} = 0$, PZT4, $d = - h_{2} /2$)

Figure 3 shows the stress intensity factors versus dimensionless crack length. The non-homogeneity parameter has a considerable effect on the SIFs amounts. The SIFs decreases gradually as the non-dimensional non-homogeneity parameter increases. This phenomena states that there is the possibility to decrease the crack opening by increasing the orthotropic FG parameter. On the other side of the coin, it can be seen that the SIFs values goes up significantly as crack length increases.

Fig. 3

Normalized stress intensity factors versus dimensionless crack length for various orthotropic non-homogeneity parameter (Uniform loading Case II, $\kappa h_{2} = 1$, PZT4, $g = 1.25$, $d = - h_{2} /2$)

In the next example, different orthotropic materials and their non-homogeneity parameters under two types of loadings namely Case I and Case II are investigated. Figures 4 and 5 depicts that the stress intensity factors for the isotropic material has considerably more values than the orthotropic material. Besides, SIFs under Case II have far more values than the ones under Case I. The results provided in this figure shows that specific amounts of FG orthotropic material can reduce the SIFs values. Also, these results illustrate that non-homogeneity parameters play an important role in the design of mechanical structures.

Fig. 4

Normalized stress intensity factors versus dimensionless crack length a (Uniform loading Case I, $\kappa h_{2} = 1$, PZT4, $d = - h_{2} /2$). b (Uniform loading Case II, $\kappa h_{2} = 1$, PZT4, $d = - h_{2} /2$)

Fig. 5

Normalized stress intensity factors versus dimensionless electric field (Uniform loading Case I, $\lambda h_{2} = 1$, $\kappa h_{2} = 1$, $d = - h_{2} /2$)

Table 4 shows the effects of the different types of loading on a single embedded crack in the FG orthotropic strip. Different non-homogeneity parameter are considered for each layer in this investigation while dimensionless crack length is assumed $a/h_{2} = 1$. The applied electrical loading is considered to be $D^{*} = 1$. As can be seen, the SIFs for Case I have approximately zero values. In all the next examples, the amount of dielectric constant is considered to be $D^{*} = 1$ so that the mediums would endure by far the least amount of SIFs.

Table 4 Comparison of different types of loading on the SIFs for PZT4 and $g = 1.25$

Figure 6 shows the effect of different piezoelectric and piezoelectric FG parameter on SIFs when crack is located in $d = h_{2} /8$. As can be seen in Fig. 6, piezoelectric material has significant effect on SIFs. Same as previous example, FG piezoelectric coating non-homogeneity parameter can reduce the amount of SIFs and decrease crack opening values.

Fig. 6

Normalized stress intensity factors versus crack length (Uniform loading Case II, $\lambda h_{2} = 1$, $g = 1.25$, $d = - h_{2} /8$)

In the next example, the effect of crack orientation on the stress intensity factors under different loading types, namely Case II (Fig. 7a) and point load (Fig. 7b), is studied. Orthotropic and isotropic materials are also taken into account to study this effect. The crack is rotated around its center which is fixed on the center line of the orthotropic layer. The maximum amount of SIFs occurs at $\theta = 0$. As can be seen the effect of the applied traction on SIFs vanishes at $\theta = \pi /2$. The results also show that the SIFs for orthotropic material have less values than the SIFs for the isotropic material at vicinity of the crack tips. Moreover, since the crack rotates in an FG layer, the left and right crack tips have different values. As expected, it shows that the left tips have less values than the right tips.

Fig. 7

Normalized stress intensity factors versus crack rotation a (Uniform loading Case II, $\kappa h_{2} = 1$, PZT4, $d = - h_{2} /2$, $a/h_{2} = 0.5$). b (Point load, $\kappa h_{2} = 1$, PZT4, $d = - h_{2} /2$, $a/h_{2} = 0.5$)

In the next example, in Fig. 8, two parallel cracks that are located in $d_{1} = - h_{2} /2$ and $d_{2} = - h_{2} /4$ are investigated. Three different types of loadings, i.e., uniform loads cases I and II and point load, are considered. Uniform loads and point load are normalized by $K_{0} = \tau_{0} \sqrt a$ and $K_{0} = \tau_{0} /\sqrt a$, respectively. As can be seen Case II allocates by far the most amount of SIFs values as opposed to Case I. It is also evident that the SIFs for crack tips, $R_{1}$ and $L_{2}$ increases and then decreases which are obviously under the effect of materials and non-homogeneity parameters.

Fig. 8

Normalized stress intensity factors for two parallel cracks versus dimensionless cracks length a (Uniform loading Case I, $\kappa h_{2} = 1$, $\lambda h_{2} = 1$, PZT4, $d_{1} = h_{2} /4$, $d_{2} = h_{2} /2$). b (Uniform loading Case II, $\kappa h_{2} = 1$, $\lambda h_{2} = 1$, PZT4, $d_{1} = h_{2} /4$, $d_{2} = h_{2} /2$). c (Point load, $\kappa h_{2} = 1$, $\lambda h_{2} = 1$, PZT4, $d_{1} = h_{2} /4$, $d_{2} = h_{2} /2$)

Figures 9 and 10 depict the variation of the dimensionless SIFs of two equal-length straight cracks with length $a/h_{2} = 0.4$ are located on the centerline of the FG orthotropic substrate. Left crack is fixed and the right crack rotates around its center. Uniform loading, Case II, is applied on the boundaries. The variation of the SIFs at crack tips $L_{1}$ and $R_{1}$ is not significant compared to the other crack tips. Also, at $\theta = \pi /2$ SIFs have by far the least amounts and are almost zero.

Fig. 9

Normalized stress intensity factors for two parallel cracks versus dimensionless electric field (Uniform loading Case I, $\kappa h_{2} = 1$, $\lambda h_{2} = 1$, PZT4, g = 1.25, $d_{1} = h_{2} /4$, $d_{2} = h_{2} /2$)

Fig. 10

Normalized stress intensity factors for a fixed and a rotating crack (Uniform loading Case II, $\kappa h_{2} = 1$, $\lambda h_{2} = 1$, PZT4, $d = - h_{2} /2$, $a/h_{2} = 0.5$)

As can be seen in Fig. 11, the stress intensity factors for two centric elliptical cracks are under two kind of tractions are investigated. The elliptical crack sectors are increasing as the degree between the crack tips and the vertical axis grows. Case II uniform loading and point load are normalized by $K_{0} = \tau_{0} \sqrt {a_{2} }$ and $K_{0} = \tau_{0} /\sqrt {a_{2} }$ respectively, where $a_{2}$ is the length of the semi-major axis of ellipse. It can be seen that the crack tips $L_{1}$ and $R_{1}$ have higher SIFs values than crack tips $L_{2}$ and $R_{2}$. Besides, the applied traction, Case II, results in a far more SIFs values than the applied point load. As expected physically, crack tips show a symmetric behavior.

Fig. 11

Normalized stress intensity factors for two centric elliptical cracks (Uniform loading Case II, $\kappa h_{2} = 1$, $\lambda h_{2} = 1$, PZT4)

In the next example, Fig. 12, three elliptical periodic cracks are taken into account. Besides, the stress intensity factor values are normalized by $K_{0} = \tau_{0} \sqrt a$ where $a$ is the half length of the major axis of the ellipse. The result illustrates that the middle curve crack has more SIFs values due to the higher interaction between the cracks tips. On the contrary, the outer crack tips $L_{1}$ and $R_{3}$ have slightly less amounts than other crack tips. Furthermore, as expected the outer and inner crack tips experience the same behavior. In the last example two edge cracks namely straight edge crack and curved edge cracks are studied (Figs. 13, 14). It can be seen that for the straight edge crack, so long as isotropic material is utilized, SIFs allocate significantly more values compared to orthotropic materials, i.e. crack propagation occurs in the medium. However, the trend for the curved edge crack is different. In this case, SIFs values correlate positively with the orthotropic parameter as opposed to the straight edge crack. Finally, as expected the SIFs values drop as thickness of the layer increases.

Fig. 12

Normalized stress intensity factors for three elliptical cracks (Uniform loading Case II, $\kappa h_{2} = 1$, $\lambda h_{2} = 1$, PZT4)

Fig. 13

Normalized stress intensity factors versus edge crack length (Uniform loading Case II, $\kappa h_{2} = 1$, $\lambda h_{2} = 1$)

Fig. 14

Normalized stress intensity factors for a curved edge crack versus thickness (Uniform loading Case II, $\kappa h_{1} = 0.1$, $\lambda h_{1} = 0.1$, $a = 7h_{1}$, $b = 5h_{1}$)

6 Conclusion

An analytical solution for an FG orthotropic strip containing a Volterra-type screw dislocation reinforced by an FG piezoelectric coating is presented. The layers are under different types of loadings. The stress fields in an FG orthotropic containing a screw dislocation are obtained. With the help of Fourier transform the stress fields are reduced to a system of integral equations with a Cauchy-type singularity. Then, by utilizing the distributed dislocation technique several examples are solved numerically to show the effects of non-homogeneity parameters, cracks configurations, and material properties on the stress intensity factors. It is concluded that

• 1. By increasing the orthotropic non-homogeneity parameters the SIFs decreases.

• 2. Isotropic material allocates considerably more SIFs values than the orthotropic material.

• 3. Case I loading has approximately zero SIFs values due to the simultaneous effect of mechanical and dielectric loadings.

• 4. By applying the point load on the boundaries, SIFs obtain far less values compared to Case II.

• 5. The effect of traction on SIFs vanishes when crack rotates to be in vertical position. The maximum amount of SIFs occurs when crack is straight.

• 6. The SIFs for curve cracks increases as the degree between crack tips and the vertical axis escalates.

Appendices

Appendix A

The functions $T_{ij}$ given in Eq. (17a) and (17b)

$$\begin{aligned} T_{11} & = {\text{e}}^{(y + \eta )\lambda } \sinh [(h_{2} + \eta )\chi_{1} ] \\ T_{12} & = G_{y} \chi_{2} \cosh (h_{1} \chi_{2} )[\chi_{1} \cosh (y\chi_{1} ) + \lambda \sinh (y\chi_{1} )] \\ T_{13} & = \left[ {G_{y} \kappa \chi_{1} \cosh (y\chi_{1} ) + \left( {G_{y} \kappa \lambda + s^{2} \alpha_{1} } \right)\sinh (y\chi_{1} )} \right]\sinh (h_{1} \chi_{2} ) \\ \end{aligned}$$

(32)

$$\begin{aligned} T_{21} & = {\text{e}}^{(y + \eta )\lambda } s\sinh [(h_{2} + \eta )\chi_{1} ] \\ T_{22} & = G_{y} \chi_{2} g^{2} \cosh (h_{1} \chi_{2} )\sinh (y\chi_{1} ) \\ T_{23} & = \left[ {\alpha_{1} \chi_{1} \cosh (y\chi_{1} ) + \left( {G_{y} \kappa g^{2} - \alpha_{1} \lambda } \right)\sinh (y\chi_{1} )} \right]\sinh (h_{1} \chi_{2} ) \\ \end{aligned}$$

(33)

$$\begin{aligned} T_{31} & = {\text{e}}^{(y + \eta )\lambda } (\chi_{1} \cosh [(h_{2} + y)\chi_{1} ] + \lambda \sinh \,[(h_{2} + y)\chi_{1} ]) \\ T_{32} & = \chi_{2} G_{y} g^{2} \cosh (h_{1} \chi_{2} )\sinh (\eta \chi_{1} ) \\ T_{33} & = \left[ {\alpha_{1} \chi_{1} \cosh (\eta \chi_{1} ) + \left( {G_{y} \kappa g^{2} - \alpha_{1} \lambda } \right)\sinh (\eta \chi_{1} )} \right]\sinh (h_{1} \chi_{2} ) \\ \end{aligned}$$

(34)

$$\begin{aligned} T_{41} & = {\text{e}}^{(y + \eta )\lambda } s\sinh [(h_{2} + \eta )\chi_{1} ] \\ T_{42} & = g^{2} G_{y} \,\chi_{2} \cosh (h_{1} \chi_{2} )\sinh (\eta \chi_{1} ) \\ T_{43} & = \left[ {\alpha_{1} \chi_{1} \cosh (\eta \chi_{1} ) + \left( {G_{y} \kappa g^{2} - \alpha_{1} \lambda } \right)\sinh (\eta \chi_{1} )} \right]\sinh (h_{1} \chi_{2} ) \\ \end{aligned}$$

(35)

Appendix B

The functions $A_{i} ,C_{i}$ and $F$ given in Eqs. (20) and (21)

$$\begin{aligned} A_{1} & = 2\chi_{2} y(\chi_{1} - \lambda )({\text{e}}^{{ - (h_{2} + y)\chi_{1} + y\lambda - h_{1} \kappa }} + {\text{e}}^{{(\lambda + \chi_{1} )y + h_{2} \chi_{1} - h_{1} \kappa }} ) \\ A_{2} & = {\text{e}}^{{(h_{2} - y)\lambda - y\chi_{1} - h_{1} \chi_{2} }} (\chi_{2} + \kappa )\left[ {(\chi_{2} - \kappa )\alpha_{1} + y(\lambda - \chi_{1} )} \right] \\ A_{3} & = {\text{e}}^{{(h_{2} + y)\lambda - y\chi_{1} - h_{1} \chi_{2} }} (\chi_{2} - \kappa )\left[ {(\chi_{2} + \kappa )\alpha_{1} - y(\lambda - \chi_{1} )} \right] \\ A_{4} & = {\text{e}}^{{(h_{2} + 3y)\lambda - y\chi_{1} + h_{1} \chi_{2} }} (\chi_{2} - \kappa )\left[ {(\chi_{2} + \kappa )\alpha_{1} - y(\lambda + \chi_{1} )} \right] \\ A_{5} & = {\text{e}}^{{(h_{2} + y)\lambda + y\chi_{1} - h_{1} \chi_{2} }} (\chi_{2} + \kappa )\left[ {(\chi_{2} - \kappa )\alpha_{1} + y(\lambda + \chi_{1} )} \right] \\ A_{6} & = {\text{e}}^{{ - (h_{2} + y)\chi_{1} + y\lambda - h_{1} \kappa }} 2D_{0} e_{15} y\left[ {\left( { - 1 + {\text{e}}^{{2\left( {h2 + y} \right)\chi_{1} }} } \right)\lambda + \left( {1 + {\text{e}}^{{2\left( {h_{2} + y} \right)\chi_{1} }} } \right)\chi_{1} } \right] \\ A_{7} & = ( - \,\chi_{2} + {\text{e}}^{{h_{1} \kappa }} [\chi_{2} \cosh (h_{1} \chi_{2} ) - \kappa \sinh (h_{1} \chi_{2} )]) \\ \end{aligned}$$

(36)

$$\begin{aligned} C_{1} & = 2g^{2} s^{2} \chi_{2} y({\text{e}}^{{(\lambda + \chi_{1} )y + h_{2} \chi_{1} - h_{1} \kappa }} - {\text{e}}^{{(\lambda - \chi_{1} )y - h_{2} \chi_{1} - h_{1} \kappa }} ) \\ C_{2} & = {\text{e}}^{{(h_{2} + y)\lambda + y\chi_{1} + h_{1} \chi_{2} }} [\alpha_{1} (\chi_{2} + \kappa ) - y(\lambda + \chi_{1} )](\chi_{2} - \kappa )(\chi_{1} - \lambda ) \\ C_{3} & = {\text{e}}^{{(h_{2} + y)\lambda + y\chi_{1} - h_{1} \chi_{2} }} s^{2} [g^{2} (\chi_{2} + \kappa )y + \alpha_{1} (\chi_{1} - \lambda )] \\ C_{4} & = {\text{e}}^{{(h_{2} + y)\lambda - y\chi_{1} + h_{1} \chi_{2} }} s^{2} [g^{2} (\chi_{2} - \kappa )y + \alpha_{1} (\chi_{1} + \lambda )] \\ C_{5} & = {\text{e}}^{{(h_{2} + y)\lambda - y\chi_{1} - h_{1} \chi_{2} }} s^{2} [g^{2} (\chi_{2} + \kappa )y - \alpha_{1} (\chi_{1} + \lambda )] \\ C_{6} & = {\text{e}}^{{ - (h_{2} + y)\chi_{1} + y\lambda - h_{1} \kappa }} 2D_{0} \left( { - \,1 + {\text{e}}^{{2(h_{2} + y)\chi_{1} }} } \right){\text{e}}_{15} g^{2} s^{2} y \\ C_{7} & = ( - \,\chi_{2} + {\text{e}}^{{h_{1} \kappa }} [\chi_{2} \cosh (h_{1} \chi_{2} ) - \kappa \sinh (h_{1} \chi_{2} )]) \\ \end{aligned}$$

(37)

$$F = 4d_{11} \pi sG_{y} \left( {g^{2} G_{y} \chi_{2} \cosh (h_{1} \chi_{2} )\sinh (h_{2} \chi_{1} ) + \left[ {\alpha_{1} \chi_{1} \cosh (h_{2} \chi_{1} ) + \left( {\alpha_{1} \lambda - g^{2} \kappa G_{y} } \right)\sinh (h_{2} \chi_{1} )} \right]\sinh (h_{1} \chi_{2} )} \right)$$

(38)

Appendix C

The kernels mentioned in Eq. (24) are given as

$$\begin{aligned} k_{ij} & = - \frac{1}{\pi }\left( {g^{2} G_{y} \left[ {\int\limits_{0}^{ + \infty } {\left\{ {\frac{{T_{21} }}{E}[T_{22} - T_{23} ] - \frac{{{\text{e}}^{{ - sg(y_{i} - y_{j} )}} }}{2}} \right\}} } \right.\sin [s(x_{i} - x_{j} )]{\text{d}}s + \left. {\frac{{(x_{i} - x_{j} )}}{{2[(x_{i} - x_{j} )^{2} + g^{2} (y_{i} - y_{j} )^{2} ]}}} \right]\cos \theta } \right. \\ \quad - \left. {G_{x} \left[ {\int\limits_{0}^{ + \infty } {\left\{ {\frac{{T_{11} }}{E}[T_{12} - T_{13} ] + \frac{{{\text{e}}^{{ - sg(y_{i} - y_{j} )}} }}{2}} \right\}} } \right.\cos [s(x_{i} - x_{j} )]{\text{d}}s - \left. {\frac{{g(y_{i} - y_{j} )}}{{2[(x_{i} - x_{j} )^{2} + g^{2} (y_{i} - y_{j} )^{2} ]}}} \right]\sin \theta } \right) \\ \end{aligned}$$

$$\begin{aligned} k_{ij} & = \frac{1}{\pi }\left( {g^{2} G_{y} \left[ {\int\limits_{0}^{ + \infty } {\left\{ {\frac{{T_{41} }}{E}[T_{42} - T_{43} ] - \frac{{{\text{e}}^{{sg(y_{i} - y_{j} )}} }}{2}} \right\}} } \right.\sin [s(x_{i} - x_{j} )]{\text{d}}s + \left. {\frac{{(x_{i} - x_{j} )}}{{2[(x_{i} - x_{j} )^{2} + g^{2} (y_{i} - y_{j} )^{2} ]}}} \right]\cos \theta } \right. \\ \quad - \left. {G_{x} \left[ {\int\limits_{0}^{ + \infty } {\left\{ {\frac{{T_{31} }}{E}[T_{32} - T_{33} ] - \frac{{{\text{e}}^{{sg(y_{i} - y_{j} )}} }}{2}} \right\}} } \right.\cos [s(x_{i} - x_{j} )]{\text{d}}s + \left. {\frac{{g( - y_{i} + y_{j} )}}{{2[(x_{i} - x_{j} )^{2} + g^{2} (y_{i} - y_{j} )^{2} ]}}} \right]\sin \theta } \right) \\ \end{aligned}$$

(39)