1 Introduction

Non-Newtonian fluids are frequently encountered in daily life and in industrial processes, for instance, in chemical, food processing and oil industries. A particular characteristic of some non-Newtonian liquids is the retention of fading “memory” upon the removal of stress which is termed as fluid’s elasticity. Viscoelastic fluids contain normal stress effects which are an expression of fluid’s elasticity which is added to the viscous effect when the fluid is set in motion. There are strong experimental manifestations to the viscoelastic behavior such as Weissenberg or rod-climbing effect. Commonly encountered examples are clay coatings, food products, inks, detergents, food gels, gums, emulsions, liquid polymers, liquid crystals, etc. One of the frequently employed viscoelastic models is the Oldroyd-B fluid model that can predict the behaviors of relaxation time, creep and normal stress differences for many polymeric liquids. In recent past, modest research is published concerning boundary layer analysis in Oldroyd-B liquid, compared with its Newtonian counterpart. Bhatnagar et al. [1] studied the boundary layer formation in Oldroyd-B fluid near a linearly stretched sheet with stream-wise pressure gradient. In this work, the authors used perturbation expansions for non-dimensional velocity and extra stress tensor components in terms of small viscoelastic fluid parameter. Further, graphical results addressing the behavior of fluid’s elasticity were obtained and deliberated. Later, Sajid et al. [2] evaluated explicit expressions of stress tensor components for Oldroyd-B model. These components were then used to formulate stagnation-point flow of Oldroyd-B fluid near stretching plate. Finally, they managed to find finite difference approximations of resulting boundary value problem. Shehzad et al. [3] considered thermophoretic particle deposition in three-dimensional Oldroyd-B fluid flow adjacent to a bi-directional deforming sheet. Series and numerical solutions for Oldroyd-B fluid motion over a stationary plate with stream-wise pressure gradient were computed by Abbasbandy et al. [4]. Effects of variable thermal conductivity on the Oldroyd-B fluid motion across an impulsively stretching surface were deliberated in Motsa and Ansari [5]. Recent attempts in the area can be stated through [6,7,8,9,10,11,12,13] and refs. there in.

Heat transfer refers to the transmission of thermal energy from one region to another as a result of temperature gradient. This phenomenon is associated with flows in wide spectrum of industrial and geophysical processes. Fourier law [14], developed in 1822, gives the relation between heat flow rate and the temperature gradient and it is recognized as fundamental law of conduction. This law gives a paradoxical prediction that any initial change would instantly alter the medium under observation and, therefore, it does not preserve the “causality principle”. This questions whether or not Fourier law gives adequate description of the heat transport phenomenon. To resolve this shortcoming, Cattaneo [15] came up with the concept of heat transmission due to thermal waves travelling at finite speed. He included a partial time derivative in Fourier model that rendered a damped hyperbolic energy equation. Such kind of heat transfer description has important implications in everyday life, in fields such as modeling skin burn [16], nanofluid flows [17] and biological materials [18]. To ensure objectivity principle, Christov [19] modified the partial time derivative in Cattaneo model with frame indifferent objective rate. Cattaneo–Christov theory still seems incomplete since it does not account for the thermal retardation time which is the time required for the build-up of temperature gradient in a volume element. Straughan [20] investigated the Christov’s relation for convection heat transfer in Newtonian fluid with gravity acting downward. Tibullo and Zampoli [21] proved uniqueness theorem for incompressible fluid flow in a bounded domain with a non-Fourier heat flux. Haddad [22] employed the Cattaneo–Christov heat flux theory to analyze thermal instability threshold for viscous flow through Brinkman porous space separated by two infinite plane surfaces. Han et al. [23] made use of analytic and numeric schemes to deal with slip flow of Maxwell fluid considering non-Fourier heat conduction. Khan et al. [24] numerically analyzed heat flux relaxation effect on Maxwell fluid flow near an exponentially deforming non-isothermal wall. Hayat et al. [25] employed non-Fourier approach to analyze fluid flow near a surface with variable thickness. An analytical investigation of Christov’s equation for unsteady MHD flow between coaxially rotating disk was made by Hayat et al. [26]. Their computations revealed that radial stretching rate has a considerable influence on velocity and temperature between the disks. Subsequent works in this area can be found in [27,28,29,30,31,32,33,34,35].

Heat transfer in boundary layer adjacent to continuously stretching surfaces with a given temperature has been a widely addressed research topic in fluid mechanics. It is important in a number of manufacturing processes such as glass-fiber and paper production, annealing of copper wire, condensation process, die forging and few others. Following the pioneering work of Crane [36], abundant material concerning interesting features of this problem is published. Magyari and Keller [37] described fluid flow over a non-isothermal surface which stretches in its own plane with exponentially varying velocity. Their results depict that structure of temperature curves is controlled by a parameter (A) measuring the exponential growth/decay of the wall temperature. After careful analysis, they concluded that meaningful solutions are possible only when this parameter is greater than a certain critical value. At this critical value of \(A\), wall temperature gradient becomes zero illustrating that no heat transfer takes place between fluid and the surface. Later, Elbashbeshy [38] revisited the similarity analysis of Ref. [37] by assuming permeable stretching surface. Viscoelastic fluid flow caused by an exponentially stretching isothermal wall was analytically explored by Khan and Sanjayanand [39]. Radiation effects in viscous flow characterized by exponentially deforming boundary were elucidated by Sajid and Hayat [40] using homotopy approach. Bhattacharyya [41] found multiple solutions for steady flow driven by an exponentially shrinking wall. Recently, several fascinating heat transfer problems involving exponentially deforming surfaces have been published (see, for instance, Liu et al. [42], Mustafa et al. [43], Weidman [44], Ahmad et al. [45], Patil et al. [46], Merkin et al. [47], etc.).

To the best of authors’ knowledge, the Oldroyd-B fluid flow due to exponentially deforming surface has not been explored in the existence of thermal relaxation effects. Thus framework of Ref. [9] has been extended by involving Cattaneo–Christov heat flux theory. We rely on homotopy analysis approach, proposed by Liao [48, 49], to find analytical approximations for velocity and temperature profiles. Additionally, we use the concept of squared residuals to compute optimal results for convergence control parameters. Furthermore, we will seek the critical range of temperature exponent parameter for which the meaningful solution cannot be found. The main interest is to elucidate flow and thermal fields in the existence of key physical attribute of the problem namely thermal relaxation time. The computational results of wall shear stress and heat transfer rate are presented and elucidated for certain values of embedded quantities. The results of this study might be beneficial in polymer processing and coating-related applications.

2 Mathematical model

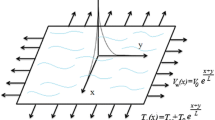
Consider a two-dimensional Oldroyd-B fluid flow over an impermeable plane wall at \(y = 0\) expanding with velocity \(u_{\text{w}} = u_{0} e^{x/L}\). The incompressible Oldroyd-B fluid is contained in the region \(y > 0\). The resulting motion of the quiescent fluid is produced solely by the stretching wall (see Fig. 1). Let the temperature at the wall vary with horizontal distance \(x\) according to \(T_{\text{w}} = T_{\infty } + T_{0} e^{Ax/2L}\), in which \(A\) is a constant whose value depends on the material properties of the fluid and \(T_{\infty }\) is the quiescent fluid temperature. A non-Fourier heat flux model due to Christov [19] is opted to analyze the thermal field. In view of these assumptions, the governing equations of Oldroyd-B motion and energy balance can be put in the following forms:

$$u_{x} + v_{y} = 0,$$
(1)
$$uu_{x} + vu_{y} + \lambda_{1} (u^{2} u_{xx} + v^{2} u_{yy} + 2uvu_{xy} ) = \nu \left[ {u_{yy} + \lambda_{2} (uu_{xyy} + vu_{yyy} - u_{x} u_{yy} + u_{y} u_{xy} )} \right],$$
(2)
$$\rho C_{p} (v_{i} T,_{i} ) = - Q_{i,i} ,$$
(3)

where \(\nu\) represents the kinematic viscosity of the fluid, \(\rho\) is the fluid density, \(\lambda_{1}\) stands for fluid relaxation time, \(\lambda_{2}\) for fluid retardation time, \(\beta_{T}\) is the volumetric expansion coefficient, \(C_{p}\) represents the specific heat capacity and \(Q_{i}\) denotes the heat flux vector. Christov [19] proposed the following heat conduction model:

$$\tau (Q_{i,t} + v_{j} Q_{i,j} - Q_{j} v_{i,j} + Q_{i} v_{j,j} ) = - Q_{i} - \kappa T_{i} ,$$
(4)

in which \(\tau\) denotes the thermal relaxation time defined as the time lag required for the onset of heat conduction in a fluid element after temperature difference is assigned through it. Taking divergence of Eq. (4) and then utilizing Eq. (3), a simple arrangement yields the following result (see Han et al. [23], Khan et al. [24], etc.):

$$(uT_{x} + vT_{y} ) + \tau \left( {\begin{array}{*{20}c} {u^{2} T_{xx} + v^{2} T_{yy} + 2uvT_{xy} + } \\ {uu_{x} T_{x} + vu_{y} T_{x} + uv_{x} T_{y} + vv_{y} T_{y} } \\ \end{array} } \right) = \alpha T_{yy} .$$
(5)
Fig. 1
figure 1

Physical configuration and coordinate system

Full size image

where α is the thermal diffusivity. Boundary conditions for problem under consideration are expressed below:

$$u(x,0) = u_{\text{w}} (x) = U_{0} \exp \left( {\frac{x}{L}} \right),v(x,0) = 0,$$
(6a)
$$T(x,0) = T_{\text{w}} (x) = T_{\infty } + T_{0} \exp \left( {\frac{Ax}{2L}} \right),$$
(6b)
$$u(x, + \infty ) = 0, T(x, + \infty ) \to T_{\infty } ,$$
(6c)

where conditions prescribed in Eq. (6a) indicate no slip and no penetration at the surface, Eq. (6b) signifies no thermal slip at the surface and Eq. (6c) shows that velocity and temperature gradients become zero far from the surface.

Let us introduce a transformation comprising non-dimensional quantities \(\psi ,\theta\) and \(\zeta\) such that:

$$\zeta = \sqrt {\frac{{U_{0} }}{2\nu L}} \exp \left( {\frac{x}{2L}} \right)y, \psi (x,y) = (2\nu LU_{0} )^{1/2} f(\zeta )\exp \left( {\frac{x}{2L}} \right), \theta (\zeta ) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}.$$
(7)

The axial and transverse velocity components are thus related to \(\psi\) according \(u = \psi_{y}\) and \(v = - \psi_{x}\) respectively. Substitution of above variables in Eqs. (2) and (5) gives rise to the following differential equations:

$$f^{\prime\prime\prime} - 2f^{{{\prime }2}} + ff^{\prime\prime} - \frac{{\beta_{1} }}{2}(4f^{{{\prime 3}}} - \zeta f^{{{\prime }2}} f^{\prime\prime} + f^{2} f^{\prime\prime\prime} - 6ff^{\prime}f^{\prime\prime}) + \frac{{\beta_{2} }}{2}(3f^{{{\prime \prime 2}}} + 2f^{\prime}f^{\prime\prime\prime} - ff^{iv} ) = 0,$$
(8)
$$\frac{1}{\Pr }\theta^{\prime\prime} + f\theta^{\prime} - Af^{\prime}\theta + \frac{\gamma }{2}\left[ {Aff^{\prime\prime}\theta - A(A + 2)f^{{{\prime }2}} \theta + (1 + 2A)ff^{\prime}\theta^{\prime} - f^{2} \theta^{\prime\prime}} \right] = 0.$$
(9)

Here \(\beta_{1}\) denotes the non-dimensional fluid relaxation time which measures the ratio of time scale of material’s response to the observation time scale, \(\beta_{2}\) represents the dimensionless retardation time which measures the time required for the build-up of shear stress in the fluid, \(\gamma\) is the non-dimensional thermal relaxation time and \(\Pr\) stands for Prandtl number which is ratio of momentum diffusion to the thermal diffusion. These parameters are defined as follows:

$$\Pr = \frac{\nu }{\alpha }, \quad \beta_{1} = \frac{{\lambda_{1} u_{\text{w}} }}{L}, \quad \beta_{2} = \frac{{\lambda_{2} u_{\text{w}} }}{L}, \quad \gamma = \frac{\tau u_w}{L}.$$
(10)

The transformed conditions are given below:

$$\begin{aligned} f = 0,\quad f^{\prime} = 1, \quad \theta = 1 \quad {\text{at}} \quad \zeta = 0, \hfill \\ f^{\prime} \to 0, \quad \theta \to 0 \quad {\text{as}} \quad \zeta \to \infty . \hfill \\ \end{aligned}$$
(11)

3 Series solutions by HAM

In this section, we look for series solutions of coupled non-linear equations \({\mathcal{N}}_{f} (f(\eta )) = 0\) (Eq. 8) and \({\mathcal{N}}_{\theta } (\theta (\eta )) = 0\) (Eq. 9) subject to the conditions (11) through homotopy analysis technique. On the basis of so-called “rule of solution expression” and the conditions (11), it is reasonable to set following initial approximations \(f_{0}\) and \(\theta_{0}\) of functions \(f\) and \(\theta\), respectively:

$$f_{0} (\zeta ) = 1 - \exp ( - \zeta ), \theta_{0} (\zeta ) = \exp ( - \zeta ).$$
(12)

Let us choose the auxiliary linear operators \({\mathcal{L}}_{f}\) and \({\mathcal{L}}_{\theta }\) of the following forms:

$${\mathcal{L}}_{f} \equiv \frac{{\partial^{3} }}{{\partial \zeta^{3} }} - \frac{\partial }{\partial \zeta }, \quad {\mathcal{L}}_{\theta } \equiv \frac{{\partial^{2} }}{{\partial \zeta^{2} }} - 1.$$
(13)

The procedure outlined in Ref. [10] is exactly followed to reduce non-linear Eqs. (8) and (9) to \(n\) linear sub-problems containing an auxiliary parameter \(\hbar\). These are solved exactly by MATHEMATICA for \(n = 1,2,3 \ldots\) and then homotopy series for \(f\) and \(\theta\) are constructed as follows:

$$f(\zeta ) = f_{0} (\zeta ) + \mathop \sum \limits_{n = 1}^{\infty } f_{n} (\zeta ),$$
(14)
$$\theta (\zeta ) = \theta_{0} (\zeta ) + \mathop \sum \limits_{n = 1}^{\infty } \theta_{n} (\zeta ),$$
(15)

where \(f_{n} (\zeta )\) and \(\theta_{n} (\zeta )\) denote the solutions for \(n\)th-order deformation equations of Eqs. (8) and (9), respectively. It is well-known that convergence of homotopy series relies on the appropriate selection of parameter \(\hbar\) (see Liao [49]). In some articles [50,51,52,53,54], the method of finding optimal value of auxiliary parameter \(\hbar\) was introduced. Following these, we define the squared residuals of Eqs. (8) and (9) as follows:

$$\Delta_{N}^{f} (\hbar ) = \int \limits_{0}^{\infty } \left[ {{\mathcal{N}}_{f} \left( {\mathop \sum \limits_{j = 0}^{N} f_{j} (\zeta )} \right)} \right]{\text{d}}\zeta ,$$
(16)
$$\Delta_{N}^{\theta } (\hbar ) = \int \limits_{0}^{\infty } \left[ {{\mathcal{N}}_{\theta } \left( {\mathop \sum \limits_{j = 0}^{N} \theta_{j} (\zeta )} \right)} \right]{\text{d}}\zeta .$$
(17)

Now we seek the values of \(\hbar\) for which squared residuals \(\Delta_{N}^{f}\) and \(\Delta_{N}^{\theta }\) are minimum. This can be done through the command Minimize of the software MATHEMATICA as explained in Liao [50]. In Tables 1 and 2, we enlist the optimal values of \(\hbar\) for functions \(f\) and \(\theta\) at different parameter values. It can be seen that reasonably accurate approximation to the exact solution is found for both low and high values of embedded parameters.

Table 1 Optimal values of \(\hbar\) for function \(f\) and corresponding squared residuals for different values of \(\beta_{1}\) and \(\beta_{2}\) at 13th-order of approximations when \(A = \gamma = 0.5\) and \(\Pr = 1\)
Full size table
Table 2 Optimal values of \(\hbar\) for functions \(f\) and \(\theta\) and corresponding squared residuals for different values of \(A, \Pr\) and \(\gamma\) at 13th-order of approximations when \(\beta_{1} = \beta_{2} = 0.5\)
Full size table

4 Results and discussion

A non-Fourier heat flux theory is utilized to model the flow and heat transfer of Oldroyd-B fluid bounded by an exponentially deforming non-isothermal surface. The arising local similarity equations have been dealt by well-known homotopy analysis technique. The accuracy of analytical scheme is validated by comparing the values of \(f^{\prime\prime}(0)\) and \(\theta^{\prime}(0)\) to those reported by Khan et al. [24] via numerical approach. Table 3 demonstrates excellent correlation between analytical and numerical results which establishes the correctness of our code. We now turn our attention to examine the role of physical parameters on the flow and thermal fields. In Table 4, we provide numerical results for temperature gradient at the wall for various parameter values. In accordance with the study [37], the similarity solutions remain physically realistic for positive values of \(A\), that is, heat flows from the stretching boundary towards the ambient fluid when \(A > 0\). Wall temperature gradient has a positive value when parameter \(A\) is less than certain value \(A_{\text{c}}\) illustrating that temperature distribution is strictly convex and forms a “hill-shaped” pattern near the boundary which is referred as “Sparrow–Gregg hill”. Table 2 indicates that magnitude of \(\theta^{\prime}(0)\) grows with increasing thermal relaxation time. Moreover, the effect of fluid relaxation time is to enhance the wall temperature gradient.

Table 3 Comparison of present computations of \(\theta^{\prime}(0)\) with those of Khan et al. [24] when \(A = 1.5\) and \(\beta_{2} = 0\)
Full size table
Table 4 Computational results of \(f^{\prime\prime}(0)\) and \(\theta^{\prime}(0)\) for various parameter values at \(\Pr = 1\)
Full size table

Figure 2 shows the evolution of similarity profile \(f^{\prime}\) for various values of Deborah number \(\beta_{1}\). For comparison purpose, the figure also includes the results for Newtonian fluid case. All the curves begin from their wall value 1 and asymptotically decay to zero outside the boundary layer. It is revealed that velocity at any location above the sheet decreases for increasing values of \(\beta_{1}\). It means that, by an increase in \(\beta_{1}\), velocity gradient at the surface is increased. Also, a considerable reduction in boundary layer thickness is depicted when \(\beta_{1}\) enlarges. Physically, large values of \(\beta_{1}\) implies that stress relaxation is slow in comparison with the observation time scale. Thus boundary layer thickness does not develop as fast as for small Deborah number.

Fig. 2
figure 2

Profiles of velocity field \(f^{\prime}(\zeta )\) for different values of \(\beta_{1}\)

Full size image

Figure 3 presents velocity curve as a function of similarity variable \(\zeta\) for varying values of Deborah number \(\beta_{2}\). As Deborah number \(\beta_{2}\) grows, \(u\)-velocity component is seen to increase at any location above the surface. This also means that momentum penetration depth is increased as the fluid retardation time grows.

Fig. 3
figure 3

Profiles of velocity field \(f^{\prime}(\zeta )\) for different values of \(\beta_{2}\)

Full size image

Figure 4 plots temperature curves, represented by \(\theta (\zeta )\), by changing the Deborah numbers \(\beta_{1}\) and \(\beta_{2}\). Our numerical results indicate that transverse velocity component \(v\) decreases with increasing \(\beta_{1}\) above the sheet. It means that less fluid is extracted from the region of lower temperature far from the boundary when \(\beta_{1}\) is increased. This in turn reduces the heat transfer rate or the wall temperature gradient. The smaller gradient \(\theta^{\prime}(0)\) yields thicker thermal boundary layer as found in the Fig. 4. We also found a slight reduction in temperature profile \(\theta\) for increasing values of retardation time \(\lambda_{2}\).

Fig. 4
figure 4

Profiles of temperature field \(\theta (\zeta )\) for various values of \(\beta_{2}\)

Full size image

Figure 5 is plotted to inspect the change in temperature distribution \(\theta (\zeta )\) as the dimensionless thermal relaxation time \(\gamma\) is varied. A considerable reduction in temperature profile is found for growing thermal relaxation time.

Fig. 5
figure 5

Profiles of temperature field \(\theta (\zeta )\) for various values of \(\gamma\)

Full size image

In Fig. 6, temperature curves are computed for different values of temperature exponent parameter \(A\). When \(A = - 2\), heat flows from the quiescent fluid towards the stretching wall, a phenomenon that is signaled in the plot of \(\theta\) by the existence of Sparrow–Gregg hills. We observe that temperature profile at \(\zeta = 0\) is strictly convex when parameter \(A\) is strictly less than some negative value \(A_{\text{c}}\) while it is strictly concave for \(A > 0\), as also noted in [37]. When \(A = A_{\text{c}}\), the temperature curve represents the adiabatic situation. As expected, heat penetration in the fluid considerably decreases for increasing values of \(A\).

Fig. 6
figure 6

Profiles of temperature field \(\theta (\zeta )\) for different values of \(A\)

Full size image

Figures 7 and 8 portray the impact of Prandtl number \(\Pr\) on the near-surface temperature for \(A = 0.5\) and \(A = - 1.5\), respectively. Temperature profile \(\theta (\zeta )\) becomes thinner when \(\Pr\) enlarges. This is not surprising since increasing Prandtl number implies slower diffusion rate which in turn reduces heat penetration into the quiescent fluid. In Fig. 8, Sparrow–Gregg hills are evident just in the wall region and height of these hills increase with increasing \(\Pr\). Similar trend is also noticed in [37] for the Newtonian fluid case.

Fig. 7
figure 7

Profiles of temperature field \(\theta (\zeta )\) for different values of \(Pr\) when \(A = 0.5\)

Full size image
Fig. 8
figure 8

Curves of wall temperature gradient \(\theta^{\prime}(0)\) for different values of \(\Pr\) when \(A = - 1.5\)

Full size image

Figure 9 demonstrates the variation in wall temperature gradient \(\theta^{\prime}(0)\) with the change in Prandtl number \(\Pr\) for different values of \(A\). The black curve is computed at \(A = A_{\text{c}} = - 0.85\) for which \(\theta^{\prime}\left( 0 \right) = 0\). This illustrates that the stretching surface becomes adiabatic when \(A = - 0.85\). When \(A < A_{\text{c}} = 0.85\), wall temperature gradient \(\theta^{\prime}(0)\) becomes positive for any value of \(\Pr\) which is an indicator of the reverse heat flow near the wall region. Irrespective of the choice of \(A\), the profile of \(\left| {\theta^{\prime}(0)} \right|\) continues to grow as \(\Pr\) increases.

Fig. 9
figure 9

Curves of wall temperature gradient \(\theta^{\prime}(0)\) for different values of \(A\)

Full size image

Figure 10 displays the graphs of \(\theta^{\prime}(0)\) versus dimensionless thermal relaxation time \(\gamma\) for varying Deborah number \(\beta_{1}\). The solid and dashed curves correspond to \(\beta_{2} = 0\) and \(\beta_{2} = 1\), respectively. Interestingly, a linear growth in the magnitude of \(\theta^{\prime}(0)\) with increasing \(\beta_{1}\) is apparent. It should be noted here that variation in \(\theta^{\prime}(0)\) with \(\beta_{1}\) increases in magnitude with increasing thermal relaxation time.

Fig. 10
figure 10

Curves of wall temperature gradient \(\theta^{\prime}(0)\) for various values of \(\gamma\)

Full size image

5 Concluding remarks

An analytical study is performed for flow of an incompressible Oldroyd-B fluid bounded by an exponentially deforming sheet. Oldroyd-B fluid model is considered to be adequate in flow description of many polymeric liquids. Thus current analysis has obvious role in polymer extrusion and metal working processes. The temperature at the surface is assumed to grow or decay exponentially with the horizontal distance \(x\). The main motivation was to inspect thermal field when the Cattaneo–Christov heat flux theory is involved. Important observations of this work are listed below:

  • Both \(u\)-velocity component and boundary layer thickness decrease/increase when stress relaxation/retardation time is enhanced.

  • The curvature of temperature field \(\theta\) near the surface is strictly convex when temperature exponent parameter \(A\) is chosen beyond a certain value \(A_{\text{c}}\) that depends on the choice of other parameters. In this case, “Sparrow–Gregg hills” appear in the curves of \(\theta (\zeta )\).

  • When \(A = A_{\text{c}}\), the stretching surface is “adiabatic” for any considered Prandtl number \(\Pr\).

  • Irrespective of the choice of parameter \(A\), heat penetration depth reduces and wall temperature gradient grows as \(\Pr\) enlarges.

  • A considerable decrease in temperature distribution is found when thermal relaxation time is increased.

  • For increasing fluid relaxation time, thermal boundary layer becomes thinner and wall temperature gradient enlarges.

  • The influences of parameters appear similar in both Cattaneo–Christov and Fourier models. However, the effects are prominent in Cattaneo–Christov model when compared with Fourier model.

  • Present analytical findings appear to be consistent with the results of available articles in limiting cases.

  • Following studies [55] and [56], current problem can be investigated for a nanoparticle working fluid in future. Further, this work can be revisited to focus on optimal results for drag coefficient and heat transfer rates (see [57] and [58] for details).