1 Introduction

Force study of linkages is of great importance, as the longitudinal, transverse forces, and bending moments in sections links can be determined by reactive forces found in the kinematic pairs.

The purpose of the force analysis of linkages is not only the definition of reactions in kinematic pairs and generalized driving forces but also the quality assessment of designed linkage for certain dynamic criteria and use this assessment to improve its design [1, 2]. Calculation of forces in the kinematic pairs of the linkages (kinetostatic analysis) is performed on the basis of constraint release mechanism and d’Alembert’s principle [1].

Methods of kinetostatic analysis of linkages can be divided into graphic-analytical and analytical. The first papers on the graphic-analytical methods of planar linkages’ kinetostatics belong to Mohr O. [3], Wittenbauer F. [4], Federhofer K. [5], and Tolle O. [6], who used graphical statics methods, replacement points, and the principle of superposition to determine the reaction forces in kinematic pairs.

The works of N.E. Zhukovsky dedicated to the study of machines and mechanisms are of extensive practical and scientific interest. We mention the work [7], which proposed an original way to solve the problems of force analysis of mechanisms of any complexity by reducing it to the equilibrium of the lever problem; L.V. Assur [8] used this method to calculate the kinetostatic parameters of three driving groups.

In papers [8,9,10,11], the L.V. Assur’s special points and the method of direct force resolution were used to calculate the kinetostatic of the complex mechanisms.

In [12] the graphic-analytical solution of the problems of speed and acceleration of planar and spatial mechanisms solved by constructing vector products and the vector components. In addition, here, the vector method was applied, for the first time, to determine the forces acting in the mechanisms.

The proposed vector method of solving the problem was further developed in [13], in which not the vector equations were used to find the normal components of the reaction but the projection of vector equations to the randomly selected coordinate axes.

C. Bagci [14] used a screw method to study the spatial mechanisms’ equilibrium under the action of given external forces.

The works [15,16,17,18,19,20] are of particular interest, where the matrix analysis is used for kinetostatic study as it leads to a handy algorithm development and future mathematical formalization, convenient when using a computer.

Currently, the computer programs such as Maple, Mathcad are widely used for kinetostatic calculation of planar linkages [21,22,23]. In [24], a method for the force analysis of the linkages in Mathcad program is proposed that allows you to analytically solve the vector force balance equations.

The methods of vector algebra are widely used for analytical study of kinematics and kinetostatics of linkages [25,26,27,28,29,30], consisting in replacing of each link of the mechanism with the appropriate vector.

At a constant angular velocity of the driving member in ω1 = const the area of movement 0 ≤ φ1 ≤ 2π, you can determine the counterweight moment and the reaction mechanism in the kinematic pairs using the kinetostatic analysis. You can define the parameters of the electric motor by the average value of the balancing point calculation and selection of bearings to be installed in the hinges by the extreme values of the responses. In addition, the analytical expressions of reactions you can be used to solve problems in the dynamics of planar linkages taking into account the forces of friction in kinematic pairs.

Let us introduce the following quality criteria: K1and K2. Let us define criteria K1 as the ratio of the driving torque to the moment of the resistance forces. The smaller the parameter, the less energy you have to spend to set the mechanism in motion. Moreover, the criterion K1 is an absolute amount of the angular speed analog of the mechanism’s output link. Let us determine the criterion K2 as the relative level of reactions in all the kinematic pairs of the mechanism. By definition, both the quality criteria depend only on the geometric dimensions of the mechanism and do not depend on the forces and moments applied to the mechanism that allows us to include these criteria in the solution of the optimal kinematic synthesis problem.

The method of vector kinetostatic analysis for planar linkages of high classes is proposed below, beginning with the second class and up to the fifth class inclusive. The results of solving the problem of kinetostatic analysis of planar linkages of high classes are obtained in vector form, which is a difference from other methods. Next, vector equations can be analytically solved in analytical Maple computing system that is to be the most convenient way for further calculations.

2 Kinetostatic analysis of planar linkages of second class

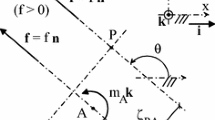
Consider a vector method for kinetostatic analysis of planar linkages of second class (Fig. 1).

Fig. 1
figure 1

Planar linkage mechanisms of second class: a four-bar linkage, b slider-crank mechanism

Full size image

Let \(\vec{R}_{ij} = - \vec{R}_{ji} \;i, j = 0, \,1, \,2,\, 3\) (the reaction of the i on the j link) be the desired reaction in the kinematic pairs and M y be the unknown counterbalancing moment on the driving member 1. Let us specify a mass of links m i , the moments of links inertia with respect to mass centers \(J_{{S_{i} }}\), as well as the forces of gravity of links \(\vec{G}_{i}\) and the moment or force of resistance on the output link M3 or F3. Let the law of motion of the driving member φ1 = φ1(t) be known and solving the problem of the kinematic analysis can determine the laws of motion of the other links of the mechanism, which means that we can find the inertial forces of mass centers \(- m_{i} \vec{W}_{{S_{i} }}\) and the moments of inertia forces of the links \(- J_{{S_{i} }} \varepsilon_{i}\). Here, \(\vec{W}_{{S_{i} }}\) is the acceleration of the center of mass at the point S i and ɛ i is the angular acceleration of the center of mass at the point S i .

2.1 Kinetostatic analysis of the four-bar linkage

Consider the kinetostatic analysis of the four-bar linkage, see Fig. 1a. Let us write the equations of equilibrium of its three links in the vector form according to the principle of d’Alembert:

$$\vec{R}_{01} + \vec{R}_{21} + \vec{G}_{1} = 0,\quad \vec{l}_{1} \times \vec{R}_{21} + M_{y} \vec{k} - J_{{S_{1} }} \varepsilon_{1} \vec{k} = 0$$
(1)
$$\vec{R}_{12} + \vec{R}_{32} + \vec{G}_{2} - m_{2} \vec{W}_{{S_{2} }} = 0,\quad (\vec{l}_{2} - \vec{r}_{2} ) \times \vec{R}_{32} - \vec{r}_{2} \times \vec{R}_{12} - J_{{S_{1} }} \varepsilon_{1} \vec{k} = 0$$
(2)
$$\vec{R}_{23} + \vec{R}_{03} + \vec{G}_{3} - m_{3} \vec{W}_{{S_{3} }} = 0,\quad (\vec{l}_{3} - \vec{r}_{3} ) \times \vec{R}_{23} - \vec{r}_{3} \times \vec{R}_{03} - J_{{S_{3} }} \varepsilon_{3} \vec{k} - M_{3} \vec{k} = 0.$$
(3)

In these equations, the \(\vec{k}\) denotes the unit vector of the coordinate axis Oz. From Eq. (1) with a known vector \(\vec{R}_{12}\), we can find a reaction from the rack O on the driving member and the balancing point:

$$\vec{R}_{01} = \vec{R}_{12} - \vec{G}_{1} ,\quad M_{y} = (\vec{k},\vec{l}_{1} ,\vec{R}_{12} ) + J_{{S_{1} }} \varepsilon_{1} .$$

To simplify further calculations, we introduce the notation:

$$\vec{P}_{i} = \vec{G}_{i} - m_{i} \vec{W}_{{S_{i} }} ,\quad \vec{J}_{i} = J_{{S_{i} }} \varepsilon_{i} \vec{k},\quad i = 2..5.$$

We will take \(\vec{R}_{12}\) for the desired reaction, and then, the Eqs. (2–3) can be written as follows:

$$\left\{ \begin{aligned} & \vec{R}_{23} = \vec{R}_{12} + \vec{P}_{2} ,\quad \vec{R}_{03} = - \vec{R}_{12} - \vec{P}_{2} - \vec{P}_{3} , \hfill \\ & (\vec{l}_{2} - \vec{r}_{2} ) \times (\vec{R}_{12} + \vec{P}_{2} ) + \vec{r}_{2} \times \vec{R}_{12} + \vec{J}_{2} = 0, \hfill \\ & (\vec{l}_{3} - \vec{r}_{3} ) \times (\vec{R}_{12} + \vec{P}_{2} ) + \vec{r}_{3} \times (\vec{R}_{12} + \vec{P}_{2} + \vec{P}_{3} ) - \vec{J}_{3} - M_{3} \vec{k} = 0 \hfill \\ \end{aligned} \right..$$
(4)

From the last two vector equations of the system (4), we can write the following system of vector equations for the desired vector (where the right-hand sides of these equations are denoted as \(\vec{p}_{i}\) for simplicity):

$$\left\{ \begin{aligned} & \vec{l}_{2} \times \vec{R}_{12} = \vec{p}_{2} = - (\vec{l}_{2} - \vec{r}_{2} ) \times \vec{P}_{2} - \vec{J}_{2} , \hfill \\ & \vec{l}_{3} \times \vec{R}_{12} = \vec{p}_{3} = - \vec{l}_{3} \times \vec{P}_{2} - \vec{r}_{3} \times \vec{P}_{3} + \vec{J}_{3} + M_{3} \vec{k} \hfill \\ \end{aligned} \right..$$
(5)

The solution of the system of vector Eq. (5) will be sought as a linear combination of the vectors \(\vec{l}_{2}\) and \(\vec{l}_{3}\), i.e., as follows:

$$\vec{R}_{12} = c_{1} \vec{l}_{2} + c_{2} \vec{l}_{3} .$$
(6)

After substituting (6) into (5), we obtain the following expressions for the scalar parameters c1 and c2:

$$c_{1} = - \frac{{\vec{k} \cdot \vec{p}_{3} }}{{(\vec{k},\vec{l}_{2} ,\vec{l}_{3} )}},\quad c_{2} = \frac{{\vec{k} \cdot \vec{p}_{2} }}{{(\vec{k},\vec{l}_{2} ,\vec{l}_{3} )}}.$$
(7)

Thus, the problem of kinetostatic analysis is completely solved; the results are obtained in vector form (7).

Consider the particular case of this problem. Quite often, it is necessary to solve the problem of static, i.e., without considering the forces of inertia and even the gravity forces of mechanism links. The same problem arises in determining the dimensionless criteria for transmission of mechanism movement. Assuming the vector \(\vec{p}_{2} = 0,\quad \vec{p}_{3} = M_{3} \vec{k}\) in the above formulas, we obtain the desired reaction in the kinematic pairs:

$$\vec{R}_{01} = \vec{R}_{12} = \vec{R}_{23} = - \vec{R}_{03} = - \frac{{M_{3} \vec{l}_{2} }}{{(\vec{k},\vec{l}_{2} ,\vec{l}_{3} )}},\quad M_{y} = - M_{3} \frac{{(\vec{k},\vec{l}_{1} ,\vec{l}_{2} )}}{{(\vec{k},\vec{l}_{2} ,\vec{l}_{3} )}}.$$

We define quality criteria K1 and K2 in the form of expressions:

$$K_{1} = \left| {\frac{{M_{y} }}{{M_{3} }}} \right| = \left| {\varphi^{\prime}_{3} } \right| = \frac{{l_{1} }}{{l_{3} }}\left| {\frac{{\sin (\varphi_{2} - \varphi_{1} )}}{{\sin (\varphi_{2} - \varphi_{3} )}}} \right|,\quad K_{2} = \left| {\frac{{R_{\hbox{max} } l_{3} }}{{M_{3} }}} \right| = l_{3} \left| {\frac{{R_{12} }}{{M_{3} }}} \right| = \frac{1}{{\left| {\sin (\varphi_{2} - \varphi_{3} )} \right|}}.$$

Both criterion functions K1(φ1) and K2(φ1) can take any non-negative values. The value of any of these parameters depends on the distance from the dead center position of the mechanism: while approaching the dead center position, the criteria values increase significantly due to the fact that the denominator sin (φ2−φ3) tends to zero. Thus, from the values of the transmission criteria K1 and K2, not only the quality of the transmission of motion and forces can be judged, but also the degree of remoteness from the danger zone when mechanism is working.

2.2 Kinetostatic analysis of the slider-crank mechanism

Consider the kinetostatic analysis of the slider-crank mechanism (Fig. 1b). Let us write the equations of equilibrium of all its links in the vector form according to the principle of d’Alembert:

$$\vec{R}_{01} + \vec{R}_{21} + \vec{G}_{1} = 0,\quad \vec{l}_{1} \times \vec{R}_{21} + M_{y} \vec{k} - J_{{S_{1} }} \varepsilon_{1} \vec{k} = 0$$
$$\vec{R}_{12} + \vec{R}_{32} + \vec{G}_{2} - m_{2} \vec{W}_{{S_{2} }} = 0,\quad (\vec{l}_{2} - \vec{r}_{2} ) \times \vec{R}_{32} - \vec{r}_{2} \times \vec{R}_{12} - J_{{S_{1} }} \varepsilon_{1} \vec{k} = 0$$
$$\vec{R}_{23} + \vec{R}_{03} + \vec{G}_{3} - m_{3} \vec{W}_{{S_{3} }} + \vec{F}_{3} = 0,\quad \sum\limits_{i}^{{}} {M_{B} } (\vec{F}_{i} ) = 0.$$
(8)

We express all the reactions in kinematic pairs and balancing moment also through the vector \(\vec{R}_{12}\):

$$\left\{ \begin{aligned} & \vec{R}_{01} = \vec{R}_{12} - \vec{G}_{1} ,\quad \vec{R}_{23} = \vec{R}_{12} + \vec{P}_{2} ,\quad \vec{R}_{03} = - \vec{R}_{12} - \vec{P}_{2} - \vec{P}_{3} - \vec{F}_{3} , \hfill \\ & M_{y} = (\vec{k},\vec{l}_{1} ,\vec{R}_{12} ) + J_{{S_{1} }} \varepsilon_{1} ,\quad (\vec{l}_{2} - \vec{r}_{2} ) \times (\vec{R}_{12} + \vec{P}_{2} ) + \vec{r}_{2} \times \vec{R}_{12} + \vec{J}_{2} = 0 \hfill \\ \end{aligned} \right..$$
(9)

The equation in the form of the system moments (8) serves only to determine the point of application of the reaction \(\vec{R}_{03}\) or the arm of the reaction against the hinge B. As a rule, this arm in many problems is equal to zero, and the reaction \(\vec{R}_{03}\) passes through the point A. We can obtain the following vector equation from the third and last system of Eq. (9):

$$\left\{ \begin{aligned} \vec{j} \times \vec{R}_{12} = \vec{a}, \hfill \\ \vec{l}_{2} \times \vec{R}_{12} = \vec{b} \hfill \\ \end{aligned} \right.,$$
(10)

where \(\vec{i},\vec{j}\) are the unit vectors of the coordinate axes Ox and Oy, respectively, and known vectors on the right side in equation are equal to

$$\begin{aligned} \vec{a} = - \vec{j} \times (\vec{P}_{2} + \vec{P}_{3} + \vec{F}_{3} ), \hfill \\ \vec{b} = - (\vec{l}_{2} - \vec{r}_{2} ) \times \vec{P}_{3} - \vec{J}_{2} . \hfill \\ \end{aligned}$$

It can be written as the solution of (10) for the reaction \(\vec{R}_{12}\):

$$\vec{R}_{12} = \frac{{(\vec{k} \cdot \vec{b})\vec{j} - (\vec{k} \cdot \vec{a})\vec{l}_{2} }}{{\vec{i} \cdot \vec{l}_{2} }}.$$

In the particular case, when we neglect the forces of inertia and weights of links, it can be obtained as follows:

$$\vec{R}_{01} = \vec{R}_{12} = \vec{R}_{23} = - \vec{R}_{03} - \vec{F}_{3} = - \frac{{F_{3} \vec{l}_{2} }}{{l_{2} \cos \varphi_{2} }},\quad M_{y} = - F_{3} l_{1} \frac{{\sin (\varphi_{2} - \varphi_{1} )}}{{\cos \varphi_{2} }}$$

and the quality criteria

$$K_{1} = \left| {\frac{{M_{y} }}{{F_{3} l_{1} }}} \right| = \left| {\frac{{S^{\prime}}}{{l_{1} }}} \right| = \left| {\frac{{\sin (\varphi_{2} - \varphi_{1} )}}{{\cos \varphi_{2} }}} \right|,\quad K_{2} = \left| {\frac{{R_{\hbox{max} } }}{{F_{3} }}} \right| = \left| {\frac{{R_{12} }}{{F_{3} }}} \right| = \frac{1}{{\left| {\cos \varphi_{2} } \right|}}.$$

2.3 Kinetostatic analysis of the rocker mechanism

Consider the rocker mechanism (Fig. 2). Let us write the equations of equilibrium of the mechanism links in the vector form according to the principle of d’Alembert:

Fig. 2
figure 2

Rocker mechanism

Full size image
$$\vec{R}_{01} + \vec{R}_{21} + \vec{P}_{1} = 0,\quad (\vec{l}_{1} - \vec{r}_{1} ) \times \vec{R}_{21} - \vec{r}_{1} \times \vec{R}_{01} + M_{y} \vec{k} - \vec{J}_{1} = 0$$
(11)
$$\vec{R}_{12} + \vec{R}_{32} + \vec{P}_{2} = 0,\quad \sum\limits_{i}^{{}} {M_{{S_{2} }} } (\vec{F}_{i} ) = 0\quad$$
$$\vec{R}_{23} + \vec{R}_{03} + \vec{P}_{3} = 0,\quad (\vec{e} + \vec{s}_{3} - \vec{r}_{3} ) \times \vec{R}_{23} - \vec{r}_{3} \times \vec{R}_{03} - \vec{J}_{3} - M_{3} \vec{k} = 0.$$

The second equation of (11) in the form of moments is only necessary to determine the point of application of the reaction \(\vec{R}_{32}\). Let us denote the desired reaction as \(\vec{R}_{12} = \vec{Z}\). Then, the above-recorded equations take the following form:

$$\vec{R}_{01} = \vec{Z} - \vec{P}_{1} ,\quad M_{y} = (\vec{k},\vec{l}_{1} ,\vec{Z}) - (\vec{k},\vec{r}_{1} ,\vec{P}_{1} ) + \vec{k} \cdot \vec{J}_{1}$$
(12)
$$\vec{R}_{23} = \vec{Z} + \vec{P}_{2} ,\quad \vec{R}_{03} = - \vec{Z} - \vec{P}_{2} - \vec{P}_{3}$$
(13)
$$(\vec{e} + \vec{s}_{3} ) \times \vec{Z} = - \vec{r}_{3} \times \vec{P}_{3} - (\vec{e} + \vec{s}_{3} ) \times \vec{P}_{2} + \vec{J}_{3} + M_{3} \vec{k}.$$

We have the following system of vector equations to determine \(\vec{Z}\)

$$\left\{ \begin{aligned} & (\vec{e} + \vec{s}_{3} ) \times \vec{Z} = \vec{p}, \hfill \\ & \vec{s}_{3} \cdot \vec{Z} = q. \hfill \\ \end{aligned} \right.$$
(14)

Here, we use the notation:

$$\vec{p} = - \vec{r}_{3} \times \vec{P}_{3} - (\vec{e} + \vec{s}_{3} ) \times \vec{P}_{2} + \vec{J}_{3} + M_{3} \vec{k},\,\,\,\,q = - \vec{s}_{3} \cdot \vec{P}_{2} .$$

The solution of (14) can be written as follows:

$$\vec{R}_{12} = \vec{Z} = \frac{{q \cdot (\vec{e} + \vec{s}_{3} )}}{{s_{3}^{2} }} + \frac{{\vec{p} \times \vec{s}_{3} }}{{s_{3}^{2} }}.$$

The remaining unknown constituents are determined by Eqs. (12) and (13).

In the particular case, when we neglect the forces of inertia and weights of links, it can be obtained as follows:

$$\vec{R}_{01} = \vec{R}_{12} = \vec{R}_{23} = - \vec{R}_{03} = \frac{{M_{3} (\vec{k} \times \vec{s}_{3} )}}{{s_{3}^{2} }},\quad M_{y} = M_{3} l_{1} \frac{{\sin (\varphi_{1} - \varphi_{3} )}}{{s_{3}^{{}} }},$$

and the motion transmission criteria

$$K_{1} = \left| {\frac{{M_{y} }}{{M_{3} }}} \right| = \left| {\varphi^{\prime}_{3} } \right| = \left| {l_{1} \frac{{\sin (\varphi_{1} - \varphi_{3} )}}{{s_{3} }}} \right|,\quad K_{2} = \left| {\frac{{R_{\hbox{max} } }}{{M_{3} }}} \right| = \left| {\frac{{R_{12} }}{{M_{3} }}} \right| = \frac{1}{{\left| {s_{3} } \right|}}.$$

For all the above cases, the program has been drawn up in Maple computer algebra system, and it was also created a new module of vector algebra to solve the problems of vector mechanics.

The test calculation was made for the four-bar linkage with the following input data: the geometric dimensions of the mechanism l1 = 0.4 m, l2 = 0.8 m, l3 = 0.7 m, x C  = 1.0 m, y C  = 0.01 m, r1 = 0.0 m, r2 = 0.4 m, r3 = 0.0 m, and α2 = 00; mass and moments of inertia of links \(m_{1} = 0.3{\text{kg}},\,\,\,m_{2} = 0.2{\text{kg}},\,\,and\,m_{3} = 0.4{\text{kg}}\), \(J_{{S_{1} }} = 0.1{\text{kgm}}^{2} ,\,\,\,J_{{S_{2} }} = 0.05{\text{kgm}}^{2} ,\,and\,J_{{S_{3} }} = 0.07{\text{kgm}}^{2}\); resistance moment on the output shaft \(M_{3} = 3{\text{HM}}\), and the angular velocity of the driving member assumed to be constant ω1 = 10 s−1.

Figure 3 shows graphs of motion transmission criteria K1 and K2, and Fig. 4a, b shows the hodograph of the reaction \(\vec{R}_{12}\) and the diagram of the balancing moment M y .

Fig. 3
figure 3

Motion transmission criteria K1, K2

Full size image
Fig. 4
figure 4

a Hodograph of the reaction \(\vec{R}_{12}\) and b balancing moment M y

Full size image

3 Kinetostatic analysis of planar linkage mechanism of third class

Consider a vector method for the kinetostatic analysis of planar linkage mechanism of third class (Fig. 5). Accepted designations are similar to that were used above.

Fig. 5
figure 5

Planar linkage mechanism of third class

Full size image

The equilibrium equations of five moving links of the mechanism have the following form:

$$\vec{R}_{01} + \vec{R}_{21} + \vec{G}_{1} = 0,\quad \vec{l}_{1} \times \vec{R}_{21} + M_{y} \vec{k} - J_{{S_{1} }} \varepsilon_{1} \vec{k} = 0$$
(15)
$$\vec{R}_{12} + \vec{R}_{32} + \vec{G}_{2} - m_{2} \vec{W}_{{S_{2} }} = 0,\quad (\vec{l}_{2} - \vec{r}_{2} ) \times \vec{R}_{32} - \vec{r}_{2} \times \vec{R}_{12} - J_{{S_{1} }} \varepsilon_{1} \vec{k} = 0$$
(16)
$$\left\{ \begin{aligned} & \vec{R}_{23} + \vec{R}_{43} + \vec{R}_{53} + \vec{G}_{3} - m_{3} \vec{W}_{{S_{3} }} = 0,\quad \hfill \\ & (\vec{l}_{3} - \vec{r}_{3} ) \times \vec{R}_{43} + (\vec{l}^{\prime}_{3} - \vec{r}_{3} ) \times \vec{R}_{53} - \vec{r}_{3} \times \vec{R}_{23} - J_{{S_{3} }} \varepsilon_{3} \vec{k} = 0 \hfill \\ \end{aligned} \right.$$
(17)
$$\vec{R}_{34} + \vec{R}_{04} + \vec{G}_{4} - m_{4} \vec{W}_{{S_{4} }} = 0,\quad (\vec{l}_{4} - \vec{r}_{4} ) \times \vec{R}_{34} - \vec{r}_{4} \times \vec{R}_{04} - M_{4} \vec{k} - J_{{S_{4} }} \varepsilon_{4} \vec{k} = 0$$
(18)
$$\vec{R}_{35} + \vec{R}_{05} + \vec{G}_{5} - m_{5} \vec{W}_{{S_{5} }} = 0,\quad (\vec{l}_{5} - \vec{r}_{5} ) \times \vec{R}_{35} - \vec{r}_{5} \times \vec{R}_{05} - M_{5} \vec{k} - J_{{S_{5} }} \varepsilon_{5} \vec{k} = 0.$$
(19)

From Eqs. (15) with a known value of \(\vec{R}_{12}\), we can find a reaction from the rack on the driving member and the balancing point:

$$\vec{R}_{01} = \vec{R}_{12} - \vec{G}_{1} ,\quad M_{y} = (\vec{k},\vec{l}_{1} ,\vec{R}_{12} ) + J_{{S_{1} }} \varepsilon_{1} .$$

For simplicity, we introduce the notation

$$\vec{P}_{i} = \vec{G}_{i} - m_{i} \vec{W}_{{S_{i} }} ,\quad \vec{J}_{i} = J_{{S_{i} }} \varepsilon_{i} \vec{k},\quad i = 2, \ldots ,5.$$

We will take \(\vec{R}_{34}\) and \(\vec{R}_{35}\) for the desired reactions and denote them as \(\vec{Z}_{1}\) and \(\vec{Z}_{2}\) to distinguish them from the others, then we can write Eqs. (15)–(19):

$$\left\{ \begin{aligned} & \vec{R}_{04} = - \vec{Z}_{1} - \vec{P}_{4} ,\quad \vec{R}_{05} = - \vec{Z}_{2} - \vec{P}_{5} , \hfill \\ & \vec{R}_{12} = \vec{Z}_{1} + \vec{Z}_{2} - \vec{P}_{2} - \vec{P}_{3} ,\quad \vec{R}_{23} = \vec{Z}_{1} + \vec{Z}_{2} - \vec{P}_{3} , \hfill \\ & (\vec{l}_{2} - \vec{r}_{2} ) \times (\vec{Z}_{1} + \vec{Z}_{2} - \vec{P}_{3} ) + \vec{r}_{2} \times (\vec{Z}_{1} + \vec{Z}_{2} - \vec{P}_{2} - \vec{P}_{3} ) + \vec{J}_{2} = 0 \hfill \\ & (\vec{l}_{3} - \vec{r}_{3} ) \times \vec{Z}_{1} + (\vec{l}^{\prime}_{3} - \vec{r}_{3} ) \times \vec{Z}_{2} + \vec{r}_{3} \times (\vec{Z}_{1} + \vec{Z}_{2} - \vec{P}_{3} ) + \vec{J}_{3} = 0 \hfill \\ & (\vec{l}_{4} - \vec{r}_{4} ) \times \vec{Z}_{1} + \vec{r}_{4} \times (\vec{Z}_{1} + \vec{P}_{4} ) - M_{4} \vec{k} - \vec{J}_{4} = 0 \hfill \\ & (\vec{l}_{5} - \vec{r}_{5} ) \times \vec{Z}_{2} + \vec{r}_{5} \times (\vec{Z}_{2} + \vec{P}_{5} ) - M_{5} \vec{k} - \vec{J}_{5} = 0 \hfill \\ \end{aligned} \right..$$
(20)

From the last four equations of the system (20), we can write the following system of vector equations for the desired vectors (where the right-hand sides of these equations are denoted as \(\vec{p}_{i}\) for simplicity):

$$\left\{ \begin{aligned} & \vec{l}_{2} \times (\vec{Z}_{1} + \vec{Z}_{2} ) = \vec{p}_{2} = \vec{l}_{2} \times \vec{P}_{3} + \vec{r}_{2} \times \vec{P}_{2} - \vec{J}_{2} \hfill \\ & \vec{l}_{3} \times \vec{Z}_{1} + \vec{l}^{\prime}_{3} \times \vec{Z}_{2} = \vec{p}_{3} = \vec{r}_{3} \times \vec{P}_{3} - \vec{J}_{3} \hfill \\ & \vec{l}_{4} \times \vec{Z}_{1} = \vec{p}_{4} = - \vec{r}_{4} \times \vec{P}_{4} + \vec{J}_{4} + M_{4} \vec{k} \hfill \\ & \vec{l}_{5} \times \vec{Z}_{2} = \vec{p}_{5} = - \vec{r}_{5} \times \vec{P}_{5} + \vec{J}_{5} + M_{5} \vec{k} \hfill \\ \end{aligned} \right..$$
(21)

The solution of system (21) can be found in the form:

$$\vec{Z}_{1} = c_{1} \vec{l}_{2} + c_{2} \vec{l}_{4} ,\quad \vec{Z}_{2} = c_{3} \vec{l}_{2} + c_{4} \vec{l}_{5} .$$

Here, the scalar parameters c i are defined by the following:

$$\begin{aligned} & c_{1} = - \frac{{\vec{k} \cdot \vec{p}_{4} }}{{(\vec{k},\vec{l}_{2} ,\vec{l}_{4} )}},\quad c_{3} = - \frac{{\vec{k} \cdot \vec{p}_{5} }}{{(\vec{k},\vec{l}_{2} ,\vec{l}_{5} )}},\quad \hfill \\ & c_{2} = \frac{{(\vec{q},\vec{l}_{2} ,\vec{l}_{5} ) - (\vec{p}_{2} ,\vec{l}^{\prime}_{3} ,\vec{l}_{5} )}}{\Delta },\quad c_{4} = - \frac{{(\vec{q},\vec{l}_{2} ,\vec{l}_{4} ) - (\vec{p}_{2} ,\vec{l}_{3} ,\vec{l}_{4} )}}{\Delta }, \hfill \\ \end{aligned}$$

where we use the notation

$$\vec{q} = \vec{p}_{3} + \vec{l}_{2} \times (c_{1} \vec{l}_{3} + c_{3} \vec{l}^{\prime}_{3} ),\quad \Delta = (\vec{l}_{2} \times \vec{l}_{5} ) \cdot (\vec{l}_{3} \times \vec{l}_{4} ) - (\vec{l}_{2} \times \vec{l}_{4} ) \cdot (\vec{l}^{\prime}_{3} \times \vec{l}_{5} ).$$

If we neglect the inertial components and weights of links \(\vec{P}_{i} = 0,\quad \vec{J}_{i} = 0\) and consider M4 = 0, then the solution is much simpler:

$$\left\{ \begin{aligned} \vec{l}_{2} \times (\vec{Z}_{1} + \vec{Z}_{2} ) = 0,\quad \vec{l}_{3} \times \vec{Z}_{1} + \vec{l}^{\prime}_{3} \times \vec{Z}_{2} = 0, \hfill \\ \vec{l}_{4} \times \vec{Z}_{1} = 0,\quad \vec{l}_{5} \times \vec{Z}_{2} = M_{5} \vec{k} \hfill \\ \end{aligned} \right.$$
$$\begin{aligned} c_{1} = 0,\quad c_{3} = - \frac{{M_{5} }}{{(\vec{k},\vec{l}_{2} ,\vec{l}_{5} )}},\quad \vec{q} = c_{3} (\vec{l}_{2} \times \vec{l}^{\prime}_{3} ),\quad \hfill \\ c_{2} = \frac{{(\vec{q},\vec{l}_{2} ,\vec{l}_{5} )}}{\Delta },\quad c_{4} = - \frac{{(\vec{q},\vec{l}_{2} ,\vec{l}_{4} )}}{\Delta } \hfill \\ \end{aligned}$$
$$\vec{Z}_{1} = c_{2} \vec{l}_{4} ,\quad \vec{Z}_{2} = c_{3} \vec{l}_{2} + c_{4} \vec{l}_{5} .$$

4 Kinetostatic analysis of planar linkage mechanism of fourth class

Consider a vector method for kinetostatic analysis of planar linkage mechanism of fourth class (Fig. 6).

Fig. 6
figure 6

Planar linkage mechanism of fourth class

Full size image

Let \(\vec{R}_{ij} = - \vec{R}_{ji} \,i, j = 0, \, 1, \ldots , \, 5\) (the reaction of the i on the j link) be the desired reaction in the kinematic pairs and M y be the unknown counterbalancing moment on the driving member 1. Let us specify a mass of links m i , the moments of links inertia with respect to mass centers \(J_{{S_{i} }}\), as well as the forces of gravity of links \(\vec{G}_{i}\) (not shown on the figure) and the moment or force of resistance on the output link M5. Let the law of motion of the driving member φ1 = φ1(t) be known. From solving the problem of the kinematic analysis, we can determine the laws of motion of the other links of the mechanism. Then, you can find the inertial forces of mass centers \(- m_{i} \vec{W}_{{S_{i} }}\) and the moments of inertia forces of the links \(- J_{{S_{i} }} \varepsilon_{i}\).

Equilibrium equations for the five mobile links based on the principle of d’Alembert mechanism can be written as follows:

$$\sum\limits_{j}^{{}} {\vec{F}_{j,i} } - m_{i} \vec{W}_{{S_{i} }} = 0,\quad \sum\limits_{j}^{{}} {M_{{S_{i} }} (\vec{F}_{j,i} } ) - J_{{S_{i} }} \varepsilon_{i} \vec{k} = 0,\quad i = 1, \ldots ,5,$$

where \(\vec{F}_{j,i}\) are the active and reactive forces acting on the link i. Let us write this for each level, considering driving member 1 as statically balanced:

$$\vec{R}_{01} + \vec{R}_{21} + \vec{G}_{1} = 0,\quad \vec{l}_{1} \times \vec{R}_{21} + M_{y} \vec{k} - J_{{S_{1} }} \varepsilon_{1} \vec{k} = 0$$
(22)
$$\left\{ \begin{aligned} & \vec{R}_{12} + \vec{R}_{32} + \vec{R}_{42} + \vec{G}_{2} - m_{2} \vec{W}_{{S_{2} }} = 0,\quad \hfill \\ & (\vec{l}_{2} - \vec{r}_{2} ) \times \vec{R}_{32} + (\vec{l}^{\prime}_{2} - \vec{r}_{2} ) \times \vec{R}_{42} - \vec{r}_{2} \times \vec{R}_{12} - J_{{S_{2} }} \varepsilon_{2} \vec{k} = 0 \hfill \\ \end{aligned} \right.$$
(23)
$$\vec{R}_{23} + \vec{R}_{53} + \vec{G}_{3} - m_{3} \vec{W}_{{S_{3} }} = 0,\quad (\vec{l}_{3} - \vec{r}_{3} ) \times \vec{R}_{53} - \vec{r}_{3} \times \vec{R}_{23} - J_{{S_{3} }} \varepsilon_{3} \vec{k} = 0$$
(24)
$$\vec{R}_{24} + \vec{R}_{54} + \vec{G}_{4} - m_{4} \vec{W}_{{S_{4} }} = 0,\quad (\vec{l}_{4} - \vec{r}_{4} ) \times \vec{R}_{54} - \vec{r}_{4} \times \vec{R}_{24} - J_{{S_{4} }} \varepsilon_{4} \vec{k} = 0$$
(25)
$$\left\{ \begin{aligned} & \vec{R}_{35} + \vec{R}_{45} + \vec{R}_{05} + \vec{G}_{5} - m_{5} \vec{W}_{{S_{5} }} = 0,\quad \hfill \\ & (\vec{l}_{5} - \vec{r}_{5} ) \times \vec{R}_{35} + (\vec{l}^{\prime}_{5} - \vec{r}_{5} ) \times \vec{R}_{45} - \vec{r}_{5} \times \vec{R}_{05} - M_{5} \vec{k} - J_{{S_{5} }} \varepsilon_{5} \vec{k} = 0 \hfill \\ \end{aligned} \right..$$
(26)

In these equations, the \(\vec{k}\) denotes the unit vector of the coordinate axis Oz. From Eqs. (22) with a known vector \(\vec{R}_{12}\), we can find a reaction from the rack (link number 0) on the driving member and the balancing point:

$$\vec{R}_{01} = \vec{R}_{12} - \vec{G}_{1} ,\quad M_{y} = (\vec{k},\vec{l}_{1} ,\vec{R}_{12} ) + J_{{S_{1} }} \varepsilon_{1} .$$

For simplicity, we introduce the notation:

$$\vec{P}_{i} = \vec{G}_{i} - m_{i} \vec{W}_{{S_{i} }} ,\quad \vec{J}_{i} = J_{{S_{i} }} \varepsilon_{i} \vec{k},\quad i = 2,\,3,\,4,\,5.$$

We will take \(\vec{R}_{35}\) and \(\vec{R}_{45}\) for the desired reactions and denote them as \(\vec{Z}_{1}\) and \(\vec{Z}_{2}\) to distinguish them from the others, then we can write Eqs. (23)–(26):

$$\left\{ \begin{aligned} & \vec{R}_{05} = - \vec{Z}_{1} - \vec{Z}_{2} - \vec{P}_{5} ,\quad \vec{R}_{24} = \vec{Z}_{2} - \vec{P}_{4} , \hfill \\ & \vec{R}_{23} = \vec{Z}_{1} - \vec{P}_{3} ,\quad \vec{R}_{12} = \vec{R}_{23} + \vec{R}_{24} - \vec{P}_{2} = \vec{Z}_{1} + \vec{Z}_{2} - \vec{P}_{2} - \vec{P}_{3} - \vec{P}_{4} ,\quad \hfill \\ & (\vec{l}_{2} - \vec{r}_{2} ) \times (\vec{Z}_{1} - \vec{P}_{3} ) + (\vec{l}^{\prime}_{2} - \vec{r}_{2} ) \times (\vec{Z}_{2} - \vec{P}_{4} ) + \vec{r}_{2} \times (\vec{Z}_{1} + \vec{Z}_{2} - \vec{P}_{2} - \vec{P}_{3} - \vec{P}_{4} ) + \vec{J}_{2} = 0 \hfill \\ & (\vec{l}_{3} - \vec{r}_{3} ) \times \vec{Z}_{1} + \vec{r}_{3} \times (\vec{Z}_{1} - \vec{P}_{3} ) + \vec{J}_{3} = 0 \hfill \\ & (\vec{l}_{4} - \vec{r}_{4} ) \times \vec{Z}_{2} + \vec{r}_{4} \times (\vec{Z}_{2} - \vec{P}_{4} ) + \vec{J}_{4} = 0 \hfill \\ & (\vec{l}_{5} - \vec{r}_{5} ) \times \vec{Z}_{1} + (\vec{l}^{\prime}_{5} - \vec{r}_{5} ) \times \vec{Z}_{2} + \vec{r}_{5} \times (\vec{Z}_{1} + \vec{Z}_{2} + \vec{P}_{5} ) - M_{5} \vec{k} - \vec{J}_{5} = 0 \hfill \\ \end{aligned} \right..$$
(27)

From the last four equations of the system (27), we can write the following system of vector equations for the desired vectors (where the right-hand sides of these equations are denoted as \(\vec{p}_{i}\) for simplicity):

$$\left\{ \begin{aligned} & \vec{l}_{2} \times \vec{Z}_{1} + \vec{l}^{\prime}_{2} \times \vec{Z}_{2} = \vec{p}_{2} = \vec{l}_{2} \times \vec{P}_{3} + \vec{l}^{\prime}_{2} \times \vec{P}_{4} + \vec{r}_{2} \times \vec{P}_{2} - \vec{J}_{2} \hfill \\ & \vec{l}_{3} \times \vec{Z}_{1} = \vec{p}_{3} = \vec{r}_{3} \times \vec{P}_{3} - \vec{J}_{3} \hfill \\ & \vec{l}_{4} \times \vec{Z}_{2} = \vec{p}_{4} = \vec{r}_{4} \times \vec{P}_{4} - \vec{J}_{4} \hfill \\ & \vec{l}_{5} \times \vec{Z}_{1} + \vec{l}^{\prime}_{5} \times \vec{Z}_{2} = \vec{p}_{5} = - \vec{r}_{5} \times \vec{P}_{5} + \vec{J}_{5} + M_{5} \vec{k} \hfill \\ \end{aligned} \right..$$
(28)

The solution of system (28) can be found in the form of a linear combination:

$$\vec{R}_{35} = \vec{Z}_{1} = a_{1} \vec{l}_{3} + b_{1} \vec{l}_{4} ,\quad \vec{R}_{45} = \vec{Z}_{2} = a_{2} \vec{l}_{3} + b_{2} \vec{l}_{4} .$$
(29)

Here, the scalar parameters a1, b1, a2, b2 are defined by the following:

$$\begin{aligned} & b_{1} = \frac{{\vec{k} \cdot \vec{p}_{3} }}{{(\vec{k},\vec{l}_{3} ,\vec{l}_{4} )}},\quad a_{2} = - \frac{{\vec{k} \cdot \vec{p}_{4} }}{{(\vec{k},\vec{l}_{3} ,\vec{l}_{4} )}},\quad \hfill \\ & a_{1} = \frac{{(\vec{q}_{2} ,\vec{l}^{\prime}_{5} ,\vec{l}_{4} ) - (\vec{q}_{5} ,\vec{l}^{\prime}_{2} ,\vec{l}_{4} )}}{\Delta },\quad b_{2} = - \frac{{(\vec{q}_{2} ,\vec{l}_{5} ,\vec{l}_{3} ) - (\vec{q}_{5} ,\vec{l}_{2} ,\vec{l}_{3} )}}{\Delta }, \hfill \\ \end{aligned}$$

where we use the notation

$$\begin{aligned} & \vec{q}_{2} = \vec{p}_{2} - b_{1} \vec{l}_{2} \times \vec{l}_{4} - a_{2} \vec{l}^{\prime}_{2} \times \vec{l}_{3} ,\quad \vec{q}_{5} = \vec{p}_{5} - b_{1} \vec{l}_{5} \times \vec{l}_{4} - a_{2} \vec{l}^{\prime}_{5} \times \vec{l}_{3} , \hfill \\ & \Delta = (\vec{l}_{2} \times \vec{l}_{3} ) \cdot (\vec{l}^{\prime}_{5} \times \vec{l}_{4} ) - (\vec{l}^{\prime}_{2} \times \vec{l}_{4} ) \cdot (\vec{l}_{5} \times \vec{l}_{3} ). \hfill \\ \end{aligned}$$

After substituting (29) in the first four equations of the system (27), we define a reaction in the kinematic pairs \(\vec{R}_{12} ,\vec{R}_{23} ,\vec{R}_{24} ,\vec{R}_{05}\), and then, from Eq. (22), we find \(\vec{R}_{01}\) and M y

$$\vec{R}_{01} = \vec{R}_{12} - \vec{G}_{1} ,\quad M_{y} = J_{{S_{1} }} \varepsilon_{1} + (\vec{k},\vec{l}_{1} ,\vec{R}_{12} ).$$

Thus, the problem of kinetostatic analysis is completely solved; the results are obtained in vector form.

Consider the particular case of this problem. Quite often, it is necessary to solve the problem of static, i.e., without considering the forces of inertia and even the gravity forces of mechanism links. If we neglect the inertial components and weights of links, i.e., \(\vec{P}_{i} = 0,\quad \vec{J}_{i} = 0\), then the solution is much simpler:

$$\left\{ \begin{aligned} & \vec{l}_{2} \times \vec{Z}_{1} + \vec{l}^{\prime}_{2} \times \vec{Z}_{2} = 0,\quad \vec{l}_{5} \times \vec{Z}_{1} + \vec{l}^{\prime}_{5} \times \vec{Z}_{2} = M_{5} \vec{k}, \hfill \\ & \vec{l}_{3} \times \vec{Z}_{1} = 0,\quad \vec{l}_{4} \times \vec{Z}_{2} = 0 \hfill \\ \end{aligned} \right.$$
$$\begin{aligned} & b_{1} = 0,\quad a_{2} = 0,\quad \vec{q}_{2} = 0,\quad \vec{q}_{5} = M_{5} \vec{k},\quad \hfill \\ & a_{1} = - \frac{{(\vec{q}_{5} ,\vec{l}^{\prime}_{2} ,\vec{l}_{4} )}}{\Delta },\quad b_{2} = \frac{{(\vec{q}_{5} ,\vec{l}_{2} ,\vec{l}_{3} )}}{\Delta } \hfill \\ \end{aligned}$$
$$\vec{R}_{23} = \vec{R}_{35} = \vec{Z}_{1} = a_{1} \vec{l}_{3} = - M_{5} \frac{{(\vec{k},\vec{l}^{\prime}_{2} ,\vec{l}_{4} )}}{\Delta }\vec{l}_{3} ,\quad \vec{R}_{24} = \vec{R}_{45} = \vec{Z}_{2} = b_{2} \vec{l}_{4} = M_{5} \frac{{(\vec{k},\vec{l}_{2} ,\vec{l}_{3} )}}{\Delta }\vec{l}_{4}$$
$$\vec{R}_{12} = \vec{R}_{01} = - \vec{R}_{05} = M_{5} \frac{{(\vec{k},\vec{l}_{2} ,\vec{l}_{3} )}}{\Delta }\vec{l}_{4} - M_{5} \frac{{(\vec{k},\vec{l}^{\prime}_{2} ,\vec{l}_{4} )}}{\Delta }\vec{l}_{3} ,\quad M_{y} = \vec{R}_{12} \cdot (\vec{k} \times \vec{l}_{1} ).$$

We can write the following expressions for the criteria of motion transmission K1 and K2.

$$\begin{aligned} & K_{1} = \left| {\frac{{M_{y} }}{{M_{5} }}} \right| = \left| {\varphi^{\prime}_{5} } \right| = \left| {\frac{{(\vec{k},\vec{l}_{2} ,\vec{l}_{3} )(\vec{k},\vec{l}_{1} ,\vec{l}_{4} ) - (\vec{k},\vec{l}^{\prime}_{2} ,\vec{l}_{4} )(\vec{k},\vec{l}_{1} ,\vec{l}_{3} )}}{{(\vec{l}_{2} \times \vec{l}_{3} ) \cdot (\vec{l}^{\prime}_{5} \times \vec{l}_{4} ) - (\vec{l}^{\prime}_{2} \times \vec{l}_{4} ) \cdot (\vec{l}_{5} \times \vec{l}_{3} )}}} \right|,\quad \hfill \\ & K_{2} = \left| {\frac{{R_{\hbox{max} } l_{5} }}{{M_{5} }}} \right| = l_{5} \left| {\frac{{\hbox{max} (|R_{12} |,|R_{24} |,|R_{23} |)}}{{M_{5} }}} \right| \hfill \\ \end{aligned}$$

Figure 7 shows graphs of motion transmission criteria K1, K2.

Fig. 7
figure 7

Criteria for force transmission K1, K2

Full size image

Figure 7 shows that the criterion value K1 reaches the maximum value at the position of the input link 1.4 rad and 4.9 rad, and the criterion value K2 reaches the maximum value at the position of the input link 1.6 and 4.9 rad. This shows that the maximum level of the reactions in all the kinematic pairs of linkage IV-th class appears in the vicinity of the angle position of the input link 4.9 rad.

5 Conclusion

Considered a vector method of determining the reactions in kinematic pairs and balancing moment can significantly simplify the problem of kinetostatic analysis of complex linkages.

A vector kinetostatic analysis method for planar linkages of high classes was developed. Computer implementation of algorithms with the use of Maple analytical calculations package was presented.

For all the planar linkages, which were considered in the work, a program in the system of analytic calculations of Maple was developed; in addition, a new module of vector algebra was also created for solving the problems of vector mechanics. Knowledge of analytical expression reactions allows most clearly meeting the challenges of the dynamics of mechanisms, taking into account the forces of friction in kinematic pairs.

The results of solving the problem of kinetostatic analysis are obtained in vector form, which is the novelty of the method.

We introduce the quality criteria, which depend only on the geometric dimensions of the linkage mechanism and do not depend on the forces and moments applied to the mechanism that allows us to use these criteria for the optimal kinematic synthesis. The quality criteria can take any non-negative values. The value of any of these parameters depends on the degree of remoteness of the mechanism from a dead position: the closer to a dead position of criteria values increases significantly. Thus, according to the values of quality, criteria can be judged not only on the quality of the transmission of motion and strength, but also on the degree of remoteness of the danger zone when working mechanism.