1 Introduction

Total hip arthroplasty (THA) implantations associated with degenerative and traumatic hip conditions, such as osteoarthritis, post-traumatic arthritis, and hip fractures, reach about 500,000 procedures performed annually in the UK and USA, and are estimated in more than one million worldwide [26, 52, 60]. In addition, the elderly population is growing as life expectancy increases; consequently, the demand for THA is increasing and is expected to grow by 174% in about 572,000 THA by the year 2030, only in the USA [43]. Furthermore, it is unclear if the number of orthopedic surgeons will be sufficient to meet this demand for health care [33]. Despite THA shows excellent clinical outcomes and is considered a successful and cost-effective procedure to relieve pain and restoring hip joint [52], some prosthesis fails, most commonly due to aseptic loosening secondary to wear or dislocation [45, 56]. Therefore, the development of computational tools with the capability to estimate bone growth and resorption when prosthetic devices are used has a remarkable importance, since these processes may contribute to implant success or failure. In this scenario, the finite-element method (FEM) has been playing a key role, being used to study and evaluate the mechanical behavior of prosthetic devices [53, 60], and to improve our understanding on the fundamentals of the mechanics of biological processes such as growth and remodeling [1, 35, 46, 58]. Through the multiplicative decomposition of the deformation gradient, the biological growth is associated with soft tissues and the remodeling process with hard tissues, while the former are treated kinematically, considering changes in volume at constant density [1, 38, 46, 54]; the latter are associated with changes in properties at constant volume [1, 35, 46, 58], such as internal structure, strength, or density [58]. In density growth case, focus of this work, the approach is of a constitutive kind using continuum nonlinear mechanics for hard tissues [1, 46].

The first work considering growth and resorption associated with gain or loss of mass, known as theory of adaptive elasticity, was presented by [19], where the traditional balance equations are enhanced by additional mass source terms, allowing bone adapts its density due to stress, strain, or energy [23, 44]. In addition, there was developed the bone maintenance theory [9,10,11, 13], motivated by the trajectorial hypothesis of bone microstructural arrangement in the principal stress directions [35, 64] and by structural optimization [1, 39, 42], to quantify the relationships between physiological loads and bone morphology, based on mathematical theories for bone adaptation to mechanical stimulus.

Several works were developed following the above-mentioned theories in prosthetic design analysis based on bone-remodeling theory [31, 63], in density prediction from stress–morphology relationships in trabecular bone [12], in the bone adaptation theory development [9], and in the numerical improvement for bone-remodeling simulations [30, 34]. However, to overcome some unstable and non-physical results using these formulations [40], a solution for the biomechanical coupled problem in terms of the mass and momentum balances using an implicit Euler backward integration scheme for the density evolution, following the isotropic functional adaptation reported by [30], was proposed to characterize density profiles in the proximal femur [39, 40, 42] and in tibia bone [50, 61], where hard tissues are characterized by an energy-driven evolution of the mass, and the mass source is specified in terms of density and strain energy.

Despite the considerable research in the field, from that we only highlighted some important contributions, the computational modeling of density growth using FEM in orthopedics biomechanics continues to be challenging, for instance, due to the constitutive laws considered [9, 35, 46, 58], the physiological loads and boundary conditions assumed [6, 22, 57, 62], and the implementation of the biomechanical problem in FEM softwares.

The aim of this study is the development and implementation of an FEM model with the capability to simulate the bone density growth and resorption processes due to mechanical stimuli. Moreover, the application of the study proposes a computational assessment tool for orthopedic specialists, focused on the simulation of a healthy femur and a femur with an implanted prosthesis submitted to loads.

For this purpose, two simulations were conducted:

  1. 1.

    In the first example, where density growth is not considered, the healthy and the prosthetic femurs will be submitted to real daily physical activity loads to found higher and lower stress regions that could be candidates for bone growth and resorption zones.

  2. 2.

    In the second example, the density growth process is considered in the simulation, to locate bone growth and resorption zones due to mechanical effects for the femur healthy condition and after a THA surgical procedure. In this situation, mechanical loads correspond to the average loads considered previously.

The density growth model developed takes into account the coupling between the biological and the mechanical effects and is based on growth and remodeling theories for biological materials. We adopted a nonlinear formulation for large deformations using the isotropic functional adaptation approach proposed by [30], used for bone density growth applications [42, 50, 61].

This paper is organized as follows Sect. 2 presented the theoretical framework and the constitutive equations for density growth within the context of continuum mechanics. Section 3 presents the set of governing equations formed by the coupling of the biological and mechanical problems and the corresponding boundary conditions. Section 4 describes how it implemented the incremental problem of density evolution embedded into the mechanical problem in COMSOL Multiphysics finite-element software using the solid mechanics and the general form PDE modules, respectively. Section 5 presents the geometrical model and the finite-element model adopted of a coupled structure–structure type along with the loads and boundary conditions, finite-element meshes, and the material properties assumed. In Sect. 6, the two biomechanical simulation examples (above mentioned) for the healthy and the prosthetic femurs are presented. In addition, in this section, the results obtained are presented and discussed. The final conclusions are summarized in Sect. 7.

2 Theoretical framework

Let consider a body \(\mathcal {B}\) capable of changing its density due to a mechanical stimulus, where two coupled processes are taking place: a mechanical one, driven by the body deformation due to loads, and a biological one, related to density changes in an energy-driven format due to a mass source.

Body motion is given by the vector field \(\mathbf {\chi }\); consequently, \({\mathbf v} =\dot{\chi }\) is the velocity field. Mapping \({\mathbf x} =\chi (\mathbf X ,t)\) is considered one-to-one in X for fixed \(\mathrm {t}\), so invertible then: \({\mathbf X} =\chi ^{-1}(\mathbf x ,t)\), being \(\mathbf X\) and \(\mathbf x\), the position vectors referred to reference and current configurations. Deformation gradient is defined as \({\mathbf F} =\nabla {\mathbf {\chi }}\) and the volumetric Jacobian of the deformation is the determinant of \(\mathbf F\), being: \({J}=\mathrm {det}(\mathbf F )\). Dot symbol and \(\nabla\) operator denote material time derivative and gradient of a quantity. The displacement \(\mathbf u\) of \(\mathbf X\) is defined as \({\mathbf u}{ (\mathbf X ,t)}=\chi (\mathbf X ,t)-{\mathbf X}\), where its gradient is related to \(\mathbf F\) through \({\mathbf F} ={\mathbf I }+\nabla {\mathbf u}\), being \(\mathbf I\) the second-order identity tensor. Density growth process is regulated by the rate of the density scalar field \(\rho _K\).

2.1 Balance equations

Mass and momentum balances are presented in the local form referred to the reference configuration. In the mass balance, the rate change of mass due to volumetric mass sources, neglecting mass fluxes [40, 50, 61], is given by

$$\begin{aligned} \dot{\rho }_K=\Gamma _K \end{aligned},$$
(1)

expressing the equilibrium of the rate change of mass \(\dot{\rho }_K\) with the mass source \(\Gamma _K\), being \(\rho _K\) the mass density.

The linear momentum balance balances the rate change of momentum \(\dot{\overline{\rho _K{\mathbf v} }}\) with the momentum contributions of traction, body forces, and mass source [23, 41, 44]; hence

$$\begin{aligned} {\dot{\overline{\rho _K{\mathbf v} }}}=\mathrm {Div}{}{\mathbf P} +{\mathbf b} +\Gamma _K{\mathbf v}, \end{aligned}$$
(2)

being \(\mathbf v\) the velocity, b the body force, and \(\mathbf P\) the first Piola–Kirchhoff stress tensor. \(\mathrm {Div}\) denotes the divergence of a quantity. Considering (1) in (2), the linear momentum balance gives

$$\begin{aligned} \rho _K\dot{\mathbf{v }}=\mathrm {Div}{} {\mathbf P} +{\mathbf b}.\end{aligned}$$
(3)

2.2 Density growth constitutive equations

In the mass balance of (1), the mass source term \(\Gamma _K\) has the following form [30]:

$$\begin{aligned} \Gamma _K=c\bigg ({\left[ \frac{\rho _K}{{\rho _K}^{*}}\right] }^{-m}{{\psi }_K}-{\psi _K}^{*}\bigg ), \end{aligned}$$
(4)

being \({\rho _K}^{*}\) the initial density, \({\psi _K}^{*}\) the stimulus attractor [9], considered as the energy saturation value for density evolution [61], m the bone adaptation process exponent [30], and c the adaptation process speed coefficient [40], assumed equals to unity. For a deeper insight on the stimulus attractor physical meaning, which is obtained from experimental data and assuming that bone mass is maintained for 10,000 walking cycles per day, the reader is addressed to [9].

The strain energy density form adopted is

$$\begin{aligned} {\psi _K}=\left[ \frac{\rho _K}{{\rho _K}^{*}}\right] ^{n}{{\psi }_K}^{\mathrm{neo}} \end{aligned}$$
(5)

with the relative density term \(\left[ {\rho _K}/{\rho _K}^{*}\right] ^{n}\) used for open-pored cell materials [13, 28], where n is the porosity exponent.

By neglecting tissues viscous effects for short-time scales (seconds or minutes order) and assuming that growth occurs for large time scales (weeks or months order), its constitutive response can be considered as hyperelastic [42], assuming also that density growth in hard tissues occurs at constant volume. Accordingly, the strain energy function considered is of a neo-Hookean type:

$$\begin{aligned} {\psi _K}^{\mathrm{neo}}=\left[ \frac{\lambda }{2}{\ln }^{2}{J}+\frac{\mu }{2}\left( {\mathbf F} ^{T}{}{ \mathbf F} :{\mathbf I} -3-2\ln {J}\right) \right], \end{aligned}$$
(6)

being \(\lambda\) and \(\mu\) the Lamé constants and \(\mathbf F ^{T}\) the transpose of \(\mathbf F\).

Piola–Kirchhoff stress can be obtained through the derivative of the strain energy with respect to the deformation gradient; hence, using (5) and (6):

$$ {\mathbf P} ={\frac{\partial {{\psi }_K}}{\partial {\mathbf F} }}={\left[ \frac{\rho _K}{{\rho _K}^{*}}\right] ^{n}}{\left[ (\lambda {\ln } {J}-\mu ){\mathbf F} ^{-T}+\mu {\mathbf F} \right],} $$
(7)

being \(\mathbf F ^{-T}\) the inverse of the transpose of \(\mathbf F\).

3 Governing equations and boundary conditions for density growth

The governing equations are obtained coupling the biological problem, defined through the mass balance, with the mechanical problem defined through the momentum balance. The biological problem expression is obtained using the strain energy of (5) for an hyperelastic material in the form of (6) and the mass source (4) in the mass balance (1). The mechanical problem expression is obtained using the Piola–Kirchhoff stress of (7) in the momentum balance (3). Finally, the biomechanical coupled problem results in

$$\begin{aligned} \dot{\rho }_K= & {} {\frac{1}{2}}\left[ \frac{\rho _K}{{\rho _K}^{*}}\right] ^{n-m}{\psi _K}^{\mathrm{neo}}-\psi _K^{*},\end{aligned}$$
(8)
$$\begin{aligned} {\mathbf {0}}= & {} {\mathrm {Div}}\left( \left[ \frac{\rho _K}{{\rho _K}^{*}}\right] ^{n}\left[ (\lambda {\ln } {J}-\mu {)\mathbf F} ^{-T}+\mu {\mathbf F} \right] \right), \end{aligned}$$
(9)

considering a quasi-static process and neglecting body forces.

The boundary conditions that supplement the above governing equations can be established as follows: let the body \(\mathcal {B}\) be given with loading surface tractions \(\bar{\tau }\) defined on \(\partial _{\tau }{\mathcal {B}}\), and with prescribed displacements \(\bar{\mathbf{u }}=0\) on \(\partial _{u}{\mathcal {B}}\), then, Neumann and Dirichlet boundary conditions (BC) for the mechanical problem are, respectively

$$\begin{aligned} {{\mathbf P} (\mathbf X ){\mathbf n} (\mathbf X )}={{\bar{\tau }}(\mathbf X ),}&\quad{{ \mathbf X} \in \partial _{\tau }{\mathcal {B}}} \\ {{\mathbf u} (\mathbf X )}={\bar{\mathbf{u }}(\mathbf X ),}&\quad {{\mathbf X} \in \partial _{u}{\mathcal {B}},} \end{aligned}$$
(10)

where \(\mathbf n\) is the unit normal to \(\partial _{\tau }{\mathcal {B}}\). Prescribed displacements \(\bar{\mathbf{u }}\) and prescribed tractions \(\bar{\tau }\) are given functions on \(\partial _{u}{\mathcal {B}}\) and \(\partial _{\tau }{\mathcal {B}}\) which are, respectively, complementary disjoints of \(\partial \mathcal {B}\). Within the mechanical problem is embedded the density growth boundary value problem given by the mass balance (1), with the initial condition:

$$\begin{aligned} \rho _K(\mathbf X ,0)={\rho _K}^{*}. \end{aligned}$$
(11)

4 Numerical application

To solve the theoretical model presented, we have used COMSOL Multiphysics v 4.4. The goal is to solve the incremental problem of density evolution due to the mass source \(\Gamma _K\) for an hyperelastic material, embedded into the mechanical problem, which is coupled to density through the deformation field generated in response to the applied load.

The coupled problem given by the nonlinear equations system formed by (8) and (9) was solved numerically using the solid mechanics mode for the mechanical problem given by the momentum balance (9) with the BC (10), and using the General Form PDE for the biological problem of density evolution given by (8) with the initial condition (11). The strain energy function was reprogrammed including the relative density term in the neo-Hookean hyperelastic strain energy. A function for the mass source term \(\Gamma _K\) was also implemented in the form of (4).

In the next sections will be presented two biomechanical application examples of a healthy and a prosthetic femur behavior submitted to loads. The former, without consider density growth for locating possible zones of growth and resorption, and the latter, considering density growth process based on the theory presented in the previous sections. All models were discretized with LagrangianFootnote 1 quadratic elements to interpolate displacements \(\mathbf u\) and the density \(\rho _K\). For the time discretization, a general-\(\alpha\) backward differentiation method was used [16]. The MUMPS solver was used [47], to solve the discrete system resulting from each time step discretization with residual tolerance levels of \(10^{-4}\), which is considered sufficient, since similar solutions were obtained at lower tolerance levels. In all models, plane stress condition was adopted.

5 Geometrical and finite-element models

5.1 Geometrical model

Fig. 1
figure 1

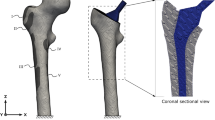
Geometrical model of HF and FP, relevant dimensions, characteristics, and main anatomical landmarks. a HF characteristics, total length, neck-shaft angle (133°), and femoral head diameter. b HF model, medullary canal diameter, and cortical wall thickness at the mid-diaphysis by medial and lateral. c FP model, prosthesis stem length, size (diameter), and head diameter. All dimensions are in millimeters

Full size image

The geometrical two-dimensional (2D) model for the healthy femur (HF) and for the femur with an implanted prosthesis (FP) is shown in Fig. 1 corresponding to a 2D slice through the HF and FP in the mid-frontal plane.

Fig. 2
figure 2

Loads, boundary conditions, and meshes for HF and FP. a Proximal part of the model domains, applied load regions for daily activity loads and abductor forces (Fab), with \({\alpha = }\) 28°. a.1 Zero displacements BC in HF and FP distal ends. a.2 Daily activity load values (x and y components) over time for 100% of one cycle for NW, US, and DS. Load function values for the three physical activities (NW, US, and DS) were taken from public database Orthoload [5], with permission. b Meshes of HF and FP proximally. b.1, b.2 Mesh details showing the coupled structure–structure model for HF and FP. The y-axis denotes the direction of an imaginary axis passing through the femoral medullary canal from distal to proximal

Full size image

Cortical and spongious tissue contours were obtained in previous works [7], and compared with femur anatomical standard dimensions of a human adult [32]. Tissue contour splines were converted to 2D surfaces to generate cortical and spongious domains.

The prosthesis is considered as a conceptual cementless type, with typical dimensions according to the specialized literature [14, 27]. It is worth to mention that cemented prosthesis conditions are not considered in this study.

The tissues and prosthesis (stem and head) geometrical domains were generated using software Solidworks version 2013 and a coupled structure–structure model was constructed using Boolean operations in COMSOL Multiphysics. Boolean operation sequence performed for the prosthetic case mimics a THA surgery, consisting in the femoral head cut (resection) followed by the prosthesis stem insertion in the medullary canal. Finally, the geometrical model obtained is adopted for the two simulation examples that will be presented in the following sections.

5.2 Example 1: finite-element model considering physical activities

First, it was implemented an FEM model without considering density growth for HF and FP, submitted to three daily physical activities normal walk (NW), going up stairs (US), and going down stairs (DS), to locate high-stress concentration zones that could be possible density growth areas. Load conditions and model meshes are shown in Fig. 2. Zero displacement BC were considered in femurs distal ends (Fig. 2a.1). Loads were applied on HF and FP heads (Fig. 2a) and the load functions were taken, with permission, from public database Orthoload [5], considering x and y components for the three load cases (Fig. 2a.2). Abductor muscle force was considered of 703 N applied on the greater trochanter [9, 39].

Cortical and spongious tissues were considered as hyperelastic, homogeneous and isotropic [18, 29, 39], and prosthesis materials, as linear elastics and isotropic, using a Titanium (Ti6Al4V) alloy and a Cobalt–Chromium (Co–Cr) alloy for the stem and the head, respectively [49, 65]; material properties are shown in Table 1. Bone density for cortical and spongious tissues was assumed as \(\rho _Kc\) = 1800 \(\mathrm {kg/{m}^{3}}\) and \(\rho _Ke\) = 600 \(\mathrm {kg/{m}^{3}}\), respectively.

The model was discretized in 27,712 elements (Fig. 2b), and solved for 118,914 degrees of freedom (DOF), after two previous mesh refinement steps until convergence was achieved. The total time for simulations was \(t_{\text {NW}}=1.103\), \(t_{\text {US}}=1.593\), and \(t_{\text {DS}}=1.439\) s, corresponding to 100% of the entire cycle of each load case [5]. The time step used was \(\Delta t=0.01\). The coupled structure–structure model, described previously, ensures stress transmission from cortical to spongious tissue for healthy condition and from prosthesis stem to cortical and spongious tissues for prosthetic condition (Fig. 2b, b.1, b.2). Bone–prosthesis interface was considered as fully bonded [8, 36].

Table 1 Material properties for cortical and spongious tissues and for prosthesis biomaterials
Full size table

6 Results and discussion

6.1 Model results considering physical activities

The interest of this work is focus in cortical bone tissue, since it is the main responsible for prosthesis stem fixation. However, some results concerning prosthesis will briefly discuss.

Results were analyzed and there were found three main critical regions, coincident in location for the three load cases. Region 1 located in medial cortical wall HF mid-diaphysis, region 2 in medial cortical wall FP mid-diaphysis, and region 3 in HF neck, as shown in Fig. 3, where it can be found the Von Mises stress distribution of analyzed load cases at times \(t_{\text {NW}}=0.55\), \(t_{\text {US}}=0.81\), and \(t_{\text {DS}}=0.8\) s, for an NW, US, and DS, respectively, where maximum stresses were attained. In addition, region 4, located in FP neck, was included in the analysis to compare critical regions for both situations, healthy and post-operative.

Fig. 3
figure 3

Von Mises stress distribution at physical activity times where maximum stresses were attained, critical regions, and stresses along medial cortical walls from proximal to distal (outer and inner cortical stresses values from point p to point d), in HF (left) and FP (right) for a, d Normal walk case (NW) at \(t=0.55\) s (the red arrows describes the displacements vector field); b, e going up stairs case (US) at \(t=0.81\) s; c, f going down stairs case (DS) at \(t=0.8\) s. Being 1, 2, 3, and 4, the critical regions. Red and blue arrows at HF medial and lateral cortical walls are only representative of compression and tension

Full size image

Higher stresses were found in HF over the medial cortical wall from mid-diaphysis to proximal for NW due to a higher bending moment when compared with US and DS, where a predominant compressive situation leads to stresses concentration in the neck (Fig. 3a–c). Also is observed that the higher stresses are located in femurs necks for the healthy condition for the three load cases (Fig. 3a–c). In contrast, in FP, the higher stresses were found in mid-diaphysis, being the most critical situation for NW, due to a higher bending moment (Fig. 3d–f). In FP neck, an unloading situation was detected proximally due to stress shielding, being critical for US activity.

There are also plotted the stresses along HF and FP medial inner and outer cortical walls (Fig. 3 right panels), from a point p located proximally in femurs necks (at lesser trochanter height) to a point d located in the mid-diaphysis. Note that the outer cortical stresses for HF shown peaks at region 3 for NW, US, and DS, then stresses remained almost constants in mid-diaphysis for NW, while decreased distally for US and DS.

Inner cortical HF stresses exhibit similar patterns for the three load cases with no significative peaks. In the FP outer cortical bone, the unloading situation is observed in region 4 for NW, US, and DS, followed by a slightly stresses increasing down to the region 2 peaks, followed by a sharply decrease distally. Inner cortical FP stresses shown the jumps due to the interfaces changes, from cortical–spongious to cortical bone–prosthesis proximally and at the stem distal tip-cortical bone (Fig. 3d–f).

As shown in Fig. 3, stresses were higher in FP medial cortical wall mid-diaphysis (region 2) than in HF analogous region for the three load cases, indicating that for a prosthetic condition, bone is significantly overloading (in about 10 MPa) in the outer cortical wall due to the higher bending moment and at inner cortical wall due to the prosthesis distal tip load transferring as previously obtained by other authors [2, 36]. We hypothesized that these critical areas (Fig. 3d–f) could be one of the causes of periprosthetic fractures that commonly occur underneath of implanted prosthesis, see, for instance, [21, 25, 26].

Regarding FP neck (region 4, Fig. 3d–f), stresses were lower (in about 17 MPa) than in the analogous HF region for the three load cases due to the unloading situation proximally (stress shielding). It was also significant that stresses over FP medial cortical wall were higher and more uniformly distributed through the cortical thickness for DS than for NW and US activities (Fig. 3d–f), suggesting that DS activity may stimulate bone in the medial cortical wall and may reduce the unloading situation in FP proximally.

Fig. 4
figure 4

Stresses and strains in HF and FP critical regions through the time for the three physical activities simulated. a–c Von Mises stress vs time of critical regions for NW, US, and DS, respectively. d–f Strains vs time of critical regions for NW, US, and DS, respectively. Intervals 10–50% NW, 15–55% US, and 50–90% DS are the higher load-level intervals determined for each physical activity

Full size image

Maximum stresses (Fig. 3) were below cortical bone compressive and tensile yield strength values (\(\sigma _{yc}\) = 115 and \(\sigma _{yt}\) = 121 MPa), without compromise bone integrity. In the prosthesis, most significative stresses were found in the neck between 70 and 97 MPa (Fig. 3d–f), in agreement with [8]. Stresses obtained were below the titanium alloy compressive and tensile yield strength (\(\sigma _{yc}\) = 970 and \(\sigma _{yt}\) = 880 MPa). Even though a fatigue analysis is required; however, fatigue is out the scope of the current work.

In addition, four probes were positioned in the regions of interest to analyze stresses and strains behavior through the time for the three load cases, as shown in Fig. 4. From the analysis of intervals: 10–50% NW, 15–55% US, and 50–90% DS, stresses were significantly higher in FP region 2 than in HF region 1 all over the referred intervals (Fig. 4a–c), confirming that bone in the mid-diaphysis is submitted to higher stress levels post-operatively (from 7 to 10 MPa overloaded), being NW activity, the most critical situation.

Regarding femoral neck, for prosthetic condition (region 4), stresses were significantly lower than for healthy condition (region 3), confirming the unloading situation (from 13 to 17 MPa less), found previously. From the strains analysis over the intervals defined above, Fig. 4d–f shows a strain increase in FP region 2 (from 130 to 274 \(\upmu \varepsilon\)) with respect to HF region 1, due to higher stress levels in the mid-diaphysis post-operatively. In FP (region 4), strains were significantly lower than for healthy condition (region 3), as a result of stress reduction (from 365 to 458 \(\upmu \varepsilon\) less). Maximum stresses and strains found in regions of interest at: 50% NW, 52% US, and 53% DS, are shown in Table 2.

Table 2 Maximum stresses and strains in HF and FP critical regions at 50\(\%\) NW, 52\(\%\) US, and 53\(\%\) DS of physical activities
Full size table

This part of the study has examined the biomechanical behavior of healthy femur and its post-operative condition after a THA surgery for three daily physical activities. From a qualitative point of view, there were found higher stresses in compressed cortical wall medially than in tensed cortical wall laterally, in agreement with [36, 62]. In addition, Von Mises stress results reproduced the typical bending stress distribution reported in the literature with maximum values located in mid-diaphysis medial cortical bone for healthy and prosthetic condition [36, 51, 62].

It is worth to mention that direct comparisons with other authors reports are often difficult, due to the load-level variability in numerical and experimental studies and also due to the material properties and the boundary conditions considered in numerical studies. However, from a quantitative point of view, Von Mises stress results shown agreement with previously results published in the literature [8, 36, 51, 62].

The Von Mises criterion was adopted as a first approximation. Despite the fact that is recommended for ductile materials, this criterion has been considered for estimate proximal femoral fracture loads and to assess hip fracture risk [20, 37]. In addition, several studies correlate Von Mises stress levels to bone mineral density for healthy and prosthetic femur [36, 55, 59].

Furthermore, strain-based criteria is suggested as sufficient to predict femoral bone behavior [37]. In this regard, a strain analysis was conducted and maximum strains obtained shown agreement with strains determined experimentally and using FEM [9, 22, 62], reporting maximum values between 1000 and 2000 \(\upmu \varepsilon\) for normal physical activities.

6.2 Example 2: density growth model

In this example, it implemented a density growth FEM model for HF and FP submitted to loads equivalent to the physical activities studied previously, following the formulation presented in Sects. 2 and 3, to predict bone density distribution, and to locate bone growth and resorption zones, for the post-operative condition.

Since total times of the physical activities studied are too small (and load values too high) for density growth process which takes place, a multiple step load type was considered [42, 61], and was applied on HF and FP heads as an average daily load, in increments of 250 N each five dimensionless units of time. To simulates an NW load level, which is the most frequent and time-consumed activity performed in daily routines, the maximum value was considered of 1850 N; moreover, a 250 N increment was added to include DS load levels (Fig. 5d).

Abductor muscle force and zero displacement BC in femurs distal ends (from previous example), and a 240 N load in \({-x}\) direction (NWx, Fig. 2a.2), were considered. Cortical and spongious tissues were treated as hyperelastic, homogeneous, and isotropic. The corresponding density variables were defined as \(\rho _Kc\) and \(\rho _Ke\) and were computed using the density evolution expression from the governing equations of Sect. 3. The corresponding mass sources \(\Gamma _Kc\) and \(\Gamma _Ke\) were implemented using the expression (4) from Sect. 2.2.

Initial density was \({\rho _K}^{*}\) = 600 \(\mathrm {kg/{m}^{3}}\) for both tissues, under homogeneous density assumption at simulation start. The stimulus attractor considered was \({\psi _K}^{*}=0.01\) MPa following [9, 39, 42] and the n and m parameter values were \(n=2\), \(m=3\) according to [39, 42, 61]. Prosthesis materials were considered according to the material properties shown in Table 1, as in the previous example. In addition, the previous example model mesh was adopted (Fig. 2b). Simulation total time was \(t=40\) dimensionless time units, and the time step for the incremental problem was \(\Delta t=0.01\).

6.2.1 Density growth model results

As in the previous example, the main interest is focus in cortical bone tissue; however, spongious bone density patterns for HF will briefly described. Figure 5a–c shows density distribution results at times \(t=15\), \(t=25\), and \(t=35\). Density distribution in HF at simulations end agrees with cortical walls and spongious bone arrange of an anatomical femur, according to [64], spongious column from the head to calcar region, and the system from lateral cortical bone to superior neck were well reproduced (Fig. 5c), see also [1, 46].

Fig. 5
figure 5

Density prediction for HF and FP, multiple step average daily load, density evolution, biological stimulus, and stresses in the regions of interest (1, 2, 3, and 4). a–c Density prediction for HF and FP at times \(t=15\), \(t=25\), and \(t=35\). At the end of simulation, cortical walls were formed in medial and lateral cortexes (in red) for HF and FP, and spongious bone areas were formed in the medullary canal (in blue) for HF. d Multiple step load \(\bar{\tau }\). First time step was divided into two sub-steps, a 100 N ramp (from \(t=0\) to 0.1) followed by a 250 N constant value (from \(t=0.1\) to 5), followed by increments of 250 N constant values. e Density evolution in the regions of interest. f Biological stimulus. g Stresses

Full size image

Ward’s triangle was reproduced well for initial simulation times while appears slightly displaced upwards at simulations end. In addition, cortical and spongious density distribution obtained agrees with previous results reported for a healthy femur [41, 42] and for post-operative femur condition after a THA [39].

An increase of density in high-stress concentration areas and a bone resorption situation associated with low-stress regions are observed in Fig. 5c, consistent with [4, 36, 39]. In addition, this phenomenon was confirmed, since significative growth and resorption regions coincide with critical stresses regions found in the previous example.

Density evolution in these regions was measured over time (Fig. 5e), exhibiting a relaxation tendency to biological equilibrium, where each load increases is followed by changes in density towards to a new equilibrium state, as obtained in [41, 42, 61]. Also is observed (in Fig. 5e), an initial resorption in regions 1 and 2 due to low-stress levels, and in region 4 due to stress-shielding effect, followed by density growth evolution in all regions, for the loading history \(\bar{\tau }\).

At simulations end, density values obtained for HF were in agreement with values reported by [3, 48]. In FP mid-diaphysis, there were found higher density values of around 1649 \(\mathrm {kg/{m}^{3}}\) in contrast with the 1615 \(\mathrm {kg/{m}^{3}}\) found in the analogous HF region, for 1850 N load (1776 and 1760 \(\mathrm {kg/{m}^{3}}\), respectively, for 2100 N), resulting from the overloading situation in the mid-diaphysis (Fig. 5e). It was expected a higher difference between the obtained density values in these regions. However, due to the complexity of the presented model, it is difficult to determine if this difference is real or if is associated with numerical uncertainties of the model without conducting a previous statistical analysis.

In FP neck, there were found lower density values of around 1118 \(\mathrm {kg/{m}^{3}}\) in contrast with the 1847 \(\mathrm {kg/{m}^{3}}\) found in the same region for HF, for 1850 N load (1259 \(\mathrm {kg/{m}^{3}}\) in contrast with 1951 \(\mathrm {kg/{m}^{3}}\) for 2100 N), confirming evidence of a significative proximal–medial bone resorption post-operatively (Fig. 5e).

In FP, as determined in the previous example, load is transferred to the stem distal tip leading to the stress-shielding phenomenon as a consequence of the mechanical system configuration. Consequently, a density growth (mass deposition) occurs at stem distal tip-cortical bone interface and a bone resorption (bone loss) take place in region 4, due to the unloading situation proximally (Fig. 5c, e), in agreement with [4, 36, 39].

Regarding biological stimulus and stress evolution, the nonlinear behavior and the relaxation behavior of these quantities towards to biological equilibrium are observed in Fig. 5f, g. Each load increase of \(\bar{\tau }\) is followed by changes in density converging to a new equilibrium state, where biological stimulus equals the attractor \({\psi _K}^{*}\), mass sources \(\Gamma _Kc\), and \(\Gamma _Ke\) vanishes and \(\rho _Kc\) and \(\rho _Ke\) undergo no further changes in cortical and spongious tissues, providing HF and FP the optimal density distributions to support the load environment simulated, in agreement with [42, 50, 61]. Note also the higher stresses values in the mid-diaphysis post-operatively compared with the same region for healthy condition, and the significative stress reduction in the neck region 4 due to the unloading situation proximally, compared with the analogous healthy region 3 (Fig. 5g). It should be highlighted that the present study was developed according to the reporting parameters and considerations for FEM studies of biological structures suggested by [24], in a consistent and reproducible manner.

Although results shown good agreement with previous contributions in the field, the proposed models have some limitations and simplifications. For instance, the two-dimensional nature of the model was chosen as a first approximation to focus the study on density growth principal effects. However, the extension to 3D is straightforward. Despite this limitation, the proposed models considering the coupling cortical–spongious, in principle, may be more accurate than models considering femur as a single domain without geometrical distinction between cortical and spongious tissues, as assumed by other authors.

Concerning abductor force simulated, it suggested the inclusion of muscles such as Illio-tibial band and Illiopsoas to attained maximal physiological relevance [22]. However, remains controversially whether muscle force must be taken into account when testing implants fixations [6]. In addition, there were considered proximal and distal parts of the femur with zero displacement BC at distal ends (lateral and medial condyles), which may also be, in principle, more accurate, realistic, and physiologically acceptable than considering only the proximal femur fixed at the mid-diaphysis, as commonly treated in the literature.

Regarding prosthesis, in the case of the anchorage stem system, which makes differences in load transfer, certainly exist several prosthesis designs in the market. However, for a 150 mm stem length of THA implant considered, no substantial geometrical variations exist among prosthesis design models [14, 27]. On the other hand, we only consider a cementless prosthesis type in this study. For a cemented case, a geometrical domain and material properties corresponding to a cement mantle between the bone and the stem surface would need to be included in the model. In addition, other phenomena such as adhesion would also need to be included. These issues will be the subject of a future research.

Homogeneous and isotropic considerations for bone tissues were adopted in a preliminary research stage. Despite this considerations are commonly assumed in hip replacements behavior studies [8, 15, 39], transversally isotropic or orthotropic bone properties can be introduced without additional complexities.

The density growth model implemented is only valid for multiple step load cases, since computational time is not related to real physical time, and density saturation for the average daily load chosen could be considered as a bone density stable condition reached by the femur for long term from a clinical point of view, as indicated in [4]. Therefore, further studies considering the cyclic nature of daily physical activities must be conducted, especially focusing on the constitutive law for the mass source. Regarding density distribution results for healthy and prosthetic condition, and despite the agreement with previous studies reported, a qualitative–quantitative validation through a direct comparison with several patient-specific medical images is also required. Therefore, the extension to the 3D model, the inclusion of additional physiological muscle forces and boundary conditions in the analysis although with a comparison with clinical cases and considering the cyclic character of daily physical activities in the density growth model are among the issues to developed in our research for future works.

7 Conclusions

A density growth model for bone tissues based on a continuum theory for biological growth and remodeling processes was presented in this work and was implemented in an FEM software to simulate bone density behavior in a healthy and a prosthetic femur due to mechanical loads.

In the model considering daily physical activities, results shown that for post-operative condition:

  1. 1.

    Bone in the mid-diaphysis is significantly overloading, situation that may lead eventually to periprosthetic fractures being more critical for a normal walk activity.

  2. 2.

    Going down stair activity is suggested to stimulate bone density growth and to reduce the unloading situation detected proximally in the medial cortical wall.

Regarding the density growth model, for healthy condition, results agree with real bone morphology and density distribution in the proximal femur. For the prosthetic femur condition:

  1. 1.

    A densification was localized in the mid-diaphysis medially due to the overloading situation generated by the stem distal tip load transmission.

  2. 2.

    A significative resorption was localized in the proximal–medial region due to stress shielding which may lead to the aseptic loosening of the implant.

Comparison of qualitative and quantitative results obtained with previous results reported by other authors was conducted showing good agreement. Therefore, from the clinical point of view, results obtained may help in the study of physiotherapy treatments, to reduce the risk of periprosthetic fractures and to achieve adequate physiological density levels during the recovery phase after surgery as well as for long term.

Finally, the implemented bone density growth model combined with the evolutive model for daily physical activities loads presented represents a potentially computational assessment tool for orthopedic surgeons. In addition, the proposed tool can be useful to identify possible zones of periprosthetic fractures and to detect zones of bone density growth and resorption due to mechanical loads, for the healthy femur and its post-operative condition after a THA procedure.