1 Introduction

As the core factor in the cold rolling process, the accurate prediction of rolling force is necessary for the increasing demands on the high-quality products. Rolling force has a significant influence on the final thickness accuracy and flatness quality of the cold rolled product [1, 2]. It is necessary to establish a high accuracy method to predict the rolling force parameters, but the non-linear nature of the cold rolling, mechanical and material phenomena make the process difficult to formulate and solve.

Until now, many attempts have been proposed to study the metal flow and to predict the required rolling force in cold rolling process. Many existing traditional rolling force models are based on the theoretical works of Karman [3], who developed the basis of rolling theory, and the equilibrium relationship equation in the micro unit was obtained by the differential equation under a certain assumption. Orowan [4] developed the differential equations of calculating unit rolling pressure based on the slab method in another stress distribution assumption. Tselikov [5] found a solution of Karman’s differential equation, the influence of the backward and forward tension stresses were taken into consideration, in his assumptions the contact arc was substituted by chord. Another analytical model of rolling force was derived by Bland-Ford [6], who avoided most of the numerical integration in Orowan’s theory. On the basis of Bland-Ford’s study, Hill [7] gave the general relation between the rolling force and the required energy in the deformation region. In Stone’s research [8], the effects of strip tension were considered based on the simplified slab analysis of deformation region, and his results became the most widely used solution of rolling force in the industrial application.

FEM (Finite Element Method) is another way to study complex deformation. Several researchers established different FEM models to analyze cold rolling process, Abdelkhales et al. [9], Nakhoul et al. [10] and Nielsen et al. [11] established viscoplastic models, and Jiang et al. [12], Zhang et al. [13] and Mei et al. [14] proposed rigid-plastic models, LEE et al. [15] and Poursian et al. [16] used the elastic–plastic models to investigate the cold rolling process. But the large computation time and huge memory capacity during calculation are the disadvantages of the FEM model, especially for personal computers [17]. ANN (Artificial Neural Networks) models had also been widely used in the control system due to their unique model structure and the inherent ability of non-linear simulation, as well as the high degree of adaptive and fault tolerance characteristics. Researchers developed BP method [18], Bayesian method [19], RBF method [20], adaptive neural method [21] and predictive network [22] to predict the cold rolling force, and Gudur et al. [23] proposed a neutral network-assisted finite model for the simulation analysis of cold rolling process. Whereas, for ANN models, the massive training data is necessary for the offline simulation, the data defects reflected for changed rolling status, in which the calculation accuracy was not always guaranteed.

Because of the high speed in obtaining the analytical solution, the upper bound method was widely used in the metal deformation process [24]. Sezek et al. [25] derived dual-stream function velocity field to analyze cold and hot plate rolling, the rigid plastic boundary of the inlet zone and spread function were both assumed in quadratic form, the required optimum rolling force and final shape from the upper bound analysis show good agreement with the experimental results. Sun et al. [26] proposed a hyperbolic sine velocity field to calculate the rolling force, and the ID yield criterion was applied to obtain the internal plastic deformation power, the online measured data was used to verify the validity of his model. An admissible velocity field of non-bonded sandwich rolling process was developed by Haghighat et al. [27], in his study, the rolling force, mean contract pressure and the final thickness of each layer were determined by the upper bound analysis.

In this paper, to obtain the analytical solution of rolling force and stress state coefficient in cold rolling process, the cylindrical velocity field and strain rate fields are proposed, and then analytical solution of rolling force is obtained by minimizing the total power. Meanwhile, the effect of frictional factor, reduction ratio and the backward or forward tense on location of neutral point and stress state coefficient are discussed, respectively. Also, the calculated results obtained by the proposed model are compared with experimental measured data and other researchers’ models.

2 Rolling process

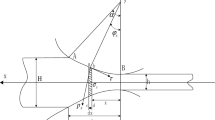
The materials starts with initial thickness h 0, and then rolled through a pair of cylindrical work rolls with roll radius R, the thickness is reduced to h 1, as shown in Fig. 1. Three regions (I, II and III) were divided by the cylindrical velocity discontinuity surfaces, S 1 and S 2. The surface S 1 was the surface jointed by the entrance contract point, and the surface S 2 was joined by the cores of the two work rolls, it was not a velocity discontinuity only because the curvature radius of the section was infinite. The axes r, θ, z of cylindrical coordinate system are chosen to describe the deformation zone. The axis z represents the width direction.

Fig. 1
figure 1

Definition sketch of the deformation region

Full size image

To simplify the calculation through the upper bound analysis, the following assumptions are employed [27]: (1) the work roll is rigid materials; (2) the sheet is symmetric on both the materials and the thickness about symmetry axis; (3) the sheets are rigid plastic materials; (4) the deformation of the sheet is plane strain, only because the change in width during was negligible during the cold rolling process; (5) the frictional factor in the surface was constant.

In the mentioned assumptions, the whole sheet was taken as rigid plastic material, the regions I and III were un-deformation regions. But in fact, in regions outside the plastic deformation zone II, the elastic deformation zone exists in regions I and III, from with Jiang’s research [28], the contribution of the rolling force in these parts was less than 3% in the total rolling force, so the assumptions of “materials are taken as rigid and moves as rigid bodies” in this study was acceptable.

The region I and III are the un-deformation regions, and in the region II, the connection line of the symmetry points in the upper and down roll were the series of arc with different curvature radius with the origins o. The materials move at speed v 0 before entering the deformation zone, and after rolling it moves at speed v 1. The cylindrical coordinate system with origins o is used to describe the positions of the velocity discontinuity surfaces, contract surface, interface and the velocity components in deformation region.

Thickness in the deformation region with angle α can be expressed as:

$$h_{\alpha } = h_{1} + 2R(1 - \cos \alpha )\;\;\;\alpha \in \left( {0,\theta } \right)$$
(1)

where α was angle between the surface tangent and the horizontal axis.

The maximum contact angle θ satisfies

$$h_{0} = h_{ 1} + 2R\left( { 1 - { \cos } \theta } \right),\theta = { \arcsin } \left( {l/R} \right) .$$
(2)

3 Upper bound analysis

3.1 Cylindrical velocity field

For cold rolling process, the shape factor of strip was b/h m  ≫ 10, so the width b can be taken as a constant value, it is assumed that there was no width spread, so the z direction was the non-deforming direction, and v z  = v θ  = 0. Because of the volume constancy, the following relation holds.

$$vh = v_{0} h_{0} = v_{1} h_{1} = v_{n} h_{n} = \dot{v}h_{n} ,$$
(3)

where h n was the thickness on the neutral, and the \(\dot{v}\) was the circumferential velocity.

From Eq. (1) and (3), the thickness in the neutral surface was:

$$h_{n} = h_{1} + 2R(1 - \cos \alpha_{n} ) .$$
(4)

So the velocity on each connection surface with the angle α can be described as:

$$\left\{ \begin{aligned} v_{r} = \frac{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( {\alpha_{n} } \right)}}{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( \alpha \right)}}\dot{v} = \frac{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( {\alpha_{n} } \right)}}{2\alpha r}\dot{v} \hfill \\ v_{\theta } = 0 \hfill \\ v_{z} = 0 \hfill \\ \end{aligned} \right. .$$
(5)

For the cold rolling process the θ is too small, so the arc length equals to the length of the chord approximately

$$S = 2s = 2\alpha r \approx h = h_{1} + 2R\left[ {1 - \cos \left( \alpha \right)} \right] .$$
(6)

For the arc in the deformation region, it satisfy the following conditions, the direction of v r and r are opposite, so the

$$ \left\{ \begin{aligned} \dot{\varepsilon }_{rr} &= - \frac{{\partial v_{r} }}{\partial r} = \left[ {\frac{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( {\alpha_{n} } \right)}}{{2\alpha r^{2} }}} \right]\\ \dot{v} &= \frac{1}{r}\left[ {\frac{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( {\alpha_{n} } \right)}}{2\alpha r}} \right]\\ \dot{v} &= \frac{2\sin \left( \alpha \right)}{S}\left[ {\frac{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( {\alpha_{n} } \right)}}{2\alpha r}} \right]\dot{v} \hfill \\ \dot{\varepsilon }_{\theta \theta } &= \frac{{v_{r} }}{r} + \frac{1}{r}\frac{{\partial v_{\theta } }}{\partial \theta } = - \frac{1}{r}\left[ {\frac{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( {\alpha_{n} } \right)}}{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( \alpha \right)}}} \right]\\ \dot{v} &= - \frac{2\sin \left( \alpha \right)}{S}\left[ {\frac{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( {\alpha_{n} } \right)}}{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( \alpha \right)}}} \right]\dot{v} \dot{\varepsilon }_{r\theta } = \dot{\varepsilon }_{zr} = \dot{\varepsilon }_{\theta z} = \dot{\varepsilon }_{zz} = 0 \hfill \\ \end{aligned} \right. . $$
(7)

Due to α ≤ θ, α ≤ 1, sinα ≈ α, so the velocity in the entry and delivery side were

$$\left\{ \begin{aligned} \left. {v_{r} } \right|_{\alpha = 0} = \frac{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( {\alpha_{n} } \right)}}{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}}}}\dot{v} = \frac{{h_{1} + 2R\left( {1 - \cos \left( {\alpha_{n} } \right)} \right)}}{{h_{1} }}\dot{v} = \frac{{h_{n} \dot{v}}}{{h_{1} }} = v_{1} \hfill \\ \left. {v_{r} } \right|_{\alpha = \theta } = \frac{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( {\alpha_{n} } \right)}}{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right) + 1 - \cos \left( \theta \right)}}} \right. \kern-0pt} {\left( {2R} \right) + 1 - \cos \left( \theta \right)}}}}\dot{v} = \frac{{h_{1} + 2R\left( {1 - \cos \left( {\alpha_{n} } \right)} \right)}}{{h_{1} + 2R\left( {1 - \cos \left( \theta \right)} \right)}}\dot{v} = \frac{{h_{n} \dot{v}}}{{h_{0} }} = v_{0} \hfill \\ \end{aligned} \right. .$$
(8)

Equations (7) and (8) show that the velocity field expressed in Eq. (5) satisfies the velocity boundary conditions and the geometric equations, so the velocity field is the kinematically admissible velocity and strain rate field.

3.2 Internal plastic deformation power

The internal plastic deformation power is:

$$\dot{W}_{i} = \frac{{2\sigma_{\text{s}} }}{\sqrt 3 }\int_{V} {\sqrt {\dot{\varepsilon }_{rr}^{2} + \dot{\varepsilon }_{r\theta }^{2} } {\text{d}}V} = \frac{{2\sigma_{\text{s}} }}{\sqrt 3 }\int_{0}^{\theta } {\sqrt 2 \dot{\varepsilon }_{rr} } RS{\text{d}}\alpha = \frac{{2\sigma_{\text{s}} \dot{v}h_{1} }}{\sqrt 3 }\left[ {1 + \frac{{2R\left( {1 - \cos \left( {\alpha_{n} } \right)} \right)}}{{h_{1} }}} \right]\ln \frac{{h_{0} }}{{h_{1} }} .$$
(9)

3.3 Frictional power

The relative sliding velocity in the contact surface can be expressed as follows:

$$\Delta v_{f} = v - \dot{v} = \frac{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( {\alpha_{n} } \right)}}{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( \alpha \right)}}\dot{v} - \dot{v} .$$
(10)

The frictional force of the contact surface was τ f  = mk, so the frictional power loss per unit width of sheet along contact surface can be determined as:

$$\begin{aligned} \dot{W}_{f} = 2\int_{s} {\tau_{f} \left| {\Delta v_{f} } \right|{\text{d}}s} = \frac{{2m\sigma_{\text{s}} }}{\sqrt 3 }\int_{s} {\left| {\Delta v_{f} } \right|{\text{d}}s} \hfill \\ \quad \;\, = \frac{{2m\sigma_{\text{s}} }}{\sqrt 3 }\left\{ {\int_{0}^{{\alpha_{n} }} {\left[ {\frac{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( {\alpha_{n} } \right)}}{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( \alpha \right)}}\dot{v} - \dot{v}} \right]R{\text{d}}\alpha } + \int_{{\alpha_{n} }}^{\theta } {\left[ {\dot{v} - \frac{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( {\alpha_{n} } \right)}}{{{{h_{1} } \mathord{\left/ {\vphantom {{h_{1} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}} + 1 - \cos \left( \alpha \right)}}\dot{v}} \right]R{\text{d}}\alpha } } \right\} \hfill \\ \quad \;\, = \frac{{2Rm\sigma_{\text{s}} \dot{v}}}{\sqrt 3 }\left\{ {\frac{{b - \cos \left( {\alpha_{n} } \right)}}{{\sqrt {b^{2} - 1} }}\left[ {2{ \arctan }\frac{{\sqrt {b^{2} - 1} \sin \left( {\alpha_{n} } \right)}}{{b\cos \left( {\alpha_{n} } \right) - 1}} - { \arctan }\frac{{\sqrt {b^{2} - 1} \sin \left( \theta \right)}}{b\cos \left( \theta \right) - 1}} \right] + \left( {\theta - 2\alpha_{n} } \right)} \right\} \hfill \\ \end{aligned}$$
(11)

where b = h 1/2R + 1.

3.4 Shear power

There was no shear power loss in exit section, according the geometry relation ds = 2R sinαdα, Δv t  = v 0 sinα, the equation for the power loss along the shear surface was:

$$\dot{W}_{s} = \int_{s} {\Delta v_{t} k{\text{d}}s} = 2Rkv_{0} \int_{s} {\sin^{2} \alpha {\text{d}}\alpha } = 4Rkv_{0} \int_{0}^{\theta } {\sin^{2} \alpha {\text{d}}\alpha } = 4Rkv_{0} \left. {\left[ {\frac{\alpha }{2} - \frac{1}{4}\sin \left( {2\alpha } \right)} \right]} \right|_{0}^{\theta } = 2Rkv_{0} \left[ {\theta - \sin \left( \theta \right)\cos \left( \theta \right)} \right] .$$
(12)

3.5 Tense power

To reduce the rolling force and the power consumption and enhance the flatness quality, the backward tense and forward tense were applied during the rolling process, the tense power can be described as:

$$\dot{W}_{t} = 4\left( {\sigma_{\text{b}} h_{0} v_{0} - \sigma_{f} h_{1} v_{1} } \right) = 4\dot{v}h_{n} \left( {\sigma_{\text{b}} - \sigma_{f} } \right) = 4\dot{v}\left[ {h_{1} + 2R - 2R\cos \left( {\alpha_{n} } \right)} \right]\left( {\sigma_{\text{b}} - \sigma_{f} } \right) .$$
(13)

3.6 Total power

Substituting Eq. (9), Eqs. (10)–(13) into the total power function \(J^{*} = \dot{W}_{i} + \dot{W}_{f} + \dot{W}_{s} + \dot{W}_{t}\), the solution of the total deformation power function can be received according to the first variation principle of rigid plastic material.

$$\begin{aligned} J^{*} = \dot{W}_{i} + \dot{W}_{f} + \dot{W}_{s} + \dot{W}_{t} \hfill \\ \;\;\; = \frac{{2\sigma_{\text{s}} \dot{v}h_{1} }}{\sqrt 3 }\left[ {1 + \frac{{2R\left( {1 - \cos \alpha_{n} } \right)}}{{h_{1} }}} \right]\ln \frac{{h_{0} }}{{h_{1} }} + 2Rkv_{0} \left[ {\theta - \sin \left( \theta \right)\cos \left( \theta \right)} \right] + 4\dot{v}\left[ {h_{1} + 2R - 2R\cos \left( {\alpha_{n} } \right)} \right]\left( {\sigma_{\text{b}} - \sigma_{f} } \right) \hfill \\ \;\;\;\;\;\; + \frac{{2Rm\sigma_{\text{s}} \dot{v}}}{\sqrt 3 }\left\{ {\frac{{b - \cos \left( {\alpha_{n} } \right)}}{{\sqrt {b^{2} - 1} }}\left[ {2{ \arctan }\frac{{\sqrt {b^{2} - 1} \sin \left( {\alpha_{n} } \right)}}{{b\cos \left( {\alpha_{n} } \right) - 1}} - { \arctan }\frac{{\sqrt {b^{2} - 1} \sin \left( \theta \right)}}{b\cos \left( \theta \right) - 1}} \right] + \left( {\theta - 2\alpha_{n} } \right)} \right\} \hfill \\ \end{aligned} .$$
(14)

Differentiating the total power with respect to the arbitrary variable α n and making the result set equal to zero, the following equation can be obtained.

$$\frac{{{\text{d}}J^{ * } }}{{{\text{d}}\alpha_{n} }} = \frac{{{\text{d}}\dot{W}_{i} }}{{{\text{d}}\alpha_{n} }} + \frac{{{\text{d}}\dot{W}_{f} }}{{{\text{d}}\alpha_{n} }} + \frac{{{\text{d}}\dot{W}_{s} }}{{{\text{d}}\alpha_{n} }} + \frac{{{\text{d}}\dot{W}_{t} }}{{{\text{d}}\alpha_{n} }} = 0 ,$$
(15)

where \(\left\{ \begin{aligned} \frac{{{\text{d}}\dot{W}_{i} \,}}{{{\text{d}}\alpha_{n} }} = \frac{{4R\sigma_{\text{s}} \dot{v}}}{\sqrt 3 }\ln \frac{{h_{0} }}{{h_{1} }}\sin \left( {\alpha_{n} } \right) \hfill \\ \frac{{{\text{d}}\dot{W}_{f} }}{{{\text{d}}\alpha_{n} }} = \frac{{2Rm\sigma_{\text{s}} \dot{v}}}{\sqrt 3 }\left\{ {\frac{{\sin \left( {\alpha_{n} } \right)}}{{\sqrt {b^{2} - 1} }}\left[ {2\arctan \frac{{\sqrt {b^{2} - 1} \sin \left( {\alpha_{n} } \right)}}{{b\cos \left( {\alpha_{n} } \right) - 1}} - \arctan \frac{{\sqrt {b^{2} - 1} \sin \left( \theta \right)}}{b\cos \left( \theta \right) - 1}} \right]} \right\} \hfill \\ \frac{{{\text{d}}\dot{W}_{s} }}{{{\text{d}}\alpha_{n} }} = 0 \hfill \\ \frac{{{\text{d}}\dot{W}_{t} }}{{{\text{d}}\alpha_{n} }} = 8\left( {\sigma_{\text{b}} - \sigma_{f} } \right)R\dot{v}\sin \left( {\alpha_{n} } \right) \hfill \\ \end{aligned} \right. .\)

The α n in different production conditions can be obtained, then the corresponding minimum rolling torque M min, rolling force P min the stress state coefficient n σ can be determined, respectively.

$$M_{ \rm{min} } = \frac{{RJ_{\rm{min} }^{*} }}{{2\nu_{R} }}, P_{ \rm{min} } = \frac{{M_{\rm{min} } }}{\lambda \cdot l}, n_{\sigma } = \frac{{P_{ \rm{min} } }}{4 \cdot w \cdot l \cdot k} ,$$
(16)

where λ is the arm factor.

From the solution of Eq. (15), we also obtained the relationship between the frictional factor m and the neutral angle α n

$$m = \frac{{2\sqrt {b^{2} - 1} \left[ {\ln \frac{{h_{0} }}{{h_{1} }} + 4\sqrt 3 \left( {\frac{{\sigma_{b} - \sigma_{f} }}{{\sigma_{s} }}} \right)} \right]}}{{\arctan \frac{{\sqrt {b^{2} - 1} \sin \left( \theta \right)}}{b\cos \left( \theta \right) - 1} - 2\arctan \frac{{\sqrt {b^{2} - 1} \sin \left( {\alpha_{n} } \right)}}{{b\cos \left( {\alpha_{n} } \right) - 1}}}} .$$
(17)

4 Results and discussion

A Microsoft Visual Studio program has been implemented to realize the calculation process of the mentioned equations, and the flow chart is given in Fig. 2.

Fig. 2
figure 2

Flow chart of the calculation process

Full size image

The bite angle was divided into 500 parts, it was small enough to describe the deformation zone, and the increasing step of the reduction ratio was 0.05 and the step of the frictional factor was 0.02 in the range, both are typically used in simulations.

The mechanical properties and the material parameters were initialized first, then the process of finding the optimal solution was finished with a series of cyclic iterative process, in which the frictional factor, the thickness reduction ratio and initial angle were included, then the required minimal total power, the rolling force and neutral point position were obtained. The following analysis was based on the calculation results.

4.1 Rolling force and power

Figure 3 shows the trend of the total power during the search of the minimum power for different frictional factor. It is shown that for the same frictional factor, the total power changes with the change of neutral angle, also the minimum of total power increases when the frictional factor increases. In other words, the required rolling force increases with increasing of the frictional factor.

Fig. 3
figure 3

Variation of total power with the neutral angle change (ɛ = 0.3)

Full size image

Figure 4 displays the proportion of each power in total power as the reduction ratio changed (m = 0.07). While the backward and forward tense stress are constant, as the reduction ratio increases, the proportion of shear power and the tense power were in a small value, the inter deformation power contributes the main proportion, which was always in a high level, and the proportion of friction power increased as the reduction ratio increasing, because the sheet used in the present paper satisfies l/h m  ≥ 1.

Fig. 4
figure 4

The proportion of each power in total power as the reduction ratio changed (m = 0.07)

Full size image

4.2 Impact of m, ɛ and σ b , σ f on the position of neutral angle

The neutral angle position (described by α n /θ) is a key parameter in the deformation zone. The following sections show the change of the location of neutral point α n /θ with the influenced factors (frictional factor m, reduction ratio ɛ and the tense stress).

Figure 5 shows the location of neutral point α n /θ is a function of the reduction ratio and the frictional factor, it shows that the neutral point moves toward the exit side when m decreases or ε increases, it means the forward slip decreases as m decreases or ε increases.

Fig. 5
figure 5

Effect of frictional factor m and reduction ε on the location of neutral point α n /θ

Full size image

Figure 6a, b illustrate the effect of backward and forward tension stresses on the location of neutral point α n /θ. As the σ b /σ s increases, the location of the neutral point moves toward the exit side, also the same trend occurs while σ f /σ s decreases. And we also found that, with the increasing of the reduction ratio, the impact of tense on the position of the neutral point was linear approximately.

Fig. 6
figure 6

a Effect of tense on the position of the neutral point α n /θ (ɛ = 0.25). b Effect of tense on the position of the neutral point α n /θ (ɛ = 0.3)

Full size image

4.3 Impact of m, ɛ and σ b , σ f on stress state coefficient

The stress state coefficient n σ is another key factor to describe the rolling status. The following sections show the relationship between the stress state coefficient n σ and the influenced factors (frictional factor m, reduction ratio ɛ and the tense stress).

Figure 7 illustrates that stress state coefficient n σ is a function of the frictional factor m and reduction ratio ε. It can be seen that n σ increases linearly as ε or m increases. The obtained results are compared to the traditional model as KopoaeB’s, Stones, Hill’s and Tselikov’s results, as shown in Fig. 8, it shows that the stress state coefficient obtained by the proposed model are in a good agreement, the maximum error was less than 6.1%.

Fig. 7
figure 7

Effect of frictional factor m and reduction ratio ε on stress state coefficient n σ

Full size image
Fig. 8
figure 8

Compare between the proposed and traditional models in stress state coefficient n σ

Full size image

Figure 9 shows the impact of the backward and forward tension on the stress state coefficient. It can be seen that n σ decreases linearly as σ b /σ s or σ f /σ s increases. Because with the increasing of the backward or forward tension stress, the value of deformation resistance of the strip decreases in a linearly way, which make the rolling force decreases.

Fig. 9
figure 9

Effect of tense stress on stress state coefficient n σ

Full size image

5 Application

5.1 Experimental work

To verify the validity of the analytical model proposed in this paper, the results obtained from Eq. (16) are compared with the actual experimental data. A series of experiments has been carried out by an experimental four-high reversing cold mill,as shown in Fig. 10. The experimental slabs (initial size: 1.35 mm × 150 mm)rolled through the pair of work rolls (Ø165 mm) with the maximum circumferential velocity in 1200 m/min, the thickness were measured by the thickness gauge in the entrance and delivery sides, the strip speed was measured by the laser speed gauge, and the rolling force were measured by the pressure sensor.

Fig. 10
figure 10

Structure of experimental four-high reversing cold mill

Full size image

The experimental material used in the experiments is SPCC steel, and the strip is reduced from 1.35 mm to 0.17 mm in five pass. The roll rolling schedule of each pass in shown in Table 1.

Table 1 Rolling schedule (h = 0.17 mm)
Full size table

The regression model of deformation resistance for the SPCC was described in Eq. (18), the regression coefficient was shown in Table 2.

$$\sigma = \left( {a_{0} + a_{1} \dot{\varepsilon }_{\sum } } \right)\left( {1 - a_{3} e^{{a_{4} \dot{\varepsilon }_{\sum } }} } \right) ,$$
(18)

where \(\dot{\varepsilon }_{\sum }\) was the cumulative reduction ratio, \(\dot{\varepsilon }_{\sum } = \frac{1}{3}\left( {\frac{{H_{0} - h_{0} }}{{H_{0} }}} \right) + \frac{2}{3}\left( {\frac{{H_{0} - h_{1} }}{{H_{0} }}} \right) .\)

Table 2 Regression coefficient of the SPCC deformation resistance model
Full size table

Taking into account the influence of backward and the forward tension, the deformation resistance is expressed further:

$$\sigma_{s} = \sigma - \left[ {\left( {1 - \beta } \right)\sigma_{b} + \beta \sigma_{f} } \right] ,$$
(19)

where β was the tense influence coefficient, β = 0.3 for cold rolling [29].

The sheet rolled in five passes based on the schedule in Tabel 1, and the actual rolling force data was collected and compared with the proposed model and the traditional models(e.g. KopoaeB’s, Hill’s and Stone’s models). All the calculated results was obtained offline.

Figure 11 shows the comparison results of the actual and the predicted rolling force, it can be seen that the proposed model and Hill’s models were in a better agreement with the actual ones, and the maximum error was less than 5.2%, meanwhile, the predicted error of KopoaeB’s and Stone’s result were about 7.0 and 9.3%. The average error and the variance were shown in Table 3, though the average error of the proposed model was higher than Hill’s model, the smaller variance showed a better stability.

Fig. 11
figure 11

Comparison of the rolling force between the proposed model actual and measured

Full size image
Table 3 The statistics of the model error in each pass
Full size table

It should be pointed out that, comparing to Hill’s model, the predicted precision in each pass were a little bigger than the actual ones in each pass, that is because the proposed method was based the upper bound method.

5.2 Industrial work

To check the accuracy of rolling force model, the calculation process has been programed and applied in the control system of one 1450 mm cold tandem mill in a domestic factory of Tangshan. The slabs were reduced from 1.8–4.0 mm to 0.18–0.5 mm, and the diameter of the work roll was 400.0 mm. Figure 12 shows the mill layout and instrument arrangement.

Fig. 12
figure 12

The 1450 mm cold tandem mill layout and instrument arrangement

Full size image

During the rolling process, the roll linear velocity is measured by the velocity sensor, and the thickness is given by the X-ray thickness gauge, the rolling force is given by the pressure sensor located over the bearing blocks of the top work roll, the strips velocity was measured by the laser speed gauge.

The frictional factor used in the experiment from the following equation [30]:

$$m = \left( {m_{0} + m_{v} + m_{r} } \right)\left( {1 + m_{w} } \right)\left( {1 + m_{\varepsilon } } \right) ,$$
(20)

where m 0 is basic value of frictional factor; m v is speed influence factor of friction; m r is roughness influence factor of friction, m w is the wear influence factor of friction; m ɛ is the reduction influence factor of friction.

The influence of work roll elastic deformation should not be ignored, so the Hitchcock’s flattening radius formula [31] should be taken into the consideration in the iteration process in Fig. 2, as:

$$R^{'} = R\left( {1 + \frac{{16(1 - \nu^{2} )}}{\pi E} \cdot \frac{F}{w\Delta h}} \right) .$$
(21)

When the roll radius deviation between two iteration calculations was smaller than the convergence value (less than 0.01%), the iteration finished. The flow chart was shown in Fig. 13.

Fig. 13
figure 13

Flow chart of the iteration process

Full size image

More than 1500 records were collected, and the comparison between the proposed model and measured ones were shown in Fig. 14.

Fig. 14
figure 14

Comparison rolling force predicted by proposed model with measured results

Full size image

Compared with the industrial actual data, the rolling force predicted by the proposed model shows a good agreement with the actual measured ones. Also we found that the proportion (predicted results greater than the actual measured ones) is about 60%, that because the method we used to calculate the rolling force was based on the upper bound analysis. The data deviation distribution histogram is given in Fig. 15, data analysis results shows that and the deviation proportion in the range of ±5.0% was 77.2%, the proportion in the range of ±10.0% reached 97.3%, the results shows that the accuracy was high, and the effectiveness of the proposed model was verified further.

Fig. 15
figure 15

Deviation distribution histogram

Full size image

The time required for the model calculation was less than 1.0 s; it means that the proposed model meets the requirement of the online control process control system of the cold rolling.

6 Conclusion

  1. 1.

    The cylindrical coordinate velocity field and the corresponding strain rate field are applied to the upper bound analysis of the cold rolling process, and the analytical solutions of rolling force and the stress state coefficient are obtained.

  2. 2.

    The neutral point moves toward the exit side while the σ b /σ s or reduction ratio ε increases, also the similar trend occurred while frictional factor m or σ f /σ s decreases. The stress state coefficient tension stress n σ decreases while the σ b /σ s or σ f /σ s increases, and the opposite trend occurred while frictional factor m and reduction ratio ε increases.

  3. 3.

    The application results from the experimental mill and the industrial plant show that the prediction precision of the proposed model was in a high level, meanwhile, the calculation speed and accuracy can meet the requirement of the process control system of the cold rolled sheet.