1 Introduction

Functionally graded materials are one of the novel class of materials whose thermo-mechanical properties vary smoothly in one or more directions based on a position-dependent function. Analysis of solid structures such as beams, plates and shells made of FGMs have attracted increasing attention due to the interesting behaviour of FG solids. A number of wealth investigations are observed through the open literature on static and dynamic analysis of circular, annular and sectorial plates. Among them, Nie and Zhong [1] developed a semi-analytical approach to treat the symmetrical bending of functionally graded annular and circular plates. Two directional FG plates whose properties vary continuously according to an exponential function in radial and thickness directions are assumed in their work. After presenting two coupled elasticity equations, a state space method in thickness direction combined with DQM technique along radial axis is used to discrete the governing equations. A modification of [1] is reported in [2] to the free vibration problem of annular plates including multi-directional non-homogeneity. First-order theory-based formulation to analyse the non-linear symmetric and asymmetric behaviour of circular FG plates is reported by Noseir and Fallah [3]. A perturbation solution in conjunction with circumferential Fourier expansion is developed to overcome the highly non-linear equilibrium equations. Reddy et al. [4] presented explicit closed-form expressions to study both thin and moderately thick annular and circular FG plates subjected to axisymmetric loading. Axisymmetric bending of thick functionally graded circular plates based on a third-order shear deformation plate theory is reported by Saidi et al. [5]. Their study covers various types of boundary conditions for outer edge of the plate and closed-form expressions are obtained for stress, deflection and moment distribution through the plate. Sahraee and Saidi [6] examined the bending and stretching of thick FG plates subjected to uniform transverse mechanical loading. Based on a fourth-order shear deformable plates theory, four coupled ordinary differential equations are established. For the case when properties are graded across the thickness, stretching–bending coupling exists through the formulation. Noseir and Fallah [7] proposed a reformulation for FGM plates in polar coordinates in which five highly coupled equilibrium equations are decoupled and represented in terms on two new PDEs known as edge zone and interior zone functions. Free vibration of annular FG plates based on the moderately thick plate theory is done by Hosseini Hashemi et al. [8]. After deriving five highly coupled partially differential equations, and employing the decoupling method proposed by Noseir an Fallah [7], closed-form explicit expressions to cover the natural frequencies of various types of FG plates covering possible combinations of free, clamped, soft and hard simply supported edges for inner and outer boundaries of the plate are presented. Assuming exponentially distributed mechanical properties for FG plates, Dong [9] investigated three-dimensional free vibration of annular FG plates via a Ritz method, where displacements are chosen as a proper sets of Chebyshev polynomials. Aghdam et al. [10] investigated the implementation of Extended Kantorovich Method (EKM) in static analysis of sectorial FG plates. Their study is limited to fully clamped plates subjected to uniformly distributed lateral mechanical loading. A polynomial Ritz-based eigenvalue analysis is performed by Tajeddini et al. [11] to study the vibration problem of annular and circular plates made of FGMs. A finite elements-based formulation is developed by Afsar and Go [12] to analyse the thermoelastic bending response of rotating FGM annular disks with radial heterogeneity.

Prediction of the bifurcation point of the solid structures subjected to in-plane mechanical or thermal loading is one of the most important factors in design. Growth of FG structures, and especially circular, annular or sectorial FG plates, have necessitated more investigation on this subject to reach a reliable design. Among the primary works on this subject, Najafizadeh and Eslami performed the buckling of thin solid circular plates made of FGMs subjected to mechanical [13] and thermal [14] loading. Their investigations are limited to the symmetrical buckling. Following Kirchhoff plate theory of thin structures, the equilibrium and stability equations in general form are obtained and eigenvalue solution of stability equations is done and closed-form phrases are reported to predict the bifurcation-point temperatures or loads of thin circular FG plates. When mechanical properties of FG plates are graded across the thickness of the plate according to power law form, Najafizadeh and Heydari [15, 16] treated the thermal and mechanical buckling load of thick FG plates based on the von-Karman non-linearity and Reddy’s third-order thick plate theory. Reliable explicit expressions are resulted in their work. A pseudo-spectral method to solve the thermally induced buckling problem of circular FG plates with variable thickness is done by Jalali et al. [17]. Based on the first-order theory of laminated plates, stability equations are solved via the Chebyshev polynomials. Ma and Wang [18] did the post-buckling and non-linear bending of circular FG plate when loading cases are symmetric. A numerical shooting method is adopted to solve the non-linear coupled ordinary differential equations. To compare the influences of three available homogenization schemes on critical buckling temperature and heat flux and also post-buckling equilibrium path of FGM solid circular plates, a Ritz-based formulation with polynomial shape functions is used by Kiani and Eslami [19]. Mechanical buckling, thermal buckling, and elastic foundation effect of mechanical buckling of sectorial plates are reported by Saidi and co-authors [20–22]. All of these works are formulated based on the first-order plate theory and five partially differential equations are established as stability equations. After decoupling equations, Levy-type solution of plates is adopted to solve the instability problem of sectorial FG plates under various boundary conditions. However, pre-buckling analysis of a plate is not well executed in [21], where the problem is posed as a primary–secondary equilibrium configuration instead of the non-linear bending. Also Li et al. [23] presented the non-linear bending and post-buckling of heated elastic FG circular plates for imperfect and perfect plates based on a shooting method. Recently, Kiani and Eslami [24, 25] discussed the thermal bifurcation and buckled configurations of an FGM circular/annular plate resting over elastic foundation. It has been shown that the fundamental buckled shape of an annular plate over a complete elastic foundation, or a circular plate over a partial/complete elastic foundation may be asymmetric. Sepahi et al. [26] adopted the GDQ method to solve the non-linear equilibrium equations of radially graded FGM annular plate. A shooting method is adopted in [27] by Aghelinejad et al. to obtain the critical buckling temperature and post-buckling equilibrium path of transversely graded annular FG plate. Reported works of [26, 27] consider only the symmetrical shape for buckling state and post-buckling regime of the clamped annular FGM plates.

Fig. 1
figure 1

Geometry of a thin annular FGM plate

Full size image

Various analytical eigenvalue analysis are reported for instability of FGM circular plates. There is, however, no analytical work covering the elastic instability of heated annular FG plates in asymmetrical shape using a single transcendental equation. Examination of the existence of asymmetrical buckling modes at the presence of symmetrical loadings and revealing the real state of the plate under the in-plane thermal loads are the main factors that are discussed in this research. Based on the classical theory of plates and the von-Karman non-linearity in polar coordinate, equilibrium equations of an annular plate are derived. Pre-buckling analysis of the plate with the assumption of immovable edges is executed and proper boundary conditions are chosen to assure the existence of bifurcation-type buckling. Stability equations of the plate are derived in general form and asymmetrical eigenvalue solution is performed. In each case of thermal loading, closed-form expressions are presented to estimate the critical buckling temperatures as well as the buckled shapes. Results show that the number of nodal diameters of clamped annular FG plates are identical with those of obtained for isotropic homogeneous plates.

2 Governing equations

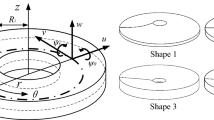
Consider an annular plate made of FGMs of thickness h, inner radii b, and outer radii a, referred to the polar coordinates \((r,\theta ,z)\), as shown in Fig. 1. As a rule of thermo-mechanical property distribution, a power law form is chosen which dictates the dispersion of ceramic volume fraction \(V_c\) and metal volume fraction \(V_m\) as follows:

$$\begin{aligned} V_{c}=\left( \dfrac{1}{2}+\dfrac{z}{h}\right) ^{k},\quad V_{m}=1-V_{c} \end{aligned}$$
(1)

Shen and Wang [28] made a comparison on the Voigt rule of mixture and Mori-Tanaka scheme for the non-linear vibration problem of rectangular FGM plates. It is shown that the difference between these two methods is negligible. Therefore, in this study the simple scheme of Voigt rule of mixture is used. Based on the Voigt rule [13, 14], thermo-mechanical properties of the FGM plate, may be expressed as the linear function of each property and volume fractions. By means of this rule and Eq. (1), a non-homogeneous property of the plate, P, as a function of thickness direction may be written as

$$\begin{aligned} P(z)=P_{m}+P_{cm}\left( \dfrac{1}{2}+\dfrac{z}{h}\right) ^{k},\quad P_{cm}=P_{c}-P_{m} \end{aligned}$$
(2)

where \(P_{m}\) and \(P_{c}\) are the corresponding properties of the metal and ceramic, respectively, and k is a non-negative constant called the power law index and shows the sharpness of property dispersion. In the present work, we assume that modulus of elasticity, E, thermal conductivity, K, and the thermal expansion coefficient, \(\alpha\), are described by Eq. (2), while Poisson’s ratio, \(\nu\), is considered to be constant across the thickness [20–22]. This assumption has been established in a large number of studies, since Poisson’s ratio generally varies in a small range.

The von-Karman-type non-linear strain-displacement relations in polar coordinate, considering the thin plate theory assumptions, are [13, 14]

$$\begin{aligned} \varepsilon _{rr} &= u_{,r}+\frac{1}{2}w_{,r}^2 \\ \varepsilon _{\theta \theta } &= \dfrac{1}{r}v_{,\theta }+\frac{1}{r}u+\frac{1}{2r^2}w_{,\theta }^2 \\ \gamma _{r\theta} &= \frac{1}{r}u_{,\theta }+v_{,r}-\frac{1}{r}v+\dfrac{1}{r}w_{,\theta }w_{,r} \end{aligned}$$
(3)

Here, \(\varepsilon _{rr}\) and \(\varepsilon _{\theta \theta }\) are the normal strains and \(\gamma _{r\theta }\) is the shear strain, and a comma indicates partial derivative. Besides, u, v and w are the radial, circumferential and lateral displacements, respectively.

Fig. 2
figure 2

Influence of the power law index on critical buckling temperature difference \(\Delta T_\mathrm{{cr}} [K]\) of fully clamped annular FG plates

Full size image

In this study, the classical plate theory with Kirchhoff assumptions is used with the following displacement field [13, 14]

$$\begin{aligned} u(r,\theta ,z) &= u_{0}(r,\theta )-zw_{0,r}(r,\theta ) \\ v(r,\theta ,z)&= v_{0}(r,\theta )-\dfrac{z}{r}w_{0,\theta }(r,\theta ) \\ w(r,\theta ,z)&= w_{0}(r,\theta ) \end{aligned}$$
(4)

where \(u_{0},\;v_{0}\), and \(w_{0}\) represent the displacements of the mid-surface \((z=0)\) along r, \(\theta\), and z directions, respectively.

Considering T and \(T_{0}\) as temperature distribution and reference temperature, respectively, the constitutive law for the FGM plate subjected to thermal loadings becomes [29]

$$\begin{aligned} \left\{ \begin{array}{c} \sigma _{rr} \\ \sigma _{\theta \theta }\\ \tau _{r\theta } \end{array}\right\} = \dfrac{E}{1-\nu ^ 2} \begin{bmatrix} 1&\nu&0 \\ \nu&1&0 \\ 0&0&\dfrac{1-\nu }{2} \\ \end{bmatrix} \left( \left\{ \begin{array}{c} \varepsilon _{rr} \\ \varepsilon _{\theta \theta }\\ \gamma _{r\theta } \end{array}\right\} -(T-T_{0})\left\{ \begin{array}{c} \alpha \\ \alpha \\ 0 \end{array}\right\} \right) \end{aligned}$$
(5)

Based on the classical plate theory, the stress resultants are related to the stresses through the following equations [13]

$$\begin{aligned} (N_{rr},N_{\theta \theta },N_{r\theta })=\int _{-\frac{h}{2}}^\frac{h}{2}(\sigma _{rr},\sigma _{\theta \theta },\tau _{r\theta })\mathrm{d}z \end{aligned}$$
$$\begin{aligned} (M_{rr},M_{\theta \theta },M_{r\theta })=\int _{-\frac{h}{2}}^\frac{h}{2}z(\sigma _{rr},\sigma _{\theta \theta },\tau _{r\theta })\mathrm{d}z \end{aligned}$$
(6)

Substituting Eqs. (3), (4), and (5) into (6) gives the stress resultants in terms of the mid-plane displacement as

$$\begin{aligned} \left\{ \begin{array}{c} N_{rr} \\ N_{\theta \theta } \\ N_{r\theta }\\ M_{rr} \\ M_{\theta \theta } \\ M_{r\theta }\end{array}\right\} = \dfrac{1}{1-\nu ^2} \times \begin{bmatrix} E_{1}&\nu E_{1}&0&E_{2}&\nu E_{2}&0 \\ \nu E_{1}&E_{1}&0&\nu E_{2}&E_{2}&0 \\ 0&0&\dfrac{1-\nu }{2}E_{1}&0&0&\dfrac{1-\nu }{2}E_{2} \\ E_{2}&\nu E_{2}&0&E_{3}&\nu E_{3}&0 \\ \nu E_{2}&E_{2}&0&\nu E_{3}&E_{3}&0 \\ 0&0&\dfrac{1-\nu }{2}E_{2}&0&0&\dfrac{1-\nu }{2}E_{3} \\ \end{bmatrix} \end{aligned}$$
$$\begin{aligned} \left\{ \begin{array}{c} u_{0,r}+\dfrac{1}{2}w_{0,r}^2 \\ \dfrac{1}{r}v_{0,\theta }+\dfrac{1}{r}u_{0}+\dfrac{1}{2r^2}w_{0,\theta }^2\\ \dfrac{1}{r}u_{0,\theta }+v_{0,r}-\dfrac{1}{r}v_{0}+\dfrac{1}{r}w_{0,r}w_{0,\theta }\\ -w_{0,rr}\\ -\dfrac{1}{r^2}w_{0,\theta \theta }-\dfrac{1}{r}w_{0,r}\\ -\dfrac{2}{r}w_{0,r\theta }+\dfrac{2}{r^2}w_{0,\theta } \end{array} \right\} - \left\{ \begin{array}{c} N^{T} \\ N^{T} \\ 0 \\ M^{T}\\ M^{T}\\ 0\end{array}\right\} \end{aligned}$$
(7)

where \(N^{T}\) and \(M^{T}\) are the thermal force and thermal moment resultants and \(E_{1}\), \(E_{2}\), and \(E_{3}\) are constants to be calculated as

$$\begin{aligned} E_{1}=\int _{-\frac{h}{2}}^\frac{h}{2}E(z)\mathrm{d}z=h\left( E_{m}+\frac{E_{cm}}{k+1}\right) =he_{1} \end{aligned}$$
$$\begin{aligned} E_{2}=\int _{-\frac{h}{2}}^\frac{h}{2}zE(z)\mathrm{d}z=h^{2}{E_{cm}}\left( \frac{1}{k+2}-\frac{1}{2k+2}\right) =h^2e_{2} \end{aligned}$$
$$\begin{aligned} E_{3}=\int _{-\frac{h}{2}}^\frac{h}{2}z^{2}E(z)\mathrm{d}z=h^{3}\left( \frac{1}{12}E_{m}+E_{cm}\left(\frac{1}{k+3}-\frac{1}{k+2}+\frac{1}{4k+4}\right)\right) =h^3e_{3} \end{aligned}$$
$$\begin{aligned} N^{T}=\dfrac{1}{1-\nu }\int _{-\frac{h}{2}}^\frac{h}{2}E(z)\alpha (z)(T-T_{0})\mathrm{d}z \end{aligned}$$
$$\begin{aligned} M^{T}=\dfrac{1}{1-\nu }\int _{-\frac{h}{2}}^\frac{h}{2}zE(z)\alpha (z)(T-T_{0})\mathrm{d}z \end{aligned}$$
(8)

The equilibrium equations of an annular FGM plate under thermal loadings may be derived on the basis of the stationary potential energy. The total virtual potential energy of the plate, \(\delta U\), is equal to the total virtual strain energy of the plate, that is,

$$\begin{aligned} \delta U=\int _b^a \int _0^{2\pi }\int _{-\frac{h}{2}}^\frac{h}{2}\left( \sigma _{rr} \delta \varepsilon _{rr}+\sigma _{\theta \theta } \delta \varepsilon _{\theta \theta }+\tau _{r\theta }\delta \gamma _{r\theta }\right) r\mathrm{d}z \mathrm{d}\theta \mathrm{d}r \end{aligned}$$
(9)

Using Eqs. (7) and (8) and employing the virtual work principle to minimize the functional of total potential energy function and performing some proper mathematical simplifications yield the expressions for the equilibrium equations of FGM plate as below

$$\begin{aligned} \delta u_{0}: N_{rr,r}+\dfrac{1}{r}N_{r\theta ,\theta }+\dfrac{1}{r}(N_{rr}-N_{\theta \theta })=0 \end{aligned}$$
$$\begin{aligned} \delta v_{0}: N_{r\theta ,r}+\dfrac{2}{r}N_{r\theta }+\dfrac{1}{r}N_{\theta \theta ,\theta }=0 \end{aligned}$$
$$\begin{aligned} \delta w_{0}&:& M_{rr,rr} + \frac{2}{r}M_{rr,r}+\frac{1}{r^2}M_{\theta \theta ,\theta \theta }-\frac{1}{r}M_{\theta \theta ,r}+\frac{2}{r}M_{r\theta , r\theta }&\quad&+\frac{2}{r^2}M_{r\theta , \theta }+ N_{rr}w_{0,rr} \\&\quad&+N_{\theta \theta }\left( \frac{1}{r^2}w_{0,\theta \theta }+\dfrac{1}{r}w_{0,r}\right) +2N_{r\theta }\left( \frac{1}{r}w_{0,r\theta }-\frac{1}{r^2} w_{0,\theta }\right) =0 \end{aligned}$$
(10)

3 Existence of bifurcation-type buckling

In the previous section, the equilibrium equations are derived for an annular FGM plate. To obtain the in-plane loads, pre-buckling analysis should be done. When a bifurcation point exists in load-deflection path of the plate, a pre-buckling configuration is revealed when the non-linear terms are omitted from Eq. (7). Consider an FGM plate that is subjected to transverse symmetrical temperature loading case.

Assume that the FGM plate exhibits a bifurcation-type buckling. Therefore, prior to buckling, plate experiences an in-plane regime of displacements. Neglecting the lateral deflection of the plate in pre-buckling state (since bifurcation exists, plate does not experience any lateral deflection) and solving the symmetrical type of the equilibrium equations in conjunction with the immovability conditions on inner and outer edges, yields

$$\begin{aligned} u_{0}^{0}(r,\theta )=0 \end{aligned}$$
(11)

Here, a superscript 0, indicates the pre-buckling conditions.

Now, by means of Eq. (7) and neglecting the lateral deflection of the plate in pre-buckling state, the following pre-buckling forces are obtained

$$\begin{aligned} N_{rr}^{0}=N_{\theta \theta }^{0}=-N^{T},\, N_{r\theta }^{0}=0 \end{aligned}$$
(12)

While the in-plane resultants are obtained, extra pre-buckling moments exist which are equal to

$$\begin{aligned} M_{rr}^{0}=M_{\theta \theta }^{0}=-M^{T},\, M_{r\theta }^{0}=0 \end{aligned}$$
(13)

These thermal moments, in general, are not zero due to the mid-plane asymmetric configuration of FG annular plates. The existence of thermal moments in pre-buckling state means that, plate bends at the onset of thermal loading. Only in a special case, extra moments vanish through the plate and that is when edges are capable of supplying moments. Among three types of boundary conditions (Free, Clamped and Simply supported) only clamped edges are capable of handling extra moments. This phenomenon arises from the fact that kinematic boundary conditions of clamping are not affected by temperature distribution. Therefore, only annular plates which are clamped at inner and outer edges show a bifurcation-type buckling under thermal loading, and only this type is considered in this paper. This conclusion is compatible with the findings of other researchers for flat beams and plates of various shapes, see e.g. [30–43]. Note that, for annular plate with both boundaries clamped, based to the Eq. (11), in pre-buckling state, all three components of displacement field are equal to zero.

4 Stability equations

The stability equations of an FG annular plate may be obtained by means of the adjacent equilibrium criterion [15, 16]. Let us assume that the state of equilibrium of FGM plate under loads is defined in terms of the displacement components \(u^{0}_{0}, v^{0}_{0}\), and \(w^{0}_{0}\). The displacement components of a neighbouring state of the stable equilibrium differ by \(u^{1}_{0}, v^{1}_{0}\), and \(w^{1}_{0}\) with respect to the equilibrium position. Thus, the total displacements of a neighbouring state are [15, 16]

$$\begin{aligned} u_{0}=u^{0}_{0}+u^{1}_{0},\quad v_{0}=v^{0}_{0}+v^{1}_{0},\quad w_{0}=w^{0}_{0}+w^{1}_{0} \end{aligned}$$
(14)

Accordingly, the stress resultants are divided into two terms representing the stable equilibrium and the adjacent state. The stress resultants with superscript 1 are linear functions of displacement with superscript 1. Considering this and using Eqs. (7) and (10), and performing proper simplifications, the stability equations become

$$\begin{aligned} N_{rr,r}^{1}+\dfrac{1}{r}N_{r\theta ,\theta }^{1}+\dfrac{1}{r}(N_{rr}^{1}-N_{\theta \theta }^{1})=0 \end{aligned}$$
$$\begin{aligned} N_{r\theta ,r}^{1}+\dfrac{2}{r}N_{r\theta }^{1}+\dfrac{1}{r}N_{\theta ,\theta }^{1}=0 \end{aligned}$$
$$\begin{aligned} &M_{rr,rr}^{1}+ \dfrac{2}{r}M_{rr,r}^{1}+\dfrac{1}{r^2}M_{\theta \theta ,\theta \theta }^{1}-\dfrac{1}{r}M_{\theta \theta ,\theta }^{1}+\dfrac{2}{r}M_{r\theta , r\theta }^{1} \\ & \quad +\dfrac{2}{r^2}M_{r\theta , \theta }^{1} + N_{rr}^{0}w_{0,rr}^{1} \nonumber \\ & \quad +N_{\theta \theta }^{0}\left( \dfrac{1}{r^2}w_{0,\theta \theta }^{1}+\dfrac{1}{r}w_{0,r}^{1}\right) \\ & \quad +2N_{r\theta }^{0}\left( \dfrac{1}{r}w_{0,r\theta }^{1}-\dfrac{1}{r^2} w_{0,\theta }^{1}\right) =0 \end{aligned}$$
(15)

The stability equations in terms of the displacement components may be obtained by substituting Eq. (7) into the above equations. Upon substitution, second and higher order terms of the incremental displacements may be omitted [14, 16]. Resulting equations are three stability equations based on the classical plate theory for an FGM plate

$$\begin{aligned} E_{1}\left( u_{0,rr}^1+\dfrac{1}{r}u_{0,r}^1-\dfrac{1}{r^2}u_{0}^{1}-\dfrac{1}{r^2}v_{0,\theta }^1+\dfrac{1}{r}v_{0,r\theta }^1\right) +\dfrac{(1-\nu )}{2}E_{1}\left( \dfrac{1}{r^2}u_{0,\theta \theta }^1-\dfrac{1}{r}v_{0,r\theta }^1-\dfrac{1}{r^2}v_{0,\theta }^{1} \right) \\ -E_{2}\left( w_{0,rrr}^1-\dfrac{1}{r^2}w_{0,r}^1+\dfrac{1}{r}w_{0,rr}^1-\dfrac{2}{r^3}w_{0,\theta \theta }^1+\dfrac{1}{r^2}w_{0,\theta \theta r}^1\right) =0 \end{aligned}$$
$$\begin{aligned} E_{1}\left( \dfrac{1}{r^2}v_{0,\theta \theta }^1+\dfrac{1}{r}u_{0,r\theta }^1+\dfrac{1}{r^2}u_{0,\theta }^{1}\right) +\dfrac{(1-\nu )}{2}E_{1}\left( v_{0,rr}^1+\dfrac{1}{r}v_{0,r}^1-\dfrac{1}{r^2}v_{0}^{1}+\dfrac{1}{r^2}u_{0,\theta }^1-\dfrac{1}{r}u_{0,r\theta }^1 \right) \\ -E_{2}\left( \dfrac{1}{r}w_{0,rr\theta }^1+\dfrac{1}{r^2}w_{0,r\theta }^1+\dfrac{1}{r^3}w_{0,\theta \theta \theta }^1\right) =0 \end{aligned}$$
$$\begin{aligned} \dfrac{E_{2}}{1-\nu ^2}\left( u_{0,rrr}^{1}+\dfrac{2}{r}u_{0,rr}^{1}-\dfrac{1}{r^2}u_{0,r}^{1}+\dfrac{1}{r^3}u_{0}^{1}+\dfrac{1}{r^3}u_{0,\theta \theta }^1+\dfrac{1}{r^2}u_{0,r\theta \theta }^1-\dfrac{1}{r^2}v_{0,r\theta }^1+\dfrac{1}{r^3}v_{0,\theta }^{1}+\dfrac{1}{r^3}v_{0,\theta \theta \theta }^{1}\right. \nonumber \\\left. +\dfrac{1}{r}v_{0,rr\theta }^{1} \right) -\dfrac{E_{3}}{1-\nu ^2}\left( w_{0,rrrr}^1+\dfrac{2}{r}w_{0,rrr}^1-\dfrac{1}{r^2}w_{0,rr}^1+\dfrac{1}{r^3}w_{0,r}^1+\dfrac{2}{r^2}w_{0,rr\theta \theta }^1-\dfrac{2}{r^3}w_{0,r\theta \theta }^1+\dfrac{4}{r^4}w_{0,\theta \theta }^1\right. \nonumber \\+\left. \dfrac{1}{r^4}w_{0,\theta \theta \theta \theta }^1\right) +N_{rr}^{0}w_{0,rr}^{1}+N_{\theta \theta }^{0}\left( \dfrac{1}{r^2}w_{0,\theta \theta }^{1}+\dfrac{1}{r}w_{0,r}^{1}\right) +2N_{r\theta }^{0}\left( \dfrac{1}{r}w_{0,r\theta }^{1}-\dfrac{1}{r^2} w_{0,\theta }^{1}\right) =0 \end{aligned}$$
(16)

With some mathematical manipulations, one may obtain an uncoupled equation in terms of the incremental lateral displacement \(w_{0}^1\). To this end

  1. 1.

    The first of Eq. (16) is differentiated with respect to r.

  2. 2.

    The first of Eq. (16) is divided by r.

  3. 3.

    The second of Eq. (16) is differentiated with respect to \(\theta\) and then divided by r.

  4. 4.

    The obtained equations in steps (1)–(3) are added and the result is multiplied by \(-\dfrac{E_{2}}{E_{1}(1-\nu ^2)}\)

  5. 5.

    The obtained equation in step (4) is added to the third of Eq. (16).

The resulting equation is an uncoupled equation in terms of \(w_{0}^{1}\)

$$\begin{aligned} &D_{k}\left( w_{0,rrrr}^1+\dfrac{2}{r}w_{0,rrr}^1-\dfrac{1}{r^2}w_{0,rr}^1+\dfrac{1}{r^3}w_{0,r}^1+\dfrac{2}{r^2}w_{0,rr\theta \theta }^1-\dfrac{2}{r^3}w_{0,r\theta \theta }^1\right. \nonumber \\ & \left. +\dfrac{4}{r^4}w_{0,\theta \theta }^1+\dfrac{1}{r^4}w_{0,\theta \theta \theta \theta }^1\right) -N_{rr}^{0}w_{0,rr}^{1}-N_{\theta \theta }^{0}\left( \dfrac{1}{r^2}w_{0,\theta \theta }^{1}+\dfrac{1}{r}w_{0,r}^{1}\right) \nonumber \\ & \quad -2N_{r\theta }^{0}\left( \dfrac{1}{r}w_{0,r\theta }^{1}-\dfrac{1}{r^2} w_{0,\theta }^{1}\right) =0 \end{aligned}$$
(17)

where \(D_k=\dfrac{E_{1}E_{3}-E^{2}_{2}}{E_{1}(1-\nu ^2)}\) is the equivalent flexural rigidity of an FGM plate. For decoupling of equilibrium or stability equations in polar coordinate based on FSDT one may refer to [7, 20–22, 44].

5 Solving the stability equation

In this section, an exact solution for stability equation (17) is presented. Substituting pre-buckling forces from Eqs. (12) into (17) gives

$$\begin{aligned} \left( \dfrac{\partial ^2}{\partial r^2}+\dfrac{1}{r}\dfrac{\partial }{\partial r}+\dfrac{1}{r^2}\dfrac{\partial ^2}{\partial \theta ^2}\right) \left( \dfrac{\partial ^2}{\partial r^2}+\dfrac{1}{r}\dfrac{\partial }{\partial r}+\dfrac{1}{r^2}\dfrac{\partial ^2}{\partial \theta ^2}+\dfrac{N^T}{D_{k}}\right) w_{0}^1 (r,\theta )=0 \end{aligned}$$
(18)

It is more convenient to introduce the following non-dimensional parameters

$$\begin{aligned} \overline{r}=\dfrac{r}{a},\quad \beta =\dfrac{b}{a},\quad \delta =\dfrac{h}{a}, \mu ^2=\dfrac{N^Ta^2}{D_{k}} \end{aligned}$$
(19)

While the in-plane load is symmetric, the buckled shape of the plate may be asymmetric [24, 25, 45, 46]. To this end, the buckling mode of the plate is considered as [47]

$$\begin{aligned} w_{0}^1(a\overline{r},\theta )=W_{n}(\overline{r})\cos (n\theta ) \end{aligned}$$
(20)

where n is the number of nodal diameters. Here, \(n=0\) indicates the symmetric buckled shape of the plate and \(n>0\) is associated with the asymmetric buckled shapes. Recalling the definition of non-dimensional parameters (19) and substituting Eqs. (20) into (18), the following ordinary differential equation is obtained

$$\begin{aligned} \left( \dfrac{\mathrm{d}^2}{\mathrm{d}\overline{r}^2}+\dfrac{1}{\overline{r}}\dfrac{\mathrm{d}}{\mathrm{d}\overline{r}}-\dfrac{n^2}{\overline{r}^2} \right) \left( \dfrac{\mathrm{d}^2}{\mathrm{d}\overline{r}^2}+\dfrac{1}{\overline{r}}\dfrac{\mathrm{d}}{\mathrm{d}\overline{r}}-\dfrac{n^2}{\overline{r}^2}+\mu ^2\right) W_{n}(\overline{r})=0 \end{aligned}$$
(21)

The exact solution of this equation is obtained as

$$\begin{aligned} W_{n}(\overline{r})=C_{1n}J_{n}(\mu \overline{r})+C_{2n}Y_{n}(\mu \overline{r})+C_{3n}\overline{r}^n+C_{4n}\left\{ \begin{array}{c} \ln \overline{r} \\ \overline{r}^{-n}\end{array}\right\} \end{aligned}$$
(22)

Here, \(C_{in}, i=1,2,3,4\) are constants to be evaluated when the boundary conditions are applied to Eq. (22). Also \(J_{n}\) and \(Y_{n}\) are the Bessel functions of the first and second kind, respectively. Note that the top form of Eq. (22) is associated with \(n=0\) (symmetric buckling) and the bottom one is related to \(n>0\) (asymmetric buckling). Equivalently, when the circumferential mode is \(n=0\), the function \(\ln (\overline{r})\) should be used where as when the circumferential mode is \(n>0\), the function \(\overline{r}^{-n}\) should be used.

As proved in the previous section, only plates with both inner and outer clamped edges exhibit bifurcation-type buckling for transverse thermal loading. For clamped annular FG plates, boundary conditions are [16]

$$\begin{aligned} W_{n}(1)=\dfrac{\mathrm{d}W_{n}}{\mathrm{d}\overline{r}}(1)=W_{n}(\beta )=\dfrac{\mathrm{d}W_{n}}{\mathrm{d}\overline{r}}(\beta )=0 \end{aligned}$$
(23)

Recalling Eq. (22), the following system of equations is obtained with the aid of boundary conditions (23)

$$\begin{aligned} \begin{bmatrix} J_{n}(\mu )&Y_{n}(\mu )&1&\left\{ \begin{array}{c} 0 \\ 1 \end{array} \right\} \\ J_{n}(\mu \beta )&Y_{n}(\mu \beta )&\beta ^n&\left\{ \begin{array}{c} Ln\beta \\ \beta ^{-n} \end{array}\right\} \\ \left[ J_{n}(\mu \overline{r})\right] ^{'}_{\overline{r}=1}&\left[ Y_{n}(\mu \overline{r})\right] ^{'}_{\overline{r}=1}&n&\left\{ \begin{array}{c} 1 \\ -n \end{array}\right\} \\ \left[ J_{n}(\mu \overline{r})\right] ^{'}_{\overline{r}=\beta }&\left[ Y_{n}(\mu \overline{r})\right] ^{'}_{\overline{r}=\beta }&n\beta ^{n-1}&\left\{ \begin{array}{c} \beta ^{-1} \\ -n\beta ^{-n-1} \end{array}\right\} \\ \end{bmatrix} \left\{ \begin{array}{c} C_{1n} \\ C_{2n}\\ C_{3n} \\ C_{4n}\end{array}\right\} = \left\{ \begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \end{array}\right\} \end{aligned}$$
(24)

To obtain a non-trivial solution, the determinant of the coefficients matrix (24) should set equal to zero. When the determinantal equation is solved, the following explicit expressions are obtained as buckling criteria of the plate

$$\begin{aligned} \dfrac{4}{\pi \mu }&-\mu \beta \ln \beta \left( J_{1}(\mu )Y_{1}(\mu \beta )-Y_{1}(\mu )J_{1}(\mu \beta ) \right) \nonumber \\&+\beta \left( J_{0}(\mu )Y_{1}(\mu \beta )-Y_{0}(\mu )J_{1}(\mu \beta ) \right) -\left( J_{1}(\mu )Y_{0}(\mu \beta )-Y_{1}(\mu )J_{0}(\mu \beta ) \right) =0 \end{aligned}$$
(25)

for \(n=0\) (symmetric buckled shape) and

$$\begin{aligned} \frac{8n}{\pi \mu }&- \mu \beta \left( \beta ^n-\beta ^{-n}\right) \left( J_{n+1}(\mu )Y_{n+1}(\mu \beta )-Y_{n+1}(\mu )J_{n+1}(\mu \beta ) \right) \\ &+ 2n\beta ^{n+1} \left( J_{n}(\mu )Y_{n+1}(\mu \beta )-Y_{n}(\mu )J_{n+1}(\mu \beta ) \right) \\&- 2n\beta ^{-n}\left( J_{n+1}(\mu )Y_{n}(\mu \beta )-Y_{n+1}(\mu )J_{n}(\mu \beta ) \right) =0 \end{aligned}$$
(26)

for \(n>0\) (asymmetric buckled shape).

Now, to obtain the non-dimensional critical buckling loads of the plate, \(n_\mathrm{{cr}}^T\), for every positive integer number n the associated determinant equation has to be solved. Finding the smallest positive root of the associated equation for each n and choosing the smallest between them yields the associated critical value of \(\mu\), which is called \(\mu _\mathrm{{cr}}\). The non-dimensional critical buckling load of the plate, according to definition (19), is evaluated as \(n_\mathrm{{cr}}^T=\mu _\mathrm{{cr}}^2\).

The temperature distribution through the plate should be known to evaluate the critical buckling temperatures.

6 Types of thermal loading

6.1 Uniform temperature rise

Consider an annular FG plate at reference temperature \(T_{0}\). When the radial extension is prevented, the uniform temperature may be raised to \(T_{0}+\Delta T\) such that the plate buckles. Substituting \(T=T_{0}+\Delta T\) in the fourth of Eq. (8) gives

$$\begin{aligned} N^{T}=\dfrac{ \Delta T h}{1-\nu }\left( E_{m}\alpha _{m}+\dfrac{E_{cm}\alpha _{m}+E_{m}\alpha _{cm}}{k+1}+\dfrac{E_{cm}\alpha _{cm}}{2k+1}\right) \end{aligned}$$
(27)

Recalling Eq. (27) and using the definition of \(n_{cr}^{T}\) and solving for \(\Delta T\), the critical buckling temperature difference of the plate in this case is obtained as

$$\begin{aligned} \Delta T_{cr}= \dfrac{\delta ^2}{(1+\nu )}\times \dfrac{e_{1}e_{3}-e_{2}^2}{Pe_{1}}n^{T}_\mathrm{{cr}} \end{aligned}$$
(28)

with

$$\begin{aligned} P=E_{m}\alpha _{m}+\dfrac{E_{m}\alpha _{cm}+E_{cm}\alpha _{m}}{k+1}+\dfrac{E_{cm}\alpha _{cm}}{2k+1} \end{aligned}$$
(29)

For an isotropic homogeneous annular plate, \((k=0)\), Eq. (28) reduces to

$$\begin{aligned} \Delta T_{cr}= \dfrac{\delta ^2}{12(1+\nu )\alpha _{c}}n^{T}_\mathrm{{cr}} \end{aligned}$$
(30)

6.2 Linear temperature across the thickness

Consider a thin FGM annular plate where the temperatures at the ceramic-rich and metal-rich surfaces are \(T_{c}\) and \(T_{m}\), respectively. The temperature distribution for the given boundary conditions is obtained by solving the heat conduction equation along the plate thickness. If the plate thickness is thin enough, the temperature distribution is approximated linear through the thickness. So the temperature as a function of thickness coordinate z can be written in the form

$$\begin{aligned} T=T_{m}+(T_{c}-T_{m})\left( \dfrac{1}{2}+\dfrac{z}{h}\right) \end{aligned}$$
(31)

Substituting Eqs. (31) into (8) and solving for \(\Delta T=T_{c}-T_{m}\) gives the critical buckling temperature difference between the metal-rich and ceramic-rich surfaces as

$$\begin{aligned} \Delta T_\mathrm{{cr}}= \dfrac{\delta ^2}{(1+\nu )}\times \dfrac{e_{1}e_{3}-e_{2}^2}{Qe_{1}}n^{T}_\mathrm{{cr}}-(T_{m}-T_{0})\dfrac{P}{Q} \end{aligned}$$
(32)

where P is defined by Eq. (29) and Q is equal to

$$\begin{aligned} Q=\dfrac{E_{m}\alpha _{m}}{2}+\dfrac{E_{m}\alpha _{cm}+E_{cm}\alpha _{m}}{k+2}+\dfrac{E_{cm}\alpha _{cm}}{2k+2} \end{aligned}$$
(33)

For an isotropic homogeneous annular plate, \((k=0)\), Eq. (32) reduces to

$$\begin{aligned} \Delta T_{cr}= \dfrac{\delta ^2}{6(1+\nu )\alpha _{c}}n^{T}_\mathrm{{cr}}-2(T_{m}-T_{0}) \end{aligned}$$
(34)

6.3 Non-linear temperature through the thickness

Assume an FGM annular plate where the temperature in ceramic-rich and metal-rich surfaces are \(T_{c}\) and \(T_{m}\), respectively. The governing equation for the steady-state one-dimensional heat conduction equation, in the absence of heat generation, becomes

$$\begin{aligned} \dfrac{\mathrm{d}}{\mathrm{d}z}\left( K(z)\dfrac{\mathrm{d}T}{\mathrm{d}z}\right) =0 \end{aligned}$$
$$\begin{aligned} T\left(\dfrac{h}{2}\right)=T_{c},\quad T\left(-\dfrac{h}{2}\right)=T_{m} \end{aligned}$$
(35)

Solving this equation via the polynomial series and taking enough terms, yields the temperature distribution across the thickness of the plate. Following the same method used for the linear temperature, the critical bucking temperature difference between the upper and lower surfaces of the plate may be evaluated as

$$\begin{aligned} \Delta T_\mathrm{{cr}}= \dfrac{\delta ^2}{(1+\nu )}\times \dfrac{e_{1}e_{3}-e_{2}^2}{Re_{1}}n^{T}_\mathrm{{cr}}-(T_{m}-T_{0})\dfrac{P}{R} \end{aligned}$$
(36)

with the following definitions

$$\begin{aligned} D=\sum _{i=0}^{N}\dfrac{\left(-\dfrac{K_{cm}}{K_{m}}\right)^{i}}{ik+1} \end{aligned}$$
$$\begin{aligned} R&=\dfrac{1}{D}\times \left\{ E_{m}\alpha _{m} \sum _{i=0}^{N}\dfrac{(-\dfrac{K_{cm}}{K_{m}})^{i}}{(ik+1)(ik+2)}\right. \nonumber \\&\quad +\left. (E_{cm}\alpha _{m}+E_{m}\alpha _{cm})\sum _{i=0}^{N}\dfrac{(-\dfrac{K_{cm}}{K_{m}})^{i}}{(ik+1)(ik+k+2)}\right. \nonumber \\&\quad +\left. E_{cm}\alpha _{cm}\sum _{i=0}^{N}\dfrac{(-\dfrac{K_{cm}}{K_{m}})^{i}}{(ik+1)(ik+2k+2)}\right\} \end{aligned}$$
(37)

where N is the number of sufficient terms to assure the convergence of the series.

For an isotropic homogeneous plate, \((k=0)\), expression (36) simplifies to

$$\begin{aligned} \Delta T_\mathrm{{cr}}= \dfrac{\delta ^2}{6(1+\nu )\alpha _{c}}n^{T}_\mathrm{{cr}}-2(T_{m}-T_{0}) \end{aligned}$$
(38)

which is similar to Eq. (34) because the solution of heat conduction equation (35) is linear across the thickness when thermal conductivity of the plate is position independent.

7 Results and discussions

To illustrate the proposed approach, a ceramic–metal functionally graded annular plate is considered. The combination of materials consists of aluminium and alumina. Material properties are assumed to be temperature independent. This assumption is established to present the critical buckling temperatures in simple closed-form expressions, otherwise, numerical techniques should be implemented to obtain the temperature profile through the plate thickness, iteratively. The elasticity modulus, the thermal expansion coefficient, and the thermal conductivity coefficient for aluminium are \(E_{m}=70\) GPa, \(\alpha _{m}=23\times 10^{-6}\)/K  and \(K_{m}=204\) W/mK, and for alumina are \(E_{c}=380\) GPa,  \(\alpha _{c}=7.4\times 10^{-6}\)/K and \(K_{c}=10.4\)  W/mK, respectively. For simplicity, Poisson’s ratio is chosen to be 0.3 [14]. The plate is assumed to be clamped at both inner and outer edges.

In Table 1, to show the validity and accuracy of the present method, the critical buckling temperature difference of thin annular isotropic plates is compared with those reported in [23] based on the numerical shooting method and results of Tani [49]. As seen, a small difference between our result and those reported in [23] is observed which is due to neglecting the asymmetrical deformation of annular plates under symmetrical in-plane loading in [23]. As seen, the comparison is well justified.

Table 1 Critical buckling temperature difference \(\Delta T_\mathrm{{cr}} [K]\) of an isotropic annular plate \((k=0)\) with \(\beta =0.5\) subjected to uniform temperature rise loading
Full size table

In another comparison study, critical buckling temperatures of solid circular plates for nonuniform thermal loading are provided. Comparison is provided in Table 2. The temperature profile through the thickness is obtained according to non-linear temperature distribution obtained from the heat conduction equation. A solid circular plate with radius to thickness ratio \(a/h=50\) is considered. Inner radius is set equal to zero. Boundary conditions on the inner edge of the plate is considered to be sliding support. It is seen that numerical results of this study match well with the results of Najafizadeh and Hedayati [50] and Prakash and Ganapathi [51].

Table 2 Critical buckling temperature difference \(\Delta T_\mathrm{{cr}} [K]\) of FG solid circular plates with \(a/h=50\) subjected to non-linear temperature distribution across the thickness
Full size table

The influence of power law index on critical buckling temperature difference of annular FG plates is depicted in Fig. 2. Geometrical parameters are chosen as \(\beta =0.25\) and \(\delta =0.02\). A 5K increase in metal-rich surface of the plate is considered, i.e. \(T_{m}-T_{0}=5K\). As seen, when the power law index of FG plates becomes larger, curves behaviour in each case of thermal loading is different. When plate is subjected to uniform temperature rise (UTR), and power law index increases up to 2, \(\Delta T_\mathrm{{cr}}\) inherits a swift descend, while for \(2<k<10\) the value of \(\Delta T_\mathrm{{cr}}\) increases very slow, and finally non-significant decrease occurs for \(k>10\). For non-linear temperature across the thickness (NLTD), \(\Delta T_\mathrm{{cr}}\) increases up for initial values of power law index and then decreases permanently. In comparison with rapid changes in \(\Delta T_\mathrm{{cr}}\) for \(k<2\), alternations for \(k>2\) are not significant. It should be pointed out that the linear temperature distribution across the thickness (LTD), which is an approximation for exact heat conduction equation (35), underestimates the critical buckling temperatures, except for \(k=0\) and \(k=\infty\), when FGM annular plate reduces to a full-metal or full-ceramic plate. In these cases, the exact solution of heat conduction equation is also linear.

Buckled configurations of clamped annular FG plates \((k=1)\) for some \(\beta\) ratios are depicted in Fig. 3. As seen for all cases, \((\beta =0.1,0.3,0.4,0.5)\) plates buckle in asymmetric modes. The associated buckling modes are \(n=1,2,3,4\), respectively. As seen, by increasing the \(\beta\) ratio, number of nodal diameters increases.

Fig. 3
figure 3

Buckled configurations of FG plates with various \(\beta\) ratios when \(k=1\). Left, Up: \(\beta =0.1\); Right, Up: \(\beta =0.2\); Left, Down: \(\beta =0.4\); Right, Down: \(\beta =0.5\)

Full size image

Table 3 presents the buckling temperature difference of thin FG annular plate subjected to UTR case for various power law index, \(\beta\) and \(\delta\) ratios. As expected, when plate becomes thicker the buckling temperatures become higher, which is due to an increase in the flexural rigidity of the plate. As seen, the critical buckling temperature becomes higher when the ratio \(\beta\) increases. It should be noted that the number of nodal points for each \(\beta\) are indicated as superscripts. As seen for all cases, asymmetric buckling configuration occurs, i.e. \(n>0\). Furthermore, the critical buckling temperature of non-homogeneous plate \((0<k<\infty )\) lies between the associated values of plates made of ceramic and metal constituents, respectively.

Table 3 Critical buckling temperature difference \(\Delta T_\mathrm{{cr}}[K]\) of annular FG plates subjected to uniform temperature rise loading for various \(\beta\) and \(\delta\) ratios
Full size table

The influence of \(\delta\) and \(\beta\) ratios on bifurcation buckling of FG plates for linear and non-linear cases of temperature distribution is depicted in Figs. 4 and 5, respectively. The linear composition of ceramic–metal is assumed for the FG annular plates. As expected, when \(\delta\) increases the critical buckling temperature of FG plates becomes higher due to an increase in the flexural rigidity of the plate. Also as \(\beta\) diminishes, \(\Delta T_\mathrm{{cr}}\) decreases permanently.

Fig. 4
figure 4

Influence of thickness and inner radius on critical buckling temperature difference of annular FG plates subjected to linear temperature distribution across the thickness

Full size image
Fig. 5
figure 5

Influence of thickness and inner radius on critical buckling temperature difference of annular FG plates subjected to heat conduction across the thickness

Full size image
Table 4 Range of \(\beta\) ratio to obtain a certain number of nodal diameters indicated as superscripts
Full size table

To obtain a clear understanding on hoop mode alternation with respect to \(\beta\) ratio, Table 4 presents the range of the \(\beta\) ratio for a specified number of nodal diameters. As one may obtain, in the range \(0.001 < \beta < 1\), piecewise increase in number of nodal diameters is observed with respect to the permanent increase of \(\beta\) ratio. At higher values of \(\beta\), number of nodal diameters changes rapidly.

8 Conclusion

In the present article the equilibrium and stability equations for a thin annular heated FG plates are obtained. The derivation is based on the classical plate theory, while the constituent materials follow the power law form of property distribution. The boundary conditions of plate on both edges are assumed to be hard clamped. Closed-form solutions are derived for the critical buckling temperatures. It is concluded that

  1. 1.

    In general, bifurcation-type buckling does not exist for annular FG plates. Boundary conditions on both inner and outer edges have a great effect on dictating the behaviour of the plate under in-plane thermal loading. Only fully clamped annular FG plates exhibit bifurcation-type buckling, where for other combinations of boundary conditions plate exhibit a non-linear bending with the presence of thermal loading.

  2. 2.

    While the temperature distribution is symmetric through the plate, buckled configurations of c lamped-clamped FG plates are all asymmetric.

  3. 3.

    The number of nodal diameters and critical buckling temperatures of FG plates increase when \(\beta\) ratio gets larger.

  4. 4.

    The number of nodal diameters of FG plates and isotropic homogeneous plates are similar to each other when the geometric parameters are kept constant.