1 Introduction

Buckling of solid structures such as beams, plates, and shells under thermal or mechanical loadings have been the subject of many studies for a long period of time. Brush and Almorth (1975) presented the nonlinear equilibrium equations and linear stability equations for these types of structures and presented the critical mechanical loads of bars, plates, and shells for some types of loadings and boundary conditions. Wang et al. (2004) presented the closed form solution for buckling of beams based on the classical, first order, and higher order displacement beam theories under compressive loads. They also studied the buckling of plates and shells under mechanical loadings. A survey in the literature shows that the problem of thermal instability of curved or straight beams subjected to temperature distribution of an arbitrary variation has not been treated in a general form. Forray (1959) expressed stresses in a closed circular ring subjected to linear temperature distribution along the thickness and uniform along the span. Formula for the elastic buckling of beams may be applied to conditions under which the proportional limit exceed when a reduced value of the modulus of elasticity corresponding to the actual stress is used (Timoshenko 1936). Carter and Gere (1962) gave some graphs for buckling coefficients of beams with single taper for various end conditions, angle of taper, and the cross sections. Culver and Preg (1968) have tabulated the buckling coefficients for singly tapered beam-columns in which the effect of torsion, including the warping restraint, is considered for the case where the loading is by end moments in the stiffer principal plane. Burgreen and Mannit (1969) and Burgreen and Megal (1971) have discussed the buckling of bimetallic beams and have pointed out some difficulties in predicting the snap-through instability of these beams. Aydogdu (2007) discussed the thermal buckling of cross-ply laminated composite beams for various boundary conditions based on the Reddy’s displacement models. He used the Ritz method for different length to thickness ratios of the beam. Khdeir (2001) studied the buckling of cross-ply laminated composite beams based on various beam theories and various edge conditions. He found that the results using third order and first order beam theories are in good agreement, while the values related to classical beam theory are not so close to those related for the shear deformable beams, specially for thick beams.

For the plate problems, Reddy and Khdier (1989) studied the buckling and vibration of composite laminated plates based on the classical, first order, and higher order displacement plate theories. They presented their results using both exact and finite element methods for various edge conditions of the plate. Mossavarali and Eslami (2002) used the higher order formulation for displacement of shear deformable plates to find the critical buckling temperature of imperfect orthotropic plates. A review of recent developments in laminated composite plates buckling was carried out by Leissa (1992) and Tauchert (1991).

Zhao et al. (2007) studied the post-buckling of simply supported rod made of functionally graded materials under uniform thermal loading using the numerical shooting method. Li et al. (2006) studied the thermal post-buckling behaviour of a fixed-fixed beam based on the Timoshenko beam theory. They found the effect of shear on buckling of homogeneous beams and used the shooting method to analyze the post-buckling behaviour of FGM beams. Rastgo et al. (2005) discussed the buckling of functionally graded material curved beams under linear thermal loading. They studied both the in-plane and out of plane buckling of curved beams. Ke et al. (2009a) presented the post-buckling of a cracked beam for hinged–hinged and clamped–hinged edge conditions based on the Timoshenko beam theory. Also, Ke et al. (2009b) presented the free vibration and mechanical buckling of cracked beams using the first order shear deformation beam theory for three types of boundary conditions.

In thermal buckling of functionally graded material plates Javaheri and Eslami (2002a, b) discussed the thermal buckling of plates based on the classical and higher order displacement plate theories. They studied four types of thermal loadings for critical bucking temperature of plates and found that the classical plate theory over-predicts the buckling behaviour of thick plates. Also, Javaheri and Eslami (2002c) expressed the mechanical buckling of plates under three types of mechanical loadings for simply supported plates in all edges. Lanhe (2004) gave thermal buckling of simply supported functionally graded plates for three types of thermal loadings based on the first order shear deformation plate theory. Samsam Shariat and Eslami (2005, 2006, 2007) discussed the buckling of perfect and imperfect simply-supported functionally graded materials plates under various types of thermal loading. They used both classical and third order displacement theories and modelled the imperfection using the double sine series. They found a closed form solution for the critical bucking temperature in each case of thermal loading. Zhao et al. (2009) discussed the uni-axial and uniform temperature rise buckling of functionally graded plates containing a circular or square hole based on the first order shear deformation plate theory for fully clamped and fully simply supported edge conditions using the Element-free Kp-Ritz formulation.

In this paper, the thermal buckling of beams made of the functionally graded material is discussed. Various types of boundary conditions and thermal loadings are considered. The Euler–Bernoulli beam theory is employed and the closed form solutions are presented for different types of boundary conditions and thermal loadings.

2 Functionally graded Euler beams

Consider a beam of functionally graded material, where the graded properties are assumed to be through the thickness direction. The volume fractions of the constituent materials, which are assumed to be ceramic of volume V c and metal of volume V m may be expressed using the power law distribution as (Praveen and Reddy 1998)

$$ V_{m}=1-V_{c}, \quad V_{c}=\left( {\frac{1}{2}}+{\frac{z}{h}}\right)^{k} $$
(1)

where h is the thickness of the beam and z is the thickness coordinate measured from the middle surface of the beam (−h/2 ≤ z ≤ h/2), k is the power law index which has the value equal or greater than zero. Note that for the upper surface, which is ceramic rich, V c (h/2) = 1 and for the lower surface, which is metal rich, V c (−h/2) = 0. Variation of V c with k and z/h is shown in Fig. 1.

Fig. 1
figure 1

Variation of ceramic volume fraction with power law index and thickness coordinate

Full size image

The value of k equal to zero represents a fully ceramic beam (V c  = 1) and k equal to infinity represents a fully metallic beam (V c  = 0).

We assume that the mechanical and thermal properties of the FGM beam are distributed based on Voigt’s rule (Suresh and Mortensen 1998). Thus, the property variation of a functionally graded material using Eq. 1 is given by

$$ P(z)=P_{m}+P_{cm}\left({\frac{1}{2}}+{\frac{z}{h}} \right)^{k} $$
(2)

where, P cm  = P c  − P m , and P m and P c are the corresponding properties of the metal and ceramic, respectively. In this analysis the material properties, such as Young’s modulus E(z), coefficient of thermal expansion α(z) and thermal conductivity K(z), may be expressed by Eq. 2.

3 Governing equations

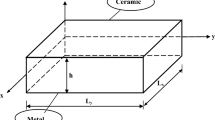
Consider a beam made of FGMs with rectangular cross section. It is assumed that the length of the beam is L, width is b, and the height is h. Rectangular Cartesian coordinates is used such that the x axis is at the left side of the beam on its middle surface and z is measured from the middle surface and is positive upward, as shown in Fig. 2. The analysis of beam is based on the classical beam theory using the Euler–Bernoulli assumptions. The displacement field for the Euler–Bernoulli beam is given as (Aydoglu 2007)

$$ \begin{aligned} \bar{u}(x,z)&=u-z{\frac{dw}{dx}}\\ \bar{w}(x,z)&=w \end{aligned} $$
(3)

where \(\bar{u}(x,z)\) and \(\bar{w}(x,z)\) are displacements of an arbitrary point of the beam along the x and z-directions, respectively, and u and w are the displacements of the mid-surface of the beam which are functions of x only. The strain–displacement relations for the beam are given in the form

$$ \varepsilon_{xx}={\frac{\partial \bar{u}}{\partial x}} +{\frac{1}{2}}\left( {\frac{\partial \bar{w}}{\partial x}}\right)^{2} $$
(4)

where ɛ xx is the axial strain. Substituting Eq. 3 into Eq. 4 reveals axial strain in the beam, which is equal to

$$ \varepsilon_{xx}={\frac{du}{dx}}+{\frac{1}{2}}\left( {\frac{dw}{dx}}\right)^{2}-z{\frac{d^{2}w}{dx^{2}}} $$
(5)

Constitutive law for a material under thermal and mechanical loads using linear thermo-elasticity can be written in the form (Zhao et al. 2007; Li et al. 2006)

$$ \sigma_{xx}=E\left( \varepsilon_{xx}-\alpha( T-T_{0}) \right) $$
(6)

In this equation σ xx is the axial stress, T 0 is the reference temperature, and T is the temperature distribution through the beam. Equations 5 and 6 are combined to give the axial stress in terms of the middle surface displacements as

$$ \sigma_{xx}=E\left({\frac{du}{dx}}+{\frac{1}{2}}\left( {\frac{dw}{dx}}\right)^{2}-z{\frac{d^{2}w}{dx^{2}}} -\alpha\left( T-T_{0}\right) \right) $$
(7)

The force and moment per unit length of the beam expressed in terms of the stress through the thickness, according to the Euler–Bernoulli beam theory, are (Zhao et al. 2007)

$$ \begin{aligned} N_{x}&=\int\limits_{\frac{-h}{2}}^{\frac{h}{2}}\sigma_{xx}dz\\ M_{x}&=\int\limits_{\frac{-h}{2}}^{\frac{h}{2}}z\sigma_{xx}dz \end{aligned} $$
(8)

Using Eqs. 2, 7, and 8 and noting that u and w are only functions of x, N x and M x are obtained as

$$ \begin{aligned} N_{x}&=E_{1}\left({\frac{du}{dx}}+{\frac{1}{2}}\left( {\frac{dw}{dx}}\right)^{2}\right) -E_{2}\;{\frac{d^{2}w}{dx^{2}}}-N_{x}^{T} \\ M_{x}&=E_{2}\left({\frac{du}{dx}}+{\frac{1}{2}}\left( {\frac{dw}{dx}}\right)^{2}\right) -E_{3}\;{\frac{d^{2}w}{dx^{2}}}-M_{x}^{T} \end{aligned} $$
(9)

where E 1, E 2, and E 3 are constants and \(N_{x}^{T}\) and \(M_{x}^{T}\) are thermal force and thermal moment resultants, which are calculated using the following relations

$$ \begin{aligned} E_{1}&=\int\limits_{\frac{-h}{2}}^{\frac{h}{2}}E(z)dz =h\left(E_{m}+{\frac{E_{cm}}{k+1}}\right)\\ E_{2}&=\int\limits_{\frac{-h}{2}}^{\frac{h}{2}}zE(z)dz =h^{2}{E_{cm}}\left({\frac{1}{k+2}}-{\frac{1}{2k+2}}\right)\\ E_{3}&=\int\limits_{\frac{-h}{2}}^{\frac{h}{2}}z^{2}E(z)dz =h^{3}\left({\frac{1}{12}}E_{m}+E_{cm}\left({\frac{1}{k+3}} -{\frac{1}{k+2}}+{\frac{1}{4k+4}}\right)\right)\\ N_{x}^{T}&=\int\limits_{\frac{-h}{2}}^{\frac{h}{2}}E(z)\alpha(z)(T-T_{0})dz \\ M_{x}^{T}&=\int\limits_{\frac{-h}{2}}^{\frac{h}{2}}zE(z)\alpha(z)(T-T_{0})dz \end{aligned} $$
(10)

Note that to find the thermal force and moment, the temperature distribution through the beam should be known.

Fig. 2
figure 2

The geometry and coordinate system of an FGM beam

Full size image

The total potential energy for a beam under thermal loads is defined as

$$ U={\frac{1}{2}}\int\limits_0^L\int\limits_{\frac{-b}{2}}^{\frac{b}{2}}\int\limits_{\frac{-h} {2}}^{\frac{h}{2}}\sigma_{xx}\left( \varepsilon_{xx}-\alpha( T-T_{0})\right) dzdydx $$
(11)

Substituting σ xx from Eq. 7 and ɛ xx from Eq. 5 into Eq. 11 and integrating with respect to z and y, gives the final form of the total potential energy of beam as

$$ \begin{aligned} U=\,&{\frac{b}{2}}\int\limits_0^L\left[ E_{1}\left({\frac{du}{dx}}+{\frac{1}{2}}\left( {\frac{dw}{dx}}\right)^{2}\right)^{2}-2E_{2}{\frac{d^{2}w}{dx^{2}}}\left( {\frac{du}{dx}}+{\frac{1}{2}}\left(\frac{dw}{dx}\right)^{2}\right)\right.\\ &\left. +E_{3}\left({\frac{d^{2}w}{dx^{2}}}\right)^{2} -2N_{x}^{T}\left( {\frac{du}{dx}}+{\frac{1}{2}}\left( {\frac{dw}{dx}}\right)^{2}\right) +2M_{x}^{T}\left({\frac{d^{2}w}{dx^{2}}}\right)+S\right]dx \end{aligned} $$
(12)

where S is

$$ S=\int\limits_{\frac{-h}{2}}^{\frac{h}{2}} E(z)\alpha^{2}(z)(T-T_{0})^{2}dz $$
(13)

To derive the equilibrium equations, the variational approach may be used. Assume that the total functional of U is F. In this case Euler’s equations are expressed as

$$ \begin{aligned} {\frac{\partial F}{\partial u}} -{\frac{d}{dx}}\left( {\frac{\partial F}{\partial( {\frac{du}{dx}})}} \right) &=0\\ {\frac{\partial F}{\partial w}}-{\frac{d}{dx}}\left( {\frac{\partial F}{\partial( {\frac{dw}{dx}})}} \right)+{\frac{d^{2}}{dx^{2}}} \left({\frac{\partial F}{\partial( {\frac{d^{2}w}{dx^{2}}})}} \right) &=0 \end{aligned} $$
(14)

The nonlinear equilibrium equations for an FGM beam using Eqs. 12 and 14 become

$$ \begin{aligned} &E_{1}\left({\frac{d^{2}u}{dx^{2}}}+{\frac{dw}{dx}}\;{\frac{d^{2}w}{dx^{2}}}\right) -E_{2}{\frac{d^{3}w}{dx^{3}}}-{\frac{dN_{x}^{T}}{dx}}=0\\ &E_{2}\left( {\frac{d^{3}u}{dx^{3}}}+{\frac{dw}{dx}}\;{\frac{d^{3}w}{dx^{3}}} +\left({\frac{d^{2}w}{dx^{2}}}\right)^{2}\right) -E_{3}{\frac{d^{4}w}{dx^{4}}}-{\frac{d^{2}M_{x}^{T}}{dx^{2}}}\\ &\quad +{\frac{d^{2}w}{dx^{2}}}\left(E_{1}\left({\frac{du}{dx}}+{\frac{1}{2}} \left({\frac{dw}{dx}}\right)^{2}\right)-E_{2}{\frac{d^{2}w}{dx^{2}}} -N_{x}^{T}\right) =0 \end{aligned} $$
(15)

To derive the stability equations, the adjacent-equilibrium criterion is used. Assume that the equilibrium state of a functionally graded beam is defined in terms of the displacement components u 0 and w 0. The displacement components of a neighboring stable state differ by u 1 and w 1 with respect to the equilibrium position. Thus, the total displacements of a neighboring state are

$$ \begin{aligned} u&=u_{0}+u_{1}\\ w&=w_{0}+w_{1} \end{aligned} $$
(16)

Substituting Eq. 16 into Eq. 15 and expanding them results into two nonlinear equations as

$$ \begin{aligned} &E_{1}\left({\frac{d^{2}u_{0}}{dx^{2}}} +{\frac{d^{2}u_{1}}{dx^{2}}}+{\frac{dw_{0}}{dx}}\;{\frac{d^{2}w_{0}}{dx^{2}}} +{\frac{dw_{0}}{dx}}\;{\frac{d^{2}w_{1}}{dx^{2}}}+{\frac{dw_{1}}{dx}}\;{\frac{d^{2}w_{0}}{dx^{2}}} +{\frac{dw_{1}}{dx}}\;{\frac{d^{2}w_{1}}{dx^{2}}}\right)\\ &\quad-E_{2}\left({\frac{d^{3}w_{0}}{dx^{3}}}+{\frac{d^{3}w_{1}}{dx^{3}}}\right) -{\frac{dN^{T}_{x}}{dx}}=0\\ &E_{2}\left({\frac{d^{3}u_{0}}{dx^{2}}}+{\frac{d^{3}u_{1}}{dx^{2}}} +{\frac{dw_{0}}{dx}}\;{\frac{d^{3}w_{0}}{dx^{3}}}+{\frac{dw_{0}}{dx}}\;{\frac{d^{3}w_{1}} {dx^{3}}}+{\frac{dw_{1}}{dx}}\;{\frac{d^{3}w_{0}}{dx^{3}}}+{\frac{dw_{1}}{dx}}\;{\frac{d^{3}w_{1}}{dx^{3}}}\right)\\ &\quad -E_{3}\left({\frac{d^{4}w_{1}}{dx^{4}}}+{\frac{d^{4}w_{0}}{dx^{4}}}\right) -{\frac{d^{2}M_{x}^{T}}{dx^{2}}}-N_{x}^{T}\left({\frac{d^{2}w_{0}} {dx^{2}}}+{\frac{d^{2}w_{1}}{dx^{2}}}\right)\\ &\quad+E_{1}\left( {\frac{d^{2}w_{1}}{dx^{2}}}+{\frac{d^{2}w_{0}}{dx^{2}}}\right) \left({\frac{du_{0}}{dx}}+{\frac{du_{1}}{dx}}+{\frac{1}{2}} \left({\frac{dw_{0}}{dx}}\right)^{2}+{\frac{1}{2}}\left( {\frac{dw_{1}}{dx}}\right)^{2} +\left( {\frac{dw_{0}}{dx}}\right)\left( {\frac{dw_{1}}{dx}}\right)\right)=0 \end{aligned} $$
(17)

The terms in the resulting equations with subscript 0 satisfy the equilibrium condition and therefore drop out of the equations. Also, the non-linear terms with subscript 1 are ignored because they are small compared to the linear terms. Deformation of the beam prior to buckling for arbitrary boundary conditions and subjected to transverse temperature loading is obtained by solving Eq. 15 with the nonlinear terms is set equal to zero (Khdeir 2001). Considering all of these mentioned above, the stability equations become

$$ \begin{aligned} E_{1}{\frac{d^{2}u_{1}}{dx^{2}}}-E_{2}{\frac{d^{3}{w_{1}}}{dx^{3}}}=0 \\ E_{2}{\frac{d^{3}u_{1}}{dx^{3}}}-E_{3}{\frac{d^{4}{w_{1}}}{dx^{4}}} -N_{x}^{T}{\frac{d^{2}{w_{1}}}{dx^{2}}}=0 \end{aligned} $$
(18)

Similar to displacements, the force resultants of a neighboring state may be related to the state of equilibrium. The stress resultants with subscript 1 are linear parts of resultants that correspond to the neighboring state. Using Eqs. 9 and 16, the expressions for N x1 and M x1 become

$$ \begin{aligned} N_{x1}&=E_{1}{\frac{du_{1}}{dx}}-E_{2}{\frac{d^{2}w_{1}}{dx^{2}}}\\ M_{x1}&=E_{2}{\frac{du_{1}}{dx}}-E_{3}{\frac{d^{2}w_{1}}{dx^{2}}} \end{aligned} $$
(19)

Combining Eq. 18 by eliminating u 1, provides an ordinary differential equation in terms of w 1, which is the stability equation of an FGM beam under thermal loading

$$ {\frac{d^{4}w_{1}}{dx^{4}}}+\mu^{2}{\frac{d^{2}w_{1}}{dx^{2}}}=0 $$
(20)

with

$$ \mu^{2}={\frac{E_{1}N_{x}^{T}}{E_{1}E_{3}-E_{2}^{2}}} $$
(21)

When the temperature distribution in the beam is a function of thickness direction only, the parameter μ is constant. In this case the exact solution of Eq. 20 is

$$ w_{1}(x)=C_{1}\sin (\mu x)+C_{2}\cos (\mu x)+C_{3}x+C_{4} $$
(22)

Using Eqs. 18, 19, and 22 the expressions for u 1, N x1, and M x1 become

$$ \begin{aligned} u_{1}(x)&={\frac{E_{2}}{E_{1}}}\mu C_{1}\cos (\mu x)-{\frac{E_{2}}{E_{1}}} \mu C_{2}\sin (\mu x)+C_{5}x+C_{6}\\ M_{x1}(x)&={\frac{{E_{1}E_{3}-E_{2}^{2}}}{E_{1}}}\mu^{2}C_{1}\sin (\mu x)+{\frac{{E_{1}E_{3}-E_{2}^{2}}}{E_{1}}}\mu^{2}C_{2}\cos (\mu x)+E_{2}C_{5}\\ N_{x1}(x)&=E_{1}C_{5} \end{aligned} $$
(23)

The constants of integration C 1–C 6 are obtained using the boundary conditions of the beam. The parameter μ must be minimized to find the minimum value of \(N_{x}^{T}\) associated with the thermal buckling load.

Five types of boundary conditions are assumed for the FGM beam. Let us consider a beam with both edges clamped. The edge conditions of the clamped–clamped FGM beam are (Khdeir 2001)

$$ u_{1}(0)=w_{1}(0)={\frac{dw_{1}}{dx}}(0)=u_{1}(L)=w_{1} (L)={\frac{dw_{1}}{dx}}(L)=0 $$
(24)

Using Eqs. 23 and 24, the constants C 1 to C 6 must satisfy the system of equations

$$ \left[\begin{array}{ccllll} 0 &1 & 0 & 1 & 0 & 0\\ \sin (\mu L) &\cos (\mu L) & L & 1 & 0 &0\\ \mu &0 & 1 & 0 & 0 & 0\\ \mu \cos (\mu L) &-\mu \sin (\mu L) & 1 & 0 & 0 &0\\ {\frac{E_{2}}{E_{1}}}\mu &0 & 0 & 0 & 0 & 1\\ {\frac{E_{2}}{E_{1}}}\mu \cos (\mu L) &-{\frac{E_{2}}{E_{1}}}\mu \sin (\mu L) & 0 & 0 & L & 1\\\ \end{array}\right] \left[ \begin{array}{l} C_{1}\\ C_{2}\\ C_{3}\\ C_{4}\\ C_{5}\\ C_{6} \end{array} \right]= \left[ \begin{array}{l} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{array} \right] $$
(25)

To have a non-trivial solution, the determinant of coefficient matrix must be set to zero, which yields

$$ \mu L(2-2\cos(\mu L)-\mu L\sin(\mu L))=0 $$
(26)

The smallest positive value of μ which satisfies Eq. 26 is \(\mu_{min}={\frac{6.28319}{L}}.\) Table 1 shows different types of boundary conditions and the minimum value of μ associated with the thermal buckling loads. Now, the critical thermal force of the beam for all cases of boundary conditions can be written in the form

$$ N_{xcr}^{T}=C{\frac{E_{1}E_{3}-E_{2}^{2}}{E_{1}L^{2}}} $$
(27)

where C is a constant and depends on the type of boundary conditions and is 39.47842 for C–C beams, 9.86960 for S–S and C–R beams, 2.46740 for S–R beams, and 20.19077 for C–S beams.

Table 1 Boundary conditions and minimum value of μ for various edge supports
Full size table

For an isotropic homogeneous beam, setting k = 0 in Eq. 27 gives

$$ N_{xcr}^{T}=C{\frac{Eh^{3}}{12L^{2}}} $$
(28)

which is a well-known relation for the critical axial buckling load of beams given in Yang (2005).

4 Types of thermal loading

4.1 Uniform temperature rise

Consider a beam at reference temperature T 0. When the axial displacement is prevented, the uniform temperature may be raised to \(T_{0}+\Updelta T\) such that the beam buckles. Substituting \(T=T_{0}+\Updelta T\) into Eq. 10 gives

$$ N_{x}^{T}= \Updelta T h\left(E_{m}\alpha_{m}+{\frac{E_{cm}\alpha_{m}+E_{m}\alpha_{cm}} {k+1}}+{\frac{E_{cm}\alpha_{cm}}{2k+1}}\right) $$
(29)

Using Eqs. 27 and 29, the critical buckling temperature \(\Updelta T_{cr}^{Uni}\) is expressed in the form

$$ \Updelta T_{cr}^{Uni}={\frac{C}{\alpha_{m}}}\left( {\frac{h}{L}}\right)^{2}{\frac{F(k,\xi)}{G(k,\xi,\zeta)}} $$
(30)

where, \(\xi={\frac{E_{cm}}{E_{m}}}, \zeta={\frac{\alpha_{cm}}{\alpha_{m}}}\). The functions F(k, ξ) and G(k, ξ, ζ) are defined as

$$ \begin{aligned} F(k,\xi)&={\frac{1}{12}}+{\frac{\xi(k^{2}+k+2)}{4(k+1)(k+2)(k+3)}} -{\frac{\xi^{2}k^{2}}{4(k+1)(k+2)^{2}(k+1+\xi)}}\\ G(k,\xi,\zeta)&=1+{\frac{\xi +\zeta}{k+1}}+{\frac{\xi \zeta}{2k+1}} \end{aligned} $$
(31)

4.2 Linear temperature through the thickness

Consider a thin FGM beam which the temperature in ceramic-rich and metal-rich surfaces are T c and T m , respectively. The temperature distribution for the given boundary conditions is obtained by solving the heat conduction equation along the beam thickness. If the beam thickness is thin enough, the temperature distribution is approximated linear through the thickness. So the temperature as a function of thickness coordinate z can be written in the form

$$ T=T_{m}+(T_{c}-T_{m})\left({\frac{1}{2}}+{\frac{z}{h}}\right) $$
(32)

Substituting Eq. 32 into Eq. 10 gives the thermal force as

$$ \begin{aligned} N_{x}^{T}=&h(T_{m}-T_{0})\left(E_{m}\alpha_{m}+ {\frac{E_{cm}\alpha_{m}+E_{m}\alpha_{cm}}{k+1}}+ {\frac{E_{cm}\alpha_{cm}}{2k+1}}\right)\\ &+h\Updelta T\left({\frac{E_{m}\alpha_{m}}{2}} +{\frac{E_{cm}\alpha_{m}+E_{m}\alpha_{cm}}{k+2}} +{\frac{E_{cm}\alpha_{cm}}{2k+2}}\right) \end{aligned} $$
(33)

where \(\Updelta T=T_{c}-T_{m}.\) Combining Eqs. 27 and 33 gives the final form for the critical buckling temperature difference through the thickness as

$$ \Updelta T_{cr}^{Linear}={\frac{C}{\alpha_{m}}}\left({\frac{h}{L}}\right)^{2} {\frac{F(k,\xi)}{H(k,\xi,\zeta)}}-(T_{m}-T_{0}){\frac{G(k,\xi,\zeta)} {H(k,\xi,\zeta)}} $$
(34)

Here, the functions F(k, ξ) and G(k, ξ, ζ) are defined in Eq. 31, and the function H(k, ξ, ζ) is defined as

$$ H(k,\xi,\zeta)={\frac{1}{2}}+{\frac{\xi +\zeta}{k+2}}+{\frac{\xi \zeta}{2k+2}} $$
(35)

4.3 Non-linear temperature through the thickness

Assume an FGM beam where the temperature in ceramic-rich and metal-rich surfaces are T c and T m , respectively. The governing equation for the steady-state one-dimensional heat conduction equation, in the absence of heat generation, becomes

$${\frac{d}{dz}}\left(K(z){\frac{dT}{dz}}\right)=0, T \left({\frac{h}{2}}\right)=T_{c}, T\left(-{\frac{h}{2}}\right)=T_{m}$$
(36)

where K(z) is given by Eq. 2. Solving this equation via polynomial series and taking the first seven terms, yields the temperature distribution across the thickness of the beam as

$$ T=T_{m}+{\frac{(T_{c}-T_{m})}{D}}\left[ \sum_{i=0}^{5}{\frac{(-1)^{i}}{ik+1}} \left( {\frac{K_{cm}}{K_{m}}}\right)^{i}\left( {\frac{1}{2}}+{\frac{z}{h}}\right)^{ik+1} \right] $$
(37)

with

$$ D=\sum_{i=0}^{5}{\frac{(-1)^{i}}{ik+1}}\left( {\frac{K_{cm}}{K_{m}}}\right)^{i} $$
(38)

Evaluating \(N_{x}^{T}\) and solving for \(\Updelta T\) gives the critical bucking temperature difference as

$$ \Updelta T_{cr}^{Non{\hbox{-}}Lin}={\frac{C}{\alpha_{m}}}\left({\frac{h}{L}}\right)^{2} {\frac{F(k,\xi)}{I(k,\xi,\zeta,\gamma)}}-(T_{m}-T_{0}){\frac{G(k,\xi,\zeta)} {I(k,\xi,\zeta,\gamma)}} $$
(39)

In this relation \(\gamma={\frac{K_{cm}}{K_{m}}}\) and the function I(k, ξ, ζ, γ) is defined as

$$ \begin{aligned} I(k,\xi,\zeta,\gamma)=&{\frac{1}{D}}\left[{\frac{1}{2}}+{\frac{1}{k+2}} \left(\xi+\zeta-{\frac{\gamma}{k+1}}\right)\right.\\ &\left. +{\frac{1}{2k+2}}\left(\xi\zeta-{\frac{\gamma\xi+\gamma\zeta}{k+1}} +{\frac{\gamma^{2}}{2k+1}}\right)+{\frac{1}{3k+2}}\left({\frac{\gamma^{2}\xi+\gamma^{2}\zeta} {2k+1}}-{\frac{\gamma^{3}}{3k+1}}-{\frac{\gamma\xi\zeta}{k+1}}\right)\right.\\ &+{\frac{1}{4k+2}}\left({\frac{\gamma^{4}}{4k+1}}-{\frac{\gamma^{3}\xi + \gamma^{3}\zeta} {3k+1}} +{\frac{\gamma^{2}\xi\zeta}{2k+1}}\right)+{\frac{1}{5k+2}}\left({\frac{\gamma^{4}\xi +\gamma^{4}\zeta}{4k+1}}\right.\\ &\left. -{\frac{\gamma^{5}}{5k+1}}-\left.{\frac{\gamma^{3}\xi\zeta}{3k+1}}\right) +{\frac{1}{6k+2}}\left({\frac{\gamma^{4}\xi\zeta}{4k+1}} -{\frac{\gamma^{5}\xi+\gamma^{5}\zeta}{5k+1}}\right)-{\frac{\gamma^{5}\xi\zeta}{(5k+1)(7k+2)}} \right] \end{aligned} $$
(40)

5 Result and discussions

Consider a ceramic–metal functionally graded beam. The combination of materials consist of aluminum and alumina. The elasticity modulus, the thermal expansion coefficient, and the thermal conductivity coefficient for aluminum are E m  = 70 GPa, α m  = 23 × 10−6/°C and K m  = 204 W/m°K and for alumina E c  = 380 GPa, α c  = 7.4 × 10−6/°C and K c  = 10.4 W/m°K, respectively. The beam is assumed under various types of boundary conditions on both sides.

Figure 3 depicts the critical bucking temperature versus L/h for a fully metallic beam made of aluminum for various types of boundary conditions subjected to the uniform temperature rise. It is apparent that, as the ratio L/h increases, the critical bucking temperature decreases. Also, the critical buckling temperature for the S–S and C–R types of boundary conditions are identical and lower than C–C and C–S beams, but larger than the value related to the S–R beams.

Fig. 3
figure 3

Critical bucking temperature versus L/h for a pure isotropic beam with various boundary conditions

Full size image

Figure 4 demonstrates the influence of the power law index k on the bucking temperature of a C–S FGM beam in the case of uniform temperature rise. By increasing the power law index k, the critical buckling temperature decreases for k < 2 and increases for 2 < k < 10 and then decreases for k > 10. It is noted that the buckling temperature of FGM beam decreases with the increase of the L/h ratio, as expected.

Fig. 4
figure 4

Critical buckling temperature versus power law index k for a C–S FGM beam

Full size image

Figure 5 shows the buckling temperature of a S–S FGM beam versus the ratio h/L with power law index k = 1. Also, it is assumed that the temperature difference between the metal-rich surface of the FGM and reference temperature is T m  − T 0 = 5°C (Javaheri and Eslami 2002b; Lanhe 2004). Three types of thermal loads are compared in this figure. It can be concluded that the critical buckling temperature for uniform temperature rise is lower than linear temperature variation through the thickness, where the latter case is also lower than the nonlinear temperature distribution through the thickness.

Fig. 5
figure 5

A comparison between different types of thermal loading

Full size image

Tables 2 and 3 show the results for an FGM beam for the linear and nonlinear cases of temperature distribution through the thickness, respectively. In these cases, boundary conditions are assumed to be C–R for beam. Results are listed for various values of k and L/h ratio. It is apparent that in both cases of thermal loading, the bucking temperature of the FGM beams decreases with the increase of L/h ratio. Also, the decrease of the critical bucking temperature decreases with the increase of this ratio. For nonlinear temperature distribution across the thickness, the buckling temperature decreases with the increase of the power law index k.

Table 2 Critical bucking temperature for a C–R FGM beam in the case of linear temperature distribution through the thickness
Full size table
Table 3 Critical bucking temperature for a C–R FGM beam in the case of non-linear temperature distribution through the thickness
Full size table

6 Conclusion

In the present article, the equilibrium and stability equations for the FGM beams with various types of boundary conditions are obtained. The derivation is based on the Euler–Bernoulli beam theory, with the assumption of power law composition for the constituent material. The buckling analysis under three types of thermal loading is presented. Closed form solutions are derived for the thermal buckling. It is concluded that:

  1. (1)

    In each case of thermal loading and boundary conditions, the critical bucking temperature for the FGM beams is lower than fully ceramic beam but greater than fully metallic beam.

  2. (2)

    The critical temperature of isotropic homogeneous beam is independent of elasticity modulus, but for an FGM beam the elasticity modulus of the constituent materials have significant effect on the critical buckling temperature.

  3. (3)

    The critical bucking temperatures for the C–R and S–S boundary conditions are identical in each case of thermal loading.

  4. (4)

    Based to the Euler–Bernoulli beam theory, the critical bucking temperature is proportional to the square of h/L ratio for both FGM and pure isotropic beams.

  5. (5)

    For functionally graded beams under uniform temperature rise, by increasing the power law index k, the critical buckling temperature decreases for k < 2 and increases for 2 < k < 10 and then decreases for k > 10.