1 Introduction

The applied structures in buildings, bridges, reservoir foundations, swimming pools, and various economic and industrial designs are formed from different components, of which the most important parts are plates. The plates in many structures are subjected to various tensile, bending, and compressive and shear loadings in various working conditions. In safe conditions, such loads cause buckling or static instability, which is very important in practice. A plate may be subjected to non-uniform load at the edges that can be applied as linear or nonlinear [1]. A comprehensive analysis was presented by Timoshenko and Gere [2] in which the linear and nonlinear buckling problems for plates with different forms under a variety of loadings and substantial presentation of the results of critical loads and buckling modes that are widely used in practical engineering design. Extensive studies about buckling of rectangular plates, being subjected to uniform in-plane loading, have been performed by Michelussi [3]. Leissa and Kang presented an exact solution for buckling analysis of a thin rectangular plate with two opposite simply-supported edges, using power series of Frobenius. In their work, the in-plane loading varies linearly along the edges. Additionally, they examined the vibration of an isotropic rectangular plate under linear load in another research [4, 5]. Javaheri and Eslami investigated the buckling of FGM plates under compressive plane load. They concluded that the critical buckling load for FGM plates increases as the ratio of width per length rises, and on the other hand, the critical load decreases as the ratio of width per thickness grows [6]. Bret and Devarakonda examined the buckling of rectangular plates with simply-supported boundary conditions at the edges which are subjected to sinusoidal loading, using Galerkin method [7]. The buckling of rectangular plates subjected to a variety of non-uniform loadings such as concentrated, local, sinusoidal, and other loadings was studied by Jana and Bhaskar [8, 9]. Wang et al. utilized the differential quadrature method to calculate the buckling load of rectangular plates which are subjected to non-uniform load at the edges. They examined cosine, linear, and parabolic shaped loads in the buckling load [10–12]. Hosseini-Hashemi applied Mindlin’s plate theory to study isotropic rectangular plate buckling under in-plane loading with different boundary conditions [13]. Kumar Panda and Ramachandra investigated the buckling of composite plates subjected to non-uniform linear and parabolic shaped loadings at the edges, using shear deformation theory [14]. Latifi et al. examined the buckling of rectangular plates made of FGM in different boundary conditions and under biaxial compressive loading. The analysis is based on the classical plate theory with large deformations [15]. Abolghasemi et al, investigated the buckling of rectangular plates under non-uniform in-plane load, using the first-order shear deformation theory. The results were compared with the numerical solutions and those of the classical theory [16]. Orthotropic plates had high efficiency in civil infrastructure and other structural applications, because, they had such advantages as high stiffness ratio and resistance versus weight. Concrete slabs with reinforced asymmetric steel on both sides are examples of orthotropic plates. Harris presented the buckling analysis of orthotropic rectangular plates which were subjected to uniaxial and in-plane loadings in two directions [17]. Hwang and Lee analyzed the buckling of orthotropic plates under optional in-plane load. They examined the behavior of the plate under non-uniform loading with various boundary conditions, using the finite element method [18]. Lopatin and Morozov investigated the buckling analysis of orthotropic plate with CCFF boundary conditions. The problem was solved via partial differential equations and Galerkin method [19, 20]. Thai and Kim applied Levy solution to the buckling analysis of orthotropic plates, using two-variable refined plate theory [21]. Jafari and Eftekhari analyzed the buckling load and the natural frequencies of rectangular orthotropic plates located on elastic foundation for various types of loadings and boundary conditions, using a combination of Ritz and differential quadrature methods [22]. It is observed that one of the main conditions of the stability of a structure is providing appropriate support for the structure, the reaction of the structures on the foundation has long been considered. In Winkler model, the elastic foundation is independently modeled, using a series of springs. Despite the effectiveness of this model, the behavior of the elastic foundation is actually continuous, but it models the independent springs to analyze the behavior of the elastic foundation [23]. To correct this deficiency, researchers used Pasternak model, which is the most common one in this area, by adding a beam or plate with lateral shear stiffness [24]. Kim examined the stability and dynamic response of a thin infinite plate resting on Pasternak foundation [25]. Saeidifar and Sadeghi presented an analytical solution for the buckling analysis of rectangular plate under uniaxial compressive loading with changes in the thickness and modulus of elasticity in the y direction [26]. Akhavan et al. introduced an exact solution for the buckling analysis of Mindlin rectangular plates under uniform in-plane linear loading on elastic foundation, assuming two opposite simply-supported edges. To extract the governing equations, the analysis method is based on Mindlin theory, considering the effect of first-order shear deformation and interaction of plate-foundation. Moreover, in two other papers, they examined the analysis of free vibration of Mindlin rectangular plates under uniform in-plane linear loading [27, 28]. Hosseini-Hashemi et al. investigated hydrostatic vibration and buckling analysis of rectangular plates resting on Pasternak foundation and subjected to in-plane loads with linear variation for different boundary conditions [29]. Bodaghi and Saidi examined the buckling behavior of rectangular plates made of FGM materials on elastic Pasternak foundation under in-plane uniaxial linear and nonlinear loadings, based on the classical theory. Using Levy solution, the buckling equation was transformed to an ordinary differential equation with variable coefficients and then was solved exactly using power series of Frobenius method [30]. Panahandeh Shahraki et al., studied the buckling of FGM cracked plates supported by Pasternak foundation [31]. Foroughi and Azhari presented the buckling and free vibration of thick FGM plates resting on Pasternak elastic foundation, using finite strip method. The buckling analysis was carried out by normal finite strip method [32]. Yaghoobi and Fereidoon presented the analysis of mechanical and thermal buckling of FGM plate on elastic foundation, supposing shear deformation theory [33]. Viswanathana and Navaneethakrishnan investigated the buckling analysis of rectangular plate with variable thickness resting on elastic foundation, using spline approximation method [34]. Lam and Wang presented common exact solutions for elastic bending, buckling, and vibration of rectangular plate, using Levy solution on two-parametric elastic foundation via Green functions [35].

According to the abovementioned literature review, several works have been published on isotropic plate buckling under uniform uniaxial or biaxial loadings, whereas the buckling of orthotropic plate with non-uniform nonlinear loading is less considered, mainly due to the complexity of the solution process. This study introduces an exact analysis for the buckling of orthotropic rectangular plates based on the classical plate theory. It is assumed that a rectangular plate is resting on Pasternak (two-parametric) elastic foundation and is subjected to non-uniform in-plane biaxial loading. Using Levy resolution, the buckling equation is reduced to an ordinary differential equation with variable coefficients. It is solved using power series of Frobenius. By applying different combinations of boundary conditions along the opposite edge of the plate, the critical buckling load is obtained. The accuracy of results is confirmed by comparing them with those of previous studies as well as the finite element method. Also, the influences of parameters such as aspect ratio, the ratio of modulus of elasticity in two different directions, the type of non-uniform loading in both uniaxial and biaxial states, the various types of boundary conditions, the foundation coefficients on the critical buckling load of plate are examined.

2 Formulation presentation

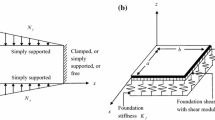
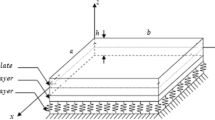
Assume a rectangular thin plate with lateral dimensions of a × b and uniform thickness of h, as shown in Fig. 1, which is simply supported at x = 0, a while the other two edges of y = 0, b have any arbitrary conditions such as the clamped (C), and simply (S) or free support (F). It is assumed that the material is orthotropic, and the main orthotropic directions are in the directions of x and y-axes. Shear modulus G of the plate and the relationship between four independent elastic constants can be expressed as follows [1]:

$$G \approx \frac{{\sqrt {E_{x} E_{y} } }}{{2\left( {1 + \sqrt {\upsilon_{x} \upsilon_{y} } } \right)}},\quad \,\frac{{\upsilon_{x} }}{{E_{x} }} = \frac{{\upsilon_{y} }}{{E_{y} }}.$$
(1)
Fig. 1
figure 1

Orthotropic rectangular plate resting on Pasternak elastic foundation

Full size image

In the plane stress condition, bending and torsional stiffness of the orthotropic plate is defined as follows [1]:

$$\begin{aligned} D_{11} & = \frac{{E_{x} h^{3} }}{{12\left( {1 - \nu_{xy} v_{yx} } \right)}},\,\quad D_{12} = D_{21} = \frac{{E_{x} v_{yx} h^{3} }}{{12\left( {1 - \nu_{xy} v_{yx} } \right)}}\,\,\,\,\,\,\, \\ D_{22} & = \frac{{E_{y} h^{3} }}{{12\left( {1 - \nu_{xy} v_{yx} } \right)}},\,\quad D_{66} = \frac{{G_{xy} h^{3} }}{12}.\,\,\, \\ \end{aligned}$$
(2)

The governing equation in the buckling of orthotropic rectangular plate under biaxial in-plane loading, regardless of the shear force N xy per unit of the length, which rests on Pasternak elastic foundation is as follows [30]:

$$\begin{aligned} & D_{11} \frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\left( {D_{12} + 2D_{66} } \right)\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + D_{22} \frac{{\partial^{4} w}}{{\partial y^{4} }} + K_{w} .w - K_{s} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) \\ & \quad - N_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }} - N_{y} \frac{{\partial^{2} w}}{{\partial y^{2} }} = 0, \\ \end{aligned}$$
(3)

where K w and K s are the coefficients of lateral and shear stiffness of the foundation, respectively. W, N x , N y are out-plane displacement, and the normal forces per unit of the length along x and y directions, respectively. To make a dimensionless form of the governing Eq. (3), the following parameters are defined as follows:

$$\begin{aligned} &\xi = \frac{x}{a} ,\,\quad \,\eta = \frac{y}{b}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{\partial \xi }{\partial x} = \frac{1}{a}\,,\quad \,\frac{\partial \eta }{\partial y} = \frac{1}{b} \hfill \\ &\frac{\partial w}{\partial x} = \frac{\partial w}{\partial \xi }\frac{\partial \xi }{\partial x} = \frac{\partial w}{\partial \xi }\left( {\frac{1}{a}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{\partial w}{\partial y} = \frac{\partial w}{\partial \eta }\frac{\partial \eta }{\partial y} = \frac{\partial w}{\partial \eta }\left( {\frac{1}{b}} \right). \hfill \\ \end{aligned}$$
(4)

Based on Levy approach, the following expansions of displacements are chosen as follows by considering that the two opposite sides of the plate are simply supported in x direction:

$$w\left( {\eta ,\xi } \right) = Y_{m} \left( \eta \right)\text{sin}\left( {m\pi \xi } \right),$$
(5)

where Y m is a function of η, and m is the number of half-waves of the shape modes in x direction. This function satisfies boundary conditions in ξ = 0, 1. Substituting the parameters of Eqs. (4) and (5) in (3), and arranging it based on the order of Y m , the following equation can be obtained:

$$\begin{aligned} & D_{22} \left( {\frac{1}{b}} \right)^{4} Y_{m}^{IV} + \left[ { - 2\left( {D_{12} + 2D_{66} } \right) \left( {\frac{m\pi }{ab}} \right)^{2} - K_{s} \left( {\frac{1}{{b^{2} }}} \right) - N_{y} \left( {\frac{1}{{b^{2} }}} \right)} \right]Y^{\prime\prime}_{m} \\ & \quad + \left[ {D_{11} \left( {\frac{m\pi }{a}} \right)^{4} + K_{w} + K_{s} \left( {\frac{m\pi }{a}} \right)^{2} + N_{x} \left( {\frac{m\pi }{a}} \right)^{2} } \right]Y_{m} = 0. \\ \end{aligned}$$
(6)

2.1 Orthotropic rectangular plate under biaxial loading

In this section, various types of non-uniform loading are examined, and the governing differential equations of plate buckling are solved by Frobenius method. The distribution of in-plane loading per unit length in direction x is considered as follows:

$$N_{x} = - \mu N_{0} \left( {a_{0} + a_{1} \eta + a_{2} \eta^{2} + a_{3} \eta^{3} + a_{4} \eta^{4} + a_{5} \eta^{5} } \right),$$
(7)

where a 1 , a 2 , a 3 , a 4 , and a 5 are determined as dependent on the type of loading. N 0 is the maximum intensity of the in-plane load per unit length. The loading in y direction is defined in the form of the mean function of loading in x direction with proportion coefficient (R) as Eq. (8):

$$\begin{aligned} N_{y} & = R \bar{N}_{x} ,\quad \,\bar{N}_{x} = \frac{1}{b}\mathop \int \limits_{0}^{b} N_{x} \text{d}y = \mathop \int \limits_{0}^{1} N_{x} \text{d}\eta \, \\ N_{y} & = - R \mu N_{0} \left( {a_{0} + \frac{{a_{1} }}{2} + \frac{{a_{2} }}{3} + \frac{{a_{3} }}{4} + \frac{{a_{4} }}{5} + \frac{{a_{5} }}{6}} \right). \\ \end{aligned}$$
(8)

In this study, five cases of loading are examined according to Fig. 2. Also, the coefficients of a i and μ can be seen for each case in Table 1.

Fig. 2
figure 2

Schematic of non-uniform loading cases of in-plane loading with boundary condition SCSC

Full size image
Table 1 Different types of loading rectangular plate
Full size table

2.2 Applying Frobenius method to governing equations

Suppose that the rectangular plate is under in-plane loading according to Fig. 2 in both x and y directions. N 0 is the intensity of compressive force (load factor per length unit). In general, to solve the governing equation by substituting Eqs. (7) and (8) in (6), the following equation can be obtained:

$$\begin{aligned} & D_{22} \left( {\frac{1}{b}} \right)^{4} Y_{m}^{IV} + \left[ { - 2\left( {D_{12} + 2D_{66} } \right)\left( {\frac{m\pi }{ab}} \right)^{2} - \frac{{K_{s} }}{{b^{2} }} + \frac{{N_{0} R\mu }}{{b^{2} }}\left( {a_{0} + \frac{{a_{1} }}{2} + \frac{{a_{2} }}{3} + \frac{{a_{3} }}{4} + \frac{{a_{4} }}{5} + \frac{{a_{5} }}{6}} \right)} \right]Y^{\prime\prime}_{m} \\ & \quad + \left[ {D_{11} \left( {\frac{m\pi }{a}} \right)^{4} + K_{w} + K_{s} \left( {\frac{m\pi }{a}} \right)^{2} - \mu N_{0} \left( {a_{0} + a_{1} \eta + a_{2} \eta^{2} + a_{3} \eta^{3} + a_{4} \eta^{4} + a_{5} \eta^{5} } \right)\left( {\frac{m\pi }{a}} \right)^{2} } \right]Y_{m} = 0. \\ \end{aligned}$$
(9)

The differential Eq. (9) can be solved exactly by the power series solution, using Frobenius method:

$$Y_{m} = \mathop \sum \limits_{n = 0}^{\infty } C_{m,n} \eta^{n} .$$
(10)

By substituting the power series of Eq. (10) in (9), the result is as follows:

$$\begin{aligned} &D_{22} \left( {\frac{1}{b}} \right)^{4} \left( {\mathop \sum \limits_{n = 4}^{\infty } n\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)C_{m,n} \eta^{n - 4} } \right) \hfill \\ &\quad+ \left[ { - 2\left( {D_{12} + 2D_{66} } \right) \left( {\frac{m\pi }{ab}} \right)^{2} - K_{s} \left( {\frac{1}{{b^{2} }}} \right)} \right. \hfill \\ &\quad\left. { + \left( {\frac{R}{{b^{2} }}} \right)\mu N_{0} \left( {a_{0} + \frac{{a_{1} }}{2} + \frac{{a_{2} }}{3} + \frac{{a_{3} }}{4} + \frac{{a_{4} }}{5} + \frac{{a_{5} }}{6}} \right)} \right]\left( {\mathop \sum \limits_{n = 2}^{\infty } n\left( {n - 1} \right)C_{m,n} \eta^{n - 2} } \right) \hfill \\ &\quad\left. { + \left[ {D_{11} \left( {\frac{m\pi }{a}} \right)^{4} + K_{w} + K_{s} \left( {\frac{m\pi }{a}} \right)^{2} } \right. - \mu N_{0} \left( {a_{0} + a_{1} \eta + a_{2} \eta^{2} + a_{3} \eta^{3} + a_{4} \eta^{4} + a_{5} \eta^{5} } \right)\left( {\frac{m\pi }{a}} \right)^{2} } \right]\left( {\mathop \sum \limits_{n = 0}^{\infty } C_{m,n} \eta^{n} } \right) = 0 \hfill \\ \end{aligned}$$
(11)

By collecting the indexes of Eq. (11), multiplying two equal sides of the equation in b 4/D 1, and considering the following dimensionless parameters, Eq. (12) results as follows:

$$\begin{aligned} &D_{11} = D_{1} \,,\,\quad D_{22} = D_{2} ,\quad \,\left( {D_{12} + 2D_{66} } \right) = D_{3} \\ &Q = \frac{a}{b} ,\quad \bar{K}_{w} = \frac{{K_{w} b^{4} }}{{D_{1} }} , \quad \bar{K}_{s} = \frac{{K_{s} b^{2} }}{{D_{1} }},\quad N_{0} = \frac{{N_{0} b^{2} }}{{D_{1} }} , \quad \beta = \frac{m\pi }{Q}. \\ \end{aligned}$$
(12)

After rearranging, Eq. (13) is obtained in the following way:

$$\begin{aligned} & \mathop \sum \limits_{n = 0}^{\infty } \left( {\left( {\frac{{D_{2} }}{{D_{1} }}\left( {n + 4} \right)\left( {n + 3} \right)\left( {n + 2} \right)\left( {n + 1} \right)C_{m,n + 4} } \right.} \right. \\ & \quad + \left[ { - 2\frac{{D_{3} }}{{D_{1} }} \left( \beta \right)^{2} - \bar{K}_{s} + \left( {a_{0} + \frac{{a_{1} }}{2} + \frac{{a_{2} }}{3} + \frac{{a_{3} }}{4} + \frac{{a_{4} }}{5} + \frac{{a_{5} }}{6}} \right)\mu R \bar{N}_{0} } \right] \\ & \quad \times \left( {n + 2} \right)\left( {n + 1} \right)C_{m,n + 2} \left. { + \left[ {\left( \beta \right)^{4} + \bar{K}_{w} + \bar{K}_{s} \left( \beta \right)^{2} - a_{0} \mu \bar{N}_{0} \left( \beta \right)^{2} } \right]C_{m,n} } \right)\eta^{n} \\ & \quad - \left( {a_{1} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,n} } \right)\eta^{n + 1} - \left( {a_{2} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,n} } \right)\eta^{n + 2} - \left( {a_{3} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,n} } \right)\eta^{n + 3} \\ & \quad - \left( {a_{4} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,n} } \right)\eta^{n + 4} \left. { - \left( {a_{5} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,n} } \right)\eta^{n + 5} } \right) = 0. \\ \end{aligned}$$
(13)

According to the same indexes for coefficient η 0, the following equation is obtained:

$$\begin{aligned} C_{m,4} & = \left( {\frac{{D_{1} }}{{24D_{2} }}} \right)\left( { - 2\left[ { - 2\frac{{D_{3} }}{{D_{1} }} \left( \beta \right)^{2} - \bar{K}_{s} + \left( {a_{0} + \frac{{a_{1} }}{2} + \frac{{a_{2} }}{3} + \frac{{a_{3} }}{4} + \frac{{a_{4} }}{5} + \frac{{a_{5} }}{6}} \right)R\mu \bar{N}_{0} } \right]} \right.C_{m,2} \\ &\quad \left. { - \left[ {\left( \beta \right)^{4} + \bar{K}_{w} + \bar{K}_{s} \left( \beta \right)^{2} - a_{0} \mu \bar{N}_{0} \left( \beta \right)^{2} } \right]C_{m,0} } \right) \\ \end{aligned}$$
(14)

and for coefficient η 1, it can be calculated that:

$$\begin{aligned} C_{m,5} & = \left( {\frac{{D_{1} }}{{120D_{2} }}} \right)\left( { - 6\left[ { - 2\frac{{D_{3} }}{{D_{1} }} \left( \beta \right)^{2} - \bar{K}_{s} + \left( {a_{0} + \frac{{a_{1} }}{2} + \frac{{a_{2} }}{3} + \frac{{a_{3} }}{4} + \frac{{a_{4} }}{5} + \frac{{a_{5} }}{6}} \right)R\mu \bar{N}_{0} } \right]} \right.C_{m,3} \\ & \quad - \left[ {\left( \beta \right)^{4} + \bar{K}_{w} + \bar{K}_{s} \left( \beta \right)^{2} - a_{0} \mu \bar{N}_{0} \left( \beta \right)^{2} } \right]C_{m,1} \left. { + \left( {a_{1} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,0} } \right)} \right) \\ \end{aligned}$$
(15)

and for coefficient η 2,

$$\begin{aligned} C_{m,6} & = \left( {\frac{{D_{1} }}{{360D_{2} }}} \right)\left( { - 12\left[ { - 2\frac{{D_{3} }}{{D_{1} }} \left( \beta \right)^{2} - \bar{K}_{s} + \left( {a_{0} + \frac{{a_{1} }}{2} + \frac{{a_{2} }}{3} + \frac{{a_{3} }}{4} + \frac{{a_{4} }}{5} + \frac{{a_{5} }}{6}} \right)R \mu \bar{N}_{0} } \right]C_{m,4} } \right. \\ & \quad - \left[ {\left( \beta \right)^{4} + \bar{K}_{w} + \bar{K}_{s} \left( \beta \right)^{2} - a_{0} \mu \bar{N}_{0} \left( \beta \right)^{2} } \right]C_{m,2} + \left( {a_{1} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,1} } \right)\left. { + \left( {a_{2} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,0} } \right)} \right) \\ \end{aligned}$$
(16)

and for the coefficient η 3,

$$\begin{aligned} C_{m,7} & = \left( {\frac{{D_{1} }}{{840D_{2} }}} \right)\left( { - 20\left[ { - 2\frac{{D_{3} }}{{D_{1} }} \left( \beta \right)^{2} - \bar{K}_{s} + \left( {a_{0} + \frac{{a_{1} }}{2} + \frac{{a_{2} }}{3} + \frac{{a_{3} }}{4} + \frac{{a_{4} }}{5} + \frac{{a_{5} }}{6}} \right)R\mu \bar{N}_{0} } \right]C_{m,5} } \right. \\ & \quad - \left[ {\left( \beta \right)^{4} + \bar{K}_{w} + \bar{K}_{s} \left( \beta \right)^{2} - a_{0} \mu \bar{N}_{0} \left( \beta \right)^{2} } \right]C_{m,3} + \left( {a_{1} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,2} } \right) \\ & \quad\left. { + \left( {a_{2} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,1} } \right) + \left( {a_{3} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,0} } \right)} \right) \\ \end{aligned}$$
(17)

and for coefficient η 4,

$$\begin{aligned} C_{m,8} & = \left( {\frac{{D_{1} }}{{1680D_{2} }}} \right)\left( { - 30\left[ { - 2\frac{{D_{3} }}{{D_{1} }} \left( \beta \right)^{2} - \bar{K}_{s} + \left( {a_{0} + \frac{{a_{1} }}{2} + \frac{{a_{2} }}{3} + \frac{{a_{3} }}{4} + \frac{{a_{4} }}{5} + \frac{{a_{5} }}{6}} \right)R\mu \bar{N}_{0} } \right]} \right.C_{m,6} \\ & \quad - \left[ {\left( \beta \right)^{4} + \bar{K}_{w} + \bar{K}_{s} \left( \beta \right)^{2} - a_{0} \mu \bar{N}_{0} \left( \beta \right)^{2} } \right]C_{m,4} + \left( {a_{1} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,3} } \right) \\ & \quad + \left( {a_{2} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,2} } \right) + \left( {a_{3} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,1} } \right)\left. { + \left( {a_{4} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,0} } \right)} \right) \\ \end{aligned}$$
(18)

and for η n η = 5, 6, 7, … equals:

$$\begin{aligned} C_{m,n + 4} &= \frac{{D_{1} }}{{D_{2} \left( {n + 4} \right)\left( {n + 3} \right)\left( {n + 2} \right)\left( {n + 1} \right)}}\left( { - \left[ { - 2\frac{{D_{3} }}{{D_{1} }} \left( \beta \right)^{2} - \bar{K}_{s} } \right.} \right. \hfill \\ &\quad\left. { + \left( {a_{0} + \frac{{a_{1} }}{2} + \frac{{a_{2} }}{3} + \frac{{a_{3} }}{4} + \frac{{a_{4} }}{5} + \frac{{a_{5} }}{6}} \right)R \mu \bar{N}_{0} } \right]\left( {n + 2} \right)\left( {n + 1} \right)C_{m,n + 2} \hfill \\&\quad - \left[ {\left( \beta \right)^{4} + \bar{K}_{w} + \bar{K}_{s} \left( \beta \right)^{2} - a_{0} \mu \bar{N}_{0} \left( \beta \right)^{2} } \right]C_{m,n} + a_{1} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,n - 1} + a_{2} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,n - 2} \hfill \\ &\quad+ a_{3} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,n - 3} \left. { + a_{4} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,n - 4} + a_{5} \mu \bar{N}_{0} \left( \beta \right)^{2} C_{m,n - 5} } \right) \hfill \\ \end{aligned}$$
(19)

Equations (14)–(19) are reversibility equations for C m,n as arbitrary coefficients when n ≥ 4.

2.3 Types of loading

Once the rectangular plate is subjected to in-plane CASE-A loading according to Fig. 2, −N 0 (load factor per length unit) is the intensity of compressing force in η = 1/2. Based on Eq. (20) to solve this state, Cosine Taylor polynomial expansion is used.

$$N_{x} = - N_{0} \text{cos}\pi \left( {\eta - \frac{1}{2}} \right)$$
(20)

and,

$$N_{x} = - N_{0} \text{cos}\pi \left( {\eta - \frac{1}{2}} \right) = - N_{0} \mathop \sum \limits_{n = 0}^{\infty } \frac{{\left( { - 1} \right)^{n} \left( {\left. {\pi \left( {\eta - \frac{1}{2}} \right)} \right)} \right.^{2n} }}{{\left( {2n} \right)!}}.$$
(20-a)

By expanding and arranging the abovementioned series, and as regards the sum of the first three terms has sufficient accuracy:

$$N_{x} = - N_{0} \left( {1 - \frac{1}{2}\pi^{2} \left( {\eta - \frac{1}{2}} \right)^{2} + \frac{1}{24}\pi^{4} \left( {\eta - \frac{1}{2}} \right)^{4} } \right)$$
(20-b)

and,

$$N_{x} = - N_{0} \left( {\frac{1}{24}\pi^{4} \eta^{4} - \frac{1}{12}\pi^{4} \eta^{3} + \left( {\frac{1}{16}\pi^{4} - \frac{1}{2}\pi^{2} } \right)\eta^{2} + \left( {\frac{1}{2}\pi^{2} - \frac{1}{48}\pi^{4} } \right)\eta + \left( {1 - \frac{1}{8}\pi^{2} + \frac{1}{384}\pi^{4} } \right)} \right).$$
(21)

By naming the terms like Table 1 as follows, the values of a i are obtained:

$$\begin{aligned} a_{0} & = 1 - \frac{1}{8}\pi^{2} + \frac{1}{384}\pi^{4} \,,\quad \,\,a_{1} = \frac{1}{2}\pi^{2} - \frac{1}{48}\pi^{4} \,,\quad \,a_{2} = \frac{1}{16}\pi^{4} - \frac{1}{2}\pi^{2} \,\,\, \\ a_{3} & = - \frac{1}{12}\pi^{4} \,,\quad \,a_{4} = \frac{1}{24}\pi^{4} ,\quad \,a_{5} = 0.\,\,\, \\ \end{aligned}$$
(22)

Generally, for the other kinds of loadings of A, B, C, D, and E, the values of a i and μ can be replaced in Eq. (9) and can be solved by Frobenius method.

3 Boundary conditions

So far, different values of C m,n are obtained by reversible relationships in terms of C m,0, C m,1, C m,2, and C m,3. To calculate the values of these coefficients, it is required to have the equations that can be achieved by applying the boundary conditions. For each edge of the plate η = 0, 1 according to the boundary conditions, two equations can be written. These two edges may admit any boundary condition (including simply, clamped, and free-edged support). For dimensionless boundary conditions, we give:

$$\begin{aligned} &{\rm Simply}\quad w = 0,\quad \,\frac{\partial w}{\partial \eta } = 0 \hfill \\ &{\rm Clamped}\quad w = 0\,,\,\quad \,\frac{\partial w}{\partial \eta } = 0 \hfill \\ &{\rm Free}\quad \frac{{\partial^{2} w}}{{\partial \eta^{2} }} + \nu \frac{{\partial^{2} w}}{{\partial \xi^{2} }} = 0\,,\quad \,\frac{{\partial^{3} w}}{{\partial \eta^{3} }} + \left( {2 - \nu } \right)\frac{{\partial^{3} w}}{{\partial \eta \partial \xi^{2} }} + \bar{K}_{s} \frac{\partial w}{\partial \eta } = 0. \hfill \\ \end{aligned}$$
(23)

By substituting Eq. (5) in (23), the following equations can be obtained:

$$\begin{aligned} &{\rm Simply}\quad Y_{m} = 0, Y^{\prime \prime }_{m} = 0 \hfill \\ &{\rm Clamped}\quad Y_{m} = 0, Y^{\prime }_{m} = 0 \hfill \\ &{\rm Free}\quad Y^{\prime\prime}_{m} - v\left( {\frac{m\pi }{Q}} \right)^{2} Y_{m} = 0,\quad Y^{\prime\prime\prime}_{m} - \left[ {\left( {2 - v} \right)\left( {\frac{m\pi }{Q}} \right)^{2} + \bar{K}_{s} } \right]Y^{\prime}_{m} = 0. \hfill \\ \end{aligned}$$
(24)

4 Critical buckling load

By applying different boundary conditions to each kind of loading, four equations with variables C m,0, C m,1, C m,2, and C m,3 are achieved. To obtain a non-trivial solution of the system, the determinant of the coefficients matrix is set to zero. By solving the eigenvalue equation, the values of dimensionless buckling loads of \(\bar{N}_{0}\) can be achieved. Substituting each \(\bar{N}_{0}\) in four homogeneous equations, the values of corresponding eigenvectors of C m,n representing the shape mode (m) can be determined. The minimum value of \(\bar{N}_{0}\) represents the critical buckling load. Numerical results of power series method are presented in the next section and are achieved according to Table 2, considering adequate term (N = 55) for convergence. In this table, N is the total number of existing terms in the power series solution method. The highlighted critical buckling load shows the best convergence values in each column with minimum N.

Table 2 Convergence test of the critical buckling load factors for orthotropic rectangular thin plate under biaxial non-uniform in-plane loading resting on Pasternak elastic foundation for CASE-A
Full size table

5 Evaluation of accuracy and reliability of results

To demonstrate the validity of the results of Frobenius solution for rectangular plate, first they have been compared with those in the literature review in Tables 3 and 4, and for all boundary conditions, validity and accuracy are observed.

Table 3 Comparison of the critical buckling load parameter (\(\bar{N}_{cr}\)) for a thin square plate (Q = 1) subjected to uniformly and linearly distributed in-plane compressive loading resting on Pasternak elastic foundation
Full size table
Table 4 Comparison of the critical buckling load parameter (\(\bar{N}_{{\text{cr}}}\)) for thin rectangular plates subjected to uniformly and linearly distributed in-plane compressive loading
Full size table

6 The analytical results and discussion

6.1 The effect of ratio of elasticity modulus and the method of loading on the critical buckling load

To examine the critical dimensionless buckling load in each type of loading according to boundary conditions, two tables are presented. In the first table, the coefficient values of Winkler and Pasternak foundations (lateral and shear stiffness) have been fixed, and the effects of boundary conditions, aspect ratio, the ratio of modulus of elasticity, and the kind of loadings as uniaxial and biaxial are investigated. Superscript numbers in parentheses represent the buckling mode. Based on Tables 5, 6, 7, 8 and 9, it can be found that the critical buckling load generally decreases as aspect ratio (Q) increases. As a result, the maximum buckling corresponds to the aspect ratio (Q = 0.5). Additionally, it can be seen that by increasing the aspect ratio, the critical buckling load factor sometimes remains constant; for example, in the Table 5 for rectangular plate (CASE-A) with the boundary condition (SCSC) and (R = 0), when E x /E y  = 0.5, the critical dimensionless buckling load \(\bar{N}_{cr} = 259.352\) is obtained for aspect ratio (Q = 0.5, m = 1), (Q = 1, m = 2), and Q = 2, m = 4. This is due to the fact that parameter β appears to determine the coefficients matrix.

Table 5 The critical buckling load factor (\(\bar{N}_{{\text{cr}}}\)) for the isotropic and orthotropic rectangular plate with different boundary conditions under axial and biaxial non-uniform in-plane loading for CASE-A
Full size table
Table 6 The critical buckling load factor (\(\bar{N}_{{\text{cr}}}\)) for the isotropic and orthotropic rectangular plate with different boundary conditions under axial and biaxial non-uniform in-plane loading for CASE-B
Full size table
Table 7 The critical buckling load factor (\(\bar{N}_{{\text{cr}}}\)) for the isotropic and orthotropic rectangular plate with different boundary conditions under axial and biaxial non-uniform in-plane loading for CASE-C
Full size table
Table 8 The critical buckling load factor (\(\bar{N}_{{\text{cr}}}\)) for the isotropic and orthotropic rectangular plate with different boundary conditions under axial and biaxial nonlinear in-plane loading for CASE-D
Full size table
Table 9 The critical buckling load factor (\(\bar{N}_{{\text{cr}}}\)) for the isotropic and orthotropic rectangular plate with different boundary conditions under axial and biaxial non-uniform in-plane loading for CASE-E
Full size table

While the ratio of coefficients of m and Q in that parameter has been chosen as a constant value, the buckling load factor does not change. It should be noted that this phenomenon is a familiar behavior in buckling of plates, that is not limited to orthotropic plates on elastic foundation. Furthermore, by increasing the aspect ratio, the critical buckling load factor remains occasionally constant, whereas the critical buckling mode increases. As it is evident in all tables, the maximum buckling mode corresponds to the aspect ratio Q = 10.

When the plate is subjected to uniaxial loading (R = 0), the critical buckling load occurs in higher modes, compared to biaxial loading. Critical buckling load values of the plate, while it is subjected to biaxial loading (there are a few exceptions), decrease in comparison with the uniaxial state. For example, in Table 7 for rectangular plate under sample loading (C) with the boundary condition SSSS when the ratio of modulus of elasticity in two different directions is 2 and the aspect ratio is Q = 2, the critical buckling load is reduced from the value of \(\bar{N}_{cr} = 111.109\) to \(\bar{N}_{cr} = 20.525\).

It can also be observed that as the ratio of the modulus of elasticity in two different directions (isotropic and orthotropic) increases, the value of dimensionless buckling load decreases. In all Tables of 5, 6, 7, 8, and 9, the maximum buckling load is associated to the plate with SCSC boundary condition. In other words, when two edges of the plate are clamped, the critical buckling load increases, compared to the simply-supported and free edges. It can also be seen in the state of uniaxial loading (R = 0) that the minimum buckling load is associated with SSSF plate.

6.2 The influence of stiffness coefficients of elastic foundation and combinations of boundary conditions on the critical buckling load

In this section, the influences of elastic foundation coefficients and boundary conditions for a rectangular orthotropic plate on the state of biaxial loading can be observed. According to Tables 10 and 11, it is obvious that the minimum buckling load is associated to the state in which there is a rectangular plate without elastic foundation. When \(\bar{K}_{W} = 100,\bar{K}_{S} = 0\), the value of buckling load increases in comparison with that of the foundationless state. As expected, when the coefficients of elastic foundation increase, the values of dimensionless critical buckling load rise, and, rising rates of these amounts for the coefficient Pasternak elastic foundation (shear stiffness coefficient) are more than those with the variation of the coefficient of Winkler elastic foundation (lateral stiffness coefficient).

Table 10 The critical buckling load factor (\(\bar{N}_{{\text{cr}}}\)) for the orthotropic rectangular plate with different boundary conditions under biaxial non-uniform in-plane loading for CASE-A versus foundation stiffness coefficients
Full size table
Table 11 The critical buckling load factor (\(\bar{N}_{{\text{cr}}}\)) for the orthotropic rectangular plate with different boundary conditions under biaxial non-uniform in-plane loading for CASE-B versus foundation stiffness coefficients
Full size table

6.3 The influence of type of loading and different combinations of boundary conditions on the critical buckling load

In Table 12, the influence of loading type on the dimensionless critical buckling load under various boundary conditions can be observed while comparing the results of the present study with those of finite element method [36].

Table 12 Comparison of buckling load (\(\bar{N}_{cr}\)) from the present method with FEM results
Full size table

According to Table 12, as observed, the results of finite element method have good agreement with Frobenius method’ solution. As it is evident, the maximum buckling load corresponding to the state of loading CASE-D, for SCSC plate is: \(\bar{N}_{cr} = 53.927\). Due to the fact that in this state of loading, a combination of tension and compression is applied to the edges, the part of the plate in tension stress improves the stability of orthotropic plate. Besides, the minimum critical buckling load is \(\bar{N}_{cr} = 17.988\) for (CASE-C). In this case, the intensity of load on the edge η = 0, 1 is −3N 0 . In the same loading condition, it can be found that maximum buckling load occurs for SCSC plate. On top of that, when one edge of the plate is free (there is one exception), the value of the critical buckling load gets more than that of SSSC, and SSSS plates.

7 The contours of critical buckling mode shapes

Displacement contour diagram (fixed displacement lines) of the critical buckling modes for orthotropic rectangular plate resting on Pasternak elastic foundation under biaxial in-plane loading and different boundary conditions are shown. As observed, for rectangular plate with boundary condition of SCSC (two clamped edges), the maximum and minimum buckling loads correspond to CASE-D and CASE-C, respectively (Fig. 3).

Fig. 3
figure 3

The Displacement contours of plate in different cases of loading for \(Q = 2,\,\,E_{x} /E_{y} = 10,\,R = 1,\,\bar{K}_{w} = 100,\bar{K}_{s} = 10\)

Full size image

8 Conclusion

In this paper, the buckling analysis of orthotropic rectangular thin plates resting on Pasternak elastic foundation with two opposite simply supported edges, and two other edges being arbitrarily restrained, was investigated. According to Levy solution and applying Frobenius method to the governing equation, the critical buckling load of the plate was obtained. The in-plane loading was assumed to have non-uniform and nonlinear distribution. As seen, Frobenius method solution is an efficient and reliable method which presents very strong and compressed process for buckling analysis. The results showed that the accuracy of this method is dependent on the number of terms of power series for achieving convergence. Some of the important results of this study are as follows:

  • It is observed that by increasing the aspect ratio, in some cases, the coefficient of critical buckling load remains constant, whereas the critical buckling mode increases.

  • When the plate is subjected to uniaxial loading (there are a few exceptions), the values of critical buckling load get more than those in the state of biaxial loading, and occur in the higher modes.

  • As the value of modulus of elasticity in two different directions increases, the values of buckling load decrease.

  • By increasing the coefficients of elastic foundation, the values of critical buckling load grow, too. Shear foundation coefficient exerts a greater influence on the buckling load in comparison with the lateral foundation coefficient.

  • The buckling load of the plate is highly dependent on the type of loading at the edges.

  • In the specified type of in-plane loading, the maximum buckling load is allocated to that of the rectangular plate with two opposite clamped edges. Moreover, it can be found out that when the plate is under uniaxial loading, the minimum buckling load occurs when the plate has a free edge.

  • The results of this study can be used as a new reference to assist researchers and engineers assess the accuracy and reliability of the results and investigate the analytical and numerical methods in the future.