1 Introduction

The purpose of this paper is to extend the analytical formulation of a new diffusion process [1–3] introducing time-dependent parameters. The motivation leading to introducing the new process comes from the formulation of a population dynamics model. Actually if we try to model the invasion process of a given species intended to conquer and occupy some territory it is advisable to consider two distinct motions with different velocities, namely the soldiers and the colonizers. Clearly, soldiers move faster than colonizers. The governing equation obtained to describe this peculiar population dynamic problem is interesting enough to be extended to the field of complex physical phenomena. The new equation, however, for the correct interpretation of the added terms, requires the presence of a flux potential that, as far as we know, has not yet been considered in the current literature.

The new potential induces the formation of a secondary flux that is function of the curvature variation of the concentration as explained in previous papers. The secondary flux requires the introduction of two new parameters, the concentration fraction incorporated in this new flux (1 − β) and a new diffusion coefficient R controlling the mass transfer time rate associated to the secondary flux. It is interesting to notice that the secondary flux may delay or accelerate the diffusion process depending on the values of the new parameters introduced in the governing equation and the initial and boundary conditions as well. The combination of the new coefficients β and R, for a given diffusion coefficient D provide a very large spectrum of possible behaviors allowing for the simulation of several process without introduction of unnecessary non-linearity.

Several types of anomalous diffusion processes have been extensively reported that could possibly be analyzed using the present approach. Delayed diffusion, to give an example, has been observed in a large number of experiments [4, 5]. The governing equations used to solve this class of problems are, however, the classical diffusion equation with source/sink terms to adjust experimental results to the analytical formulation. Integro-differential equations have also been used particularly for reaction diffusion processes with time delay [6]. Other approaches make use of nonlinear diffusion coefficients to help the interpretation of experimental results. Recent experimental and theoretical works in the fields of plasma physics [7, 8] superconductors [9] and the efflux mechanism of cholesterol via aqueous diffusion [10, 11] show clearly that the classical diffusion equation doesn’t represent satisfactorily the physics of the phenomena. However, the time variation characteristics reported for these three last cases suggest that the theory presented here may be of some help. It may be particularly helpful in biological phenomena due to energy exchanges coming from the biochemical reactions occurring simultaneously with the diffusion process. Osmotic processes [12] and flow in porous media [13] are other examples where anomalous diffusion can be found.

In this paper, we will extend the theory to the case where a key parameter, namely β, that defines the volumes of the two sets moving with distinct velocities, is function of time. We may consider this behavior as an evolutionary process. The influence of anisotropy introducing a perturbation on the secondary flux will also be presented.

2 The basics of the diffusion model

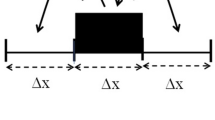
Consider a discrete model consisting of a row of cells such that each cell can communicate with the neighboring ones. Let the contents of each cell be partly redistributed to the adjacent cells in equal portions and partly retained in the cell at each time step. Figure 1 represents the distribution process for a characteristic time step Δt. The fundamental idea is therefore to assume that the contents of a cell n at a time t changes at each time interval Δt such that a fraction β is equally redistributed to the right, n + 1, and left, n − 1, neighboring cells while the remaining portion stays temporarily confined in the same cell n. The set of equations derived with the help of the discrete approach representing this distribution law reads:

$$\begin{aligned} &q_{n}^{t} = \left( {1 - \beta } \right)q_{n}^{t - 1} + \frac{1}{2}\beta q_{n - 1}^{t - 1} + \frac{1}{2}\beta q_{n + 1}^{t - 1} \\ &q_{n}^{t + 1} = \left( {1 - \beta } \right)q_{n}^{t} + \frac{1}{2}\beta q_{n - 1}^{t} + \frac{1}{2}\beta q_{n + 1}^{t} \\ \end{aligned}$$

where \(0 \le \beta \le 1\). Clearly with β = 1 the above equations represent the discrete formulation scheme leading to the well-known second order classical diffusion equation. But with \(\beta \ne 1\) a new equation is obtained. After the proper operations and assuming the continuity requirements for the function q(x, t) we get [2, 3]:

$$\frac{\partial q}{\partial t} = \beta D\frac{{\partial^{2} q}}{{\partial x^{2} }} - \left( {1 - \beta } \right)\beta R\frac{{\partial^{4} q}}{{\partial x^{4} }}$$
(1)
Fig. 1
figure 1

Contents redistribution scheme for a generalized cell n

Full size image

The fourth order term with negative sign introduces the effect of retention. The coefficients D and R are generalized constants. It is important to keep the parameters β and β(1 − β) explicitly in the equation because they are control parameters expressing the balance between diffusion and retention when both are activated simultaneously. The retention effect reaches its maximum effect for β = 0.5. Clearly, retention cannot be activated without diffusion, that is, while diffusion can take place without retention, the complementary process, that is, retention without diffusion is not possible.

According to the derivation above the effect of temporary retention cannot be consistently modeled without the presence of the fourth order differential term. It is also remarkable that the discrete approach shows that non-linear terms are not required to represent temporary retention for the case of homogeneous isotropic media. This means, as it should be expected, that temporary retention belongs to the class of primary phenomena and, in general, is not a secondary perturbation on the diffusion process as usually assumed for modeling anomalous diffusion.

Note that we are defining temporary retention and not sinks that would subtract a fraction of particles definitively from the system.

Equation (1) shows clearly the existence of two different diffusion processes. The variable q(x, t) represents the mass concentration and it is not difficult to see that two distinct velocity potentials come into play one of them corresponding to the second order differential term and the other one corresponding to the fourth order differential term. Particles belonging to the fraction β follow the classical Fick’s law, it is the primary flux that will be called Ψ 1 and particles belonging to the fraction (1 − β) follow a new law, it is the secondary flux that will be called Ψ 2. Note that throughout this paper the fraction β will be considered independent of x. Considering Eq. (1) and anticipating the mathematical structure of the integrand in the mass conservation principle it is not difficult to see that the fluxes are given respectively by:

$${\varvec{\Psi}}_{1} = - D\frac{{\partial q\left( {x,t} \right)}}{\partial x}{\mathbf{e}}_{1}$$
$${\varvec{\Psi}}_{2} = R\beta \frac{{\partial^{3} q\left( {x,t} \right)}}{{\partial x^{3} }}{\mathbf{e}}_{1}$$

Indeed if we assume these two laws for the flux rates corresponding, Ψ 1 to the fraction of particles β diffusing according to Fick’s law and Ψ 2 ruling the complementary fraction (1 − β) the mass conservation principle gives:

$$\int\limits_{V} {\frac{{q\left( {x,t +\Delta t} \right) - q\left( {x,t} \right)}}{{\Delta t}}{\text{d}}s + } \int\limits_{\partial V} {\left[ {\beta {\varvec{\Psi}}_{1} + \left( {1 - \beta } \right){\varvec{\Psi}}_{2} } \right] \cdot {\text{e}}_{1} \,{\text{d}}s} = 0$$

This leads immediately to:

$$\frac{{\partial q\left( {x,t} \right)}}{\partial t} = \frac{\partial }{\partial x}\left[ {\beta D\frac{{\partial p\left( {x,t} \right)}}{\partial x}} \right] - \frac{\partial }{\partial x}\left[ {\beta \left( {1 - \beta } \right)R\frac{{\partial^{3} p\left( {x,t} \right)}}{{\partial x^{3} }}} \right]$$
(2)

D and R are respectively the diffusion and reactivity coefficients that can be functions of x and t. The physical meaning of the primary flux is well known, namely, the particle concentration distribution tends to smooth out along the space variable. The particles move from higher concentration regions toward lower concentration regions. The secondary flux is concerned with the curvature variation of the concentration distribution. Recall that the curvature of the function q(x, t) is proportional to the second derivative \(\left( {{{\partial^{2} q} \mathord{\left/ {\vphantom {{\partial^{2} q} {\partial x^{2} }}} \right. \kern-0pt} {\partial x^{2} }}} \right)\) of the concentration. Therefore, the secondary flux grows with the increase in the curvature.

Figure 2 shows two possible configurations of the concentration function. The secondary flux is always oriented in the direction of increasing curvature of the concentration profile. Since increasing curvature means local accumulation, the secondary flux may be interpreted as a process that favors local concentration. It is also remarkable that the intensity of the secondary flux increases linearly with the fraction β of particles belonging to the primary flux. Therefore, the fraction β is a control parameter for the intensity of the secondary flux.

Fig. 2
figure 2

Direction of the secondary flux as function of the curvature variation. Secondary and primary fluxes may be in the same direction or opposite to each other

Full size image

In this paper, we will consider diffusion in an isotropic medium, therefore D and R constants, but the fraction β may vary in time. That is, we are considering a dynamical process where particles may move from the set defined by β to the set defined by (1 − β) and vice versa.

In previous papers [2, 3] we have introduced the bi-flux hypothesis for isotropic media with time independent coefficients. It was shown that the bi-flux assumption might be correlated with two set of particles scattering in two different energy states for β constant.

Let us now consider a particular system to illustrate the behavior of the concentration variation where all parameters (β, D, R) are constant, the domain of definition is given by \(x \ge 0\) and t ≥ 0. The initial condition reads:

$$q\left( {x,0} \right) = q_{0} \exp \left( { - kx} \right)$$

and the boundary conditions are given by:

$$\left. {{{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right|_{x = 0} = - kq_{0} {\text{e}}^{{Dk^{2} \rho t}} \quad {\text{and}}\quad \left. {{{\partial^{3} p} \mathord{\left/ {\vphantom {{\partial p} {\partial x}}} \right. \kern-0pt} {\partial x^{3} }}} \right|_{x = 0} = - q_{0} k^{3} {\text{e}}^{{Dk^{2} \rho t}}$$

and as x → ∞ the function an all the derivatives vanish. Under these assumptions the solution of Eq. (1) reads:

$$q\left( {x,t} \right) = q_{0} \exp \left( { - kx + Dk^{2} \rho t} \right)$$
(3)

where \(\rho = \beta \left( {1 - \left( {1 - \beta } \right)r} \right)\) and r = Rk 2/D.

The primary flux and the secondary flux are:

$${\varvec{\Psi}}_{1} = - q_{0} k\exp \left( { - kx + Dk^{2} \rho t} \right)\quad {\text{and}}\quad {\varvec{\Psi}}_{2} = - \beta q_{0} k^{3} \exp \left( { - kx + Dk^{2} \rho t} \right)$$

Equation (3) is the function of the concentration variation with space and time. The time variation is controlled by the parameter ρ. For positive values of ρ, the density grows with time for all x. If ρ is negative, the concentration decreases and tends to zero as t → ∞ (Fig. 3).The parameter ρ is a function of β. For β = 1 we have ρ = 1 and the solution reproduces the classical result, the concentration increases at a rate Dk 2. If β = 0 there is no diffusion, the system is stationary. Now if 0 < β < 1 the roots of ρ are β 1 = 0 and β 2 = 1 − 1/r. Now if r < 1 the root β 2 is negative and in the interval 0 < β < 1 the values of ρ will be positive as shown in the Fig. 4. This means that the concentration will increase steadily although at a lower rate as compared with the classical diffusion, that is ρ < Dk 2. This is due to the secondary flux that in this case has the opposite direction of the primary flux, removing particles from the system. Nevertheless the evolution in time is characterized as a densification process. Now if r > 1 there is a root in the interval (0, 1) and for β < (1 − 1/r) we have ρ < 0. This means that we have a rarefaction process, that is, the particles removed from the process due to the secondary flux exceed the number of particles injected by the primary flux. The concentration decrease to zero as t → ∞. Particularly for β = 1 − 1/r the process is stationary corresponding to a stagnation point. Figure 4 shows the variation of ρ/Dk 2 with β for some values of r.

Fig. 3
figure 3

Solution of the concentration distribution for q(x, t) = q 0exp(−kx + Dk 2 ρt) with ρ > 0. Mass is added to the system

Full size image
Fig. 4
figure 4

Variation of the concentration parameter ρ/Dk2 with the diffusing fraction β for different values of r. Points on the horizontal axis correspond to stagnation, points above and below the horizontal axis correspond to densification and rarefaction respectively

Full size image

Finally for r = 1 the curve ρ/Dk 2 is tangent to the horizontal axis. It is a limiting curve or a separatrix. All the curves above this separatrix correspond to densification processes. Curves below the separatrix cross the horizontal axis ρ/Dk 2 = 0 at β = β stag and enter a region where rarefaction prevails. That is ρ/Dk 2 < 0 for β < β stag, where β stag = (1 − 1/r).

3 The bi-flux process under two excitation states

Let us explain first what we understand by excitation state. Consider a particle moving with linear velocity v and rotating with angular velocity ω. The linear momentum p and the angular momentum L are given respectively by \({\mathbf{p}} = m{\mathbf{v}}\) and \({\mathbf{L}} = m\bar{d}^{2} {\varvec{\upomega}}\) where m is the mass of the particle and \(\bar{d}\) is the effective gyration radius. Let us call active energy or translational energy the kinetic energy associated to the linear momentum. That is if p is the linear momentum of a given particle P, its active energy is \(e_{\text{p}} = {{{\mathbf{p}}^{2} } \mathord{\left/ {\vphantom {{{\mathbf{p}}^{2} } {2m}}} \right. \kern-0pt} {2m}}\) where m is the mass of the particle. The rotational energy e ω corresponds to the kinetic energy generated by the angular momentum L, that is \(e_{\omega } = {{{\mathbf{L}}^{2} } \mathord{\left/ {\vphantom {{{\mathbf{L}}^{2} } {2m}}} \right. \kern-0pt} {2m}}\bar{d}^{2}\). Any particle may be moving with linear momentum p and angular momentum L, the total energy e however remains constant, e = e p + e ω  = constant. We will consider that energy conservation is true for all particles under consideration, that is, the system is conservative.

Now suppose that we have a system consisting of N particles where the particles are divided into two subsets, N 1 = βN and N 2 = (1 − β)N. The energy density or specific energy (energy/volume) corresponding to N 1 and N 2 are respectively, \(E_{1} = \beta {{{\varvec{\Psi}}_{1}^{2} } \mathord{\left/ {\vphantom {{{\varvec{\Psi}}_{1}^{2} } {2q}}} \right. \kern-0pt} {2q}}\) and \(E_{2} = \left( {1 - \beta } \right)\left( {{{{\varvec{\Psi}}_{2}^{2} } \mathord{\left/ {\vphantom {{{\varvec{\Psi}}_{2}^{2} } {2q}}} \right. \kern-0pt} {2q}} + E_{\omega } \left( \beta \right)} \right)\). Therefore, we assume that all particles excited in the state E 1 do not rotate, all kinetic energy is stored as active energy, while the kinetic energy corresponding to the state E 2 is stored as active energy and rotational energy E ω (β) as well. Note that since the system is conservative we have E = E 1 + E 2 → constant. We may consider the rotational energy as a hidden form of energy and the parameter (1 − β) as the probability of occurrence of rotational energy. Indeed for pure Fickian processes (1 − β) = 0 there is no rotational energy in the system, E ω(1) = 0, and for (1 − β) = 1 all energy is stored as rotational energy E ω(0) = E. Let us call \(E_{\omega } \left( 0 \right) = E_{\omega }^{ * }\). Recall that if β = 0 then Ψ 2 = 0. The contribution of the rotational energy of all particles to E 2 is wrapped up in the energy density term E ω(β).

Suppose now that we are dealing with a dynamic system, that is, there is a continuous internal energy exchange in the system E 1 ↔ E 2. The energy distribution is clearly controlled by the parameter β. Therefore, to perform the analysis of a dynamical diffusion process as exposed above in an isotropic medium it suffices to assume the fraction β(t) varying in time and the diffusing particles distributed between two time-dependent energy states. Note that Eq. (1) still holds for β = β(t).

As suggested above, in diffusion processes particles collide continuously exchanging linear momentum and angular momentum. In principle, at each collision, active energy may be converted into rotational energy and the other way around. In our particular universe, we will consider two distinct and opposite phase states. The phase state S1 is such that active energy is always converted into rotational energy while in the phase state S2 rotational energy is always converted into active energy. Let us introduce the following rules that apply in our particular universe.

  1. 1.

    In an isolated system the total kinetic energy remains constant, therefore, \(E_{1} + E_{2} = \beta {{{\varvec{\Psi}}_{1}^{2} } \mathord{\left/ {\vphantom {{{\varvec{\Psi}}_{1}^{2} } {2q}}} \right. \kern-0pt} {2q}} + \left( {1 - \beta } \right)\left( {{{{\varvec{\Psi}}_{2}^{2} } \mathord{\left/ {\vphantom {{{\varvec{\Psi}}_{2}^{2} } {2q}}} \right. \kern-0pt} {2q}} + E_{\omega } \left( \beta \right)} \right) = {\text{constant}}\) for all t.

  2. 2.

    In an isolated system subjected to the phase state S1 the rotational energy increases and the active energy decreases continuously. Therefore, in an isolated system S1 \(\mathop {\lim }\limits_{t \to \infty } E_{1} \to 0\;{\text{and}}\;\mathop {\lim }\limits_{t \to \infty } E_{2} \to \mathop {\lim }\limits_{t \to \infty } E_{\omega } \left( \beta \right)\). This means that β = β(t) is a function of time and β(t) → 0 as t → ∞.

  3. 3.

    In an isolated system subjected to the phase state S2 the active energy increases and the rotational energy decreases continuously. Therefore, in an isolated system S2 \(\mathop {\lim }\limits_{t \to \infty } E_{1} \to E\;{\text{and}}\;\mathop {\lim }\limits_{t \to \infty } E_{\omega } \left( \beta \right) \to 0\). This means that β = β(t) is a function of time and β(t) → 1 as t → ∞.

According to the hypothesis introduced above, a complex diffusion process consisting of a very large number of micro-states is reduced to two fundamental non-stationary states governed by a primary volumetric flow rate Ψ 1 and a secondary volumetric flow rate Ψ 2 that represent the overall average of micro-states (see “Appendix”). If the system is in the phase state S1 as time increases it tends to the stationary state E ω. For a system in the phase state S2, all particles will be excited in the energy state E 1 after a sufficient long time. Now as β = β(t) is function of time, as time varies the parameter 0 < β < 1 covers the whole energy distribution spectrum for both cases.

4 The energy transfer principle

4.1 Isolated system in the phase state S1

Consider a one-dimensional problem defined in some interval x ∈ [a, b]. Let us assume that the distribution of particles in states E 1 and E 2 is independent of x but may vary in time. The system is isolated and according to the model exposed in the previous section the system tends to rest meaning that the total active energy tends to zero as t → ∞. Since the system is isotropic, the linear momentum tends uniformly to zero for all x as t → ∞, that is \(\mathop {\lim }\limits_{t \to \infty } {\mathbf{p}}\left( {x,t} \right) \to 0\). Consequently \(\mathop {\lim }\limits_{t \to \infty } \beta \left( {x,t} \right) \to 0\). Under these conditions, let us find an expression for the decay of the fraction β as function of time. Clearly the probability of interaction among particles is proportional to β inducing a reduction of particles in state E 1. That is, the variation δβ is proportional to β. This means that the change of the excitation state, active energy into rotational energy (p → L), is more intense when the number of particles in state E 1 is large β ≫ 0.

Besides the probability of interaction among particles the rate of the variation δβ depends on the energy contained in the state E 1 or alternatively on complementary state E 2. Let T(t) be the variable that measures the active energy contained in the state E 1. It might be an indirect measure of the linear momentum of the particles in the system. Since the system is isolated and the total energy is constant, T(t) is also an indirect measure of the rotational energy. Let E ω (T) represent the rotational energy. Clearly E ω (T) is decreasing functions of T (Fig. 5).

Fig. 5
figure 5

Variation of the rotational energy with the parameter T

Full size image

At very large energy levels T ≫ 0 the rate of variation of the rotational energy E ω (T) with respect to the energy parameter T is low. But for T small big variations of the angular momentum occurs for relatively low decrease of the energy parameter T. Therefore, it is reasonable to assume as a first approximation:

$$E_{\omega } \left( T \right) = F\left( {\frac{{T_{0} }}{T}} \right)$$
(4)

The variation δβ depends therefore on two determinant parameters:

  1. 1.

    The fraction of particles in the state E ω given by β.

  2. 2.

    The variation of the rotational energy given by −δ(E ω (T)). The negative sign meaning that β decreases as E ω increases.

With the hypotheses above, it is possible to define the variation of β:

$$\delta \beta = \beta \frac{{\left( { - \delta E_{\omega } } \right)}}{{K_{0} }}\;\quad{\text{where}}\,K_{0} \,{\text{is}}\,{\text{a}}\,{\text{given}}\,{\text{energy}}\,{\text{parameter}}$$

Now with Eq. (4) we may write:

$$\delta E_{\omega } = - \frac{{T_{0} }}{{T^{2} }}\frac{{{\text{d}}F}}{{{\text{d}}u}}\delta T\;\quad{\text{where}}\;u = T_{0} /T$$

Introducing the expression above in the equation for δβ we get:

$$\delta \beta = \beta \frac{1}{{K_{0} }}\frac{{T_{0} }}{{T^{2} }}\frac{{{\text{d}}F}}{{{\text{d}}u}}\delta \left( T \right)$$

After integration:

$$\beta = \exp \left( {\int {\left( {\frac{{T_{0} }}{{K_{0} }}\frac{1}{T}F_{u} } \right)\frac{1}{T}\frac{\partial T}{\partial t}{\text{d}}t} } \right)$$
(5)

where \(F_{u} = {{{\text{d}}F} \mathord{\left/ {\vphantom {{{\text{d}}F} {{\text{d}}u}}} \right. \kern-0pt} {{\text{d}}u}}\). Now define:

$$S_{\omega } = \frac{1}{T}F_{u}$$

The function S ω may be understood as the entropy referring to the present theory applied to isolated systems. Introducing this expression in (5) we get:

$$\beta = \exp \left( {\frac{{T_{0} }}{{K_{0} }}\int {S_{\omega } \frac{\partial }{\partial t}\ln T{\text{d}}t} } \right)$$

With:

$$\frac{\partial }{\partial t}\ln T = g\left( {S_{\omega } } \right)\quad {\text{and}}\quad \frac{{K_{0} }}{{T_{0} }} = S_{0}$$

We finally obtain:

$$\beta = \exp \left( {\int {\frac{{S_{\omega } }}{{S_{0} }}g\left( {S_{\omega } } \right){\text{d}}t} } \right)$$

Assuming now the simplest expression for the energy E ω (T), that is, according to (4) E ω (T) = K 1(T 0/T), \(F_{u} = K_{1}\) and with (5) it is readily obtained:

$$\beta = \exp \left( { - \frac{1}{{S_{0} }}\int {\frac{{\partial S_{\omega } }}{\partial t}{\text{d}}t} } \right)$$
(6-a)

That after integration gives the general expression:

$$\beta = \exp \left[ { - \frac{{S_{\omega } (t)}}{{S_{0} }}} \right]$$
(6-b)

Therefore, \(S_{\omega } = - S_{0} \ln \beta \;or\;S_{\omega } = S_{0} \ln \left( {{{N_{1} } \mathord{\left/ {\vphantom {{N_{1} } N}} \right. \kern-0pt} N}} \right)\). We will call the variable S ω as ω-entropy. It is a measure of the relative organization of particles in two states S1 and S2. \(S_{\omega }\) indicates the equivalent number of particles excited in a pure rotational energy state or likewise at rest, meaning x i  = constant (i = 1,2,3), in a given inertial frame. That is, as \(S_{\omega } \to \infty\) or similarly β → 0 the relative distances among all particles tend to remain fixed and the system approaches a stationary state. If it would be only possible to measure the active energy, then for very large values of \(S_{\omega }\) an external observer would conclude that the system is inactive or “dead”. Maybe only the mass could be detected and the rotational energy stored in the system would be hidden, it would be a kind of “dark energy”.

Since the active energy for this system is a decreasing function of time and the variation rate of change is inversely proportional to the active energy level it is reasonable to admit that \({{\partial S_{\omega } } / {\partial t = U_{0} t}}\) where U 0 is a constant of the system. From which follows \(S_{\omega } = {{U_{0} t^{2} } / 2}\), and finally:

$$\beta = \exp \left( { - {{t^{2} } / {\tau_{0}^{2} }}} \right)\;{\text{where}}\;{{U_{0} } /{2S_{0}}} = {1 / {\tau_{0}^{2} }}.$$

4.2 Isolated system in the phase state S2

This system, sustained by the phase state S2 has the opposite property of the previous one, that is, the collision between two particles always transforms angular momentum into linear momentum but not the other way around. This means that ultimately the initial rotational energy will be totally converted into active energy. Suppose that initially the total energy in the system is stored under the form of rotational energy \({\text{E}}_{\omega }^{ * }\).That is, the fraction β increases gradually from β(0) = 0 up to β(t *) = 1 which is the maximum possible value. We want to analyze the behavior of the phase change up to t = t*.

The evolution of the fraction β, with a first approximation for the energy function, is given by the expression (6-a) derived before with the exponent multiplied by −1. Indeed we have now \(S_{\omega } \left( 0 \right) > S_{\omega } (t)\) for all t > 0 and consequently \(\delta \beta = \beta \left( {\delta E_{\omega } } \right)\) which explains the change in sign. Now the simplest approximation for the variation of the ω-entropy coherent with the variation for S1 is given by \({{\partial S_{\omega } } / {\partial t}} = - \hat{U}_{0} t^{ - 3}\). Note that now the ω-entropy is a decreasing function of time given by \(S_{\omega } = {{\hat{U}_{0} t^{ - 2} } / 2}\). Therefore, we may write from (6-b):

$$\beta = \exp \left( { - {{\tau_{0}^{2} } / {t^{2} }}} \right)\;{\text{where}}\;{{\hat{U}_{0} } /{2S_{0}}} = {\tau_{0}^{2}}.$$

Note that under the above assumptions t* → ∞.

This case, the S2 phase state, is more complex than the first one S1. The transfer of rotational energy to active energy is not so easy and would require an external potential field to initiate and probably to sustain the process. Therefore, the present approach is only a first approximation. Note that the phase S1 is related to extinction while S2 is related to creation which is always more difficult to be analyzed and simulated.

5 Selected examples

Consider the bi-flux diffusion process defined on the interval [−1, 1] for an isotropic supporting medium. If the fraction β is function of time the governing equation is:

$$\frac{\partial q}{\partial x} = \beta \left( t \right)D\frac{{\partial^{2} q}}{{\partial x^{2} }} - \left( {1 - \beta \left( t \right)} \right)\beta \left( t \right)R\frac{{\partial^{4} q}}{{\partial x^{4} }}$$

Assume that the primary and secondary fluxes vanish at the boundaries, x = 1 and x = −1. The boundary conditions therefore read:

$$\left. {\frac{\partial q}{\partial x}} \right|_{x = \pm 1} = 0\quad {\text{and}}\quad \left. {\frac{{\partial^{3} q}}{{\partial x^{3} }}} \right|_{x = \pm 1} = 0$$

Let the initial condition be:

$$q\left( {x,0} \right) = 0.25\left( {1 + \cos \left( {\pi x} \right)} \right)\quad - \, 1 \le x \le 1$$

Suppose that initially, t = 0, the system is subjected to a pure Fickian process, that is, only the primary flux exists. Since there is no energy exchange with the surroundings, according to our hypothesis, the primary flux will decrease and the secondary flux will increase as time increases. Energy is continuously transferred from the primary flux to the secondary flux. Now for an isolated system starting with a full Fickian diffusion regime, that is β(0) = 1 Eq. (6-a) prevails, that is:

$$\beta = \exp \left( { - {t / {\tau_{0} }}} \right)^{2}$$

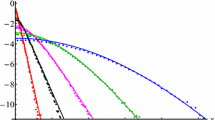
The diffusion and reactivity coefficients are taken D = 0.1 and R = 0.008 respectively. Figure 6 shows the concentration profile for different values of the parameter τ 0. For values relatively high, \(\tau_{0} = {1 / {\sqrt 2 }}\) the freezing process is low and stabilizes close to the uniform solution, that is, \(\mathop {q(x,t)}\limits_{\lim t \to \infty } = {\text{const}}.\) Note that both fluxes are blocked at the ends x =+1 and x = −1 and the diffusion process imposes q(x, t) constant as t → ∞. As the value of τ 0 decreases, the freezing progression is quicker. For τ 0 = 0, 1 there is almost no time to initiate the diffusion process and the density distribution after a sufficient long time is almost the same as the initial conditions. Figure 7 shows the time variation of the concentration at x = 0. For values of τ 0 < 0.1, the steady state is reached very quickly and the final concentration distribution remain close to the initial condition. Since β goes to zero as time increases in all the cases, the primary flux will vanish and the concentration profile q(x, t) will freeze for very large t. It is interesting to observe that the gradient of the concentration alone is not determinant to trigger the diffusion process, it is also necessary the presence of particles in state E 1. If the system has attained the limiting state \(E_{2} = E_{\omega }^{ * }\), than there is no flow irrespective of the concentration profile.

Fig. 6
figure 6

Evolution of the concentration profile in an isolated system. Energy is being transferred from S1 to S2 at different rates 1/τ0. For 1/τ0 = 0, β = 1, Fickian diffusion

Full size image
Fig. 7
figure 7

Evolution in time of the concentration at x = 0 for different values of τ 0

Full size image

Now consider the second case where the system belongs to the phase state S2 initially free of active energy but subjected to a continuous influx of active energy at the expense of rotational energy. Let the boundary conditions be the same as before and take the following initial condition:

$$q\left( {x,0} \right) = 0.25\left( {2 - \cos \left( {\pi x} \right)} \right)$$

Initially the system is inactive; there is no flux at all, neither primary nor secondary. Now, since rotational energy is being continuously transformed into active energy the fraction β will steadily increase. The law governing this behavior is given by \(\beta = \exp \left( { - {{\tau_{0}^{2} } / {t^{2} }}} \right)\) as explained before. Figure 8 shows the evolution of the bi-flux process for different values of τ 0. For very low energy transfer rates, τ 0 large, the system tends to equilibrium very slowly. For low values of τ 0, the system behaves almost like a pure Fickian process. Note that since there is no flow at the boundaries the system tends to the steady state with the concentration q(x, t) constant along the domain [−1, 1]. The variation of the concentration with time, q(0, t), at x = 0, for various values of τ 0 is shown in Fig. 9. Here the fraction β of particles belonging to the Fickian diffusion increases steadily in time. Therefore, eventually the final concentration profile will coincide with the expected profile for a Fickian process that is a uniform distribution on the region −1 < x < 1. The evolution of q(0, t) shown in the Fig. 9 shows clearly this tendency.

Fig. 8
figure 8

Evolution of the concentration profile q(x, t) for a non-conservative system. Energy is being continuously transferred to the system at different rates τ 0. For τ 0 = 0, β = 1, Fickian

Full size image
Fig. 9
figure 9

Evolution in time of the concentration at x = 0 for different values of τ 0

Full size image

The influence of anisotropy in the secondary flow may be examined taking R as a function of x. Consider the problem defined above where the Fick’s diffusion decays exponentially at a rate exp(−2/t 2) as shown in Fig. 6. Let R be defined as follows:

$$\begin{aligned} &{\text{For}}\quad - 1 \le x \le 0\quad R(x) = 0.008 \hfill \\ &{\text{For}}\quad 0 \le x \le 1\quad R(x) = 0.008 + 80x \hfill \\ \end{aligned}$$

Now since the reactivity coefficient is function of x the Eq. (2) prevails. Solving this equation the solution shown in the Fig. 10 shows the disturbance in the solution introduced by this type of anisotropy. High values of the reactivity coefficient for the interval 0 ≤ x ≤ 1 tends to accelerate the diffusion process. The concentration distribution is displaced to the right showing a clearly asymmetric dispersal on the x axis. For this case, the reactivity coefficient induces a preference of the flux towards the right. For living organisms, this could represent better competitive conditions on the right side of the domain. It is also interesting to note that the variation of R(x) speeds up the concentration evolution q(x, t) for x > 0 also indicating the preference for this interval of the domain. The steady state as t → ∞ tends to an asymmetric distribution with preference for the right.

Fig. 10
figure 10

a Solution foran anisotropic medium; b solution for an isotropic medium For both cases β = exp(−2/t2) and D = 0.1

Full size image

6 A Gedankenexperiment

Although there is not yet a concrete experiment to test the theory, there are situations where the bi-flux theory is the best model. Indeed, suppose a group of bikers initially gathered on a relatively small region of a straight road. The bikers and the respective bikes are all similar. The bikes carry an inertia wheel or more precisely a flywheel assembled on the rear axle. The bikers may couple or uncouple the flywheel to the rear wheel through a device connected to the handlebar. The flywheel is initially at rest and disconnected from the rear wheel. Therefore, all the energy expended by the bikers is used to gain linear momentum.

Now let us assume that the natural tendency of the bikers is to avoid clustering. Therefore, they will disperse traveling from places with high bikers concentration to places with low bikers concentration. Then it is acceptable to introduce for this behavior the same law governing the ordinary diffusion processes. It is assumed that the track is uniform along all the trajectory traveled by the bikers and that all bikers react similarly when exposed to the same circumstances. This is to say that the diffusion coefficient is constant for the dispersion process.

Now suppose that at some given time, a fraction (1 − β) of the total number of bikers receive a signal requiring that they delay the scattering process. Subsequently they couple the flywheel to the rear wheel while keeping pedaling the bikes with the same energy. Clearly, a fraction of that energy will be transferred to activate the flywheel angular momentum that is now integrated to the system. Consequently, the linear momentum will decrease and the flux rate as well.

This second group certainly moves according to a new law. The bikers concentration cannot be precisely determined by the classical diffusion model anymore.

Generalizing the diffusion equation and introducing new physical constants, as the diffusion coefficient D(x, t, αi) as function of space or time, or both, would lack of scientific consistency. Indeed, despite the fact that the parameters α i could be determined by comparing analytical results with experiments, this procedure is nevertheless artificial. Adjusting experimental results to analytical results is not a warranty that the theory describes correctly the physical phenomenon. If this kind of solution were to be applied to this case, the best that we could expect would be a mean value for the bikers concentration. The real phenomenon would be lost and the diffusion coefficient would not be a physical constant but a parameter adjusted to a specific case. The bi-flux process cannot be simulated with a second order PDE. Therefore, to solve this problem the bi-flux approach is the more adequate. The fourth order equation is a better approximation to model the real physical phenomenon. It introduces a new variable, namely the distribution parameter β that determines the fraction of particles scattering according to the Fick’s law. Now, it is not impossible that the diffusion coefficient, even if independent of x and t, may, in some particular cases, be a function of the concentration β. This is another advantage of the new approach that allows for the variation of the diffusion coefficient with the fraction of particles scattering according to the Fick’s law.

To the best of our knowledge, the theory presented here is new and therefore there are no related experimental results. Population dynamics and capital flow are two types of phenomenon that call for a bi-flux theory. However, experiments and parameter identification that would help to validate the models are still missing.

There are other theories that introduce a fourth term in the diffusion process. These theories assume a second order approximation for the diffusion coefficient that leads to a nonlinear fourth order PDE [14]. The expanded governing equation for these cases refines the results of the classical theory, however, the assumption of a single flow process is preserved. In the theory proposed here, the fourth order equation is not associated to second order effects. It represents a parallel behavior comparable to the main diffusion process.

7 Conclusion

It was shown that the more realistic dynamical behavior of particles scattering in a substrate comprising the contribution of both, the linear momentum and angular momentum, to the kinetic energy can be taken into account. The variation of the rotational energy contribution is obtained indirectly through the variation of the translational kinetic energy given by the secondary flux Ψ 2. It is remarkable that the introduction of the rotational energy in the dynamics of the particles requires the introduction of the secondary flux Ψ 2 and therefore the introduction of the fourth order equation to model the diffusion phenomenon.

Since for real systems the translational and rotational energies are function of time it is necessary to introduce the variable β as function of time as well. As shown in the preceding sections the theory uses the fundamental kinematical principles of mechanics in a particular “universe” in order to derive a consistent time variation for the fraction β. The solution leads to the introduction of the variable S ω which is entropy equivalent in the new “universe” that tends spontaneously to a peculiar energy state, with increasing values of S ω , provided that it is isolated from external energy sources. We believe that the reasoning leading to this new variable S ω , despite the fact that the limiting states may be ideal states, helps to better understand the notion of entropy of the classical thermodynamics. Consider for instance an isolated system, if for t = 0 the rotational energy vanishes then β = 1, the ω-entropy is ln(1) = 0 and the translational or active energy is at the maximum level. As time increases the system goes through all possible combinations of micro-states and the entropy increases without limit as β tends to zero. The maximum entropy corresponds to the state where all kinetic energy is stored as rotational energy and translational energy vanishes. Therefore, the maximum ω-entropy corresponds to a state where the distances among all particles remain constant reaching a freezing configuration. This state is consistent with the classical thermodynamics assumption of absolute zero temperature. The universe “stands still” in some inertial reference frame. Now suppose that the observable fraction of kinetic energy is only the energy associated to the linear momentum, then the “stationary” universe in the state \(E_{\omega }^{ * }\) is invisible and the energy stored in this state is a kind of “dark energy”, it is non-observable. Maybe the better interpretation of the ω-entropy is a state where translational energy is irrecoverable or rotational energy is irreversible. Another interesting observation is that the state \(E_{\omega }^{ * }\) may be reached with a non-uniform concentration profile, than it is possible to have ∂q/∂x ≠ 0 and no motion. This means that the rotational energy somehow cancels the potential energy required to induce the Fickian flux.

Another essential contribution of this theory is the introduction of active behavior of the particles. Changing of states may be only possible if particles interact or if they may change state due to some internal property. Therefore, this new approach is a better model for biological systems and energized particles diffusing in a particular energy field.

The abnormal diffusion of enzymes reported recently indicates that the perturbation is due the thermal energy released from a particular reaction taking place in the enzyme itself [15]. The new observed behavior is modeled with the classical second order theory where the diffusion coefficient is considered as a particular function of the reaction rate. It is expected to obtain the net diffusion coefficient as the authors correctly sustain. Assuming the classical solution an adjusted diffusion coefficient is determined using experimental observations. The new coefficient is proposed as D = D 0 + αV. Again, despite the fact that the experiments reported in the paper are conducted under extremely care, the coefficients determined experimentally may not reflect the real physicochemical behavior. The net value of the diffusion coefficient could be the mean value obtained from the two distinct fluxes, primary and subsidiary.

Maybe the theory introduced here could be of some help provided that the chemical reaction modifying the diffusion process is progressive in time, that is, the reaction is not triggered simultaneously for all the particles which apparently is the case. But to perform this analysis the measurements should be different in order to evaluate the new variable β and the new reactivity coefficient R.

The bi-flux diffusion process as described here is an open research theme. The determination of the parameters β and R presents a considerable challenge. Preliminary analysis using the inverse approach technique suggests a close interdependence between these variables [16, 17]. Also the inclusion of sources and sinks will certainly expand the applicability spectrum of the theory.

We believe that the present theory is worthwhile being explored and improved. It opens several opportunities to people interested in both theoretical and experimental work.