1 Introduction

In Oil Reservoir Engineering applications one problem of great interest is the dynamic optimization of production scheduling, considering constraints at total field rate meaning that all wells share common injection and production units. The waterflooding optimal management problem, which is by far the most commonly used method to improve oil recovery, is studied here. The objective is to maximize the exploitation of the field using as controls the rates of injector and producer wells.

The application of different optimization techniques in the field of upstream in the oil industry began in the 1950s and has been developing ever since. There are three major lines of study within the context of optimization of oil production [1]. One highlights the operation of oil fields, related to equipment and production facilities and wells. Another is related to the development oil field, related to quantity and distribution of development of wells (not exploration). The last one is related to the management oil field through the dynamic allocation of the flows of the wells.

There is a vast literature on the dynamic rate allocation optimization for waterflooding. One may classify the methods according to the degree of intrusion into the simulator code. The highly intrusive methods make use of the adjoint technique to compute the gradient of the objective function [2], and are among the most efficient methods [3–6].

Adjoint methods require a large programming effort to be implemented and are not available in all commercial simulator codes at the present time. The semi-intrusive methods make use of reduced order models [7, 8], or time of flight concept in streamline simulators to equalize water breakthrough in groups of producer wells [9]. Finally the non-intrusive methods use the simulator as a black-box and are purely data driven.

Algorithms typically use evolutionary techniques [10–12], pattern search methods [13] and surrogate-based methods [14]. Another class of derivative-free algorithms use approximate gradients of the objective function based on stochastic methods [15] and ensemble methods [16], which may be corrected by additional finite difference computations [17] or be incorporated into a quadratic interpolation model [18].

Some researchers believe that the creation of hybrid methods can result in tools that succeed in the optimization process. Hybridization is already common practice in many fields. A hybrid algorithm may arise from the combination of two (or more) different strategies to solve one task. In principle, each strategy can be used independently, but this would produce solutions concentrated only in some specific characteristics. If the combination is efficient, unlike the independent use, chances are for a better solution to be found more quickly.

Güyagüler [19] proposed a hybrid optimization technique, based on the genetic algorithm (GA) with the polytope algorithm (simplex) and the Kriging technique. Hybridization of genetic algorithm with simplex introduced hill climbing into the stochastic search and also allowed the use of proxies created and calibrated iteratively throughout the run and adopting simple surrogate models in place of expensive numerical simulations.

The choices of available algorithms to assist in the optimization process are numerous; however, the type of algorithm to be considered often depends on the characteristics of the problem. The optimization performed with the hybrid strategy considered here in is implemented in two steps. In the first step, a global search algorithm is responsible for identifying the region where the global optimum may be located. In the second step, a local search algorithm refines the solution found on the previous step. To perform a global search, a genetic algorithm (GA) was considered [20], and to perform the local search a sequential approximate optimization (SAO) was used [21, 22]. Kriging-based surrogates are used in both stages.

Some considerations are taken to improve the performance of the GA. Some of them are related to constraints handling, because it is well known that evolutionary algorithms have difficulty to deal with it. Other one is related to the surrogate model where the search process is performed, since it has an interest in a good characterization of the behavior of real functions, in the entire domain, without wasting evaluations on points from unpromising regions.

The main idea is to combine techniques into a tool where the user does not need to provide many settings to achieve the optimal solution of the problems.

2 Multimodality issues

The presence of multimodality in functions in some problems is characteristics that hinder the work of mathematical programming algorithms; therefore, to find the optimal solution for such problems, such algorithms need to be applied to multiple starting points. Various attempts represent multiple executions where different solutions can be found with no guarantee that the solution is the global optimum of the problem. Considering this, we could say that mathematical programming algorithm would not be the best alternative to solve problems in which one seeks a global optimal solution and the involved function present multimodality characteristics.

Because of the difficulties, an alternative would be to adopt more robust search methods to deal with multimodality. In general, classes of algorithms that can perform this task are the evolutionary algorithms. However, the computational cost for this is quite high; therefore, when considering practical engineering problems, the use of such schemes is not a feasible option to be considered.

In short, we can say that both approaches mentioned above have useful features to obtain optimal solutions; however, the negative characteristics of them, in some situations, can avoid their use. To overcome the difficulties, and explore the positive aspects of the algorithms, an option that comes up is a combination of methods to create hybrid strategies and perform the search process.

3 Waterflooding problem

3.1 Definition

Waterflooding is the most commonly used method to improve oil recovery and maintain the reservoir at a proper pressure level. Optimization techniques can be applied to improve waterflooding sweep efficiency through the propagation of the water front. In this sense, one problem of great interest is the dynamic optimization of producing scheduling, leading to optimal rate allocation to the injectors and producers. In this problem, the net present value (NPV) is considered as the objective function and the constraints are related to the rates: total filed, limit values and voidage-type replacement [23].

3.2 Mathematical formulation

Mathematically the waterflooding problem can be formulated as follows:

$$ \begin{aligned} {\text{Maximize: }} & {\text{ NPV}} = f({\varvec{q}}) = \sum\limits_{t = 0}^{T} {\left[ {\frac{1}{{(1 + d)^{t} }} \cdot F_{t} ({\varvec{q}}_{t} )} \right]} \\ {\text{subject}}\;{\text{to: }}\,& \sum\limits_{p \in P} {q_{p,t} } \le Q_{l,\hbox{max} } ,\quad t = 1, \ldots ,n_{t} \\ & \sum\limits_{p \in I} {q_{p,t} } \le Q_{inj,\hbox{max} } ,\quad t = 1, \ldots ,n_{t} \\ & q_{p,t}^{l} \le q_{p,t} \le q_{p,t}^{u} ,\quad p = 1, \ldots ,n_{w} ,\quad t = 1, \ldots ,n_{t} \\ & \sum\limits_{p \in P} {q_{p,t} } \le \sum\limits_{p \in I} {\alpha \cdot q_{p,t} } \le \delta \cdot \sum\limits_{p \in P} {q_{p,t} } ,\quad t = 1, \ldots ,n_{t} \\ \end{aligned} $$
(1)

where \( {\varvec{q}} = [{\varvec{q}}{_{1}}^{T} {\varvec{q}}{_{2}}^{T} \ldots {\varvec{q}}_{{n_{t} }}^{T} ] \) is the vector of well rates for all control cycles; \( {\varvec{q}}_{t} = [{q_{1,t}} , \, {q_{2,t}} , \ldots, {q_{{n_{w} ,t}}} ] \) is the vector of well rates at control cycle t; q p,t is the liquid rate of well p at control cycle t; n t is the total number of control cycles; and n w is the total number of wells. In the objective function d is the discount rate and τ t is the time at the end of the tth control cycle. The cash flow at control cycle t, which represents the oil revenue minus the cost of water injection and water production, is given by

$$ F({\varvec{q}}_{t} ) = \Delta \tau_{t} \left[ {\sum\limits_{p \in P} {(r_{\text{o}} q_{{{\text{p}},t}}^{\text{o}} - c_{\text{w}} q_{{{\text{p}},t}}^{\text{w}} )} - \sum\limits_{p \in I} {(c_{\text{wi}} q_{{{\text{p}},t}} )} } \right], $$
(2)

where Δτ t is the time size of the tth control cycle; P and I are the sets of production and injection wells, respectively; q o p,t and q w p,t are the average oil and water rates at the pth production well at tth control cycle; r o is the oil price; c w and c wi are the costs of producing and injecting water. Q l,max is the maximum allowed total production liquid rate and Q inj,max is the maximum allowed total injection rate of the field. Superscripts l and u denote, respectively, the lower and upper bounds of design variables. Superscripts o and w denote, respectively, oil and water phases.

The last constraint requires that, for all cycles, the total injection rate belongs to an interval that goes from the total production rate to δ times this value, where δ ≥ 1 is the over injection parameter and α is the ratio between Q inj,max and Q l,max. This is a more general form of the so-called voidage replacement constraint used by many researchers as a means to maintain the reservoir properly pressurized [3, 24–26]. Although reduction of the voidage replacement fraction, at the end of the production period may improve NPV [27], this practice may produce undesirable effects, such as drop pressure on the reservoir, consequently, this would result on the production of gas on it [28]. This constraint is not a mandatory part of the optimization process and may be deleted from the formulation if the user deems appropriate.

The design variables are the well rates in each control cycle. Let well rates be scaled by their respective maximum allowable field rates:

$$ x_{p,t} = {{q_{p,t} } \mathord{\left/ {\vphantom {{q_{p,t} } {Q_{{{\text{l}},\hbox{max} }} }}} \right. \kern-0pt} {Q_{{{\text{l}},\hbox{max} }} }},\quad p \in P;\quad x_{p,t} = q_{p,t} /Q_{inj,\hbox{max} } ,\quad p \in I. $$
(3)

Design variables, x p,t , are then the allocated rate for well p at time at cycle t. We consider two alternative formulations for this problem: full capacity operation (FCO) and non-full capacity operation (NCO) [29].

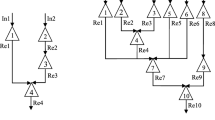
The commonly used approach to these problems is to subdivide the concession period into a number of control cycles, n t , whose switching times are fixed (see Fig. 1).

Fig. 1
figure 1

Control cycles’ switching times

Full size image

Another step to make both of the mentioned strategies (FCO and NCO) more flexible is to consider the time of control switching as design variables. Although the number of design variables increases, the time of control switching can be made more intelligent, matching events like optimum water breakthrough, pressure needs of the reservoir and shutting-in of wells or the whole field. Also, due to this additional flexibility it is possible to obtain optimal management schedules with less control cycles.

Under previous paragraph considerations, the time interval of each control cycle, except for the last, is a design variable as depicted in Fig. 1. Scaling the time intervals by the concession period, T, one gets

$$ x_{\Delta \tau ,t} = \Delta \tau_{t} /T,\quad t = 1, \ldots ,n_{t} - 1. $$
(4)

Henceforth, we will call the previously defined fixed time strategies as FCO-FT and NCO-FT and the strategies which considers the time of control switching as design variables as FCO-VT and NCO-VT.

A general formulation for the waterflooding problem, considering all variables scaled, can be formulated as follows:

$$ \begin{aligned} {\text{Maximize: }} & {\text{NPV}} = f(x) = \sum\limits_{t = 0}^{T} {\left[ {\frac{1}{{(1 + d)^{t} }} \cdot F_{t} (x_{t} )} \right]} \\ {\text{subject}}\;{\text{to}}{:}\; & \sum\limits_{p \in P} {x_{p,t} } \le 1,\quad t = 1 \ldots n_{t} \\ & \sum\limits_{p \in I} {x_{p,t} } \le 1,\quad t = 1 \ldots n_{t} \\ & \sum\limits_{t = 1}^{{n_{t} - 1}} {x_{\Delta \tau ,t} } \le 1 \\ & x_{p,t}^{l} \le x_{p,t} \le x_{p,t}^{u} ,\quad p = 1 \ldots n_{w} ,\quad t = 1 \ldots n_{t} \\ & x_{\Delta \tau ,t}^{l} \le x_{\Delta \tau ,t} \le x_{\Delta \tau ,t}^{u} ,\quad t = 1 \ldots n_{t} - 1, \\ & \sum\limits_{p \in P} {x_{p,t} } \le \sum\limits_{p \in I} {\alpha \cdot x_{p,t} } \le \delta \cdot \sum\limits_{p \in P} {x_{p,t} } ,\quad t = 1 \ldots n_{t} \\ \end{aligned} $$
(5)

Computation of the objective functions of the above problems requires a complete reservoir simulation. As simulations can take several hours to run, the optimization algorithm is coupled to surrogate models constructed as described in the following sections.

4 Optimization strategies

4.1 Approximations: surrogate models

The surrogate functions have been used aiming a fast computation, and also to get a smooth and/or simplified function for the computationally expensive models (high fidelity). The essential is that high-fidelity functions (costly) can be replaced by simpler functions, which are used during the optimization process.

The Kriging data fitting scheme is the approach used in this work to build the surrogate models. The main idea of this model is to assume that errors are not independent but rather assume that they are correlated to the distance between corresponding points modeled by a Gaussian process around each sample point. The main advantages of this scheme are to easily accommodate irregularly distributed sample data, and the ability to model multimodal functions with many peaks and valleys. Moreover, Kriging models provide exact interpolation at the sample points [23].

Kriging technique involves interpolation or numerical regression (polynomial) of a set of results generated from the real model [30, 31]. Therefore, to build such a model, the first step is to generate a set of points (sample) that are unique and limited by the boundaries of the design space. This technique is known in the literature as design of experiments (DOE) [30, 31]. The most common approaches are: Latin Hypercube (LHS), Quasi-Monte Carlo (QMC), and Latinized Centroidal Voronoi Tessellation (LCVT) [32]. It has been found that for the specific problem of optimized waterflooding management LCVT outperforms the others in general and is, therefore, used in this study [33].

Once m sample points are generated, predictor expressions are developed to evaluate the function at untried design points. This is based on the “ordinary Kriging” approach which models the true function as [31]:

$$ f({\varvec{x}}) = \beta + Z({\varvec{x}}) $$
(6)

where β is an unknown constant and Z(x) is a Gaussian random function with zero mean and variance σ 2.

After the construction of the approximation form, some model assessment strategies are required to check if a generated model is adequate. Such measure also provides some guidelines for selecting the best approximation model. The strategies considered are the same detailed in [23].

4.2 Hybrid strategy

4.2.1 Global search: genetic algorithm (GA)

As previously mentioned, a GA, implementation from MATLAB, is the global strategy considered on optimization process. GAs, as powerful and broadly applicable stochastic search and optimization techniques, are perhaps the most widely known types of evolutionary computation methods today. In the past decade, the GA community has turned much of attention to optimization problems in industrial engineering resulting in a large field of research and applications [34].

In general, a genetic algorithm has five basic components, as summarized by Michalewicz [35]:

  • A genetic representation of solutions to the problem;

  • A way to create an initial population of solutions;

  • An evolution function rating solutions in terms of their fitness;

  • Genetic operators that alter the genetic composition of children during reproduction;

  • Values for the parameters of GA.

In general, GAs follow the steps below:

  1. 1.

    Generation of initial population;

  2. 2.

    Fitness evaluation for all individuals in population;

  3. 3.

    Application of genetic operators to generate new population (selection, crossover and mutation);

  4. 4.

    Checking convergence; if not reached, return to step 2 and repeat the process.

It is well known that evolutionary algorithms have problems to deal with constrained optimization, and it is not different in GA. Some techniques have been developed in attempt to overcome this difficulty. In most applications of GAs to constrained optimization problems, the penalty function method has been used [36]. In this work is used an adaptive penalty method [37] which does not require any type of user-defined penalty parameter and uses information from the population. Moreover, to make the global search procedure more effective a filter scheme is proposed in which the level of feasibility in the initial population is assured.

4.2.1.1 Constraints handling

Constraint handling methods used in classical optimization algorithms can be classified into two groups [36]: (i) generic methods that do not exploit the mathematical structure (whether linear or nonlinear) of the constraint, and (ii) specific methods that are only applicable to a special type of constraints. Generic methods, such as the penalty function method, the Lagrange multiplier method, and the complex search method [38, 39] are popular, because each one of them can be easily applied to any problem without much change in the algorithm. However, the performance of these methods in most cases is not satisfactory.

On other hand, specific methods for constraints handling, such as the cutting plane method, the reduced gradient method, and the gradient projection method [38, 39], are applicable either to problems only having convex feasible regions or to problems having a few variables.

Since GAs are generic search methods, most applications of them to constraint optimization problems have used the penalty function. The penalty function approach involves a number of penalty parameters which must be set right in any problem to obtain feasible solutions. This dependency of GAs performance on penalty parameters has led researchers to develop sophisticated penalty function approaches such as multi-level penalty functions [40], dynamic penalty functions [41], and penalty functions involving temperature-based evolution for penalty parameters with repair operators [42]. All these approaches require extensive experimentation for setting up appropriate parameters needed to define the penalty function [36].

In special situations, closed genetic operators (in the sense that when applied to feasible parents they produce feasible offspring) can be designed if enough design space knowledge is available [43]. Special decoders [44]—that always generate feasible individuals from any given genotype—have been devised, but no applications considering implicit constraints have been published.

The GA from the MATLAB global optimization toolbox has some alternatives to deal with constrained problems, but in this work, two alternatives of constraints handling were considered because the available methods could not find results for the studied cases.

Chromosome repairing procedure: For this process, initially a randomly population is generated. After this, the level of violation related to the linear constraints defined in Eq. (5) is verified. From this stage two parameters (λ l, λ u) are created. The first one is called inferior activation parameter, which refers to the individuals that activate the constraints by lower bounds

$$ {\varvec{A}} \cdot (\lambda^{l} {\varvec{x}}) = {\varvec{b}}^{l} $$
(7)

The second parameter is created in a similar way. It is called superior activation parameter, which refers to the individuals that activate the constraints by upper bounds

$$ {\varvec{A}} \cdot (\lambda^{u} {\varvec{x}}) = {\varvec{b}}^{u} $$
(8)

Next, a randomly value λ in the interval [λ l, λ u] is picked. This λ is named feasibility parameter. These parameters are generated for each unfeasible individual in the initial population. The use of λ guarantees that the imposed constraints will not be violated, but it is not correct to affirm that the individual is completely in feasible region because some of its coordinates could be out of its limits.

After the application of the feasibility parameter, the coordinates of the individual are ranked to be corrected if necessary. The coordinates are ranked in a descending order. In case of any coordinate be out of the limits, a coordinate correction is made to send the individual to the feasible region.

In case of upper bound violation, the excess is relocated to the next feasible coordinate as the design variables rank goes on. When more than one coordinate violate the limits, the excess is summed to be redistributed. When the lower bound is violated, the amount necessary to bring it to the lower bound value is taken from the next feasible coordinates.

After an unfeasible individual be transformed into a feasible one, its coordinates are relocated in the chromosome (the original positions). To consider this process is crucial for creating the initial population. The GA implementation considered here presents difficulty to solve the waterflooding problem, when it was used without any feasible individual in the initial population. In various tests considered, the optimization process has been finished without any feasible solution found.

It is important to mention that the above procedure is used to create the initial population for GA and to create some feasible samples to build the global surrogate model used in the global search of the optimization process (more details in Sect. 4.2.1.2).

The chromosome repairing is a good choice to handling the linear constraints, although it cannot be used as the only method for this task, because it would interfere directly in the search process. For example, if there are violated children generated by the crossover operator, they would be genetically modified by the repairing process, and this would change the main characteristics of the GA, in a sense that every violated children generated would be subjected to a kind of driven mutation process. It would happen in the children generated by the mutation operator too.

Adaptive penalty method: The adaptive penalty method (APM) presented in [39] adaptively quantifies the penalty coefficients of each constraint using information from the population such as the average value of the objective function and the level of violation of each constraint. The fitness function is written as:

$$ F({\varvec{x}}) = \left\{ {\begin{array}{*{20}ll} {f({\varvec{x}})} & {{\text{if}}\;{\varvec{x}}\;{\text{is}}\;{\text{feasible}},} \\ {\bar{f}({\varvec{x}}) + \sum\nolimits_{j = 1}^{m} {\gamma_{j} v_{j} ({\varvec{x}})} } & {\text{otherwise}} \\ \end{array} } \right. $$
(9)

where

$$ \bar{f}({\varvec{x}}) = \left\{ {\begin{array}{*{20}ll} {f({\varvec{x}})} & {{\text{if }}f({\varvec{x}}) > \langle f({\varvec{x}})\rangle ,} \\ {\langle f({\varvec{x}})\rangle } & {\text{otherwise}} \\ \end{array} } \right. $$
(10)

where 〈f(x)〉 is the average of the objective function values in the current population and γ j is the penalty parameter for the jth constraint, and m is the number of constraints. It is defined at each generation by:

$$ \gamma_{j} = |\langle f({\varvec{x}})\rangle |\frac{{\langle v_{l} ({\varvec{x}})\rangle }}{{\sum\limits_{l = 1}^{m} {[\langle v_{l} ({\varvec{x}})\rangle ]^{2} } }} $$
(11)

and 〈v j (x)〉 is the violation of the lth constraint averaged over the current population. The idea is that the values of the penalty coefficients should be distributed in a way that those constraints which are more difficult to be satisfied should have a relatively higher penalty coefficient. Details of the proposed definition can be seen in [43].

To make clearer, consider Fig. 2 in which both feasible and infeasible solutions are shown. Among the six infeasible solutions, the individuals #3, #4, #5 and #6 have their objective function values (represented by opened circles), less than the average objective function and, according to the proposed method (see Eq. 10), this leads to \( \bar{f}({\varvec{x}}) = \langle f({\varvec{x}})\rangle \). The solutions #1 and #2 have objective function values which are greater than the population objective function average. Thus, for this case \( \bar{f}({\varvec{x}}) = f({\varvec{x}}) \).

Fig. 2
figure 2

A pictorial description of the function \( \bar{f}(\varvec{x}) \)

Full size image
4.2.1.2 Adaptive surrogate model

The definition of a surrogate model that can define the overall behavior of the functions involved in the problem is not trivial, since it has an interest in a good characterization of the behavior of real functions without wasting evaluations on points from unpromising regions. In addition, when considering constrained optimization, the requirements are increased because it is important to build surrogate models that can represent the behavior from the real functions in feasible region while representing unfeasible region reasonably, since, in general, the global solution is located within the limits of the feasible region.

An alternative is to create a “weak” surrogate model which is enriched as the search process is performed. A scheme of surrogate model with addition of points on waterflooding optimization problem was considered with the particle swarm algorithm in the master thesis presented by Souza [45]. A similar scheme is considered in this work.

Initially, two samples are created: the first one is the initial sample, which has a representative number of points which belongs to the feasible region (it was considered 60 %—just a little more than half of the samples); and the second is the “update” sample, which has only feasible points to update the surrogate model (both samples are created with the chromosome repairing procedure help—previously mentioned).

The initial surrogate model is created with the initial sample; the optimization is performed with the GA on it. When the search is finished, the consistency of the solution is checked. If the accuracy of the model is not satisfactory, the model is updated with addition of new samples. The samples taken to update the model consist on the solution found by the GA and some points from the update sample (in this work where chosen three points randomly). The model is updated until there are points available on the update sample or the consistency of the solution is reached.

The consideration of the “solution” point to update the model improves the representation of the behavior on the region where it was found by GA; however, it should not be considered alone as it can be a local optimum. The addition of feasible samples improves model in other feasible regions.

The computational aspects of this strategy can be summarized as follows:

  1. 1.

    Create the initial sample (with 60 % in feasible region) and the update sample;

  2. 2.

    Compute the function evaluations of the initial sample;

  3. 3.

    Construct a global surrogate model for the functions;

  4. 4.

    Optimize the problem using GA with the approximated functions;

  5. 5.

    Evaluate the solution found by GA on the real function;

  6. 6.

    Check the global convergence criteria of the strategy:

6.1. If reached, the process is finished;

6.2. Otherwise, the solution found by GA is added to the initial sample as well as the points taken from the update sample (three points, which are evaluated on real functions), and returns to step 3.

4.2.2 Local search: sequential approximate optimization (SAO)

A local strategy named Sequential Approximate Optimization (SAO) is used to compose the hybrid strategy in this study. The SAO methodology decomposes the original optimization problem into a sequence of optimization subproblems, confined to small subregions of optimization design space, called trust regions, whose extents are adaptively managed by the SAO strategy depending on surrogate accuracy [21, 46]. Surrogate functions (low cost) are created and used by the optimizer. Mathematically, each subproblem, at the kth SAO iteration, is defined as:

$$ \begin{aligned} {\text{Maximize:}}\; & \, \hat{f}^{k} (x) \\ {\text{subject}}\;{\text{to}}{:}\,& \hat{g}_{i}^{k} (x) \le 0,\quad i = 1 \ldots m \\ & \hat{h}_{j}^{k} (x) = 0,\quad j = 1 \ldots n \\ & {\varvec{Ax}} \le {\varvec{b}} \\ & \left\| {x - x_{c}^{k} } \right\|_{\infty } \le \Delta^{k} \\ & x^{l} \le x \le x^{u} \\ \end{aligned} $$
(12)

In the above equations, \( \hat{f}^{k} (x) \), \( \hat{g}_{i}^{k} ({\varvec{x}}) \) and \( \hat{h}_{j}^{k} ({\varvec{x}}) \) are, respectively, the surrogate objective and the constraints functions constructed for the current iteration, A and b are the matrix and right-hand side of linear constraints, \( x_{\text{c}}^{k} \) is the center point of the trust region, Δk is the size of the trust region at the current iteration, and x l and x u are, respectively, the lower and upper bounds of the design variables. The initial trust region is a subregion taken from the entire domain which considers the initial point é central point.

Each subproblem formulated in Eq. (12) defines SAO iteration. The main steps involved in the computations are:

  1. 1.

    Compute the expensive and/or non-smooth objective function and constraints at the central point in the subregion;

  2. 2.

    Construct surrogate model in the subregion;

  3. 3.

    Optimize within the subregion using the surrogate objective function and constraints;

  4. 4.

    Compute the true objective function and constraints at the optimum identified in step 3;

  5. 5.

    Check for convergence;

  6. 6.

    Move/shrink/expand the subregion according to the accuracy of the approximated model compared to the true function and constraint values;

  7. 7.

    Impose local consistency;

  8. 8.

    Check for overall optimization convergence. If it is achieved stop the SAO procedure; otherwise return to step 3.

To update the trust region size for each optimization subproblem the approach considered takes into consideration the accuracy of surrogate functions against the true functions. For more details see [23]. More details about the SAO algorithm can be checked in [22, 23].

5 Examples

In this section, the tools described previously are employed in a study case. The studies are conducted using MATLAB. The reservoir numerical simulations are performed using IMEX Commercial Software from CMG [47].

5.1 Brush Canyon Outcrop Synthetic Case

This reservoir is composed of a complex geologic model constructed from geostatistical techniques and data from outcrop, which is close to a real reservoir model, although it is a synthetic case where the first studies were presented in [10].

The generated model reproduces typical of a depositional turbidity formations system in deep water, representing the most important type of reservoir found in sedimentary basins along the Brazilian coast. The petrophysical parameters were correlated, as can be seen in [48].

The features and the main characteristics of the model for this reservoir are presented in Table 1 and in Fig. 3.

Table 1 Summary of model characteristics
Full size table
Fig. 3
figure 3

Brush Canyon Outcrop model (permeability field)

Full size image

Although the model incorporates a high degree of uncertainty, it is not considered in the studies performed here.

For the optimization problem, the production of the platform is limited to 5000 m3/day, and the total injected water is limited to 5750 m3/day. As the well rates are the design variables, the boundaries are imposed as the limitations on these rates.

For the producers, the rates can vary from 0 to 900 m3/day, and for the injectors, the rates can vary from 0 to 1500 m3/day. Normalizing the boundaries according the Eq. (3) gives to the producers a range of 0 ≤ x p,t  ≤ 0.18, t = 1…n t , p ε P, while gives to the injectors a range of 0 ≤ x p,t  ≤ 0.2609, t = 1…n t , p ε I.

The concession period is 24 years, and when considering the time of control switching as design variable, the related design variables are normalized according the Eq. (4).

A simplified version of VPL is used considering the revenues from the oil, and the production and injection costs (see Eqs. 1, 2). To calculate the NPV it is considered: \( r_{\text{o}} = 25.00/{\text{m}}^{3} , \) \( c_{\text{w}} = 5.00/{\text{m}}^{3} \), \( c_{\text{wi}} = 2.00/{\text{m}}^{3} \) and 0.093 as internal return rate.

Next sections present solutions for two operation strategies: full capacity/fixed time (FCO-FT) and non-full capacity/variable time (NCO-VT). Normalized producer rates in the base case for all strategies are: x p,t  = 0.143, t = 1…n t , p ∊ P, while for all injectors, x p,t  = 0.2, t = 1…n t , p ∊ I. These values correspond to uniform rate allocation to all wells. The corresponding NPV value is $2.6209 × 108.

5.1.1 Optimal solution: FCO-FT case

This section discusses solutions obtained for the fixed time, full capacity operation of the example. Two different numbers of control cycles were considered as shown in Fig. 4. In this case, the number of design variables is ten per control cycle, two less than the total number of wells.

Fig. 4
figure 4

Control cycles considered on concession period

Full size image

The consideration of these two cases with different number of control cycles did not provide a big difference in the results obtained. The explanation for this can be perceived from Fig. 5.

Fig. 5
figure 5

Performance of FCO-FT with different control cycles

Full size image

Considering the hybrid strategy, the result found for the NPV, by the GA in the global search, was \( \$ 2.7173 \times 10^{8} \), which does not represent great improvement when comparing with the base case.

Taking the solution provided by the GA, and considering this solution as the initial point, for SAO in the local search, our best fixed time result for final NPV is \( \$ 3.1767 \times 10^{8} \), which represents a 21.21 % of improvement over the base case.

For this case, a better result was already found. It is presented by Horowitz [23]. The NPV found in that work was \( \$ 3.2282 \times 10^{8} \), which represents a 23.17 % of improvement over the base case (more details for this result can be found in [23]).

Tables 2 and 3 list optimum well rates for the case with six control cycles, which involves 60 independent design variables. As can be readily seen producer wells P-6, P-8, P-10, and P-12 are all operating at their maximum liquid rate. Figure. 6 shows the optimal rates of the remaining producers.

Table 2 Optimization results for producer wells for six control cycles on FCO-FT case
Full size table
Table 3 Optimization results for injector wells for six control cycles on FCO-FT case
Full size table
Fig. 6
figure 6

Rate controls of selected well. a Producer wells and b injector wells

Full size image

5.1.2 Optimal solution: NCO-VT case

Increasing the number of variables could afford an improvement on the NPV over the one on the base case, but, as can be seen in Fig. 5, it was considered six times more design variables and the result was not so different.

As mentioned in the mathematical formulation of the problem, a step that makes the production strategies more flexible is to consider the time of control switching as design variables. Although the number of design variables increases, the time of control switching can be made more intelligent. Due to this additional flexibility it is possible to obtain optimal management schedules with less control cycles.

For this reason, this case considers the non-full capacity with variable time operation. Only the case with three control cycles is discussed. In this case, the range for the time of control switching variables is \( 0 \le x_{\Delta \tau ,t} \le 0.4 \), t = 1…n t  − 1, and the limits for the rates are the same presented in the FCO-FT case. The total number of design variables now is 38. The over injection parameter is taken as δ = 1.15 (see Eq. 1).

Again, the proposed methodology was considered. The result found for the NPV, by the GA in the global search, was \( \$ 3.5578 \times 10^{8} \), and now, it represents a great improvement when comparing with the base case. But it is not the final result.

Considering this solution as the initial point, for SAO in the local search, our best result for final NPV is \( \$ 3.6233 \times 10^{8} \), which is 14 % higher than the two previous solutions (FCO-FT cases), and corresponding to 38.25 % improvement when compared to the base case.

A result for this case can also be found in Horowitz [23]. The NPV found in that work was \( \$ 3.6100 \times 10^{8} \), which represents a 37.74 % of improvement over the base case (more details for this result can be found in [23]).

Tables 4 and 5 show the values of the design variables, and the results obtained in both case can also be compared in Fig. 7.

Table 4 Optimization results for producer wells for six control cycles on NCO-VT case
Full size table
Table 5 Optimization results for injector wells for six control cycles on NCO-VT case
Full size table
Fig. 7
figure 7

Performance of NCO-FT with different control cycles

Full size image

The most flexible management strategy is NCO-VT, which creates more opportunities to increase NPV by the possibility of shutting-in and late starting of production and injection wells. The inclusion of control cycle duration in the formulation is effective in reducing significantly the number of design variables while maintaining recovery efficiency. On the other hand, it has been observed that this technique increases the nonlinearity of the problem which may become multimodal.

6 Conclusions

The optimization of waterflooding management problem needs a large amount of function evaluation which means a large amount of reservoir simulation. It is computationally expensive. A powerful strategy to tackle this problem is the use of surrogate models based on data fitting techniques. Extensive comparative studies of performance in waterflooding problems indicate that LCVT sampling coupled with Kriging data fitting is the technique of choice to construct an effective surrogate model to deal with this kind of problems.

A hybrid global/local optimization strategy is used to solve the problem performing the optimization process in two steps, a global search (performed by GA) followed by a local search (performed by SAO). Although the SAO is an efficient optimization method, the hybrid methodology considered here overcomes the need to perform several initial point tries on reservoir optimization problems.

The waterflooding problem is formulated using liquid rates of wells as controllable variables. Duration of control cycles may also be included as design variables. The objective function is a simplified NPV. Different operational conditions may be modeled such as Full Capacity Operation (FCO) and Non-full Capacity Operation (NCO). In FCO, both injection and production units are forced operate at their maximum capacity at all times whereas in NCO this condition is relaxed.

The most flexible management strategy is NCO with variable duration of control cycles. This creates more opportunities to increase NPV by the possibility of shutting-in and late starting of production and injection wells. The inclusion of control cycle duration in the formulation is effective in reducing significantly the number of design variables while maintaining recovery efficiency. On the other hand, it has been observed that this technique increases the nonlinearity of the problem which may become multimodal.

The cases considered involve a high nonlinear objective function and also presents several constraints functions. These aspects together turn out the problem too difficult to be solved by the GA (in charge of the first stage of the optimization). To improve its performance, some tools were considered to increase the capability to find a good feasible solution.