Desert seismic random noise reduction framework based on improved PSO–SVM

Abstract

As one of the major regions of carbonate rock oil–gas exploration in western China, Tazhong area of the Tarim Basin has severe environment and complex ground surface conditions, hence the signal to noise ratio (SNR) of the field seismic data is extremely low. To improve the SNR of desert seismic data is a crucial step in the following work. However, the random noise in desert seismic characterizes by non-stationary, non-gaussian, non-linear and low frequency, which are very different from the random Gaussian noise. In addition, the effective signals of desert seismic generally share the same frequency band with strong random noise. These all make some traditional denoising methods cannot suppress it well. Therefore, a new noise suppression framework based on improved PSO–SVM is proposed in this paper. First, we extract the correlation of noisy desert seismic data to form feature vector. Subsequently, the model of improved PSO–SVM was built to classify the extracted feature, thereby identifying the position of the seismic events. Finally, second-order TGV filter was applied for obtaining denoised results. We perform tests on synthetic and field desert seismic record and the denoising results show that the proposed method can effectively preserve effective signals and eliminate random noise.

1 Introduction

Tazhong area of Tarim Basin in western China is one of the main areas for carbonate oil–gas exploration. Since this area is covered by desert with harsh environment and complex surface conditions, the SNR of the field record is extremely low. With the continuous development of seismic exploration technology, the requirements for the quality of seismic data are becoming higher and higher. To improve the SNR of desert seismic data has become an important aspect of the processing work. Different from mountain land, forest belt and other regions, the sand layer in the desert region is loose. This leads to the desert seismic noise possesses strong energy. Additionally, the loose sand will absorb most of high-frequency noise. This results in the consequence that desert seismic noise mainly characterizes by low-frequency. In sum, the waveform of random noise in desert areas is similar to effective signals, and it characterizes by low-frequency, narrow frequency-band, the frequency-band overlap between random noise and effective signals, etc. These all make the desert noise more difficult to be suppressed.

Thus far, various effective denoising methods have been developed in different application fields, and the more mature methods include adaptive filtering (Ristau and Moon 2001; Jeng et al. 2009), empirical modal decomposition (Bekara and Baan 2009), singular value decomposition (SVD) (Deng et al. 2008), polynomial fitting (Yuan and Wang 2013), wavelet transform (WT) (Hongying et al. 2013; Tian et al. 2015), Shearlet transform (Zhang et al. 2015), f-k filtering (Naghizadeh 2012), time–frequency peak filtering (Elboth et al. 2010), etc. Meanwhile, these methods have not only been limited to the simple and direct application, but also expanded to some improved algorithms or algorithms combined with other methods to achieve the desired denoising. Though these methods have achieved better practical applications, each method for denoising is mainly for suppression of random Gaussian noise. Due to the characteristics of desert seismic random noise, the existing various signal processing technologies cannot cope with complex and low-quality desert seismic data at this stage. Therefore, it is very urgent to find a new method which can effectively suppress the desert seismic random noise.

With the advancement of science and technology, machine learning (ML) has been applied in many fields, such as image processing, industrial fault diagnosis, speech signal processing and so on (Jung et al. 2010, 2011; Omran et al. 2004; Archana and Elangovan 2014). ML has been also widely used in the field of seismic signal processing. Noureddine et al. (2008) proposed a method of feedback connection artificial neural network to reduce the noise of seismic data. Juan and Francois (2011) proposed a method of machine learning for seismic phase classification. Bui Quang et al. (2015) used hidden Markov model to classify the seismic event. Dan et al. (2016) utilized fuzzy C-means clustering algorithm to pick first arrival time point of micro-seismic data. The advantage of ML is that the prediction can be realized under the circumstance that the prediction relationship cannot be described by a specific analytical expression. Though the specific analytical expressions cannot be used to describe the relationship between input and output, machine learning algorithm can establish the nonlinear relationship between input and output, which makes the machine learning algorithm be used to establish the nonlinear prediction model. In recent years, neural network, deep learning and other new machine learning methods have also provided effective solutions to practical problems. However, almost all of these methods require a large number of training samples, and there may be a larger “false alarm rate” and “missing alarm rate” when there are a small number of samples.

Support vector machine (SVM) (Vapnik 1999) is a machine learning method based on statistical theory, which is suitable for obtaining the optimal solution under limited samples, and the data acquired in our experiment performed happens to be the case of small-volume samples. Its basic idea is to map the low-dimensional input spatial data to the high-dimensional characteristic space through using kernel function, and then convert the low-dimensional linear inseparable problems into linearly separable ones in the high-dimensional space.

Denoising is a process to separate out effective signal from noise. In fact, it is also a course of identification and classification. How to accurately classify is the vital for denoising. In this paper, the excellent classification performance of SVM was exploited to identify the events submerged in strong noise. It is generally known that the performance of SVM is largely dependent on its parameters such as the penalty parameter C and the kernel function parameters g. As a result, an effective and intelligent method should be employed to obtain the optimal parameters of SVM. Particle swarm optimization (PSO) was first put forward by Kennedy and Eberhart (1995), Vashishtha (2016). It is a global optimization technique inspired by social behavior of bird flocking or fish schooling. In this paper, we try to use an improved PSO to find the optimal parameters for the SVM model. After identifying the desert seismic events, the second-order total generalized variation (TGV) filter (Knoll et al. 2011) was used for denoising to get the ideal result. Such denoising processing serves as a seeking energy minimization processing in TGV model, which draws upon the better ability of high order derivative for distinction noise and effective signal. In a word, our method first extracts the correlations of noisy desert seismic data to form feature vectors. In addition, we have established an improved PSO–SVM model, which is the optimal signal and noise recognition model. Next, the second-order TGV filter, which keeps the signals better, was employed to obtain denoised results. Finally, the proposed method was proven valid and feasible by both synthetic data experiments and field data experiments.

2 Theory and method

2.1 Seismic random noise of desert

In the desert zone of the Tarim basin, it is almost flat and there is little vegetation. The desert noise is divided into three categories according to the reason that the noise generates: natural noise, near-field cultural noise and far-field cultural noise, respectively. The natural noise is generated mainly by the friction between the wind and the ground; the near-field noise is mainly caused by machines and human footsteps around geophones; the far-field noise sources are mainly man-made physical processes far from the receiver. The characteristics of the desert seismic random noise are non-stationary, non-linear, low-frequency, which are totally different from the white Gaussian noise. Additionally, the effective signal and the strong random noise of the desert seismic data are overlapped in frequency domain (for details, see Li and Li 2016; Zhong et al. 2019).

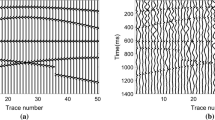
In order to more intuitively present the characterization of desert noise, we take actual desert noise record as an example. Figure 1a shows the time-domain waveform of the record, which is composed of 3000 sampling points. Figure 1b shows the power spectrum, which is obtained by the PWELCH method. It can be seen that the power spectrum of the data is consistent, and its frequency-band range is approximately 0–40 Hz. Figure 1c shows the amplitude distribution. It can be found the amplitude centralize around in (− 3, 3). The other statistical characteristics are listed in Table 1. The mean is close to 0. The variance is small, which indicates the dispersion degree is low. The skewness is more than 0, which means the probability density curve is more to the right than the normal distribution. The kurtosis is less than 3, which means the probability density curve is lower than the normal distribution.

Fig. 1

a Field noise record in the desert of Tarim, b power spectrum, c amplitude distribution

Table 1 Statistical characteristic

2.2 Feature extraction of desert seismic signal

It is difficult to classify noisy data directly because the frequency and amplitude of the desert seismic random noise are similar to effective signals. Effective feature extraction of noisy desert seismic data is the key to classification. In our research, the correlation $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\gamma }$ is extracted as the feature of desert seismic signal. The correlation is a statistical indicator reflecting the degree of linear correlation between variables. It was defined as:

$$\gamma \left( {\tau_{1} ,\tau_{2} } \right) = \frac{{\text{cov} (\tau_{1} ,\tau_{2} )}}{{\sqrt {\text{var} [\tau_{1} \left] {\text{var} [\tau_{2} } \right]} }}$$

(1)

where $\text{cov} (\tau_{1} ,\tau_{2} )$ is the covariance of $\tau_{1}$ and $\tau_{2}$; $\text{var} [ \tau_{1} ]$ and $\text{var} [ \tau_{2} ]$ are the variances of $\tau_{1}$ and $\tau_{2}$ respectively; $\tau_{1}$ and $\tau_{2}$ are the variables. Here, suppose $f_{o} (i) = \{ f_{o} (1),f_{o} (2), \ldots ,f_{o} (n)\}$ is a desert seismic signal with $n$ data points, we selected each consecutive 3 data points as each variable $\tau$. Using Eq. (1), the correlation $\gamma$ can be calculated to form the feature vector $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {Q}_{p}$, as shown in the following expression:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {Q}_{p} = \left\{ {\gamma \left( {\tau_{1} ,\tau_{2} } \right)} \right\}\quad \left( {p \in 1,2} \right)$$

(2)

In order to more observably analyze the feature of desert seismic signal, we generate a set of synthetic data as shown in Fig. 2. Its SNR is − 7.63 dB and dominant frequency of effective signals is 30 Hz. It could be observed from Fig. 2 that the random noise in desert seismic signal was mainly at low frequency, and they have a large difference and there were no rules. We selected the 5th, 19th, 20th, 34th and 47th trace (the blue lines in Fig. 2) with larger differences for correlation calculation, as shown in Fig. 3. The blue lines are the noisy signals, and the red lines are the corresponding correlation value. It can be seen that the distribution of the correlation value of effective signal and noise was different, especially, the first sub-wave of the 19th and 20th was destroyed by the strong noise, and the position of effective signals couldn’t be distinguished visually. Hence, it demonstrated that correlation could be used as the feature vector of seismic signal identification.

Fig. 2

Synthetic noisy desert seismic signals

Fig. 3

Feature extraction. (Color figure online)

2.3 Support vector machine (SVM)

SVM has a very excellent generalization performance because it could independently find the support vectors to constructing a hyperplane for classification according VC dimension theory and the principle of structural risk minimization. In addition, it avoids the network structure selection, over-learning, under-learning and other problems of artificial neural network and other theories. The basic idea of SVM algorithm is to map input data in low-dimensional space to high-dimensional feature space through nonlinear mapping, so as to make it linearly separable, and solve the optimal discriminant function in high-dimensional space and determine the classification boundary. Considering a two-class problem, the training sample $m_{o}$ can be expressed as follows:

$$m_{o} = \{ (x_{i} ,y_{i} )|x_{i} \in R^{n} ,y_{i} \in \{ 0, + 1\} ,i = 1,2,3 \ldots l\}$$

(3)

where $x_{i}$ represents the input feature vector of desert seismic signal; $y_{i}$ is either 0 or + 1, which is denoted as effective desert seismic signal or random noise. SVM classifies the samples by using the optimal classification hyper-plane $\begin{array}{*{20}c}\varvec{\omega}\\ \end{array} x_{i} + b = 0$, and the two samples closest to the optimal classification hyper-plane are called support vector. The sum of the distance between the support vector and the optimal hyper-plane is $\frac{2}{{\left\| {\begin{array}{*{20}c}\varvec{\omega}\\ \end{array} } \right\|}}$, and according to the principle of structural risk minimization, the sum of the distance should be maximized. Therefore, the problem of solving the optimal hyperplane is transformed into the following optimization problem:

$$\begin{aligned} & \hbox{min} \frac{1}{2}\left\|\varvec{\omega}\right\|^{2} \\ & y_{i} \left( {\varvec{\omega x}_{i} + b} \right) \ge 1 \\ \end{aligned}$$

(4)

where $\omega$ is the normal vector of the optimal classified hyper-plane; $b \in {\mathbf{R}}$ is the classification threshold.

For most cases of training sample set are linearly indivisible, SVM introduces non-negative slack variable $\xi_{i}$ and penalty factor C. After conducting nonlinear mapping through kernel function, the above objective function was changed into:

$$\begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{\omega},b,\xi }} \frac{1}{2}\varvec{\omega}^{\text{T}}\varvec{\omega}\text{ + }C\sum\limits_{i = 1}^{l} {\xi_{i} } \\ & y_{i} \left( {\varvec{\omega}^{\text{T}} \phi \left( {\varvec{x}_{i} } \right) + b} \right) \ge 1 - \xi_{i} \\ & \xi_{i} \ge 0 \\ \end{aligned}$$

(5)

Lagrange multiplier method was adopted to solve the above minimum problem, and Lagrange function was established as follows:

$$J\left( {\varvec{\omega},b,\alpha } \right) = \frac{1}{2}\varvec{\omega}^{T}\varvec{\omega}+ C\sum\limits_{i = 1}^{l} {\xi_{i} } - \sum\limits_{i = 1}^{l} {\alpha_{i} } \left[ {y_{i} \left( {\varvec{\omega}^{T} \phi \left( {\varvec{x}_{i} } \right) + b} \right) - 1 + \xi_{i} } \right]$$

(6)

where $\alpha_{i}$ is Lagrange multiplier and $\alpha_{i}$ > 0.

Seek the partial derivatives of $\varvec{\omega}$ and b in Formula (6) and set them to zero, respectively. Then substitute the results into Formula (6) to obtain the dual problem of the original problem:

$$\begin{aligned} & \mathop {\hbox{max} }\limits_{\alpha } Q\left( \alpha \right) = \sum\limits_{i = 1}^{l} {\left( {1 - \xi_{i} } \right)\alpha_{i} } + C_{i} \sum\limits_{i = 1}^{l} {\xi_{i} } - \frac{1}{2}\sum\limits_{i = 1}^{l} {\sum\limits_{j - 1}^{l} {\alpha_{i} \alpha_{j} y_{i} y_{j} \phi } \left( {x_{i}^{\text{T}} } \right)\phi \left( {x_{j} } \right)} \\ & \sum\limits_{j - 1}^{l} {\alpha_{i} y_{i} = 0,0 \le \alpha_{i} \le C} \\ \end{aligned}$$

(7)

Solve the above dual problem, obtain the optimal Lagrange multiplier $\alpha_{i}^{ * }$, and further acquire the discriminant function:

$$Y = \text{sgn} \left( {\sum\limits_{i = 1}^{l} {\alpha_{i}^{*} y_{i} \left( {\varphi (x_{i} )} \right)^{T} \varphi (x) + b} } \right),$$

(8)

where $x$ is the test sample.

Define $K\left( {\varvec{x}_{i} ,\varvec{x}} \right) = (\phi (\varvec{x}_{i} ))^{\text{T}} \phi (\varvec{x})$ as the kernel function, and the most widely used kernel function is the Gaussian radial basis function (RBF):

$$K(x_{i} ,x) = \exp ( - g\left\| {x_{i} - x} \right\|^{2} ),$$

(9)

where $g$ is the width of kernel function. It could be seen from the above derivation process that the value of penalty factor C and kernel function width g was the main factor affecting the recognition performance of SVM. In the actual classification, parameter C was reflected in the fact that, the generalization ability of SVM classifier would weaken when the value of C increased, and the decrease of C would make the classifier become underfitting. The parameter g reflected the dispersion situation that the original data was mapped to the high-dimensional space. If g was too large, the projection of the kernel function in the high-dimensional space would become smaller, which reduced the classifier’s ability to classify linearly indivisible data. However, if $g$ was too small, the projected area of kernel function in the high-dimension space would easily increase, which reduced the generalization ability of the classifier. Therefore, in order to improve the recognition accuracy, the value of the optimal penalty factor C and kernel function width g should be determined. In this paper, C and g were regarded as the optimization objects, and the identification accuracy was taken as the fitness function, and the improved particle swarm optimization algorithm was used to seek the optimal C and $g$.

2.4 Improved particle swarm optimization (PSO)

Particle swarm optimization (PSO) algorithm is a new swarm intelligence algorithm, in which particles find the global optimal solution by changing their speed and position according to the optimal position of individuals and swarms, and evaluate the performance of particles through a pre-defined fitness function. Assuming that the particle swarm whose population size is $m$ searches in a n-dimensional space, if the optimal position of the individual particle so far is $Pbest$, and the optimal position of the swarm is $Gbest$.

The flying speed $V_{i}$ and position $P_{i}$ of particles can be adjusted according to the following formula:

$$V_{i} (t + 1) = \eta \times V_{i} (t) + c_{1} \times r_{1} \times (Pbest - P_{i} ) + c_{2} \times r_{2} \times (Gbest - P_{i} )$$

(10)

$$P_{i} \left( {t + 1} \right) = P_{i} \left( t \right) + H_{O} \left( {1 - t/t_{\hbox{max} } } \right)V_{i} \left( {t + 1} \right)$$

(11)

where $P_{i}$ is the current position of the particles; $t$ is the iterations; $\eta$ is inertial weight coefficient; Constant $c_{1}$ and $c_{2}$ are learning factors; $r_{1}$ and $r_{2}$ are random numbers uniformly distributed within the range of [0,1]; Flight constant H₀ is generally 1.6. After setting the initial value of the particles, the optimal particle position could be found by the mutual iteration of formula (10) and formula (11) until the maximum iterations.

PSO is a popular parameter optimization tool, but its searching precision cannot meet our needs. Therefore, we adjust the inertia weight coefficient of particles to enhance the global search performance of PSO algorithm. Generally, the larger the inertia weight value was, the stronger the algorithm’s global search ability would be; otherwise, the algorithm’s local search ability would be stronger. The ideal PSO algorithm is that it has stronger global search ability at the early stage but stronger local search ability at the later stage. Therefore, the value of $\upeta$ of PSO algorithm in this paper could be adjusted by using the following linear strategy:

$$\upeta(t) =\upeta_{\hbox{max} } - (\upeta_{\hbox{max} } -\upeta_{\hbox{min} } ) \cdot \frac{t}{{t_{\hbox{max} } }}$$

(12)

The improved particle swarm optimization algorithm was used to optimize the SVM algorithm, and whether the sample classification results were consistent with the actual classifications was regarded as the fitness function of the PSO. Assuming that $F_{rec}$ was the classification results of the training set, $F_{act}$ was the actual classification, and l was the training set sample size, then the fitness function of particles could be defined as:

$$F = \tfrac{1}{l}\sum\limits_{i = 1}^{l} {(F_{rec} (i) = F_{act} (i))}$$

(13)

The fitness value of particles indicated the similarity between data objects in each classification. The higher the fitness value was, the more accurate the classification results would be.

To illustrate the clustering performance of the PSO–SVM method, we select the 47th trace synthetic data of the Fig. 2 as an example. As shown in Fig. 4, there are noise-free data, noisy signal, SVM clustering result and PSO–SVM clustering result, respectively. We can see that the PSO–SVM method has the more accurate clustering performance than the SVM method. In addition, we also calculate the clustering accuracy rate adopting the average of running 200 times. The results are shown in Table 2. We can see that the detection accuracy rate of the PSO–SVM method is always higher than the SVM method under the different SNR. In order to intuitively observe the detection accuracy rate, we plot the line chart of the Table 2 as seen in Fig. 5. It is can be seen that in the different SNRs, the green line chart is always above the red line chart. These all prove that the PSO–SVM method has the better accuracy.

Fig. 4

The clustering result of the 47th trace

Table 2 The clustering accuracy rate

Fig. 5

The line chart of accuracy

2.5 Second-order total generalized variation (TGV) denoising model

Total variation (TV) model, as a classical filter, explains the de-noising process from a novel perspective, which converts the de-noising problem into the energy minimization problem. Though TV model have better de-noising effects, its results can not only preserve the marginal information of signals but also generate a “staircase effect”. To address this defect of TV model, Bredies et al. proposed a new mathematical model: generalized total variation (TGV). As a high-order variation model, TGV can approximate free-order piecewise polynomial functions, which effectively overcame the defect that TV model is easy to generate staircase effect. Meanwhile, TGV itself also has many excellent properties, for example, it is rotation-invariant, convex, lower semi-continuous and so on. Second-order TGV model is adopted in this paper. Assuming that the desert seismic noisy record could be expressed as:

$$f_{o} (i,j) = f(i,j) + n(i,j)$$

(14)

where $f_{o} (i,j)$ is the desert seismic signal containing noise; $f(i,j)$ is the pure desert seismic signal; $n(i,j)$ is the desert random noise; $i = 1 \ldots N$ is the sampling point; and $j = 1 \ldots D$ is the channel order. Therefore, the random noise suppression model of desert seismic based on second-order TGV is as follows:

$$\mathop {\hbox{min} }\limits_{\Omega } TGV_{\alpha } (f) + \tfrac{\beta }{2}\int_{\Omega } {(f - f_{0} )dx}$$

(15)

where $TGV_{\alpha }^{2} (f) = \mathop {\hbox{min} }\limits_{\lambda } \alpha_{1} \left\| {\nabla f - \lambda } \right\|_{1} + \alpha_{0} \left\| {\varepsilon (\lambda )} \right\|_{1}$ is the second-order TGV regular terms; the second item is the data fidelity term; $\beta$ is the regularization parameter; $\nabla f$ is the gradient of desert seismic signal; $\lambda$ is a random variable, and $\Omega$ is the data size.

2.6 Process of denoising

Combining the above-mentioned contents, the specific steps of low-frequency desert seismic random noise suppression framework based on the improved PSO–SVM are summarized as follows:

• 1. Construct training sample set. According to Eq. (1), calculate the correlation $\gamma$ of noisy desert seismic data to construct its feature vector $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {Q}_{p}$. Afterwards, set the labels according to the differences of the effective signals and random noise feature.

• 2. Train the improved PSO–SVM model. Put the feature vector $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {Q}_{p}$ and the corresponding training labels into SVM, and then use the improved PSO to optimize SVM parameters.

• 3. Calculate the feature vectors of the test sample set, and then employ the improved PSO–SVM model for classification to get the contained effective signal points and without the effective signal points.

• 4. By means of the second-order TGV filter, we obtained the denoised results.

3 Application to desert seismic data

3.1 Testing on synthetic data

In order to test the feasibility and effectiveness of the proposed method, we present a synthetic data set shown in Fig. 6a. This synthetic record composed of six reflection events with the dominant frequencies of 25 Hz, 22 Hz, 20 Hz, 18 Hz. The sampling number is 500, and the horizontal distance between adjoin channels is 50 m. Figure 6b is the real desert noise, which is collected in the Tarim desert region. This desert noise is added to the pure synthetic seismic record and we get a synthetic noisy record with SNR of − 7.58 dB shown in Fig. 6c. We can see that the events are almost submerged by the strong noise. In this experiment, we conduct the wavelet denoised method, shearlet denoised method, f-x method, TGV denoised model and proposed denoising method on the noisy record. The denoised results are shown in Fig. 6d–h, respectively.

Fig. 6

Synthetic desert seismic data processing results a pure signal, b desert noise, c synthetic noisy data, d denoised result of wavelet, e denoised result of shearlet, f denoised result of f-x, g denoised result of TGV, h denoised result of proposed method

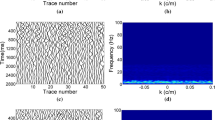
From the Fig. 6d, we can see that the wavelet method is poor to suppress the desert seismic random noise. For the shearlet method, it can suppress the noise better than the wavelet, that is because the multi-direction of the shearlet. However, there is still much random noise in Fig. 6e. Visually, though Fig. 6f, g have a little better result, it is still not very ideal. Figure 6h shows the result of the proposed method. We can see that the denoising effect is very obvious. It proves that the proposed method can accurately confirm the position of effective desert seismic signal, and effectively denoise the random noise on the Ricker wavelets. For further analysis, we also map the F-K spectrum of noise-free signal, desert noise, noisy record, and denoising records as shown in Fig. 7a–h, respectively. Figure 7a shows the frequency of the noise-free is dominated in 0–40 Hz. Figure 7b shows the frequency of the noise is dominated in 0–30 Hz. It indicates that there is overlap between the noise-free signal and the noise in the frequency domain. We can see that Fig. 7h is very similar to Fig. 7a, which means the proposed method can effectively identify the effective signal from the complex records and suppress the random noise.

Fig. 7

F-K spectrum a noise-free signal, b desert noise, c synthetic noisy signal, d result of wavelet, e result of shearlet, f result of f-x, g result of TGV, h result of proposed method

In order to better observe the denoised results, we extract the 30th trace from denoised results to compare with the pure signal. Figure 8a–e shows the comparison of the amplitudes of the signal waveform in time domain. Notice that the denoised signal of the proposed method is closer to the noise-free signal and the amplitude value of noise is minimum.

Fig. 8

Amplitude comparison of signals of the 30th trace a result of wavelet, b result of shearlet, c result of f-x, d result of TGV, e result of proposed method

In addition, the signal-to-noise ratio (SNR) is used as a measure of five denoising algorithms’ performance, which is defined as:

$$SNR = 101\log \frac{{\sum\nolimits_{i,j} {\left| {f(\hat{i},j)} \right|^{2} } }}{{\sum\nolimits_{i,j} {\left| {f_{0} - \hat{f}} \right|^{2} } }}$$

(16)

As shown in Table 3, we make a comparison among these methods under different noise level conditions in SNR. The data are collected from an average of ten runs. Examining the results in Table 3, we can clearly see that the proposed algorithm always outperforms the other four methods. In order to more intuitively observe, we plot the line chart of the Table 3 as seen in Fig. 9. It is can be seen that in the different SNRs, the green line chart is always above others line chart.

Table 3 SNRs of different methods

Fig. 9

The line chart of selected method for various input SNR

3.2 Analysis of real desert seismic data

The proposed method is finally tested with the desert seismic data in a certain area of China (see Fig. 10a) to further investigate the feasibility. We can see that the effective signals are submerged by strong noise. The SNR of this data is very low. We apply the wavelet denoised method, shearlet denoised method, f-x method, TGV method and proposed denoising method to this desert seismic data. The denoised results are shown in Fig. 10b–f respectively. From Fig. 10b–d, we cannot observe clear event, especially in green and blue rectangles. This is because both effective desert seismic signals and random noise are attenuated. As seen in Fig. 10e, TGV method can remove most random, but some weak desert seismic signals are not effectively recovered. Notice green and blue rectangles, although the events are emerged, but they are not continuous. Figure 10f shows the result of the proposed method. We can see clear and distinguishable events. In conclusion, the experiment verifies the effectiveness of the proposed method.

Fig. 10

Comparison of results of real desert seismic data a real desert seismic data, b result of wavelet, c result of shearlet, d result of f-x, e result of TGV, f result of proposed method

4 Conclusion

In this paper, a novel algorithm for desert seismic random noise reduction was proposed based on improved PSO–SVM. SVM is a supervised learning method in accordance with the statistical learning theory and the principle of structural risk minimization, exhibiting huge advantages in solving small sample, nonlinear and high dimensional pattern recognition problems. First, the correlation was extracted as the feature vector. Subsequently, the improved PSO was employed to optimize the SVM parameters. Finally, second-order TGV was applied for obtaining optimal denoising results. Compared with traditional methods, this proposed denoising framework can accurately detect the effective signals and finally achieve excellent de-noising effects. At last, both synthetic experiment results and real data results indicated that the new method could effectively remove the random noise from the desert seismic signals.