1 Introduction

Multivariate statistical methods act as a powerful tool of lithology determination in hydrocarbon exploration. Factor analysis is capable of extracting unobserved, latent petrophysical information from well log data. By correlating the calculated factors to petrophysical parameters, new approaches are being developed for the better modeling of hydrocarbon reserves. Bücker et al. (2000) suggested the use of factor analysis for a fast and objective evaluation of lithology from logging while drilling data. Odokuma-Alonge and Adekoya (2013) applied the same statistical method for the interpretation of stream sediments using geochemical data. Coimbra et al. (2017) used Principal Component Analysis as a related method to calibrate and contrast stratigraphic patterns in bulk elemental abundances. Szabó (2011) used factor analysis for shale volume calculation in unconsolidated shaly-sand hydrocarbon formations. Based on this study, Szabó and Dobróka (2013) found a strong exponential relation between a statistical factor explaining the most part of variance of the input well-logging data and the shale content for different North-American and Hungarian wells. The applicability of factor analysis was also indicated by Asfahani (2014) for the classification of Syrian basaltic formations. Szabó et al. (2014) confirmed for the results of shale volume estimation by core data.

The traditional method of factor analysis normally solves a maximum likelihood problem to extract the statistical factors (Beauducel et al. 2016). In this study, we offer an alternative approach, which treats the factor analysis as an inverse problem. In the frame of the inversion-based factor analysis, the observed well logs are approximated by calculated data directly computed from the factors, and the misfit between them is continuously optimized in an iterative process. For the computer-based minimization process, one of the most favorable methods are the global optimization methods. Sen and Stoffa (1995) provided a detailed description on the applicability of global optimization techniques used in geophysics including Simulated Annealing (SA). Soupiosa et al. (2011) utilized the Genetic Algorithms as a similar method to SA for seismic travel time inversion. Shaw and Srivastava (2007) successfully applied Particle Swarm Optimization as a third group of global optimization methods for inverting direct current, induced polarization and magnetotelluric data. The Simulated Annealing algorithm is an adaptation of the Metropolis algorithm (Metropolis et al. 1953) that is based on the annealing of solids in a heat bath. Analogously to the metallurgical process, SA is often used to solve multivariate optimization problems. Yin and Hodges (2007) suggested the use of SA for the inversion of electromagnetic data to eliminate the strongly start model dependent nature of traditional linearized inversion algorithms, e.g. the Marquardt–Levenberg method (Marquardt 1963). Szűcs et al. (2006) proved that in the characterization of groundwater formations, the geophysical inverse problem could be effectively solved by the Very Fast Simulated Annealing method. In this study, factor analysis is combined with SA to calculate the statistical factors more accurately and improve the fit between the measured and calculated well logs. By choosing suitable control parameters, SA allows the estimation of the factor variables in a convergent iterative procedure.

2 Simulated Annealing assisted factor analysis

SA is a random search technique used for approximating the global optimum of an objective function. The SA algorithm is based on the analogy between the simulation of the annealing of solids and the problem of solving multivariate optimization problems (van Laarhoven and Aarts 1987). Annealing denotes a physical process in which a solid is heated up by increasing the temperature to a maximum value. At this stage, all particles of the solid randomly arrange themselves in the liquid phase. Then, a slow cooling is carried out by slowly lowering the temperature. In this way, all particles organize themselves in the low energy ground state of a corresponding lattice, provided the maximum temperature is sufficiently high and the cooling is sufficiently slow. If the cooling schedule is too rapid, then the solid is not allowed to reach thermal equilibrium at a given temperature, and defects can be frozen into the solid and a metastable amorphous structure is reached (in our point of view a local minimum) rather than the lowest possible energy crystalline lattice structure (global minimum). Since the number of atoms are in the order of 1023, there are many possibilities for reaching an imperfect structure, in other words, a local minimum, but there is only one global minimum (perfect crystalline lattice structure). The analogy with geophysical inversion problems is obvious as we have a great number of measured and calculated data and we look for the absolute minimum of an objective function related to the data misfit with many local minima.

Factor analysis is generally used to describe several measured quantities with potentially fewer unobserved variables. In well log analysis, the measured well logs represent the input variables, which are simultaneously processed to extract the statistical factors. The scores of a given factor plotted against depth called a factor log can be associated with petrophysical parameters by regression analysis. In this study, we derive the shale volume from the factor logs in different sedimentary formations deposited along the Alaska Peninsula, USA.

In the first step, open-hole wireline logging data are standardized and put into the data matrix D, in such a way that each column contains data of different logging tools

$$ {\mathbf{D}} = \left( {\begin{array}{*{20}c} {\mathop D\nolimits_{11} } & {\mathop D\nolimits_{12} } & \cdots & {\mathop D\nolimits_{1K} } \\ {\mathop D\nolimits_{21} } & {\mathop D\nolimits_{22} } & \cdots & {\mathop D\nolimits_{2K} } \\ \vdots & \vdots & \vdots & \vdots \\ {\mathop D\nolimits_{i1} } & {\mathop D\nolimits_{i2} } & \cdots & {\mathop D\nolimits_{iK} } \\ \vdots & \vdots & \vdots & \vdots \\ {\mathop D\nolimits_{N1} } & {\mathop D\nolimits_{N2} } & \cdots & {\mathop D\nolimits_{NK} } \\ \end{array} } \right), $$
(1)

where K is the number of different types of well logs and N is the total number of observed depths. The basis of factor analysis is the following decomposition of matrix D

$$ {\mathbf{D}} = {\mathbf{FL}}^{\text{T}} + {\mathbf{E}}, $$
(2)

where F denotes the N-by-M matrix of factor scores, L represents the K-by-M matrix of factor loadings and E denotes the N-by-K residual matrix. Based on Eq. (2), the observed variables are derived as the linear combination of the factors. The factor loadings quantify the correlation relation between the observed variables and the extracted factors. The largest part of the total data variance is represented by the first column of the matrix F, which is called the first factor log. The factor loadings can be estimated by the non-iterative approach of Jöreskog (2007)

$$ {\mathbf{L}} = \left( {diag{\mathbf{S}}^{ - 1} } \right)^{ - 1/2} {\varvec{\Omega}}\left( {{\varvec{\Gamma}} - \theta {\mathbf{I}}} \right)^{1/2} {\mathbf{U,}} $$
(3)

where \( {\varvec{\Gamma}} \) denotes the diagonal matrix of the first M number of sorted eigenvalues of the sample covariance matrix S, \( {\varvec{\Omega}} \) is the matrix of the first M number of eigenvectors and U is an arbitrarily chosen M-by-M orthogonal matrix.

We alter the traditional method (Bartlett 1937) of factor analysis by using the SA algorithm to calculate the factor scores. The combined method has been chosen to call as FA-SA. In the first step of this optimization problem, the model of factor analysis defined in Eq. (2) is rearranged

$$ {\mathbf{d}} = {\widetilde{\mathbf{L}}\mathbf{f}} + {\mathbf{e}}, $$
(4)

where d denotes the KN length vector of observed (standardized) data, \( {\widetilde{\mathbf{L}}} \) is the NK-by-NM matrix of factor loadings, f is the MN length vector of factor scores and e is the KN length vector of residuals. At first, all data are put into a column vector, from where the matrix \( {\widetilde{\mathbf{L}}} \) is estimated by Eq. (3) and then rotated with the varimax algorithm developed by Kaiser (1958). This orthogonal rotation simplifies the interpretation of factors by giving to each factor a few large loadings and many small loadings. Then the vector of factor scores f is estimated by the FA-SA algorithm. To solve the inverse problem and estimate the factor scores, an objective function needs to be defined, the minimization of which finds the optimal solution. We choose the objective function, named energy function in the terminology of optimization theory, based on the L2 norm as

$$ E = \frac{1}{NK}\sum\limits_{i = 1}^{NK} {\left( {{\mathbf{d}}_{i}^{(m)} - {\mathbf{d}}_{i}^{(c)} } \right)^{2} = \hbox{min} } , $$
(5)

where \( {\mathbf{d}}_{{}}^{(m)} \) and \( {\mathbf{d}}_{{}}^{(c)} \) denote the measured and calculated (standardized) well-logging data vectors, respectively. In the modified model of factor analysis, the term of \( {\widetilde{\mathbf{L}}\mathbf{f}} \) represents the calculated data and D denotes the measured data. The former multiplication allows the estimation of the theoretical values of well logs, which can be considered as the solution of the forward problem. During the iterative procedure, we keep the values of factor loadings fixed to minimize the CPU time, and only the factor scores are updated. In each iteration, a randomly generated number (b) is added to any of the factor scores in vector f

$$ {\mathbf{f}}_{j}^{(new)} = {\mathbf{f}}_{j}^{(old)} + b\quad (j = 1, \ldots ,NM), $$
(6)

where parameter b is smaller than the maximal perturbation (bmax) that has to be defined in the initialization of the FA-SA algorithm. In the current procedure, we select the initial values of factor scores as zero. If the energy difference of factor models—estimated in two subsequent iterations (ΔE) according to Eq. (5)—is negative (i.e. better fit between the observed and calculated data), the new model is accepted and the process is continued with the new energy state. However, in the reverse case (if ΔE > 0), the probability of acceptance is given by the formula P a  = exp(− ΔE/T), where T is the current temperature of the artificial system with no physical meaning. The new factor model is accepted only when a randomly generated number from the range of 0 and 1 is smaller than P a . This acceptance rule for new energy states is referred to as the Metropolis criterion (Metropolis et al. 1953). This is a fundamental part of the FA-SA algorithm as it prevents the search from being stuck in a local minimum of function E in Eq. (5). During the annealing process, the temperature of the system is reduced iteratively according to Geman and Geman (1984)

$$ T^{(new)} = T^{(old)} /\ln (1 + q), $$
(7)

where q denotes the number of iterations already computed. The maximal perturbation term (bmax) is also reduced according to bmax = bmax · ε, where ε is an arbitrary chosen constant from the interval of 0 and 1. These steps are repeated in each iteration until the pre-defined maximal number of iteration steps is reached and then the values of factor scores in the last iteration step are accepted as the solution. The factors estimated by the FA-SA algorithm are directly used to reveal hidden petrophysical information from the well-logging data set. Szabó and Dobróka (2013) showed that the shale volume (in percent) correlates strongly to the first factor log (F1) scaled into the range of 0 and 100

$$ V_{sh} = 2.76e^{{0.037F_{1} }} , $$
(8)

the validity of which is verified in Alaska coastal sediments in Sect. 3. According to Eq. (8), the first factor has been identified as a lithologic indicator. Shale volume can also be independently calculated by a series expansion based inversion method (Dobróka et al. 2016). Szabó and Dobróka (2017) confirmed the validity of Eq. (8) by a series expansion based interval inversion procedure.

3 Field examples

3.1 Milky River Formation

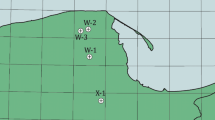
The FA-SA method is tested in two hydrocarbon exploratory wells drilled in Alaska, USA shown in Fig. 1. First, we investigate Well-1 that penetrated the Milky River Formation, which is mainly built up of conglomerates, sandstone and mudstone and was formed in a shallow marine environment in the Pliocene age. It has high porosity and high permeability. As the input of factor analysis, we utilized the natural gamma-ray intensity (GR), density (RHOB), caliper (CAL), deep induction resistivity (ILD), spontaneous potential (SP) and neutron-porosity (NPHIS) logs. At the beginning of the statistical procedure, the factor loadings are calculated by Jöreskog’s non-iterative approach using Eq. (3). Table 1 contains the resultant factor loadings representing the impact of the different well logs on the extracted factors for Well-1.

Fig. 1
figure 1

The location of the investigated wells

Full size image
Table 1 Rotated factor loadings estimated in Well-1
Full size table

As Table 1 shows, the deep resistivity and the spontaneous potential logs have the highest loads on the first factor and unusually the load of the natural gamma-ray intensity is only − 0.5213. From the first factor considered as lithological indicator, we would expect the natural gamma-ray intensity to have higher load, but in this formation, the abundance of lithic detritus causes a mineralogical overlap between sandstones and mudstones. Therefore, the natural gamma-ray tool which response is mainly due to some aspect of mineralogy recorded only little or no difference between sandstone and mudstone and this causes the relatively low factor loading of the natural gamma-ray intensity on the first factor.

Then the factor scores are estimated by the FA-SA algorithm. In the step of initialization, we define the objective function, also called the energy function according to Eq. (5) and set the initial temperature (T0) to 0.00015, cooling schedule according to Eq. (7), maximal parameter perturbation (b max ) to 0.5, perturbation reduction parameter (\( \varepsilon \)) to 0.98 and the maximal number of iteration steps. Figure 2a shows the decrease of the difference between the measured and calculated well logs by the iterations steps and Fig. 2b presents the temperature decrease of the system. The difference between the measured and calculated reached a minimum at about eighty thousand iterations, which took approximately 5 min on a quad-core based workstation. The continuous decrease of the value of the objective function indicates the highly stable nature of the FA-SA method.

Fig. 2
figure 2

a Development of convergence of the FA-SA procedure for Well-1, b temperature of the system during the procedure

Full size image

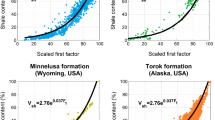
Figure 3 presents the relation between the first factor and the shale volume estimated by the FA-SA method utilizing Eq. (8). The regression coefficients of the suggested exponential relation agree well with earlier studies (Szabó and Dobróka 2013). The same coefficients in different formations shows consistent results and confirm the applicability of the method.

Fig. 3
figure 3

Regression relation between the scaled first factor and the shale volume for Well-1

Full size image

Shale volume derived from the FA-SA method is shown in Fig. 4. On tracks 1–6, the standardized (input) well logs (black solid line) and the calculated logs (red dotted line) can be seen. Track 7 is the scaled first factor log, while next to it on the right the shale volume calculated from the first factor log (red solid line) is compared to that of calculated by deterministic modeling using the SP log (purple dotted line).

Fig. 4
figure 4

The results of FA-SA for Well-1. (Color figure online)

Full size image

The fit between the observed and calculated well logs is quite good. Theoretical well logs represented by red dashed lines were directly calculated as the multiplication of the rotated factor loadings and factor scores. The shale volume calculated by the FA-SA method also agrees well with the results of deterministic analysis. These results indicate the applicability of the FA-SA method for shale volume estimation in shallow marine sedimentary formations.

3.2 Bear Lake Formation

In case of Well-2, the penetrated horizon is the Bear Lake Formation, which is of Miocene age, and consists mainly of sandstones, conglomerates and thin mudstones. It formed in neritic to tidal flat environments and it can be characterized by high porosity and moderate permeability. The inputs of the factor analysis were the caliper (CAL), interval transit time (DT), natural gamma-ray intensity (GR), deep induction resistivity (ILD), neutron-porosity (NPHIS), density (RHOB) and spontaneous potential (SP) logs. The FA-SA procedure run by the same control parameters as in Well-1. Table 2 contains the factor loadings related to three factors in case of Well-2.

Table 2 Rotated factor loadings calculated in Well-2
Full size table

In this case, not just the deep resistivity and the spontaneous potential logs have high loads on the first factor, but both the gamma-ray intensity and the caliper logs, too. We implemented the caliper log into the procedure, because washouts and the thickening of the mudcake might have strong relation in some cases to lithology. As we can see in this example, the caliper log affects highly the lithology-sensitive first factor. Figure 5 shows the decrease of the value of energy function by the iteration steps. It reached a minimum at about ninety thousand iterations in approximately 4 min. In this case, the FA-SA method again proves to be very stable in the iteration process. The cooling schedule was identical as in Fig. 2b which indicates the highly adaptive nature of this approach.

Fig. 5
figure 5

The decrease of the model energy by the iteration steps for Well-2

Full size image

The regression function of the first factor and the shale volume estimated by the FA-SA method is illustrated in Fig. 6, which refers to a strong relation also for Well-2.

Fig. 6
figure 6

Regression relation between the first factor and the shale volume for Well-2

Full size image

The interpretation results of the FA-SA method applied to Well-2 is shown in Fig. 7. The first seven columns from the left represents the input well logs (black solid line) and the calculated logs (red dotted line), the next is the scaled first factor log (blue solid line), and on the very right the shale volume calculated from the first factor log (red solid line) can be compared to the shale volume calculated by deterministic modeling (purple dotted line). Here the calculated logs again fit the measured data acceptably well. In conclusion, the shale volume calculated by the FA-SA method is consistent with the shale volume calculated by deterministic modeling.

Fig. 7
figure 7

The results of FA-SA for Well-2. (Color figure online)

Full size image

4 Discussion and conclusions

The study presents the results of the newly developed method (FA-SA) of factor analysis assisted by the Simulated Annealing technique. With a global optimization approach, this method transforms the measured well logs into factor logs in a reliable way. One finds that the first factor log calculated by the FA-SA method strongly correlates with the independently calculated shale volume of different coastal formations. However, it should be noted, that as it is a general method, it should work in most lithologies. Based on the factor loadings, in both examples the second factor log is influenced by porosity sensitive logs such as RHOB, NPHIS and DT, two of which, RHOB and DT, are also sensitive to elastic properties, which might be the basis of further studies. The implementation of the FA-SA allows also for the estimation of the theoretical values of well logs, which neglects the preliminary knowledge of zone parameters and other petrophysical information. It also proves to be very stable in the iteration process and delivers the results within some minutes for sections of few hundred meters. Therefore, the statistical method can serve as an alternative tool for calculating shale volume in the oilfield. With the further improvement of the mathematical algorithm of the FA-SA method, we intend to give a robust solution, so that it can also be utilized for highly noisy data sets with arbitrary (e.g. not normally distributed) statistical distributions.