Lax–Wendroff consistency of finite volume schemes for systems of non linear conservation laws: extension to staggered schemes

Abstract

We prove in this paper the Lax–Wendroff consistency of a general finite volume convection operator acting on discrete functions which are possibly not piecewise-constant over the cells of the mesh and over the time steps. It yields an extension of the Lax–Wendroff theorem for general colocated or non-colocated schemes. This result is obtained for general polygonal or polyhedral meshes, under assumptions which, for usual practical cases, essentially boil down to a flux-consistency constraint; this latter is, up to our knowledge, novel and compares the discrete flux at a face to the mean value over the adjacent cell of the continuous flux function applied to the discrete unknown function. We first briefly show how this result copes with multipoint colocated schemes on general meshes. We then apply it to prove the consistency of a finite volume discretisation of a convection operator featuring a (convected) scalar variable and a (convecting) velocity field, with a staggered approximation, i.e. with a cell-centred approximation of the scalar variable and a face-centred approximation of the velocity.

1 Introduction

The well-known Lax–Wendroff theorem [11] states that, on uniform 1D grids, if the approximate solutions of a flux-consistent and conservative cell-centred finite volume (FV) scheme for a system of conservation laws converge a.e. and boundedly as the mesh and time steps tend to zero, then the limit is a weak solution of the conservation law; we call this property “Lax–Wendroff consistency” (or LW-consistency for short); it is also stated in a different form [12, Section 12.10], with a BV bound assumption on the scheme. The Lax–Wendroff theorem is an “if-theorem”, which fails to solve the convergence issue for FV schemes since compactness is lacking. Nevertheless, it introduces two crucial tools for the analysis of FV schemes, namely the conservativity and consistency of the numerical fluxes; note that this analysis cannot be handled by the famous Lax–Richtmyer theorem, even in the linear case and even if the exact solution is assumed to be regular, as soon as the mesh is non uniform, see e.g. [4] for more on this subject. Moreover, the Lax–Wendroff theorem remains a useful tool to check whether a particular scheme gives a reasonable approximation when no estimates on the approximate solutions are available to yield some compactness, such as in the case of general hyperbolic systems. The Lax–Wendroff theorem was generalised to non uniform 1D or Cartesian meshes in [3, Theorem 21.2]. In a recent work [1], the Lax–Wendroff theorem is extended to obtain some error estimates for higher order schemes on uniform 1D meshes. The case of general (and, in particular, unstructured) discretisations has been also been tackled over the past decades: [10, 6, Section 4.2.2] [2, 5]. In [2], a quasi-uniformity assumption is required on the mesh, but the flux is only required to be continuous, while in [5], there is no uniformity assumption on the mesh but the flux is supposed to be locally Lipschitz continuous or at least locally “Lipschitz-diagonal” continuous, see Sect. 3 below and [5, Remark 5.2]. In all the above cited works, the scheme is supposed to be colocated, in the sense that the discrete unknowns are associated to the cells of the mesh, so these results may not be used directly to cope with staggered approximations, for instance.

The aim of this paper is to address more general approximations, including those of co-located or staggered type; indeed, we prove the LW-consistency of a generic finite volume convection operator acting on discrete functions that are possibly not piecewise-constant over the cells of the mesh and over the time steps; the result is otained under sufficient conditions which, in usual cases, turn to essentially boil down to a new flux consistency requirement; this LW-consistency result is stated in Theorem 2.1 below. The flux consistency constraint, formulated by Assertion (11), demands a control on the difference between the discrete flux at a face (or edge) and the mean value over the adjacent cell of the continuous flux function applied to the discrete unknown function. Theorem 2.1 is valid for general polygonal or polyhedral meshes without any supplementary assumptions on the mesh; as a by product of this work, we thus also obtain a consistency result for colocated schemes (i.e. schemes using only piecewise-constant per cell unknowns) with possibly relaxed assumptions for the mesh compared to [5]. However, let us note that the proof that the assumption (11) is satisfied is usually based on the control of the difference between the numerical solution and its space or time translates, see [5, Section 4] and that these latter results may require some regularity assumptions on the mesh, see also Remark 2.2.

This paper is organized as follows. We state and prove the general consistency result in Sect. 2. We then apply it in Sect. 3 to the colocated case and then, in Sect. 4, to a staggered discretisation; precisely speaking, we show the consistency of a finite volume discretisation of a nonlinear convection operator for a scalar variable $\rho$ of the form $\partial _t \beta (\rho ) + {\mathrm {div}}(g(\rho ){{\varvec{u}}})$, where $\beta$ and g are regular functions and ${{\varvec{u}}}$ is a velocity field, and where we use a cell-centred approximation for $\rho$ and a face-centred approximation of ${{\varvec{u}}}$.

2 The general LW-consistency result

The aim is to prove the LW-consistency of finite volume approximations of nonlinear convective terms which appear in most models of fluid flow. The general context is the following. Given a numerical scheme which yields some approximate solutions to the system of conservative partial differential equations, we assume that these approximate solutions converge to some functions strongly in $L^1$, and we wish to show that the limit is indeed a solution to the system, at least in a weak sense. In order to do so, the usual idea is to multiply the numerical scheme by an interpolate of a smooth function, sum over the cells of the mesh and over the time steps and show that passing to the limit, we get a weak formulation of the system of partial differential equations. The theorem that we prove below is a mean to prove that one may indeed pass to the limit in the terms that involve nonlinear convection operators. Let us begin with an example. Consider the barotropic Euler equations, which read:

$$\begin{aligned}&\partial _t {\bar{\rho }} + {\mathrm {div}}({\bar{\rho }} {\bar{{{\varvec{u}}}}}) = 0, \end{aligned}$$

(1a)

$$\begin{aligned}&\partial _t({\bar{\rho }} {\bar{{{\varvec{u}}}}})+ {\mathrm {div}}({\bar{\rho }} {\bar{{{\varvec{u}}}}} \otimes {\bar{{{\varvec{u}}}}}) + \varvec{\nabla }{\bar{p}} = 0, \end{aligned}$$

(1b)

where ${\bar{\rho }}$ is the density, ${\bar{{{\varvec{u}}}}}$ the velocity and ${\bar{p}}$ the pressure, which, for barotropic flows, is a function of ${\bar{\rho }}$ only: ${\bar{p}}= {\mathfrak {p}}({\bar{\rho }})$. Here and in the remainder of the paper, we use overlined letters when referring to the solution of the continuous problem, while non overlined letters will be used for discrete unknowns. This system of equations is supplemented by an initial condition and suitable boundary conditions if $\Omega$ is bounded. An entropy weak solution of the system satisfies the Eq. (1) and also satisfies (in a weak sense, which includes the initial condition) the following entropy condition:

$$\begin{aligned} \partial _t {\bar{E}} + {\mathrm {div}}(({\bar{E}} + {\bar{p}}) {\bar{{{\varvec{u}}}}})\le 0, \text{ with } {\bar{E}} = \frac{1}{2} {\bar{\rho }} |{\bar{{{\varvec{u}}}}}|^2 + {\mathcal {H}} ({\bar{\rho }}) \text{ and } {\mathcal {H}}(s) = s \int \dfrac{{\mathfrak {p}}(s)}{s^2} \ ds. \end{aligned}$$

(2)

The weak consistency of staggered finite volume schemes for this system of equations discretised on multi-dimensional Cartesian or unstructured meshes has been the object of several recent papers, see e.g. [8, 9]. The system (1) and (2) may be written as

$$\begin{aligned}&\bar{{\mathcal {C}}}_1({\bar{\rho }},{\bar{{{\varvec{u}}}}}) = 0, \end{aligned}$$

(3a)

$$\begin{aligned}&\bar{{\mathcal {C}}}_2({\bar{\rho }},{\bar{{{\varvec{u}}}}}) + \varvec{\nabla }{\bar{p}} = 0, \end{aligned}$$

(3b)

$$\begin{aligned}&\bar{{\mathcal {C}}}_3({\bar{E}},{\bar{{{\varvec{u}}}}}) + {\mathrm {div}}({\bar{p}} {\bar{{{\varvec{u}}}}} ) \le 0, \end{aligned}$$

(3c)

with $\bar{{\mathcal {C}}}_1({\bar{\rho }},{\bar{{{\varvec{u}}}}}) = \partial _t {\bar{\rho }} + {\mathrm {div}}({\bar{\rho }} {\bar{{{\varvec{u}}}}})$, $\bar{{\mathcal {C}}}_2({\bar{\rho }},{\bar{{{\varvec{u}}}}}) = \partial _t({\bar{\rho }} {\bar{{{\varvec{u}}}}})+ {\mathrm {div}}({\bar{\rho }} {\bar{{{\varvec{u}}}}} \otimes {\bar{{{\varvec{u}}}}})$, and $\bar{{\mathcal {C}}}_3({\bar{E}},{\bar{{{\varvec{u}}}}}) = \partial _t {\bar{E}} + {\mathrm {div}}({\bar{E}} {\bar{{{\varvec{u}}}}})$. In the above cited works, the system is discretised with an explicit or implicit in time scheme, and the convection operators ${\mathcal {C}}_1$ and ${\mathcal {C}}_2$ by a first or second order finite volume scheme. In fact, the system of the barotropic equations can be discretised by different schemes: explicit or implicit, colocated meshes or staggered meshes, using a Riemann solver or using an equation-by- equation procedure. In all cases, the consistency study will have to deal with each of the discrete non linear convection operator ${\mathcal {C}}_i$ associated to $\bar{{\mathcal {C}}}_i$. The present work aims at simplifying the proofs of consistency by giving a general result for any nonlinear convection term, discretised on a colocated or staggered mesh, thereby extending our previous result of [5] to staggered meshes. Theorem 2.1 below is an efficient tool to this purpose; it may be used for any of the terms in (3), and is specifically useful to tackle the terms featuring discrete variables with different space approximations, as the operators ${\mathcal {C}}_i$ of these equations in case of staggered discretizations. We emphasize that both implicit or explicit schemes may be addressed, since the proof deals separately with the discrete time operator and the discrete space divergence operator.

Let us then turn to the general setting; we suppose that:

$$\begin{aligned} \Omega \subset \mathbb {R}^d,\ d= 1, 2,3,\ T \in (0,+\infty ), \ p \in \mathbb {N}^*,\ \beta \in C^0(\mathbb {R}^p, \mathbb {R}),\ {{\varvec{f}}}\in C^0(\mathbb {R}^p, \mathbb {R}^d). \end{aligned}$$

(4)

We consider the conservative convection operator $\bar{{\mathcal {C}}}({\bar{U}})$ acting on a vector ${\bar{U}} \in \mathbb {R}^p$ of functions, real-valued, and defined (in the distributional sense), for ${\bar{U}} \in L^\infty (\Omega \times (0,T), \mathbb {R}^p)$, by:

$$\begin{aligned} \bar{{\mathcal {C}}} ({\bar{U}}):&\quad \Omega \times (0,T) \rightarrow \mathbb {R}, \nonumber \\&\quad ({\varvec{x}},t) \mapsto \partial _t(\beta ({\bar{U}}))({\varvec{x}},t) + {\mathrm {div}}({{\varvec{f}}}({\bar{U}}))({\varvec{x}},t). \end{aligned}$$

(5)

Note that, here and throughout the paper, we use $\beta ({\bar{U}})$ (resp. ${{\varvec{f}}}({\bar{U}})$) to denote the function $\beta \circ {\bar{U}}$ obtained by composition of $\beta$ and ${\bar{U}}$ (resp. ${{\varvec{f}}}$ and ${\bar{U}}$), so, for instance, $\beta ({\bar{U}})({\varvec{x}},t)$ stands for $\beta ({\bar{U}}({\varvec{x}},t))$. In the above example of the barotropic Euler equations (1), we have, for $i = 1,2$, $\bar{{\mathcal {C}}}_i({\bar{U}}) = \partial _t(\beta _i({\bar{U}})) + {\mathrm {div}}({{\varvec{f}}}_i({\bar{U}}))$, with ${\bar{U}} = ({\bar{\rho }}, {\bar{{{\varvec{u}}}}})$, $\beta _1( {\bar{U}}) = {\bar{\rho }}$, ${{\varvec{f}}}_1({\bar{U}}) = {\bar{\rho }} {\bar{{{\varvec{u}}}}}$, $\beta _2({\bar{U}}) = {\bar{\rho }} {\bar{{{\varvec{u}}}}}$, and ${{\varvec{f}}}_2({\bar{U}}) = {\bar{\rho }} {\bar{{{\varvec{u}}}}} \otimes {\bar{{{\varvec{u}}}}}$ (in fact, to match precisely the formalism of Eq. (4), these last two functions have to be considered as d functions, one for each velocity component, associated to d convection operators, which has no consequence for the matter at hand).

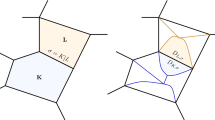
Let us denote by ${\mathcal {P}}$ a mesh of the domain $\Omega$, consisting of a set of disjoint open polyhedral or polygonal subsets of $\Omega$, called cells, whose union of closures is ${\bar{\Omega }}$ (Fig. 1). To avoid cumbersome notations, we assume that any pair of adjacent cells shares a whole face (in 3D) or edge (in 2D), and not only a part of it; however this assumption is not necessary for the result of Theorem 2.1 to hold. Throughout the paper and when the space dimension is not specified, we use "face" to define the interface between two cells; for a face $\zeta$, $|\zeta |$ stands for its $(d-1)$-dimensional measure in 2D and 3D, and we set $|\zeta |=1$ by convention in one space dimension. The notation |P| stands for the d-dimensional measure of a cell P. We denote by $\delta ({\mathcal {P}})$ the space step, defined by

$$\begin{aligned} \delta ({\mathcal {P}}) = \max _{P \in {\mathcal {P}}}\ {\mathrm {diam}}(P). \end{aligned}$$

Let ${{\mathfrak {F}}}$ denote the set of faces of the mesh, and ${{\mathfrak {F}}}_{\mathrm {int}}$ denote the set of faces that are not located on the boundary $\partial \Omega$; for a given cell $P \in {\mathcal {P}}$, let ${{\mathfrak {F}}}(P)$ be the set of faces of P. Let $t_0 = 0< t_1< \ldots < t_N = T$ be a partition of (0, T), denoted by ${{\mathcal {T}}}$; for such a partition ${{\mathcal {T}}}$, we define the time step by $\delta t = \max \,\{t_{n+1} - t_n, n \in \llbracket 0, N-1 \rrbracket \}$, where $\llbracket 0, N-1 \rrbracket$ denotes the set of integers n such that $0 \le n \le N-1$.

The unknown is supposed to be represented by a function $U \in L^\infty (\Omega \times (0,T), \mathbb {R}^p)$. For a colocated FV scheme, it is the piecewise constant function defined by $U(x,t) = U_K^n$ for $x \in K$ and $t\in ]t_n,t_{n+1}[$. For a FV staggered scheme for a system of equations, each component of U is piecewise constant on each associated mesh. But U could also be a piecewise affine function, for instance if say, a DG scheme is used. We emphasize that for non colocated schemes, some unknowns are not piecewise-constant over the cells of the mesh and over the time steps. For instance, when using staggered discretisations in fluid flow simulations, if P is a primal cell, the velocity is possibly discontinuous along surfaces or lines included in P (see the example developed in Sect. 4). The discrete convection operator that we consider here takes the following form:

$$\begin{aligned} {\mathcal {C}}(U) :&\quad \Omega \times (0,T) \rightarrow \mathbb {R}, \\&\quad ({\varvec{x}},t) \mapsto {\mathcal {C}}(U)_P^n, \text{ for } {\varvec{x}}\in P,\ P \in {\mathcal {P}}, \text{ and } t \in (t_n,t_{n+1}),\ n \in \llbracket 0, N-1 \rrbracket , \end{aligned}$$

with

$$\begin{aligned} {\mathcal {C}}(U)_P^n = (\eth _t \beta )_P^n + \frac{1}{|P|} \sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta |\ {{\varvec{F}}}_\zeta ^n \cdot {\varvec{n}}_{P,\zeta }, \end{aligned}$$

where $\bigl \{\beta _P^n,\ P \in {\mathcal {P}},\ n \in \llbracket 0, N \rrbracket \bigr \}$ is a family of real numbers,

$$\begin{aligned} (\eth _t \beta )_P^n = \frac{\beta _P^{n+1} - \beta _P^n}{t_{n+1} - t_n},\ n \in \llbracket 0, N-1 \rrbracket , \end{aligned}$$

(6)

$\bigl \{{{\varvec{F}}}_\zeta ^n,\ \zeta \in {{\mathfrak {F}}},\ n \in \llbracket 0, N-1 \rrbracket \bigr \}$ is a family of real vectors of $\mathbb {R}^d$ and ${\varvec{n}}_{P,\zeta }$ stands for the normal vector to $\zeta$ pointing outward P. Note that this form of the flux implies that the scheme is conservative. Of course, the real numbers $\bigl \{\beta _P^n,\ P \in {\mathcal {P}},\ n \in \llbracket 0, N \rrbracket \bigr \}$ and $\bigl \{{{\varvec{F}}}_\zeta ^n,\ \zeta \in {{\mathfrak {F}}},\ n \in \llbracket 0, N-1 \rrbracket \bigr \}$ are related to the unknown U; it is the object of Theorem 2.1 below to state precisely the assumptions that must be satisfied by these quantities to ensure the consistency of the discrete convection operator.

Fig. 1

An example of a two-dimensional mesh and associated notations: P and Q are two generic cells, $P, Q \in {\mathcal {P}}$, with ${\mathcal {P}}$ the set of cells, $\zeta =P|Q$ is the face separating P and Q, $\zeta \in {{\mathfrak {F}}}$, with ${{\mathfrak {F}}}$ the set of faces and ${\varvec{n}}_{P,\zeta }$ is the normal to $\zeta$ pointing outward P

Theorem 2.1

(LW-consistency for a multi-dimensional conservative convection operator) Under the assumptions (4), let $({\mathcal {P}}^{(m)},{{\mathcal {T}}}^{(m)})_{m\in \mathbb {N}}$ be a sequence of possibly non uniform space-time discretisations, with $\delta ({\mathcal {P}}^{(m)})$ and $\delta t^{(m)}$ tending to zero as $m\rightarrow +\infty$, and let $(U^{(m)})_{m\in \mathbb {N}}$ be the associated sequence of discrete functions. We suppose that the sequence $(U^{(m)})_{m\in \mathbb {N}}$ is bounded and converges to a limit:

$$\begin{aligned}&\exists \ C^u \in \mathbb {R}_+^* \text{ s.t. } \Vert U^{(m)}\Vert _\infty \le C^u,\ \forall {m\in \mathbb {N}}, \end{aligned}$$

(7)

$$\begin{aligned}&\exists \ {\bar{U}} \in L^\infty (\Omega \times (0,T), \mathbb {R}^p) \text{ s.t. } \Vert U^{(m)}- {\bar{U}} \Vert _{L^1(\Omega \times (0,T), \mathbb {R}^p)} \rightarrow 0 \text{ as } m \rightarrow +\infty . \end{aligned}$$

(8)

We also assume that the family $\{ (\beta ^{(m)})_P^n,\ P \in {\mathcal {P}}^{(m)},\ n \in \llbracket 0, N^{(m)}\rrbracket ,\ {m\in \mathbb {N}}\}$ is bounded. In addition, let $U_0 \in L^\infty (\Omega ,\mathbb {R}^p)$ and let us suppose that, as $m \rightarrow + \infty$,

$$\begin{aligned}&\qquad \qquad \qquad \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} \int _P \bigl ((\beta ^{(m)})_P^0 - \beta (U_0)({\varvec{x}}) \bigr )\ \varphi ({\varvec{x}}) \ \mathrm {d}{\varvec{x}}\rightarrow 0, \text{ for } \text{ any } \varphi \in C_c^\infty (\Omega ), \end{aligned}$$

(9)

$$\begin{aligned}&\qquad \qquad \qquad \sum _{n=1}^{N^{(m)}} \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} \int _{t_{n-1}}^{t_n} \int _P \Bigl ( (\beta ^{(m)})_P^n - \beta (U^{(m)})({\varvec{x}},t) \Bigr )\ \varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\rightarrow 0,\nonumber \\&\qquad \qquad \qquad \quad \quad \text{ for } \text{ any } \varphi \in C_c^\infty \bigl (\Omega \times [0,T)\bigr ), \end{aligned}$$

(10)

$$\begin{aligned}&\sum _{n=0}^{N^{(m)}-1} \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} \frac{{\mathrm {diam}}(P)}{|P|} \sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta |\ \int _{t_n}^{t_{n+1}} \int _P \Bigl | \Big (({{\varvec{F}}}^{(m)})_{\zeta }^n -{{\varvec{f}}}(U^m)({\varvec{x}},t) \Big ) \cdot {\varvec{n}}_{P,\zeta } \Bigr | \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\rightarrow 0, \end{aligned}$$

(11)

where ${\mathcal {P}}_{\mathrm {int}}^{(m)}$ denotes the set of cells of ${\mathcal {P}}^{(m)}$ that have no face on the boundary $\partial \Omega$. Then, for any $\varphi \in C_c^\infty (\Omega \times [0,T))$,

$$\begin{aligned}&\int _0^T \int _\Omega {\mathcal {C}}^{(m)}(U^{(m)})\ {\mathcal {I}}^{(m)}(\varphi )({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\rightarrow -\int _\Omega \beta (U_0)({\varvec{x}})\ \varphi ({\varvec{x}},0) \ \mathrm {d}{\varvec{x}}\nonumber \\&\qquad - \int _0^T \int _\Omega \Big (\beta ({\bar{U}})({\varvec{x}},t)\ \partial _t \varphi ({\varvec{x}},t) + \ {{\varvec{f}}}({\bar{U}})({\varvec{x}},t) \cdot \varvec{\nabla }\varphi ({\varvec{x}},t) \Big ) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\quad \text{ as } m \rightarrow + \infty , \end{aligned}$$

(12)

where ${\mathcal {I}}^{(m)}(\varphi )$ is an interpolate of $\varphi$ defined a.e. by

$$\begin{aligned} {\mathcal {I}}^{(m)}(\varphi )({\varvec{x}},t)= & {} \varphi _P^n \text{ for } {\varvec{x}}\in P \text{ and } t \in (t_n, t_{n +1}), \nonumber \\ \text{ with } \varphi _P^n= & {} \frac{1}{|P|} \int _P \varphi ({\varvec{x}},t_n)\ \mathrm {d}{\varvec{x}},\quad \text{ for } P \in {\mathcal {P}} \text{ and } n \in \llbracket 0, N-1 \rrbracket . \end{aligned}$$

(13)

Before we give the proof of Theorem 2.1, let us first briefly comment on its assumptions.

Remark 2.2

(Flux consistency) The required flux consistency is stated by Assertion (11), which requires the flux $({{\varvec{F}}}^{(m)})_{\zeta }^n$ through a face $\zeta$ of a cell P to be close to the mean value over P of the actual flux function ${{\varvec{f}}}$ applied to the unknown. For a scheme involving only cell unknowns, for instance, the quantity $({{\varvec{F}}}^{(m)})_{\zeta }^n$ is generally a function of the unknowns in the cell P and in the neighbouring cells, and checking the assumption (11) amounts to bound the difference between the unknowns and their translates. Note that, while Theorem 2.1 holds for very general meshes, as we have already mentioned in the introduction, some regularity assumptions on the sequence of meshes may be required at this step.

To clarify this point, let us consider a simple one-dimensional problem for the scalar unknown u, with $\beta (u) = f(u) = u$, leading to the linear convection operator ${\mathcal {C}}(u) = \partial _t u + \partial _x u$, which we discretise with the first-order explicit-in-time upwind scheme. Let us suppose that the discrete functions are defined by $u(x,t)=u_P^n$ for $x \in P$ and $t \in (t_n,t_{n+1})$. Then, for ${\varvec{x}}\in P$ and $t \in (t_n,t_{n+1})$, $|(({{\varvec{F}}}^{(m)})_{\zeta }^n -{{\varvec{f}}}(U^m)({\varvec{x}},t)) \cdot {\varvec{n}}_{P,\zeta }| = |(u^{(m)})_{P^-}^n -(u^{(m)})_P^n|$ where $P^-$ is the left cell to P when $\zeta$ is its left face, and $|(({{\varvec{F}}}^{(m)})_{\zeta }^n -{{\varvec{f}}}(U^m)({\varvec{x}},t)) \cdot {\varvec{n}}_{P,\zeta }| = 0$ otherwise (disregarding the boundary cells, according to the formulation of the theorem). Checking Assumption (11) thus consists in proving that the term $R^{(m)}$ defined by

$$\begin{aligned} R^{(m)}= \sum _{n=0}^{N^{(m)}-1} (t_{n+1} - t_n) \sum _{P \in {\mathcal {P}}^{(m)}} {\mathrm {diam}}(P)\ |u^n_P -u^n_{P^-}| \end{aligned}$$

tends to zero as m tends to $+\infty$. This is implied by the convergence in $L^1(\Omega \times (0,T))$ of the sequence of discrete solutions provided that the ratio $|P|/|P^-|$ is bounded independently of m for the sequence of meshes under consideration [5, Section 4]. More elaborate example of application, using colocated then staggered meshes, are provided below, in Sects. 3 and 4 respectively.

Remark 2.3

(Disregarding boundary cells in Assumption (11)) Since the support of the test function $\varphi$ is compact in $\Omega \times [0,T)$, for $\delta ({\mathcal {P}}^{(m)})$ small enough, $\varphi$ vanishes in the boundary cells. Consequently, it is clear from the proof of the theorem below (see the expression (15) of the term $X_2^{(m)}$) that boundary cells may be excluded in the sum in Assertion (11). This is the reason why only the cells in ${\mathcal {P}}_{\mathrm {int}}^{(m)}$ are considered in Assumption (11). For numerical fluxes involving wider stencils (for instance in the case of higher order schemes), one could in fact reduce the set of involved cells furthermore.

Remark 2.4

(Regularity of $\beta$ and ${{\varvec{f}}}$) The proof of Theorem 2.1 holds if $\beta$ and ${{\varvec{f}}}$ are only continuous functions, which is the assumption made in the present section; however, to prove Assertions (10) and (11), a locally Lipschitz-diagonal continuity (see Definition 3.1 below) is often required, as in Sects. 3 and 4.

Remark 2.5

(Stronger convergence assumptions on $\{ (\beta ^{(m)})_{m\in \mathbb {N}}\}$) In most situations, stronger convergence properties hold for $(\beta ^{(m)})_{m\in \mathbb {N}}$, in the sense that the LW-convergence assumptions (9) and (10) are implied by the following strong convergence assumptions:

$$\begin{aligned}&\sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} \int _P |(\beta ^{(m)})_P^0 - \beta (U_0({\varvec{x}})) | \ \mathrm {d}{\varvec{x}}\rightarrow 0 \text{ as } m \rightarrow + \infty , \\&\sum _{n=0}^{N_m-1} \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} \int _{t_n}^{t_{n+1}} \int _P |(\beta ^{(m)})_P^n - \beta (U^{(m)}({\varvec{x}},t)) | \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\rightarrow 0 \text{ as } m \rightarrow + \infty . \end{aligned}$$

This is the case, for instance, for the convection operators considered in Sects. 3 and 4 below. However, there are cases where the convergence of $\beta ^{(m)}$ is only weak, see for instance the reconstructed kinetic energy for the full compressible Euler equations in [8].

Remark 2.6

(On the interpolate of the test function) Note that in the definition (13) of ${\mathcal {I}}^{(m)}(\varphi )$ in (12), the quantities $\varphi _P^n,\ n \in \llbracket 0, N \rrbracket$, may be also defined as

$$\begin{aligned} \varphi _P^n = \frac{1}{|P|} \int _P \varphi ({\varvec{x}},t_{n+1}) \ \mathrm {d}{\varvec{x}}, \end{aligned}$$

with minor changes in the arguments of the present section, essentially a slightly different assumption (10), which reads:

$$\begin{aligned} \sum _{n=1}^{N^{(m)}} \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} \int _{t_{n-1}}^{t_n} \int _P \Bigl ( (\beta ^{(m)})_P^{n-1} - \beta (U^{(m)})({\varvec{x}},t) \Bigr )\ \varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\rightarrow 0,\\ \quad \text{ for } \text{ any } \varphi \in C_c^\infty \bigl (\Omega \times [0,T)\bigr ). \end{aligned}$$

For instance, for a scalar problem, if the discrete function is defined as $u({\varvec{x}},t)=u^{n-1}_P$ for ${\varvec{x}}\in P$ and $t \in [t_{n-1},t_n)$ (choice often used in explicit schemes) and $\beta _P^{n-1}$ is defined in the scheme as $\beta (u^{n-1}_P)$, this assumption is trivially satisfied, since $(\beta ^{(m)})_P^{n-1} = \beta (U^{(m)})({\varvec{x}},t)$ in $P \times (t_{n-1},t_n)$, while checking the original assumption (10) needs to bound the time translates of the discrete solution. This is however an easy task, under a very mild regularity assumption for the time discretisation (see Sect. 4 below). The opposite situation occurs (i.e. this is Assumption (10) which is now trivially satisfied) if the discrete function is defined as $u({\varvec{x}},t)=u^n_P$ for ${\varvec{x}}\in P$ and $t \in [t_{n-1},t_n)$, which is often done for implicit schemes.

Proof of Theorem 2.1

Theorem 2.1 is the consequence of the two following lemmas, which prove respectively the convergence of the time derivative part and the space derivative part. Let us decompose

$$\begin{aligned}&\int _0^T \int _\Omega {\mathcal {C}}^{(m)}(U^{(m)})\ {\mathcal {I}}^{(m)}(\varphi )({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t= X_1^{(m)}+ X_2^{(m)}, \text{ with } \nonumber \\&\qquad X_1^{(m)}= \sum _{n=0}^{N^{(m)}-1} (t_{n+1} - t_n) \sum _{P \in {\mathcal {P}}^{(m)}}|P| (\eth _t \beta ^{(m)})_P^n\ \varphi _P^n, \end{aligned}$$

(14)

$$\begin{aligned}&\qquad X_2^{(m)}= \sum _{n=0}^{N^{(m)}-1} (t_{n+1} - t_n) \sum _{P \in {\mathcal {P}}^{(m)}}\ \sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta |\ ({{\varvec{F}}}^{(m)})_\zeta ^n \cdot {\varvec{n}}_{P,\zeta }\ \varphi _P^n. \end{aligned}$$

(15)

Then, by Lemma 2.7 below,

$$\begin{aligned} X_1^{(m)}\rightarrow - \int _\Omega \beta (U_0)({\varvec{x}})\ \varphi ({\varvec{x}},0) \ \mathrm {d}{\varvec{x}}- \int _0^T \int _\Omega \beta ({\bar{U}})({\varvec{x}},t)\ \partial _t \varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\quad \text{ as } m\rightarrow +\infty , \end{aligned}$$

and by Lemma 2.8 below,

$$\begin{aligned} X_2^{(m)}\rightarrow - \int _0^T \int _\Omega {{\varvec{f}}}({\bar{U}})({\varvec{x}},t) \cdot \varvec{\nabla }\varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\quad \text{ as } m\rightarrow +\infty , \end{aligned}$$

which concludes the proof. $\square$

Lemma 2.7

(LW-consistency, time derivative) Let the sequence $(X_1^{(m)})_{m\in \mathbb {N}}$ be defined by (14). Then, under the assumptions and notations of Theorem 2.1,

$$\begin{aligned} X_1^{(m)}\rightarrow - \int _\Omega \beta (U_0)({\varvec{x}})\ \varphi ({\varvec{x}},0) \ \mathrm {d}{\varvec{x}}- \int _0^T \int _\Omega \beta ({\bar{U}})({\varvec{x}},t)\ \partial _t \varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\quad \text{ as } m\rightarrow +\infty . \end{aligned}$$

Proof

By the definition (6) of $\eth _t^n \beta _P^{(m)}({\varvec{x}},t)$ and thanks to a discrete integration by parts, we get that

$$\begin{aligned} X_1^{(m)}= - \sum _{P \in {\mathcal {P}}^{(m)}} |P| \ (\beta ^{(m)})_P^0\ \varphi _P^0 - \sum _{n=1}^{N^{(m)}} (t_n - t_{n-1}) \sum _{P \in {\mathcal {P}}^{(m)}} |P|\ (\beta ^{(m)})_P^n\ \frac{\varphi _P^n - \varphi _P^{n-1}}{t_n - t_{n-1}}. \end{aligned}$$

Let us write the first term of the right-hand side as

$$\begin{aligned} - \sum _{P \in {\mathcal {P}}^{(m)}} |P| \ (\beta ^{(m)})_P^0\ \varphi _P^0= & {} -\sum _{P \in {\mathcal {P}}^{(m)}} \int _P (\beta ^{(m)})_P^0\ \bigl (\varphi _P^0-\varphi ({\varvec{x}},0)\bigr ) \ \mathrm {d}{\varvec{x}}\\&-\sum _{P \in {\mathcal {P}}^{(m)}} \int _P (\beta ^{(m)})_P^0\ \varphi ({\varvec{x}},0) \ \mathrm {d}{\varvec{x}}. \end{aligned}$$

On the one hand, the piecewise-constant function equal to $\varphi _P^0$ on each cell $P\in {\mathcal {P}}^{(m)}$ converges to $\varphi ({\varvec{x}},0)$ in $L^\infty (\Omega )$ as m tends to $+\infty$, and $(\beta ^{(m)})^0$ is supposed to be bounded; the first integral at the right-hand side thus tends to zero. Hence, invoking Assumption (9) for the second integral,

$$\begin{aligned} - \sum _{P \in {\mathcal {P}}^{(m)}} |P| \ (\beta ^{(m)})_P^0\ \varphi _P^0 \rightarrow - \int _\Omega \beta (U_0)({\varvec{x}})\ \varphi ({\varvec{x}},0) \ \mathrm {d}{\varvec{x}}\quad \text{ as } m\rightarrow +\infty . \end{aligned}$$

Let the piecewise constant function $\eth _t^{(m)}\varphi : \Omega \times (0,T) \rightarrow \mathbb {R}^d$ be defined by

$$\begin{aligned} \eth _t^{(m)}\varphi ({\varvec{x}},t) = \dfrac{\varphi _P^{n+1} - \varphi _P^n}{t_{n+1} - t_n} \text{ for } ({\varvec{x}},t) \in P \times (t_n,t_{n+1}). \end{aligned}$$

The function $\eth _t^{(m)}\varphi$ converges uniformly to $\partial _t \varphi$ in $L^\infty (\Omega \times (0,T))$. The second term of $X_1^{(m)}$ may be decomposed as

$$\begin{aligned} -\sum _{n=1}^{N^{(m)}} (t_n - t_{n-1}) \sum _{P \in {\mathcal {P}}^{(m)}} |P|\ (\beta ^{(m)})_P^n\ \frac{\varphi _P^n - \varphi _P^{n-1}}{t_n - t_{n-1}}= Y_1^{(m)}+ Y_2^{(m)}\end{aligned}$$

with

$$\begin{aligned}&Y_1^{(m)}= -\sum _{n=1}^{N^{(m)}} \sum _{P \in {\mathcal {P}}^{(m)}} \int _{t_{n-1}}^{t_n} \int _P (\beta ^{(m)})_P^n\ \bigl (\eth _t^{(m)}\varphi ({\varvec{x}},t)- \partial _t \varphi ({\varvec{x}},t)\bigr ) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t, \\&Y_2^{(m)}= - \sum _{n=1}^{N^{(m)}} \sum _{P \in {\mathcal {P}}^{(m)}} \int _{t_{n-1}}^{t_n} \int _P (\beta ^{(m)})_P^n\ \partial _t \varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t. \end{aligned}$$

Since the family $\{ (\beta ^{(m)})_P^n,\ P \in {\mathcal {P}}^{(m)},\ n \in \llbracket 0, N^{(m)}\rrbracket ,\ {m\in \mathbb {N}}\}$ is assumed to be bounded, the uniform convergence of $\eth _t^{(m)}\varphi$ to $\partial _t\varphi$ yields that the sequence $(Y_1^{(m)})_{m\in \mathbb {N}}$ tends to zero. Invoking the assumption (10), the continuity of $\beta$ and the convergence of $(U^{(m)})_{m\in \mathbb {N}}$ to ${\bar{U}}$, we get that

$$\begin{aligned} \lim _{m \rightarrow +\infty } X_1^{(m)}= \lim _{m \rightarrow +\infty } Y_2^{(m)}= - \int _0^T \int _\Omega \beta ({\bar{U}})({\varvec{x}},t)\ \partial _t \varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t. \end{aligned}$$

$\square$

Lemma 2.8

(LW-consistency, space derivative) Let the sequence $(X_2^{(m)})_{m\in \mathbb {N}}$ be defined by (15). Then, under the assumptions and notations of Theorem 2.1,

$$\begin{aligned} X_2^{(m)}\rightarrow - \int _0^T \int _\Omega {{\varvec{f}}}({\bar{U}})({\varvec{x}},t) \cdot \varvec{\nabla }\varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\quad \text{ as } m\rightarrow +\infty . \end{aligned}$$

Proof

Since $\varphi$ is compactly supported and since $\delta ({\mathcal {P}}^{(m)}) \rightarrow 0$ as $m \rightarrow 0$, there exists $M \in \mathbb {N}$ such that for $m \ge M$, $\varphi _P^n = 0$ for all ${\varvec{x}}\in {\mathcal {P}}^{(m)}\setminus {\mathcal {P}}_{\mathrm {int}}^{(m)}$. Moreover, since for a face $\zeta$ separating P and $P'$, one has ${\varvec{n}}_{P,\zeta }= - {\varvec{n}}_{P',\zeta }$, we get that

$$\begin{aligned} X_2^{(m)}= & {} \sum _{n=0}^{N^{(m)}-1} (t_n - t_{n-1}) \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}}\ \sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta | \ ({{\varvec{F}}}^{(m)})_\zeta ^n \cdot {\varvec{n}}_{P,\zeta }\ \varphi _P^n \\= & {} \sum _{n=0}^{N^{(m)}-1} (t_n - t_{n-1}) \sum _{P_{\mathrm {int}} \in {\mathcal {P}}^{(m)}} A_P^n \end{aligned}$$

with

$$\begin{aligned} A_P^n =\sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta |\ ({{\varvec{F}}}^{(m)})_{\zeta }^n \cdot {\varvec{n}}_{P,\zeta } \ (\varphi _P^n -\varphi _\zeta ^n), \end{aligned}$$

where $\varphi _\zeta ^n$ denotes the mean value of $\varphi ({\varvec{x}},t_n)$ over $\zeta$. For any ${\varvec{x}}\in P$, $t \in [t_n, t_{n+1})$, we decompose $A_P^n$ as

$$\begin{aligned} \begin{array}{l} A_P^n = B_P^n({\varvec{x}},t)+R_P^n({\varvec{x}},t) \text{ with } \\ \displaystyle B^n({\varvec{x}},t) = \sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta |\ {{\varvec{f}}}(U^{(m)})({\varvec{x}},t) \cdot {\varvec{n}}_{P,\zeta } \ (\varphi _P^n -\varphi _\zeta ^n), \\ \displaystyle R_P^n({\varvec{x}},t) = \sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta |\ \Bigl ( ({{\varvec{F}}}^{(m)})_\zeta ^n - {{\varvec{f}}}(U^{(m)})({\varvec{x}},t) \Bigr ) \cdot {\varvec{n}}_{P,\zeta } \ (\varphi _P^n -\varphi _\zeta ^n). \end{array} \end{aligned}$$

(16)

Since $\sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta |\ {\varvec{n}}_{P,\zeta } =0$, we have

$$\begin{aligned} B_P^n({\varvec{x}},t)= & {} -\sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta |\ {{\varvec{f}}}(U^{(m)})({\varvec{x}},t) \cdot {\varvec{n}}_{P,\zeta } \ \varphi _\zeta ^n = - |P|\ {{\varvec{f}}}(U^{(m)})({\varvec{x}},t) \cdot (\varvec{\nabla }\varphi )_P^n, \nonumber \\ \text{ with } (\varvec{\nabla }\varphi )_P^n= & {} \dfrac{1}{|P|} \sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta |\ \varphi _\zeta ^n\ {\varvec{n}}_{P,\zeta } = \dfrac{1}{|P|} \int _P \varvec{\nabla }\varphi ({\varvec{x}},t_n) \ \mathrm {d}{\varvec{x}}. \end{aligned}$$

(17)

Note that the piecewise constant function $\varvec{\nabla }^{(m)}\varphi :\ \Omega \times (0,T) \rightarrow \mathbb {R}^d$ defined by

$$\begin{aligned} \varvec{\nabla }^{(m)}\varphi ({\varvec{x}},t) = (\varvec{\nabla }\varphi )_P^n \text{ for } ({\varvec{x}},t) \in P \times (t_n,t_{n+1}) \end{aligned}$$

converges uniformly to $\varvec{\nabla }\varphi$ in $L^\infty (\Omega \times (0,T))^d$.

Owing to (16), we have

$$\begin{aligned} A_P^n = \frac{1}{(t_{n+1} - t_n) \ |P|} \Bigl (\int _{t_n}^{t_{n+1}} \int _P B_P^n({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t+ \int _{t_n}^{t_{n+1}} \int _P R_P^n({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\Bigr ), \end{aligned}$$

and, thanks to (17),

$$\begin{aligned} X_2^{(m)}= & {} \sum _{n=0}^{N^{(m)}-1} \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} \frac{1}{|P|} \Bigl (\int _{t_n}^{t_{n+1}} \int _P B_P^n({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t+ \int _{t_n}^{t_{n+1}} \int _P R_P^n({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\Bigr ) \nonumber \\= & {} -\int _0^T \int _\Omega {{\varvec{f}}}(U^{(m)})({\varvec{x}},t) \cdot \varvec{\nabla }^{(m)}\varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\nonumber \\&+ \sum _{n=0}^{N^{(m)}-1} \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} \frac{1}{|P|} \int _{t_n}^{t_{n+1}} \int _P R_P^n({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t. \end{aligned}$$

(18)

Then, thanks to the boundedness and convergence assumptions on $U^{(m)}$ and to the uniform convergence of $\varvec{\nabla }^{(m)}\varphi$ to $\varvec{\nabla }\varphi$, the first term tends to $-\int _0^T \int _\Omega {{\varvec{f}}}({\bar{U}})({\varvec{x}},t) \cdot \varvec{\nabla }\varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t$ as $m \rightarrow +\infty$. Since $|\varphi _\zeta ^n - \varphi _P^n | \le C_\varphi \, {\mathrm {diam}}(P)$, with $C_\varphi$ depending only on $\varphi$, we get, for any ${\varvec{x}}\in P$ and $t \in (t_n,t_{n+1})$,

$$\begin{aligned} |R_P^n({\varvec{x}},t)| \le C_\varphi \ \sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta |\ \Bigl | \Bigl ( ({{\varvec{F}}}^{(m)})_\zeta ^n - {{\varvec{f}}}(U^{(m)})({\varvec{x}},t) \Bigr ) \cdot {\varvec{n}}_{P,\zeta } \Bigr |\ {\mathrm {diam}}(P). \end{aligned}$$

The second term of the right-hand side of Relation (18) thus tends to 0 as $m \rightarrow +\infty$ thanks to the assumption (11), which concludes the proof. $\square$

3 Application to a colocated scheme

In this section, we apply Theorem 2.1 to a first specific case, namely the case of a convection operator for a single scalar unknown ${\bar{u}}$, with a piecewise-constant discretisation of the unknown. We are going to prove a general consistency result for multipoint schemes, assuming minimal regularity of the mesh.

The considered convection operator reads:

$$\begin{aligned} \bar{{\mathcal {C}}} ({\bar{u}}):&\quad \Omega \times (0,T) \rightarrow \mathbb {R}, \nonumber \\&\quad ({\varvec{x}},t) \mapsto \partial _t(\beta ({\bar{u}}))({\varvec{x}},t) + {\mathrm {div}}({{\varvec{f}}}({\bar{u}}))({\varvec{x}},t), \end{aligned}$$

(19)

where $\Omega \subset \mathbb {R}^d$, $d= 1$, 2, 3, $T \in (0,+\infty )$, $\beta \in C^0(\mathbb {R}, \mathbb {R})$, ${{\varvec{f}}}\in C^0(\mathbb {R}, \mathbb {R}^d)$. The functions $\beta$ and ${{\varvec{f}}}$ are supposed to be locally-Lipschitz. The discrete unknowns are $(u_P^n)_{P \in {\mathcal {P}},\ n \in \llbracket 0, N-1 \rrbracket }$ and the discrete convection operator reads:

$$\begin{aligned} {\mathcal {C}}(u) :&\quad \Omega \times (0,T) \rightarrow \mathbb {R},\nonumber \\&\qquad ({\varvec{x}},t) \mapsto \frac{\beta (u_P^{n+1}) - \beta (u_P^n)}{t_{n+1} - t_n} + \frac{1}{|P|} \sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta |\ {{\varvec{F}}}_\zeta ^n \cdot {\varvec{n}}_{P,\zeta }, \nonumber \\&\qquad \text{ for } {\varvec{x}}\in P,\ P \in {\mathcal {P}}, \text{ and } t \in (t_n,t_{n+1}),\ n \in \llbracket 0, N-1 \rrbracket . \end{aligned}$$

(20)

For a face $\zeta$ of the mesh, we denote by ${\mathcal {S}}_\zeta$ a set of cells, and suppose that the flux ${{\varvec{F}}}_\zeta ^n$ reads

$$\begin{aligned} {{\varvec{F}}}_\zeta ^n = {{\varvec{F}}}_{\zeta ,n}\bigl ((u_L^n)_{L \in {\mathcal {S}}_\zeta } \bigr ). \end{aligned}$$

The set ${\mathcal {S}}_\zeta$ is often referred to as the stencil of the scheme. We denote by $(a)_{L \in {\mathcal {S}}_\zeta }$ the family of real numbers whose cardinal is the same as ${\mathcal {S}}_\zeta$ and whose elements are all equal to a. The flux is supposed to satisfy the usual consistency assumption:

$$\begin{aligned} \text{ for } a \in \mathbb {R},\ \forall \zeta \in {{\mathfrak {F}}}, \qquad {{\varvec{F}}}_{\zeta ,n}\bigl ((a)_{L \in {\mathcal {S}}_\zeta }\bigr ) = {{\varvec{f}}}(a). \end{aligned}$$

(21)

In addition, we suppose the following local “Lip-diag“ (for Lipschitz-diagonal) property of the flux:

Definition 3.1

(Local Lipschitz-diagonal continuity) The numerical flux function ${{\varvec{F}}}_{\zeta ,n}$ is said to be locally Lipschitz-diagonal continuous, or Lip-diag, if for any bounded interval $I\subset \mathbb {R}$, there exists $C_I \in \mathbb {R}_+$ depending only on I such that, for any $n\in \llbracket 0, N-1 \rrbracket$, for any face $\zeta \in {{\mathfrak {F}}}$, for any family $(u_L)_{L \in {\mathcal {S}}_\zeta } \subset I$, and for any P adjacent cell to $\zeta$,

$$\begin{aligned} \bigl | {{\varvec{F}}}_{\zeta ,n}\bigl ((u_L^n)_{L \in {\mathcal {S}}_\zeta } \bigr ) - {{\varvec{f}}}(u_P^n) \bigr | \le C_I\ \sum _{L \in {\mathcal {S}}_\zeta } |u_L^n - u_P^n|. \end{aligned}$$

(22)

Note that this condition is weaker than the local Lipschitz-continuity of the numerical flux function ${{\varvec{F}}}_{\zeta ,n}$. For $P \in {\mathcal {P}}$, we denote by ${\mathcal {N}}_1(P)$ the set of the neighbours of P, i.e. the cells of ${\mathcal {P}}$ sharing a face with P; for $\ell >1$, we define ${\mathcal {N}}_\ell (P)$ as the set of the cells sharing a face with a cell of ${\mathcal {N}}_{\ell -1}(P)$. We assume that there exists ${\bar{\ell }} \in \mathbb {N}$ such that

$$\begin{aligned} \forall \zeta \in {{\mathfrak {F}}}, \text{ for } \text{ any } \text{ cell } P \text{ adjacent } \text{ to } \zeta ,\ {\mathcal {S}}_\zeta \subset {\mathcal {N}}_{{\bar{\ell }}} (P). \end{aligned}$$

(23)

The integer ${\bar{\ell }}$ characterizes the compactness of the stencil of the scheme. The initial value for the scalar unknowm u is defined by

$$\begin{aligned} u_P^0 = \frac{1}{|P|}\ \int _P u_0({\varvec{x}}) \ \mathrm {d}{\varvec{x}},\qquad \forall P \in {\mathcal {P}}, \end{aligned}$$

(24)

where $u_0$ is a given function of $L^1(\Omega )$. Finally, we define the discrete function associated to the unknowns as:

$$\begin{aligned} u({\varvec{x}},t) = u_P^n \quad \text{ for } {\varvec{x}}\in P,\ P \in {\mathcal {P}}, \ t \in [t_n,t_{n+1}),\ n \in \llbracket 0, N-1 \rrbracket . \end{aligned}$$

The consistency result for the discrete convection operator is given in the next lemma; it uses the following regularity parameters of the mesh:

$$\begin{aligned} \theta _1({\mathcal {P}}) = \max _{P \in {\mathcal {P}}} \frac{{\mathrm {diam}}(P)^d}{|P|}, \quad \theta _2({\mathcal {P}}) = \max \Bigl \{ \frac{|P|}{|Q|},\ P \text{ and } Q \text{ adjacent } \text{ cells } \text{ of } {\mathcal {P}} \Bigr \}. \end{aligned}$$

We also measure the regularity of the time discretisation by the parameter $\theta _3({{\mathcal {T}}})$ defined by

$$\begin{aligned} \theta _3({{\mathcal {T}}}) = \max _{1 \le n \le N-1} \Bigl \{ \frac{t_{n+1}-t_n}{t_n-t_{n-1}}, \frac{t_n-t_{n-1}}{t_{n+1}-t_n} \Bigl \}. \end{aligned}$$

Lemma 3.2

[Consistency, colocated scheme] Consider a sequence of space and time discretisations $({\mathcal {P}}^{(m)})_{m\in \mathbb {N}}$ and $({{\mathcal {T}}}^{(m)})_{m\in \mathbb {N}}$ , with $\delta ({\mathcal {P}}^{(m)})$ and $\delta t^{(m)}$ tending to zero; let $(u^{(m)})_{m\in \mathbb {N}}$ be an associated sequence of discrete functions, and let ${\mathcal {C}}^{(m)}(u^{(m)})$ be the associated sequence of discrete convection operators defined by (20). We assume that for each $m \in \mathbb {N}$, (21)–(24) hold with, in (23), ${\bar{\ell }}$ independent of m. We also suppose that

$$\begin{aligned} \exists \ \theta \in \mathbb {R} \text{ such } \text{ that } \max \{\theta _1({\mathcal {P}}^{(m)}),\ \theta _2({\mathcal {P}}^{(m)}),\ \theta _3({{\mathcal {T}}}^{(m)}),\ m \in \mathbb {N}\} \le \theta , \end{aligned}$$

(25)

and that the number of faces of each cell of the meshes ${\mathcal {P}}^{(m)}$ is bounded independently of m. Finally, we suppose that the sequence $(u^{(m)})_{m\in \mathbb {N}}$ is bounded in $L^\infty (\Omega \times (0,T))$, and that, when m tends to $+\infty$, it converges in $L^1(\Omega \times (0,T))$ to ${\bar{u}} \in L^\infty (\Omega \times (0,T))$. Then, for any function $\varphi \in C^\infty _c(\Omega \times [0,T))$,

$$\begin{aligned}&\int _0^T \int _\Omega {\mathcal {C}}^{(m)}(U^{(m)})({\varvec{x}},t)\ {\mathcal {I}}^{(m)}(\varphi ) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\rightarrow -\int _\Omega \beta (u_0)({\varvec{x}})\ \varphi ({\varvec{x}},0) \ \mathrm {d}{\varvec{x}}\\&\quad - \int _0^T \int _\Omega \Bigl (\beta ({\bar{u}})({\varvec{x}},t)\ \partial _t \varphi ({\varvec{x}},t) + \ \bigl ({{\varvec{f}}}({\bar{u}})\bigr )({\varvec{x}},t) \cdot \varvec{\nabla }\varphi ({\varvec{x}},t) \Bigr ) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\quad \text{ as } m \rightarrow + \infty . \end{aligned}$$

Proof

Let $m_u \in \mathbb {R}$ and $M_u \in \mathbb {R}$ be two real numbers such that

$$\begin{aligned} m_u \le (u^{(m)})_P^n\le M_u,\ \forall P \in {\mathcal {P}}^{(m)},\ n \in \llbracket 0, N^{(m)}\rrbracket ,\ \forall m \in \mathbb {N}, \end{aligned}$$

and let $C_\beta$ be the Lipschitz modulus of $\beta$ over the interval $[m_u,M_u]$. We check the assumptions of Theorem 2.1. The consistency of the initialization with the initial condition (Assumption (9)) follows from its definition (24); indeed, for any $\varphi \in C_c^\infty (\Omega )$,

$$\begin{aligned} \Bigl | \sum _{P \in {\mathcal {P}}^{(m)}} \int _P \bigl ((\beta ^{(m)})_P^0 - \beta (u_0)({\varvec{x}}) \bigr )\ \varphi ({\varvec{x}}) \ \mathrm {d}{\varvec{x}}\Bigr | \le C_\beta \ \Vert \varphi \Vert _{L^\infty (\Omega )} \sum _{P \in {\mathcal {P}}^{(m)}} \int _P |u_0({\varvec{x}})-u^0_P| \ \mathrm {d}{\varvec{x}}, \end{aligned}$$

and thus tends to zero for any function $u_0 \in L^1(\Omega )$. Since $(\beta ^{(m)})_P^n = \beta ((u^{(m)})_P^n)$, the left-hand side of Assertion (10) reads, with $\varphi \in C_c^\infty (\Omega \times [0,T))$:

$$\begin{aligned} R^{(m)}_t= & {} \sum _{n=1}^{N^{(m)}} \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} \int _{t_{n-1}}^{t_n} \int _P \Bigl ( (\beta ^{(m)})_P^n - \beta (u^{(m)})({\varvec{x}},t) \Bigr )\ \varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\\= & {} \sum _{n=1}^{N^{(m)}} \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} \int _{t_{n-1}}^{t_n} \int _P \Bigl ( \beta \bigl ((u^{(m)})_P^n\bigr ) - \beta \bigl ( (u^{(m)})_P^{n-1} \bigr ) \Bigr )\ \varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t. \end{aligned}$$

We thus have

$$\begin{aligned} |R^{(m)}_t| \le C_\beta \ \Vert \varphi \Vert _{L^\infty (\Omega \times [0,T))} \sum _{n=1}^{N^{(m)}} (t_n - t_{n-1}) \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}}|P|\ |(u^{(m)})_P^n - (u^{(m)})_P^{n-1}|, \end{aligned}$$

and thus $R^{(m)}_t$ tends to zero thanks to the assumed regularity of the sequence of time discretisations, invoking the bound of the time-translates of a converging sequence of functions of $L^1(\Omega \times (0,T))$ stated by Lemma A.1 in Appendix. We now check Assumption (11). For $n \in \llbracket 0, N^{(m)}\rrbracket$, $P \in {\mathcal {P}}^{(m)}_{\mathrm {int}}$ and $\zeta \in {{\mathfrak {F}}}(P)$, let

$$\begin{aligned} R_{P,\zeta }^n = \frac{1}{|P|} \int _{t_n}^{t_{n+1}} \int _P \Bigl | \Big ( ({{\varvec{F}}}^{(m)})_\zeta ^n -{{\varvec{f}}}(u^{(m)}) ({\varvec{x}},t) \Big ) \cdot {\varvec{n}}_{P,\zeta } \Bigr | \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\end{aligned}$$

and let

$$\begin{aligned} R^{(m)}= \sum _{n=0}^{N^{(m)}-1} \sum _{P \in {\mathcal {P}}^{(m)}_{\mathrm {int}}} {{\mathrm {diam}}(P)} \sum _{\zeta \in {{\mathfrak {F}}}} |\zeta | \ R_{P,\zeta }^n. \end{aligned}$$

By definition of the discrete flux and the discrete functions, we get:

$$\begin{aligned} R_{P,\zeta }^n = \frac{1}{|P|} \int _{t_n}^{t_{n+1}} \int _P \Bigl | \Big ( {{\varvec{F}}}_{\zeta ,n}\Bigl (\bigl ((u^{(m)})_L^n\bigr )_{L \in {\mathcal {S}}_\zeta } \Bigr ) -{{\varvec{f}}}\bigl ((u^{(m)})_P^n\bigr ) \Big ) \cdot {\varvec{n}}_{P,\zeta } \Bigr | \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t. \end{aligned}$$

Thanks to Assumption (22), we thus have

$$\begin{aligned} R_{P,\zeta }^n \le (t_{n+1} - t_n)\ C_{[m_u,M_u]}\ \sum _{L \in {\mathcal {S}}_\zeta } |u_L^n - u_P^n|. \end{aligned}$$

The remainder term $R^{(m)}$ is thus a collection of differences between the values taken by the unknown in two different cells. In order to apply Lemma A.3 of the appendix, we need to evaluate, for $P \in {\mathcal {P}}^{(m)}$, the sum $\omega _P$ of the weights multiplying the jumps where $(u^{(m)})_P^n$ appears. We first notice that, thanks to the assumed regularity of the mesh, for $Q \in {\mathcal {P}}^{(m)}$ and $\zeta$ a face of Q, ${\mathrm {diam}}(Q)\ |\zeta | \le {\mathrm {diam}}(Q)^d \le \theta \ |Q|$. For P to appear in a difference associated to a face of a cell Q, we need, by assumption, that $P \in {\mathcal {N}}_{{\bar{\ell }}}(Q)$; this in turn requires that $Q \in {\mathcal {N}}_{{\bar{\ell }}}(P)$. The sum $\omega _P$ thus satisfies:

$$\begin{aligned} \omega _P \le \theta \sum _{L \in {\mathcal {N}}_{{\bar{\ell }}}(P)} |L|, \end{aligned}$$

and, invoking once again the regularity constraints on the mesh:

$$\begin{aligned} \omega _P \le \theta ^{{\bar{\ell }}+1}\ \mathrm {card} (N_{{\bar{\ell }}}(P))\ |P|. \end{aligned}$$

The proof is thus complete thanks to Lemma A.3, since we have supposed that the number of faces of the cells is uniformly bounded, and then so is $\mathrm {card} (N_{{\bar{\ell }}}(P))$. $\square$

4 An example of application for staggered discretisations

The interest of Theorem 2.1 lies in the fact that it may deal with terms combining several variables, associated to different meshes and time discretisations. A typical example of a such a case is the balance equation for the entropy in barotropic compressible flows (2), where the entropy E is a nonlinear function of the density $\rho$ and the velocity ${{\varvec{u}}}$ which, in staggered discretisation, are approximated on different meshes, and may also be evaluated at different time levels. Hence, Theorem 2.1 is a suitable tool to prove the consistency of this equation. In this section, we focus on a similar but simpler problem, namely a staggered discretisation of a convection operator combining the time derivative of the function of a single scalar variable and a space divergence term, with a flux obtained as the product of another function of this scalar variable with the velocity.

We suppose that $\Omega$ is an open bounded polygonal set of $\mathbb {R}^2$, and consider the following convection operator:

$$\begin{aligned} {\mathcal {C}}({\bar{U}}) :&\quad \Omega \times (0,T) \rightarrow \mathbb {R}, \nonumber \\&\quad ({\varvec{x}},t) \mapsto \partial _t(\beta ({\bar{q}}))({\varvec{x}},t) + {\mathrm {div}}\bigl (g({\bar{q}})\,{\bar{{{\varvec{v}}}}} \bigr )({\varvec{x}},t), \end{aligned}$$

(26)

with ${\bar{U}} = ({\bar{q}},{\bar{{{\varvec{v}}}}}) \ : \Omega \times (0,T) \rightarrow \mathbb {R}\times \mathbb {R}^2$, ${{\varvec{f}}}({\bar{U}}) = {{\varvec{f}}}({\bar{q}},{\bar{{{\varvec{v}}}}}) = g({\bar{q}})\,{\bar{{{\varvec{v}}}}}$, where $\beta :\ \mathbb {R}\rightarrow \mathbb {R}$ and $g :\ \mathbb {R}\rightarrow \mathbb {R}$ are locally Lipschitz-continuous real functions. Note that, for instance, the convection term of Eq. (1a) may be written as (26) with ${\bar{U}} = ({\bar{\rho }}, {\bar{{{\varvec{u}}}}})$, $\beta (s) = s$ and $g(s) = s$.

In order to discretise this convection operator, we consider two types of staggered arrangements. In both arrangements, the scalar unknowns are located at the centre of the cells. However, these arrangements differ in the use of the vector unknowns. The first discretisation uses the whole velocity vector unknown on each edge of the mesh; this corresponds to the Rannacher–Turek (RT) discrete unknowns in the finite element setting [13]. The second discretisation uses only the normal component of the velocity on each edge; this latter arrangement of the discrete unknowns is very often referred to as the Marker-and-Cell (MAC) scheme [7]. Hence we will refer to the first arrangement as the RT case, and the second as the MAC case. Such discretisations are called staggered and are widely used in computational fluid dynamics; an example of the implementation of a staggered discretisation for the solution of the barotropic and full Euler equations may be found e.g. in [8, 9].

We suppose that the mesh is composed either of general quadrangles (RT case), or of rectangles (MAC case). We recall that ${{\mathfrak {F}}}$ stands for the set of edges of the mesh, and the internal edge separating the cells P and Q is denoted by $\zeta =P|Q$. This mesh will be referred to in the following as the primal mesh.

We also introduce now one or two dual meshes, depending on the case.

• RT case In this case, the (unique) dual mesh consists in a new partition of $\Omega$ indexed by the elements of ${{\mathfrak {F}}}$, i.e. $\Omega =\cup _{\zeta \in {{\mathfrak {F}}}} D_\zeta$. For an internal edge $\zeta =P|Q$, the set $D_\zeta$ is supposed to be a subset of $P \cup Q$ and we define $D_{P,\zeta }=D_\zeta \cap P$, so that $D_\zeta =D_{P,\zeta } \cup D_{Q,\zeta }$ (see Fig. 2); for an external edge $\zeta$ of a cell P, $D_\zeta$ is a subset of P, and $D_\zeta =D_{P,\zeta }$. The cells $(D_\zeta )_{\zeta \in {{\mathfrak {F}}}}$ are referred to as the dual or diamond cells, and $D_{P,\zeta }$ as half dual cells or half diamond cells. For a rectangular cell P, we define $D_{P,\zeta }$ as the simplex having the mass centre of P as vertex and the edge $\zeta$ as basis; this definition is extended to general primal meshes by supposing that $|D_{P,\zeta }|$ is still equal to |P|/4 and that the sub-cells connectivities (i.e. the way the half-dual cells share a common edge) is left unchanged. Note that the actual geometry of the dual cells does not need to be specified (and a dual cell may not be a polytope, a dual edge being possibly curved).

• MAC case In this case, two dual meshes are considered, each of them consisting in a partition of $\Omega$ indexed by the vertical and horizontal elements of ${{\mathfrak {F}}}$, i.e. $\Omega =\cup _{\zeta \in {{\mathfrak {F}}}^{(i)}} D_\zeta$, $i=1,2$, where ${{\mathfrak {F}}}^{(1)}$ (resp. ${{\mathfrak {F}}}^{(2)}$) denotes the set of vertical (resp. horizontal) edges. The cells $(D_\zeta )_{\zeta \in {{\mathfrak {F}}}}$ are still referred to as the dual cells. They are no longer diamond shaped; indeed, a half dual cell $D_{P,\zeta }$ is now half of the rectangle P with side $\zeta$ (see Fig. 3). As in the former case, for an internal edge $\zeta =P|Q$, the dual cell $D_\zeta$ is the subset of $P \cup Q$ defined as $D_\zeta =D_{P,\zeta } \cup D_{Q,\zeta }$; for an external edge $\zeta$ of a cell P, $D_\zeta$ is a subset of P, and $D_\zeta =D_{P,\zeta }$.

Fig. 2

Primal and dual meshes and associated notations for the quadrangular mesh and Rannacher–Turek like unknowns

Fig. 3

Primal and dual meshes and associated notations for the MAC case. Left: the primal cells; the edges $\zeta$ and $\zeta '$ belong to ${{\mathfrak {F}}}^{(1)}$ and the edges $\kappa$ and $\kappa '$ to ${{\mathfrak {F}}}^{(2)}$ Center: the dual cells associated to ${{\mathfrak {F}}}^{(1)}$ Right: the dual cells associated to ${{\mathfrak {F}}}^{(2)}$

The scalar unknown q is associated to the primal cells:

$$\begin{aligned} q({\varvec{x}},t) = q_P^n \quad \text{ for } {\varvec{x}}\in P,\ P \in {\mathcal {P}}, \ t \in [t_n,t_{n+1}),\ n \in \llbracket 0, N-1 \rrbracket . \end{aligned}$$

The unknowns corresponding to the vector-valued unknown ${{\varvec{v}}}$ are located at the centre of the edges in the RT case; in the MAC case, the unknowns associated to the ith component of ${{\varvec{v}}}$ are located at the centre of the edges of the ith dual mesh. Hence the associated approximate vector function reads:

• RT case—the whole vector unknown is associated to each dual cell :

  $$\begin{aligned} {{\varvec{v}}}({\varvec{x}},t) = {{\varvec{v}}}_\zeta ^n \quad \text{ for } {\varvec{x}}\in D_\zeta ,\ \zeta \in {{\mathfrak {F}}},\ t \in [t_n,t_{n+1}),\ n \in \llbracket 0, N-1 \rrbracket . \end{aligned}$$

• MAC case—the ith component of the vector unknown is associated to the cells of the ith dual mesh, so that ${{\varvec{v}}}({\varvec{x}},t) = (v_1({\varvec{x}},t),\ v_2({\varvec{x}},t))^t$ where, for $i=1,\ 2$,

  $$\begin{aligned} v_i({\varvec{x}},t) = v_\zeta ^n, \text{ for } {\varvec{x}}\in D_\zeta ,\ \zeta \in {{\mathfrak {F}}}^{(i)} \text{ and } t \in [t_n,t_{n+1}),\ n \in \llbracket 0, N-1 \rrbracket . \end{aligned}$$

Let ${{\varvec{e}}}^{(i)}$ denote the ith unit vector of the canonical basis of $\mathbb {R}^2$; with the notations of the previous section, the considered discrete convection operator reads:

$$\begin{aligned}&{\mathcal {C}}_{{\mathcal {P}}}(q,{{\varvec{v}}})_P^n = (\eth _t \beta )_P^n + \frac{1}{|P|} \sum _{\zeta \in {{\mathfrak {F}}}(P)} |\zeta |\ {{\varvec{F}}}_\zeta ^n \cdot {\varvec{n}}_{P,\zeta }, \text{ with } \beta _P^n = \beta (q_P^n) \text{ and } {{\varvec{F}}}_\zeta ^n \\&\quad = {{\varvec{f}}}(q_\zeta ^n,{{\varvec{v}}}_\zeta ^n ) = g(q_\zeta ^n) \ {{\varvec{v}}}_\zeta ^n \\&\qquad \text{ where } {{\varvec{v}}}_\zeta ^n \text{ is } {\left\{ \begin{array}{ll} \text{ the } \text{ vector } \text{ of } \text{ discrete } \text{ unknowns } &{} \text{ in } \text{ the } \text{ RT } \text{ case }, \\ \text{ defined } \text{ as } v_\zeta ^n \ {{\varvec{e}}}^{(i)} \text{ for } \zeta \in {{\mathfrak {F}}}^{(i)},\ i = 1 \text{ or } 2, &{} \text{ in } \text{ the } \text{ MAC } \text{ case }, \end{array}\right. } \end{aligned}$$

and, for $\zeta =P|Q$, $q_\zeta ^n$ stands for a convex combination of $q_P^n$ and $q_Q^n$. For instance the upwind choice would be $q_\zeta ^n= q_P^n$ if $v_\zeta ^n \ge 0$ and $q_\zeta ^n= q_Q^n$ otherwise. Note that for the LW-consistency result, any convex combination works, but this is not so for the stability of the scheme, for which some unpwinding is required.

The initial value for the scalar unknown q is defined by

$$\begin{aligned} q_P^0 = \frac{1}{|P|}\ \int _P q_0({\varvec{x}}) \ \mathrm {d}{\varvec{x}}. \end{aligned}$$

(27)

The consistency result for the discrete convection operator is given in the next lemma; it uses the same regularity parameters of the mesh as in the colocated case, which we recall:

$$\begin{aligned} \theta _1({\mathcal {P}}) = \max _{P \in {\mathcal {P}}} \frac{{\mathrm {diam}}(P)^2}{|P|}, \quad \theta _2({\mathcal {P}}) = \max \Bigl \{ \frac{|P|}{|Q|},\ P \text{ and } Q \text{ adjacent } \text{ cells } \text{ of } {\mathcal {P}} \Bigr \}. \end{aligned}$$

Note that in the MAC case (in fact, for a Cartesian grid), the regularity parameter $\theta _1({\mathcal {P}})$ controls the ratio between the two dimensions (i.e. the height and the width) of a cell. For a rectangular computational domain, we thus observe that the ratio $|\zeta |/|\zeta '|$, for $(\zeta ,\zeta ') \in ({{\mathfrak {F}}}^{(i)})^2$, $i = 1$, 2, is bounded by $\theta _1({\mathcal {P}})^2$, which is a quasi-uniformity property of the mesh. This also implies that $\theta _2({\mathcal {P}}) \le \theta _1({\mathcal {P}})^2$, and so the second regularity parameter is useless. It may easily be checked that similar relations holds for a general MAC scheme, i.e. a union of matching Cartesian grids, with powers of $\theta _1({\mathcal {P}})$ possibly higher than 2. Hence, the regularity of a MAC mesh (or of a Cartesian grid) may be equivalently measured by

$$\begin{aligned} \theta ({\mathcal {P}}) = \max \Bigl \{\frac{{\bar{h}}^{(1)}}{{\underline{h}}^{(2)}},\ \frac{{\bar{h}}^{(2)}}{{\underline{h}}^{(1)}} \Bigr \}, \end{aligned}$$

with, for $i = 1$, 2, ${\bar{h}}^{(i)}=\max \{ |\zeta |,\ \zeta \in {{\mathfrak {F}}}^{(i)} \}$ and ${\underline{h}}^{(i)}=\min \{ |\zeta |,\ \zeta \in {{\mathfrak {F}}}^{(i)} \}$.

We also measure the regularity of the time discretisation by the parameter $\theta _3({{\mathcal {T}}})$ defined by

$$\begin{aligned} \theta _3({{\mathcal {T}}}) = \max _{1 \le n \le N-1} \Bigl \{ \frac{t_{n+1}-t_n}{t_n-t_{n-1}}, \frac{t_n-t_{n-1}}{t_{n+1}-t_n} \Bigl \}. \end{aligned}$$

Lemma 4.1

(Consistency, staggered scheme) Let a sequence of discretisations $({\mathcal {P}}^{(m)})_{m\in \mathbb {N}}$ and $({{\mathcal {T}}}^{(m)})_{m\in \mathbb {N}}$ be given, with $\delta ({\mathcal {P}}^{(m)})$ and $\delta t^{(m)}$ tending to zero, and let $(q^{(m)},{{\varvec{v}}}^{(m)})_{m\in \mathbb {N}}$ be the associated sequence of discrete functions. We suppose that

$$\begin{aligned} \exists \ \theta \in \mathbb {R} \text{ such } \text{ that } \max \{\theta _1({\mathcal {P}}^{(m)}),\ \theta _2({\mathcal {P}}^{(m)}),\ \theta _3({{\mathcal {T}}}^{(m)}),\ m \in \mathbb {N}\} \le \theta . \end{aligned}$$

(28)

We suppose that the sequences $(q^{(m)})_{m\in \mathbb {N}}$ and $({{\varvec{v}}}^{(m)})_{m\in \mathbb {N}}$ are bounded in $L^\infty (\Omega \times (0,T))$ and $L^\infty (\Omega \times (0,T))^2$ respectively, and that, when m tends to $+\infty$, they converge in $L^p(\Omega \times (0,T))$ and $L^p(\Omega \times (0,T))^2$, $1 \le p < +\infty$, to ${\bar{q}} \in L^\infty (\Omega \times (0,T))$ and ${\bar{{{\varvec{v}}}}} \in L^\infty (\Omega \times (0,T))^2$ respectively. Then, for any function $\varphi \in C^\infty _c(\Omega \times [0,T))$,

$$\begin{aligned}&\int _0^T \int _\Omega {\mathcal {C}}^{(m)}(U^{(m)})({\varvec{x}},t)\ {\mathcal {I}}^{(m)}(\varphi ) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\rightarrow -\int _\Omega \beta (q_0)({\varvec{x}})\ \varphi ({\varvec{x}},0) \ \mathrm {d}{\varvec{x}}\\&\quad - \int _0^T \int _\Omega \Bigl (\beta ({\bar{q}})({\varvec{x}},t)\ \partial _t \varphi ({\varvec{x}},t) + \ \bigl (g({\bar{q}})\, {\bar{{{\varvec{v}}}}})\bigr )({\varvec{x}},t) \cdot \varvec{\nabla }\varphi ({\varvec{x}},t) \Bigr ) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\quad \text{ as } m \rightarrow + \infty . \end{aligned}$$

Proof

In this proof, we denote by $C_\beta$ and $C_g$ the Lipschitz modulus of $\beta$ and g respectively on the interval $[m_q, M_q]$, where $m_q \in \mathbb {R}$ and $M_q \in \mathbb {R}$ are such that

$$\begin{aligned} m_q \le (q^{(m)})_P^n\le M_q,\ \forall P \in {\mathcal {P}}^{(m)},\ n \in \llbracket 0, N^{(m)}\rrbracket ,\ \forall m \in \mathbb {N}. \end{aligned}$$

The proof of this lemma relies on Theorem 2.1. The consistency of the initialization with the initial condition (Assumption (9)) follows from its definition (27); indeed, for any $\varphi \in C_c^\infty (\Omega )$,

$$\begin{aligned} \Bigl | \sum _{P \in {\mathcal {P}}^{(m)}} \int _P \bigl ((\beta ^{(m)})_P^0 - \beta (q_0)({\varvec{x}}) \bigr )\ \varphi ({\varvec{x}}) \ \mathrm {d}{\varvec{x}}\Bigr | \le C_\beta \ \Vert \varphi \Vert _{L^\infty (\Omega )} \sum _{P \in {\mathcal {P}}^{(m)}} \int _P |q_0({\varvec{x}})-q^0_P|, \end{aligned}$$

and thus tends to zero for any function $q_0 \in L^1(\Omega )$. Since $(\beta ^{(m)})_P^n = \beta ((q^{(m)})_P^n)$, the left-hand side of Assertion (10) reads, with $\varphi \in C_c^\infty (\Omega \times [0,T))$:

$$\begin{aligned} R^{(m)}_t= & {} \sum _{n=1}^{N^{(m)}} \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} \int _{t_{n-1}}^{t_n} \int _P \Bigl ( (\beta ^{(m)})_P^n - \beta (U^{(m)})({\varvec{x}},t) \Bigr )\ \varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\\= & {} \sum _{n=1}^{N^{(m)}} \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} \int _{t_{n-1}}^{t_n} \int _P \Bigl ( \beta \bigl ((q^{(m)})_P^n\bigr ) - \beta \bigl ( (q^{(m)})_P^{n-1} \bigr ) \Bigr )\ \varphi ({\varvec{x}},t) \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t. \end{aligned}$$

We thus have

$$\begin{aligned} |R^{(m)}_t| \le C_\beta \ \Vert \varphi \Vert _{L^\infty (\Omega \times [0,T))} \sum _{n=1}^{N^{(m)}} (t_n - t_{n-1}) \sum _{P \in {\mathcal {P}}_{\mathrm {int}}^{(m)}} |(q^{(m)})_P^n - (q^{(m)})_P^{n-1}|, \end{aligned}$$

and thus $R^{(m)}_t$ tends to zero thanks to the assumed regularity of the sequence of time discretisations, invoking the bound of the time-translates of a converging sequence of functions of $L^1(\Omega \times (0,T))$ stated by Lemma A.1 in Appendix.

We now check Assumption (11). For $n \in \llbracket 0, N^{(m)}\rrbracket$, $P \in {\mathcal {P}}^{(m)}_{\mathrm {int}}$ and $\zeta \in {{\mathfrak {F}}}(P)$, let

$$\begin{aligned} R_{P,\zeta }^n = \frac{1}{|P|} \int _{t_n}^{t_{n+1}} \int _P \Bigl | \Big ( ({{\varvec{F}}}^{(m)})_{\zeta }^n -{{\varvec{f}}}(q^{(m)},{{\varvec{v}}}^{(m)}) ({\varvec{x}},t) \Big ) \cdot {\varvec{n}}_{P,\zeta } \Bigr | \ \mathrm {d}{\varvec{x}}\ \mathrm {d} t\end{aligned}$$

and let

$$\begin{aligned} R^{(m)}= \sum _{n=0}^{N^{(m)}-1} \sum _{P \in {\mathcal {P}}^{(m)}_{\mathrm {int}}} {{\mathrm {diam}}(P)} \sum _{\zeta \in {{\mathfrak {F}}}} | \zeta | \ R_{P,\zeta }^n. \end{aligned}$$

We now express $R_{P,\zeta }^n$, for the RT and MAC discretisations successively.

• RT case—in the case of general quadrangular meshes with the whole vector unknowns located on the edges, we have

  $$\begin{aligned} ({{\varvec{F}}}^{(m)})_\zeta ^n = g(q_\zeta ^n)\, {{\varvec{v}}}_\zeta ^n \quad \text{ and } \quad {{\varvec{f}}}(q^{(m)},{{\varvec{v}}}^{(m)})({\varvec{x}},t) = g(q_P^n)\ {{\varvec{v}}}_{\zeta '}^n \text{ for } {\varvec{x}}\in D_{P,\zeta '},\ \zeta ' \in {{\mathfrak {F}}}(P). \end{aligned}$$

  We thus get, denoting by $\vert {{\varvec{a}}}\vert$ the Euclidean norm of any vector ${{\varvec{a}}}\in \mathbb {R}^2$,

  $$\begin{aligned} \Big | \Big (({{\varvec{F}}}^{(m)})_{\zeta }^n - {{\varvec{f}}}(U^{(m)})({\varvec{x}},t)\Big )\cdot {\varvec{n}}_{P,\zeta } \Big | \le \bigl | g(q_\zeta ^n)\, {{\varvec{v}}}_\zeta ^n - g(q_P^n)\ {{\varvec{v}}}_{\zeta '}^n \bigr | \text{ for } {\varvec{x}}\in D_{P,\zeta '},\ \zeta ' \in {{\mathfrak {F}}}(P). \end{aligned}$$

  Let Q be the primal cell such that $\zeta = P|Q$. Since $q_\zeta ^n$ is a convex combination of $q_P^n$ and $q_Q^n$, we thus get, for ${\varvec{x}}\in P$, and $t \in [t_n t_{n+1})$,

  $$\begin{aligned} \Big | \Big (({{\varvec{F}}}^{(m)})_{\zeta }^n - {{\varvec{f}}}(U^{(m)})({\varvec{x}},t)\Big )\cdot {\varvec{n}}_{P,\zeta } \Big | \le C\ \Bigl (|q^n_P - q^n_Q| + \sum _{\zeta ' \in {{\mathfrak {F}}}(P)} \vert {{\varvec{v}}}_\zeta ^n-{{\varvec{v}}}_{\zeta '}^n \vert \Bigr ), \end{aligned}$$

  where C only depends on $\Vert q^{(m)}\Vert _{L^\infty (\Omega \times (0,T))}$, $\Vert {{\varvec{v}}}^{(m)}\Vert _{L^\infty (\Omega \times (0,T))^2}$ and $C_g$. Integrating over $P \times (t_n,t_{n+1})$, we obtain

  $$\begin{aligned} R_{P,\zeta }^n \le C\ (t_{n+1}- t_n) \Bigl (|q^n_P - q^n_Q| + \sum _{\zeta ' \in {{\mathfrak {F}}}(P)} \vert {{\varvec{v}}}_\zeta ^n-{{\varvec{v}}}_{\zeta '}^n \vert \Bigr ). \end{aligned}$$

• MAC case—in this case, the velocity components are piecewise constant on different grids. Let i be the index such that $\zeta \in {{\mathfrak {F}}}^{(i)}$, and let $\zeta '$ be the other edge of P normal to ${{\varvec{e}}}^{(i)}$, i.e. the opposite of $\zeta$ in P. We have

  $$\begin{aligned} ({{\varvec{F}}}^{(m)})_{\zeta }^n \cdot {\varvec{n}}_{P,\zeta } = g(q_\zeta ^n)\, v_\zeta ^n \ \delta _\zeta \quad \text{ and } \quad {{\varvec{f}}}(q^{(m)},{{\varvec{v}}}^{(m)})({\varvec{x}},t) = {\left\{ \begin{array}{ll} g(q_P^n) \ v_{\zeta }^n\ \delta _\zeta \text{ if } {\varvec{x}}\in D_{P,\zeta }, \\ g(q_P^n) \ v_{\zeta '}^n\ \delta _\zeta \text{ if } {\varvec{x}}\in D_{P,\zeta '}, \end{array}\right. } \end{aligned}$$

  with $\delta _\zeta = {\varvec{n}}_{P,\zeta } \cdot {{\varvec{e}}}^{(i)}$. We thus get

  $$\begin{aligned} \Big | \Big (({{\varvec{F}}}^{(m)})_{\zeta }^n - {{\varvec{f}}}(U^{(m)})({\varvec{x}},t)\Big )\cdot {\varvec{n}}_{P,\zeta } \Big | = {\left\{ \begin{array}{ll} \bigl | g(q_\zeta ^n)\, {{\varvec{v}}}_\zeta ^n - g(q_P^n) \ v_{\zeta }^n \bigr | \text{ if } {\varvec{x}}\in D_{P,\zeta }, \\ \bigl | g(q_\zeta ^n)\, {{\varvec{v}}}_\zeta ^n - g(q_P^n) \ v_{\zeta '}^n \bigr | \text{ if } {\varvec{x}}\in D_{P,\zeta '}, \end{array}\right. } \end{aligned}$$

  and hence, for ${\varvec{x}}\in P$, and $t \in [t_n t_{n+1})$, denoting by Q the primal cell such that $\zeta = P|Q$,

  $$\begin{aligned} \Big | \Big (({{\varvec{F}}}^{(m)})_{\zeta }^n - {{\varvec{f}}}(U^{(m)})({\varvec{x}},t)\Big )\cdot {\varvec{n}}_{P,\zeta } \Big | \le C\ \bigl ( |q_P^n - q_Q^n | + \ |v_\zeta ^n - v_{\zeta '}^n | \bigr ), \end{aligned}$$

  where C only depends on $\Vert q^{(m)}\Vert _{L^\infty (\Omega \times (0,T))}$, $\Vert {{\varvec{v}}}^{(m)}\Vert _{L^\infty (\Omega \times (0,T))^2}$ and $C_g$. Therefore, integrating over $P \times (t_n,t_{n+1})$, we finally get

  $$\begin{aligned} R_{P,\zeta }^n \le C\ (t_{n+1}- t_n)\ \Bigl (|q^n_P - q^n_Q| + \vert {{\varvec{v}}}_\zeta ^n-{{\varvec{v}}}_{\zeta '}^n \vert \Bigr ). \end{aligned}$$

Note that, in these computations, we have not addressed the case where $\zeta$ is an external edge, taking benefit of the fact that, in the expression of $R^{(m)}$, the sum is restricted to the internal cells.

From the definition of $R^{(m)}$, we thus get that, for both cases, it satisfies the following inequality:

$$\begin{aligned} R^{(m)}\le C\ \bigl ( R_1^{(m)}+ R_2^{(m)}\bigr ), \end{aligned}$$

with

$$\begin{aligned} R_1^{(m)}= \ \sum _{n=0}^{N^{(m)}-1} (t_{n+1} - t_n) \sum _{P \in {\mathcal {P}}^{(m)}} {\mathrm {diam}}(P) \ \sum _{\begin{array}{c} \zeta \in {{\mathfrak {F}}}(P), \\ \zeta =P|Q \end{array}} |\zeta |\ |q^n_P - q^n_Q|, \end{aligned}$$

and

$$\begin{aligned} R_2^{(m)}= {\left\{ \begin{array}{ll} \displaystyle \sum _{n=0}^{N^{(m)}-1} (t_{n+1} - t_n) \sum _{P \in {\mathcal {P}}^{(m)}} {\mathrm {diam}}(P) \sum _{\{\zeta , \zeta '\} \subset {{\mathfrak {F}}}(P)^2} (|\zeta | + |\zeta '|)\ \vert {{\varvec{v}}}_\zeta ^n-{{\varvec{v}}}_{\zeta '}^n \vert &{} \text{ in } \text{ the } \text{ RT } \text{ case },\\ \displaystyle \sum _{n=0}^{N^{(m)}-1} (t_{n+1} - t_n) \sum _{P \in {\mathcal {P}}^{(m)}} {\mathrm {diam}}(P) \sum _{\begin{array}{c} i=1,2, \\ \{\zeta , \zeta '\} \subset {{\mathfrak {F}}}^{(i)}(P)^2 \end{array}} (|\zeta | + |\zeta '|)\ \vert v_\zeta ^n-v_{\zeta '}^n \vert&\text{ in } \text{ the } \text{ MAC } \text{ case }. \end{array}\right. } \end{aligned}$$

There only remains to prove that $R_1^{(m)}$ and $R_2^{(m)}$ tend to zero as m tends to $+\infty$. Reordering the summation in $R_1^{(m)}$, we get that

$$\begin{aligned} R_1^{(m)}= \sum _{n=0}^{N^{(m)}-1} (t_{n+1} - t_n)\ \sum _{\begin{array}{c} \zeta \in {{\mathfrak {F}}}_{\mathrm {int}}^{(m)}, \\ \zeta =P|Q \end{array}} \omega _\zeta \ |q^n_P - q^n_Q|, \quad \text{ with } \omega _\zeta = \Bigl ({\mathrm {diam}}(P) + {\mathrm {diam}}(Q)\Bigr )\ |\zeta |. \end{aligned}$$

Lemma A.1 states that $R_1^{(m)}$ tends to zero if the weight $\omega _\zeta$ is controlled by both |P| and |Q|; since we have $\omega _\zeta \le 2 \bigl (\max ({\mathrm {diam}}(P),{\mathrm {diam}}(Q))\bigr )^2$, this is easily obtained using Assumption (28).

Fig. 4

Left: the primal edges $\zeta$ and $\zeta '$ are adjacent. Right: the primal edges $\zeta$ and $\zeta '$ are opposite

As to the term $R_2^{(m)}$, let us start with the RT case. We have:

$$\begin{aligned} \sum _{\{\zeta , \zeta '\} \subset {{\mathfrak {F}}}(P)^2} (|\zeta | + |\zeta '|)\ \vert {{\varvec{v}}}_\zeta ^n-{{\varvec{v}}}_{\zeta '}^n \vert \le 2\,{\mathrm {diam}}(P) \sum _{\{\zeta , \zeta '\} \subset {{\mathfrak {F}}}(P)^2}\vert {{\varvec{v}}}_\zeta ^n-{{\varvec{v}}}_{\zeta '}^n \vert , \end{aligned}$$

We distinguish two cases for the subsets $\{\zeta , \zeta '\}) \subset {{\mathfrak {F}}}(P)^2$ that appear in the summation: either the dual cells $D_\zeta$ and $D_\zeta '$ share a common (dual) edge $\eta =\zeta |\zeta ' \in {{\mathfrak {F}}}^*$, where ${{\mathfrak {F}}}^*$ denotes the set of edges of the dual mesh, or they are opposite edges in the quadrilateral cell P; in this latter case, we may write that

$$\begin{aligned} |{{\varvec{v}}}_{\zeta }^n - {{\varvec{v}}}_{\zeta '}^n| \le |{{\varvec{v}}}_{\zeta }^n - {{\varvec{v}}}_{\zeta ''}^n| + |{{\varvec{v}}}_{\zeta ''}^n - {{\varvec{v}}}_{\zeta '}^n|, \end{aligned}$$

where $\zeta '' \in {{\mathfrak {F}}}(P)$ is such that the dual cell $D_{\zeta ''}$ shares a common (dual) edge $\eta$ (resp. $\eta '$) $\in {{\mathfrak {F}}}^*$ with $D_{\zeta }$ (resp. $D_{\zeta '}$) as shown in Fig. 4. There is one jump between two adjacent faces that appears directly in the summation over $\{\zeta , \zeta '\}) \subset {{\mathfrak {F}}}(P)^2$, and at most two coming from the decompositions of the jumps needed for pairs of opposite edges, so that altogether,

$$\begin{aligned} \sum _{(\zeta , \zeta ') \in {{\mathfrak {F}}}(P)^2} (|\zeta | + |\zeta '|)\ \vert {{\varvec{v}}}_\zeta ^n-{{\varvec{v}}}_{\zeta '}^n \vert \le 6\ {\mathrm {diam}}(P) \sum _{\eta = \zeta |\zeta '\in {{\mathfrak {F}}}^*(P)} \vert {{\varvec{v}}}_\zeta ^n-{{\varvec{v}}}_{\zeta '}^n \vert , \end{aligned}$$

with ${{\mathfrak {F}}}^*(P)$ the edges of the dual mesh included in P. We thus get

$$\begin{aligned} R_2^{(m)}\le 6\ \sum _{n=0}^{N^{(m)}-1} (t_{n+1} - t_n) \sum _{\eta = \zeta |\zeta '\in {{\mathfrak {F}}}^*} {\mathrm {diam}}(P_\eta )^2\ \vert {{\varvec{v}}}_\zeta ^n-{{\varvec{v}}}_{\zeta '}^n \vert , \end{aligned}$$

where $P_\eta$ stands for the primal cell in which $\eta$ is included. The right-hand side of this inequality is thus a collection of jumps across the dual edges, with, for an edge $\eta$, a weight given by

$$\begin{aligned} \omega _\eta = 6\ {\mathrm {diam}}(P_\eta )^2. \end{aligned}$$

Thanks to Lemma A.1, $R_2^{(m)}$ tends to zero when m tends to $+\infty$ if $\omega _\eta$ is controlled by both $|D_\zeta |$ and $|D_{\zeta '}|$; this is indeed the case thanks to Assumption (28), since $|D_\zeta | \ge |P_\eta |/4$ and $|D_{\zeta '}| \ge |P_\eta |/4$.

Let us now turn to the MAC case, which is in fact simpler; indeed, the differences of velocities appearing in the expression of $R_2^{(m)}$ are all jumps across dual edges, and we may thus recast $R_2^{(m)}$ as

$$\begin{aligned} R_2^{(m)}= \sum _{n=0}^{N^{(m)}-1} (t_{n+1} - t_n) \sum _{i=1}^2 \quad \sum _{\eta = \zeta |\zeta '\in {{\mathfrak {F}}}^{(i,*)}} {\mathrm {diam}}(P_\eta )\ (|\zeta | + |\zeta '|)\ \vert v_\zeta ^n-v_{\zeta '}^n \vert , \end{aligned}$$

where, once again, $P_\eta$ is the primal cell in which lies $\eta$ (note that this sum only involves a subset of the dual edges, which corresponds of the dual edges included in primal cell), and ${{\mathfrak {F}}}^{(1,*)}$ (resp. ${{\mathfrak {F}}}^{(2,*)}$) denotes the set of vertical (respectively horizontal) dual edges. We thus again have a collection of jumps across the dual edges, with, for an edge $\eta$ included in a primal cell $P_\eta$ and separating the dual cells $D_\zeta$ and $D_{\zeta '}$, a weight given by

$$\begin{aligned} \omega _\eta = {\mathrm {diam}}(P_\eta ) \ \bigl (|\zeta | + |\zeta '|\bigr ). \end{aligned}$$

Thus, again thanks to Lemma A.1, $R_2^{(m)}$ tends to zero when m tends to $+\infty$ since, remarking that $|D_\zeta | \ge |P_\eta |/2$, $|D_{\zeta '}| \ge |P_\eta |/2$ and $\omega _\eta \le 2 {\mathrm {diam}}(P_\eta )^2$, so the weight $\omega _\eta$ is controlled by both $|D_\zeta |$ and $|D_{\zeta '}|$ thanks to Assumption (28). $\square$

Remark 4.2

(On the required regularity of the time discretisation) The assumption $\theta _3({{\mathcal {T}}}^{(m)}) \le \theta$, for $m \in \mathbb {N}$, may be avoided thanks to a different choice of the interpolation of the test function (see Remark 2.6). However, this assumption is very mild (in fact, we do not have in mind any scheme where the ratio between two consecutive time-steps is likely to blow up when refining the discretisation).

Appendix A. Convergence of discrete functions in \(L^1\)

We recall a result proven in [5, Lemma 4.3]. To facilitate its use in the proof of Lemma 4.1, it is rephrased here under more general forms than in [5] (see Remark A.2 below for the differences).

Let ${\mathcal {M}}$ be a conforming mesh of the domain $\Omega$ of $\mathbb {R}^d$, $d=1,2,3$, in polygonal or polyhedral subsets, and ${{\mathcal {T}}}=(t_i)_{i \in \llbracket 0, N \rrbracket }$ be a time discretisation of the interval (0, T), i.e. a sequence of real numbers such that $0=t_0< \dots< t_n < \dots t_N=T$. We denote by $\delta t_{{\mathcal {T}}}$ the time step, defined by $\delta t_{{\mathcal {T}}}= \max \{t_{n+1}-t_n,\ n \in \llbracket 0, N-1 \rrbracket \}$. For $u \in L^1(\Omega \times (0,T))$, $K \in {{\mathcal {M}}}$ and n such that $n \in \llbracket 0, N-1 \rrbracket$, let $u_K^n$ be the mean value of u over $K \times (t_n,t_{n+1})$. We denote by ${{\mathcal {E}}}_{\mathrm{int}}$ the set of internal faces of the mesh and the face $\sigma \in {{\mathcal {E}}}_{\mathrm{int}}$ separating the cells K and L is denoted by $\sigma =K|L$. We define the following quantity:

$$\begin{aligned} T_{{{\mathcal {M}}},{{\mathcal {T}}}} \, u= \sum _{n=0}^{N-1} (t_{n+1}-t_n) \sum _{\begin{array}{c} \sigma \in {{\mathcal {E}}}_{\mathrm{int}}\\ \sigma =K|L \end{array}} \omega _\sigma \ |u_K^n-u_L^n| + \sum _{n=0}^{N-2} \delta _{n+1/2}\ \sum _{K\in {{\mathcal {M}}}} |K|\ |u_K^{n+1}-u_K^n|, \end{aligned}$$

(29)

where $(\omega _\sigma )_{\sigma \in {{\mathcal {E}}}_{\mathrm{int}}}$ and $(\delta _{n+1/2})_{n \in \llbracket 0, N-2 \rrbracket }$ are two sets of non-negative weights. We introduce the two following parameters:

$$\begin{aligned} \theta _{{\mathcal {M}}}=\max _{K \in {{\mathcal {M}}}} \max _{\sigma \in {{\mathcal {E}}}_{\mathrm{int}}(K)}\ \frac{\omega _\sigma }{|K|}, \quad \theta _{{{\mathcal {T}}}}= \max _{n \in \llbracket 0, N-2 \rrbracket }\ \Bigl \{ \frac{\delta _{n+1/2}}{t_{n+1} - t_n},\ \frac{\delta _{n+1/2}}{t_{n+2} - t_{n+1}}\Bigl \}, \end{aligned}$$

(30)

with ${{\mathcal {E}}}_{\mathrm{int}}(K)$ the set of internal faces of K. We denote by $\delta ({{\mathcal {M}}})$ the space step characterizing ${{\mathcal {M}}}$, i.e. $\delta ({{\mathcal {M}}}) = \max _{K \in {{\mathcal {M}}}} {\mathrm {diam}}(K)$. Then the following convergence result holds.

Lemma A.1

Let $\theta >0$ and $({{\mathcal {M}}}^{(m)})_{m \in \mathbb {N}}$ be a sequence of meshes and for each $m \in \mathbb {N}$, $\theta _{{{\mathcal {M}}}^{(m)}}$ be defined by (30). We assume that $\theta _{{{\mathcal {M}}}^{(m)}} \le \theta$ for all $m \in \mathbb {N}$ and $\lim _{m \rightarrow +\infty } \delta ({{\mathcal {M}}}^{(m)}) =0$. We suppose that the number of faces of a cell $K \in {{\mathcal {M}}}^{(m)}$ is bounded independently from $m \in \mathbb {N}$. For $m \in \mathbb {N}$, we suppose given a time discretisation ${{\mathcal {T}}}^{(m)}$, and suppose that $\delta t_{{{\mathcal {T}}}^{(m)}}$ also tends to zero when m tends to $+\infty$, and that $\theta _{{{\mathcal {T}}}^{(m)}} \le \theta$ for all $m \in \mathbb {N}$. Let $u \in L^1(\Omega \times (0,T))$ and $(u_p)_{p \in \mathbb {N}}$ be a sequence of functions of $L^1(\Omega \times (0,T))$ such that $u_p \rightarrow u$ in $L^1(\Omega \times (0,T))$ as $p \rightarrow +\infty$.

Then $T_{{{\mathcal {M}}}^{(m)},{{\mathcal {T}}}^{(m)}}\, u_p$ defined by (29) tends to zero when m tends to $+\infty$ uniformly with respect to $p \in \mathbb {N}$.

Remark A.2

The difference between Lemma A.1 and the formulation of the same convergence result in [5] lies in the definition of the weight of the jumps, which is more general in Lemma A.1. Indeed, the weight of the jumps through the faces featured in the definition of $T_{{{\mathcal {M}}},{{\mathcal {T}}}}\, u$ are defined in [5, Lemma 4.3] as a function of the volume of some dual cells associated to the faces, but a careful examination of the proof itself shows that the introduction of a dual mesh is in fact useless. Therefore, the proof of Lemma [5, Lemma 4.3] readily extends to prove Lemma A.1.

This generalization is in most cases sufficient. However, we may go one step further, still with minor modifications of the proof of [5], as follows. Let ${\mathcal {S}}_x$ be a set of cardinal 2 - subsets of ${\mathcal {M}}$, and ${\mathcal {S}}_t$ be a set of cardinal 2 - subsets of $\llbracket 0, N-1 \rrbracket$. Let ${\widetilde{T}}_{{{\mathcal {M}}},{{\mathcal {T}}}}\, u$ be defined by

$$\begin{aligned} {\widetilde{T}}_{{{\mathcal {M}}},{{\mathcal {T}}}}\, u= \sum _{n=0}^{N-1} (t_{n+1}-t_n) \sum _{\{K,L\} \in {\mathcal {S}}_x} \omega _{K,L}\ |u^n_L - u^n_K| + \sum _{\{p,q\} \in {\mathcal {S}}_t}\ \delta _{p,q}\ \sum _{K\in {{\mathcal {M}}}} |K|\ |u^p_K - u^q_K|,\nonumber \\ \end{aligned}$$

(31)

where $(\omega _{K,L})_{\{K,L\} \in {\mathcal {S}}_x}$ and $(\delta _{p,q})_{\{p,q\} \in {\mathcal {S}}_t}$ are two sets of non-negative weights. We introduce the two following parameters:

$$\begin{aligned} \begin{array}{l} \displaystyle \theta _{{\mathcal {M}}}=\max _{K \in {{\mathcal {M}}}} \frac{1}{|K|}\ \sum _{\begin{array}{c} L \in {\mathcal {M}}\\ \{K,L\} \in {\mathcal {S}}_x \end{array}} \omega _{K,L},\qquad \theta _{{{\mathcal {T}}}}= \max _{n \in \llbracket 0, N-1 \rrbracket }\ \frac{1}{t_{n+1} - t_n}\ \sum _{\begin{array}{c} p \in \llbracket 0, N-1 \rrbracket \\ { \{n,p\} \in {\mathcal {S}}_t} \end{array}} \delta _{n,p}. \end{array} \end{aligned}$$

(32)

For $\{K,L\} \in {\mathcal {S}}_x$ and $\{p,q\}\in {\mathcal {S}}_t$, let

$$\begin{aligned} {\mathfrak {d}} (\{K,L\}) = \max _{({\varvec{x}},{\varvec{y}}) \in K \times L} |{\varvec{y}}-{\varvec{x}}|, \quad {\mathfrak {d}}(\{p,q\})={\left\{ \begin{array}{ll} t_{q+1}-t_p &{} \text{ if } q >p,\\ t_{p+1}-t_q &{} \text{ otherwise } \end{array}\right. } \end{aligned}$$

and let

$$\begin{aligned} {\mathfrak {d}}({{\mathcal {M}}}) = \max _{\{K,L\} \in {\mathcal {S}}_x} {\mathfrak {d}} (\{K,L\}),\quad {\mathfrak {d}}({{\mathcal {T}}}) = \max _{\{p,q\} \in {\mathcal {S}}_t} {\mathfrak {d}} (\{p,q\}). \end{aligned}$$

Then the following convergence result holds.

Lemma A.3

Let $({{\mathcal {M}}}^{(m)})_{m \in \mathbb {N}}$ and $({{\mathcal {T}}}^{(m)})_{m \in \mathbb {N}}$ be a given sequence of meshes and time discretisations. Let us suppose there exists $\theta > 0$ such that $\theta _{{{\mathcal {M}}}^{(m)}} \le \theta$ and $\theta _{{{\mathcal {T}}}^{(m)}} \le \theta$ for all $m \in \mathbb {N}$, with $\theta _{{{\mathcal {M}}}^{(m)}}$ and $\theta _{{{\mathcal {T}}}^{(m)}}$ given by Eq. (32). Let us assume that ${\mathfrak {d}}({{\mathcal {M}}}^{(m)})$ and ${\mathfrak {d}}({{\mathcal {T}}}^{(m)})$ tend to zero when m tends to $+\infty$. Let $u \in L^1(\Omega \times (0,T))$ and $(u_p)_{p \in \mathbb {N}}$ be a sequence of functions of $L^1(\Omega \times (0,T))$ such that $u_p \rightarrow u$ in $L^1(\Omega \times (0,T))$ as $p \rightarrow +\infty$.

Then ${\widetilde{T}}_{{{\mathcal {M}}}^{(m)},{{\mathcal {T}}}^{(m)}}\, u_p$ defined by (31) tends to zero when m tends to $+\infty$ uniformly with respect to $p \in \mathbb {N}$.