Numerical solution of the Bagley–Torvik equation using Laguerre polynomials

Abstract

The Laplace transform and Laguerre polynomials are applied to the solution of the Bagley–Torvik equation. We first convert the fractional differential equation into the algebraic equation by Laplace transform. Then, we find the numerical inversion of Laplace transform by Laguerre polynomials. The fractional derivative is described in the Caputo sense. Numerical examples are provided to demonstrate the accuracy and efficiency of the method.

1 Introduction

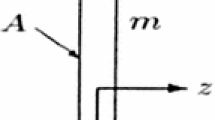
In modeling the motion of a rigid plate immersed in Newtonian fluid, Torvik and Begley [23] considered the fractional differential equation

$$\begin{aligned} Ay''(t)+BD^{\frac{3}{2}}y(t)+Cy(t)=f(t), \end{aligned}$$

(1)

subject to

$$\begin{aligned} y(0)=a_{0},\quad y'(0)=a_{1}. \end{aligned}$$

(2)

Here, y(t) represents the displacement of the plate of mass M and surface area S. The constants A, B, and C are given by

$$\begin{aligned} A=M, \quad B=2S\sqrt{\mu \rho }, \end{aligned}$$

where $\mu$ and $\rho$ are the viscosity and density, respectively, of the fluid in which the plate is immersed, and

$$\begin{aligned} C=k \end{aligned}$$

where k is the stiffness of the spring to which the plate is attached. Finally, f(t) represents the loading force. The operator $D^{\alpha }$ is the Caputo fractional derivative. The equation of existence and uniqueness of the solution to this initial value problem have been discussed in [12, 20].

Fractional differential equations have been found to be more realistic in modeling a variety of physical phenomena, engineering processes, biological systems, and financial products such as signal identification and image processing, optical systems, thermal system materials, control systems, etc. [13, 26]. A considerable amount of work has been invested in determining numerical solutions of the Bagley–Torvik equation. Podlubny [16] has investigated the solution of this problem and proposed a numerical method in his book. Ray and Bera [19] applied the Adomian decomposition method to solve the Bagley–Torvik equation and obtained the same solution as that of Podlubny by Green’s function. Diethelm and Ford [6] solved the problem with Adams predictor and corrector method. Cenesiz et al. [3, 10] proposed a new generalization of the Taylor collocation method for the numerical solution of a class of fractional-order differential equations. Li and Ray [11, 18] derived the Haar wavelet operational matrix of the fractional-order integration and applied the method to the Bagley–Torvik equation. Sakar et al. [21] presented a new reproducing kernel Hilbert space method for boundary value problem of fractional Bagley–Torvik equation. In [2, 7, 14, 15], Chebyshev polynomial and hybrid functions were considered to find an approximate solution for the problem. Most recently, Balaji and Hariharan, Srivastava et al. [1, 22] introduced wavelet methods to solve fractional-order differential equations including the Bagley–Torvik equation.

2 Basic definitions

In this section, we give some definitions and properties of the fractional calculus and Laplace transform.

Definition 1

A real function $f(t),t>0,$ is said to be in the space $C_{\mu },\mu \in R,$ if there exists a real number $p>\mu ,$ such that $f(t)=t^{p}h_{1}(t),$ where $f_{1}(t)\in C(0,\infty ),$ and it is said to be in space $C^{n}_{\mu }$ if and only if $f^{(n)}\in C_{\mu },n\in N.$

Definition 2

The fractional derivative $D^{\alpha }$ of f(t) in the Caputo’s sense is defined as

$$\begin{aligned} D^{\alpha }f(t)=\frac{1}{\varGamma (n-\alpha )}\int _{0}^{t} (t-\tau )^{n-\alpha -1}f^{(n)}(\tau )d(\tau ), \end{aligned}$$

(3)

for $n-1< \alpha \le n,n\in N,t>0,f(t)\in C_{-1}^{n}.$

Definition 3

The Laplace transform of a function f(t), $t>0$ is defined as

$$\begin{aligned} {\mathcal {L}}[f(t)]=F(s)=\int _{0}^{+\infty }\mathrm{e}^{-st}f(t)dt, \quad Re(s)>\sigma _{0}, \end{aligned}$$

(4)

where $\sigma _{0}$ is the abscissa of convergence.

It has following properties:

$$\begin{aligned} {\mathcal {L}}[af(t)+bg(t)]=a{\mathcal {L}}[f(t)]+b{\mathcal {L}}[g(t)], \end{aligned}$$

(5)

where a, b are constants.

Theorem 1

The Laplace transform ${\mathcal {L}}[f(t)]$ of the Caputo derivative is defined as [16]

$$\begin{aligned} {\mathcal {L}}[D^{\alpha }f(t)]=s^{\alpha }F(s)-\sum ^{n-1}_{k=0} s^{\alpha -k-1}f^{(k)}(0), \end{aligned}$$

(6)

for $~n-1<\alpha \le n.$

3 Solution of the Bagley–Torvik equation

In this section, we solve the Bagley–Torvik equation (1) and (2) using Laplace transform and Laguerre polynomial. First, we apply the Laplace transform to both sides of (1)

$$\begin{aligned} {\mathcal {L}}[Ay''(t)]+{\mathcal {L}}\left[ BD^{\frac{3}{2}}y(t)\right] + {\mathcal {L}}[Cy(t)]={\mathcal {L}}[f(t)]. \end{aligned}$$

(7)

Using the (5), (6), and initial conditions given in (2), we get

$$\begin{aligned} {\mathcal {L}}[y(t)]=\frac{{\mathcal {L}}[f(t)]+Asa_{0}+Aa_{1}+ Bs^{\frac{1}{2}}a_{0}+Bs^{-\frac{1}{2}}a_{1}}{As^{2}+ Bs^{\frac{3}{2}}+C}. \end{aligned}$$

(8)

The solution is followed by numerical inversion of Laplace transform. In [8, 9, 24, 25], an algorithm for numerical inversion of Laplace transform is given. The method is based on the Laguerre expansion of y(t).

$$\begin{aligned} y(t)=\mathrm{e}^{\sigma t}\sum ^{\infty }_{k=0}c_{k}\mathrm{e}^{-bt}L_{k}(2bt), \end{aligned}$$

(9)

where $L_{k}(2bt)$ is the Laguerre polynomial of degree k, while $\sigma > \sigma _{0}$ and $b>0$ are parameters of the series, and the coefficients $c_{k}$ are the Taylor coefficients of

$$\begin{aligned} \varPhi (z)=\frac{2b}{1-z}F\left( \sigma +\frac{2b}{1-z}-b\right) =\sum ^{+\infty }_{n=0}c_{n}z^{n}, \quad |z|<R, \end{aligned}$$

(10)

where R is the radius of convergence of the series on the right side in (10). Theoretical estimates for the optimal parameters $\sigma$ and b were derived in [25], and a subroutine for computing them may be found in [9]. Numerically, the $c_{k}$ can be computed using the equally accurate mid-point rule which avoids the singular point. The $c_{k}$ is given by

$$\begin{aligned} c_{k}=\frac{\mathrm{e}^{-ikh/2}}{2N}\sum ^{N-1}_{j=-N}{\varPhi }(\mathrm{e}^{i\theta _{j+1/2}}) \mathrm{e}^{ik\theta _{j}}, \quad k=0,1,2,\ldots ,N-1, \end{aligned}$$

where $\theta _{j}=jh, h=\pi /N$. This can be computed as a FFT of length 2N. The corresponding approximation to y(t) given by (9) is

$$\begin{aligned} y_{N}(t)=\mathrm{e}^{\sigma t}\sum ^{N}_{k=0}c_{k}\mathrm{e}^{-bt}L_{k}(2bt). \end{aligned}$$

(11)

Naturally, besides the choices for $\sigma$ and b, the success or failure of such an algorithm depends on the accuracy of the approximations $c_{k}$ and on how many N of these are calculated.

4 Error analysis

In this section, we analyze the error of the method described in Sect. 3. In [25] the author identified three sources of error associated with the Laguerre expansion. First, there is the truncation error arising from truncating the series to N terms. Second, the expansion coefficients $c_{i}$ are computed numerically and not analytically. This particular error is referred to as the discretization error. Third, the inversion of the Laplace transform is well known to be an ill-conditioned problem. Thus, the actual expression employed in estimating y(t) is

$$\begin{aligned} {\widetilde{y}}_{N}(t)=\mathrm{e}^{\sigma t}\sum ^{N}_{k=0}{\widetilde{c}}_{k}(1+\epsilon _{k})\mathrm{e}^{-bt}L_{k}(2bt), \end{aligned}$$

where $\epsilon _{k}$ denotes the relative error in the floating point representation of computed coefficients. We define the absolute error e(x) as the difference between the function y(t) and its computed solution. Considering the fact that $|\mathrm{e}^{-bx}L_{k}(2bx)|\le 1$, we get

$$\begin{aligned} e(t)=\mid y(t)-{\widetilde{y}}_{N}(t)\mid \le \mathrm{e}^{\sigma t}(T+D+C), \end{aligned}$$

where

$$\begin{aligned} T=\sum _{k=N}^{\infty }|c_{k}|, D=\sum _{k=0}^{N-1}|c_{k}-{\widetilde{c}}_{k}|, C=\epsilon \sum _{k=0}^{N-1}|{\widetilde{c}}_{k}|, \end{aligned}$$

are the truncation, discretization, and conditioning error bounds, respectively. $\epsilon$ is the machine round-off unit so that for each k, $|\epsilon _{k}|\le \epsilon$. From [5, 25], the discretization error can be neglected when compared with the truncation and conditioning errors. Therefore, we mainly refer to the truncation error T and conditioning error C. In [4, 25], the upper bound of T and C were given

$$\begin{aligned} T\le \frac{k(r)}{r^{N}(r-1)}, \quad C\le \epsilon \frac{rk(r)}{r-1}, \end{aligned}$$

which is valid for each $r\in (1,R)$. Therefore, we can get the following error bounds

$$\begin{aligned} e(x)\le \frac{k(r)}{r^{N}(r-1)}+\epsilon \frac{rk(r)}{r-1}. \end{aligned}$$

5 Numerical examples

In this section, we demonstrate the effectiveness and simplicity of the proposed method with three examples.

Example 1

First, we consider the following Bagley–Torvik equation

$$\begin{aligned} y''(t)+y^{\frac{3}{2}}(t)+y(t)=\frac{2t^{1/2}}{\varGamma (3/2)}+t^{2}-t, \end{aligned}$$

with the initial conditions

$$\begin{aligned} y(0)=0,\quad y'(0)=1, \end{aligned}$$

where the exact solution is $y(t)=t^2-t$. We apply the method described in Sect. 3 with $N=4,8,16$ and different values of $\sigma$, b to solve the problem. The results are listed in Tables 1 and 2.

Table 1 The absolute errors between the exact and approximate solutions with $\sigma =1, b=1$

Table 2 The absolute errors between the exact and approximate solutions with the optimal $\sigma$ and b

Example 2

In this example, we consider the following equation

$$\begin{aligned} y''(t)+\frac{1}{2}D^{\frac{3}{2}}y(t)+\frac{1}{2}y(t)=g(t) \end{aligned}$$

subject to the initial condition $y(0)=0, y'(0)=0$, where

$$\begin{aligned} g(t)=\left\{ \begin{array}{ll} 8, &{}\quad 0\le t \le 1; \\ 0, &{}\quad t>1. \end{array} \right. \end{aligned}$$

The problem was considered in [3, 14, 17, 18]. We applied the present method to solve the problem with $N=8,16,32$. The numerical solutions obtained by the present method and other numerical methods such as the wavelet method [18] and hybrid functions method [14] are given in Tables 3, 4. Clearly, the numerical results show that the present method is effective and its accuracy is comparable with existing methods. The numerical results with $N=8,16,32$ and the exact solution are plotted in Fig. 1. The approximate solutions using the present method show excellent agreement with the exact solutions.

Table 3 Comparison of the numerical results of the wavelet and present method for Example 2

Table 4 Comparison of the numerical results of the hybrid function and present method for Example 2

Fig. 1

Exact solution and numerical solution for $N=8,16,32$

Table 5 Comparison of the maximum absolute errors for different values of $\alpha$ for Example 3

Table 6 Comparison of the absolute errors with $\alpha =1$ for different values of N for Example 3

Table 7 Comparison of the absolute errors with $\alpha =4\pi$ for different values of N for Example 3

Fig. 2

Exact solution and numerical solution for $N=16, \alpha =1$

Fig. 3

Exact solution and numerical solution for $N=32, \alpha =4\pi$

Example 3

Consider the following Bagley–Torvik equation

$$\begin{aligned} y''(t)+y^{\frac{3}{2}}(t)+y(t)=f(t), \end{aligned}$$

with the initial conditions

$$\begin{aligned} y(0)=0,\quad y'(0)=\alpha , \end{aligned}$$

where the exact solution is $y(t)=sin(\alpha t)$. This problem has been considered in [7]. We applied the present method to solve the problem with various choices of $\alpha$ and N. In Table 5, we compared the maximum absolute errors of the approximate solutions obtained by the present method and the Chebyshev collocation method in [7]. Tables 6, 7 also show that the approximate solutions using the present method are consistent with the exact solutions for $\alpha =1$, and $4\pi$. In Figs. 2, 3, we plot the approximate solutions by the proposed method for different values of $\alpha$ and the exact solution.

6 Conclusion

In this work, we used a method based on Laplace transform and Laguerre polynomials to solve the Bagley–Torvik equation. The numerical solution obtained using the proposed method shows that this method can solve the problem effectively. The results prove that the proposed method is a very powerful, efficient, and simple mathematical tool for solving fractional differential equations in the field of Newtonian fluids.