Sinc-Galerkin solution to the clamped plate eigenvalue problem

Abstract

We propose an accurate and computationally efficient numerical technique for solving the biharmonic eigenvalue problem. The technique is based on the sinc-Galerkin approximation method to solve the clamped plate problem. Numerical experiments for plates with various aspect ratios are reported, and comparisons are made with other methods in literature. The calculated results accord well with those published earlier, which proves the accuracy and validity of the proposed method.

1 Introduction

Eigenvalue problems such as plate vibration problems have attracted much research using a wide range of methods. However, exact solutions are available only for certain boundary conditions and domain configurations, hence approximate solutions are of great importance when analytical methods fail or become too cumbersome.

A large number of numerical methods have been developed to obtain solutions for many rectangular plate problems with different boundary conditions [23, 26, 29, 37–39]. A boundary homotopy method was used in [46] to obtain strict bounds for the N lowest eigenvalues of the clamped plate equation in the unit square. Some of these methods can only provide upper bounds for the eigenvalues. For example, spectral Legendre-Galerkin method [6] was used to provide highly accurate solution to the biharmonic eigenvalue problem for the clamped unit-square plate and buckling plate problems. Another method that always gives upper bounds for the eigenvalues is the Rayleigh-Ritz method [48]. Recently, Gavalas and El-Raheb [21] extended the method for eigenvalue problems with discontinuous boundary conditions applied to vibration of rectangular plates. Also, the method was applied in [8] for the vibration analysis of exponential functionally graded rectangular plates in thermal environment. On the other hand, the superposition method developed by Gorman [24] gives lower bound results to the same problem. This method has been successfully applied for the analysis of undamped out-of-plane vibrations of single isotropic plates [22]. Other successful numerical methods include the spline finite strip method by Fan and Cheung [19], the Galerkin approach by Chia [11] and Leipholz [27], the least squares technique [45], meshless methods [4, 13], and finite element methods [1, 10]. Differential quadrature (DQ) methods [2, 9] have been successfully applied in the vibration analysis. A generalized differential quadrature (GDQ) method was introduced by Shu and Richards [41] to simplify the calculation of the weighting coefficients of the derivatives approximation.

The biharmonic boundary value problem

$$\begin{aligned} \frac{\partial ^{4}{u}}{\partial {x}^{4}}+2 \frac{\partial ^{4}{u}}{\partial {x}^{2}\partial {y}^{2}} +\frac{\partial ^{4}{u}}{\partial {y}^{4}}= f(x,y),\quad (x,y)\in \Omega \equiv (a,b)\times (c,d), \end{aligned}$$

subject to the nonhomogeneous boundary conditions

$$\begin{aligned} \left. u\right| _{\partial {\Omega } }= g(x,y), \quad \left. \frac{\partial {u }}{\partial n} \right| _{\partial \Omega } = h(x,y) \end{aligned}$$

(where $\frac{\partial {u }}{\partial n}$ is the outward normal derivative) was solved using the sinc-Galerkin method in [18]. In this paper, we apply the sinc-Galerkin method to solve the biharmonic eigenvalue problem

$$\begin{aligned} \frac{\partial ^{4}{u}}{\partial {x}^{4}}+2 \frac{\partial ^{4}{u}}{\partial {x}^{2}\partial {y}^{2}} +\frac{\partial ^{4}{u}}{\partial {y}^{4}}= \lambda u ,\quad (x,y)\in \Omega \equiv (a,b)\times (c,d), \end{aligned}$$

subject to the following boundary conditions for a clamped plate

$$\begin{aligned} \left. u\right| _{\partial {\Omega } }= \left. \frac{\partial {u }}{\partial n} \right| _{\partial \Omega } = 0. \end{aligned}$$

In recent years, a lot of attention has been devoted to the study of the sinc method to investigate various scientific models. It is possible to solve two point boundary value problems [5, 34], initial-value problems [3], fourth-order differential equations [40], sixth-order boundary-value problems [17], nonlinear higher-order boundary-value problems [16], partial differential equations [32], eigenvalue problems, singular problem-like Poisson [47], linear Fredholm integro-differential equations [33], linear and nonlinear Volterra integro-differential equations [35], linear and nonlinear system of second-order boundary value problems [14], as well as Troesch’s problem [15] by using sinc methods. The comparison of finite difference, spectral and sinc-convolution treatments was considered in [12].

The outline of the paper is as follows. Section 2, contains notations, definitions and some results of sinc function theory. In Sect. 3, the sinc-Galerkin approach to the clamped plate eigenvalue problem is presented. In Sect. 4, we verify the reliability of the proposed algorithm by numerical results obtained and comparisons with published results in literature. Conclusions are given in Sect. 5.

2 Preliminaries and fundamentals

The books [31, 43] provide excellent overviews of methods based on sinc functions for solving ordinary and partial differential equations and integral equations. The goal of this section is to recall notations and definitions of the sinc function, state some known results, and derive useful formulas that are important for this paper.

The sinc function is defined on the whole real line by

$$\begin{aligned} \text{ sinc } (x)=\frac{\sin (\pi x)}{\pi x}, \quad -\infty<x<\infty . \end{aligned}$$

For $h>0$, the translated sinc functions with evenly spaced nodes are given as

$$\begin{aligned} S(k,h)(x)=\text{ sinc }\left( \frac{x-kh}{h}\right) ,\quad \text{ k }=0,\pm 1,\pm 2,\ldots \end{aligned}$$

If f is defined on the real line, then for $h>0$ the series

$$\begin{aligned} C(f,h)=\sum _{k=-\infty }^{\infty } f(hk) \text{ sinc }\left( \frac{x-hk}{h}\right) , \end{aligned}$$

is called the Whittaker cardinal expansion of f whenever this series converges. The properties of Whittaker cardinal expansions have been studied and are thoroughly surveyed in [43]. These properties are derived in the infinite strip $D_d$ of the complex plane where for $d>0$

$$\begin{aligned} D_d=\left\{ {\zeta =\xi +i\eta :|\eta |<d\le \frac{\pi }{2}}\right\} . \end{aligned}$$

(2.1)

To construct approximations on the interval (a, b) which are used in this paper, we consider the conformal map [43]

$$\begin{aligned} \phi (z)=\ln \left( \frac{z-a}{b-z}\right) , \end{aligned}$$

(2.2)

The map $\phi$ carries the eye-shaped region

$$\begin{aligned} D_{E}=\left\{ z=x+iy:\left| \text{ arg }\left( \frac{z-a}{b-z}\right) \right| <d\le \frac{\pi }{2}\right\} , \end{aligned}$$

(2.3)

onto the infinite strip $D_d$.

The “mesh sizes” h represent the mesh sizes in $D_d$ for the uniform grids $\{kh\}$, $k=0,\pm 1,\pm 2,\ldots$. The sinc grid points $z_k\in (a,b)$ in $D_E$ will be denoted by $x_k$ because they are real, and are given by

$$\begin{aligned} x_k=\phi ^{-1}(kh)=\frac{a+b\,e^{kh}}{1+e^{kh}}, \end{aligned}$$

(2.4)

The class of functions suitable for sinc interpolation and quadrature is denoted by B(D) and defined below.

Definition 2.1

[43] Let B(D) be the class of functions F that are analytic in D, satisfy

$$\begin{aligned} \int _{\psi (L+t)} |F(z)dz|\rightarrow 0,\quad \text{ as } \; t=\pm \infty , \end{aligned}$$

where

$$\begin{aligned} L=\left\{ iy:|y|<d \le \frac{\pi }{2}\right\} , \end{aligned}$$

and on the boundary of D (denoted $\partial D$) satisfy

$$\begin{aligned} N(F)=\int _{\partial D_E}|F(z)dz|<\infty . \end{aligned}$$

The following theorem provides the error bounds of sinc interpolation and quadrature formulae for functions in B(D).

Theorem 2.1

[43]Let $\Gamma$ be (a, b). Let $F\in B(D)$ and $\tau _{j}=\psi (jh)=\phi ^{-1}(jh),\quad j=0,\pm 1,\pm 2,\ldots ,$. Let there exist positive constants $\alpha$, $\beta$ and C such that

$$\begin{aligned} \left| \frac{F(\tau )}{\phi '(\tau )} \right| \le C {\left\{ \begin{array}{ll} \exp (-\alpha |\phi (\tau )|),\quad \tau \in \psi ((-\infty ,0)), \\ \exp (-\beta |\phi (\tau )|),\quad \tau \in \psi ((0,\infty )). \end{array}\right. } \end{aligned}$$

(2.5)

then the error bound is

$$\begin{aligned} \left| \int _{\Gamma }F(\tau ) d\tau -h\sum _{j=-M}^{N}\frac{F(\tau _j)}{\phi '(\tau _j)}\right| \le C \left( \frac{e^{-\alpha M h}}{\alpha }+\frac{e^{-\beta N h}}{\beta }\right) +\left| I_F\right| . \end{aligned}$$

(2.6)

Making the selections

$$\begin{aligned} h=\sqrt{\frac{\pi d}{\alpha M}},\quad \text{ and }\quad N\equiv \left[ \left| \frac{\alpha }{\beta } M+1\right| \right] , \end{aligned}$$

where [x] is the integer part of x,  then

$$\begin{aligned} \int _\Gamma F(\tau ) d \tau =h\sum _{j=-M}^{N} \frac{F(\tau _j)}{\phi '(\tau _j)}+O\left( e^{-(\pi \alpha d M)^{1/2}}\right) . \end{aligned}$$

The sinc-Galerkin method requires that the derivatives of composite sinc functions be evaluated at the nodes. We need the following lemma.

Lemma 2.1

[31, 43] Let $\phi$ be the conformal one-to-one mapping of the simply connected domain $D_E$ onto $D_d,$ given by (2.2). Then

$$\begin{aligned} \delta _{jk}^{(0)}=\left[ S(j,h)\circ \phi (x)\right] |_{x=x_k}= \left\{ \begin{array}{ll} 1,&{}\quad \text{ j }=k,\\ 0,&{}\quad \text{ j }\ne k, \end{array} \right. \end{aligned}$$

(2.7)

$$\begin{aligned} \delta _{jk}^{(1)}=h\frac{d}{d\phi }\left[ S(j,h)\circ \phi (x)\right] |_{x=x_k}= \left\{ \begin{array}{ll} 0,&{}\quad \text{ j }=k,\\ \frac{(-1)^{k-j}}{k-j},&{}\quad \text{ j }\ne k, \end{array} \right. \end{aligned}$$

(2.8)

$$\begin{aligned} \delta _{jk}^{(2)}=h^2\frac{d^2}{d\phi ^2}\left[ S(j,h)\circ \phi (x)\right] |_{x=x_k}= \left\{ \begin{array}{ll} \frac{-\pi ^2}{3},&{}\quad \text{ j }=k,\\ \frac{-2(-1)^{k-j}}{(k-j)^2},&{}\quad \text{ j }\ne k. \end{array} \right. \end{aligned}$$

(2.9)

$$\begin{aligned} \begin{array}{ll} \delta _{jk}^{(3)}&{}=h^3\left[ \frac{d^3}{d\phi ^3}\left[ S(j,h)\circ \phi (x)\right] \right] _{x=x_k}\\ &{}= \left\{ \begin{array}{ll} 0, &{} \quad \text{ j }=k,\\ \frac{(-1)^{k-j}}{(k-j)^3}\left[ 6-\pi ^2(k-j)^2\right] , &{}\quad \text{ j }\ne k, \end{array} \right. \end{array} \end{aligned}$$

(2.10)

$$\begin{aligned} \begin{array}{ll} \delta _{jk}^{(4)}&{}=h^4\left[ \frac{d^4}{d\phi ^4}\left[ S(j,h)\circ \phi (x)\right] \right] _{x=x_k}\\ &{}= \left\{ \begin{array}{ll} \frac{\pi ^4}{5}, &{} \quad \text{ j }=k,\\ \frac{-4(-1)^{k-j}}{(k-j)^4}\left[ 6-\pi ^2(k-j)^2\right] , &{}\quad \text{ j }\ne k, \end{array} \right. \end{array} \end{aligned}$$

(2.11)

3 The Sinc-Galerkin approach to the biharmonic eigenvalue problem

The equation of motion for the undamped free vibration of a plate may be written as [44]

$$\begin{aligned} \frac{\partial ^{4}{u}}{\partial {\bar{x}}^{4}}+2 \frac{\partial ^{4}{u}}{\partial {\bar{x}}^{2}\partial {\bar{y}}^{2}} +\frac{\partial ^{4}{u}}{\partial {\bar{y}}^{4}}+\frac{\rho }{D} \frac{\partial ^{2}{u}}{\partial {t}^{2}}=0 \end{aligned}$$

(3.1)

where u is the transverse displacement at a point defined by the coordinates $(\bar{x},\bar{y})\in (0,a)\times (0,b)$ where a and b are the plate dimensions, at any given time t, D is the flexural rigidity of the plate and $\rho$ is the mass of the plate per unit area of its surface.

For a plate of constant thickness $\sigma$ and material properties E (Young’s modulus of elasticity) and $\nu$ (Poisson’s ratio), the flexural rigidity D is given by

$$\begin{aligned} D = \frac{E\,\sigma ^{3}}{12(1-\nu ^{2})} \end{aligned}$$

Assuming harmonic vibration, we may write

$$\begin{aligned} u(\bar{x},\bar{y},t) = U(\bar{x},\bar{y})sin(\omega t) \end{aligned}$$

(3.2)

where $U(\bar{x},\bar{y})$ is a shape function satisfying the fully clamped plate boundary conditions and describing the shape of the deflected middle surface of the vibrating plate, and $\omega$ is a natural circular frequency of the plate. Substituting for u in Eq. (3.1), we obtain

$$\begin{aligned} \frac{\partial ^{4}{U}}{\partial {\bar{x}}^{4}}+2 \frac{\partial ^{4}{U}}{\partial {\bar{x}}^{2}\partial {\bar{y}}^{2}} +\frac{\partial ^{4}{U}}{\partial {\bar{y}}^{4}}-\frac{\rho \omega ^{2}}{D} U = 0 \end{aligned}$$

(3.3)

For convenience, the governing Eq. (3.3) is expressed in dimensionless form. Define the dimensionless coordinates x and y, where $x = \bar{x}/a$ and $y = \bar{y}/b$. Equation (3.3) may be then written as

$$\begin{aligned} LU \equiv \frac{\partial ^{4}{U}}{\partial {y}^{4}}+ 2\Phi ^{2} \frac{\partial ^{4}{U}}{\partial {x}^{2}\partial {y}^{2}} +\Phi ^{4} \frac{\partial ^{4}{U}}{\partial {x}^{4}}-\Phi ^{4} \lambda ^2 U = 0, \end{aligned}$$

(3.4)

where $\left( \Phi = b/a \right)$ is the plate aspect ratio, and the non-dimensional frequency parameter, $\lambda$ of the plate may be expressed as

$$\begin{aligned} \lambda = \omega a^2 \sqrt{\frac{\rho }{D}} \end{aligned}$$

(3.5)

The assumed sinc approximate solution to the eigenvalue problem (3.4) takes the form:

$$\begin{aligned} U_{n}(x,y)=\sum _{j=-M}^{N}\sum _{i=-M}^{N}U_{ij}\,S_{ij}(x,y),\quad n=M+N+1 \end{aligned}$$

(3.6)

where the basis functions $\left\{ S_{ij}(x,y)\right\}$ for $-M \le i,j \le N$ are given as simple product basis functions of one dimensional sinc basis

$$\begin{aligned} \begin{array}{ll} S_{ij}(x,y)&{}=S_i(x)S_j(y)\\ &{}=[S(i,h_x) \circ \phi _1(x)][S(j,h_y)\circ \phi _2(y)] \end{array} \end{aligned}$$

(3.7)

where $\phi$ be as before.

The assumed approximate solution satisfies the clamped plate boundary conditions

$$\begin{aligned} \left. U \right| _{\Gamma } = \left. \frac{\partial {U}}{\partial {n}} \right| _{\Gamma }=0 \end{aligned}$$

where $\Gamma$ is the boundary of the new dimensionless domain, $\Omega \equiv (0,1)\times (0,1)$, and n is the outward normal to the boundary.

We use the Galerkin scheme to determine the unknown coefficients $\left\{ U_{ij}\right\}$ in (3.6). First, we define the inner product of two functions f and g by

$$\begin{aligned} \left<f,g\right>=\int _{0}^{1}\int _{0}^{1}\, f(x,y)\,g(x,y)\,w(x)\,v(y)\,dx\, dy, \end{aligned}$$

where $w(x)=\frac{1}{[\phi _1'(x)]^2}$ and $v(y)=\frac{1}{[\phi _2'(x)]^2}$ are the weight functions in the direction of the x-axis and y-axis, respectively.

The discrete Galerkin system is then given by

$$\begin{aligned} \langle LU_{n}, S_{kl} \rangle = \Phi ^{4} \lambda ^{2}\langle U_{n}, S_{kl}\rangle ,\quad -M\le k,l\le N \end{aligned}$$

(3.8)

Instead of substituting the approximate solution given by (3.6) into (3.8), we first analyze the equation

$$\begin{aligned} \left<\Phi ^{4}U_{xxxx},S_k \,S_l\right>+\left<2\, \Phi ^{2} U_{xxyy},S_k S_l\right>+\left<U_{yyyy},S_k\, S_l\right>=\left<\Phi ^{4} \lambda ^2 U,S_k\, S_l\right> \end{aligned}$$

(3.9)

The method of approximating the integrals in (3.9) begins by integrating by parts to transfer all derivatives from U to $S_{kl}$. We are lead to the following theorem

Theorem 3.1

The following relations hold

$$\begin{aligned} \left<\Phi ^{4} U_{xxxx},S_k\, S_l\right>\approx h_x h_y \Phi ^{4} \frac{v(y_l)}{\phi _2'(y_l)}\sum _{i=-M}^{N}\sum _{j=0}^4\frac{U(x_i,y_l)}{\phi _1'(x_i)}\left[ \frac{1}{h_x^j}\delta _{ki}^{(j)}\mu _j\right] , \end{aligned}$$

(3.10)

$$\begin{aligned} \left<U_{yyyy},S_k S_l\right>\approx h_x h_y\frac{w(x_k)}{\phi _1'(x_k)}\sum _{i=-M}^{N}\sum _{j=0}^4\frac{U(x_k,y_i)}{\phi _2'(y_i)}\left[ \frac{1}{h_y^j}\delta _{li}^{(j)}\eta _j\right] , \end{aligned}$$

(3.11)

$$\begin{aligned} \left<2\ \Phi ^{2} u_{xxyy},S_k S_l\right>\approx 2 \Phi ^{2} h_x\,h_y\,\sum _{j=-M}^{N}\,\sum _{i=-M}^{N}\, \sum _{r=0}^2\,\,\sum _{p=0}^2\,\,\frac{\tau _r\,\xi _p \,U(x_i,y_j)}{h_x^r\,h_y^p\,\phi '_1(x_i)\,\phi '_2(y_i)}\,\delta _{ki}^{(r)}\,\delta _{lj}^{(p)}, \end{aligned}$$

(3.12)

and

$$\begin{aligned} \left<\Phi ^{4} \lambda ^2 U , S_k S_l \right> \approx \Phi ^{4} \lambda ^2\, h_x\,h_y\,\frac{w(x_k)\, U(x_k,y_l)\,v(y_l)}{\phi '_1(x_k)\,\phi '_2(y_j)} \end{aligned}$$

(3.13)

for some functions $\mu _j,$ $\eta _j,$ $\xi _p$ and $\tau _r$ to be determined.

Proof

The proof is given in Appendix 1. $\square$

Replacing each term of (3.9) with the corresponding approximations defined in (3.10), (3.11), (3.12) and  (3.13) and replacing $U(x_k,y_l)$ by $U_{kl}$ and dividing by $h_x\,h_y$, we obtain the following theorem

Theorem 3.2

If the assumed approximate solution of the boundary-value problem (3.1) is (3.6), then the discrete sinc-Galerkin system for the determination of the unknown coefficients $\left\{ U_{kl},\, k=-M,\ldots , N,\quad l=-M,\ldots , N \right\}$ is given by

$$\begin{aligned}&\Phi ^{4} \frac{v(y_l)}{\phi _2'(y_l)}\sum _{i=-M}^{N}\sum _{j=0}^4\frac{U_{il}}{\phi _1'(x_i)}\left[ \frac{1}{h_x^j}\delta _{ki}^{(j)}\mu _j\right] \nonumber \\&\qquad + \;2\, \Phi ^{2}\sum _{j=-M}^{N}\,\sum _{i=-M}^{N}\,\sum _{r=0}^2\,\,\sum _{p=0}^2\,\,\frac{\tau _r\,\xi _p\,\,\delta _{ki}^{(r)}\,\delta _{lj}^{(p)}}{h_x^r\,h_y^p\,\phi '_1(x_i)\,\phi '_2(y_j)}\,U_{ij} \nonumber \\&\qquad + \;\frac{w(x_k)}{\phi _1'(x_k)}\sum _{i=-M}^{N}\sum _{j=0}^4\frac{U_{ki}}{\phi _2'(y_i)}\left[ \frac{1}{h_y^j}\delta _{li}^{(j)}\eta _j\right] = \Phi ^{4} \lambda ^2\, \frac{w(x_k)\, U(x_k,y_l)\,v(y_l)}{\phi '_1(x_k)\,\phi '_2(y_l)}\quad \quad \quad \end{aligned}$$

(3.14)

Recall the notation of Toepleitz matrices [25]. Let $I_{n}^{(P)}$, $P=0,1,2,3,4$ be the $n\times n$ matrices $I^{(P)}$, with jk-th entry $\delta _{jk}^{(P)}$ as given by equations (2.7)–(2.11). Further, $D(g_x)$ is an $n \times n$ diagonal matrix whose diagonal entries are $[g_{-M}, g_{-M+1}, \dots , g_{N}]^T$. Lastly, the $n\times n$ matrix $\mathbf U$ has kl-th entries given by $U_{kl}$. Introducing this notation in Eq. (3.14) leads to the matrix form

$$\begin{aligned} \mathbf A \,\mathbf X +\mathbf C \, \mathbf X \, \mathbf E +\mathbf X \, \mathbf B =\lambda ^2\,\mathbf X \end{aligned}$$

(3.15)

where $\mathbf A ,\, \mathbf B ,\,\mathbf C ,\,\mathbf E$ and $\mathbf X$ are matrices of size $n \times n$, and given by

$$\begin{aligned} \mathbf A= & {} \mathbf D (\phi '_1)\sum _{i=0}^4 \left[ \frac{1}{h_x^i}{} \mathbf I _{n}^{(i)}{} \mathbf D \left( \frac{\mu _i}{{\phi '_1}^2w}\right) \right] \mathbf D (\phi _1'), \\ \mathbf B= & {} \left( \frac{1}{\Phi ^{4}}\right) \mathbf D (\phi '_2)\sum _{i=0}^4 \left[ \frac{1}{h_y^i}{} \mathbf I _{n}^{(i)}{} \mathbf D \left( \frac{\eta _i}{{\phi '_2}^2\,v}\right) \right] ^T\mathbf D (\phi _2'), \\ \mathbf C= & {} \left( \frac{2}{\Phi ^{2}}\right) \,\mathbf D (\phi '_1)\,\sum _{i=0}^2 \left[ \frac{1}{h_x^i}{} \mathbf I _{n}^{(i)}{} \mathbf D \left( \frac{\tau _i}{{\phi '_1}^2\,w}\right) \right] \,\mathbf D (\phi '_1) \\ \mathbf E= & {} \mathbf D (\phi '_2)\,\sum _{i=0}^2 \left[ \frac{1}{h_y^i}{} \mathbf I _{n}^{(i)}{} \mathbf D \left( \frac{\xi _i}{{\phi '_2}^2\,v}\right) \right] ^T\,\mathbf D (\phi '_2) \end{aligned}$$

and

$$\begin{aligned} \mathbf X =\mathbf D (w)\,\mathbf U \,\mathbf D (v), \end{aligned}$$

The last step is to convert the matrix equation (3.15) to a matrix eigenvalue problem. This is done via vectorization of (3.15) using Kronecker matrix products [36]. This yields the algebraic eigenvalue problem

$$\begin{aligned} \mathbf M \,z = \lambda ^2 \, z \end{aligned}$$

(3.16)

where

$$\begin{aligned} \mathbf M = \mathbf I _n\otimes \mathbf A + \mathbf E ^T \otimes \mathbf C + \mathbf B ^T\otimes \mathbf I _n \end{aligned}$$

From the above equation, the values of $\lambda$ defined in Eq. (3.5) can be obtained from the eigenvalues of matrix M.

4 Numerical results and discussions

For purposes of comparison, contrast and performance, we consider the computation of $\lambda$ for the square plate and rectangular plates of various aspect ratios, $\Phi$. For all cases, we have made the selections, $d = \pi /2$, $\alpha = 0.5$ and $h = \pi /\sqrt{M}$.

• Case 1 In this case, a clamped square plate is considered. In Table 1, we report the calculated values of $\lambda _1, \lambda _2, \lambda _3$ and $\lambda _4$ using different number of sinc basis functions with $M = 5,\,10,\,15,\ldots ,50$.

It is worth noting that clamped plate eigenvalue problem has no exact solution. Hence, we further use the results obtained in Table 1 to find the limit values $\left\{ \lambda ^{*}_1,\,\lambda ^{*}_2,\,\lambda ^{*}_3,\,\lambda ^{*}_4\right\}$ using the minimal polynomial extrapolation (MPE) approach [7, 42]. The obtained limit values are reported in Table 2 along with the strict lower bounds, $\underline{\lambda }_j$ and upper bounds, $\overline{\lambda }_j$ obtained in [46].

Table 1 Convergence of the computed values of $\lambda$ for the square plate using different M

Table 2 Minimal polynomial extrapolation limits of $\lambda$ for the square plate compared to the strict lower and upper bounds of [46]

Since we are using the Galerkin scheme, we note from the results in Table 1 that our method converges to the accurate upper bound. We define an approximate relative error (ARE) by

$$\begin{aligned} e_i = \frac{\left| \lambda _\mathrm {sinc}-\lambda _i^{*}\right| }{\lambda _i^{*}},\qquad i = 1,\ldots ,4. \end{aligned}$$

(4.1)

Fig. 1

Approximate relative error of the calculated $\lambda _i,\; i = 1,\ldots ,4$

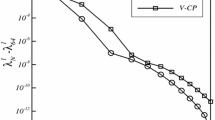
The exponential convergence rate shown in Fig. 1 for the ARE of the first four frequency paramters verifies the validity and accuracy of the proposed scheme. The shapes of the corresponding eigenmodes are shown in Fig. 2.

Fig. 2

Eigenmodes of the clamped square plate: a The first mode, $\lambda _1 \simeq 35.985$. b The second mode, $\lambda _2 \simeq 73.394$. c The third mode, $\lambda _3 \simeq 73.394$. d The fourth mode, $\lambda _4 \simeq 108.217$

Table 3 Comparison of the first four frequency parameters for clamped square plate

The results in Table 3 also show good agreement with those obtained by other methods; the Rayleigh–Ritz method with displacement components expressed in simple algebraic polynomial forms [8], the Rayleigh–Ritz method together with natural co-ordinate regions and normalized beam characteristic orthogonal polynomials [20], the Ritz method with 36 terms containing the products of beam functions [28], and Rayleigh–Ritz procedure for minimization of the energy function derived using Mindlin’s plate theory [30].

• Case 2 In this case, we consider clamped rectangular plates with different aspect ratios $\Phi = 2/3, 1.5$ and 2.5. The calculated values of $\lambda _i,\,\, i = 1,\ldots ,4$ for $\Phi = 2/3$ and 1.5 are reported in Tables 4 and 5, respectively.

The mode shapes for the rectangular plate with an aspect ration, $\Phi = 1.5$ are shown in Fig. 3.

Table 4 Convergence of the computed values of $\lambda$ for clamped rectangular plate with an aspect ratio $\Phi = 2/3$

Table 5 Convergence of the computed values of $\lambda$ for clamped rectangular plate with an aspect ratio $\Phi = 1.5$

Fig. 3

Mode shapes of clamped rectangular plate with $\Phi =1.5$: a The first mode, $\lambda _1 \simeq 27.005$. b The second mode, $\lambda _2 \simeq 41.704$. c The third mode, $\lambda _3 \simeq 66.125$. d The fourth mode, $\lambda _4 \simeq 66.527$

Table 6 Convergence of the computed values of $\lambda$ for clamped rectangular plate with an aspect ratio $\Phi = 2.5$

In Table 6, the values of $\lambda$ for the case of a clamped rectangular plate with $\Phi = 2.5$ are reported. The calculated values of the first four frequency parameters for the cases of $\Phi = 2/3, 1.5$ and 2.5 are listed in Table 7, compared with those obtained by other approaches in [8, 20, 28, 30].

Table 7 Comparison of the first four frequency parameters for clamped rectangular plates with different aspect ratios

Based on the limit values obtained using the MPE method, the approximate relative errors are defined for each case of $\Phi = 2/3, 1.5$ and 2.5 by (4.1). The values of the AREs are listed in Table 8.

Table 8 Approximate relative errors for clamped plates with different aspect ratios

5 Conclusion

In this paper, the sinc-Galerkin method was applied to solve the biharmonic eigenvalue problem. Clamped thin square and rectangular plates with various aspect ratios were considered. The calculated results for these cases accord well with those published earlier. In addition, compared to the strict lower and upper bounds available for the square plate, the sinc-Galerkin has a high convergence rate. This proves the accuracy and validity of the sinc-Galerkin method.

Appendix 1: Proof of Theorem 3.1

For $U_{xxxx}$, the inner product with sinc basis element is given by

$$\begin{aligned} \left<\Phi ^{4} U_{xxxx},S_k S_l\right>=\Phi ^{4} \int _{0}^1 \int _0^1 U_{xxxx}(x,y)S_k(x)S_l(y)w(x)v(y)dx dy. \end{aligned}$$

Integrating by parts to remove the fourth order derivatives from the dependent variable U leads to the equality.

$$\begin{aligned} \left<\Phi ^{4} U_{xxxx},S_k S_l\right>= B_{x}+\Phi ^{4} \int _{0}^1 \int _0^1 U(x,y)\left[ S_k(x)S_l(y)w(x)v(y)\right] _{xxxx}dx dy. \end{aligned}$$

(5.1)

where the boundary term is

$$\begin{aligned} B_x=\Phi ^{4} \int _0^1\left[ U_{xxx}(S_kS_lwv)-U_{xx}(S_kS_lwv)_x +U_x(S_kS_lwv)_{xx}-U(S_kS_lwv)_{xxx}\right] _0^1 dy. \end{aligned}$$

The boundary terms in Eq. (5.1) vanished. Continuing only with the remaining integral in (5.1) and expanding the derivative results in

$$\begin{aligned} \left<\Phi ^{4} U_{xxxx},S_k S_l\right>=\Phi ^{4} \int _{0}^1 \int _0^1 \sum _{i=0}^4U(x,y)\left[ S_k^{(i)}\mu _i\right] S_l v(y) dx dy. \end{aligned}$$

(5.2)

where $S_k^{(i)}$ denotes the ith derivative of $S_k$ with respect to the $\phi _1$ and

$$\begin{aligned} \mu _4= & {} (\phi _1')^{4}w, \\ \mu _3= & {} 6(\phi '_1)^2\phi ''_1w+4(\phi '_1)^3w', \\ \mu _2= & {} 3(\phi ''_1)^2w+4\phi '_1\phi '''_1w+12\phi _1'\phi _1''w'+6(\phi _1')^2w'', \\ \mu _1= & {} \phi _1''''w+4\phi _1'''w'+6\phi _1''w''+4\phi _1'w'''. \end{aligned}$$

and

$$\begin{aligned} \mu _0=w'''' \end{aligned}$$

Applying the sinc quadrature in the x-domain and y-domain to Eq. (5.2) yields Eq. (3.10).

The inner product for $U_{yyyy}$ may be handled in a similar manner. This gives the expression (3.11) where

$$\begin{aligned} \eta _4= & {} (\phi _2')^{4}v, \\ \eta _3= & {} 6(\phi '_2)^2\phi ''_2v+4(\phi '_2)^3v', \\ \eta _2= & {} 3(\phi ''_2)^2v+4\phi '_2\phi '''_2v+12\phi _2'\phi _2''v'+6(\phi _2')^2v'', \\ \eta _1= & {} \phi _2''''v+4\phi _2'''v'+6\phi _2''v''+4\phi _2'v'''. \end{aligned}$$

and

$$\begin{aligned} \eta _0=v'''' \end{aligned}$$

For $U_{xxyy}$, the inner product with sinc basis element is given by

$$\begin{aligned} \left<2\,\Phi ^{2} u_{xxyy},S_k\, S_l\right>=2\,\Phi ^{2} \int _{0}^1 \int _0^1 \,U_{xxyy}(x,y)\,S_k(x)\,S_l(y)\,w(x)\,v(y)\,dx \,dy. \end{aligned}$$

Integrating by parts to remove the fourth derivatives from the dependent variable U leads to the equality

$$\begin{aligned} \left<2\,\Phi ^{2} U_{xxyy},S_k \,S_l\right> = B_{xy}+ \Phi ^{2} \int _{0}^1 \int _0^1 U(x,y)\,\left[ 2\,S_k(x)\,S_l(y)\,w(x)\,v(y)\right] _{xxyy}\,dx\, dy. \end{aligned}$$

(5.3)

where the boundary term is

$$\begin{aligned} B_{xy}= & {} \Phi ^{2}\int _0^1\left[ U_{xyy}(S_k\,S_l\,w\,v)-U_{yy}(S_k\,S_l\,w\,v)_x\right] _0^1 dy \\&+ \; \int _0^1\left[ U_{y}(S_k\,S_l\,w\,v)_{xx}- U(S_k\,S_l\,w\,v)_{xxy}\right] _0^1 dx=0 \end{aligned}$$

Continuing with the remaining integral in (5.3) and expanding the derivative result in

$$\begin{aligned} \left<2\,\Phi ^{2} U_{xxyy},S_k S_l\right>=2\,\Phi ^{2} \int _{0}^1\int _0^1 \sum _{r=0}^2\,\,\sum _{p=0}^2\,\,U(x,y)S_k^{(r)}\,S_l^{(p)}\,\,\tau _r\,\xi _p\, \,dx\, dy. \end{aligned}$$

(5.4)

where

$$\begin{aligned} \tau _2=(\phi _1')^2\,w,\quad \tau _1=2\phi _1'w'+\phi _1''w,\quad \tau _0=w'', \end{aligned}$$

and

$$\begin{aligned} \xi _2=(\phi _2')^2v,\quad \xi _1=2\phi _2'v'+\phi _2''v,\quad \xi _0=v'' \end{aligned}$$

Applying the sinc quadrature in the x-domain and y-domain to the Eq. (5.4) yields Eq. (3.12).

For $\Phi ^{4} \lambda ^2 U(x,y)$, the inner product is

$$\begin{aligned} \left<\Phi ^{4} \lambda ^2 U ,S_k S_l\right>=\Phi ^{4} \int _0^1\int _0^1 \lambda ^2 U(x,y)S_k S_lw(x)v(y)dx dy \end{aligned}$$

(5.5)

Applying the sinc quadrature to (5.5) yields

$$\begin{aligned} \left<\Phi ^{4} \lambda ^2 U ,S_k S_l\right>\approx \Phi ^{4} \lambda ^2 h_x h_y\frac{w(x_k)U(x_k,y_l)v(y_l)}{\phi _1'(x_k)\phi _2'(y_l)} \end{aligned}$$

(5.6)

as given in Eq. (3.13).