An efficient technique for finding the eigenvalues and the eigenelements of fourth-order Sturm-Liouville problems

Abstract

In this paper an efficient method based on Legendre-Galerkin method for computing the eigenvalues of fourth-order Sturm-Liouville problem subject to a kind of fixed boundary conditions is developed. Properties of Legendre polynomials are first presented, these properties are then utilized to reduce the eigenvalues of fourth-order Sturm-Liouville problem to some linear algebraic equations. The method is computationally attractive, and applications are demonstrated through an illustrative example and a comparisons with other methods are made.

1 Introduction

The present work describes Legendre-Galerkin method for finding the eigenvalues and the eigenelements of fourth-order Sturm-Liouville problems of the form

$$\begin{aligned} \left[ p_1(x)\, \frac{d^2u}{dx^2}\right] ''-\left[ s(x)\, \frac{d u}{dx }\right] '=\left[ \lambda w(x)-q(x)\right] u(x), \quad a<x< b, \end{aligned}$$

(1.1)

subject to one of the following pairs of homogenous boundary conditions:

$$\begin{aligned} \begin{array}{ll} (1)&{} u(a)=u'(a)=u(b)=u'(b)=0\quad \\ (2)&{} u(a)=u''(a)=u(b)=u''(b)=0\quad \,\,\,\,\\ (3)&{} u''(a)=u'''(a)=u''(b)=u'''(b)=0\,\\ (4)&{} u(a)=u'(a)=u(b)=u''(b)=0\quad \quad \\ \end{array} \end{aligned}$$

(1.2)

where $\lambda$ is a parameter is independent on x and $p_1(x), q(x), s(x)$ and w(x) are piecewise continuous functions and $p_1(x)$ and w(x) are positive.

The Sturm-Liouville problems arise throughout applied mathematics, classical and quantum mechanics. Most of physical phenomena, can describe by PDEs in several dimensions. This leads to a Sturm-Liouville problem when the equations are separable. The Sturm-Liouville boundary value problems for ODEs play an important role in both the theory and applications of physical, biological and chemical phenomena [10].

In elasticity, this equation is associated to the steady-state Euler-Bernoulli beam equation for the deflection u of a vibrating beam, with the other quantities involved having physical meaning, e.g. $p > 0$ is the flexural rigidity of the beam, $p_1u''$ is the bending moment and $(\lambda w-q)$ is the frequency of vibration.

It is well known that (1.1) has an infinite sequence of eigenvalues $(\lambda _k)_{k\ge 1}$ which are bounded from below by a constant $\lambda _0$, i.e.

$$\begin{aligned} \lambda _0\le \lambda _1\le \lambda _2\le \cdots \le \lambda _k\le \cdots \end{aligned}$$

(1.3)

with $\lim \nolimits _{k\rightarrow \infty }\lambda _k=\infty$ and each eigenvalues has multiplicity at most 2. For more details see [11, 12]. In applications, there are more types of boundary conditions commonly used with (1.1) discussed in [5, 13].

In most cases, it is not possible to obtain the eigenvalues of the problem analytically. However, there are various approximate methods for solving special types of Sturm-Liouville problems as, for example, Adomian decomposition method [4], the homotopy analysis method [2], variational iteration method [3], spectral parameter power series method [14], Extended sampling method [9], finite difference and Numerov’s methods [6], differential quadrature method [1], Chebyshev spectral collocation method [10], Haar wavelet method [13] and polynomial expansion method [5].

In recent years, a lot of attention has been devoted to the study of Legendre methods to investigate various scientific models. Using these methods made it possible to solve differential equations of Lane-Emden type [16], second and fourth order equations [18], Cahn-Hilliard equations with Neumann boundary conditions [19], Fredholm integral [21], Helmholtz equation [22], second kind Volterra integral equations [20], high-order linear Fredholm integro-differential [23] and Abels integral equation [17].

Legendre methods for ordinary differential equations has many salient features due to the properties of the basis functions and the manner in which the problem is discretized. The approximating discrete system depends only on parameters of the differential equation. The approximation rate of Legendre polynomials is $n^{-k}$ where n is the number of Legendre polynomial elements used, and k is a positive constant. The efficiency of the method has been formally proved by many researchers [15, 24, 25].

The paper is organized as follows: in Sect. 2, we present the preliminaries of Legendre polynomials. Section 3 presents the convergence of Legendre polynomials and error estimation for Legendre-Galerkin method. Section 4 is devoted to derivation of the discrete system. Section 5 shows the accuracy of the proposed method using numerical examples and making comparisons with other methods. Section 6 gives a brief conclusion. Note that we have computed the numerical results by Mathematica programming.

2 Preliminaries and fundamentals

Orthogonal polynomials have very useful properties in the solution of mathematical and physical problems. They provide a natural way to solve, expand, and interpret solutions to many types of important differential and integro-differential equations. Legendre polynomials are one of the most common orthogonal polynomial set.

Legendre polynomials $P_n(x)$ satisfy Legendre differential equation

$$\begin{aligned} \frac{d}{dx}\left[ (1-x^2)\frac{d}{dx}P_n(x)\right] +n(n+1)P_n(x)=0, -1\le x \le 1, n\ge 0, \end{aligned}$$

(2.1)

with recurrence relations

$$\begin{aligned} (n+1)P_{n+1}(x)=(2n+1)xP_n(x)-nP_{n-1}(x), \end{aligned}$$

(2.2)

and the orthogonality on $[-1, 1]$

$$\begin{aligned} \int _{-1}^{1}P_m(x)P_n(x)dx= {\left\{ \begin{array}{ll} 1, &{} \text {if}\,\,\,m=n, \\ 0, &{} \text {if}\,\,\,m\ne n. \end{array}\right. } \end{aligned}$$

(2.3)

Theorem 2.1

[15] Let n and m be any two integer numbers such that $n,m\le N$, then

• (i)
  $$\begin{aligned} \int _{-1}^{1}P'_n(x)P_m(x)dx&= {\left\{ \begin{array}{ll} 2, &{}{if}\, \, n=m+i, \\ 0, &{} {if}\, \, n\ne m+i\; or \;m\ge n.\end{array}\right. } \end{aligned}$$
• (ii)
  $$\begin{aligned} \int _{-1}^{1}x P'_n(x)P_m(x)dx&={\left\{ \begin{array}{ll} \dfrac{2n}{2n+1}, &{} if\,\, m=n,\\ 0, &{} {if}\,\, n=m+i\;or\; m>n,\\ 2, &{} {if}\,\, n\ne m+i.\end{array}\right. } \end{aligned}$$
• (iii)
  $$\begin{aligned} \int _{-1}^{1}xP_n(x)P_m(x)dx&= {\left\{ \begin{array}{ll} \dfrac{2 (m - 1)}{(2 m - 1) (2 m - 3)}, &{} {if} \; n= m-1, \\ \dfrac{2 (n - 1)}{(2 n - 1) (2 n - 3)}, &{} {if}\; n=m+1.\, \end{array}\right. } \end{aligned}$$
• (iv)
  $$\begin{aligned} \int _{-1}^{1}P''_n(x)P_m(x)dx&= {\left\{ \begin{array}{ll} n(n+1)-m(m+1), &{} {if} \; n\ne m+i, \\ 0, &{} {if} \; n=m+i\; or \;m\ge n. \end{array}\right. } \end{aligned}$$
• (v)
  $$\begin{aligned} \int _{-1}^{1}x P''_n(x)P_m(x)dx&= {\left\{ \begin{array}{ll} n(n+1)-m(m+1)-2, &{} {if} \; n=m+i, \\ 0, &{} {if} \; n\ne m+i\; or \;m\ge n. \end{array}\right. } \end{aligned}$$
• (vi)
  $$\begin{aligned} \int _{-1}^{1}x^2 P''_n(x)P_m(x)dx&= {\left\{ \begin{array}{ll} \frac{2n(n-1)}{2n+1}, &{} {if} \; m= n, \\ n(n+1)-m(m+1)-4, &{} {if} \; n= m+i+1,\\ 0, &{} {if} \; n\ne m+i+1\; or\; m>n. \end{array}\right. } \end{aligned}$$
• (vii)
  $$\begin{aligned} \int _{-1}^{1}x^2 P_n(x)P_m(x)dx = {\left\{ \begin{array}{ll} \dfrac{4n^2+4n-2}{(2n+3)(2n+1)(2n-1)} , &{} {if} \; n=m, \\ \dfrac{2(n+2)(n+1)}{(2n+5)(2n+3)(2n+1)} , &{} {if} \; n = m-2,\\ \dfrac{2n(n-1)}{(2n+1)(2n-1)(2n-3)} , &{} {if} \; n=m+2. \end{array}\right. } \end{aligned}$$

where $i=1,3,5,\ldots ,2k+1\le N-m$.

Theorem 2.2

Let n and m be any two integer numbers such that $n,m\le N$, then

• (i)
  $$\begin{aligned}&\int _{-1}^{1}x^3P_n(x)P_m(x)dx\\&\quad = {\left\{ \begin{array}{ll} \frac{2n(m-2)(m-1)}{(2m-1)(2m-3)(2m-5)(2n-1)}, &{} {if} \; n= m-3\; or\; m=n-3, \\ \frac{2\left( m(6n^3-19n^2+9n+7)-2n^3+5n^2-n-2\right) }{(2m+1)(2m-1)(2m-3)(2m-5)(2n-1)}, &{} {if} \; n=m-1\; or \;m=n-1. \end{array}\right. } \end{aligned}$$
• (ii)
  $$\begin{aligned}&\int _{-1}^{1}x^4 P_n(x)P_m(x)dx \\&\quad = {\left\{ \begin{array}{ll} \frac{2m(m+1)(n-2)(n-1)}{(2n-3)(2n-1)(2n+3)(2n+1)(2n-1)} , &{} {if} \; n=m+4\, or\, m=n\!+\!4,\\ \frac{\Lambda (n,m)}{{(2m-3)(2m-1)(2m+1)(2n-3)(2n-1)(2n+1)}}, &{}{if} \; n=m\!+\!2\;or\;m=n\!+\!2, \\ \frac{\Upsilon (n,m)}{{(2 n-1)^2 ( 2 n-3) ( 2 n+1) ( 2 n+3) ( 2 m-5) (2 m-3) ( 2 m-1) (2 m+1)}}, &{} {if} \; n = m.\\ \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} \Upsilon (n,m)= & {} 2\left( m^3(4n^2-4n-2)+m^2(4n^3-12n^2+4n+5)\right. \\&\left. +\,m(-4n^3+4n^2+4n-1)+(-2n^3+5n^2-n-2)\right) , \end{aligned}$$

$$\begin{aligned} \Lambda (n,m)= & {} 2 \Big (8 n^5 (2 + m - 5 n^2 + 2 n^3) + 2 m n (27 + m - 29 m^2 + 10 m^3)\\&+\, n^2 (189 - 102 m - 670 m^2 \!+\! 690 m^3 - 164 m^4) \!+\!3 (-9 \!+\! 25 m^2 - 20 m^3 + 4 m^4)\\&-\, 2 n^3 (22 + 41 m - 57 m^2 - 2 m^3 + 8 m^4)\\&\,+\, 4 n^4 (-21 + 18 m + 74 m^2 - 82 m^3 + 20 m^4))\Big ), \end{aligned}$$

and $i=1,3,5,\ldots ,2k+1\le N-m-1.$

Proof

By recalling Eq. (2.2) twice for (i) and three times for (ii) beside the orthogonality relation (2.3), Theorem 2.2 can be proved. $\square$

To solve the fourth-order equation, we need the following theorem.

Theorem 2.3

[26] Let n and m be any two integer numbers such that $n,m\le N$, then

• (i)
  
• (ii)
  

3 Convergence and error estimation

3.1 Convergence of Legendre polynomial

Lemma 3.1

[24, 25] Let $x(t)\in H^k(-1, 1)$ (a Sobolev space) and let $x_n(t)=\sum _{i=0}^{n} a_i P_i(t)$ be the best approximation polynomial of x(t) in the $L^2$-norm, then

$$\begin{aligned} ||x(t)-x_n(t)||_{L^2[-1, 1]}\le c_0 n^{-k}||x(t)||_{H^k(-1, 1)}, \end{aligned}$$

where

$$\begin{aligned} ||x(t)||_{L_2[-1, 1]}=\left( \int _{-1}^{1}x^2(t)dt\right) ^{1/2}, \end{aligned}$$

$$\begin{aligned} ||x(t)||_{H^k(-1, 1)}=\left( \sum _{i=0}^{k}\int _{-1}^{1}|x^{(i)}(t)|^{2}dt\right) ^{1/2}. \end{aligned}$$

and $c_0$ is a positive constant, which depends on the selected norm and is independent of x(t) and n.

By regard to the Lemma 3.1 we conclude that approximation rate of Legendre polynomials is $n^{-k}$

3.2 Error estimation of Legendre-Galerkin method

In this subsection an error estimator for Legendre-Galerkin approximate solution of a Sturm-Liouville equation is obtained. Let us call $e_n(x)=u(x)-u_n(x)$ as the error function of Legendre approximation $u_n(x)$ to u(x), where u(x) is the exact solution of (1.1) with one boundary from (1.2). Hence, $u_n(x)$ satisfies the following problem

$$\begin{aligned} \left( p_1(x) u_n''(x)\right) ''-\left( s(x)u_n'(x)\right) '=\left( \lambda w(x)-q(x)\right) u_n(x)+H_n(x), \,\, x\in (a,b), \end{aligned}$$

(3.1)

with one boundary condition from (1.2)

$$\begin{aligned} u_n(a)=u'_n(a)=u_n(b)=u'_n(b)=0, \end{aligned}$$

(3.2)

where $H_n$ is a perturbation term associated with $u_n(x)$ and can be obtained by substituting $u_n(x)$ into the equation

$$\begin{aligned} H_n(x)=\left( p_1(x) u_n''(x)\right) ''-\left( s(x)u_n'(x)\right) '-\left( \lambda w(x)-q(x)\right) u_n(x). \end{aligned}$$

(3.3)

We proceed to find an approximation $e_{n,N}(x)$ to the $e_n(x)$ in the same way as in Sect. 4 for the solution (1.1) and (1.2).

Subtracting (3.1) and (3.2) from (1.1) and (1.2), respectively, the error function $e_n(x)$ satisfies the equation

$$\begin{aligned} \left( p_1(x) e_n''(x)\right) ''-\left( s(x)e_n'(x)\right) '=\left( \lambda w(x)-q(x)\right) e_n(x)+H_n(x), \end{aligned}$$

(3.4)

with boundary conditions

$$\begin{aligned} \begin{array}{l} (1)\,\, e_n(a)=e_n'(a)=e_n(b)=e_n'(b)=0.\quad \quad \\ (2)\,\, e_n(a)=e_n''(a)=e_n(b)=e_n''(b)=0.\quad \,\,\,\,\,\,\\ (3)\,\, e_n''(a)=e_n'''(a)=e_n''(b)=e_n'''(b)=0.\quad \,\,\,\,\\ (4)\,\, e_n(a)=e_n'(a)=e_n(b)=e_n''(b)=0.\quad \quad \\ \end{array} \end{aligned}$$

(3.5)

By solving this problem in the same way as Sect. 4, we get the approximation $e_{n,N}(x)$. It should be noted that in order to construct Legendre approximation $e_{n,N}(x)$ to $e_n(x)$.

4 Legendre-Galerkin method

4.1 Eigenvalues computation

In this subsection, we explain how Legendre bases are used beside Galerkin method to find the eignvalues of (1.1) with one boundary conditions from (1.2).

First, let us rewrite (1.1) in the following form

$$\begin{aligned} u^{(4)}(x)+\mu _3(x)u'''(x)+\mu _2(x)u''(x)+\mu _1(x)u'(x)+\mu _0(x)u(x)=\lambda W(x)u(x), \end{aligned}$$

(4.1)

where

$$\begin{aligned} \mu _3(x)= & {} 2\frac{p_1'(x)}{p_1(x)},\,\, \mu _2(x)=\frac{p_1''(x)-s(x)}{p_1(x)},\,\, \mu _1(x)=-\frac{s'(x)}{p_1(x)},\,\, \mu _0(x)=\frac{q(x)}{p_1(x)}\\&\text{ and }\,\, \,W(x)=\frac{w(x)}{p_1(x)} \end{aligned}$$

are defined on the interval $a\le x\le b$ and $\lambda$ is a parameter is independent on x.

Second, we must transform the solution domain from [a, b] to $[-1,1]$ by using the linear transformation $x=\frac{b-a}{2}X+\frac{b+a}{2}$. So, the Eq. (1.1) can be written as

$$\begin{aligned} \left( \frac{2}{b-a}\right) ^4u^{(4)}(X)+2\left( \frac{2}{b-a}\right) ^3\mu _3(X)u'''(X)+\left( \frac{2}{b-a}\right) ^2\mu _2(X)u''(X)\nonumber \\ +\left( \frac{2}{b-a}\right) \mu _1(X)u'(X)+\mu _0(X)u(X)=\lambda W(X)u(X), \,\,\, -1\le X \le 1, \end{aligned}$$

(4.2)

subject to one of the following homogenous boundary conditions

$$\begin{aligned} \begin{array}{ll} 1. &{} u(-1)=u'(-1)=u(1)=u'(1)=0.\quad \quad \\ 2. &{} u(-1)=u''(-1)=u(1)=u''(1)=0.\quad \\ 3. &{} u''(-1)=u'''(-1)=u''(1)=u'''(1)=0.\qquad \\ 4. &{} u(-1)=u'(-1)=u(1)=u''(1)=0.\qquad \\ \end{array} \end{aligned}$$

(4.3)

where $X:=(\frac{2}{b-a})x-1.$

Assume the solution of the Eq. (4.2) is approximate by the finite expansion of Legendre basis function with $n+1$ undetermined coefficients $\{c_0, c_1, \ldots , c_n\}$

$$\begin{aligned} u_n(X)=\sum _{j=0}^{n} c_j P_j(X). \end{aligned}$$

(4.4)

We can reduce the Eq. (4.2) by orthogonalizing the residual with respect to the basis functions

$$\begin{aligned}&\left( \frac{2}{b-a}\right) ^4\langle u^{(4)}(X),P_r(X)\rangle +2\left( \frac{2}{b-a}\right) ^3 \langle \mu _3(X)u'''(X),P_r(X)\rangle \nonumber \\&\qquad +\left( \frac{2}{b-a}\right) ^2 \langle \mu _2(X)u''(X),P_r(X)\rangle +\left( \frac{2}{b-a}\right) \langle \mu _1(X)u'(X),P_r(X)\rangle \nonumber \\&\qquad +\,\langle \mu _0(X)u(X),P_r(X)\rangle =\lambda \langle W(X) u(X),P_r(X)\rangle , \end{aligned}$$

(4.5)

where

$$\begin{aligned} \langle \zeta , \eta \rangle =\int _{-1}^{1}\zeta \cdot \eta \, dX. \end{aligned}$$

The method of approximating the integrals in (4.5) begins by integrating by parts to transfer all derivatives from u to $P_r$. The approximation of the last four inner products on the left-hand side of (4.5) has been thoroughly treated in [15]. We will list them for convenience

$$\begin{aligned} \left\langle \mu _2(X)\,u''(X), P_r(X)\right\rangle =B_{T,2} +\int _{-1}^{1}u(X)[\mu _2(X)P_r(X)]''dX, \end{aligned}$$

(4.6)

where

$$\begin{aligned} B_{T,2}={\left\{ \begin{array}{ll} 0, &{}\mathrm{in~ case~ (1),}\\ \left[ \mu _2(X) u'(X) P_r(X)\right] _{-1}^{1}, &{} \mathrm{in ~case~ (2),}\\ \left[ \mu _2(X) u'(X) P_r(X)\right] _{-1}^{1}-\left[ u'(X) \left( \mu _2(X) P_r(X)\right) '\right] _{-1}^{1}, &{} \mathrm{in ~case~ (3),}\\ \mu _2(1) u(1)P_r(1), &{} \mathrm{in~ case~ (4).}\\ \end{array}\right. } \end{aligned}$$

$$\begin{aligned} \left\langle \mu _1(X)\,u'(X), P_r(X)\right\rangle =B_{T,1} -\int _{-1}^{1}u(X)[\mu _1(X)P_r(X)]'dX, \end{aligned}$$

(4.7)

where

$$\begin{aligned} B_{T,1}={\left\{ \begin{array}{ll} \left[ \mu _1(X) u(X) P_r(X)\right] _{-1}^{1}, &{} \mathrm{in ~case ~(3),}\\ 0, &{} \mathrm{in~ case ~(1),~ (2)~ and~ (4).}\\ \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \left\langle S(X)\,u(X), P_r(X)\right\rangle =\int _{-1}^{1}\mu (X)\,u(X)\,P_r(X)\,dX, \end{aligned}$$

(4.8)

To solve the Eqs. (1.1)–(1.2), we need the following lemma

Lemma 4.1

The following relations hold

• (i)
  $$\begin{aligned} \left\langle u^{(4)}(X),P_r(X)\right\rangle =\sum \limits _{k=2}^{3}(-1)^{k+1}\left[ u^{(k)}(X) P_r^{(3-k)}(X)\right] _{-1}^{1} +\int _{-1}^{1}u(X)P_r^{(4)}(X)dX,\nonumber \\ \end{aligned}$$

  (4.9)
• (ii)
  $$\begin{aligned}&\left\langle \mu _3(X)\,u'''(X), P_r(X)\right\rangle =B_{T,3} -\int _{-1}^{1}u(X)[\mu _3(X)P_r(X)]'''dX, \end{aligned}$$

  (4.10)

where

$$\begin{aligned} B_{T,3}={\left\{ \begin{array}{ll} \left[ \mu _3(X) u''(X) P_r(X)\right] _{-1}^{1}, &{} \mathrm{in~ case~ (1),}\\ -\left[ (\mu _3(X)P_r(X))' u'(X) \right] _{-1}^{1}, &{} \mathrm{in~ case ~(2),}\\ -\left[ (\mu _3(X)P_r(X))' u'(X)\right] _{-1}^{1}+\left[ (\mu _3(X)P_r(X))''u(X)\right] _{-1}^{1}, &{} \mathrm{in~ case~ (3),}\\ -\mu _3(-1) u(-1)P_r(-1)-(\mu _3(1)P_r(1))' u'(1), &{} \mathrm{in~ case~ (4).}\\ \end{array}\right. } \end{aligned}$$

Proof

For $u^{(4)}$, the inner product with Legendre basis elements is given by

$$\begin{aligned} \left<u^{(4)},P_r(X)\right>=\int _{-1}^1u^{(4)}P_r(X)dX. \end{aligned}$$

Integrating by parts to remove the fourth derivatives from the dependent variable u leads to the equality

$$\begin{aligned} \left\langle u^{(4)}(X),P_r(X)\right\rangle =B_{T,4}+b_{T,4}+\int _{-1}^{1}u(X)P_r^{(4)}(X)dX, \end{aligned}$$

(4.11)

where the boundary terms are

Case (1)

$$\begin{aligned} B_{T,4}= & {} \left[ \sum \limits _{k=0}^{1}(-1)^{k+1}\,u^{(k)}(X) P_r^{(3-k)}(X)\right] _{-1}^{1}=0,\\ b_{T,4}= & {} \sum \limits _{k=2}^{3}(-1)^{k+1}\left[ u^{(k)}(X) P_r^{(3-k)}(X)\right] _{-1}^{1}. \end{aligned}$$

Case (2)

$$\begin{aligned} B_{T,4}= & {} \left[ \sum \limits _{k=0}^{2}-\,u^{(k)}(X) P_r^{(3-k)}(X)\right] _{-1}^{1}=0,\, k=even,\\ b_{T,4}= & {} \sum \limits _{k=0}^{2}\left[ u^{(k+1)}(X) P_r^{(2-k)}(X)\right] _{-1}^{1},\, k=even. \end{aligned}$$

Case (3)

$$\begin{aligned} B_{T,4}= & {} \left[ \sum \limits _{k=2}^{3}(-1)^{k+1}\,u^{(k)}(X) P_r^{(3-k)}(X)\right] _{-1}^{1}=0,\\ b_{T,4}= & {} \sum \limits _{k=0}^{1}(-1)^{k+1}\left[ u^{(k)}(X) P_r^{(3-k)}(X)\right] _{-1}^{1}. \end{aligned}$$

Case (4)

$$\begin{aligned} B_{T,4}= & {} \left[ u(X)P_r'''(X)\right] _{-1}^{1}-\left[ u'(-1)P_r''(-1)\right] -\left[ u''(1)P_r'(1)\right] =0,\\ b_{T,4}= & {} \left[ u'''(X)P_r(X)\right] _{-1}^{1}+\left[ u''(-1)P_r'(-1)\right] +\left[ u'(1)P_r''(1)\right] . \end{aligned}$$

Then (4.11) may be written as (4.9). In the same way, Lemma 4.1(ii) can be proved. $\square$

Replacing each term of (4.5) with the approximation defined in (4.6)–(4.10), we obtain the following theorem

Theorem 4.2

If the assumed approximate solution of (1.1) with the boundary-value problem case (1) is (4.4), then the discrete Legendre-Galerkin system for the determination of the unknown coefficients $\{c_j\}_{j=0}^n$ is given by

$$\begin{aligned}&\sum \limits _{j=0}^{n} \left[ \left( \frac{2}{b-a}\right) ^4\left[ \sum \limits _{k=2}^{3}(-1)^{k+1}\left[ P_j^{(k)}(X) P_r^{(3-k)} (X)\right] {_{-1}^{1}}+ \int _{-1}^{1} P_j(X)P''''_r(X)\,dX\right] \right. \nonumber \\&\left. \quad +\left( \frac{2}{b-a}\right) ^3\left[ \left[ \mu _3(X) P_j''(X) P_r(X)\right] _{-1}^{1}-\int _{-1}^{1}P_j(X)[\mu _3(X)P_r(X)]'''dX\right] \right. \nonumber \\&\left. \quad +\left( \frac{2}{b-a}\right) ^2\int _{-1}^{1} P_j(X)\left[ \mu _2(X)P_r(X)\right] ''\,dX\right. \nonumber \\&\left. \quad +\frac{2}{b-a}\int _{-1}^{1} P_j(X)\left[ \mu _1(X)P_r(X)\right] 'dX\right. \nonumber \\&\left. \quad +\int _{-1}^{1} P_j(X)\mu _0(X)P_r(X)dX \right] \,c_j=\lambda \sum _{j=0}^{n}\left[ \int _{-1}^{1} W(X)P_j(X)P_r(X)dX\right] c_j. \end{aligned}$$

(4.12)

The system in (4.12) takes the matrix form

$$\begin{aligned} \mathbf {Ac} = \lambda \,\mathbf {Bc}, \end{aligned}$$

(4.13)

where

$$\begin{aligned} \mathbf {A}=\left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} e_{0,\,0}+v_{0,\,0}+w_{0,\,0} &{} e_{1,\,0}+v_{1,\,0}+w_{1,\,0} &{} \ldots &{} e_{n,\,0}+v_{n,\,0}+w_{n,\,0} \\ e_{0,\,1}+v_{0,\,1}+w_{0,\,1} &{} e_{1,\,1}+v_{1,\,1}+w_{1,\,1} &{} \ldots &{} e_{n,\,1}+v_{n,\,1}+w_{n,\,1} \\ e_{0,\,2}+v_{0,\,2}+w_{0,\,2} &{} e_{1,\,2}+v_{1,\,2}+w_{1,\,2} &{} \ldots &{} e_{n,\,2}+v_{n,\,2}+w_{n,\,2} \\ e_{0,\,3}+v_{0,\,3}+w_{0,\,3} &{} e_{1,\,3}+v_{1,\,3}+w_{1,\,3} &{} \ldots &{} e_{n,\,3}+v_{n,\,3}+w_{n,\,3}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ e_{0,\,n}+v_{0,\,n}+w_{0,\,n} &{} e_{1,\,n}+v_{1,\,n}+w_{1,\,n} &{}\ldots &{} e_{n,\,n}+v_{n,\,n}+w_{n,\,n}\\ \end{array} \right) ,\quad \end{aligned}$$

(4.14)

and

$$\begin{aligned} \mathbf {B}= & {} \sum _{j=0}^{n}\int _{-1}^{1} W(X)P_j(X)P_r(X)dX,\\ e_{j,r}= & {} \left( \frac{2}{b-a}\right) ^4\int _{-1}^{1} P_j(X)P''''_r(X)dX-2\left( \frac{2}{b-a}\right) ^3\int _{-1}^{1}P_j(X)[\mu _3(X)P_r(X)]'''dX\\&+\left( \frac{2}{b-a}\right) ^2\int _{-1}^{1} P_j(X)\left[ \mu _2(X)P_r(X)\right] ''dX \!-\!\frac{2}{b-a}\int _{-1}^{1} P_j(X)\left[ \mu _1(X)P_r(X)\right] 'dX\\&+\int _{-1}^{1} P_j(X)\mu _0(X)P_r(X)dX,\\ v_{j,r}= & {} \left( \frac{2}{b-a}\right) ^4\left[ \sum \limits _{k=2}^{3}(-1)^{k+1}P_j^{(k)}(X) P_r^{(3-k)} (X)\right] _{-1}^{1}, \\ w_{j,r}= & {} 2\left( \frac{2}{b-a}\right) ^3\left[ \mu _3(X) P_j''(X) P_r(X)\right] _{-1}^{1}. \end{aligned}$$

$e_{j,r}$ can be evaluated from theorems and lemmas in Sect. 2 and the boundary term and $v_{j,r}$ can be calculated as

$$\begin{aligned} \sum \limits _{k=2}^{3} (-1)^{k}\left[ P_j^{(k)}(X) P_r^{(3-k)}(X) \right] _{-1}^{1}= & {} \frac{1}{16}\left[ (r(r+1))(1-(-1)^{n+r+j-1})\right] \prod \limits _{i=0}^{3}(j-i+2)\\&-\frac{1}{48}\left[ \left( 1+(-1)^{n+r+j}\right) \right] \prod \limits _{i=0}^{5}(j-i+3). \end{aligned}$$

By multiplying (4.13) by $B^{-1}$ yields the equivalent system

$$\begin{aligned} \mathbf {\Phi c} = \lambda \,\mathbf {c}, \end{aligned}$$

(4.15)

where

$$\begin{aligned} \mathbf {\Phi }=\mathbf {B^{-1}A}. \end{aligned}$$

From Eq. (4.15), the values of $\lambda$ can be obtained from the eigenvalues of matrix $\mathbf {\Phi }$. This can be done by using various methods.

In the same manner, to solve (1.1) with other boundary of (1.2), we can rewrite the Theorem 4.2 after applying the remainder three homogeneous boundary value problem.

4.2 Eigenfunction computation

This subsection illustrates how eigenfunctions can be computed. The main point of calculation associate an initial condition to problem (1.1). We compute the eigenfunctions as solutions to the initial value problems with the initial conditions

$$\begin{aligned} \left( u(-1),u'(-1),u''(-1),u'''(-1)\right) =\left\{ \begin{array}{ll} (0,0,1,\beta ), &{} for~ case ~(1) ~and ~(4) , \\ (0,1,0,\beta ), &{} for~ case~ (2) ,\\ (1,\beta ,0,0), &{} for~ case~ (3) . \\ \end{array}\right. \end{aligned}$$

We normalize the eigenfunction using $u'(x)=1$ for case (2), $u(x)=1$ for case (3) and $u''(x)=1$ for case (1) and (4). If we denote ${u_1}_n(x, \lambda )$ and ${u_2}_n(x, \lambda )$ the solutions corresponding to initial conditions (0, 0, 1, 0) and (0, 0, 1, 1) respectively for case (1) and (4), (0, 1, 0, 0) and (0, 1, 0, 1) respectively for case (2) and (1, 0, 0, 0) and (1, 1, 0, 0) respectively for case (3). Then the eigenfunctions u(x) given by

$$\begin{aligned} u_n(x)={u_1}_n(x)+\beta {u_2}_n(x). \end{aligned}$$

By applying the boundary conditions, $\beta$ can be evaluated as

$$\begin{aligned} \beta =\left\{ \begin{array}{ll} -\dfrac{{u_1}_n(1,\lambda )}{{u_2}_n(1,\lambda )}, &{} for ~case ~(1),~ (2)~ and ~(4) , \\ -\dfrac{{u''_1}_n(1,\lambda )}{{u''_2}_n(1,\lambda )}, &{} for~ case ~(3) . \end{array}\right. \end{aligned}$$

So, we can write the eigenfunctions $u_n(x)$ as

$$\begin{aligned} u_n(x)=\left\{ \begin{array}{ll} {u_1}_n(x,\lambda )-\dfrac{{u_1}_n(1,\lambda )}{{u_2}_n(1,\lambda )}{u_2}_n(x,\lambda ), &{} for ~case~ (1),~ (2) ~and~ (4) , \\ {u_1}_n(x,\lambda )-\dfrac{{u''_1}_n(1,\lambda )}{{u''_2}_n(1,\lambda )}{u_2}_n(x,\lambda ), &{} for~ case ~(3) . \end{array}\right. \end{aligned}$$

5 Numerical examples

The six examples included in this section were selected in order to illustrate the performance of Legendre-Galerkin method to find the eigenvalues of the regular Sturm-Liouville problem. We compare our method once with the exact solution and other with the methods introduced in [1–10]. It is shown that Legendre-Galerkin method yields better results. Here, we used of the Mathematica 10 package to calculate the eigenvalues and eigenfunction problem (1.1) with one boundary condition of (1.2). The computational codes were conducted on an Intel(R) Core(TM) i3 CPU with power 2.40 GHz, equipped with 4 GB of RAM.

Example 1

[1–5] Consider the eigenvalue problem

$$\begin{aligned} u^{(4)}(x)=\lambda u(x), \qquad \qquad 0\le x \le 1, \end{aligned}$$

subject to the boundary conditions

$$\begin{aligned} \begin{array}{ll} u(0)&{}= u'(0)=0,\\ u(1)&{}= u''(1)=0. \end{array} \end{aligned}$$

The exact eigenvalues in the latter case can be obtained by solving

$$\begin{aligned} \tanh \root 4 \of {\lambda }-\tan \root 4 \of {\lambda }=0. \end{aligned}$$

CPU time of calculating the eigenfunction and the comparison between Legendre-Galerkin method with other methods is tabulated in Table 1. The first four eigenfunctions have been computed using Legendre-Galerkin method and are displayed in Fig. 1. When the estimate error $e_n(x)$ is calculated for the first four eigenfunctions, we find $e_n(x)=0$.

Table 1 Comparison of eigenvalues and CPU time (s) for Example 1

Fig. 1

The first four eigenfunctions for Example 1

Example 2

[3, 5] Consider the eigenvalue problem

$$\begin{aligned} u^{(4)}(x)=\lambda u(x), \qquad 0\le x \le 1, \end{aligned}$$

subject to the boundary conditions

$$\begin{aligned} \begin{array}{ll} u''(0)&{}= u'''(0)=0,\\ u''(1)&{}= u'''(1)=0. \end{array} \end{aligned}$$

The exact eigenvalues in the latter case can be obtained by solving

$$\begin{aligned} \cos \root 4 \of {\lambda }\cosh \root 4 \of {\lambda }-1=0. \end{aligned}$$

The comparison between the exact value of the eigenvalues and Legendre-Galerkin method with other methods is tabulated in Table 2. CPU time of calculating the eigenfunction listed in Table 2. We are normalizing the eigenfunctions using $u'(0)=1$. Figure 2 produces the first eight eigenfunction. When the estimate error $e_n(x)$ is calculated for the first four eigenfunctions, we find $e_n(x)=0$.

Table 2 Comparison of eigenvalues and CPU time (s) for Example 2

Fig. 2

The first eight eigenfunctions for Example 2

Example 3

[6] Let us consider the fourth order Sturm-Liouville problems of order four

$$\begin{aligned} u^{(4)}(x)+\,u(x)=\lambda u(x),\qquad 0<x <1, \end{aligned}$$

subject to the boundary conditions

$$\begin{aligned} \begin{array}{ll} u(0)&{}=u(1)=0,\\ u''(0)&{}= u''(1)=0. \end{array} \end{aligned}$$

The exact eigenvalues of this problem are given in

$$\begin{aligned} \lambda _k=(k\pi )^4, \quad k=1,2,3,\ldots \end{aligned}$$

Table 3 lists the CPU time in second for the proposed method beside the comparison between Legendre-Galerkin method (LGM) and each of the methods in [6] with the exact value of the eigenvalues. These methods are finite difference method (FDM), modified Numerovs method (MNM) and boundary value method (BVM) of order 10. Figure 3 presents the first six eigenfunctions. The estimate error $e_n(x)=0$ for the first six eigenfunctions.

Table 3 Comparison of eigenvalues for Example 3

Fig. 3

The first six eigenfunctions for Example 3

Example 4

[5, 7] Let us consider the fourth order Sturm-Liouville problems of order four

$$\begin{aligned} \left( (1+ax)^3u''(x)\right) ''-\lambda (1+ax) u(x)=0,\quad 0\le x \le 1, \end{aligned}$$

subject to the boundary conditions

$$\begin{aligned} \begin{array}{ll} u(0)&{}=u(1)=0,\\ u'(0)&{}= u'(1)=0, \end{array} \end{aligned}$$

where a is a parameter. Table 4 shows the CPU time of Legendre-Galerkin for calculating eigenvalues and the comparison of the approximations of first three eigenvalues square root $\sqrt{\lambda }$ between Legendre-Galerkin method (LGM) and each of the methods in [5, 7].

Table 4 Comparison of eigenvalues and CPU time (s) for Example 4

Table 5 Comparison of eigenvalues and CPU time (s) for Example 5

Example 5

[8] Let us consider the fourth order Sturm-Liouville problems which is simplified Cahn-Hilliard equation of order four

$$\begin{aligned} \left( (1.1-x^2)u''(x)\right) ''+20u''(x)=\lambda u(x),\qquad -1\le x \le 1, \end{aligned}$$

subject the Dirichlet boundary conditions

$$\begin{aligned} \begin{array}{ll} u(-1)&{}=u(1)=0,\\ u'(-1)&{}= u'(1)=0. \end{array} \end{aligned}$$

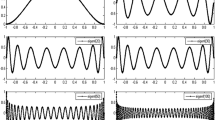
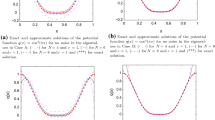
Table 5 presents the comparison of the approximations of eigenvalues between Legendre-Galerkin method (LGM) andexact dynamic stiffness method analogy in [8]. CPU time for Legendre-Galerkin method is listed in Table 5. Figure 4 shows the first six eigenfunctions. Figure 4 displays the estimate error $e_n(x)$ for first three eigenfunctions.

Example 6

[1, 4, 5, 9, 10] Next we consider the following fourth-order eigenvalue problems with variable coefficients

$$\begin{aligned} u^{(4)}(x)-0.02x^2u''(x)-0.04xu'(x)+(0.0001x^4-0.02)u(x)=\lambda u(x),\qquad 0\le x \le 5, \end{aligned}$$

subject the Dirichlet boundary conditions

$$\begin{aligned} \begin{array}{ll} u(0)&{}=u(5)=0,\\ u'(0)&{}= u'(5)=0. \end{array} \end{aligned}$$

The numerical results of first five eigenvalues $\lambda$ obtained by the Adomian decomposition method (ADM) [4], polynomial-based differential quadrature method (PDQM) [1], the polynomial expansion method (PEM) [5], the extended sampling method (ESM) [9] and Chebyshev differentiation matrices method (CDMM) [10] are listed in Table 6 beside Legendre-Galerkin Method (LGM). As compared to the existing results, we can find that the accuracy of proposed method is very satisfactory. The CPU time for the current work is compared with the program 40, page 151 [27] and Chebyshev spectral collocation method [10]. As it is shown in Table 6, the CPU time for the proposed method in this work has less cost than the one introduced in Refs. [10, 27]. Figure 5a shows the first six eigenfunctions. The estimate error $e_n(x)$ for first three eigenfunctions displays in Fig. 5b.

Fig. 4

a The first six eigenfunctions for Example 5. b The estimate error for first three eigenfunctions for Example 5

Table 6 Comparison of eigenvalues and CPU time (s) for Example 6

Fig. 5

a The first six eigenfunctions for Example 6. b The estimate error for first three eigenfunctions for Example 6

6 Conclusion

In this paper, Legendre-Galerkin method has been successfully used for finding the solution of linear fourth-order Sturm-Liouville problems. The results in the previous section indicate that our procedure can be used to obtain accurate numerical solutions of linear Sturm-Liouville problems with very little computational effort. The effectiveness of the method has been confirmed by comparing our eigenvalues with the exact values and/or other numerical methods. It was shown that the method is easy to implement and produces accurate results for eigenfunctions. The estimate error $e_n(x)$ for eigenfunctions is calculated to prove the accuracy of Legender-Galerkin method for finding eigenfunctions.