Eggbeater dynamics on symplectic surfaces of genus 2 and 3

Abstract

The group $Ham(M,\omega )$ of all Hamiltonian diffeomorphisms of a symplectic manifold $(M,\omega )$ plays a central role in symplectic geometry. This group is endowed with the Hofer metric. In this paper we study two aspects of the geometry of $Ham(M,\omega )$, in the case where M is a closed surface of genus 2 or 3. First, we prove that there exist diffeomorphisms in $Ham(M,\omega )$ arbitrarily far from being a k-th power, with respect to the metric, for any $k \ge 2$. This part generalizes previous work by Polterovich and Shelukhin. Second, we show that the free group on two generators embeds into the asymptotic cone of $Ham(M,\omega )$. This part extends previous work by Alvarez-Gavela et al. Both extensions are based on two results from geometric group theory regarding incompressibility of surface embeddings.

Résumé

Le groupe $Ham(M,\omega )$ de tous les difféomorphismes hamiltoniens d’une variété symplectique $(M,\omega )$ joue un rôle central en géométrie symplectique. Ce groupe est muni par la métrique de Hofer. Dans cet article, nous étudions deux aspects de la géométrie de $Ham(M,\omega )$, dans le cas où M est une surface fermée de genre 2 ou 3. Premièrement, nous démontrons qu’il existe des difféomorphismes dans $Ham(M,\omega )$ arbitrairement loin d’être une puissance k, par rapport à la métrique, pour tout $k \ge 2$. Cette partie généralise les travaux précédents de Polterovich et de Shelukhin. Deuxièmement, nous montrons que le groupe libre à deux générateurs admet un plongement dans le cône asymptotique de $Ham(M,\omega )$. Cette partie étend les travaux précédents d’Alvarez-Gavela et al. Les deux extensions sont basées sur deux résultats de la théorie géométrique des groupes concernant l’incompressibilité des plongements de surfaces.

1 Introduction and main results

1.1 Introduction

Recall that a symplectic manifold is a smooth even-dimensional manifold M, equipped with a closed non-degenerate differential 2-form $\omega$. Symplectic manifolds serve as models of phase spaces of classical mechanics. The group of all automorphisms of a symplectic manifold, i.e. maps $M \rightarrow M$ which preserve $\omega$, contains a subgroup of all physically possible mechanical motions. This is the group of Hamiltonian diffeomorphisms, denoted $Ham(M,\omega )$, which plays a central role in symplectic topology and Hamiltonian dynamics.

In 1990 H. Hofer introduced a remarkable bi-invariant Finsler metric on Ham (see [6]). Studying coarse geometry of the metric space Ham is an important problem of modern symplectic topology and is still far from well-understood. This paper takes a step in this direction.

Let us briefly outline our main results. Denote by $Powers_k \subset Ham$ the set of elements admitting a root of degree k. It has been shown in [11] that for surfaces of genus $\ge 4$ the complement $Ham \setminus Powers_k$ contains an arbitrarily large ball, with respect to the metric introduced by Hofer. We extend this result to surfaces of genus 2 and 3.

Further, according to [2], any asymptotic cone (in the sense of Gromov, see [5]) of a group with a bi-invariant metric has a natural group structure. It has been shown in [1] that for a surface M of genus $\ge 4$, any such cone of $Ham(M,\omega )$ contains a free group with 2 generators. We extend this result to surfaces of genus 2 and 3.

The proofs of the above-mentioned results on surfaces of genus $\ge 4$ involve Floer homology of non-contractible closed orbits on the surface and are proved by considering special elements of Ham, the so-called eggbeater maps (see [4, 11]), which originate in chaotic dynamics. An algebraic analysis of non-contractible closed orbits of these maps plays an important role in the proof. This is exactly the place where we had to modify the original arguments, in order to extend the results to the cases of genera 2 and 3. Our main innovations are two algebraic results about homomorphisms from a free group into a surface group (see Lemma 1.3 and Claim 4.1 below).

1.2 Preliminaries

Recall that Hofer’s metric on $Ham(M,\omega )$ is defined as

$$\begin{aligned} d_H(f,g) = \inf _H \int _0^1 \left( \max _M H_t - \min _M H_t \right) dt , \end{aligned}$$

for $f,g \in Ham(M,\omega )$, where the infimum is taken over all smooth $H: S^1 \times M \rightarrow {\mathbb {R}}$ that generate $f^{-1}g$ and where $H_t = H(t,\cdot )$. This is a bi-invariant metric on Ham(M) and the fact that it is a genuine metric, as opposed to a pseudo-metric, is non-trivial (see [6, 7]). Hofer’s norm of a diffeomorphism is its Hofer distance to the identity and is denoted

$$\begin{aligned} ||\cdot ||_H = d_H(id,\cdot ) . \end{aligned}$$

The focus of this paper is the metric space $(Ham(M), d_H)$. The question whether for every symplectic manifold Ham(M) has infinite diameter with respect to Hofer’s metric is an important open problem in this field; it is conjectured (see discussion in 14.2 of [9]) that the answer to this question is positive for every closed symplectic manifold M. The conjecture has been partially confirmed (see [9, 10, 13]).

Rather than asking about the diameter of the group Ham(M), one can ask about the supremum of distances $d_H(f,X)$ for some subset of interest $X \subset Ham(M)$. A natural set X to ask this question for is $Aut(M,\omega )$, the set of autonomous (i.e. "time-independent") Hamiltonian diffeomorphisms, and another interesting family of sets are the sets $Powers_k = \{\psi ^k | \psi \in Ham(M,\omega )\}$ of Hamiltonian diffeomorphisms which admit $k^{th}$ roots, for $k \ge 2$ an integer. The quantities queried are the following:

$$\begin{aligned} aut(M,\omega ) = \sup _{\phi \in Ham(M, \omega )} d_H(\phi , Aut(M, \omega )) ,\\ powers_k(M,\omega ) = \sup _{\phi \in Ham(M, \omega )} d_H(\phi , Powers_k(M,\omega )) . \end{aligned}$$

Note that for a symplectic manifold M, showing that $aut(M) = \infty$ or that for any $k \ge 2$, $powers_k(M) = \infty$ would answer the Hamiltonian diameter question for M.

L. Polterovich and E. Shelukhin conjectured in [11] that $aut(M) = \infty$ for all closed symplectic manifolds and made a first step in that direction: they show that symplectic surfaces M of genus $\ge 4$ have $powers_k(M) = \infty$ for all $k \ge 2$. One of the results in this paper states this is also true for symplectic surfaces of genera 2, 3 (see Theorem 1.1 below).

Our second result concerns the coarse structure of the metric space $(Ham(M), d_H)$. To state it we need the notions of the asymptotic cone of a metric space, which is an important notion in coarse geometry, and of ultrafilters and ultralimits (see [5]). A filter on a partially ordered set $(P,\le )$ is a non-empty proper subset $F \subset P$ that is upward closed and downward directed, i.e. if $x \in F, y \in P, x \le y$ then $y \in F$ and also $\forall x,y \in F \ \exists z \in F$ such that $z \le x,y$. A non-principal ultrafilter on $(P,\le )$ is a filter F on $(P,\le )$ such that there is no filter $F^\prime$ on P with $F \subset F^\prime \subset P$ and such that F is not of the form $\{x \in P | y \le x\}$ for any $y \in P$. Given a metric space (X, d), an ultrafilter ${\mathcal {U}}$ on the power set of the natural numbers $2^{\mathbb {N}}$ (equipped with the inclusion order) and a sequence of points $(x_n)$ in X, a point $x \in X$ is the ${\mathcal {U}}$-ultralimit of $(x_n)$, denoted $\lim _{\mathcal {U}} x_n$, if for any $\epsilon > 0$, $\{n | d(x_n,x) \le \epsilon \} \in {\mathcal {U}}$. The ultralimit does not necessarily exist, but can be shown to exist if $(x_n)$ is bounded.

Let (X, d) be a metric space, fix ${\mathcal {U}}$ a non-principal ultrafilter on $2^{\mathbb {N}}$, and fix some basepoint $x_0 \in X$. The asymptotic cone of (X, d) is a metric space $Cone_{\mathcal {U}}(X,d)$ whose underlying set is

$$\begin{aligned} \left\{ \left( x_k \right) _{k \in {\mathbb {N}}} \in X^{\mathbb {N}}\big | \exists C > 0 \ s.t.\ \forall k: \frac{d(x_k,x_0)}{k} < C \right\} \bigg / \thicksim , \end{aligned}$$

where $(x_k) \sim (y_k)$ if $\lim _{\mathcal {U}} \frac{d(x_k,y_k)}{k} = 0$, and whose metric is

$$\begin{aligned} d_{\mathcal {U}} ([(x_k)], [(y_k)]) = \lim _{\mathcal {U}} \frac{d(x_k,y_k)}{k} . \end{aligned}$$

Assume additionally that X is a group and that d is a bi-invariant metric. Then $Cone_{\mathcal {U}}(X,d)$ is also a group, with multiplication

$$\begin{aligned}{}[(x_k)] \cdot [(y_k)] = [(x_k \cdot y_k)] . \end{aligned}$$

Since d is bi-invariant, this multiplication is well defined and $d_{\mathcal {U}}$ is also bi-invariant.

Elements of the asymptotic cone represent directions (or rather, velocities) in which one can go to infinity in the base space X. For example, bounded metric spaces all have asymptotic cones which are single points, and on the other hand, the asymptotic cone of the hyperbolic plane is a tree with uncountably many branches at each point. The asymptotic cone is an invariant of the coarse structure, or the large-scale properties of a metric space, in the sense that quasi-isometric spaces have the same asymptotic cones (see [12] for more on coarse structure, asymptotic cones, and quasi-isometry).

The focus of this paper is the geometry of Ham(M) for $(M,\omega )$ a symplectic manifold, therefore we consider $Cone_{\mathcal {U}}(Ham(M), d_H)$ for a non-principal ultrafilter ${\mathcal {U}}$ on $2^{\mathbb {N}}$. In [1], D. Alvarez-Gavela et al. show that given a symplectic surface M of genus $\ge 4$, there exists a monomorphism $F_2 \hookrightarrow Cone_{\mathcal {U}}(Ham(M))$, where $F_2$ is the free group on two generators, and therefore $Cone_{\mathcal {U}}(Ham(M))$ has a subgroup isomorphic to $F_2$. The second result in this paper states this is also true for symplectic surfaces of genera 2,3 (see Theorem 1.2 below).

We turn now to our main results.

1.3 Results

The following results are generalizations of previous theorems appearing in [1, 11]: specifically, Theorem 1.1 is a generalization of Theorem 1.3 in [11] and Theorem 1.2 is a generalization of Theorem 1.1 in [1]. The original theorems are the same as stated here, except for their assumptions on the surface $\Sigma$: while the original theorems hold for all closed symplectic surfaces $\Sigma$ of genus $\ge 4$, the theorems presented here hold for closed symplectic surfaces of genera 2 and 3.

Theorem 1.1

Let $\Sigma$ be a closed oriented surface of genus 2 or 3, equipped with an area form $\sigma$, and $k \ge 2$ an integer. Then $powers_k(\Sigma , \sigma ) = \infty$.

Theorem 1.2

Let $\Sigma$ be a closed oriented surface of genus 2 or 3, equipped with an area form $\sigma$. Then for any non-principal ultrafilter ${\mathcal {U}}$ on $2^{\mathbb {N}}$, there exists a monomorphism $F_2 \hookrightarrow Cone_{\mathcal {U}}(Ham(\Sigma ), d_H)$.

We remark that since $aut(M) \ge powers_k(M)$, Theorem 1.1 implies that $aut(\Sigma , \sigma ) = \infty$ for any closed oriented surface $\Sigma$ of genus 2 or 3 with an area form $\sigma$. We remark further that the above results survive stabilization by a closed aspherical symplectic manifold. That is, if $(M,\omega )$ is a symplectic manifold with $\pi _2(M) = 0$ and $\Sigma$ is as above, then the results also hold for the symplectic manifold $(\Sigma \times M, \sigma \oplus \omega )$. This is shown in the same way as in [1, 11].

In the proofs of our results we closely follow [1, 11]. Specifically, we use the same construction called eggbeater maps (see [4, 11]). We will outline the proofs of the original theorems and give an in-depth explanation of the changed parts in Sect. 3. An alternative proof of the theorems in genus 3 is presented in Sect. 4.

1.4 Outline of the proofs for genera 2,3

In this subsection we present a short outline of the proofs of the theorems. The full details of the proofs are given in Sect. 3.

Fig. 1

The manifold C used in the proof

Fig. 2

The profile of the map $f: C_* \rightarrow C_*$

Fig. 3

The neighborhood of an intersection of $C_V$ and $C_H$, with the profile of $f_V \circ f_H$ pictured. The map $f_V \circ f_H$ is a shear along $C_H$ (1) and then a shear along $C_V$ (2)

Denote by $C = C_V \bigcup C_H$ the union of two identical annuli (see Fig. 1) and by $C_*$ a single such annulus. Let $f: C_* \rightarrow C_*$ be a piecewise-linear shear map along the axis of $C_*$, whose profile consists of two straight lines (see Fig. 2). Applying the map f on $C_V$ and $C_H$, one gets two shear maps $f_V,f_H: C \rightarrow C$ with support in $C_V,C_H$ respectively. Composing the maps $f_V,f_H$ and their inverses several times in some specific order yields a map $C \rightarrow C$ called an egg-beater map. Figure 3 depicts the profile of such an egg-beater map $f_V \circ f_H$ in the neighborhood of one of the intersections of $C_V$ and $C_H$.

The proofs of both results, Theorem 1.1 and Theorem 1.2, are based on counting the fixed points of the egg-beater map in C whose orbits belong to some suitably selected free homotopy classes $\alpha _k \in \pi _0({\mathscr {L}}C)$, where ${\mathscr {L}}X$ is the free loop space of a space X, and studying the Floer homology of these orbits. Using this tool, it can be shown that if there are not too many such fixed points and some condition on the actions of their orbits holds, then the theorems themselves hold. This is all done in [1, 11].

However, in order to get results on a closed oriented surface $\Sigma _g$ of genus g, this construction must be embedded in $\Sigma _g$, using an embedding denoted $i: C \hookrightarrow \Sigma _g$, and a similar analysis done there. In this step, one might encounter a new problem: consider $\tau _i: \pi _0({\mathscr {L}}C) \rightarrow \pi _0({\mathscr {L}}\Sigma _g)$, the mapping induced by i. The mapping $\tau _i$ might not be injective. In this case, the previous analysis done on C will no longer hold and one must then re-count fixed points in $\Sigma _g$, since the number of fixed points of the egg-beater map on $\Sigma _g$ in class $\alpha \in \pi _0({\mathscr {L}}\Sigma _g)$ is the number of fixed points of the egg-beater map on C in all the classes $\tau _i^{-1}(\alpha )$, which might be too much for these methods to work.

Originally, in genus $g \ge 4$, this problem did not arise, since if $g \ge 4$ one can find an embedding i such that $\tau _i$ is injective. In fact, one can also find an embedding $i_3$ into $\Sigma _3$ with $\tau _{i_3}$ injective; this approach is shown in Sect. 4. It is likely that there also exists an embedding $i_2$ into $\Sigma _2$ with an injective $\tau _{i_2}$. However, this isn’t proven in this paper.

The results for genera 2 and 3 are proven in Sect. 3 by placing bounds on the non-injectivity of $\tau _i$, using a wisely chosen i and an algebraic lemma. More precisely, note that injectivity of $\tau _i$ can be translated to a claim on images of conjugacy classes of $\pi _1(C)$ under the homomorphism $i_*: \pi _1(C) \rightarrow \pi _1(\Sigma _2)$ induced by i. One may choose i such that the induced homomorphism $i_*: F_3 = \langle a,b,c \rangle \rightarrow \langle g_1,g_2,g_3,g_4 | [g_1,g_2][g_3,g_4] \rangle$ is the following:

$$\begin{aligned}&a \mapsto g_1 g_3 ,\\&b \mapsto g_2 g_1^{-1} g_2^{-1} g_3 ,\\&c \mapsto g_3 . \end{aligned}$$

The main novel ingredient of the results of this paper is the following lemma:

Lemma 1.3

Let $p \in {\mathbb {Z}}_{\ge 1}$. For all $1 \le j \le p$, let $k_j,l_j \in {\mathbb {Z}}, u_j,v_j \in \{0,1\}, 0 \ne m_j,n_j \in {\mathbb {Z}}$. Consider the homomorphism $i_*: F_3 \rightarrow \pi _1(\Sigma _2)$ given above. Let $\delta = \Pi _j a^{k_j}c^{-u_j}b^{l_j}c^{v_j} \in F_3$ and $\beta = \Pi _j a^{m_j}b^{n_j} \in F_3$.

If $i_* \delta , i_* \beta$ are conjugates (in $\pi _1(\Sigma _2)$), then so are $\delta , \beta$ (in $F_3$).

This lemma gives bounds on the non-injectivity of $\tau _i$: different conjugacy classes having a specific form cannot have the same image under $\tau _i$. One may show that all orbits of the egg-beater map have free homotopy classes of this specific form (see Claim 3.13). This allows us to count fixed points of the egg-beater map in $\Sigma _g$ whose orbits are in specific free homotopy classes $\alpha _k$ by counting the corresponding fixed points in C whose orbits are in $\tau _i^{-1}(\alpha _k)$. This calculation was carried out in [1, 11] and shows that there are not too many such fixed points and that the condition on their actions mentioned above holds. Therefore, using the Floer homology tool, one can prove Theorem 1.1 and Theorem 1.2.

A different approach is shown in Sect. 4. Instead of bounding the non-injectivity of $\tau _i$, a different embedding $i_3$ into a surface of genus 3 is defined. The embedding $i_3$ has a restriction $i_3 \restriction _C$ that can be shown to induce an injective $\tau _{i_3 \restriction _C}$ (see Claim 4.1). With this injectivity in hand, the above discussion yields the desired result on the number of fixed points of the egg-beater map.

Section 2 contains the proof of Lemma 1.3 and a related result. The proofs of the theorems for genera 2 and 3, using the lemma, can be found in Sect. 3. Proofs of the theorems for genus 3, using injectivity of the induced map $\tau _{i_3}$ of the suitably-defined embedding $i_3$, are found in Sect. 4.

2 Proof of the lemma

Let us recall the notation in chapter IV of [8]. Let G, H be finitely presentable groups, let $A< G, B < H$ be isomorphic subgroups and let $\psi : A \xrightarrow {\sim } B$ be an isomorphism. The free product of G, H with respect to $\psi$ (or free product of G, H with amalgamation), denoted $\langle G * H, A = B, \psi \rangle$, is defined as follows. If $G = \langle S_1 | R_1 \rangle , H = \langle S_2 | R_2 \rangle$ are finite presentations with $S_1 \cap S_2 = \emptyset$, then the free product with amalgamation is defined to be

$$\begin{aligned} \langle G * H, A = B, \psi \rangle = \langle S_1 \cup S_2 | R_1, R_2, \{a \psi (a)^{-1} | a \in A\} \rangle . \end{aligned}$$

The groups G and H are called the factors of $\langle G * H, A = B, \psi \rangle$.

Free products with amalgamation occur naturally in topology: let X be a topological space with open cover $\{Y,Z\}$ such that $Y \cap Z$ is connected and denote $G = \pi _1(Y), H = \pi _1(Z)$. Consider $A = \pi _1(Y \cap Z) < G$ and $B = \pi _1(Y \cap Z) < H$. Denote also by $\psi : A \xrightarrow {\sim } B$ the natural isomorphism. Then by the van Kampen theorem,

$$\begin{aligned} \pi _1(X) = \langle G * H, A = B, \psi \rangle . \end{aligned}$$

Free products with amalgamation have a certain uniqueness property of conjugacy classes, which will be stated soon. First, we must recall the definition of cyclically reduced elements.

Definition 2.1

A sequence $c_1,...,c_n$ (with $n \ge 0$) of elements of $\langle G*H, A=B, \phi \rangle$ is called reduced if:

• 1. Each $c_i$ is in one of the factors G or H.

• 2. Successive $c_i,c_{i+1}$ come from different factors.

• 3. If $n > 1$, no $c_i$ is in A or B.

• 4. If $n = 1$, $c_1 \ne 1$.

A sequence $c_1,...,c_n$ of elements of $\langle G * H, A = B, \phi \rangle$ is called cyclically reduced if all its cyclic permutations (i.e. $c_2,...,c_n,c_1$, etc.) are reduced.

An element $u \in \langle G * H, A = B, \phi \rangle$ is called cyclically reduced if there exists a cyclically reduced sequence $c_1,...,c_n$ such that $u = c_1 \cdot ... \cdot c_n$. In this case the sequence $(c_i)_{i=1}^n$ is said to represent u.

We remark that every element of $\langle G * H, A = B, \phi \rangle$ is conjugate to a cyclically reduced element, which is not necessarily unique. Recall the following theorem (Theorem 2.8 in chapter IV of [8]):

Theorem (Conjugacy Theorem for Free Products with Amalgamation)

Let $P = \langle G * H, A = B, \phi \rangle$ be a free product with amalgamation. Let $u \in P$ be a cyclically reduced element and let $c_1, ..., c_n$ be any cyclically reduced sequence with $u = c_1 \cdot ... \cdot c_n$, where $n \ge 2$. Then every cyclically reduced conjugate of u can be obtained by cyclically permuting $c_1 \cdot \cdot \cdot c_n$ and then conjugating by an element of the amalgamated part A. That is, if $v \in P$ is cyclically reduced and conjugate to u, then $\exists 0 \le k < n$ and $\exists a \in A$ such that $v = a \cdot c_k \cdot ... \cdot c_n \cdot c_1 \cdot ... \cdot c_{k-1} \cdot a^{-1}$.

Denote the conjugacy relation in a group by $\sim$. For any group G denote the conjugacy class of an element $x \in G$ by $[x]_G$.

The Conjugacy Theorem implies one can define a length on elements of $P = \langle G*H , A=B, \phi \rangle$ by

$$\begin{aligned}&len: P \rightarrow {\mathbb {Z}}_{\ge 0} ,\\&\quad u \mapsto n , \end{aligned}$$

where n is the length of a cyclically reduced sequence $c_1,...,c_n$ such that $u \sim \Pi _j c_j$. This is well defined by the Conjugacy Theorem and is obviously conjugation-invariant. Note that $len(u) = 0 \iff u = 1$ and $len(u) = 1$ if and only if u is conjugate to an element of $G \cup H \subset P$.

Let us denote the following groups:

$$\begin{aligned}&H_1 = \langle g_1, g_2 \rangle \simeq F_2 , \ H_2 = \langle g_3, g_4 \rangle \simeq F_2 ,\\&\quad A = \langle [g_1,g_2] \rangle< H_1 , \ B = \langle [g_3,g_4] \rangle < H_2 , \end{aligned}$$

and denote by $\phi : A \rightarrow B$ the isomorphism $[g_1,g_2] \mapsto [g_3,g_4]^{-1}$. Let $F_3 = \langle a,b,c \rangle$ be the free group with three generators and let $\pi _1(\Sigma _2) = \langle g_1,g_2,g_3,g_4 | [g_1,g_2][g_3,g_4] \rangle = \langle H_1 * H_2, A = B, \phi \rangle$ be the first homotopy group of a closed oriented surface of genus 2.

Consider the homomorphism $\varphi : F_3 \rightarrow \pi _1(\Sigma _2)$ defined by

$$\begin{aligned}&a \mapsto g_1 ,\\&b \mapsto g_2 g_1 g_2^{-1} ,\\&c \mapsto g_3 . \end{aligned}$$

The next claim gives a restriction on non-injectivity of conjugacy classes by $\varphi$.

Claim 2.2

Let $r,s \in F_3$ and assume that $\varphi (r) \sim \varphi (s)$ in $\pi _1(\Sigma _2)$ and $r \not \sim s$ in $F_3$. Then exactly one of the following holds:

• $\exists 0 \ne j \in {\mathbb {Z}}$ such that $\varphi (r),\varphi (s)$ are conjugate to $g_1^j$ (in $\pi _1(\Sigma _2)$).

• $\exists 0 \ne j \in {\mathbb {Z}}$ such that $\varphi (r),\varphi (s)$ are conjugate to $g_3^j$ (in $\pi _1(\Sigma _2)$).

In other words, the only conjugacy classes in $F_3$ merged by the homomorphism $\varphi$ are the classes $[c^j]_{F_3}$ which merge with $[(ab^{-1}c)^j]_{F_3}$ and $[a^j]_{F_3}$ which merge with $[b^j]_{F_3}$ ($0 \ne j \in {\mathbb {Z}}$). These correspond to the following conjugacy classes in $\pi _1(\Sigma _2)$: $[g_3^j]_{\pi _1(\Sigma _2)} = [g_4 g_3^j g_4^{-1}]_{\pi _1(\Sigma _2)}$ and $[g_1^j]_{\pi _1(\Sigma _2)} = [g_2 g_1^j g_2^{-1}]_{\pi _1(\Sigma _2)}$.

Proof

Note that $\varphi (a)$ and $\varphi (b)$ are both elements in the same factor $H_1$ and $\varphi (c) \in H_2$. Partition r and s into sequences according to the partition $\{a,b\} \cup \{c\}$, i.e. concatenate consecutive symbols from $\langle a,b \rangle$, then perform the following steps in order on each sequence, until no steps can be performed:

• If the sequence has length $>1$ and has elements of the form $(ab^{-1})^j$ (for some $j \in {\mathbb {Z}}$), concatenate these elements to the previous and next elements in the sequence; do this for all occurrences of $(ab^{-1})^j$. I.e, if the sequence is $g'_1, h'_1, ab^{-1}, h'_2, (ab^{-1})^{-2}, h'_3$ (with all $g'_i \in \langle a,b \rangle , h'_i \in \langle c \rangle$), then the resulting sequence after this step will be $g'_1, h'_1 ab^{-1} h'_2 (ab^{-1})^{-2} h'_3$.

• If the sequence has length $>1$ and the first and last elements of the sequence are from the same factor (in the partition $\{a,b\},\{c\}$), concatenate them cyclically: i.e, if the sequence is ab, c, b, the resulting sequence after this step will be bab, c.

Doing this results in sequences $(r_i)_{i=1}^n,(s_i)_{i=1}^m$ such that $r \sim \Pi _i r_i, s \sim \Pi _i s_i$ (in $F_3$) and the sequences $(\varphi (r_i)), (\varphi (s_i))$ are cyclically reduced in $\pi _1(\Sigma _2)$, since the only way to generate an element of A or B from images of a, b, c is $\varphi (ab^{-1})^j = [g_1,g_2]^j \in A$; this can be seen from the definition of $\varphi$.

For example, if r were the element $abcba^{-1}cac^{-1}b \in F_3$, we first partition according to $\{a,b\},\{c\}$ to get a sequence $ab, c, ba^{-1}, c, a, c^{-1}, b$, then concatenate powers of $ab^{-1}$ to get $ab, cba^{-1}c, a, c^{-1}, b$, and finally concatenate the first and last elements to get the sequence $(r_i)_{i=1}^4 = bab, cba^{-1}c, a, c^{-1}$. Note that the resulting sequence is not uniquely defined, but any sequence which is the result of these steps will do for our purposes.

Now $(\varphi (r_i))$ and $(\varphi (s_i))$ are cyclically reduced sequences of $\pi _1(\Sigma _2)$ and $\Pi _{i=1}^m \varphi (s_i) \sim \varphi (s) \sim \varphi (r) \sim \Pi _{i=1}^n \varphi (r_i)$. Assume $n \ge 2$, we will reach a contradiction. By the Conjugacy Theorem for Free Products with Amalgamation, $\exists \alpha \in A, 0 \le k < n$ such that

$$\begin{aligned} \Pi _i \varphi (s_i) = \alpha \cdot \varphi (r_k) \varphi (r_{k+1}) ... \varphi (r_n) \varphi (r_1) ... \varphi (r_{k-2}) \varphi (r_{k-1}) \cdot \alpha ^{-1} . \end{aligned}$$

(1)

Since $A \subset {{\,\mathrm{Im}\,}}\varphi$, $\alpha = \varphi (\sigma )$ for some $\sigma \in F_3$. Therefore, pulling back Eq. 1 through $\varphi$, we get the following equation in $F_3$:

$$\begin{aligned} \Pi _i s_i = \sigma \cdot r_k r_{k+1} ... r_{k-2} r_{k-1} \sigma ^{-1} . \end{aligned}$$

Note that this can be done since $\varphi$ is a monomorphism.

Now, it can be seen that $s \sim \Pi _i s_i = \sigma r_k r_{k+1} ... r_{k-2} r_{k-1} \sigma ^{-1} \sim r$ in $F_3$, contradicting our assumption. Therefore, $n \le 1$. By symmetry of the above argument with respect to r and s, we see that $m \le 1$ as well. If $m = 0$ or $n = 0$, we get that either $r=1$ or $s=1$, which is a contradiction to the assumptions, so $m = n = 1$.

Since $n = m = 1$, our sequences from above are $(r_i) = (r), (s_i) = (s)$, so by construction $\varphi (r), \varphi (s)$ are in one of the factors $H_1,H_2$. We shall consider the case $\varphi (r),\varphi (s) \in H_1$ and conclude that $\exists j \in {\mathbb {Z}}: \varphi (r),\varphi (s) \sim g_1^j$ in $\pi _1(\Sigma _2)$. The other case, where $\varphi (r),\varphi (s) \in H_2$ and we conclude that $\exists j \in {\mathbb {Z}}: \varphi (r),\varphi (s) \sim g_3^j$ in $\pi _1(\Sigma _2)$), is analogous.

Since $\varphi (r),\varphi (s) \in H_1$, note that $r,s \in \langle a,b \rangle$. Recall, it was assumed that $r \not \sim s$ and $\varphi (r) \sim \varphi (s)$, and we want to show that $\exists j \in {\mathbb {Z}}: \varphi (r), \varphi (s) \sim g_1^j$. Denote $G = \langle a,b \rangle$ and $\psi = \varphi \restriction _G : G \rightarrow H_1$. Note that the conjugacy classes of G are:

• 1. $[1]_G$,

• 2. $[\Pi _i a^{k_i}b^{l_i}]_G$ for some $0 \ne k_i,l_i \in {\mathbb {Z}}$,

• 3. $[a^k]_G$ for some $0 \ne k \in {\mathbb {Z}}$,

• 4. $[b^l]_G$ for some $0 \ne l \in {\mathbb {Z}}$,

where some of the conjugacy classes listed in case 2 above are not distinct (for example $[aba^2b^2]_G = [a^2b^2ab]_G$), but this will not matter to our argument. Define ${\tilde{\psi }}$, a function from the set of conjugacy classes of G to the set of conjugacy classes of $H_1$, by

$$\begin{aligned} {\tilde{\psi }}([x]_G) = [\psi (x)]_{H_1} . \end{aligned}$$

Our assumptions can be rewritten as $[r]_G \ne [s]_G, {\tilde{\psi }}([r]_G) = {\tilde{\psi }}([s]_G)$ and we want to show ${\tilde{\psi }}([r]_G) = [g_1^j]_{H_1}$ for some $0 \ne j \in {\mathbb {Z}}$. Calculate ${\tilde{\psi }}$ for all the conjugacy classes of G as listed above:

• 1. ${\tilde{\psi }}([1]_G) = [1]_{H_1}$,

• 2. ${\tilde{\psi }}([\Pi _i a^{k_i}b^{l_i}]_G) = [\Pi _i g_1^{k_i} g_2 g_1^{l_i} g_2^{-1}]_{H_1}$ ($\forall i: 0 \ne k_i,l_i \in {\mathbb {Z}}$),

• 3. ${\tilde{\psi }}([a^k]_G) = [g_1^k]_{H_1}$ ($0 \ne k \in {\mathbb {Z}}$),

• 4. ${\tilde{\psi }}([b^l]_G) = [g_2 g_1^l g_2^{-1}]_{H_1} = [g_1^l]_{H_1}$ ($0 \ne l \in {\mathbb {Z}}$).

Therefore:

• 1. If ${\tilde{\psi }}([r]_G) = {\tilde{\psi }}([s]_G) = [1]_{H_1}$ then $\psi (r) = \psi (s) = 1$ and then $r = s = 1$ (since $\psi$ is a monomorphism), in contradiction.

• 2. If ${\tilde{\psi }}([r]_G) = {\tilde{\psi }}([s]_G) = [\Pi _i g_1^{k_i} g_2 g_1^{l_i} g_2^{-1}]_{H_1}$, then $[r]_G = [s]_G = [\Pi _i a^{k_i}b^{l_i}]_G$, in contradiction.

The only cases which are left are ${\tilde{\psi }}([r]_G) = {\tilde{\psi }}([s]_G) = [g_1^j]$ for some $0 \ne j \in {\mathbb {Z}}$. $\square$

Remark

In exactly the same way, one can prove the following:

Let $n \ge 2$ and define

$$\begin{aligned} \varphi : F_{2n-1}= & {} \langle a_1,...,a_{2n-1} \rangle \rightarrow \pi _1(\Sigma _n) = \langle g_1,...,g_{2n} | [g_1,g_2][g_3,g_4]...[g_{2n-1},g_{2n}] \rangle ,\\&a_{2i-1} \mapsto g_{2i-1} \ (\forall 1 \le i \le n) ,\\&a_{2i} \mapsto g_{2i} g_{2i-1} g_{2i}^{-1} \ (\forall 1 \le i < n). \end{aligned}$$

Let $r,s \in F_{2n-1}$ and assume that $\varphi (r) \sim \varphi (s)$ in $\pi _1(\Sigma _n)$ and $r \not \sim s$ in $F_{2n-1}$. Then $\exists 1 \le i \le n, 0 \ne j \in {\mathbb {Z}}$ such that $\varphi (r),\varphi (s) \sim g_{2i-1}^j$ in $\pi _1(\Sigma _n)$.

The lemma is a corollary of Claim 2.2.

Proof of Lemma 1.3

Define

$$\begin{aligned}&A : F_3 \rightarrow F_3 ,\\&\quad a \mapsto ac ,\\&\quad b \mapsto b^{-1}c ,\\&\quad c \mapsto c . \end{aligned}$$

This is an automorphism of $F_3$. Note that $i_* = \varphi \circ A$ (with $\varphi$ as defined above). We want to use Claim 2.2 with $r = A(\beta ), s = A(\delta )$:

$$\begin{aligned}&A(\beta ) = (ac)^{m_1} (b^{-1}c)^{n_1} ... (ac)^{m_p} (b^{-1}c)^{n_p} ,\\&\quad A(\delta ) = (ac)^{k_1} c^{-u_1} (b^{-1}c)^{l_1} c^{v_1} ... (ac)^{k_p} c^{-u_p} (b^{-1}c)^{l_p} c^{v_p} . \end{aligned}$$

Assume by contradiction that $\delta \not \sim \beta$ in $F_3$. Then $A(\beta ) \not \sim A(\delta )$ in $F_3$, since A is an automorphism of $F_3$, and then by Claim 2.2, $\exists 0 \ne j \in {\mathbb {Z}}$ such that one of the following holds:

• $[A(\beta )]_{F_3} = [c^j]_{F_3}$,

• $[A(\beta )]_{F_3} = [(ab^{-1}c)^j]_{F_3}$,

• $[A(\beta )]_{F_3} = [b^j]_{F_3}$,

• $[A(\beta )]_{F_3} = [a^j]_{F_3}$.

To see that, for example, $[A(\beta )]_{F_3} = [c^j]_{F_3}$ leads to a contradiction, consider the projection

$$\begin{aligned}&p_{a,b} : \langle a,b,c \rangle \rightarrow \langle a,b \rangle ,\\&\quad a \mapsto a, b \mapsto b, c \mapsto 1 . \end{aligned}$$

If $[A(\beta )]_{F_3} = [c^j]_{F_3}$, then

$$\begin{aligned}{}[(a)^{m_1} (b^{-1})^{n_1} ... (a)^{m_p} (b^{-1})^{n_p}]_{\langle a,b \rangle }= & {} [p_{a,b}(A(\beta ))]_{\langle a,b \rangle } \\= & {} [p_{a,b}(c^j)]_{\langle a,b \rangle } = [1]_{\langle a,b \rangle } . \end{aligned}$$

This implies that at least one of the $m_i,n_i$ is 0, else no cancellation can occur in the word $(a)^{m_1} (b^{-1})^{n_1} ... (a)^{m_p} (b^{-1})^{n_p}$. This is a contradiction to the assumption $\forall i: 0 \ne m_i,n_i$.

The other three cases are dealt with similarly: the case $[A(\beta )]_{F_3} = [(ab^{-1}c)^j]_{F_3}$ using the projection

$$\begin{aligned}&p_{ab^{-1}c,c} : \langle a,b,c \rangle \rightarrow \langle a,b \rangle ,\\&\quad ab^{-1}c \mapsto a, c \mapsto b, a \mapsto 1 \end{aligned}$$

(note this is well defined since $\{ab^{-1}c, a, c\}$ is a basis of $F_3$); and the cases $[A(\beta )]_{F_3} = [b^j]_{F_3}$, $[A(\beta )]_{F_3} = [a^j]_{F_3}$ using $p_{a,b}$ defined above.

Since all cases lead to a contradiction we conclude that $\delta \sim \beta$ in $F_3$, as desired. $\square$

Recall $\pi _1(\Sigma _2) = \langle H_1*H_2 , A=B , \phi \rangle$ and recall the definition of $len: \pi _1(\Sigma _2) \rightarrow {\mathbb {Z}}_{\ge 0}$. We will also make use of the following claim:

Claim 2.3

Let $r \in {\mathbb {N}}, k_i \in {\mathbb {Z}}$ for $i \in \{1,...,2r\}$ with $|k_i| \ge 2$ for all i and consider $\pi _1(\Sigma _2) = \langle g_1,g_2,g_3,g_4 | [g_1,g_2][g_3,g_4] \rangle$. Then

$$\begin{aligned} len \left( \Pi _{i=1}^r (g_1 g_3)^{k_{2i-1}} (g_2 g_1^{-1} g_2^{-1}g_3)^{k_{2i}} \right) > 1 . \end{aligned}$$

Proof

Denote $\epsilon _i = sign(k_i) = \frac{k_i}{|k_i|}$. Consider

$$\begin{aligned}&p_{13}: \pi _1(\Sigma _2) \rightarrow F_2 = \langle h_1, h_3 \rangle ,\\&\quad g_1 \mapsto h_1 ,\\&\quad g_3 \mapsto h_3 ,\\&\quad g_2, g_4 \mapsto 1 . \end{aligned}$$

Denote $w = \Pi _{i=1}^r (g_1 g_3)^{k_{2i-1}} (g_2 g_1^{-1} g_2^{-1} g_3)^{k_{2i}}$. Assume by contradiction $len(w) \le 1$. Note that $p_{13}$ preserves factors, i.e. $p_{13}(H_1) = \langle h_1 \rangle , p_{13}(H_2) = \langle h_3 \rangle$. If $len(w) = 0$, then $w = 1$, so $p_{13}(w) = 1$, and then $len(p_{13}(w)) = 0$. Else, $len(w) = 1$, so $w \sim c_1$ with $c_1 \in H_1 < \pi _1(\Sigma _2)$ or $c_1 \in H_2 < \pi _1(\Sigma _2)$. Without loss of generality, assume $c_1 \in H_1$. Then $p_{13}(w) \sim p_{13}(c_1) \in p_{13}(H_1) = \langle h_1 \rangle$, and then $len(p_{13}(w)) \le 1$. One reaches the same conclusion in both cases: $len(p_{13}(w)) \le 1$ (note that this is len in $F_2$, which is a free product of ${\mathbb {Z}}= \langle h_1 \rangle$ with ${\mathbb {Z}}= \langle h_3 \rangle$ and so is trivially a free product with amalgamation). As a remark, this procedure can be applied for any factor-preserving homomorphism $\psi$ to get $len(g) \ge len(\psi (g))$.

Consider $p_{13}(w)$:

$$\begin{aligned} p_{13}(w) = \Pi _{i=1}^r (h_1 h_3)^{k_{2i-1}} (h_1^{-1} h_3)^{k_{2i}} . \end{aligned}$$

This element is made of blocks: $(h_1 h_3)^{k_j}$ or $(h_1^{-1} h_3)^{k_j}$. Each of these blocks is reduced, so the only cancellations in the form of $p_{13}(w)$ given above can happen between two blocks. These are the options for cancellations between two blocks:

• If the first block is $(h_1 h_3)^{k_i}$ and the second is $(h_1^{-1} h_3)^{k_{i+1}}$, one of the following holds:

  • * $\epsilon _i = \epsilon _{i+1} = 1$: in this case, $(h_1 h_3)^{k_i} (h_1^{-1} h_3)^{k_{i+1}} = (h_1 h_3)^{|k_i|} (h_1^{-1} h_3)^{|k_{i+1}|}$ and we can see there is no cancellation between the two blocks.

  • * $\epsilon _i = -\epsilon _{i+1} = 1$: in this case, we have cancellation. Indeed, $(h_1 h_3)^{k_i} (h_1^{-1} h_3)^{k_{i+1}} = (h_1 h_3)^{|k_i|-1} h_1 h_1 (h_1^{-1} h_3)^{-|k_{i+1}|+1} \ (*)$.

  • * $-\epsilon _i = \epsilon _{i+1} = 1$: in this case, $(h_1 h_3)^{k_i} (h_1^{-1} h_3)^{k_{i+1}} = (h_1 h_3)^{-|k_i|} (h_1^{-1} h_3)^{|k_{i+1}|}$ and we can see there is no cancellation between the two blocks.

  • * $\epsilon _i = \epsilon _{i+1} = -1$: in this case, $(h_1 h_3)^{k_i} (h_1^{-1} h_3)^{k_{i+1}} = (h_1 h_3)^{-|k_i|} (h_1^{-1} h_3)^{-|k_{i+1}|}$ and we can see there is no cancellation between the two blocks.

  Every cancellation of type $(*)$ results in a reduced block starting and ending with $h_1$. Before it comes either $h_3$ or $h_1$ (since $(h_1^{-1} h_3)^{k_{i-1}}$ ends with one of these symbols) and after it comes either $h_1$ or $h_3^{-1}$ (for similar reasons). Thus after a cancellation of this type, none of the two ends of the resulting reduced block can be cancelled any further.

• If the first block is $(h_1^{-1} h_3)^{k_i}$ and the second is $(h_1 h_3)^{k_{i+1}}$, one of the following holds:

  • * $\epsilon _i = \epsilon _{i+1} = 1$: in this case, $(h_1^{-1} h_3)^{k_i} (h_1 h_3)^{k_{i+1}} = (h_1^{-1} h_3)^{|k_i|} (h_1 h_3)^{|k_{i+1}|}$ and we can see there is no cancellation between the two blocks.

  • * $\epsilon _i = -\epsilon _{i+1} = 1$: in this case, we have cancellation. Indeed, $(h_1^{-1} h_3)^{k_i} (h_1 h_3)^{k_{i+1}} = (h_1^{-1} h_3)^{|k_i|-1} h_1^{-1} h_1^{-1} (h_1 h_3)^{-|k_{i+1}|+1} \ (**)$.

  • * $-\epsilon _i = \epsilon _{i+1} = 1$: in this case, $(h_1^{-1} h_3)^{k_i} (h_1 h_3)^{k_{i+1}} = (h_1^{-1} h_3)^{-|k_i|} (h_1 h_3)^{|k_{i+1}|}$ and we can see there is no cancellation between the two blocks.

  • * $\epsilon _i = \epsilon _{i+1} = -1$: in this case, $(h_1^{-1} h_3)^{k_i} (h_1 h_3)^{k_{i+1}} = (h_1^{-1} h_3)^{-|k_i|} (h_1 h_3)^{-|k_{i+1}|}$ and we can see there is no cancellation between the two blocks.

  Every cancellation of type $(**)$ results in a reduced block starting and ending with $h_1^{-1}$. Before it comes either $h_3$ or $h_1^{-1}$ and after it comes either $h_1^{-1}$ or $h_3^{-1}$ (for reasons similar to above). Thus after a cancellation of this type, none of the two ends of the resulting reduced block can be cancelled any further.

Therefore, after at most $2r-1$ cancellations one reaches a reduced word. If it is not cyclically reduced, conjugate by the first block and perform one more reduction to get a cyclically reduced word v, conjugate to $p_{13}(w)$. Since every reduced block $(*)$ or $(**)$ above has length at least 2 and these are inserted without cancellations to our word v, we have $len(p_{13}(w)) = len(v) \ge 2 > 1$. This is a contradiction, so the initial assumption $len(w) \le 1$ is false. $\square$

3 Proof of the theorems

3.1 Additional definitions

In the proofs of the results, we shall use the following definitions.

Definition 3.1

A continuous map between two manifolds $f: M \rightarrow N$ induces a map $\tau _f: \pi _0({\mathscr {L}}M) \rightarrow \pi _0({\mathscr {L}}N)$ by $\tau _f([\gamma ]) = [f \circ \gamma ]$, for $\gamma : S^1 \rightarrow M$.

For any manifold M and point $x \in M$, define the map

$$\begin{aligned}&\eta _{M,x} : \pi _1(M,x) \rightarrow \pi _0({\mathscr {L}}M) , \\&\quad [{\tilde{\gamma }}]_{\pi _1(M,x)} \mapsto [{\tilde{\gamma }}]_{\pi _0({\mathscr {L}}M)}. \end{aligned}$$

where ${\tilde{\gamma }}: S^1 \rightarrow M$ is a loop.

Note that the following diagram commutes for any continuous map $f: M \rightarrow N$:

Note additionally that for $\alpha , \beta \in \pi _1(M,x)$, $\eta _{M,x}(\alpha ) = \eta _{M,x}(\beta )$ if and only if $\alpha$ and $\beta$ are conjugate in $\pi _1(M,x)$.

Definition 3.2

A word $w \in F_2 = \langle V,H \rangle$ is called balanced if it is of the form $w = V^{N_1} H^{M_1} ... V^{N_r} H^{M_r}$ for some $r \in {\mathbb {N}}$, $N_j,M_j \in {\mathbb {Z}}\setminus \{0\}$.

Note that any balanced word is cyclically reduced.

Definition 3.3

Let $\varphi : M \rightarrow M$ be a diffeomorphism. A fixed point x of $\varphi$ is called non-degenerate if $d\varphi _x$ does not have 1 as an eigenvalue.

The egg-beater construction uses dynamics on a space C which is then embedded into a surface of genus 2. Thus we shall use the following definitions of pushing forward the dynamics along the embedding.

Let X, Y be compact topological spaces and $i: X \hookrightarrow Y$ a continuous embedding. Let $f: X \rightarrow {\mathbb {R}}$ be a continuous map on X and assume the following condition holds:

$$\begin{aligned} \text {for any path-component }C of Y \setminus i(X), f \restriction _{i^{-1}(\partial C)} \text { is constant.} \end{aligned}$$

(2)

Let $C_y$ be the path-component of Y that contains $y \in Y$ and denote $D_i = \bigcup _{y \in {{\,\mathrm{Im}\,}}(i)} C_y \subseteq Y$. For all $y \in D_i$ let $\gamma _{i,y}: [0,1] \rightarrow C_y$ be a continuous path with $\gamma _{i,y}(0) = y$, $\gamma _{i,y}(1) \in {{\,\mathrm{Im}\,}}(i)$, and such that if $\gamma _{i,y}(t) \in {{\,\mathrm{Im}\,}}(i)$ for some $t \in [0,1]$, then $\gamma _{i,y} \restriction _{[t,1]}$ is constant. Note that if $y \in {{\,\mathrm{Im}\,}}(i)$, then $\gamma _{i,y} \equiv y$.

Denote the following, not necessarily continuous, map:

$$\begin{aligned}&b_i: D_i \rightarrow {{\,\mathrm{Im}\,}}(i) ,\\&\quad y \mapsto \gamma _{i,y}(1) . \end{aligned}$$

Define the following map, the pushforward of f through i:

$$\begin{aligned}&i_* f: D_i \rightarrow {\mathbb {R}},\\&\quad y \mapsto f \circ i^{-1} \circ b_i(y) . \end{aligned}$$

By Condition 2, this is a continuous map $D_i \rightarrow {\mathbb {R}}$ which is constant on $Y \setminus i(X)$ and doesn’t depend on the choice of the $\gamma _{i,y}$s. Note also that if f is smooth and constant in a neighborhood of $i^{-1}(\partial \ i(X))$ then $i_* f$ is also smooth.

Assume additionally that X, Y are symplectic manifolds, i is a symplectomorphism, and $f: S^1 \times X \rightarrow {\mathbb {R}}$ is a Hamiltonian function. Then f induces the time-one-map of its flow; let it be denoted $F: X \rightarrow X$. The pushforward of F through i is denoted $i_* F: Y \rightarrow Y$ and is the time-one-map of the flow induced by $i_* f$.

3.2 Review of the original proofs (genus $\ge 4$)

3.2.1 Outline of the original proofs and dependencies of claims

First we shall outline the proofs of the original theorems, 1.3 from [11] and 1.1 from [1]. For concreteness, their statements are given here.

Theorem 3.4

[Theorem 1.3 from [11]] Let $\Sigma _4$ be a closed oriented surface of genus $\ge 4$, equipped with an area form $\sigma _4$, and $k \ge 2$ an integer. Then $powers_k(\Sigma _4,\sigma _4) = \infty$.

Theorem 3.5

[Theorem 1.1 from [1]] Let $\Sigma _4$ be a closed oriented surface of genus $\ge 4$, equipped with an area form $\sigma _4$. Then for any non-principal ultrafilter ${\mathcal {U}}$ on $2^{\mathbb {N}}$, there exists a monomorphism $F_2 \hookrightarrow Cone_{\mathcal {U}}(Ham(\Sigma _4),d_H)$.

Both their proofs involve several intermediate results. For clarity, Fig. 4 lists the dependencies between these results. The proofs are based on a specific construction of a manifold C, an embedding $i: C \hookrightarrow \Sigma _4$, and some dynamics on C, which induce dynamics on $\Sigma _4$. These constructions are all sketched in Sect. 1.4 and given in detail further in this subsection. Propositions 3.7, 3.8 (which are Propositions 5.11 of [1] and 5.1 of [11] respectively) are claims on the dynamics on $\Sigma _4$ and Claims 3.9, 3.10 are the respective claims on the dynamics on C.

The deductions marked $**$ use "hard" Floer homology and persistence modules and do not depend on the genus of $\Sigma _4$. Therefore they can be taken as is to the case where the surface is of genus 2,3. The deductions marked $*$ are a consequence of the fact that i is constructed to be incompressible, i.e. it induces injections $\pi _1(C) \hookrightarrow \pi _1(\Sigma _4)$ and $\pi _0({\mathscr {L}}C) \hookrightarrow \pi _0({\mathscr {L}}\Sigma _4)$. This condition will not hold in the case where $\Sigma$ is of genus 2,3 (see Sect. 3.3 below) and this is exactly where Lemma 1.3 comes into play. Claims 3.9, 3.10 are proved directly by careful analysis of the dynamics on C.

This subsection details the construction $i: C \hookrightarrow \Sigma _4$, the dynamics on C and $\Sigma _4$, states all the above claims and propositions, and outlines their proofs. For full details, see [11] and [1]; we describe their work bottom-up, with respect to the directions of Fig. 4.

Fig. 4

Dependencies between original intermediate results

The manifold C mentioned above is the union of two annuli $[-1,1] \times {\mathbb {R}}/L{\mathbb {Z}}$ for some $L>4$, which intersect in two squares, see Fig. 5 below. A special map, called an eggbeater map, is defined on C (see definition later in this subsection). In order to get results for a symplectic surface M, we need an embedding $i: C \hookrightarrow M$, which will induce eggbeater dynamics on M.

Since M is symplectic it is orientable and this leaves little choice for its homeomorphism type: the genus of M determines it. Topologically, one can always think of i as first embedding C into the sphere and then adding some handles. The results here use Floer homology, where basic objects of interest are homotopy classes of free loops in the manifold. Thus we want the embedding i to have the property that homotopy classes of different orbits of the dynamics on C will be pushed by i to different homotopy classes in M, so that we will be able to distinguish between different orbits with Floer homology tools.

Since the only choice in the embedding is how many handles to add and in which components of $M \setminus i(C)$ to attach them, we want every such component to have at least one end of a handle - otherwise, it will be contractible. There are four such components (consider Fig. 5), so for this method to work we need M to be of genus at least 2. The original construction, found in [11] and presented later in this subsection, uses a surface of genus at least 4 and adds at least one handle in every such component. This produces results for surfaces of genus $\ge 4$ and has the added benefit that it makes i incompressible, so that different free homotopy classes of loops in C do not merge under i. However, this is not efficient if we want to minimize the genus. A slightly more efficient construction is found in Sect. 3.3 and produces results for surfaces of genus 2,3.

Both of the original proofs of Theorems 3.4 and 3.5 use a construction of a sequence of homomorphisms $\Phi _k: F_2 \rightarrow Ham(\Sigma _4)$ (indexed by $k \in {\mathbb {N}}$). Every such Hamiltonian diffeomorphism $\Phi _k(w)$ is generated by a specific Hamiltonian denoted $H_{k,w}$ and the Hamiltonian isotopy generated by $H_{k,w}$ is denoted $\phi _{k,w}(t)$. All of these are specified exactly later in this subsection. Note that these homomorphisms depend on the surface $\Sigma _4$ - the proofs for the generalized theorems (in Sect. 3.3) will use similar but different homomorphisms.

This sequence $\Phi _k$ induces a homomorphism

$$\begin{aligned}&F_2 \rightarrow Cone_{\mathcal {U}}(Ham(\Sigma ), d_H) , \\&\quad w \mapsto [(\Phi _k(w))_{k=1}^\infty ] . \end{aligned}$$

To show this is a monomorphism, and so prove Theorem 3.5, for any $1 \ne w \in F_2$ one needs to show that $\lim _{\mathcal {U}} \frac{d_H(\Phi _k(w), id_\Sigma )}{k} = \lim _{\mathcal {U}} \frac{|| \Phi _k(w) ||_H}{k} > 0$. This is done in Theorem 3.6:

Theorem 3.6

[Theorem 2.1 from [1]] Let $1 \ne w \in F_2 = \langle H,V \rangle$. Then there exist constants $C = C(w) > 0, k_0 = k_0(w) \in {\mathbb {N}}$ such that for any $k > k_0$:

$$\begin{aligned} || \Phi _k(w) ||_H \ge C \cdot k. \end{aligned}$$

Corollary

Theorem 3.6 implies Theorem 3.5.

In addition to the above sequence $\Phi _k$, a collection of free homotopy classes $\alpha _{k,w} \in \pi _0({\mathscr {L}}C)$, indexed by $k \in {\mathbb {N}}, w \in F_2$; and another collection of free homotopy classes $\alpha _k^\prime \in \pi _0({\mathscr {L}}C)$, indexed by $k \in K$, are specified, where $K \subset {\mathbb {N}}$ is some unbounded subset to be specified later in this subsection.

Fig. 5

The paths $q_1, q_2, q_3, q_4$ in C

To prove Theorems 3.4, 3.6, the following propositions are used:

Proposition 3.7

[Proposition 5.11 from [1]] Let $w = \Pi _{j=1}^r V^{N_j} H^{M_j} \in F_2$ be a balanced word. For large enough $k \in {\mathbb {N}}$, there are $2^{2r}$ non-degenerate fixed points of $\Phi _k(w)$ whose orbits have free homotopy class $\tau _i(\alpha _{k,w})$ (i.e. $[t \mapsto \phi _{k,w}(t)(z_0)]_{\pi _0({\mathscr {L}}\Sigma _4)} = \tau _i(\alpha _{k,w})$ for $z_0$ a non-degenerate fixed point of $\Phi _k(w)$), and these fixed points are indexed by $\mathbf {\epsilon } = (\epsilon _0,...,\epsilon _{2r-1}) \in \{\pm 1\}^{2r}$, with the fixed point associated to sign vector $\mathbf {\epsilon }$ denoted $z(\mathbf {\epsilon })$. The action and Conley-Zehnder index of the point $z(\mathbf {\epsilon })$ are

$$\begin{aligned}&{\mathcal {A}}(z(\mathbf {\epsilon })) = Lk \sum _{j=1}^r \left( \epsilon _{2j-2} N_j \left( 1-\frac{1}{2|N_j|}\right) ^2 + \epsilon _{2j-1} M_j \left( 1-\frac{1}{2|M_j|}\right) ^2 \right) + O(1) , \end{aligned}$$

(3)

$$\begin{aligned}&\mu _{CZ}(z(\mathbf {\epsilon })) = 1 + \frac{1}{2} \sum _{j=1}^r \left( \epsilon _{2j-2} sign(N_j) + \epsilon _{2j-1} sign(M_j) \right) , \end{aligned}$$

(4)

where the action of a fixed point is understood to be that of its orbit under $\phi _{k,w}$, the action and Conley-Zehnder index are with respect to the Hamiltonian $H_{k,w}$, and where the O notation in Eq. 3 is as $k \rightarrow \infty$.

Proposition 3.8

[Proposition 5.1 from [11]] Let $w = (VH)^r \in F_2$ for some $r \in {\mathbb {N}}$. For large enough $k \in K$, there are $2^{2r}$ non-degenerate fixed points of $\Phi _k(w)$ whose orbits have free homotopy class $\tau _i(\alpha _k^\prime )$, and fixed points in different orbits have action gaps that grow linearly with k. That is, for such fixed points in different orbits y, z,

$$\begin{aligned} | {\mathcal {A}}(y) - {\mathcal {A}}(z) | \ge c \cdot k + O(1) , \end{aligned}$$

as $k \rightarrow \infty$, for some global constant $c > 0$.

Note that both propositions depend on the definition of the embedding i, which will be recalled later in this subsection.

Given Proposition 3.8, Theorem 3.4 is proven in Sect. 5.1 of [11] and given Proposition 3.7, Theorem 3.6 is proven in Sect. 5.4 of [1] (the case where w is not conjugate to a power of V or H requires Proposition 3.7, the case where w is conjugate to a power of V or H does not use it). The remainder of this subsection is devoted to outlining the construction of $\Phi _k, \phi _{k,w}, \alpha _{k,w}, \alpha _k^\prime$ and the proof of Propositions 3.7, 3.8, as proven in [1, 11].

3.2.2 The geometric construction

Let $\Sigma _4$ be a surface of genus $\ge 4$. Consider the cylinder $C_*=[-1,1]\times {\mathbb {R}}/L{\mathbb {Z}}$, for $L > 4$, with coordinates x, y and the standard symplectic form $dx\wedge dy$. Let $C_V,C_H$ be two copies of $C_*$. Consider the squares

$$\begin{aligned} S_0^\prime = [-1,1]\times [-1,1]/L{\mathbb {Z}}, \ S_1^\prime = [-1,1]\times [L/2-1,L/2+1]/L{\mathbb {Z}}\end{aligned}$$

in $C_*$. They give four squares $S_{V,0},S_{V,1}\subset C_V$ and $S_{H,0},S_{H,1}\subset C_H$. Define the symplectomorphism $VH_{0,1}:S_{V,0}\bigsqcup S_{V,1} \rightarrow S_{H,0} \bigsqcup S_{H,1}$ given by $VH\bigsqcup VH^\prime$, where

$$\begin{aligned}&VH:S_{V,0}\rightarrow S_{H,0} : (x,[y]) \mapsto (-y,[x]) ,\\&\quad VH^\prime : S_{V,1}\rightarrow S_{H,1} : (x,[y]) \mapsto (y-L/2, [-x+L/2]) . \end{aligned}$$

Define

$$\begin{aligned} C = C_V \bigcup _{VH_{0,1}} C_H . \end{aligned}$$

This is a symplectic manifold with symplectic form $\omega _0 = dx \wedge dy$ on every copy of the cylinder $C_*$. Denote by $C_V: C_* \hookrightarrow C, \ C_H: C_* \hookrightarrow C$ the two injections induced by the above union.

Denote by $S_0,S_1 \subset C$ the identification of the squares $S_{V,0},S_{H,0}$ and $S_{V,1},S_{H,1}$. In fact, $S_0 \cup S_1 = C_V \cap C_H$. Fix two points $s_0 \in S_0, s_1 \in S_1$. Define 4 paths: two paths $q_1,q_3$ from $s_0$ to $s_1$ and two paths $q_2,q_4$ from $s_1$ to $s_0$ (see Fig. 5), $q_1, q_2$ are paths on $C_V$ and $q_3,q_4$ are paths on $C_H$.

Note that $\pi _1(C,s_0) \simeq F_3$, the free group on 3 generators. The 3 generators a, b, c of $\pi _1(C,s_0)$ are taken to be:

$$\begin{aligned} a= & {} [q_1 \# q_2]_{\pi _1(C,s_0)} , \\ b= & {} [q_3 \# q_4]_{\pi _1(C,s_0)} , \\ c= & {} [q_3 \# q_2]_{\pi _1(C,s_0)} , \end{aligned}$$

where the $\#$ sign is used for path concatenation: $q\#q^\prime$ is the concatenation of paths q and then $q^\prime$, if $q(1) = q^\prime (0)$.

Consider the function $u_0: [-1,1] \rightarrow {\mathbb {R}}$, $u_0(s) = 1 - |s|$. Take an even, non-negative, sufficiently $C^0$-close smoothing u to $u_0$ such that u is supported away from $\{\pm 1\}$ and both $u-u_0$ and $\int _{-1}^t (u(s)-u_0(s)) ds$ are supported in a sufficiently small neighborhood of $\{\pm 1, 0\}$. For $k \in {\mathbb {N}}$, define

$$\begin{aligned} f= & {} f_k: C_* \rightarrow C_* , \\ f(x,[y])= & {} (x,[y + k L \cdot u(x)]) . \end{aligned}$$

This mapping is a Hamiltonian diffeomorphism on $C_*$ with Hamiltonian

$$\begin{aligned} h_k(x,[y]) = -\frac{k}{2} + k \int _{-1}^x u(s) ds . \end{aligned}$$

Denote $f_{k,V} = (c_V)_* f_k$, $f_{k,H} = (c_H)_* f_k$. Note that these are two Hamiltonian diffeomorphisms on C, one supported on $C_V$ and the other on $C_H$, both supported away from $\partial C$. Define a homomorphism

$$\begin{aligned}&\Psi _k: F_2 = \langle V,H \rangle \rightarrow Ham_c(C,\omega _0) ,\\&V \mapsto f_{k,V}, H \mapsto f_{k,H} , \end{aligned}$$

where $Ham_c(M,\omega )$ denotes the group of Hamiltonian diffeomorphisms of a symplectic manifold $(M,\omega )$ which are supported in the interior of M. Note that the image of a word $w = V^{N_1} H^{M_1} ... V^{N_r} H^{M_r} \in F_2$ is $f_{k,H}^{M_r} \circ f_{k,V}^{N_r} \circ ... \circ f_{k,H}^{M_1} \circ f_{k,V}^{N_1}$. These images are called eggbeater maps.

Pushing forward the flow generated by $h_k$ to C, one gets flows on $C_V$ and $C_H$ whose time-one-maps are $f_{k,V}$ and $f_{k,H}$. Concatenating these in the order induced by w (as in the construction of $\Psi _k(w)$), one gets a flow $\psi _{k,w}(t): C \rightarrow C$, whose time-one-map is $\Psi _k(w)$. Denote the Hamiltonian that generates this flow $G_{k,w}: S^1 \times C \rightarrow {\mathbb {R}}$.

Consider a symplectic embedding $i: C \hookrightarrow \Sigma _4$ such that $i_*: \pi _1(C) \rightarrow \pi _1(\Sigma _4)$ and $\tau _i: \pi _0({\mathscr {L}}C) \rightarrow \pi _0({\mathscr {L}}\Sigma _4)$ are both injective and such that each component of $\partial C$ separates $\Sigma _4$. For example, one can embed C into ${\mathbb {R}}^2$, add at least one handle in every connected component of ${\mathbb {R}}^2 \setminus C$, and compactify by adding the point at infinity (see the construction in [11] and [1]). This is the point where Lemma 1.3 is used when generalizing the propositions to surfaces of genus 2,3 (see Sect. 3.3). Note that the pairs $i, f_{k,V}$ and $i, f_{k,H}$ satisfy Condition 2.

The homomorphisms $\Phi _k: F_2 \rightarrow Ham(\Sigma _4)$ will be defined by $\Phi _k(w) = i_* \Psi _k(w)$. The mapping $\Phi _k(w)$ is indeed a diffeomorphism, because of the assumptions on u, and is Hamiltonian, since it is generated by the Hamiltonian $H_{k,w} = i_* G_{k,w}$.

Given $k \in {\mathbb {N}}, w = V^{N_1} H^{M_1} ... V^{N_r} H^{M_r} \in F_2$, set the free homotopy classes $\alpha _{k,w}$ to be

$$\begin{aligned} \alpha _{k,w} = \eta _{C,s_0}(\beta _{k,w}) \in \pi _0({\mathscr {L}}C) , \end{aligned}$$

where

$$\begin{aligned} \beta _{k,w} = \Pi _{j=1}^r a^{k \cdot sign(N_j)} b^{k \cdot sign(M_j)} \in \pi _1(C,s_0) \end{aligned}$$

and $sign: {\mathbb {Z}}\rightarrow \{0, \pm 1\}$ is

$$\begin{aligned} n \mapsto \left\{ \begin{array}{ll} \frac{n}{|n|} &{} n \ne 0 \\ 0 &{} n = 0 \end{array}\right. . \end{aligned}$$

Additionally, choose $\nu _j,\mu _j \in (0,1)$ for $j=1,...,r$ such that $\frac{\nu _j}{L},\frac{\mu _j}{L} \in {\mathbb {Q}}$ for all j and the values $\sum _{j=0}^{r-1} (\epsilon _{2j+1}(1-\mu _{j+1})^2 - \epsilon _{2j+4}(1-\nu _{j+1})^2)$ are all distinct, for all sign vectors $\mathbf {\epsilon }= (\epsilon _0,...,\epsilon _{2r-1}) \in \{\pm 1\}^{2r}$. For these choices, the set $K \subset {\mathbb {N}}$ from Proposition 3.8 is taken to be $K = \left\{ k \in {\mathbb {N}}\mid \forall j: \frac{\mu _j k}{L}, \frac{\nu _j k}{L} \in {\mathbb {Z}}\right\}$.

For $k \in K$ set

$$\begin{aligned} \alpha _k^\prime = \eta _{C,s_0}(\beta _k^\prime ) \in \pi _0({\mathscr {L}}C) , \end{aligned}$$

where

$$\begin{aligned} \beta _k^\prime = \Pi _{j=1}^r a^{\frac{\nu _j k}{L}} b^{\frac{\mu _j k}{L}} \in \pi _1(C,s_0) . \end{aligned}$$

From this point on, it is assumed that any index k of $\alpha _k^\prime$ or $\beta _k^\prime$ is in the subset K, since otherwise $\alpha _k^\prime , \beta _k^\prime$ are not well-defined. This will also be explicitly stated.

The outline of the proofs of Propositions 3.7, 3.8 is as follows. Since any non-degenerate fixed point of $\Phi _k(w)$ must lie in ${{\,\mathrm{Im}\,}}i$ and in addition $i: C \rightarrow \Sigma _4$, $i_*: \pi _1(C,s_0) \rightarrow \pi _1(\Sigma _4,i(s_0))$ and $\tau _i: \pi _0({\mathscr {L}}C) \rightarrow \pi _0({\mathscr {L}}\Sigma _4)$ are all injective, it is enough to prove versions of Propositions 3.7, 3.8 on C, i.e. prove the following claims:

Claim 3.9

Let $w = \Pi _{j=1}^r V^{N_j} H^{M_j} \in F_2$ be balanced. For large enough $k \in {\mathbb {N}}$, there are $2^{2r}$ non-degenerate fixed points of $\Psi _k(w)$ whose orbits have free homotopy class $\alpha _{k,w}$. These fixed points have actions (with respect to $G_{k,w}$) and Conley-Zehnder indices as in Eqs. 3,4.

Claim 3.10

Let $w = (VH)^r \in F_2$ for some $r \in {\mathbb {N}}$. For large enough $k \in K$, there are $2^{2r}$ fixed points of $\Psi _k(w)$ whose orbits have free homotopy class $\alpha _k^\prime$. Such fixed points in different orbits have action gaps (with respect to $G_{k,w}$) that grow linearly with k as $k \rightarrow \infty$.

This is proven in two steps. First, one proves these claims with respect to a piecewise-linear version $\psi _{k,w}^\prime (t)$ of the isotopy $\psi _{k,w}(t)$. This is done in Sect. 5.1 of [1] and in Sect. 5 of [11], by analysis of the dynamics on C. Then, one shows that the non-degenerate fixed points of $\Psi _k(w)$ are exactly those of $\psi _{k,w}^\prime (1)$, for k large enough. This is done in Sect. 5.3 of [1].

3.3 Proof of the new theorems (genera 2,3)

The new proofs are very similar to the original ones, with the following changes. The interesting dynamics, which we want to keep, is the eggbeater dynamics, but we will need to change our construction of $i, C, \psi _{k,w}$ a bit to accommodate for the fact that the genus of the surface is now 2 or 3.

More concretely, let $\Sigma$ be a surface of genus 2 or 3 with area form $\sigma$. The following data will be defined:

• a symplectic surface $(D,\omega )$ that contains C from the original construction (i.e. $e_2: C \hookrightarrow D$ is a symplectic embedding that induces an embedding $\tau _{e_2}: \pi _0({\mathscr {L}}C) \hookrightarrow \pi _0({\mathscr {L}}D)$),

• an injection $i_2: D \hookrightarrow \Sigma$, and

• homomorphisms $\Xi _k: F_2 \rightarrow Ham_c(D, \omega )$ indexed by $k \in {\mathbb {N}}$, with $\Xi _k(w)$ the time-one-map of the flow $\xi _{k,w}(t): D \rightarrow D$, such that for all $k \in {\mathbb {N}}, w \in F_2$: $\xi _{k,w}(t) \restriction _C = \psi _{k,w}(t)$.

The Hamiltonian generating $\xi _{k,w}(t)$ will be denoted $F_{k,w}: S^1 \times D \rightarrow {\mathbb {R}}$. These data will specify the dynamics on D. In order to work on $\Sigma$, the dynamics will be pushed forward by $i_2$. This will result in a Hamiltonian $(i_2)_* F_{k,w}: S^1 \times \Sigma \rightarrow {\mathbb {R}}$ and the flow and time-one-map it generates, denoted $(i_2)_* \xi _{k,w}(t): \Sigma \rightarrow \Sigma$ and $(i_2)_* \Xi _k(w): \Sigma \rightarrow \Sigma$.

The confused reader may consult the diagram in Fig. 6, which indicates the different surfaces mentioned till now and the injections between them, together with the Hamiltonians on them, the flows these Hamiltonians generate, and their time-one-maps.

Fig. 6

The surfaces, Hamiltonians, flows and time-one-maps in the proof

All these data will be explicitly defined in Sect. 3.3.1.

With these constructions in hand we will prove new versions of Propositions 3.7, 3.8 and these will imply the generalized Theorems 1.1, 1.2. These dependencies are depicted in Fig. 7. The deductions marked $**$ can be taken as is from the proofs for surfaces of genus $\ge 4$ in [1, 11]. The deductions marked $*$ will now require justification, since $i_2$ will no longer be incompressible. Since Claims 3.9, 3.10 were already established (see proof in [1, 11] or sketch in Sect. 3.2), we have to show why they imply Propositions 3.11, 3.12. This is done in Sect. 3.3.2 and uses Lemma 1.3.

Fig. 7

Dependencies between generalized intermediate results

Propositions 3.11, 3.12, which by the above discussion imply the main theorems of this paper, are stated here.

Proposition 3.11

Let $w = \Pi _{j=1}^r V^{N_j} H^{M_j} \in F_2 = \langle H,V \rangle$ be balanced. For large enough $k \in {\mathbb {N}}$, there are $2^{2r}$ non-degenerate fixed points of $(i_2)_* \Xi _k(w)$ in $\Sigma$ whose orbits have free homotopy class $\tau _{i_2}(\alpha _{k,w})$. Such fixed points have actions and Conley-Zehnder indices as in Eqs. 3,4.

Proposition 3.12

Let $w = (VH)^r \in F_2$ for some $r \in {\mathbb {N}}$. For large enough $k \in K$, there are $2^{2r}$ fixed points of $(i_2)_* \Xi _k(w)$ in $\Sigma$ whose orbits have free homotopy class $\tau _{i_2}(\alpha _k^\prime )$. Such fixed points in different orbits have action gaps that grow linearly with k, that is, for such fixed points y, z in different orbits:

$$\begin{aligned} | {\mathcal {A}}(y) - {\mathcal {A}}(z) | \ge c \cdot k + O(1) , \end{aligned}$$

as $k \rightarrow \infty$, for some global constant $c > 0$. The set $K \subset {\mathbb {N}}$ is as defined in Sect. 3.2.

Note that since $\pi _0({\mathscr {L}}C) \subset \pi _0({\mathscr {L}}D)$, the expressions $\tau _{i_2}(\alpha _{k,w})$ and $\tau _{i_2}(\alpha _k^\prime )$ are well-defined.

3.3.1 The construction

In a sense, the proof for $\Sigma$ of genus 2 is harder than for genus 3. In the following, we will show the proof for $\Sigma$ of genus 2 and comment on the differences to the proof for genus 3 surfaces when they arise.

Consider C, defined in Sect. 3.2.2, and two additional copies of the cylinder $C_*$, $C_1$ and $C_2$. Our manifold D will be $D = C \bigsqcup C_1 \bigsqcup C_2$, equipped with the standard symplectic form $\omega _0 = dx \wedge dy$ on every component. Denote the symplectic inclusions $C_* \hookrightarrow C_1,C_2$ by $c_1,c_2$ respectively. Note that the additional annuli, $C_1$ and $C_2$, are needed to make sure that $i_2$ and $F_{k,w}$ satisfy Condition 2; that is, to enable $F_{k,w} \circ i_2^{-1}: {{\,\mathrm{Im}\,}}(i_2) \rightarrow {\mathbb {R}}$ to be extended by a locally constant function to a function on all of $\Sigma$.

The symplectic embedding $i_2:(D,\omega _0) \hookrightarrow (\Sigma , \sigma )$ is built in stages. First define $i_2$ on C: embed C symplectically into ${\mathbb {R}}^2$, embed the plane ${\mathbb {R}}^2$ into $S^2$, and then add 2 handles as shown in Fig. 8. That is, C separates the sphere into 4 connected components, each having two neighbors; connect any two non-neighboring components with a handle. In the case of genus 3, add a handle inside the ’outside’ component to obtain a surface of genus 3 (we will refer to this handle as the extra handle). This defines $i_2 \restriction _C$. Define $i_2$ on $C_1 \bigsqcup C_2$ by embedding each of them symplectically into one of the non-extra handles (with $C_1$ and $C_2$ on different handles), such that the images $i_2(C_1), i_2(C_2)$ are not contractible. The orientation of the embeddings $i_2\restriction _{C_1}, i_2\restriction _{C_2}$ and which goes on which handle, will be defined immediately. The embedding $i_2$ can be seen in Fig. 8.

Fig. 8

adding handles on $S^2$ after embedding C: this whole figure is in $S^2$

Fig. 9

the generators of $\pi _1(\Sigma , i_2(s_0))$, dashed lines only for readability

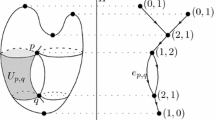
Recall $s_0 \in C$ and a, b, c, the generators of $\pi _1(C, s_0)$. Fix some $s^\prime _k \in C_k$ for $k=1,2$. The generators of $\pi _1(C_k,s^\prime _k) = {\mathbb {Z}}$ are denoted $d_k$. These are positively oriented, i.e. $d_k = [t\mapsto (0,Lt) \in C_k]$ as elements in $\pi _1(C_k,s_k^\prime )$. Denote the generators of $\pi _1(\Sigma , i_2(s_0))$ by $g_1,..,g_4$, such that $\pi _1 (\Sigma , i_2(s_0)) = \left\langle g_1,g_2,g_3,g_4\big |[g_1,g_2] [g_3,g_4] \right\rangle$ and the loops $g_1$ and $g_3$ go around the two handles (see Fig. 9). In the case where $\Sigma$ is of genus 3, denote $\pi _1(\Sigma , i_2(s_0)) = \langle g_1, ..., g_6 | [g_1,g_2] [g_3,g_4] [g_5,g_6] \rangle$, such that the loops $g_1$ and $g_3$ still go around the two non-extra handles (the same as in Fig. 9) and such that $g_5$ goes around the extra handle. The loops $g_{k+1}$ go along the handle that the loops $g_k$ go around (for $k = 1,3,5$), oriented such that $[g_1,g_2][g_3,g_4][g_5,g_6] = 1$ in $\pi _1(\Sigma , i_2(s_0))$.

Choose the image of $C_1$ to be contained in the handle that the loop $g_1 \in \pi _1(\Sigma , i_2(s_0))$ goes around (in Figs. 8 and 9 this is the upper handle), and so $i_2(C_2)$ is contained in the handle that the loop $g_3$ goes around. Since the image of $C_1$ is located on a handle, is non-contractible, and $i_2$ is an embedding, one can choose how to orient the image of $C_1$:

$$\begin{aligned} \tau _{i_2} \circ \eta _{C_1,s_1^\prime } (d_1) = \eta _{\Sigma , i_2(s_0)} (g_1) \text { or } \tau _{i_2} \circ \eta _{C_1,s_1^\prime } (d_1) = \eta _{\Sigma , i_2(s_0)} (g_1^{-1}) , \end{aligned}$$

and similarly one can choose the orientation of $i_2(C_2)$:

$$\begin{aligned} \tau _{i_2} \circ \eta _{C_2,s_2^\prime } (d_2) = \eta _{\Sigma , i_2(s_0)} (g_3) \text { or } \tau _{i_2} \circ \eta _{C_2,s_2^\prime } (d_2) = \eta _{\Sigma , i_2(s_0)} (g_3^{-1}) . \end{aligned}$$

Choose the orientation of the embeddings $i_2\restriction _{C_1}, i_2\restriction _{C_2}$ to be such that the elements $d_1,d_2$ map to $\eta _{\Sigma , i_2(s_0)} (g_1)$ and $\eta _{\Sigma , i_2(s_0)} (g_3^{-1})$ respectively under $\tau _{i_2} \circ \eta _{C_k, s_k^\prime }$ (for $k = 1,2$). This concludes the definition of the embedding $i_2$.

By construction of $i_2: D \hookrightarrow \Sigma$, the pushforward $(i_2)_*: \pi _1(D, s_0) \rightarrow \pi _1(\Sigma , i_2(s_0))$ acts on the generators a, b, c of $\pi _1(D,s_0)$ so:

$$\begin{aligned}&a \mapsto g_1 g_3 , \\&b \mapsto g_2 g_1^{-1} g_2^{-1} g_3 , \\&c \mapsto g_3 . \end{aligned}$$

In order to define the Hamiltonian $F_{k,w}$ on D, a similar procedure as the one that defines $G_{k,w}$ is followed. Recall $h = h_k: C_* \rightarrow {\mathbb {R}}$, the Hamiltonian on $C_*$:

$$\begin{aligned} (x,[y]) \mapsto -\frac{k}{2} + k \int _{-1}^x u(s) ds , \end{aligned}$$

defined in Sect. 3.2. Note that the pairs $e_2 \circ c_V, h_k$ and $e_2 \circ c_H, h_k$ satisfy Condition 2. Define two autonomous Hamiltonians on D:

$$\begin{aligned}&g_{k,V}: D \rightarrow {\mathbb {R}}, \\&\quad g_{k,V} = (e_2 \circ c_V)_* h_k \bigsqcup - (c_1)_* h_k \bigsqcup (c_2)_* h_k ; \\&\quad g_{k,H}: D \rightarrow {\mathbb {R}}, \\&\quad g_{k,H} = (e_2 \circ c_H)_* h_k \bigsqcup (c_1)_* h_k \bigsqcup (c_2)_* h_k . \\ \end{aligned}$$

Given $w \in F_2 = \langle V,H \rangle$, define $\xi _{k,w}(t)$, the flow on D, as the concatenation of the flows induced by $g_{k,V}, g_{k,H}$, in the order induced by w. The Hamiltonian which induces this flow is denoted $F_{k,w}: S^1 \times D \rightarrow {\mathbb {R}}$ and its time-one-map is $\Xi _k(w): D \rightarrow D$. Another equivalent way to define $\Xi _k(w)$ is to denote the time-one-maps of $g_{k,V}$, $g_{k,H}$ by $g_{k,V}^\prime , g_{k,H}^\prime$ respectively and define the homomorphism

$$\begin{aligned}&\Xi _k: F_2 \rightarrow Ham_c(D,\omega _0) , \\&\quad V \mapsto g_{k,V}^\prime , H \mapsto g_{k,H}^\prime . \end{aligned}$$

Next, note that $F_{k,w}$ and $i_2$ satisfy Condition 2 for all k, w. Therefore we can define the pushforwards $(i_2)_* F_{k,w}: S^1 \times \Sigma \rightarrow {\mathbb {R}}, (i_2)_* \xi _{k,w}: {\mathbb {R}}\times \Sigma \rightarrow \Sigma , (i_2)_* \Xi _k(w): \Sigma \rightarrow \Sigma$.

3.3.2 Proof of Propositions 3.11, 3.12

First we state a few helper claims and use them to prove Propositions 3.11, 3.12. Then, we will show the proofs of the claims. For the rest of this subsection, fix some $2 \le k \in {\mathbb {N}}, w = V^{N_1} H^{M_1} ... V^{N_r} H^{M_r} \in F_2$ balanced. Recall that $\alpha _{k,w} = \eta _{C,s_0}(\beta _{k,w})$, $\alpha _k^\prime = \eta _{C,s_0}(\beta _k^\prime )$, and also note that since the connected component of $s_0$ in D is $e_2(C)$. We shall abuse notation and denote $\pi _1(C,s_0) = \pi _1(D,s_0), \eta _{C,s_0} = \eta _{D,s_0}$, etc.

The first claim characterizes all egg-beater orbits in C in terms of their free homotopy classes.

Claim 3.13

Let ${\tilde{\gamma }} : S^1 \rightarrow C$ be a closed $\psi _{k,w}$-orbit. Then there exist $k_1,...,k_r, l_1,...,l_r \in {\mathbb {Z}}$, $u_1,...,u_r, v_1,...,v_r \in \{0,1\}$ such that $[{\tilde{\gamma }}]_{\pi _0({\mathscr {L}}C)} = \eta _{C,s_0}(\Pi _{m=1}^r a^{k_m}c^{-u_m}b^{l_m}c^{v_m})$.

The second claim provides a partial injectivity property of $\tau _{i_2}$.

Claim 3.14

Let $\gamma = \eta _{D,s_0}(\Pi _{m=1}^r a^{k_m}c^{-u_m}b^{l_m}c^{v_m}) \in \pi _0({\mathscr {L}}D)$ for some $k_1,...,k_r,l_1,...,l_r \in {\mathbb {Z}}$, $u_1,...,u_r,v_1,...,v_r \in \{0,1\}$ and assume $\tau _{i_2}(\gamma ) = \tau _{i_2}(\alpha _{k,w})$. Then $\gamma = \alpha _{k,w}$.

Alternatively, if $k \in K$, assume $\tau _{i_2}(\gamma ) = \tau _{i_2}(\alpha _k^\prime )$. Then $\gamma = \alpha _k^\prime$.

The third claim will allow us to focus our calculations to $\xi _{k,w}$-orbits in D which are in fact in $e_2(C)$.

Claim 3.15

Let $k \in {\mathbb {N}}$ be large enough and let $z \in \Sigma$ be a non-degenerate fixed point of $(i_2)_* \Xi _k(w)$ whose $(i_2)_* \xi _{k,w}$-orbit is in the class $\tau _{i_2}(\alpha _{k,w})$, i.e. $[(i_2)_* \xi _{k,w}(t) (z)]_{\pi _0({\mathscr {L}}\Sigma )} = \tau _{i_2}(\alpha _{k,w})$.

Alternatively, let $k \in K$ be large enough and let $z \in \Sigma$ be a non-degenerate fixed point of $(i_2)_* \Xi _k(w)$ whose $(i_2)_* \xi _{k,w}$-orbit is in the class $\tau _{i_2}(\alpha _k^\prime )$.

In both cases, $z \in i_2(C)$.

We now prove Propositions 3.11 and 3.12.

Proof of Propositions 3.11, 3.12

Recall that Claims 3.9, 3.10, proven in [1, 11], are analogous to these propositions, but set in C. We want to show why they imply that these propositions hold in $\Sigma$. The proofs for both propositions are very similar, so we present them simultaneously.

Let ${\tilde{\gamma }}: S^1 \rightarrow \Sigma$ be a closed orbit of $(i_2)_* \xi _{k,w}(t)$ in the class $\tau _{i_2}(\alpha _{k,w})$ (or $\tau _{i_2}(\alpha _k^\prime )$, in the case where $k \in K$) such that $z = {\tilde{\gamma }}(0)$ is a non-degenerate fixed point of $(i_2)_* \Xi _k(w)$. By Claim 3.15, if k is large enough then $z \in i_2(C)$ and therefore $y = i_2^{-1}(z) \in C$ is uniquely defined. Denote by $\tilde{\gamma _y} : S^1 \rightarrow C$ the $\xi _{k,w}(t)$-orbit of y. By Claim 3.13, there exist $k_1,...,k_r, l_1,...,l_r \in {\mathbb {Z}}, u_1,...,u_r, v_1,...,v_r \in \{0,1\}$ such that

$$\begin{aligned}{}[\tilde{\gamma _y}]_{\pi _0({\mathscr {L}}C)} = \eta _{C,s_0}(\Pi _{m=1}^r a^{k_m}c^{-u_m}b^{l_m}c^{v_m}) . \end{aligned}$$

Since $\tau _{i_2}([\tilde{\gamma _y}]_{\pi _0({\mathscr {L}}C)}) = [{\tilde{\gamma }}]_{\pi _0({\mathscr {L}}\Sigma )} = \tau _{i_2}(\alpha _{k,w})$ (or $\tau _{i_2}(\alpha _k^\prime )$), one has $[\tilde{\gamma _y}]_{\pi _0({\mathscr {L}}C)} = \alpha _{k,w}$ (or $[\tilde{\gamma _y}]_{\pi _0({\mathscr {L}}C)} = \alpha _k^\prime$) by Claim 3.14.

Thus non-degenerate fixed points of $(i_2)_* \Xi _k(w)$ in $\Sigma$ whose orbits are in the class $\tau _{i_2}(\alpha _{k,w})$ correspond in a 1-1 manner to non-degenerate fixed points of $\Xi _k(w)$ in D whose orbits are in the class $\alpha _{k,w}$ (and there is a similar correspondence for the classes $\tau _{i_2}(\alpha _k^\prime )$ and $\alpha _k^\prime$). Note that since Claim 3.14 uses Lemma 1.3, this is the point where the algebraic Lemma 1.3 enters the proof.

Therefore it is enough to restrict the analysis to the dynamics on D, and further, to the dynamics on C, since $z \in i_2(C)$. By Claim 3.9, for large enough k there are $2^{2r}$ non-degenerate fixed points of $\Xi _k(w)$ in the class $\alpha _{k,w}$, indexed by $\mathbf {\epsilon } = (\epsilon _0,...,\epsilon _{2r-1}) \in \{\pm 1\}^{2r}$, such that their actions and Conley-Zehnder indices are given by Eqs. 3,4. Since $i_2$ preserves actions and Conley-Zehnder indices by construction, this proves Proposition 3.11.

Similarly, setting $w = (VH)^r$, by Claim 3.10 for large enough $k \in K$ there are $2^{2r}$ non-degenerate fixed points of $\Xi _k(w)$ in the class $\alpha _k^\prime$, such that fixed points in different orbits have action gaps that grow linearly with k. The injection $i_2$ preserves actions, so this proves Proposition 3.12. $\square$

We finish this section with the proofs of the claims.

Proof of Claim 3.13

Denote $z = {\tilde{\gamma }}(0)$. Recall that $\psi _{k,w}^\prime$ is the piecewise-linear version of $\psi _{k,w}$ defined in Sect. 3.2 and that it is the concatenation of some autonomous Hamiltonian isotopies $f_{0,V}^{N_1t}, f_{0,H}^{M_1t}, ...$, while $\psi _{k,w}$ is their composition. Thus ${\tilde{\gamma }}$ and $t \mapsto \psi _{k,w}^\prime (t) (z)$ are freely homotopic loops in C.

Therefore it is enough to show there exist some integers $k_1,...,k_r, l_1,...,l_r \in {\mathbb {Z}}$ and $u_1,...,u_r, v_1,...,v_r \in \{0,1\}$ such that $[t \mapsto \psi _{k,w}^\prime (t) (z)]_{\pi _0({\mathscr {L}}C)} = \eta _{C,s_0}(\Pi _{m=1}^r a^{k_m} c^{-u_m} b^{l_m} c^{v_m})$, since homotopic loops have the same $\eta _{C,s_0}$-images. This is shown in the proof of Lemma 4.2 in [1] - in their notation, $\psi _{k,w}^\prime (t)$ is denoted $\phi ^t$ and $k_\mu , l_\mu , u_\mu , v_\mu$ are denoted $n_\mu , m_\mu , \epsilon _\mu , \nu _\mu$ respectively, for $1 \le \mu \le r$ (note we do not need the whole statement of Lemma 4.2). $\square$

Proof of Claim 3.14

The two assumptions are similar and the proofs for the two cases are the same. For concreteness, assume $\tau _{i_2}(\gamma ) = \tau _{i_2}(\alpha _{k,w})$, the other case is analogous.

Let $\delta \in \pi _1(C,s_0)$ be any element such that $\gamma = \eta _{C,s_0}(\delta )$. By assumption, $\tau _{i_2}(\gamma ) = \tau _{i_2}(\alpha _{k,w})$. Commutativity implies $\eta _{\Sigma ,i_2(s_0)}((i_2)_* \delta ) = \eta _{\Sigma ,i_2(s_0)}((i_2)_* \beta _{k,w})$, so one sees that $(i_2)_* \delta$ and $(i_2)_* \beta _{k,w}$ are conjugate in $\pi _1(\Sigma , i_2(s_0))$.

In the case where the genus of $\Sigma$ is 2, recall that $\pi _1(D,s_0) = F_3$ and that $(i_2)_* : F_3 \rightarrow \pi _1(\Sigma , i_2(s_0))$ is exactly the same homomorphism as in the requirements of Lemma 1.3.

In the case where the genus of $\Sigma$ is 3, denote

$$\begin{aligned}&p_{1234}: \pi _1(\Sigma , i_2(s_0)) \rightarrow \langle g_1,g_2,g_3,g_4 | [g_1,g_2][g_3,g_4] \rangle , \\&\quad g_1 \mapsto g_1, g_2 \mapsto g_2, g_3 \mapsto g_3, g_4 \mapsto g_4 , \\&\quad g_5,g_6 \mapsto 1 , \end{aligned}$$

and note that $p_{1234} \circ (i_2)_*$ is exactly the homomorphism as in the requirements of Lemma 1.3. Since the elements $(i_2)_* \delta , (i_2)_* \beta _{k,w}$ are conjugate in $\pi _1(\Sigma , i_2(s_0))$, so are their images $(p_{1234} \circ (i_2)_*) (\delta ), (p_{1234} \circ (i_2)_*) (\beta _{k,w})$ conjugate in $\langle g_1,g_2,g_3,g_4 | [g_1,g_2][g_3,g_4] \rangle$.

In both cases, we get by Lemma 1.3 that $\delta$ and $\beta _{k,w}$ are conjugate in $\pi _1(D,s_0)$, so $\gamma = \eta _{D,s_0}(\delta ) = \eta _{D,s_0}(\beta _{k,w}) = \alpha _{k,w}$ by definition of $\eta _{D,s_0}$. $\square$

Proof of Claim 3.15

Under both of the assumptions (that the orbit of z is in the class $\tau _{i_2}(\alpha _{k,w})$ or $\tau _{i_2}(\alpha _k^\prime )$), the orbit of z is in the class $\eta _{\Sigma , i_2(s_0)}(\Pi _{m=1}^r (g_1 g_3)^{k_{2m-1}} (g_2 g_1^{-1} g_2^{-1} g_3)^{k_{2m}})$ for some sequence $k_1,...,k_{2r} \in {\mathbb {Z}}$, since $(i_2)_*(a) = g_1 g_3, (i_2)_*(b) = g_2 g_1^{-1} g_2^{-1} g_3$. Note that for large enough k, the elements $k_m$ in this sequence all satisfy $|k_m| \ge 2$.

As noted in Sect. 2, $\pi _1(\Sigma )$ is a free product of $H_1 = \langle g_1,g_2 \rangle , H_2 = \langle g_3,g_4 \rangle$ with amalgamation of subgroups $A = \langle [g_1,g_2] \rangle , B = \langle [g_3,g_4] \rangle$ by the isomorphism

$$\begin{aligned}&\phi : A \rightarrow B ,\\&\quad [g_1,g_2] \mapsto [g_3,g_4]^{-1} . \end{aligned}$$

In the case where the genus of $\Sigma$ is 3, $\pi _1(\Sigma )$ is a free product of $H_1 = \langle g_1,g_2 \rangle , H_2 = \langle g_3,g_4,g_5,g_6 \rangle$ with amalgamation of subgroups $A = \langle [g_1,g_2] \rangle , B = \langle [g_3,g_4][g_5,g_6] \rangle$ by the isomorphism

$$\begin{aligned}&\phi : A \rightarrow B ,\\&\quad [g_1,g_2] \mapsto ([g_3,g_4][g_5,g_6])^{-1} . \end{aligned}$$

Note that $z \in i_2(D)$, otherwise z is a degenerate fixed point. Assume by contradiction $z \in i_2(C_1 \cup C_2)$. Denote the orbit of z under $(i_2)_* \xi _{k,w}(t)$ by ${\tilde{\gamma }}: S^1 \rightarrow \Sigma$.

If $z \in i_2(C_1)$, then ${\tilde{\gamma }}(t) \in i_2(C_1)$ for all t, since ${\tilde{\gamma }}(t) \in i_2(D)$ for all t, and $C_1$ is a connected component of D. This means ${\tilde{\gamma }}$ is (freely) homotopic to some loop ${\tilde{\delta }}: S^1 \rightarrow \Sigma$ based in $i_2(s_0)$ with $[{\tilde{\delta }}]_{\pi _1(\Sigma ,i_2(s_0))} = g_1^n$ for some $n \in {\mathbb {Z}}$, since by construction $\tau _{i_2} \circ \eta _{C_1, s_1^\prime } (d_1) = \eta _{\Sigma ,i_2(s_0)} (g_1)$ (recall that $d_1$ is the homotopy class of a loop going around $i_2(C_1)$ once). Therefore,

$$\begin{aligned} \eta _{\Sigma , i_2(s_0)} \left( \Pi _{m=1}^r (g_1 g_3)^{k_{2m-1}} (g_2 g_1^{-1} g_2^{-1}g_3)^{k_{2m}} \right) = [{\tilde{\gamma }}]_{\pi _0({\mathscr {L}}\Sigma )} = [{\tilde{\delta }}]_{\pi _0({\mathscr {L}}\Sigma )} = \eta _{\Sigma , i_2(s_0)}(g_1^n) , \end{aligned}$$

and so $\Pi _{m=1}^r (g_1 g_3)^{k_{2m-1}} (g_2 g_1^{-1} g_2^{-1}g_3)^{k_{2m}} \sim g_1^n$.

Note that $(g_1^n)$, a sequence with a single element, is a cyclically reduced sequence of $\langle H_1*H_2 , A=B, \phi \rangle$, so $g_1^n$ is a cyclically reduced element, with $len(g_1^n) = 1$. Recall that w is given in cyclically reduced form, thus $\forall \ 1 \le m \le r: M_m, N_m \ne 0$. Since for all m, $|k_m| \ge 2$, by Claim 2.3 it can be seen that $len \left( \Pi _{m=1}^r (g_1 g_3)^{k_{2m-1}} (g_2 g_1^{-1} g_2^{-1}g_3)^{k_{2m}} \right) > 1$, in contradiction. If the genus of $\Sigma$ is 3, then note that $p_{1234}$ (defined in the proof of Claim 3.14) preserves factors (in the sense of the proof of Claim 2.3), which means that

$$\begin{aligned}&len(\Pi _{m=1}^r (g_1 g_3)^{k_{2m-1}} (g_2 g_1^{-1} g_2^{-1}g_3)^{k_{2m}}) = \\&\quad = len(p_{1234}(\Pi _{m=1}^r (g_1 g_3)^{k_{2m-1}} (g_2 g_1^{-1} g_2^{-1}g_3)^{k_{2m}})) > 1 , \end{aligned}$$

by Claim 2.3. This is again a contradiction. Therefore $z \not \in i_2(C_1)$.

Likewise, assume $z \in i_2(C_2)$. Similarly to the previous case, there is a conjugacy between $\Pi _{m=1}^r (g_1 g_3)^{k_{2m-1}} (g_2 g_1^{-1} g_2^{-1}g_3)^{k_{2m}}$ and $g_3^n$ in $\pi _1(\Sigma , i_2(s_0))$ for some $n \in {\mathbb {Z}}$. As before, $len(\Pi _{m=1}^r (g_1 g_3)^{k_{2m-1}} (g_2 g_1^{-1} g_2^{-1}g_3)^{k_{2m}}) > 1$ and $len(g_3^n) = 1$, but len is conjugation-invariant, so this is a contradiction.

All cases lead to a contradiction, therefore $z \in i_2(C)$. $\square$

4 Incompressibility in genus 3

This section describes an embedding $i_3$ of an egg-beater-like surface $E = C \bigsqcup C_1 \bigsqcup C_2 \bigsqcup C_3$ to a closed orientable surface $\Sigma _3$ of genus 3 such that $i_3 \restriction _C$ is incompressible, i.e. $(i_3 \restriction _C)_*: \pi _1(C) \rightarrow \pi _1(\Sigma _3)$ and $\tau _{i_3 \restriction _C}: \pi _0({\mathscr {L}}C) \rightarrow \pi _0({\mathscr {L}}\Sigma _3)$ are both injective. This incompressibility will imply Theorems 1.1, 1.2 by following the original proofs in [11] and [1]. Notation from previous sections is used in this section.

4.1 The egg-beater surface and map and the embedding

Recall the egg-beater surface $D = C_V \bigcup _{VH_{0,1}} C_H \bigsqcup C_1 \bigsqcup C_2$ defined in Sect. 3 and the cylinder $C_* = [-1,1] \times {\mathbb {R}}/ L{\mathbb {Z}}$. Let $C_3$ be another copy of $C_*$ and define $E = D \bigsqcup C_3$, with the symplectic form $dx \wedge dy$ on every component. Denote by $c_3: C_* \rightarrow E, e_3: D \rightarrow E$ the symplectic inclusions, i.e. $e_3 \bigsqcup c_3: D \bigsqcup C_* \rightarrow E$ is the identity.

The embedding $i_3: E \hookrightarrow \Sigma _3$ is defined in two parts. First, embed C symplectically into $S^2$. Note that C separates the sphere into 4 connected components. Choose any one of these components and connect it with handles to the other 3 components, with one handle each. The result is a genus 3 surface $\Sigma _3$, this defines $i_3 \restriction _C$. Define $i_3$ on $C_1 \bigsqcup C_2 \bigsqcup C_3$ by symplectically embedding each of them on a different handle. The embedding $i_3$ can be seen in Fig. 10 and the generators of $\pi _1(\Sigma _3,i_3(s_0)) = \langle g_1,...,g_6 | [g_1,g_2][g_3,g_4][g_5,g_6] \rangle$ can be seen in Fig. 11. The orientations of $i_3 \restriction _{C_j}$ for $j=1,2,3$ are chosen such that

$$\begin{aligned}&\tau _{e_3 \circ c_1} [t \mapsto (0,Lt)]_{\pi _0({\mathscr {L}}C_*)} = \eta _{\Sigma _3,i_3(s_0)}(g_1) ,\\&\quad \tau _{e_3 \circ c_2} [t \mapsto (0,Lt)]_{\pi _0({\mathscr {L}}C_*)} = \eta _{\Sigma _3,i_3(s_0)}(g_3) ,\\&\quad \tau _{c_3} [t \mapsto (0,Lt)]_{\pi _0({\mathscr {L}}C_*)} = \eta _{\Sigma _3,i_3(s_0)}(g_5) . \end{aligned}$$

The various cylinders, egg-beater surfaces and closed surfaces mentioned in this paper and the embeddings between them are summarized in Fig. 12.

Fig. 10

The embedding $i_3$. This figure is embedded in $S^2$

Fig. 11

The generators of $\pi _1(\Sigma _3,i_3(s_0))$, dashed lines only for visibility

Fig. 12

Embeddings between the surfaces

As can be seen in Fig. 11, the induced homomorphism $(i_3)_*: F_3 \rightarrow \pi _1(\Sigma _3,i_3(s_0))$ acts on the generators a, b, c of $F_3$ so:

$$\begin{aligned}&a \mapsto g_1 g_3 ,\\&\quad b \mapsto g_3 g_5 ,\\&\quad c \mapsto g_3 , \end{aligned}$$

where $a,b,c \in \pi _1(C,s_0)$ are as defined in Sect. 3.2.

The following claim is key in proving Theorems 1.1, 1.2 in genus 3.

Claim 4.1

The map $i_3 \restriction _C$ is incompressible, i.e. $(i_3 \restriction _C)_*$ and $\tau _{i_3 \restriction _C}$ are injective.

Define the egg-beater maps on E as follows:

$$\begin{aligned}&\Theta _k: F_2 \rightarrow Ham_c(E) ,\\&\quad V \mapsto (e_3 \circ e_2 \circ c_V)_* f_k \bigsqcup -(e_3 \circ c_1)_* f_k \bigsqcup -(e_3 \circ c_2)_* f_k \bigsqcup 0 \restriction _{C_3} ,\\&\quad H \mapsto (e_3 \circ e_2 \circ c_H)_* f_k \bigsqcup 0 \restriction _{C_1} \bigsqcup -(e_3 \circ c_2)_* f_k \bigsqcup -(c_3)_* f_k . \end{aligned}$$

These are Hamiltonian diffeomorphisms: $\Theta _k(V)$ can be seen to be generated by the Hamiltonian

$$\begin{aligned} (e_3 \circ e_2 \circ c_V)_* h_k \bigsqcup -(e_3 \circ c_1)_* h_k \bigsqcup -(e_3 \circ c_2)_* h_k \bigsqcup 0 \restriction _{C_3} , \end{aligned}$$

and $\Theta _k(H)$ by the Hamiltonian

$$\begin{aligned} (e_3 \circ e_2 \circ c_H)_* h_k \bigsqcup 0 \restriction _{C_1} \bigsqcup -(e_3 \circ c_2)_* h_k \bigsqcup -(c_3)_* h_k . \end{aligned}$$

The egg-beater maps on $\Sigma _3$ are $(i_3)_* \Theta _k(w)$, for $w \in F_2$.

4.2 Proof of Claim 4.1

In this proof we will use Dehn’s algorithm for the word problem for one-relator groups, see [3]. Recall that all surface groups are groups of this type.

Theorem 4.2

[Dehn’s algorithm for the word problem of a one-relator group] Let $G = \langle S | r \rangle$ be a finitely generated one-relator group, where $S = S^{-1} = \{s_1,...,s_n\}$ is a finite symbol set and r is a freely reduced word of length l on the symbols of S. Let $w = \Pi _{j=1}^k s_{i_j}$ be a freely reduced word of length $k>0$ on the symbol set S, i.e. for any j, $s_{i_j} \ne s_{i_{j+1}}^{-1}$.

If $w = 1$ in the group G, then w has a subword v of length at least $\left\lfloor \frac{l}{2} \right\rfloor + 1$, which is also a subword of a cyclic permutation of r or of $r^{-1}$.

Note that the notion of length of a word w used by Dehn is not exactly the same as the one introduced in Sect. 2. Dehn’s notion refers to the minimal number of elements of S to be multiplied in G to get the word w.

We are now ready to prove Claim 4.1.

Proof of Claim 4.1

Consider the automorphism $I: F_3 \rightarrow F_3$ given by

$$\begin{aligned}&a \mapsto ac ,\\&b \mapsto cb ,\\&c \mapsto c , \end{aligned}$$

and denote by $\varphi : F_3 \rightarrow \pi _1(\Sigma _3,i_3(s_0))$ the following homomorphism:

$$\begin{aligned}&a \mapsto g_1 ,\\&b \mapsto g_5 ,\\&c \mapsto g_3 . \end{aligned}$$

Note that $(i_3 \restriction _C)_* = \varphi \circ I$. By this decomposition, one can see that $(i_3 \restriction _C)_*$ is injective. Since I is an isomorphism, it preserves conjugacy classes, and so $i_3 \restriction _C$ is incompressible if and only if $\varphi$ preserves conjugacy classes, i.e. if and only if for all $x,y \in F_3$ which are not conjugates, $\varphi (x),\varphi (y) \in \pi _1(\Sigma _3,i_3(s_0))$ also are not conjugates.

Recall the definitions and the statement of the Conjugacy Theorem for Free Products with Amalgamation, given in Sect. 2. The conjugacy relation, in any group, will again be denoted by $\sim$. Assume by contradiction that there exist $x,y \in F_3$ such that $x \not \sim y$ and $\varphi (x) \sim \varphi (y)$. In order for the concept of cyclically reduced elements of $F_3$ to be defined, consider $F_3 = \langle a,b,c \rangle$ as the free product $\left\langle \left\langle R \right\rangle * \left\langle S \right\rangle \right\rangle$, for some two proper subsets $R \bigsqcup S = \{a,b,c\}$. This partition of $\{a,b,c\}$ gives a well-defined concept of cyclically reduced sequences of elements of $F_3$ and also a well defined length function $len = len_{R,S} : F_3 \rightarrow {\mathbb {Z}}_{\ge 0}$, defined in Sect. 2. Without loss of generality assume x, y are cyclically reduced. We will reach a contradiction.

First, consider the case where for all partitions R, S, $len_{R,S}(x), len_{R,S}(y) < 2$. If $len_{R,S}(x) = 0$ or $len_{R,S}(y) = 0$, then $x = 1$ or $y = 1$ respectively, and therefore $\varphi (x) = 1$ or $\varphi (y) = 1$ respectively. This implies that $\varphi (x) = \varphi (y) = 1$ and by injectivity of $\varphi$, $x = y = 1$, in contradiction. Therefore in this case we get that for all partitions R, S, $len_{R,S}(x) = len_{R,S}(y) = 1$. This implies that there exist $r, s \in \{a,b,c\}$ such that $x \sim r^n, y \sim s^m$ for some $m,n \in {\mathbb {Z}}$. By passing to the abelianization ${\mathbb {Z}}^6$ of $\pi _1(\Sigma _3)$, one sees that in fact $r^n = s^m$, so $x \sim y$, in contradiction. Therefore there exists a proper partition $R \bigsqcup S = \{a,b,c\}$ such that $len_{R,S}(x) \ge 2$ or $len_{R,S}(y) \ge 2$. By symmetry between x and y and between a, b, c one may assume that $R = \{a\}, S = \{b,c\}$ and $len_{R,S}(x) \ge 2$.

Denote the groups $G = \langle g_1,g_2 \rangle \simeq F_2$, $H = \langle g_3,...,g_6 \rangle \simeq F_4$, subgroups $A = \langle [g_1,g_2] \rangle < G$, $B = \langle [g_3,g_4][g_5,g_6] \rangle < H$, and the isomorphism

$$\begin{aligned}&\psi : A \xrightarrow {\sim } B ,\\&\quad [g_1,g_2] \mapsto ([g_3,g_4][g_5,g_6])^{-1} . \end{aligned}$$

Note that $\pi _1(\Sigma _3) = \langle G * H, A = B, \psi \rangle$ and that $\varphi$ preserves factors in the sense of Sect. 2. With respect to this decomposition, $\varphi (x), \varphi (y)$ are also cyclically reduced, since x, y are. Let $(x_1,...,x_n)$ be a cyclically reduced sequence representing x (i.e. $x = \Pi _{i=1}^n x_i$).

Since $\varphi (x) \sim \varphi (y)$, by the Conjugacy Theorem for Free Products with Amalgamation, there exist $\mu \in A, 1 \le k \le n$ such that

$$\begin{aligned} \varphi (y) = \mu \cdot \Pi _{i=k}^{k-1} \varphi (x_i) \cdot \mu ^{-1} := \mu \cdot \varphi (x_k) \cdot ... \cdot \varphi (x_n) \cdot \varphi (x_1) \cdot ... \cdot \varphi (x_{k-1}) \mu ^{-1}, \end{aligned}$$

and since $A = \langle [g_1,g_2] \rangle$, we see that $\varphi (y) = [g_1,g_2]^l \cdot \Pi _{i=k}^{k-1} \varphi (x_i) \cdot [g_1,g_2]^{-l}$ for some $l \in {\mathbb {Z}}$.

If $l = 0$, $\varphi (y) = \Pi _{i=k}^{k-1} \varphi (x_i)$. Since $\varphi$ is injective, this equation can be pulled back to $F_3$ to get $y = \Pi _{i=k}^{k-1} x_i \sim x$, in contradiction. Thus $l \ne 0$. Without loss of generality one can assume $l > 0$, the other case is treated in the same manner.

Since $Im(\varphi ) = \langle g_1, g_3, g_5 \rangle$, denote

$$\begin{aligned} \varphi (x_k) = f_1, \varphi (x_{k+1}) = f_2, ..., \varphi (x_n) = f_{n-k+1}, \varphi (x_1) = f_{n-k+2}, ..., \varphi (x_{k-1}) = f_n , \end{aligned}$$

with every $f_j \in \{g_1,g_3,g_5\}^{\pm 1}$. Similarly, since $Im(\varphi ) = \langle g_1, g_3, g_5 \rangle$, let $\varphi (y) = \left( \Pi _{j=1}^m f_j'\right) ^{-1}$, with all $f_j' \in \{g_1,g_3,g_5\}^{\pm 1}$ and where the word $\Pi _{j=1}^m f_j'$ is freely reduced. Our equation now reads

$$\begin{aligned}{}[g_1,g_2]^l \cdot \Pi _{j=1}^n f_j \cdot [g_1,g_2]^{-l} \cdot \Pi _{j=1}^m f_j' = 1 . \end{aligned}$$

(5)

Let w be the word on the symbols $\{g_1,...,g_6\}^{\pm 1}$ that is the free reduction of the LHS of Eq. 5. Note that $\Pi _{j=1}^n f_j, \Pi _{j=1}^m f_j'$ are freely reduced and they contain no elements $g_2^{\pm 1}$. Therefore the subwords $[g_1,g_2]^l$ and $[g_1,g_2]^{-l}$ haven’t been fully reduced in the reduction that results in w, i.e. w contains at least one instance of the subword $g_2 g_1^{-1} g_2^{-1}$ (note that the $g_1$ at the beginning of the $[g_1,g_2]$ may have been reduced). Specifically, w is not the empty word.

Recall that the single relator in the group $\pi _1(\Sigma _3, i_3(s_0))$ is $r_\Sigma = [g_1,g_2][g_3,g_4][g_5,g_6]$, of length 12. Since w doesn’t contain any occurrences of $g_4^{\pm 1}$ and $g_6^{\pm 1}$, one sees that w cannot contain a subword a cyclic permutation of $r_\Sigma$ or its inverse that is of length at least 7, since every such subword contains either $g_4^{\pm 1}$ or $g_6^{\pm 1}$ or both. By Dehn’s algorithm, we now see that $w = 1$ in the group $\pi _1(\Sigma _3, i_3(s_0))$ is a contradiction. This concludes the proof. $\square$