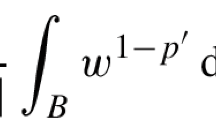Bergman Projections Induced by Doubling Weights on the Unit Ball of ${\mathbb {C}}^n$

Abstract

Let $p>1$ and $\omega ,\upsilon \in {\mathcal {D}}$. The boundedness of $P_\omega :L^\infty ({\mathbb {B}})\rightarrow {\mathcal {B}}({\mathbb {B}})$ and $P_\omega (P_\omega ^+):L^p({\mathbb {B}},\upsilon dV)\rightarrow L^p({\mathbb {B}},\upsilon dV)$ are investigated in this paper.

1 Introduction

Let ${\mathbb {B}}$ be the open unit ball of ${\mathbb {C}}^n$ and ${\mathbb {S}}$ the boundary of ${\mathbb {B}}$. When $n=1$, ${\mathbb {B}}$ is the open unit disk in the complex plane ${\mathbb {C}}$ and always denoted by ${\mathbb {D}}$. Let $H( {\mathbb {B}})$ denote the space of all holomorphic functions on ${\mathbb {B}}$. For any two points

$$\begin{aligned} z=(z_1,z_2,\ldots ,z_n)\quad \text{ and }\quad w=(w_1,w_2,\ldots ,w_n) \end{aligned}$$

in ${\mathbb {C}}^n$, define $\langle z,w \rangle =z_1\overline{w_1}+\cdots +z_n\overline{w_n}$ and $|z|=\sqrt{\langle z,z \rangle }=\sqrt{|z_1|^2+\cdots +|z_n|^2}$.

Suppose $\omega$ is a radial weight ( i.e., $\omega$ is a positive, measurable and integrable function on [0, 1) and $\omega (z)=\omega (|z|)$ for all $z\in {\mathbb {B}}$). Let ${\hat{\omega }}(r)=\int _r^1\omega (t)dt$. We say that

• $\omega$ is a doubling weight, denoted by $\omega \in \hat{{\mathcal {D}}}$, if there is a constant $C>0$ such that

  $$\begin{aligned} {\hat{\omega }}(r)<C{\hat{\omega }}\left( \frac{1+r}{2}\right) ,\quad \text{ when } 0\le r<1; \end{aligned}$$

• $\omega$ is a regular weight, denoted by $\omega \in {\mathcal {R}}$, if $\omega$ is continuous and there exist $C>0$ and $\delta \in (0,1)$ such that

  $$\begin{aligned} \frac{1}{C}<\frac{{\hat{\omega }}(t)}{(1-t)\omega (t)}<C,\quad \text{ when } t\in (\delta ,1); \end{aligned}$$

• $\omega$ is a rapidly increasing weight, denoted by $\omega \in {\mathcal {I}}$, if (see [10])

  $$\begin{aligned} \lim _{r\rightarrow 1} \frac{{\hat{\omega }}(r)}{(1-r)\omega (r)}=\infty ; \end{aligned}$$

• $\omega$ is a reverse doubling weight, denoted by $\omega \in {\check{{\mathcal {D}}}}$, if there exist $K>1$ and $C>1$, such that

  $$\begin{aligned} {\hat{\omega }}(t)\ge C{\hat{\omega }}\left( 1-\frac{1-t}{K}\right) ,\quad t\in (0,1). \end{aligned}$$

  (1)

See [9, 10] and the references therein for more details about ${\mathcal {I}},{\mathcal {R}}$, $\hat{{\mathcal {D}}}$. Let ${\mathcal {D}}=\hat{{\mathcal {D}}}\cap {\check{{\mathcal {D}}}}$. More information about ${\check{{\mathcal {D}}}}$ and ${\mathcal {D}}$ can be found in [7, 14].

Let $d\sigma$ and dV be the normalized surface and volume measures on ${\mathbb {S}}$ and ${\mathbb {B}}$, respectively. For $0<p< \infty$, the Hardy space $H^p( {\mathbb {B}})$(or $H^p$) is the space consisting of all functions $f\in H( {\mathbb {B}})$ such that

$$\begin{aligned} \Vert f\Vert _{H^p}=\sup _{0<r<1}M_p(r,f)<\infty , \end{aligned}$$

where

$$\begin{aligned} M_p(r,f)=\left( \int _{ {\mathbb {S}}}|f(r\xi )|^pd\sigma (\xi )\right) ^{1/p}, \quad 0<p<\infty . \end{aligned}$$

$H^\infty$ is the space consisting of all $f\in H( {\mathbb {B}})$ such that $\Vert f\Vert _{H^\infty }=\sup _{z\in {\mathbb {B}}}|f(z)|<\infty$.

For any $f\in H( {\mathbb {B}})$, let $\Re f$ be the radial derivative of f, that is,

$$\begin{aligned} \Re f(z)=\sum _{k=1}^n z_k\frac{\partial f}{\partial z_k}(z),\quad z=(z_1,z_2,\ldots ,z_n)\in {\mathbb {B}}. \end{aligned}$$

Then the Bloch space ${\mathcal {B}}( {\mathbb {B}})$ consists of all $f\in H( {\mathbb {B}})$ such that

$$\begin{aligned} \Vert f\Vert _{{\mathcal {B}}( {\mathbb {B}})}=|f(0)|+\sup _{z\in {\mathbb {B}}}(1-|z|^2)|\Re f(z)|<\infty . \end{aligned}$$

When $n=1$, $\Vert \cdot \Vert _{{\mathcal {B}}({\mathbb {D}})}$ differs from the norm defined in the classical way, but the two norms are equivalent. See [19] for example. We denote ${\mathcal {B}}( {\mathbb {B}})$ by ${\mathcal {B}}$ for simplicity.

Suppose $\mu$ is a positive Borel measure on ${\mathbb {B}}$ and $0<p<\infty$. The Lebesgue space $L^p( {\mathbb {B}},d\mu )$ consists of all measurable complex functions f on ${\mathbb {B}}$ such that $|f|^p$ is integrable with respect to $\mu$, that is, $f\in L^p( {\mathbb {B}},d\mu )$ if and only if

$$\begin{aligned} \Vert f\Vert _{L^p( {\mathbb {B}},d\mu )}=\left( \int _ {\mathbb {B}}|f(z)|^pd\mu (z)\right) ^{1/p}<\infty . \end{aligned}$$

$L^\infty ( {\mathbb {B}},d\mu )$ consists of all measurable complex functions f on ${\mathbb {B}}$ such that f is essentially bounded, that is, $f\in L^\infty ( {\mathbb {B}},d\mu )$ if and only if

$$\begin{aligned} \Vert f\Vert _{L^\infty ( {\mathbb {B}}, d\mu )}=\inf _{E\subset {\mathbb {B}},\mu (E)=0}\sup _{z\in {\mathbb {B}}\backslash E}|f(z)|<\infty . \end{aligned}$$

More details about $L^p( {\mathbb {B}},d\mu )$ can be found in [18, 20]. For a positive and measurable function $\omega$ on ${\mathbb {B}}$, letting $d\mu (z)=\omega (z)dV(z)$, $\mu$ is a Borel measure on ${\mathbb {B}}$ if $\omega \in L^1( {\mathbb {B}},dV)$. Then, we will write $L^p( {\mathbb {B}},d\mu )$ as $L^p( {\mathbb {B}},\omega dV)$. When $n=1$ and $z\in {\mathbb {D}}$, let $dV(z)=\frac{1}{\pi }dA(z)$ be the normalized area measure on ${\mathbb {D}}$. Then we can define the Lebesgue space on the unit disk in the same way.

In [10], Peláez and Rättyä introduced a new class of weighted Bergman spaces $A_\omega ^p({\mathbb {D}})$, which is induced by rapidly increasing weights $\omega$ in ${\mathbb {D}}$. That is

$$\begin{aligned} A_\omega ^p({{\mathbb {D}}})=L^p({\mathbb {D}},\omega dA)\cap H({\mathbb {D}}),\quad \text{ where } 0<p<\infty . \end{aligned}$$

See [9,10,11,12,13, 15, 16] for more results on $A_\omega ^p({\mathbb {D}})$ with $\omega \in \hat{{\mathcal {D}}}$. In [4], we extended some results of the Bergman space $A_\omega ^p({\mathbb {D}})$ to the unit ball ${\mathbb {B}}$ of ${\mathbb {C}}^n$. That is,

$$\begin{aligned} A_\omega ^p( {\mathbb {B}})=L^p( {\mathbb {B}},\omega dA)\cap H( {\mathbb {B}}),\quad \text{ where } 0<p<\infty . \end{aligned}$$

In brief, let $A_\omega ^p=A_\omega ^p( {\mathbb {B}})$. As a subspace of $L^p( {\mathbb {B}},\omega dV)$, the norm on $A_\omega ^p$ will be written as $\Vert \cdot \Vert _{A_\omega ^p}$. It is easy to check that $A_\omega ^p$ is a Banach space when $p\ge 1$ and a complete metric space with distance $\rho (f,g)=\Vert f-g\Vert _{A_\omega ^p}^p$ when $0<p<1$. When $\alpha >-1$ and $c_\alpha =\Gamma (n+\alpha +1)/[\Gamma (n+1)\Gamma (\alpha +1)]$, if $\omega (z)=c_\alpha (1-|z|^2)^\alpha$, the space $A_\omega ^p$ becomes the classical weighted Bergman space $A_\alpha ^p$, and we write $dV_\alpha (z)=c_\alpha (1-|z|^2)^\alpha dV(z)$. When $\alpha =0$, $A^p_0=A^p$ is the standard Bergman space. See [18, 20] for the theory of $H^p$ and $A_\alpha ^p$.

When $p=2$, the space $A_\omega ^2$ is a Hilbert space with the inner product

$$\begin{aligned} \langle f,g \rangle _{A_\omega ^2}=\int _ {\mathbb {B}}f(z)\overline{g(z)}\omega (z)dV(z) \quad \text{ for } \text{ all } f,g\in A_\omega ^2. \end{aligned}$$

In a standard way, for every $z\in {\mathbb {B}}$, the point evaluation $L_z f=f(z)$ is a bounded linear functional on $A_\omega ^2$. By Riesz’s Representation Theorem, we see that there exists a unique function $B_z^\omega$ such that

$$\begin{aligned} f(z)=\langle f, B_z^\omega \rangle _{A_\omega ^2}=\int _ {\mathbb {B}}f(w)\overline{B_z^\omega (w)}\omega (w)dV(w)\quad \text{ for } \text{ all } f\in A_\omega ^2. \end{aligned}$$

For any $f\in L^1( {\mathbb {B}},\omega dV)$, the Bergman projection $P_\omega f$ is defined by

$$\begin{aligned} P_\omega f(z)=\int _ {\mathbb {B}}f(\xi )\overline{B_z^\omega (\xi )}\omega (\xi )dV(\xi ), \end{aligned}$$

while the maximal Bergman projection $P_\omega ^+$ is defined by

$$\begin{aligned} P_\omega ^+(f)(z)=\int _ {\mathbb {B}}f(\xi )\left| B_z^\omega (\xi )\right| \omega (\xi )dV(\xi ). \end{aligned}$$

When $\omega (z)=c_\alpha (1-|z|^2)^\alpha (\alpha >-1)$, $P_\omega$ and $P_\omega ^+$ will be denoted by $P_\alpha$ and $P_\alpha ^+$, respectively.

The study of the Bergman projection has a long history. If $s\in {\mathbb {C}}$ such that $\Re s>-1$ for all $f\in L^1( {\mathbb {B}},dV)$, let

$$\begin{aligned} T_s f (z)=\frac{\Gamma (n+s+1)}{\Gamma (n+1)\Gamma (s+1)}\int _{ {\mathbb {B}}}\frac{(1-|w|^2)^s}{(1-\langle z,w\rangle )^{n+1+s}}f(w)dV(w). \end{aligned}$$

Obviously, when $s=0$, we have $T_0=P_0$. In [5], Forelli and Rudin proved that $T_s$ is bounded on $L^p( {\mathbb {B}},dV)$ if and only if $(1+\Re s)p>1$ under the assumption that $1\le p<\infty$. In [3], Choe proved that $T_s$ is bounded on $L^p( {\mathbb {B}}, dV_\alpha )$ if and only if $(1+\Re s)p>1+\alpha$ when $p\ge 1$ and $\alpha >-1$. From [20, Thm. 2.11], we see that $P_\alpha$ is bounded on $L^p( {\mathbb {B}},dV_\beta )$ if and only if $p(\alpha +1)>\beta +1$ when $p\ge 1, \alpha ,\beta \in (-1,\infty )$. In [8], Liu gave a sharp estimate for the norm of $P_0$ on $L^p( {\mathbb {B}},dV)$.

In the setting of the unit disk, Bekollé and Bonami showed that, if $1<p<\infty$, $\upsilon$ is positive on ${\mathbb {D}}$ and $\int _{\mathbb {D}}\upsilon (z)dA_\alpha (z)<\infty$, $P_\alpha : L^p({\mathbb {D}}, \upsilon dA_\alpha )\rightarrow L^p({\mathbb {D}}, \upsilon dA_\alpha )$ is bounded if and only if $\upsilon$ satisfies the Bekollé–Bonami condition, see [1, 2]. The result was extended in [17] for some $\omega \in {\mathcal {R}}$. In [13], the Bergman projections $P_\omega$ and the maximal Bergman projection $P_\omega ^+$ on some function spaces on ${\mathbb {D}}$ were studied when $\omega \in {\mathcal {R}}$. In [14], Peláez and Rättyä studied Bergman projections and the maximal Bergman projection $P_\omega ^+$ induced by radial weights $\omega$ on some function spaces on ${\mathbb {D}}$.

Motivated by [13, 14], in this paper we investigate the boundedness of $P_\omega :L^\infty ( {\mathbb {B}},dV)\rightarrow {\mathcal {B}}( {\mathbb {B}})$ and $P_\omega (P_\omega ^+):L^p( {\mathbb {B}},\upsilon dV)\rightarrow L^p( {\mathbb {B}},\upsilon dV)$ on the unit ball of ${\mathbb {C}}^n$ with $p>1$ and $\omega ,\upsilon \in {\mathcal {D}}$.

This paper is organized as follows. In Sect. 2, we recall some results and notation. In Sect. 3, we give some estimates for $B_z^\omega$ with $\omega \in \hat{{\mathcal {D}}}$. In Sect. 4, we investigate the boundedness of $P_\omega$ and $P_\omega ^+$ with $\omega \in {\mathcal {D}}$.

Throughout this paper, the letter C will denote a constant which may differ from one occurrence to the other. The notation $A \lesssim B$ means that there is a positive constant C such that $A\le CB$. The notation $A \approx B$ means $A\lesssim B$ and $B\lesssim A$.

2 Preliminary Results

For any $\xi ,\tau \in {\overline{ {\mathbb {B}}}}$, let $d(\xi ,\tau )=|1-\langle \xi ,\tau \rangle |^{1/2}$. Then $d(\cdot ,\cdot )$ is the non-isotropic metric. For $r>0$ and $\xi \in {\mathbb {S}}$, let

$$\begin{aligned} Q(\xi ,r)=\left\{ \eta \in {\mathbb {S}}:|1-\langle \xi ,\eta \rangle |\le r^2\right\} . \end{aligned}$$

$Q(\xi ,r)$ is a ball in ${\mathbb {S}}$ for all $\xi \in {\mathbb {S}}$ and $r\in (0,1)$. More information about $d(\cdot ,\cdot )$ and $Q(\xi ,r)$ can be found in [18, 20].

For any $a\in {\mathbb {B}}\backslash \{0\}$, let $Q_a=Q({a}/{|a|},\sqrt{1-|a|})$ and

$$\begin{aligned} S_a=S(Q_{a})=\left\{ z\in {\mathbb {B}}:\frac{z}{|z|}\in Q_{a},|a|<|z|<1\right\} . \end{aligned}$$

When $a=0$, let $Q_a= {\mathbb {S}}$ and $S_a= {\mathbb {B}}$. We call $S_a$ the Carleson block. See [4] for more information about the Carleson block. As usual, for a measurable set $E\subset {\mathbb {B}}$, $\omega (E)=\int _E \omega (z)dV(z)$.

Lemma 1

Let $\omega$ be a radial weight.

• (i) The following statements are equivalent.

  • (a) $\omega \in \hat{{\mathcal {D}}}$;

  • (b) there is a constant $b>0$ such that ${\hat{\omega }}(t)/(1-t)^b$ is essentially increasing;

  • (c) for all $x\ge 1$, $\int _0^1 s^x\omega (s)ds\approx {\hat{\omega }}(1-1/x)$.

• (ii) $\omega \in {\check{{\mathcal {D}}}}$ if and only if there is a constant $a>0$ such that ${\hat{\omega }}(t)/(1-t)^a$ is essentially decreasing.

• (iii) If $\omega$ is continuous, then $\omega \in {\mathcal {R}}$ if and only if there are $-1<a<b<+\infty$ and $\delta \in [0,1)$, such that

  $$\begin{aligned} \frac{{\omega }(t)}{(1-t)^b} \nearrow \infty , \quad \text{ and }\quad \frac{{\omega }(t)}{(1-t)^a}\searrow 0,\quad \text{ when } \delta \le t<1 . \end{aligned}$$

  (2)

Lemma 1 plays an important role in this research and can be found in many papers. Here, we refer to [7, Lem. B, Lem. C] and observation (v) in [10, Lem. 1.1].

For any radial weight $\omega$, its associated weight $\omega ^*$ is defined by

$$\begin{aligned}\omega ^*(z)=\int _{|z|}^1 \omega (s)\log \frac{s}{|z|}sds, \quad z\in {\mathbb {D}}\backslash \{0\}.\end{aligned}$$

The following lemma gives some properties and applications of $\omega ^*$.

Lemma 2

Let $\omega \in \hat{{\mathcal {D}}}$. The following statements hold.

• (i) $\omega ^*(r)\approx (1-r)\int _r^1 \omega (t)dt$ when $r\in (1/2,1)$.

• (ii) For any $\alpha >-2$, $(1-t)^\alpha \omega ^*(t)\in {\mathcal {R}}$.

• (iii) $\omega (S_a)\approx (1-|a|)^n\int _{|a|}^1 \omega (r)dr$.

• (iv) ${\hat{\omega }}(z)\approx {\hat{\omega }}(a)$, if $1/C<(1-|z|)/(1-|a|)<C$ for some fixed $C>1$.

Proof

(i) and (ii) are [10, Lem. 1.6, Lem. 1.7], respectively. (iii) was proved in [4]. (iv) can be proved directly by (i), (ii) and Lemma 1. For the benefit of readers, we give a proof here.

Suppose $\omega \in \hat{{\mathcal {D}}}$. Then there exist $a,b>-1$ and $\delta \in (0,1)$ such that (2) holds for $\omega ^*$. Then, for all $\delta<x\le y<1$ such that $1/C\le (1-x)/(1-y)\le C$, we have

$$\begin{aligned} 1\approx \left( \frac{1-x}{1-y}\right) ^a \le \frac{\omega ^*(x)}{\omega ^*(y)} \le \left( \frac{1-x}{1-y}\right) ^b \approx 1. \end{aligned}$$

If $x\le \delta$ and $1/C\le (1-x)/(1-y)\le C$, ${\hat{\omega }}(x)\approx {\hat{\omega }}(y)$ is obvious. So,

$$\begin{aligned} {\hat{\omega }}(z)\approx {\hat{\omega }}(a),\quad \text{ if } \frac{1}{C}<\frac{1-|z|}{1-|a|}<C. \end{aligned}$$

The proof is complete. $\square$

For a Banach space or a complete metric space X and a positive Borel measure $\mu$ on ${\mathbb {B}}$, we say that $\mu$ is a q-Carleson measure for X if the identity operator $I_d:X\rightarrow L_\mu ^q$ is bounded. When $0<p\le q<\infty$ and $\omega \in \hat{{\mathcal {D}}}$, a characterization of the q-Carleson measure for $A_\omega ^p$ was given in [4].

Theorem A

Let $0<p\le q<\infty$, $\omega \in \hat{{\mathcal {D}}}$, and $\mu$ be a positive Borel measure on ${\mathbb {B}}$. Then $\mu$ is a q-Carleson measure for $A_\omega ^p$ if and only if

$$\begin{aligned} \sup _{a\in {\mathbb {B}}} \frac{\mu (S_a)}{(\omega (S_a))^{\frac{q}{p}}}<\infty . \end{aligned}$$

(3)

Moreover, if $\mu$ is a q-Carleson measure for $A_\omega ^p$, then the identity operator $I_d:A_\omega ^p\rightarrow L_\mu ^q$ satisfies

$$\begin{aligned} \Vert I_d\Vert _{A_\omega ^p\rightarrow L_\mu ^q}^q \approx \sup _{a\in {\mathbb {B}}} \frac{\mu (S_a)}{(\omega (S_a))^{{q/p}}}. \end{aligned}$$

3 Some Estimates About $B_z^\omega$ with $\omega \in \hat{{\mathcal {D}}}$

In this section, we consider the reproducing kernel of $A_\omega ^2$ and give some estimates for it. Let’s recall some notations. For all $f\in H( {\mathbb {B}})$, the Taylor series of f at origin, which converges absolutely and uniformly on each compact subset of ${\mathbb {B}}$, is

$$\begin{aligned} f(z)=\sum _{m}a_mz^m, \quad z\in {\mathbb {B}}. \end{aligned}$$

Here the summation is over all multi-indexs $m=(m_1,m_2,\ldots ,m_n)$, $m_k$ is a non-negative integer and $z^m=z_1^{m_1}z_2^{m_2}\cdots z_{n}^{m_n}$. Let $|m|=m_1+m_2+\cdots +m_n$, $m!=m_1!m_2!\cdots m_n!$ and $f_k(z)=\sum _{|m|=k }a_mz^m$. Then the Taylor series of f can be written as $f(z)=\sum _{k=0}^\infty f_k(z)$, which is called the homogeneous expansion of f.

Lemma 3

Let $\omega \in \hat{{\mathcal {D}}}$. Then

$$\begin{aligned} B_z^\omega (w)=\frac{1}{2n!}\sum _{k=0}^\infty \frac{(n-1+k)!}{k!\omega _{2n+2k-1}} \langle w,z\rangle ^k \end{aligned}$$

and

$$\begin{aligned} \Vert B_z^\omega \Vert _{{\mathcal {B}}}\approx \frac{1}{\omega (S_z)}\approx \Vert B_z^\omega \Vert _{H^\infty },\quad z\in {\mathbb {B}}. \end{aligned}$$

Here and henceforth, $\omega _s=\int _0^1 r^s\omega (r)dr$.

Proof

Suppose $f\in A_\omega ^2$ and $f(z)=\sum _{m}a_mz^m$, $z\in {\mathbb {B}}$. For any fixed $z\in {\mathbb {B}}$, let

$$\begin{aligned} B_z^\omega (w)=\sum _{m}b_m(z)w^m. \end{aligned}$$

By [20, Lem. 1.8, Lem. 1.11], we have

$$\begin{aligned} f(z)&=\int _ {\mathbb {B}}f(w)\overline{B_z^\omega (w)}\omega (w)dV(w) \\&=2n\sum _{m} \frac{(n-1)!m!}{(n-1+|m|)!} a_m\overline{b_m(z)}\int _0^1 r^{2n+2|m|-1} \omega (r)dr \\&=2n!\sum _{m} \frac{m!}{(n-1+|m|)!} a_m\overline{b_m(z)}\omega _{2n+2|m|-1}. \end{aligned}$$

Set

$$\begin{aligned} z^m= \frac{2 n!m!}{(n-1+|m|)!} \omega _{2n+2|m|-1}\overline{b_m(z)}. \end{aligned}$$

Then,

$$\begin{aligned} B_z^\omega (w)&=\frac{1}{2 n!}\sum _{k=0}^\infty \frac{(n-1+k)!}{k! \omega _{2n+2k-1}} \sum _{|m|=k} \frac{|m|!}{m!} w^m\overline{z}^m \\&=\frac{1}{2n!}\sum _{k=0}^\infty \frac{(n-1+k)!}{k!\omega _{2n+2k-1}} \langle w,z\rangle ^k. \end{aligned}$$

Therefore,

$$\begin{aligned} \Re B_z^\omega (w) =\frac{1}{2n!}\sum _{k=1}^\infty \frac{(n-1+k)!}{(k-1)!\omega _{2n+2k-1}} \langle w,z\rangle ^k. \end{aligned}$$

By Stirling’s estimate and Lemma 1, when $1/2\le |z|<1$, we obtain

$$\begin{aligned} |B_z^\omega (w)| \lesssim \sum _{k=1}^\infty \frac{k^{n-1}|z|^{k}}{\omega _{2n+2k-1}} \approx \sum _{k=n}^\infty \frac{(k+1)^{n-1}|z|^{k}}{\omega _{2k+1}} \end{aligned}$$

and

$$\begin{aligned} |\Re B_z^\omega (z)| \approx \sum _{k=1}^\infty \frac{k^n|z|^{2k}}{\omega _{2n+2k-1}} \approx \sum _{k=n+1}^\infty \frac{(k+1)^n|z|^{2k}}{\omega _{2k+1}}. \end{aligned}$$

Let ${\hat{\omega }}_\alpha (t)=(1-t)^\alpha {\hat{\omega }}(t)$ for any fixed $\alpha \in {{\mathbb {R}}}$. Using [13, eq. (20)] and Lemma 2, we get

$$\begin{aligned} \sum _{k=n}^\infty \frac{(k+1)^{n-1}|z|^{k}}{\omega _{2k+1}} \approx \int _0^{|z|}\frac{1}{{\hat{\omega }}_{n+1}(t)}dt \lesssim \frac{1}{(1-|z|)^n{\hat{\omega }}(z)} \approx \frac{1}{\omega (S_z)} \end{aligned}$$

and

$$\begin{aligned} \sum _{k=n+1}^\infty \frac{(k+1)^n|z|^{2k}}{\omega _{2k+1}} \approx \int _0^{|z|^2}\frac{1}{(1-t)^{n+2}{\hat{\omega }}(t)}dt. \end{aligned}$$

By Lemma 1, there exists a constant $b>0$ such that ${\hat{\omega }}(t)/(1-t)^b$ is essentially increasing. So, by Lemma 2,

$$\begin{aligned} \int _0^{|z|^2}\frac{1}{(1-t)^{n+2}{\hat{\omega }}(t)}dt \gtrsim \frac{(1-|z|^2)^b}{{\hat{\omega }}(|z|^2)} \int _0^{|z|^2}\frac{1}{(1-t)^{n+2+b}}dt \gtrsim \frac{1}{(1-|z|)\omega (S_z)}. \end{aligned}$$

Therefore, when $1/2\le |z|<1$, we have

$$\begin{aligned} \Vert B_z^\omega \Vert _{H^\infty } \lesssim \frac{1}{\omega (S_z)}, \quad \frac{1}{\omega (S_z)}\lesssim \Vert B_z^\omega \Vert _{\mathcal {B}}. \end{aligned}$$

(4)

When $|z|<1/2$, since $\omega (S_z)\approx 1$, $\Vert B_z^\omega \Vert _{{\mathcal {B}}}\ge |B_z^\omega (0)|\gtrsim 1$, and

$$\begin{aligned} |B_z^\omega (w)|\le \frac{1}{2n!}\sum _{k=0}^\infty \frac{(n-1+k)!}{k!\omega _{2n+2k-1}}\frac{1}{2^k}<\infty , \end{aligned}$$

(4) also holds. By the fact that $\Vert f\Vert _{{\mathcal {B}}}\lesssim \Vert f\Vert _{H^\infty }$, we obtain the desired result. The proof is complete. $\square$

Lemma 4

Let $0<p<\infty$, $\omega ,\upsilon \in \hat{{\mathcal {D}}}$. Then the following assertions hold.

• (i) When $|rz|>1/4$,

  $$\begin{aligned} M_p^p(r, B_z^\omega ) \approx \int _{0}^{r|z|} \frac{1}{{\hat{\omega }}(t)^p (1-t)^{np-n+1}}dt \end{aligned}$$

  and

  $$\begin{aligned} M_p^p(r, \Re B_z^\omega ) \approx \int _{0}^{r|z|} \frac{1}{{\hat{\omega }}(t)^p (1-t)^{(n+1)p-n+1}}dt. \end{aligned}$$

• (ii) When $|z|>6/7$,

  $$\begin{aligned} \Vert B_z^\omega \Vert _{A_\upsilon ^p}^p \approx \int _{0}^{|z|} \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{np-n+1}}dt \end{aligned}$$

  and

  $$\begin{aligned} \Vert \Re B_z^\omega \Vert _{A_\upsilon ^p}^p\approx \int _0^{|z|} \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{(n+1)p-n+1}}dt. \end{aligned}$$

Proof

When $n=1$, the lemma was proved in [13], so we always assume $n\ge 2$. Since we will use some results on $A_\omega ^p({\mathbb {D}})$, for brief, the symbol $A_\omega ^p$ only means $A_\omega ^p( {\mathbb {B}})$ with $n\ge 2$. Meanwhile, let $B_z^{\omega ,1}$ denote the reproducing kernel of $A_\omega ^2({\mathbb {D}})$. Recall that, on the unit disk, $dA_\alpha (z)=c_\alpha (1-|z|^2)^\alpha dA(z)$, where dA(z) is the normalized area measure on ${\mathbb {D}}$.

By Lemma 3,

$$\begin{aligned} \Re B_z^\omega (w)=\frac{1}{2n!}\sum _{k=1}^\infty \frac{(n-1+k)!}{(k-1)!\omega _{2n+2k-1}}\langle w,z\rangle ^k. \end{aligned}$$

Let $e_1=(1,0,\ldots ,0)$. When $|rz|>0$, by a rotation transformation and [20, Lem. 1.9], we have

$$\begin{aligned} M_p^p(r, \Re B_z^\omega )= & {} M_p^p(r, \Re B_{|z|e_1}^\omega ) {=}\frac{1}{2n!}\int _{ {\mathbb {S}}}\left| \sum _{k=1}^\infty \frac{(n-1+k)!}{(k-1)!\omega _{2n+2k-1}}\langle r\eta ,|z|e_1\rangle ^k\right| ^p d\sigma (\eta ) \\\approx & {} \int _{{\mathbb {D}}} \left| \sum _{k=1}^\infty \frac{(n-1+k)! }{(k-1)!\omega _{2n+2k-1}}(r|z|\xi )^k\right| ^p (1-|\xi |^2)^{n-2}dA(\xi ) \\= & {} \frac{1}{|rz|^{(n-1)p}} \int _{{\mathbb {D}}} \left| \sum _{k=1}^\infty \frac{|rz|^{n+k-1}(\xi ^{n+k-1})^{(n)} }{\omega _{2(n+k-1)+1}}\right| ^p |\xi |^pdA_{n-2}(\xi ) \\\approx & {} \frac{1}{|rz|^{(n-1)p}} \int _{{\mathbb {D}}} \left| \sum _{k=0}^\infty \frac{|rz|^{k}(\xi ^{k})^{(n)} }{\omega _{2k+1}}\right| ^p dA_{n-2}(\xi ) \\= & {} \frac{1}{|rz|^{(n-1)p}} \Vert (B_{r|z|}^{\omega ,1})^{(n)}\Vert _{A_{n-2}^p({\mathbb {D}})}^p. \end{aligned}$$

When $r|z|>1/4$, by [13, Thm. 1],

$$\begin{aligned} M_p^p(r, \Re B_z^\omega ) \approx \int _{0}^{r|z|} \frac{(1-t)^{n-1}}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)}}dt =\int _{0}^{r|z|} \frac{1}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}}dt. \end{aligned}$$

Therefore, when $|z|>6/7$, by Fubini’s theorem we obtain

$$\begin{aligned} \Vert \Re B_z^\omega \Vert _{A_\upsilon ^p}^p&\approx \int _{1/2}^1 r^{2n-1}\upsilon (r)M_p^p(r,\Re B_z^\omega )dr =\int _0^{|z|} \frac{\int _{\max \{t/|z|,1/2\}}^1 r^{2n-1}\upsilon (r)dr}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} dt. \end{aligned}$$

When $0\le t\le |z|/2$,

$$\begin{aligned} \int _{\max \{t/|z|,1/2\}}^1 r^{2n-1}\upsilon (r)dr =\int _\frac{1}{2}^1 r^{2n-1}\upsilon (r)dr\approx 1\approx {\hat{\upsilon }}(t). \end{aligned}$$

(5)

When $|z|/2\le t\le |z|$, we get

$$\begin{aligned} \int _{\max \{t/|z|,1/2\}}^1 r^{2n-1}\upsilon (r)dr =\int _\frac{t}{|z|}^1 r^{2n-1}\upsilon (r)dr \le {\hat{\upsilon }}(t). \end{aligned}$$

(6)

By Lemma 1 and the fact that $\upsilon \in \hat{{\mathcal {D}}}$, there exists a constant $b>0$ such that $\frac{{\hat{\upsilon }}(t)}{(1-t)^b}$ is essentially increasing. So,

$$\begin{aligned} \int _{|z|/2}^{|z|} \frac{\int _{\max \{t/|z|,1/2\}}^1 r^{2n-1}\upsilon (r)dr}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} dt \gtrsim&\int _{|z|/2}^{2|z|-1} \frac{{\hat{\upsilon }}(\frac{t}{|z|})}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} dt \nonumber \\ \gtrsim&\int _{|z|/2}^{2|z|-1} \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} \left( \frac{1-\frac{t}{|z|}}{1-t}\right) ^b dt \nonumber \\ \gtrsim&\int _{|z|/2}^{2|z|-1} \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} dt, \end{aligned}$$

(7)

where the last estimate follows from

$$\begin{aligned} \frac{1}{|z|}\frac{|z|-t}{1-t}\ge \frac{1}{|z|}\frac{|z|-(2|z|-1)}{1-(2|z|-1)}\gtrsim 1\quad \text{ for } \text{ all } t\in \left( \frac{|z|}{2},2|z|-1\right) \text{ and } |z|>\frac{6}{7}. \end{aligned}$$

Meanwhile, $\omega ,\upsilon \in \hat{{\mathcal {D}}}$ and Lemma 2 imply

$$\begin{aligned} \int _{|z|/2}^{2|z|-1} \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}}dt\ge & {} \int _{4|z|-3}^{2|z|-1} \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}}dt \nonumber \\\approx & {} \frac{{\hat{\upsilon }}(2|z|-1)}{{\hat{\omega }}(2|z|-1)^p (1-|z|)^{p(n+1)-n}} \nonumber \\\approx & {} \int _{2|z|-1}^{|z|} \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}}dt. \end{aligned}$$

(8)

Then (7) and (8) imply that

$$\begin{aligned} \int _{|z|/2}^{|z|} \frac{\int _{\max \{t/|z|,1/2\}}^1 r^{2n-1}\upsilon (r)dr}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} dt&\gtrsim 2\int _{|z|/2}^{2|z|-1} \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} dt \nonumber \\&\gtrsim \left( \int _{|z|/2}^{2|z|-1}+\int _{2|z|-1}^{|z|}\right) \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} dt \nonumber \\&= \int _{|z|/2}^{|z|} \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} dt. \end{aligned}$$

(9)

So, if $|z|>6/7$, by (5) and (6),

$$\begin{aligned} \int _0^{|z|} \frac{\int _{\max \{t/|z|,1/2\}}^1 r^{2n-1}\upsilon (r)dr}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} dt \lesssim \int _0^{|z|} \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} dt. \end{aligned}$$

By (5) and (9), we get

$$\begin{aligned} \int _0^{|z|} \frac{\int _{\max \{t/|z|,1/2\}}^1 r^{2n-1}\upsilon (r)dr}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} dt&\gtrsim \int _0^{|z|} \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}} dt. \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert \Re B_z^\omega \Vert _{A_\upsilon ^p}^p&\approx \int _0^{|z|} \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p (1-t)^{p(n+1)-n+1}}dt. \end{aligned}$$

The rest of the lemma can be proved in the same way. The proof is complete. $\square$

4 Main Results and Proofs

In this section, we give the main results and proofs of this paper. We note that

$$\begin{aligned} \Vert f\Vert _{L^\infty ( {\mathbb {B}},\omega dV)}=\Vert f\Vert _{L^\infty ( {\mathbb {B}},dV)}, \end{aligned}$$

when $\omega \in \hat{{\mathcal {D}}}$. So, let $L^\infty = L^\infty ( {\mathbb {B}},\omega dV)=L^\infty ( {\mathbb {B}},dV)$ in this section.

Theorem 1

When $\omega \in {\mathcal {D}}$, $P_\omega :L^\infty \rightarrow {\mathcal {B}}$ is bounded and onto.

Proof

For all $f\in L^\infty$, by Lemma 4,

$$\begin{aligned} |\Re (P_\omega f)(z)| \le \int _ {\mathbb {B}}|f(w)||\Re B_z^\omega (w)|\omega (w)dV(w) \le \Vert f\Vert _{L^\infty }\Vert \Re B_z^\omega \Vert _{A_\omega ^1} \lesssim \frac{\Vert f\Vert _{L^\infty }}{1-|z|}. \end{aligned}$$

So, $P_\omega :L^\infty \rightarrow {\mathcal {B}}$ is bounded.

By [4, eq. (14)], we see that

$$\begin{aligned} \Vert f\Vert _{A_\omega ^2}^2 =\omega ( {\mathbb {B}})|f(0)|^2+ 4 \int _{ {\mathbb {B}}}\frac{|\Re f(z)|^2 }{|z|^{2n}} \omega ^{n*}(z)dV(z), \end{aligned}$$

where

$$\begin{aligned} \omega ^{n*}(z):=\int _{|z|}^1 r^{2n-1}\log \frac{r}{|z|}\omega (r)dr. \end{aligned}$$

So, for $f,g\in A_\omega ^2$,

$$\begin{aligned} \langle f,g\rangle _{A_\omega ^2}=\omega ( {\mathbb {B}})f(0)\overline{g(0)} + 4\int _{ {\mathbb {B}}} \frac{\Re f(z)\overline{\Re g(z)}}{|z|^{2n}}\omega ^{n*}(z)dV(z). \end{aligned}$$

(10)

Let

$$\begin{aligned} W_1(t):=\frac{{\hat{\omega }}(t)}{1-t},\quad \text{ and } W_1(z):=W_1(|z|). \end{aligned}$$

Since $\omega \in {\mathcal {D}}$, by Lemma 1, there are constants $a,b>0$ such that ${\hat{\omega }}(t)/(1-t)^a$ is essentially decreasing and ${\hat{\omega }}(t)/(1-t)^b$ is essentially increasing. Thus,

$$\begin{aligned} \int _r^1 \frac{{\hat{\omega }}(t)}{1-t}dt\lesssim \frac{{\hat{\omega }}(r)}{(1-r)^a}\int _r^1 (1-t)^{a-1}dt\approx {\hat{\omega }}(r) \end{aligned}$$

and

$$\begin{aligned} \int _r^1 \frac{{\hat{\omega }}(t)}{1-t}dt\gtrsim \frac{{\hat{\omega }}(r)}{(1-r)^b}\int _r^1 (1-t)^{b-1}dt\approx {\hat{\omega }}(r). \end{aligned}$$

Then,

$$\begin{aligned} \hat{W_1}(r)=\int _r^1 \frac{{\hat{\omega }}(t)}{1-t}dt \approx {\hat{\omega }}(r)=(1-r)W_1(r). \end{aligned}$$

Therefore, $W_1\in {\mathcal {R}}$. By Lemma 2 and Theorem A, $\Vert \cdot \Vert _{A_\omega ^p}\approx \Vert \cdot \Vert _{A_{W_1}^p}$. Then for all $p>0$, by [6, Thm. 1], we get

$$\begin{aligned} \Vert f\Vert _{A_\omega ^p}^p\approx \Vert f\Vert _{A_{W_1}^p}^p\approx |f(0)|^p+\int _ {\mathbb {B}}|\Re f(z)|^p(1-|z|)^p W_1(z)dV(z). \end{aligned}$$

(11)

For any $f\in H( {\mathbb {B}})$ and $|z|\le 1/2$, let $f_r(z)=f(rz)$ for $r\in (0,1)$. By Cauchy’s fomula, see [20, Thm. 4.1] for example, we have

$$\begin{aligned} f(z)=f_{3/4}\left( \frac{4z}{3}\right) =\int _ {\mathbb {S}}\frac{f_{{3/4}}(\eta )}{\left( 1-\langle \frac{4z}{3},\eta \rangle \right) ^n}d\sigma (\eta ). \end{aligned}$$

After a calculation, when $|z|\le 1/2$,

$$\begin{aligned} |f(z)|\lesssim \Vert f\Vert _{A_\omega ^1},\quad |\Re f(z)|\lesssim |z|\Vert f_{{3/4}}\Vert _{H^\infty },\quad \text{ and }\quad |\Re f(z)|\lesssim |z|\Vert f\Vert _{A_\omega ^1}. \end{aligned}$$

We note that, when $|z|\ge 1/2$,

$$\begin{aligned} \omega ^{n*}(z)=\int _{|z|}^1 t^{2n-1}\log \frac{t}{|z|}\omega (t)dt\approx \int _{|z|}^1 t\log \frac{t}{|z|}\omega (t)dt=\omega ^*(z). \end{aligned}$$

So, when $g\in {\mathcal {B}}$ and $f\in A_\omega ^1$, by (10), (11) and Lemma 2, there exists a $C=C(n,\omega ,g)$, such that

$$\begin{aligned} |\langle f_r,g\rangle _{A_\omega ^2}|&\le C\left( \Vert f_r\Vert _{A_\omega ^1}+\Vert f_r\Vert _{A_\omega ^1}\int _{\frac{1}{2} {\mathbb {B}}} \frac{\omega ^{n*}(z)}{|z|^{2n-2}}dV(z) +\int _{ {\mathbb {B}}\backslash \frac{1}{2} {\mathbb {B}}} \frac{|\Re f_r(z){\Re g(z)}|}{|z|^{2n}}\omega ^{n*}(z)dV(z) \right) \\&\approx \Vert f_r\Vert _{A_\omega ^1}+ \int _{ {\mathbb {B}}\backslash \frac{1}{2} {\mathbb {B}}} {|\Re f_r(z){\Re g(z)}|}(1-|z|){\hat{\omega }}(z)dV(z) \\&\le \Vert f_r\Vert _{A_\omega ^1}+ \Vert g\Vert _{\mathcal {B}}\int _{ {\mathbb {B}}} {|\Re f_r(z)|}{\hat{\omega }}(z)dV(z) \\&\approx \Vert f_r\Vert _{A_\omega ^1}+ \Vert g\Vert _{\mathcal {B}}\int _{ {\mathbb {B}}} {|\Re f_r(z)|}(1-|z|)W_1(z)dV(z) \\&\lesssim \Vert f\Vert _{A_\omega ^1}+\Vert g\Vert _{\mathcal {B}}\Vert f\Vert _{A_\omega ^1}. \end{aligned}$$

Therefore, $g\in {\mathcal {B}}$ induces a bounded linear functional on $A_\omega ^1$ defined by $F_g(f)=\lim \nolimits _{r\rightarrow 1}\langle f_r,g\rangle _{A_\omega ^2}$ for all $f\in A_\omega ^1$.

On the other hand, the Hahn–Banach theorem and the well known fact (see [19, Thm. 1.1] for example) that

$$\begin{aligned} (L^1( {\mathbb {B}},\omega dV))^*\simeq L^\infty ( {\mathbb {B}},\omega dV) \end{aligned}$$

guarantee the existence of $\varphi \in L^\infty$ such that

$$\begin{aligned} \lim \limits _{r\rightarrow 1}\langle f_r,g\rangle _{A_\omega ^2}= F_g(f)=\int _ {\mathbb {B}}f(z)\overline{\varphi (z)}\omega (z)dV(z) =\lim _{r\rightarrow 1}\int _ {\mathbb {B}}f_r(z)\overline{\varphi (z)}\omega (z)dV(z) \end{aligned}$$

for all $f\in A_\omega ^1$. Since $P_\omega$ is self-adjoint and $P_\omega (f_r)=f_r$, we have

$$\begin{aligned} \int _ {\mathbb {B}}f_r(z)\overline{\varphi (z)}\omega (z)dV(z) =\int _ {\mathbb {B}}P_\omega (f_r)(z)\overline{\varphi (z)}\omega (z)dV(z) =\int _ {\mathbb {B}}f_r(z)\overline{P_\omega (\varphi )(z)}\omega (z)dV(z). \end{aligned}$$

By the first part of the proof, $P_\omega \varphi \in {\mathcal {B}}$. Thus, $g-P_\omega \varphi \in {\mathcal {B}}$ and represents the zero functional. So, $g=P_\omega \varphi$. The proof is complete. $\square$

Remark 1

By the above proof, we see that $P_\omega :L^\infty \rightarrow {\mathcal {B}}$ is bounded when $\omega \in \hat{{\mathcal {D}}}$.

Theorem 2

Suppose $1<p<\infty$ and $\omega ,\upsilon \in {\mathcal {D}}$. Let $q=p/(p-1)$. Then the following statements are equivalent:

• (i) $P_\omega ^+: L_\upsilon ^p\rightarrow L_\upsilon ^p$ is bounded;

• (ii) $P_\omega : L_\upsilon ^p\rightarrow L_\upsilon ^p$ is bounded;

• (iii) $\displaystyle M:=\sup \limits _{0\le r<1} \frac{{\hat{\upsilon }}(r)^{1/p}}{{\hat{\omega }}(r)} \left( \int _r^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{1/q}<\infty ;$

• (iv) $\displaystyle N:=\sup \limits _{0\le r<1} \left( \int _0^r \frac{\upsilon (s)}{{\hat{\omega }}(s)^p}s^{2n-1}ds+1\right) ^{1/p}\left( \int _r^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{1/q}<\infty$.

Proof

When $n=1$, the theorem was first proved in [13] and improved in [7, 14]. So, we always assume that $n\ge 2$.

$(i)\Rightarrow (ii)$. It is obvious.

$(ii)\Rightarrow (iii)$. Suppose that (ii) holds. Let $P_\omega ^*$ be the adjoint of $P_\omega$ with respect to $\langle \cdot ,\cdot \rangle _{L_\upsilon ^2}$. For all $f,g\in L^\infty$, by Fubini’s Theorem,

$$\begin{aligned} \langle f, P_\omega ^*g\rangle _{L_\upsilon ^2}&=\langle P_\omega f,g\rangle _{L_\upsilon ^2} =\int _{ {\mathbb {B}}} P_\omega f(z)\overline{g(z)}\upsilon (z)dV(z)\\&=\int _ {\mathbb {B}}\left( \int _ {\mathbb {B}}f(\xi )\overline{B_z^\omega (\xi )}\omega (\xi )dV(\xi )\right) \overline{g(z)}\upsilon (z)dV(z) \\&=\int _ {\mathbb {B}}\left( \int _ {\mathbb {B}}\overline{g(z)B_z^\omega (\xi )}\upsilon (z)dV(z)\right) f(\xi )\omega (\xi )dV(\xi )\\&=\int _ {\mathbb {B}}\left( \overline{\frac{\omega (\xi )}{\upsilon (\xi )}\int _ {\mathbb {B}}{g(z)B_z^\omega (\xi )}\upsilon (z)dV(z)}\right) f(\xi )\upsilon (\xi )dV(\xi ). \end{aligned}$$

Since $L^\infty$ is dense in $L^p_\upsilon$ and $L_\upsilon ^q$, by the last equality we get

$$\begin{aligned} P_\omega ^*(g)(\xi )=\frac{\omega (\xi )}{\upsilon (\xi )}\int _ {\mathbb {B}}{g(z)B_z^\omega (\xi )}\upsilon (z)dV(z),\quad g\in L_\upsilon ^q. \end{aligned}$$

(12)

By the assumption, $P_\omega ^*$ is bounded on $L_\upsilon ^q$. Let $g_j(z)=z_1^j$, where $z=(z_1,z_2,\ldots ,z_n)$ and $j\in {\mathbb {N}}\cup \{0\}$. By [20, Lem. 1.11] and Lemma 3,

$$\begin{aligned} P_\omega ^*(g_j)(\xi )&=\frac{\omega (\xi )}{\upsilon (\xi )}\int _ {\mathbb {B}}{g_j(z)B_z^\omega (\xi )}\upsilon (z)dV(z) \\&=\frac{1}{2n!}\frac{\omega (\xi )}{\upsilon (\xi )}\sum _{k=0}^\infty \frac{(n-1+k)!}{k!\omega _{2n+2k-1}} \int _ {\mathbb {B}}g_j(z) \langle \xi ,z\rangle ^k\upsilon (z)dV(z) \\&=\frac{2n}{2n!}\frac{\omega (\xi )}{\upsilon (\xi )}\sum _{k=0}^\infty \frac{(n-1+k)!}{k!\omega _{2n+2k-1}} \int _0^1 r^{2n+k+j-1} \upsilon (r)dr\int _ {\mathbb {S}}\eta _1^j \langle \xi ,\eta \rangle ^kd\sigma (\eta ) \\&=\xi _1^j\frac{\omega (\xi )}{\upsilon (\xi )} \frac{\upsilon _{2n+2j-1}}{\omega _{2n+2j-1}}\frac{(n-1+j)!}{j!(n-1)!}\frac{(n-1)!j!}{(n-1+j)!}\\&=\xi _1^j\frac{\omega (\xi )}{\upsilon (\xi )} \frac{\upsilon _{2n+2j-1}}{\omega _{2n+2j-1}}. \end{aligned}$$

By Lemmas 1 and 2, we obtain

$$\begin{aligned} \Vert g_j\Vert _{L_\upsilon ^q}^q&=\int _{ {\mathbb {B}}}|z_1|^{qj}\upsilon (z)dV(z) =2n\int _0^1 r^{2n+qj-1}\upsilon (r)dr\int _{ {\mathbb {S}}}|\eta _1|^{qj}d\sigma (\eta ) \\&=2n {\upsilon }_{2n+qj-1} \int _{ {\mathbb {S}}}|\eta _1|^{qj}d\sigma (\eta )\\&\approx {\upsilon }_{2n+2j-1} \int _{ {\mathbb {S}}}|\eta _1|^{qj}d\sigma (\eta ), \end{aligned}$$

which implies that

$$\begin{aligned} \Vert P_\omega ^*(g_j)\Vert _{L_\upsilon ^q}^q&=\left( \frac{\upsilon _{2n+2j-1}}{\omega _{2n+2j-1}}\right) ^q\int _{ {\mathbb {B}}} |\xi _1|^{jq}\frac{\omega ^q(\xi )}{\upsilon ^{q-1}(\xi )} dV(\xi ) \\&\approx \left( \frac{\upsilon _{2n+2j-1}}{\omega _{2n+2j-1}}\right) ^q\int _0^1 r^{2n+qj-1}\frac{\omega ^q(r)}{\upsilon ^{q-1}(r)}dr\int _ {\mathbb {S}}|\eta _1|^{jq} d\sigma (\eta ) \\&\gtrsim \Vert g_j\Vert _{L_\upsilon ^q}^q\frac{\upsilon _{2n+2j-1}^{q-1}}{\omega _{2n+2j-1}^q}\int _{1-\frac{1}{2j+1}}^1 \frac{\omega ^q(r)}{\upsilon ^{q-1}(r)}r^{2n-1}dr \\&\approx \Vert g_j\Vert _{L_\upsilon ^q}^q\frac{\upsilon _{2j+1}^{q-1}}{\omega _{2j+1}^q}\int _{1-\frac{1}{2j+1}}^1 \frac{\omega ^q(r)}{\upsilon ^{q-1}(r)}r^{2n-1}dr. \end{aligned}$$

Let $r_j=1-1/(2j+1)$. We get

$$\begin{aligned} \Vert P_\omega ^*(g_j)\Vert _{L_\upsilon ^q}^q \gtrsim \Vert g_j\Vert _{L_\upsilon ^q}^q\frac{{\hat{\upsilon }}(r_j)^{q-1}}{{\hat{\omega }}(r_j)^q}\int _{r_j}^1 \frac{\omega ^q(r)}{\upsilon ^{q-1}(r)}r^{2n-1}dr . \end{aligned}$$

Let

$$\begin{aligned} H(t)=\frac{{\hat{\upsilon }}(t)^{q-1}}{{\hat{\omega }}(t)^q}\int _{t}^1 \frac{\omega ^q(r)}{\upsilon ^{q-1}(r)}r^{2n-1}dr. \end{aligned}$$

When $r_j\le t< r_{j+1}$, $H(t)\lesssim H(r_j)$. Thus, by the assumption, we get $\sup _{t\ge 0} H(t)<\infty$, as desired.

$(iii)\Rightarrow (i)$. Suppose that (iii) holds. For $z\in {\mathbb {B}}$, let

$$\begin{aligned} h(z)=\upsilon (z)^{1/p}\left( \int _{|z|}^1 \frac{\omega (s)^{q}}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{1/(pq)}. \end{aligned}$$

By the assumption we have

$$\begin{aligned} \int _t^1 \left( \frac{\omega (s)}{h(s)}\right) ^q s^{2n-1}ds = q\left( \int _t^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}} s^{2n-1}ds\right) ^{1/q} \lesssim M\frac{{\hat{\omega }}(t)}{{\hat{\upsilon }}(t)^{1/p}}. \end{aligned}$$

(13)

If $r|z|\le 1/4$, by Lemma 3,

$$\begin{aligned} M_1(r,B_z^\omega )\le \Vert B_{rz}^\omega \Vert _{H^\infty }\approx \frac{1}{{\hat{\omega }}(S_{rz})}\approx 1. \end{aligned}$$

If $r|z|>1/4$, by Lemma 1, there exists a constant $a>0$ such that ${\hat{\omega }}(t)/(1-t)^a$ is essentially decreasing. Then by Lemma 4,

$$\begin{aligned} M_1(r,B_z^\omega )\lesssim \int _0^{r|z|}\frac{dt}{{\hat{\omega }}(t)(1-t)}\lesssim \frac{(1-r|z|)^a}{{\hat{\omega }}(r|z|)}\int _0^{r|z|}\frac{dt}{(1-t)^{a+1}}\approx \frac{1}{{\hat{\omega }}(r|z|)}. \end{aligned}$$

So, for all $r\in (0,1)$ and $z\in {\mathbb {B}}$,

$$\begin{aligned} M_1(r,B_z^\omega )\lesssim 1+ \int _0^{r|z|}\frac{1}{{\hat{\omega }}(t)(1-t)}dt\lesssim \frac{1}{{\hat{\omega }}(r|z|)}. \end{aligned}$$

(14)

Hence, by (13), (14), Fubini’s theorem and Lemma 1, we obtain

$$\begin{aligned} \int _ {\mathbb {B}}|B_z^\omega (\xi )|\left( \frac{\omega (\xi )}{h(\xi )}\right) ^qdV(\xi )&=2n \int _0^1 \left( \frac{\omega (r)}{h(r)}\right) ^q r^{2n-1} M_1(r, B_z^\omega )dr \\&\lesssim \int _0^1 \left( \frac{\omega (r)}{h(r)}\right) ^q r^{2n-1}\left( 1+ \int _0^{r|z|}\frac{1}{{\hat{\omega }}(t)(1-t)}dt\right) dr \\&\lesssim M\frac{{\hat{\omega }}(0)}{{\hat{\upsilon }}(0)^{1/p}}+\int _0^{|z|}\frac{1}{{\hat{\omega }}(t)(1-t)}\int _{\frac{t}{|z|}}^1 \left( \frac{\omega (r)}{h(r)}\right) ^q r^{2n-1} drdt \\&\le M\frac{{\hat{\omega }}(0)}{{\hat{\upsilon }}(0)^{1/p}}+\int _0^{|z|}\frac{1}{{\hat{\omega }}(t)(1-t)}\int _{t}^1 \left( \frac{\omega (r)}{h(r)}\right) ^q r^{2n-1} drdt \\&\lesssim M+M \int _0^{|z|}\frac{1}{{\hat{\upsilon }}(t)^{1/p}(1-t)}dt \lesssim \frac{M}{{\hat{\upsilon }}(|z|)^{1/p}}. \end{aligned}$$

Therefore, Hölder’s inequality and Fubini’s theorem imply that

$$\begin{aligned} \Vert P_\omega ^+(f)\Vert _{L_\upsilon ^p}^p&=\int _ {\mathbb {B}}\upsilon (z)\left| \int _ {\mathbb {B}}f(\xi ) |B_z^\omega (\xi )|\omega (\xi )dV(\xi ) \right| ^pdV(z) \nonumber \\&\le \int _ {\mathbb {B}}\left( \int _ {\mathbb {B}}|f(\xi )|^p h(\xi )^p |B_z^\omega (\xi )|dV(\xi )\right) \nonumber \\&\quad \times \left( \int _ {\mathbb {B}}|B_z^\omega (\xi )|\left( \frac{\omega (\xi )}{h(\xi )}\right) ^qdV(\xi )\right) ^{p/q}\upsilon (z)dV(z) \nonumber \\&\lesssim M^\frac{p}{q}\int _ {\mathbb {B}}\left( \int _ {\mathbb {B}}|f(\xi )|^p h(\xi )^p |B_z^\omega (\xi )|dV(\xi )\right) \frac{\upsilon (z)}{{\hat{\upsilon }}(z)^{1/q}}dV(z) \nonumber \\&=M^\frac{p}{q}\int _ {\mathbb {B}}|f(\xi )|^p h(\xi )^p\left( \int _ {\mathbb {B}}|B_z^\omega (\xi )|\frac{\upsilon (z)}{{\hat{\upsilon }}(z)^{1/q}}dV(z) \right) dV(\xi ). \end{aligned}$$

(15)

Since $|B_z^\omega (\xi )|=|B_\xi ^\omega (z)|$, by (14) we get

$$\begin{aligned} \int _{ {\mathbb {B}}\backslash |\xi | {\mathbb {B}}} |B_z^\omega (\xi )|\frac{\upsilon (z)}{{\hat{\upsilon }}(z)^{1/q}}dV(z)&\lesssim \int _{|\xi |}^1 \frac{\upsilon (r)}{{\hat{\upsilon }}(r)^{1/q}}M_1(r,B_\xi ^\omega )dr \lesssim \frac{{\hat{\upsilon }}(\xi )^{1/p}}{{\hat{\omega }}(\xi )}, \end{aligned}$$

(16)

and

$$\begin{aligned}&\int _{ |\xi | {\mathbb {B}}} |B_z^\omega (\xi )|\frac{\upsilon (z)}{{\hat{\upsilon }}(z)^{1/q}}dV(z) \lesssim \int _0^{|\xi |}\frac{\upsilon (r)}{{\hat{\upsilon }}(r)^{1/q}}\frac{1}{{\hat{\omega }}(r|\xi |)}r^{2n-1}dr\nonumber \\&\quad \lesssim \int _0^{|\xi |} \frac{\upsilon (r)}{{\hat{\upsilon }}(r)^{1/q}{\hat{\omega }}(r)}r^{2n-1}dr. \end{aligned}$$

(17)

By the assumption, we have

$$\begin{aligned} \int _0^1\frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds<\infty ,\quad \int _0^{1/2} \frac{\upsilon (t)}{{\hat{\omega }}(t)^p} t^{2n-1}dt>0,\quad \int _{1/2}^1 \frac{\upsilon (t)}{{\hat{\omega }}(t)^p} t^{2n-1}dt>0. \end{aligned}$$

(18)

When $r\le 1/2$,

$$\begin{aligned} {\hat{\omega }}(r)\approx 1\approx {\hat{\upsilon }}(r)^{1/p}\left( \int _r^{1} \frac{\omega (t)^q}{\upsilon (t)^{q-1}} t^{2n-1}dt\right) ^{1/q}. \end{aligned}$$

When $r>1/2$, by Hölder’s inequality,

$$\begin{aligned} {\hat{\omega }}(r)= & {} \int _r^1\omega (t)dt \le {\hat{\upsilon }}(r)^{1/p}\left( \int _r^1 \frac{\omega (t)^q}{\upsilon (t)^{q-1}}dt\right) ^{1/q}\\\approx & {} {\hat{\upsilon }}(r)^{1/p}\left( \int _r^1 \frac{\omega (t)^q}{\upsilon (t)^{q-1}}t^{2n-1}dt\right) ^{1/q}. \end{aligned}$$

Then, for all $r\in (0,1)$,

$$\begin{aligned} \frac{{\hat{\omega }}(r)^p}{{\hat{\upsilon }}(r)}\int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}t^{2n-1}dt \lesssim \left( \int _r^1 \frac{\omega (t)^q}{\upsilon (t)^{q-1}}t^{2n-1}dt\right) ^{p/q}\int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p} t^{2n-1}dt. \end{aligned}$$

(19)

Now, we claim that

$$\begin{aligned} K_*:=\sup _{0\le r<1} \left( \int _r^1 \frac{\omega (t)^q}{\upsilon (t)^{q-1}}t^{2n-1}dt\right) ^{1/q} \left( \int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}t^{2n-1}dt\right) ^{1/p}<\infty . \end{aligned}$$

(20)

Take this for granted for a moment. Using (19) and (20), we have

$$\begin{aligned} \int _0^{|\xi |} \frac{\upsilon (r)}{{\hat{\upsilon }}(r)^{1/q}{\hat{\omega }}(r)}r^{2n-1}dr&\le \int _0^{|\xi |} \frac{\upsilon (r)}{{\hat{\omega }}(r)} \left( \frac{K_*^p}{{\hat{\omega }}(r)^p\int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}t^{2n-1}dt}\right) ^{1/q}r^{2n-1}dr \nonumber \\&=K_*^{p-1}\int _0^{|\xi |} \frac{\upsilon (r)}{{\hat{\omega }}(r)^p} \left( \int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}t^{2n-1}dt\right) ^{{-1/q}}r^{2n-1}dr \nonumber \\&\approx K_*^{p-1} \left( \int _0^{|\xi |} \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}t^{2n-1}dt\right) ^{1/p}. \end{aligned}$$

(21)

By (16), (17), (20) and (21),

$$\begin{aligned}&h(\xi )^p\int _{ {\mathbb {B}}\backslash |\xi | {\mathbb {B}}} |B_z^\omega (\xi )|\frac{\upsilon (z)}{{\hat{\upsilon }}(z)^{1/q}}dV(z)\nonumber \\&\lesssim \upsilon (\xi ) \left( \int _{|\xi |}^1 \frac{\omega (t)^q}{\upsilon (t)^{q-1}}t^{2n-1}dt\right) ^{1/q} \frac{{\hat{\upsilon }}(\xi )^{1/p}}{{\hat{\omega }}(\xi )} \le M \upsilon (\xi ), \end{aligned}$$

(22)

and

$$\begin{aligned}&h(\xi )^p\int _{ |\xi | {\mathbb {B}}} |B_z^\omega (\xi )|\frac{\upsilon (z)}{{\hat{\upsilon }}(z)^{1/q}}dV(z)\nonumber \\&\lesssim K_*^{p-1} \upsilon (\xi ) \left( \int _{|\xi |}^1 \frac{\omega (t)^q}{\upsilon (t)^{q-1}}t^{2n-1}dt\right) ^{1/q} \left( \int _0^{|\xi |} \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}t^{2n-1}dt\right) ^{1/p} \nonumber \\&\le K_*^p\upsilon (\xi ). \end{aligned}$$

(23)

So, by (15), (22) and (23),

$$\begin{aligned} \Vert P_\omega ^+(f)\Vert _{L_\upsilon ^p}^p&\lesssim \int _ {\mathbb {B}}|f(\xi )|^p \upsilon (\xi ) dV(\xi )=\Vert f\Vert _{L_\upsilon ^p}^p. \end{aligned}$$

Now, we prove that (20) holds. Assume $r>1/2$. An integration by parts and Hölder’s inequality give

$$\begin{aligned} \int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}t^{2n-1}dt&\le \int _0^{1/2} \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}dt +\int _\frac{1}{2}^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}dt \\&\lesssim 1+\int _{1/2}^r \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p} \frac{\omega (t)}{\upsilon (t)^{1/p}} \frac{\upsilon (t)^{1/p}}{{\hat{\omega }}(t)}t^{2n-1} dt \\&\le 1+ \left( \int _0^r \left( \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p} \frac{\omega (t)}{\upsilon (t)^{1/p}} \right) ^q t^{2n-1}dt\right) ^{1/q} \left( \int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p} t^{2n-1}dt\right) ^{1/p} \\&= 1+ J_1^{1/q} \left( \int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p} t^{2n-1}dt\right) ^{1/p}, \end{aligned}$$

where

$$\begin{aligned} J_1=\int _0^r \left( \frac{{\hat{\upsilon }}(t)}{{\hat{\omega }}(t)^p} \frac{\omega (t)}{\upsilon (t)^{1/p}} \right) ^q t^{2n-1}dt. \end{aligned}$$

Since

$$\begin{aligned} J_1&=\int _0^r \left( \frac{{\hat{\upsilon }}(t)^{1/p}}{{\hat{\omega }}(t)}\left( \int _t^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{1/q}\right) ^{pq} \frac{ \frac{\omega (t)^q}{\upsilon (t)^{q-1}} }{\left( \int _t^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^p}t^{2n-1} dt \\&\lesssim \frac{M^{pq} }{\left( \int _r^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{p-1}}, \end{aligned}$$

we obtain

$$\begin{aligned} \int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}t^{2n-1}dt \lesssim 1+ M^p {\left( \int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p} t^{2n-1}dt\right) ^{1/p} } {\left( \int _r^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{-p/q^2}}. \end{aligned}$$

Hence

$$\begin{aligned}&\left( \int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}t^{2n-1}dt\right) ^{1/p}\\&\quad \lesssim 1+ M {\left( \int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p} t^{2n-1}dt\right) ^{1/p^2} } {\left( \int _r^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{-1/q^2}}. \end{aligned}$$

Multiplying the expression by $\left( \int _r^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{1/q}$, we have

$$\begin{aligned} J_2(r) \lesssim&\left( \int _r^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{1/q} +MJ_2(r)^{1/p}, \end{aligned}$$

where

$$\begin{aligned} J_2(r)=\left( \int _r^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{1/q}\left( \int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}t^{2n-1}dt\right) ^{1/p}. \end{aligned}$$

Using (18), we get

$$\begin{aligned} J_2(r)^{1/q} \lesssim {\left( \int _r^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{1/q^2}}{\left( \int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p} t^{2n-1}dt\right) ^{-1/p^2}} +M<\infty . \end{aligned}$$

Therefore,

$$\begin{aligned} \sup _{r>1/2} \left( \int _r^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{1/q}\left( \int _0^r \frac{\upsilon (t)}{{\hat{\omega }}(t)^p}t^{2n-1}dt\right) ^{1/p} <\infty . \end{aligned}$$

When $r\le 1/2$, (20) holds obviously.

$(iii)\Rightarrow (iv)$. Using (18) and (20), we get the desired result.

$(iv)\Rightarrow (iii)$. Assume that (iv) holds, that is,

$$\begin{aligned} N:=\sup \limits _{0\le r<1} \left( \int _0^r \frac{\upsilon (s)}{{\hat{\omega }}(s)^p}s^{2n-1}ds+1\right) ^{1/p}\left( \int _r^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{1/q}<\infty . \end{aligned}$$

Since $\omega \in {\mathcal {D}}$, by Lemma 1, there exists $b>0$ such that ${\hat{\omega }}(r)^p/(1-r)^b$ is essentially increasing. Then

$$\begin{aligned} \int _0^r \frac{\upsilon (s)}{{\hat{\omega }}(s)^p}s^{2n-1}ds\gtrsim \frac{(1-r)^b}{{\hat{\omega }}(r)^p}\int _0^r \frac{\upsilon (s)}{(1-s)^b}s^{2n-1}ds. \end{aligned}$$

Since $\upsilon \in {\mathcal {D}}$, there exist $C>1$ and $K>1$ such that

$$\begin{aligned} {\hat{\upsilon }}(r)\ge C{\hat{\upsilon }}\left( 1-\frac{1-r}{K}\right) . \end{aligned}$$

Let $r_k=1-K^{-k}$, $k=0,1,2,\ldots$. For any $r_2\le r<1$, there is an integer $x=x(r)$ such that $r_x\le r<r_{x+1}$. Then

$$\begin{aligned} (1-r)^b\int _0^r \frac{\upsilon (s)}{(1-s)^b}s^{2n-1}ds&\ge \sum _{k=0}^{x-1}\int _{r_{k}}^{r_{k+1}} \left( \frac{1-r}{1-s}\right) ^b\upsilon (s)s^{2n-1}ds\\&\ge \sum _{k=0}^{x-1}r_k^{2n-1}\left( \frac{1-r_{x+1}}{1-r_k}\right) ^b\left( {\hat{\upsilon }}(r_k)-{\hat{\upsilon }}(r_{k+1})\right) \\&\ge \sum _{k=0}^{x-1}r_k^{2n-1}\frac{C-1}{CK^{(x+1-k)b}}{\hat{\upsilon }}(r_k)\\&\ge \sum _{k=0}^{x-1}r_k^{2n-1}\frac{(C-1)C^{x-1-k}}{K^{(x+1-k)b}}{\hat{\upsilon }}(r_x)\\&\ge {\hat{\upsilon }}(r)\frac{C-1}{C^2}\sum _{s=2}^{x+1} r_{x+1-s}^{2n-1}\left( \frac{C}{K^b}\right) ^s \\&\ge r_{x-1}^{2n-1}{\hat{\upsilon }}(r)\frac{C-1}{K^{2b}} \ge r_1^{2n-1}{\hat{\upsilon }}(r)\frac{C-1}{K^{2b}}. \end{aligned}$$

So, when $r\ge r_2$,

$$\begin{aligned} \int _0^r \frac{\upsilon (s)}{{\hat{\omega }}(s)^p}s^{2n-1}ds\gtrsim \frac{{\hat{\upsilon }}(r)}{{\hat{\omega }}(r)^p}. \end{aligned}$$

Therefore,

$$\begin{aligned} \sup \limits _{r_2\le r<1} \frac{{\hat{\upsilon }}(r)^{1/p}}{{\hat{\omega }}(r)} \left( \int _r^1 \frac{\omega (s)^q}{\upsilon (s)^{q-1}}s^{2n-1}ds\right) ^{1/q}<\infty . \end{aligned}$$

When $r< r_2$, (iii) holds obviously. The proof is complete. $\square$