The $\gamma$-diagonally dominant degree of Schur complements and its applications

Abstract

In this paper, we obtain a new estimate for the (product) $\gamma$-diagonally dominant degree of the Schur complement of matrices. As applications we discuss the localization of eigenvalues of the Schur complement and present several upper and lower bounds for the determinant of strictly $\gamma$-diagonally dominant matrices, which generalizes the corresponding results of Liu and Zhang (SIAM J. Matrix Anal. Appl. 27 (2005) 665-674).

1 Introduction

To begin with, we recall several well-known subclasses of nonsingular H-matrices. Let $A\in \mathbb {C}^{n\times n}$ and $N\equiv \{1,2,\ldots ,n\}$. Given $\alpha \subseteq N$, denote

$$\begin{aligned} P_i(A)=\sum \limits _{j\in N,j\ne i}|a_{ij}|, \quad S_i(A)=\sum \limits _{j\in N,j\ne i}|a_{ji}|, \quad i=1,2,\ldots ,n, \end{aligned}$$

and

$$\begin{aligned} P_i^\alpha (A)=\sum \limits _{j\in \alpha ,j\ne i}|a_{ij}|, \quad S_i^\alpha (A)=\sum \limits _{j\in \alpha ,j\ne i}|a_{ji}|, \quad i=1,2,\ldots ,n. \end{aligned}$$

Given $\gamma \in [0,1]$, take

$$\begin{aligned} N_\gamma (A)=\{i\in N:|a_{ii}|>\gamma P_i(A)+(1-\gamma ) S_i(A)\}. \end{aligned}$$

(1.1)

A is called a (row) strictly diagonally dominant matrix if

$$\begin{aligned} |a_{ii}|> P_i(A), \quad \forall ~i\in N. \end{aligned}$$

(1.2)

A is called a doubly strictly diagonally dominant matrix if

$$\begin{aligned} |a_{ii}||a_{jj}|> P_i(A)P_j(A), \quad \forall ~i, j\in N \text {~and~}i\ne j. \end{aligned}$$

(1.3)

A is called a strictly $\gamma$-diagonally dominant matrix ($SD^\gamma _n$) if there exists $\gamma \in [0,1]$ such that

$$\begin{aligned} |a_{ii}|>\gamma P_i(A)+(1-\gamma )S_i(A), \quad \forall ~i\in N. \end{aligned}$$

(1.4)

A is called a product strictly $\gamma$-diagonally dominant matrix ($SPD^\gamma _n$) if there exists $\gamma \in [0,1]$ such that

$$\begin{aligned} |a_{ii}|> [P_i(A)]^\gamma [S_i(A)]^{1-\gamma }, \quad \forall ~i\in N. \end{aligned}$$

(1.5)

Given $\gamma \in [0,1]$ and $1\le i<j\le n$, define the diagonally dominant degree (Liu and Zhang 2005; Cui et al. 2017) with respect to the i-th, the doubly diagonally dominant degree (Liu et al. 2012; Gu et al. 2021) with respect to the ith and jth, the $\gamma$-diagonally dominant degree (Liu and Huang 2010; Liu et al. 2010) with respect to the i-th and the product $\gamma$-diagonally dominant degree (Liu and Huang 2010; Liu et al. 2010) with respect to the i-th of A as $|a_{ii}|-P_i(A)$, $|a_{ii}a_{jj}|-P_i(A)P_j(A)$, $|a_{ii}|-\gamma P_i(A)-(1-\gamma )S_i(A)$ and $|a_{ii}|-[P_i(A)]^\gamma [S_i(A)]^{1-\gamma }$, respectively. In this way, we may define other kinds of dominant degrees, for example, Nekrasov diagonally dominant degree (Liu et al. 2022, 2018). It is clear that the positivity of these dominant degrees could characterize the corresponding classes of matrices.

The Schur complement is a useful tool in many fields such as control theory, numerical algebra, big data, polynomial optimization, magnetic resonance imaging and simulation (Li 2000; Zhang 2006; Sang 2021). To solve the large scale linear systems efficiently, the authors (Liu and Huang 2010; Liu et al. 2010) proposed a kind of iteration called the Schur-based iteration, which reduces the order of the involved matrices by the Schur complement. The closure property and the eigenvalue distribution of the Schur complement play an important role in determining the convergence of iteration methods. The properties of the eigenvalues of the Schur complement has been studied extensively in Liu and Zhang (2005); Li et al. (2017); Cvetković and Nedović (2012); Smith (1992); Zhang et al. (2007); Liu and Huang (2004); Li et al. (2022); Song and Gao (2023) and the references therein. It has been proved in Carlson and Markham (1979); Liu and Huang (2004); Li and Tsatsomeros (1997); Liu et al. (2004) that Schur complements of strictly diagonally dominant matrices are also strictly diagonally dominant and the same property holds for nonsingular H-matrices, doubly strictly diagonally dominant matrices, generalized doubly diagonally dominant matrices (S-strictly diagonally dominant matrices). However, this closeness property does not hold for (product) strictly $\gamma$-diagonally dominant matrices (Liu and Huang 2010), Nekrasov matrices (Liu et al. 2018) or hence more matrix classes based on these structures. While, the authors (Liu and Huang 2010; Liu et al. 2010; Zhou et al. 2022; Liu et al. 2018; Cvetković and Nedović 2009; Li et al. 2022; Song and Gao 2023) presented several sufficient conditions under which Schur complements of (product) strictly $\gamma$-diagonally dominant matrices, Nekrasov matrices, Dashnic-Zusmanovich type matrices, Cvetković-Kostić-Varga type matrices are still in the same original class, respectively.

The disc separations of the Schur complement compares with that of the original matrix and show that each Geršgorin disc of the Schur complement is paired with a particular Geršgorin disc of the original matrix. For more details of the famous Geršgorin disc, see (Varga 2004). Alternatively, we may consider the disc separations as the estimates (lower bounds) of the differences between the diagonally dominant degrees of the Schur complement and that of the original matrix. Roughly speaking, if these differences are all positive, the closeness property holds; otherwise, the estimates also provide sufficient conditions ensuring the schur complement is in the same matrix class (Liu et al. 2022, 2018).

In Liu and Huang (2010); Liu et al. (2010); Zhang et al. (2013); Cui et al. (2017); Zhou et al. (2022) the authors improved the disc separations of strictly diagonally dominant matrices, and gave the lower bounds of the $\gamma$-diagonally dominant degrees of the Schur complement minus that of the original matrix. These results require the involved indices are strictly diagonally dominant in both row and column (the condition is a little weaker in Zhou et al. (2022)). In this paper, we present several new estimates for the differences between the corresponding $\gamma$-diagonally dominant degrees of the Schur complement and of the original matrix under some more natural conditions. As applications, we give the localization of eigenvalues of the Schur complement and present some upper and lower bounds for the determinant of strictly $\gamma$-diagonally dominant matrices.

The rest of the paper is organized as follows. In Sect. 2, we gave some notations and technical lemmas. In Sect. 3, we present the $\gamma$ (product $\gamma$)-diagonally dominant degree on the Schur complement of $\gamma$ (product $\gamma$)-diagonally dominant matrices. In Sect. 4, the disc theorems for the Schur complements of $\gamma$ (product $\gamma$)-diagonally dominant matrices are obtained by applying the diagonally dominant degree on the Schur complement. In Sect. 5, we give some upper and lower bounds for the determinants of strictly $\gamma$-diagonally dominant matrices, which generalizes the results in (Liu and Zhang 2005, Theorem 3).

2 Notations and Lemmas

For $A=(a_{ij})\in \mathbb {C}^{n\times n}$, the comparison matrix $\mu (A)=(m_{ij})\in \mathbb {C}^{n\times n}$ is defined as

$$\begin{aligned} m_{ij}=\left\{ \begin{array}{r} |a_{ij}|,~~if ~i=j,\\ -|a_{ij}|,~~if ~i\ne j.\\ \end{array} \right. \end{aligned}$$

A matrix A is an M-matrix if it can be split into the form $A=sI-B$, where I is an identity matrix, B is a nonnegative matrix and $s>\rho (B)$. A matrix A is an H-matrix if $\mu (A)$ is an M-matrix.

Lemma 2.1

(Horn and Johnson (1990),[p. 117]) If A is an H-matrix, then $[\mu (A)]^{-1}\ge |A^{-1}|.$

For non-empty index sets $\alpha , \beta \subseteq N$, we denote by $A(\alpha ,\beta )$ the submatrix of $A\in \mathbb {C}^{n\times n}$ lying in the rows indexed by $\alpha$ and the columns indexed by $\beta$. In particular, $A(\alpha ,\alpha )$ is abbreviated as $A(\alpha )$. Assuming that $A(\alpha )$ is nonsingular, the Schur complement of A with respect to $A(\alpha )$, which is denoted by $A/A(\alpha )$ or simply $A/\alpha$, is defined to be

$$\begin{aligned} A(\bar{\alpha })-A(\bar{\alpha },\alpha )[A(\alpha )]^{-1}A(\alpha ,\bar{\alpha }). \end{aligned}$$

Let $\alpha =\{i_1,i_2,\ldots ,i_k\}\subseteq N$ and $\bar{\alpha }=N-\alpha =\{j_1,j_2,\ldots ,j_l\}$. Denote by $|\alpha |$ the cardinality of $\alpha$. It is clear that $|\alpha |=k$. For the sake of convenience, denote

$$\begin{aligned} \overrightarrow{x}_{j_s}^*:=(a_{j_s i_1},a_{j_si_2},\ldots , a_{j_si_k}),~|\overrightarrow{x}_{j_s}^*|:=\left( |a_{j_s i_1}|,|a_{j_s i_2}|,\ldots , |a_{j_s i_k}|\right) ,\\ \overrightarrow{y}_{j_s}:=(a_{i_1j_s},a_{i_2j_s},\ldots , a_{i_kj_s})^T,~|\overrightarrow{y}_{j_s}|:=(|a_{i_1j_s}|,|a_{i_2j_s}|,\ldots , |a_{i_kj_s}|)^T. \end{aligned}$$

Given any $\gamma \in [0,1]$ and $\alpha \subseteq N$, denote

$$\begin{aligned}{} & {} t_i(A)=\frac{\gamma P_i(A)+(1-\gamma )S_i(A)}{|a_{ii}|}, \end{aligned}$$

(2.1)

$$\begin{aligned}{} & {} mx^r_{j_0}(A,\alpha )=\sum \limits _{i\in \alpha }t_{i}(A)\left[ \gamma |a_{j_0i}|+(1-\gamma )\sum \limits _{j\in \bar{\alpha }}|a_{ij}|\right] , \end{aligned}$$

(2.2)

$$\begin{aligned}{} & {} mx^c_{j_0}(A,\alpha )=\sum \limits _{i\in \alpha }t_{i}(A)\left[ \gamma \sum \limits _{j\in \bar{\alpha }}|a_{ji}|+(1-\gamma )|a_{ij_0}|\right] . \end{aligned}$$

(2.3)

Lemma 2.2

Let $A \in \mathbb {C}^{n\times n}$, let $\alpha =\{i_1,i_2,\ldots ,i_k\}\subseteq N_{\gamma }(A)$ and $\bar{\alpha }=N-\alpha =\{j_1,j_2,\ldots ,j_l\}$ with $1\le k<n$. For each $t\in \{1,2,\ldots , l\}$, denote

$$\begin{aligned} B_t\equiv \begin{bmatrix} &{}&{}&{}-\sum \limits _{s=1}^{l}|a_{i_1j_s}|\\ &{}\mu [A(\alpha )]&{}&{}\vdots \\ &{}&{}&{}-\sum \limits _{s=1}^{l}|a_{i_kj_s}|\\ -|a_{j_ti_1}|&{}\ldots &{}-|a_{j_ti_k}|&{}x \end{bmatrix}. \end{aligned}$$

Then $B_t$ is an M-matrix and $det(B_t)>0$, if

$$\begin{aligned} x> \sum \limits _{u=1}^{k}t_{i_u}(A)\left[ \gamma |a_{j_ti_u}|+(1-\gamma )\sum \limits _{s=1}^l|a_{i_uj_s}|\right] =ms^r_{j_t}(A,\alpha ). \end{aligned}$$

(2.4)

Proof

It is sufficient to show that there exists a positive diagonal matrix D such that $DB_tD$ is in $SD^\gamma _{k+1}$. Since $x> ms^r_{j_t}(A,\alpha )$ and $\alpha \subseteq N$, take $\varepsilon >0$ such that

$$\begin{aligned} x>\sum \limits _{u=1}^{k}(t_{i_u}(A)+\varepsilon )\left[ \gamma |a_{j_ti_u}|+(1-\gamma )\sum \limits _{s=1}^l|a_{i_uj_s}|\right] , \end{aligned}$$

(2.5)

and

$$\begin{aligned} t_{i_u}(A)+\varepsilon <1, \quad u=1,2,\ldots ,k. \end{aligned}$$

(2.6)

We construct $D=diag(d_1,d_2,\ldots ,d_{k+1})$, where

$$\begin{aligned} d_{u}=\left\{ \begin{array}{r} t_{i_u}(A)+\varepsilon ,~~if ~1\le u\le k,\\ 1,~~if ~u= k+1.\\ \end{array} \right. \end{aligned}$$

Let $C=DB_tD=(c_{ij})$. For $u=1,2,\ldots , k+1$, by (2.6), we have

$$\begin{aligned} P_{u}(C)\le d_u P_u(B_t)\quad \text {and}\quad S_{u}(C)\le d_u S_u(B_t). \end{aligned}$$

(2.7)

Let $B_t=(b_{ij})$. Then for $1\le u\le k$, we have

$$\begin{aligned} |c_{uu}|= & {} d_u^2|b_{uu}|\\= & {} \left[ t_{i_u}(A)+\varepsilon \right] ^2|a_{i_ui_u}|\\= & {} \left[ t_{i_u}(A)+\varepsilon \right] \left[ |a_{i_ui_u}|\varepsilon +\gamma P_{i_u}(A)+(1-\gamma )S_{i_u}(A)\right] \\> & {} \left[ t_{i_u}(A)+\varepsilon \right] \left[ \gamma P_{i_u}(A)+(1-\gamma )S_{i_u}(A)\right] \\\ge & {} \left[ t_{i_u}(A)+\varepsilon \right] [\gamma P_{u}(B_t)+(1-\gamma )S_{u}(B_t)]\\\ge & {} \gamma P_{u}(C)+(1-\gamma )S_{u}(C). \end{aligned}$$

For $u=k+1$, by (2.5) and (2.6) we have

$$\begin{aligned} |c_{uu}|=1^2|b_{uu}|= x> & {} \sum \limits _{v=1}^{k}(t_{i_v}(A)+\varepsilon )\left[ \gamma |a_{j_ti_v}|+(1-\gamma )\sum \limits _{s=1}^{l}|a_{i_vj_s}|\right] \\= & {} \sum \limits _{v=1}^{k}(t_{i_v}(A)+\varepsilon )\left[ \gamma |b_{uv}|+(1-\gamma )|b_{vu}|\right] \\= & {} \gamma P_u(C)+(1-\gamma )S_u(C). \end{aligned}$$

Therefore, $C\in SD_{k+1}^{\gamma }$, and hence $B_t$ is a nonsingular H-matrix. Since $B_t=\mu (B_t)$, $B_t$ ia an M-matrix. It follows from (Horn and Johnson 1990, Theorem 2.5.4) that $det(B_t)>0$. $\square$

Lemma 2.3

Let $a_1> a_2\ge 0$, $b_1> b_2\ge 0$ and $0\le \gamma \le 1$. Then

$$\begin{aligned} (a_1+a_2)^\gamma (b_1+b_2)^{1-\gamma }\ge a_1^{\gamma } b_1^{1-\gamma }+a_2^\gamma b_2^{1-\gamma }, \end{aligned}$$

(2.8)

and

$$\begin{aligned} (a_1-a_2)^\gamma (b_1-b_2)^{1-\gamma }\le a_1^\gamma b_1^{1-\gamma }-a_2^\gamma b_2^{1-\gamma }. \end{aligned}$$

(2.9)

Proof

For $\gamma =0$ and $\gamma =1$, the above inequalities hold trivially. If $a_2=0$ or $b_2=0$, the above inequalities also hold trivially. Now suppose $0<\gamma <1$, $a_1> a_2> 0$ and $b_1> b_2>0$. Let $a_i=x_i^{1/\gamma }$ and $b_i=y_i^{1/(1-\gamma )}$ for $i=1,2$. By the well-known Hölder inequality (Horn and Johnson 1985, p. 536) we have

$$\begin{aligned} a_1^\gamma b_1^{1-\gamma }+a_2^\gamma b_2^{1-\gamma }= & {} x_1y_1+x_2y_2\le (x_1^{1/\gamma }+x_2^{1/\gamma })^\gamma \left( y_1^{1/(1-\gamma )}+y_2^{1/(1-\gamma )}\right) ^{1-\gamma }\\= & {} (a_1+a_2)^\gamma (b_1+b_2)^{1-\gamma }, \end{aligned}$$

which leads to (2.8). Note that (2.8) only requires that $a_1,a_2,b_1,b_2>0$.

Let $s=a_1-a_2$ and $t=b_1-b_2$. It is clear that $s,t>0$. By (2.8) we have

$$\begin{aligned} a_1^\gamma b_1^{1-\gamma }=(s+a_2)^\gamma (t+b_2)^{1-\gamma }\ge s^\gamma t^{1-\gamma }+a_2^\gamma b_2^{1-\gamma }=(a_1-a_2)^\gamma (b_1-b_2)^{1-\gamma }+a_2^\gamma b_2^{1-\gamma }, \end{aligned}$$

which leads to (2.9). $\square$

3 Disc separation of the Schur complement

In this section, we present the lower and upper bounds for the $\gamma$- and the product $\gamma$-diagonally dominant degrees of the Schur complent in terms of the entries of original matrices. We need the following notations. Given $\gamma \in [0,1]$ and $\alpha \subseteq N$, denote

$$\begin{aligned} w_{j}^r=P_j^{\alpha }(A)-mx^{r}_j(A,\alpha ),\quad w_{j}^c=S_j^{\alpha }(A)-mx^{c}_j(A,\alpha ),\quad w_{j}=\gamma w_{j}^r+(1-\gamma )w_{j}^c. \end{aligned}$$

One of our main results in this section is as follows.

Theorem 3.1

Let $A =(a_{ij})\in \mathbb {C}^{n\times n}$, and let $\alpha =\{i_1,i_2,\ldots ,i_k\}\subseteq N_{\gamma }(A)$ and $\bar{\alpha }=N-\alpha =\{j_1,j_2,\ldots ,j_l\}$ with $1\le k<n$. Set $A/\alpha =(a'_{ts})$. For $1\le t\le l$, we have

$$\begin{aligned}&\hspace{2.5em}|a'_{tt}|-\gamma P_t(A/\alpha )-(1-\gamma )S_t(A/\alpha ) \ge |a_{j_{t}j_{t}}|-\gamma P_{j_{t}}(A)-(1-\gamma )S_{j_{t}}(A)+w_{j_{t}} \end{aligned}$$

(3.1)

and

$$\begin{aligned}&\hspace{2.5em}|a'_{tt}|+\gamma P_t(A/\alpha )+(1-\gamma )S_t(A/\alpha ) \le |a_{j_{t}j_{t}}|+\gamma P_{j_{t}}(A)+(1-\gamma )S_{j_{t}}(A)-w_{j_{t}}. \end{aligned}$$

(3.2)

Proof

Let $B_t$ be the matrix constructed in Lemma 2.2. First we prove

$$\begin{aligned} mx^r_{j_t}(A,\alpha )\ge |\overrightarrow{x}_{j_t}^*|\{\mu [A(\alpha )]\}^{-1}\left( \sum \limits _{s=1}^{l}|\overrightarrow{y}_{j_s}|\right) . \end{aligned}$$

(3.3)

Since $B_t/\{1,2,\ldots ,k\}=x-|\overrightarrow{x}_{j_t}^*|\{\mu [A(\alpha )]\}^{-1}\left( \sum \limits _{s=1}^{l}|\overrightarrow{y}_{j_s}|\right)$, it is sufficient to prove $B_t/\{1,2,\ldots ,k\}\ge 0$ when $x=mx^r_{j_t}(A)$. Let $x=mx^r_{j_t}(A,\alpha )+\varepsilon$. For any $\varepsilon >0$, by Lemma 2.2, $det(B_{t})>0$. Note that $\mu (A(\alpha ))=B_t(\{1,2,\ldots ,k\})$ is an M-matrix and hence $det[\mu (A(\alpha ))]>0$. It is well-known that

$$\begin{aligned} det(B_t)=det[\mu (A(\alpha ))]\cdot det(B_t/\{1,2,\ldots ,k\}), \end{aligned}$$

which implies that $B_t/\{1,2,\ldots ,k\}>0$. We obtain (3.3) when $\varepsilon \rightarrow 0^+$. Adopting the same arguments, we obtain

$$\begin{aligned} mx^c_{j_t}(A)\ge \left( \sum \limits _{s=1}^{l}|\overrightarrow{x}^*_{j_s}|\right) \mu [A(\alpha )]^{-1}|\overrightarrow{y}_{j_t}|. \end{aligned}$$

(3.4)

Then we have

$$\begin{aligned}{} & {} |a'_{tt}|-\gamma P_t(A/\alpha )-(1-\gamma )S_t(A/\alpha )\\= & {} |a'_{tt}|-\gamma \sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}|a_{ts}'|-(1-\gamma )\sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}|a_{st}'|\\= & {} \left| a_{j_tj_t}-\overrightarrow{x}_{j_t}^*A(\alpha )^{-1}\overrightarrow{y}_{j_t}\right| -\gamma \sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}|a_{j_tj_s}\\{} & {} -\overrightarrow{x}_{j_t}^*A(\alpha )^{-1}\overrightarrow{y}_{j_s}|-(1-\gamma )\sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}|a_{j_sj_t}-\overrightarrow{x}_{j_s}^*A(\alpha )^{-1}\overrightarrow{y}_{j_t}|\\\ge & {} |a_{j_tj_t}|-|\overrightarrow{x}^*_{j_t}A(\alpha )^{-1}\overrightarrow{y}_{j_t}|-\gamma \sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}|a_{j_tj_s}|-\gamma \sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}|\overrightarrow{x}^*_{j_t}A(\alpha )^{-1}\overrightarrow{y}_{j_s}|\\{} & {} -(1-\gamma )\sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}|a_{j_sj_t}|-(1-\gamma )\sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}|\overrightarrow{x}^*_{j_s}A(\alpha )^{-1}\overrightarrow{y}_{j_t}|\\= & {} |a_{j_tj_t}|-\gamma P_{j_t}^{\bar{\alpha }}(A)-(1-\gamma )S_{j_t}^{\bar{\alpha }}(A)-\gamma \sum \limits _{s=1}^{l}|\overrightarrow{x}^*_{j_t}A(\alpha )^{-1}\overrightarrow{y}_{j_s}|\\{} & {} -(1-\gamma )\sum \limits _{s=1}^{l}|\overrightarrow{x}^*_{j_s}A(\alpha )^{-1}\overrightarrow{y}_{j_t}|\\\ge & {} |a_{j_tj_t}|-\gamma P_{j_t}^{\bar{\alpha }}(A)-(1-\gamma )S_{j_t}^{\bar{\alpha }}(A)-\gamma \sum \limits _{s=1}^{l}|\overrightarrow{x}^*_{j_t}|\mu (A(\alpha ))^{-1}|\overrightarrow{y}_{j_s}|\\{} & {} -(1-\gamma )\sum \limits _{s=1}^{l}|\overrightarrow{x}^*_{j_s}|\mu (A(\alpha ))^{-1}|\overrightarrow{y}_{j_t}|\\= & {} |a_{j_tj_t}|-\gamma P_{j_t}^{\bar{\alpha }}(A)-(1-\gamma )S_{j_t}^{\bar{\alpha }}(A)\\{} & {} -\gamma |\overrightarrow{x}^*_{j_t}|\mu (A(\alpha ))^{-1}\left( \sum \limits _{s=1}^{l}|\overrightarrow{y}_{j_s}|\right) -(1-\gamma )\left( \sum \limits _{s=1}^{l}|\overrightarrow{x}^*_{j_s}|\right) \mu (A(\alpha ))^{-1}|\overrightarrow{y}_{j_t}|\\\ge & {} |a_{j_tj_t}|-\gamma [P_{j_t}^{\bar{\alpha }}(A)+mx_{j_t}^r(A,\alpha )]-(1-\gamma )[S_{j_t}^{\bar{\alpha }}(A)+mx_{j_t}^c(A,\alpha )]\\= & {} |a_{j_tj_t}|-\gamma P_{j_t}(A)-(1-\gamma )S_{j_t}(A)+\gamma [P_{j_t}^{\alpha }(A)-mx_{j_t}^r(A,\alpha )]\\{} & {} +(1-\gamma )[S_{j_t}^{\alpha }(A)-mx_{j_t}^c(A,\alpha )]\\= & {} |a_{j_tj_t}|-\gamma P_{j_t}(A)-(1-\gamma )S_{j_t}(A)+w_{j_t}. \end{aligned}$$

Similarly, we can get (3.2). The proof is completed. $\square$

Corollary 3.1

Given $\gamma \in [0,1]$, let $A \in SD_{n}^\gamma$, $\alpha =\{i_1,i_2,\ldots ,i_k\}\subseteq N$ and $\bar{\alpha }=N-\alpha =\{j_1,j_2,\ldots ,j_l\}$ with $1\le k<n$. If $w_{j_t}\ge 0$ for all $t\in \{1,2,,\ldots ,l\}$, then $A/\alpha \in SD_{n-k}^{\gamma }$.

Corollary 3.2

Given $\gamma \in [0,1]$, let $A \in SD_{n}^\gamma$, $\alpha =\{i_1,i_2,\ldots ,i_k\}\subseteq N$ and $\bar{\alpha }=N-\alpha =\{j_1,j_2,\ldots ,j_l\}$ with $1\le k<n$. If

$$\begin{aligned} |a_{j_tj_t}|>\gamma P_{j_t}(A)+(1-\gamma )S_{j_t}(A)-w_{j_t},\quad t=1,\ldots ,l, \end{aligned}$$

then $A/\alpha \in SD_{n-k}^\gamma$.

Recalling the definitions of $w_j,w_j^r,w_j^c,mx_j^r(A,\alpha ),mx_j^c(A,\alpha ),t_i(A)$, we find $w_j$ increases as $|a_{i_si_s}|$ goes bigger, and when all $|a_{i_si_s}|$ are big enough we always have $w_j\ge 0$. Hence Corollary 3.1 implies that if each $|a_{i_si_s}|$ is large sufficiently, Schur complements of matrices in $SD^{\gamma }_n$ are still in $SD^{\gamma }_{n-k}$; while Corollary 3.2 tells us that the same result holds if each $|a_{j_tj_t}|$ is large sufficiently.

Example 3.1

   Let $\gamma =0.7$, $\alpha =\{3,4\}$ and

$$\begin{aligned} A=\left( \begin{array}{ccccc} 20&{}\,\, 4&{}\,\, 1&{}\,\,2\\ 2&{}\,\,16&{}\,\,1&{}\,\,0\\ 1&{}\,\,1&{}\,\,10&{}\,\,10\\ 0&{}\,\,1&{}\,\,0&{}\,\,5\\ \end{array} \right) . \end{aligned}$$

It is clear that $\bar{\alpha }=\{1,2\}$. Then $i_1=3$, $i_2=4$, $j_1=1$ and $j_2=2$. By directed computation, we have

	$P_{j_t}(A)$	$S_{j_t}(A)$	$w_{j_t}$
$j_1=1$	7	3	0.3374
$j_2=2$	3	6	−0.8972

Since

$$\begin{aligned} 20>0.7\times 7+0.3\times 3-0.3374\quad \text {and}\quad 16>0.7\times 3+0.3\times 6+0.8972, \end{aligned}$$

by Corollary 3.2, we have $A/\alpha \in SD^\gamma _2$. Since $|a_{33}|<P_3(A)$, the corresponding results in Cui et al. (2017); Liu and Huang (2010); Liu et al. (2010); Zhang et al. (2013) are not applicable. Since $A(\alpha )$ is not diagonally dominant in column, the corresponding result in Zhou et al. (2022) is not applicable.

Notice that $A/\alpha$ is a number and $w_{n}^r=w_{n}^c=mx_{n}^r(A,\alpha )=mx_{n}^c(A,\alpha )$ when $|\alpha |=n-1$. It follows immediately the following corollary from Theorem 3.1.

Corollary 3.3

Given $0\le \gamma \le 1$, let $A =(a_{ij})\in SD_{n}^\gamma$, and take $\alpha =\{1,2,\ldots ,n-1\}$. Then

$$\begin{aligned}&\hspace{2.5em}|a_{nn}|+mx_{n}^r(A,\alpha )\ge |A/\alpha | \ge |a_{nn}|-mx_{n}^r(A,\alpha ). \end{aligned}$$

(3.5)

Proof

Since $A/\alpha =a'_{11}$ is a number, $P_{1}(A/\alpha )=S_{1}(A/\alpha )=0$. Moreover, $P_n(A)=P_n^{\alpha }(A)$ and $S_n(A)=S_n^{\alpha }(A)$. By Theorem 3.1, we get (3.5). $\square$

To get the corresponding results for the product $\gamma$-diagonally dominant matrices, we need the following technical lemma.

Lemma 3.1

Let $A =(a_{ij})\in \mathbb {C}^{n\times n}$. Given $0\le \gamma \le 1$, let $\alpha =\{i_1,i_2,\ldots ,i_k\}\subseteq N_{\gamma }(A)$ and $\bar{\alpha }=N-\alpha =\{j_1,j_2,\ldots ,j_l\}$ with $1\le k<n$. Set $A/\alpha =(a'_{ts})$. If for all $1\le t\le l$, $P_{j_t}(A)>w^r_{j_t}\ge 0$ and $S_{j_t}(A)>w^c_{j_t}\ge 0$, then we have

$$\begin{aligned} |\overrightarrow{x}_{j_t}^*A(\alpha )^{-1}\overrightarrow{y}_{j_t}|+[P_t(A/\alpha )]^\gamma [S_t(A/\alpha )]^{1-\gamma }\le \left[ P_{j_t}(A)-w^r_{j_t}\right] ^\gamma \left[ S_{j_t}(A)-w^c_{j_t}\right] ^{1-\gamma }. \end{aligned}$$

(3.6)

Proof

Since $\alpha \subseteq N_\gamma (A)$, $A(\alpha )\in SD_k^{\gamma }$. It follows that $\{\mu [A(\alpha )]\}^{-1}\ge |A(\alpha )^{-1}|$. Then we have

$$\begin{aligned} |\overrightarrow{x}_{j_t}^*A(\alpha )^{-1}\overrightarrow{y}_{j_t}|\le |\overrightarrow{x}_{j_t}^*|\{\mu [A(\alpha )]\}^{-1}|\overrightarrow{y}_{j_t}|. \end{aligned}$$

(3.7)

By the definition of Schur complements, we have

$$\begin{aligned} P_t(A/\alpha )= & {} \sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}|a_{j_tj_s}-\overrightarrow{x}_{j_t}^*A(\alpha )^{-1}\overrightarrow{y}_{j_s}|\\\le & {} \sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}\left[ |a_{j_tj_s}|+|\overrightarrow{x}_{j_t}^*A(\alpha )^{-1}\overrightarrow{y}_{j_s}|\right] \\\le & {} \sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}|a_{j_tj_s}|+|\overrightarrow{x}_{j_t}^*||A(\alpha )^{-1}|\sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}|\overrightarrow{y}_{j_s}|\\\le & {} P_{j_t}^{\bar{\alpha }}(A)+|\overrightarrow{x}_{j_t}^*|\{\mu [A(\alpha )]\}^{-1}\sum \limits _{\begin{array}{c} s=1\\ s\ne t \end{array}}^{l}|\overrightarrow{y}_{j_s}|. \end{aligned}$$

Recalling the definition of $w_{j_t}^r$ and (3.3), we have

$$\begin{aligned} P_t(A/\alpha )\le P_{j_t}(A)-w_{j_t}^r-|\overrightarrow{x}_{j_t}^*|\{\mu [A(\alpha )]\}^{-1}|\overrightarrow{y}_{j_t}|. \end{aligned}$$

(3.8)

Applying the same arguments, we obtain

$$\begin{aligned} S_t(A/\alpha )\le S_{j_t}(A)-w_{j_t}^c-|\overrightarrow{x}_{j_t}^*|\{\mu [A(\alpha )]\}^{-1}|\overrightarrow{y}_{j_t}|. \end{aligned}$$

(3.9)

By Lemma 2.3, we get

$$\begin{aligned}{}[P_t(A/\alpha )]^\gamma [S_t(A/\alpha )]^{1-\gamma }\le & {} \left[ P_{j_t}(A)-w_{j_t}^r-|\overrightarrow{x}_{j_t}^*|\{\mu [A(\alpha )]\}^{-1}|\overrightarrow{y}_{j_t}|\right] ^\gamma \\{} & {} \times \left[ S_{j_t}(A)-w_{j_t}^c-|\overrightarrow{x}_{j_t}^*|\{\mu [A(\alpha )]\}^{-1}|\overrightarrow{y}_{j_t}|\right] ^{1-\gamma }\\\le & {} \left[ P_{j_t}(A)-w_{j_t}^r\right] ^\gamma \left[ S_{j_t}(A)-w_{j_t}^c\right] ^{1-\gamma }-|\overrightarrow{x}_{j_t}^*|\{\mu [A(\alpha )]\}^{-1}|\overrightarrow{y}_{j_t}|, \end{aligned}$$

which leads to (3.6). $\square$

Theorem 3.2

Let $A =(a_{ij})\in \mathbb {C}^{n\times n}$. Given $0\le \gamma \le 1$, let $\alpha =\{i_1,i_2,\ldots ,i_k\}\subseteq N_\gamma (A)$ and $\bar{\alpha }=N-\alpha =\{j_1,j_2,\ldots ,j_l\}$ with $1\le k<n$. Set $A/\alpha =(a'_{ts})$. If for all $1\le t\le l$, $P_{j_t}(A)>w^r_{j_t}\ge 0$ and $S_{j_t}(A)>w^c_{j_t}\ge 0$, then we have

$$\begin{aligned}&\hspace{2.5em}|a'_{tt}|- [P_t(A/\alpha )]^\gamma [S_t(A/\alpha )]^{1-\gamma } \ge |a_{j_tj_t}|-\left[ P_{j_t}(A)\right] ^\gamma \left[ S_{j_t}(A)\right] ^{1-\gamma }+\left( w^r_{j_t}\right) ^\gamma \left( w^c_{j_t}\right) ^{1-\gamma } \end{aligned}$$

(3.10)

$$\begin{aligned}&\hspace{2.5em}|a'_{tt}|+[P_t(A/\alpha )]^\gamma [S_t(A/\alpha )]^{1-\gamma } \le |a_{j_tj_t}|+\left[ P_{j_t}(A)\right] ^\gamma \left[ S_{j_t}(A)\right] ^{1-\gamma }-\left( w^r_{j_t}\right) ^\gamma \left( w^c_{j_t}\right) ^{1-\gamma }. \end{aligned}$$

(3.11)

Proof

By the definition of the Schur complement,

$$\begin{aligned}{} & {} |a'_{tt}|- [P_t(A/\alpha )]^\gamma [S_t(A/\alpha )]^{1-\gamma }\\= & {} |a_{j_tj_t}-\overrightarrow{x}_{j_t}^*A(\alpha )^{-1}\overrightarrow{y}_{j_t}|- [P_t(A/\alpha )]^\gamma [S_t(A/\alpha )]^{1-\gamma }\\\ge & {} |a_{j_tj_t}|-|\overrightarrow{x}_{j_t}^*A(\alpha )^{-1}\overrightarrow{y}_{j_t}|- [P_t(A/\alpha )]^\gamma [S_t(A/\alpha )]^{1-\gamma }. \end{aligned}$$

By Lemma 3.1 and Lemma 2.3 we get

$$\begin{aligned} |a'_{tt}|- [P_t(A/\alpha )]^\gamma [S_t(A/\alpha )]^{1-\gamma }\ge & {} |a_{j_tj_t}|-\left[ P_{j_t}(A)-w^r_{j_t}\right] ^\gamma \left[ S_{j_t}(A)-w^c_{j_t}\right] ^{1-\gamma }\\\ge & {} |a_{j_tj_t}|-\left[ P_{j_t}(A)\right] ^\gamma \left[ S_{j_t}(A)\right] ^{1-\gamma }+(w^r_{j_t})^\gamma (w^c_{j_t})^{1-\gamma }. \end{aligned}$$

Similarly, we obtain

$$\begin{aligned} |a'_{tt}|+ [P_t(A/\alpha )]^\gamma [S_t(A/\alpha )]^{1-\gamma }\le & {} |a_{j_tj_t}|+\left[ P_{j_t}(A)-w^r_{j_t}\right] ^\gamma \left[ S_{j_t}(A)-w^c_{j_t}\right] ^{1-\gamma }\\\le & {} |a_{j_tj_t}|+\left[ P_{j_t}(A)\right] ^\gamma \left[ S_{j_t}(A)\right] ^{1-\gamma }-(w^r_{j_t})^\gamma (w^c_{j_t})^{1-\gamma }. \end{aligned}$$

The proof is completed. $\square$

Remark that the conditions that $P_{j_t}(A)>w^r_{j_t}$ and $S_{j_t}(A)>w^c_{j_t}$ in Lemma 3.1 and Theorem 3.2 are easily satisfied since we always have $P_{j_t}(A)\ge P_{j_t}^\alpha (A)\ge w^r_{j_t}$ and $S_{j_t}(A)\ge S_{j_t}^\alpha (A)\ge w^c_{j_t}$.

4 Distribution for eigenvalues

In this section, we present some locations for eigenvalues of the Schur complement by the entries of the original matrix.

Lemma 4.1

(Ostrowski (1951)) Let $A \in \mathbb {C}^{n\times n}$ and $0 \le \gamma \le 1$. Then, for every eigenvalue $\lambda$ of A, there exists $0 \le i \le n$ such that

$$\begin{aligned} |\lambda -a_{ii}|\le \left[ P_{i}(A)\right] ^\gamma \left[ S_{i}(A)\right] ^{1-\gamma }. \end{aligned}$$

Theorem 4.1

Let $A=(a_{ij}) \in \mathbb {C}^{n\times n}$. Given $0\le \gamma \le 1$, let $\alpha =\{i_1,i_2,\ldots ,i_k\}\subseteq N_\gamma (A)$ and $\bar{\alpha }=N-\alpha =\{j_1,j_2,\ldots ,j_l\}$ with $1\le k<n$. Set $A/\alpha =(a'_{ts})$. If for all $1\le t\le l$, $P_{j_t}(A)>w_{j_t}^r\ge 0$ and $S_{j_t}(A)>w_{j_t}^c\ge 0$, then for every eigenvalue $\lambda$ of $A/\alpha$, there exists $1\le t\le n-k$ such that

$$\begin{aligned} |\lambda -a_{j_tj_t}|\le \left[ P_{j_t}(A)\right] ^\gamma \cdot \left[ S_{j_t}(A)\right] ^{1-\gamma }-\left( w^r_{j_t}\right) ^\gamma \left( w^c_{j_t}\right) ^{1-\gamma }. \end{aligned}$$

(4.1)

Proof

By Lemma 4.1, for any eigenvalue $\lambda$ of $A/\alpha$, there exists $0 \le t \le n-k$ such that

$$\begin{aligned} |\lambda -a'_{tt}|\le P_{t}^\gamma (A/\alpha )S_{t}^{1-\gamma }(A/\alpha ). \end{aligned}$$

Since $\alpha \subseteq N_\gamma (A)$, $A(\alpha )\in SD_k^{\gamma }$. It follows that $\{\mu [A(\alpha )]\}^{-1}\ge |A(\alpha )^{-1}|$. Now we have

$$\begin{aligned} 0\ge & {} |\lambda -a'_{tt}|- P_{t}^\gamma (A/\alpha )S_{t}^{1-\gamma }(A/\alpha )\nonumber \\= & {} \left| \lambda -a_{j_tj_t}+\overrightarrow{x}^*_{j_t}[A(\alpha )]^{-1}\overrightarrow{y}_{j_t}\right| - P_{t}^\gamma (A/\alpha )S_{t}^{1-\gamma }(A/\alpha )\nonumber \\\ge & {} |\lambda -a_{j_tj_t}|-|\overrightarrow{x}^*_{j_t}[A(\alpha )]^{-1}\overrightarrow{y}_{j_t}|-P_{t}^\gamma (A/\alpha )S_{t}^{1-\gamma }(A/\alpha )\nonumber \\\ge & {} \left| \lambda -a_{j_tj_t}\right| - [P_{j_t}(A)-w^r_{j_t}]^\gamma [S_{j_t}(A)-w^c_{j_t}]^{1-\gamma }\\\ge & {} \left| \lambda -a_{j_tj_t}\right| - [P_{j_t}(A)]^\gamma [S_{j_t}(A)]^{1-\gamma }+\left( w^r_{j_t}\right) ^\gamma \left( w^c_{j_t}\right) ^{1-\gamma },\nonumber \end{aligned}$$

(4.2)

which implies (4.1). Note that (4.2) is derived from Lemma 3.1. The proof is completed. $\square$

Adopting the theorem of the arithmetic and geometric means on (4.2), we get the following result immediately.

Corollary 4.1

Let $A=(a_{ij}) \in \mathbb {C}^{n\times n}$. Given $0\le \gamma \le 1$, let $\alpha =\{i_1,i_2,\ldots ,i_k\}\subseteq N_\gamma (A)$ and $\bar{\alpha }=N-\alpha =\{j_1,j_2,\ldots ,j_l\}$ with $1\le k<n$. Set $A/\alpha =(a'_{ts})$. If for all $1\le t\le l$, $P_{j_t}(A)>w_{j_t}^r\ge 0$ and $S_{j_t}(A)>w_{j_t}^c\ge 0$, then for every eigenvalue $\lambda$ of $A/\alpha$, there exists $1\le t\le n-k$ such that

$$\begin{aligned} |\lambda -a_{j_tj_t}|\le \gamma P_{j_{t}}(A)+(1-\gamma )S_{j_{t}}(A)-w_{j_t}. \end{aligned}$$

(4.3)

Next, we give a numerical example to estimate eigenvalues of the Schur complement with the entries of the original matrix to show the advantages of our results.

Example 4.1

Let

$$\begin{aligned}&\hspace{2.5em}A=\left( \begin{array}{ccccc} 15&{}\,2&{}\,0&{}\,5&{}\,1\\ 5&{}\,19&{}\,0&{}\,20&{}\,0\\ 0&{}\,0&{}\,20&{}\,10&{}\,1\\ 0&{}\,0&{}\,10&{}\,100&{}\,5\\ 1&{}\,2&{}\,1&{}5&{}\,30\\ \end{array} \right) ,\quad \alpha =\{2,4\},\quad \gamma =0.2.&\end{aligned}$$

Then we get $\bar{\alpha }=\{1,3,5\}$ and the following table.

	$P_{j_t}(A)$	$S_{j_t}(A)$	$w_{j_t}^r$	$w_{j_t}^c$	$w_{j_t}$
$j_1=1$	8	6	0.5511	3.5284	2.9329
$j_2=3$	11	11	3.3737	5.4547	5.0385
$j_3=5$	9	7	0.5511	3.8547	3.1940

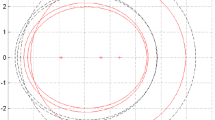
By Theorem 4.1, the eigenvalue $\lambda$ of $A/\alpha$ are in the union of the three discs as follows.

$$\begin{aligned} \lambda \in \{z:|z-15|\le 3.9214\}\cup \{z:|z-20|\le 6.0451\}\cup \{z:|z-30|\le 4.7484\}\equiv \Gamma _1. \end{aligned}$$

By Corollary 4.1, the eigenvalue $\lambda$ of $A/\alpha$ are in the union of the three discs as follows.

$$\begin{aligned} \lambda \in \{z:|z-15|\le 3.4671\}\cup \{z:|z-20|\le 5.9615\}\cup \{z:|z-30|\le 4.206\}\equiv \Gamma _2. \end{aligned}$$

Notice that $\Gamma _2$ is not necessarily contained in $\Gamma _1$. Since the second row is not diagonally dominant, the corresponding results in Cui et al. (2017); Liu and Huang (2010); Liu et al. (2010); Zhang et al. (2013) are not applicable. Since $A(\alpha )$ is not diagonally dominant in row, the corresponding result in Zhou et al. (2022) is not applicable.

Fig. 1

The red and black dotted lines denote the corresponding discs of $\Gamma _1$ and $\Gamma _2$, respectively

5 Bounds for determinants

Let $\{j_1,j_2,\ldots ,j_n\}$ be a rearrangement of the elements in $N=\{1,2,\ldots ,n\}$. Denote $\alpha _1=\{j_n\},\alpha _2=\{j_{n-1},j_n\},\ldots ,\alpha _n=\{j_1,j_2,\ldots ,j_n\}=N$. Then $\alpha _{n-k+1}- \alpha _{n-k}=\{j_k\}$, $k=1,2,\ldots ,n$, with $\alpha _0=\emptyset$. Let $\mathcal {J}$ represent any rearrangement $\{j_1,j_2,\ldots ,j_n\}$ of the elements in N with $\alpha _1,\alpha _2,\ldots ,\alpha _n$ defined as above. By using disc separation of the Schur complement, Liu and Zhang (2005) presented the lower and upper bounds for determinants of the strictly diagonally dominant matrices as follows.

Theorem 5.1

Let $A\in SD_n$. Then

$$\begin{aligned} |det(A)|\ge \max \limits _{\mathcal {J}}\prod \limits _{k=1}^{n} \left\{ |a_{j_kj_k}|-\max \limits _{i\in \alpha _{n-k}}\frac{P_i^{\alpha _{n-k+1}}(A)}{|a_{ii}|}P_{j_k}^{\alpha _{n-k+1}}(A)\right\} , \end{aligned}$$

and

$$\begin{aligned} |det(A)|\le \max \limits _{\mathcal {J}}\prod \limits _{k=1}^{n} \left\{ |a_{j_kj_k}|+\max \limits _{i\in \alpha _{n-k}}\frac{P_i^{\alpha _{n-k+1}}(A)}{|a_{ii}|}P_{j_k}^{\alpha _{n-k+1}}(A)\right\} . \end{aligned}$$

In this section we present some upper and lower bounds for the determinants of the strictly $\gamma$-diagonally dominant matrices as an application of the new estimate of the $\gamma$-dominant degree of Schur complements.

Theorem 5.2

Let $A\in SD_n^{\gamma }$. Then

$$\begin{aligned} |det(A)|\ge \max \limits _{\mathcal {J}}\prod \limits _{k=1}^{n} \left\{ |a_{j_kj_k}|-mx_{j_k}^r[A(\alpha _{n-k+1}),\alpha _{n-k}]\right\} , \end{aligned}$$

(5.1)

and

$$\begin{aligned} |det(A)|\le \min \limits _{\mathcal {J}}\prod \limits _{k=1}^{n} \left\{ |a_{j_kj_k}|+mx_{j_k}^r[A(\alpha _{n-k+1}),\alpha _{n-k}]\right\} . \end{aligned}$$

(5.2)

Proof

For the first inequality, since $\alpha _{n-k}$ is contained in $\alpha _{n-k+1}$ and $\alpha _{n-k+1}- \alpha _{n-k}=\{j_k\}$, we have, by Corollary 3.3, for each k

$$\begin{aligned} |A(\alpha _{n-k+1})/\alpha _{n-k}|\ge |a_{j_kj_k}|-mx^r_{j_k}[A(\alpha _{n-k+1}),\alpha _{n-k}]>0. \end{aligned}$$

To be explicitly,

$$\begin{aligned} mx^r_{j_k}[A(\alpha _{n-k+1}),\alpha _{n-k}]=\sum \limits _{t=k+1}^nt_{j_t}[A(\alpha _{n-k+1})]\cdot [\gamma |a_{j_kj_t}|+(1-\gamma )|a_{j_tj_k}|]. \end{aligned}$$

It follows that

$$\begin{aligned} |det(A)|= & {} \left| \frac{det(A)}{det[A(\alpha _{n-1})]}\right| \left| \frac{det[A(\alpha _{n-1})]}{det[A(\alpha _{n-2})]}\right| \ldots \left| \frac{det[A(\alpha _{2})]}{det[A(\alpha _{1})]}\right| |det[A(\alpha _1)]|\\= & {} \left| det(A/\alpha _{n-1})\right| \left| det[A(\alpha _{n-1})/\alpha _{n-2}]\right| \ldots \left| det[A(\alpha _{2})/\alpha _{1}]\right| det[A(\alpha _1)]|\\\ge & {} |a_{j_nj_n}|\prod \limits _{k=1}^{n-1}\left\{ |a_{j_kj_k}|-mx^r_{j_k}[A(\alpha _{n-k+1}),\alpha _{n-k}]\right\} . \end{aligned}$$

This implies (5.1). The inequality (5.2) in the theorem is similarly proven. $\square$

Remark that if $\gamma =1$, we obtain that

$$\begin{aligned} |det(A)|\ge & {} \max \limits _{\mathcal {J}}\prod \limits _{k=1}^{n} \left\{ |a_{j_kj_k}|-\sum \limits _{i\in \alpha _{n-k}}|a_{j_ki}|\frac{P_i^{\alpha _{n-k+1}}(A)}{|a_{ii}|}\right\} \nonumber \\\ge & {} \max \limits _{\mathcal {J}}\prod \limits _{k=1}^{n} \left\{ |a_{j_kj_k}|-\max \limits _{i\in \alpha _{n-k}}\frac{P_i^{\alpha _{n-k+1}}(A)}{|a_{ii}|}P_{j_k}^{\alpha _{n-k+1}}(A)\right\} , \end{aligned}$$

(5.3)

and

$$\begin{aligned} |det(A)|\le & {} \max \limits _{\mathcal {J}}\prod \limits _{k=1}^{n} \left\{ |a_{j_kj_k}|+\sum \limits _{i\in \alpha _{n-k}}|a_{j_ki}|\frac{P_i^{\alpha _{n-k+1}}(A)}{|a_{ii}|}\right\} \nonumber \\\le & {} \max \limits _{\mathcal {J}}\prod \limits _{k=1}^{n} \left\{ |a_{j_kj_k}|+\max \limits _{i\in \alpha _{n-k}}\frac{P_i^{\alpha _{n-k+1}}(A)}{|a_{ii}|}P_{j_k}^{\alpha _{n-k+1}}(A)\right\} . \end{aligned}$$

(5.4)

We can see that our results improve (Liu and Zhang 2005, Theorem 3) when $\gamma =1$. Moreover, Theorem 5.2 has a wider range of applications.

Notice that when $A\in SD_n^{\gamma }$, for any $1\le k\le n$ and $t\in \{k+1,k+2,\ldots ,n\}$,

$$\begin{aligned} 0\le t_{j_t}[A(\alpha _{n-k+1})]<1. \end{aligned}$$

We have the following claim immediately from the theorem.

Corollary 5.1

Let $A\in SD_n^{\gamma }$. Then

$$\begin{aligned} |det(A)|\ge \max \limits _{\mathcal {J}}\prod \limits _{k=1}^{n} \left\{ |a_{j_kj_k}|-\sum \limits _{t=k+1}^n[\gamma |a_{j_kj_t}|+(1-\gamma )|a_{j_tj_k}|]\right\} , \end{aligned}$$

(5.5)

and

$$\begin{aligned} |det(A)|\le \min \limits _{\mathcal {J}}\prod \limits _{k=1}^{n} \left\{ |a_{j_kj_k}|+\sum \limits _{t=k+1}^n[\gamma |a_{j_kj_t}|+(1-\gamma )|a_{j_tj_k}|]\right\} , \end{aligned}$$

(5.6)

where we let $\sum \limits _{t=k+1}^n[\gamma |a_{j_kj_t}|+(1-\gamma )|a_{j_tj_k}|]=0$ when $k=n$.

Example 5.1

Let $n=3$ and take $j_1=3$, $j_2=1$ and $j_3=2$. With $\alpha _1=\{j_3\}=\{2\}$, $\alpha _2=\{j_3,j_2\}=\{1,2\}$, and $\alpha _3=\{j_3,j_2,j_1\}=\{1,2,3\}$, by Corollary 5.1, we have for any $A\in SD_3^{\gamma }$,

$$\begin{aligned} |det(A)|\ge |a_{22}|\cdot [|a_{11}|-\gamma |a_{12}|-(1-\gamma )|a_{21}|]\cdot [|a_{33}|-\gamma (|a_{31}|+|a_{32}|)-(1-\gamma )(|a_{13}|+|a_{23}|)], \end{aligned}$$

and

$$\begin{aligned} |det(A)|\le |a_{22}|\cdot [|a_{11}|+\gamma |a_{12}|+(1-\gamma )|a_{21}|]\cdot [|a_{33}|+\gamma (|a_{31}|+|a_{32}|)+(1-\gamma )(|a_{13}|+|a_{23}|)]. \end{aligned}$$