Evaluation of a finite element formulation for the shallow water equations with numerical smoothing in the Gulf of San Jorge

Abstract

The shallow water equations (SWE) are a time-dependent system of non-linear partial differential equations utilized for fluid motion where the horizontal length scales are much greater than the fluid depth. The numerical solution of the SWE usually requires complex schemes and methods to deal with the instabilities proper to the system. This paper is concerned with a simple method to solve the SWE, utilizing continuous linear finite elements, no-slip closed boundary, and nested open boundary conditions, and a stabilization technique known as numerical smoothing. First, we describe the governing equations, the finite element model, and the chosen discretization. Then we solve a 2D test case of an elliptical paraboloid and analyze its convergence comparing with provided analytical solutions. Finally, we apply the model to the northern region of the Gulf of San Jorge (Argentina), optimize parameters, and validate it with collected data from an acoustic Doppler current profiler (ADCP) of two spatial points during one tidal $M_2$ period.

1 Introduction

The shallow water equations (SWE) are used to describe flow in bodies of water where the horizontal length scales are much greater than the fluid depth and are characterized by flows where horizontal velocities dominates the flow field. SWE have wide applications in ocean and coastal engineering (Dinápoli et al. 2020; Valseth and Dawson 2022; Kliem et al. 2006), and it is applied to a variety of physical phenomena such as tides in oceans (Flather and Heaps 1975; Rizal 2000; Casulli and Walters 2000), breaking waves on shallow beaches (if dispersion is included) (Barros et al. 2011), surges (Dube et al. 1985), dam-break wave modeling (Zoppou and Roberts 2000), and flooding (Costabile et al. 2017).

In the present study, we apply a finite element method (FEM) to solve the SWE and describe the current circulation in the northern region of the Gulf of San Jorge (GSJ). The GSJ is the largest coastal embayment of the Patagonian Shelf (PS), one of the most biologically productive portions of the South Atlantic Ocean, this area is very influential to the economic, social, and ecological health of the region (Marrari et al. 2017). Therefore, integrating information referred to the circulation patterns, physical, chemical, and biological processes and their influence on the coastal ecosystem, will contribute to a comprehensive understanding of the Gulf and its influence on the region.

Recent studies as Palma et al. (2020) showed that the GSJ circulation is mainly shaped by tidal forcing, and modulated by wind forcing and intrusions from the Patagonian Shelf. The (finite difference) model utilized was based on ROMS-Agrif (Debreu et al. 2012), with a resolution about 2km; therefore, the model proposed in this paper combines the tidal forcing output of this model with an unstructured finite element model to acquire higher resolution results in a particular sector of the GSJ. To validate the results, rather than an elevation comparison, we advantageously used velocity data that were collected from two locations by an acoustic Doppler current profiler (ADCP) to contrast with the model output.

Different numerical methods have been tested and developed with passing of the years, finite difference schemes (FDM) (Flather and Heaps 1975; Casulli 1990), finite element methods (FEM) (Hanert et al. 2005; Zienkiewicz and Ortiz 1995), finite volume methods (FVM) (Chippada et al. 1998), finite spectral element (Iskandarani et al. 1995), spectral element in time (or periodic galerkin) (Kawahara and Hasegawa 1978), and lattice boltzmann modeling (Tubbs 2010) among others. The most used methods are FDM, FVM, and FEM. We are particularly interested in the application of FEM in coastal wetlands and gulf regions. The FEM provides several advantages: the boundary curves with complicated geometric shape and the underwater topography with irregular rise-and-falls can be satisfactorily fitted; differences in material properties between subdomains, if any, can be considered; and various types of boundary conditions can be fulfilled. Though the main disadvantage of the FEM is its low speed in solving a time-dependent evolution problem; in particular, the implicit FEM has to solve a large-scale, sparse linear system of equations in each time step (Larson and Bengzon 2013).

Finite element methods for solving the SWE have been evolving since the decade of the 70’s. One of the firsts articles to address the problem exclusively was (Brebbia and Partridge 1976), in which it is noted that the SWE have stability issues, and a stabilization technique was needed; however, this approach did not get further tests neither implementations. The next improvement was achieved by Lynch and Gray (1979), they developed a model that deals with the stabilization problems transforming the original SWE into a wave equation, this approach is nowadays widely used to solve realistic and complex shallow water flow problems, the work in Luettich et al. (1992) for example, employed the generalized wave continuity equation in the advanced circulation model (ADCIRC).

The aim of this work is to apply a model that solves the SWE in its original form, providing a contribution to model benchmarking and the performance of simple models. A version of linear finite elements was implemented that manages the stabilization issues with numerical smoothing. This technique was proposed in Brebbia and Partridge (1976) and applied to the North Sea, but to our knowledge, has not been used in other complex problems nor has been tested enough with available analytical solutions for the SWE.

The paper is organized as follows. We first present the model equations and the finite element discretization in Sects. 2 and 3, respectively. In Sect. 4, we test the model in an elliptical paraboloid and in Sect. 5, a detailed explanation of the implementation in the Gulf of San Jorge is given, where parameter optimization and validation with current velocities are reviewed. Conclusions are discussed in Sect. 6.

2 Governing equations

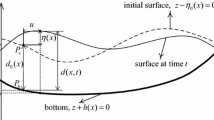
We consider the following formulation of the shallow water problem (Pinder and Gray 1977): Let $\Omega$ be the two-dimensional model domain, we seek the east–west velocity $u(x_1, x_2, t)$, the south–north velocity $v(x_1, x_2, t)$ and the surface elevation $\eta (x_1,x_2,t)$ which are solutions of the following equations:

$$\begin{aligned} 0&=\frac{\partial \eta }{\partial t}+\frac{\partial Hu}{\partial x_1}+\frac{\partial Hv}{\partial x_2}, \end{aligned}$$

(1)

$$\begin{aligned} 0&=\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x_1}+ v\frac{\partial u}{\partial x_2}-fv+g \frac{\partial \eta }{\partial x_1}-\frac{c_\omega \omega ^2}{H}\cos (\zeta )+c_du\gamma , \end{aligned}$$

(2)

$$\begin{aligned} 0&=\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x_1}+ v\frac{\partial v}{\partial x_2}+fu+g \frac{\partial \eta }{\partial x_2}-\frac{c_\omega \omega ^2}{H}\sin (\zeta )+c_dv\gamma , \end{aligned}$$

(3)

where $H=h+\eta$ is the total depth, h is the reference depth of the fluid, f is the Coriolis parameter, $c_{\omega }$ is the wind drag coefficient, $c_d$ is the bottom friction coefficient, g is the gravitational acceleration, $\omega$ is the wind velocity magnitude, $\zeta$ is the angle between the $x_1$ axis and the wind velocity vector, and $\gamma =\frac{\sqrt{u^2+v^2}}{H}.$

The initial conditions are:

$$\begin{aligned} \eta (\textbf{x},0)=\eta _0(\textbf{x}), \quad u(\textbf{x},0)=u_0(\textbf{x}), \quad v(\textbf{x},0)=v_0(\textbf{x}), \end{aligned}$$

for $\textbf{x}\in \Omega$. The boundary conditions are:

$$\begin{aligned} \eta (\textbf{x},t)=\eta _B(\textbf{x},t), \quad u(\textbf{x},t)=u_B(\textbf{x},t), \quad v(\textbf{x},t)=v_B(\textbf{x},t), \end{aligned}$$

for $(\textbf{x},t)\in \partial \Omega \times (0,T]$.

3 Finite element $P_1$ - $P_1$ model

A standard weak formulation leads to: $\eta (\cdot ,t),u(\cdot ,t),v(\cdot ,t)\in H^1(\Omega )$ satisfying the previous boundary conditions, such that

$$\begin{aligned} 0=&\int _\Omega \frac{\partial \eta }{\partial t}\psi _{\eta } -\int _\Omega hu\frac{\partial \psi _{\eta }}{\partial x_1} -\int _\Omega hv\frac{\partial \psi _{\eta }}{\partial x_2} -\int _\Omega \eta u\frac{\partial \psi _{\eta }}{\partial x_1} -\int _\Omega \eta v\frac{\partial \psi _{\eta }}{\partial x_2} ,\\ 0=&\int _\Omega \frac{\partial u}{\partial t}\psi _u+\int _\Omega u\frac{\partial u}{\partial x_1}\psi _u+ \int _\Omega v\frac{\partial u}{\partial x_2}\psi _u-\int _\Omega fv\psi _u+\int _\Omega g \frac{\partial \eta }{\partial x_1}\psi _u\\&-\int _\Omega \frac{c_\omega \omega ^2}{H}\cos (\zeta )\psi _u+\int _\Omega c_d\gamma u\psi _u,\\ 0=&\int _\Omega \frac{\partial v}{\partial t}\psi _v+\int _\Omega u\frac{\partial v}{\partial x_1}\psi _v+ \int _\Omega v\frac{\partial v}{\partial x_2}\psi _v+\int _\Omega fu\psi _v+\int _\Omega g \frac{\partial \eta }{\partial x_2}\psi _v\\&-\int _\Omega \frac{c_\omega \omega ^2}{H}\sin (\zeta )\psi _v+\int _\Omega c_d\gamma v\psi _v, \end{aligned}$$

for all $\psi _{\eta }\in H^1_0(\Omega )$ and $\psi _u,\psi _v\in L^2(\Omega )$.

We approximate the space $L^2(\Omega )$ by V, where for a triangulation $\mathcal {K} = \{K_1,\ldots ,K_{n_t}\}$ such that $\Omega =\cup _{\ell =1}^{n_t} K_\ell$, we define:

$$\begin{aligned} V=\{\psi :\Omega \rightarrow \mathbb {R}\mid \psi |_K\in \mathcal {P}_1(K),\, \forall K \in \mathcal {K}\}\cap C(\Omega ), \end{aligned}$$

where $\mathcal {P}_1(K)$ is the space of polynomials of degree 1 in K, and $C(\Omega )$ the continuous functions from $\Omega$ to $\mathbb {R}$. Then, for example, approximate:

$$\begin{aligned} \eta (\textbf{x},t)\approx \sum _{i=1}^{n_p} \upeta _i(t)\varphi _i(\textbf{x}),\quad \psi _\eta (\textbf{x}) \approx \sum _{i=1}^{n_p}\varsigma _i^\eta \varphi _i(\textbf{x}) \end{aligned}$$

where $\{\varphi _i\}_{i=1}^{n_p}$ is a base of V and $n_p$ is the total number of nodes determined by $\mathcal {K}$, obtaining a continuous Bubnov-Galerkin formulation.

To obtain a linear system of equations in space, several functions were approximated by an average of their value at the vertices of each triangle. Specifically, for a general $\phi :\Omega \rightarrow \mathbb {R}$ define:

$$\begin{aligned} a_{ij}(\phi )&=\sum _{\ell =1}^{n_t} \bar{\phi }_{K_\ell } \int _{K_\ell } \varphi _i\varphi _j,&b_{i}(\phi )&=\sum _{\ell =1}^{n_t} \bar{\phi }_{K_\ell } \int _{K_\ell } \varphi _i,\\ m^{1}_{ij}(\phi )&=\sum _{\ell =1}^{n_t} \bar{\phi }_{K_\ell } \int _{K_\ell } \varphi _i\frac{\partial \varphi _j}{\partial x_1},&m^{2}_{ij}(\phi )&=\sum _{\ell =1}^{n_t} \bar{\phi }_{K_\ell } \int _{K_\ell } \varphi _i\frac{\partial \varphi _j}{\partial x_2}, \\ \end{aligned}$$

where $\bar{\phi }_{K_\ell }=(\phi (x_1)+\phi (x_2)+\phi (x_3))/3$ for the vertices $x_1, x_2, x_3$ of $K_\ell \in \mathcal {K}$. Then we construct the matrices $A(\phi ),$ $M^1(\phi )$, $M^2(\phi )$ and the vector $b(\phi )$ (Larson and Bengzon 2013). Replacing $\eta$, u, v, $\psi _\eta$, $\psi _u$, and $\psi _v$ for their approximation in the weak formulation, gives the system:

$$\begin{aligned} 0=\tilde{A}\texttt{w}'(t)+\tilde{B}(t)\texttt{w}(t) - \tilde{d}(t). \end{aligned}$$

(4)

where $\texttt{w}=(\upeta ,\texttt{u},\texttt{v})^T$,

$$\begin{aligned} \tilde{A}= & {} \left[ \begin{array}{ccc} A(1)&{} &{} \\ &{}A(1)&{}\\ &{} &{} A(1) \end{array}\right] ,\qquad \tilde{d}=\left[ \begin{array}{c} 0 \\ b(\hat{c})\\ b(\hat{s}) \end{array}\right] ,\\ \tilde{B}= & {} \left[ \begin{array}{ccc} - (M^{1}(u) + M^{2}(v))^T &{} -(M^{1}(h))^T &{} -(M^{2}(h))^T \\ M^1(g) &{} M_{\gamma } &{} - A(f)\\ M^2(g) &{} A(f) &{} M_{\gamma } \end{array}\right] , \end{aligned}$$

with $M_{\gamma }= M^1(u)+ M^2(v) + A(c_d\gamma )$, $\hat{c}=\frac{c_\omega \omega ^2}{H}\cos (\zeta )$ and $\hat{s}=\frac{c_\omega \omega ^2}{H}\sin (\zeta )$.

Remark 1

H tends to zero when approximating to the coastline; thus, to manage the terms where there is a division by H,  we use a maximum between H and a positive constant $H_{\max }$ (Flather and Heaps 1975).

Because of the Dirichlet boundary conditions, we only need to find out the values of the unknowns $\texttt{w}$ in the interior nodes, and utilize the information from the boundary. If we denote by $\mathcal {I}$ and $\mathcal {B}$ the subset of interior and boundary nodes, respectively, the equation (4) can be written as:

$$\begin{aligned} \begin{array}{cc} 0=&{}\tilde{A}_{\mathcal {I}\mathcal {I}}\texttt{w}'_\mathcal {I}(t) + \tilde{A}_{\mathcal {I}\mathcal {B}}\texttt{w}'_\mathcal {B}(t) +\tilde{B}_{\mathcal {I}\mathcal {I}}(t)\texttt{w}_\mathcal {I}(t) +\tilde{B}_{\mathcal {I}\mathcal {B}}(t)\texttt{w}_\mathcal {B}(t) - \tilde{d}_\mathcal {I}(t),\\ 0=&{}\tilde{A}_{\mathcal {B}\mathcal {I}}\texttt{w}'_\mathcal {I}(t) + \tilde{A}_{\mathcal {B}\mathcal {B}}\texttt{w}'_\mathcal {B}(t) +\tilde{B}_{\mathcal {B}\mathcal {I}}(t)\texttt{w}_\mathcal {I}(t) +\tilde{B}_{\mathcal {B}\mathcal {B}}(t)\texttt{w}_\mathcal {B}(t) - \tilde{d}_\mathcal {B}(t). \end{array} \end{aligned}$$

(5)

Then using the second equation to replace $\texttt{w}'_\mathcal {B}(t)$ in the first equation:

$$\begin{aligned} \begin{array}{lll} 0&{}=&{}\tilde{A}_{\mathcal {I} \mathcal {I}}\texttt{w}'_\mathcal {I}(t) + \tilde{A}_{\mathcal {I} \mathcal {B}}\tilde{A}_{\mathcal {B} \mathcal {B}}^{-1}\left( \tilde{d}_\mathcal {B}(t) - \tilde{B}_{\mathcal {B} \mathcal {I}}(t)\texttt{w}_\mathcal {I}(t) -\tilde{B}_{\mathcal {B} \mathcal {B}}(t)\texttt{w}_\mathcal {B}(t)\right) \\ &{}&{}- \tilde{A}_{\mathcal {I} \mathcal {B}}\tilde{A}_{\mathcal {B} \mathcal {B}}^{-1}\tilde{A}_{\mathcal {B} \mathcal {I}}\texttt{w}'_\mathcal {I}(t) +\tilde{B}_{\mathcal {I} \mathcal {I}}(t)\texttt{w}_\mathcal {I}(t) +\tilde{B}_{\mathcal {I} \mathcal {B}}(t)\texttt{w}_\mathcal {B}(t) - \tilde{d}_\mathcal {I}(t)\\ &{}=&{}\left( \tilde{A}_{\mathcal {I} \mathcal {I}} - \tilde{A}_{\mathcal {I} \mathcal {B}}\tilde{A}_{\mathcal {B} \mathcal {B}}^{-1}\tilde{A}_{\mathcal {B} \mathcal {I}} \right) \texttt{w}'_\mathcal {I}(t) + \left( \tilde{B}_{\mathcal {I} \mathcal {I}}(t) - \tilde{A}_{\mathcal {I} \mathcal {B}}\tilde{A}_{\mathcal {B} \mathcal {B}}^{-1}\tilde{B}_{\mathcal {B} \mathcal {I}}(t)\right) \texttt{w}_\mathcal {I}(t)\\ &{}&{}+ \left( \tilde{B}_{\mathcal {I} \mathcal {B}}(t) - \tilde{A}_{\mathcal {I} \mathcal {B}}\tilde{A}_{\mathcal {B} \mathcal {B}}^{-1}\tilde{B}_{\mathcal {B} \mathcal {B}}(t) \right) \texttt{w}_\mathcal {B}(t) - \left( \tilde{d}_\mathcal {I}(t) - \tilde{A}_{\mathcal {I} \mathcal {B}}\tilde{A}_{\mathcal {B} \mathcal {B}}^{-1} \tilde{d}_\mathcal {B}(t)\right) . \end{array} \nonumber \\ \end{aligned}$$

(6)

Now, to solve this system, we will proceed to discretize (6) in time. We write the time-dependent functions as a convex combination of two time steps, the actual time $n-1$ and the new time we want to compute, n. Then, for example, $\texttt{w}(t)\approx \theta \texttt{w}^n+(1-\theta )\texttt{w}^{n-1},$ where $\theta \in [0,1], n=0,\ldots ,m,$ $m\in \mathbb {N},$ and $\texttt{w}^0 = \texttt{w}(0),$ $\texttt{w}^m=\texttt{w}(T).$

To keep the system linear, we take the discretization of ${\tilde{B}}$ explicitly, similarly to Flather and Heaps (1975) i.e., $\tilde{B}(t)\approx {\tilde{B}}^{n-1}.$ For the time derivative we use a classical Euler method to obtain $\displaystyle \frac{d \texttt{w}}{d t}\approx \frac{\texttt{w}^n-\texttt{w}^{n-1}}{\Delta t}$.

Applying the time discretization to the linear system (6), we obtain:

$$\begin{aligned} \left( \frac{\tilde{A}_{\mathcal {I}\mathcal {I}}-{\tilde{A}}_PA_{\mathcal {B}\mathcal {I}}}{\Delta t}+\theta ({\tilde{B}}_{\mathcal {I}\mathcal {I}}^{n-1}-{\tilde{A}}_PB_{\mathcal {B}\mathcal {I}}^{n-1})\right) \texttt{w}_{\mathcal {I}}^n=b, \end{aligned}$$

(7)

where

$$\begin{aligned} b=&-\biggl (-\frac{\tilde{A}_{\mathcal {I}\mathcal {I}}-{\tilde{A}}_PA_{\mathcal {B}\mathcal {I}}}{\Delta t}\texttt{w}_{\mathcal {I}}^{n-1}+(1-\theta )({\tilde{B}}_{\mathcal {I}\mathcal {I}}^{n-1}-{\tilde{A}}_PB_{\mathcal {B}\mathcal {I}}^{n-1})\texttt{w}_{\mathcal {I}}^{n-1}\\&+\theta ({\tilde{B}}_{\mathcal {I}\mathcal {B}}^{n-1}-{\tilde{A}}_PB_{\mathcal {B}\mathcal {B}}^{n-1})\texttt{w}_{\mathcal {B}}^n+(1-\theta )({\tilde{B}}_{\mathcal {I}\mathcal {B}}^{n-1}-{\tilde{A}}_PB_{\mathcal {B}\mathcal {B}}^{n-1})\texttt{w}_{\mathcal {B}}^{n-1}\\&-\theta ({\tilde{d}}_{\mathcal {I}}^n-{\tilde{A}}_P{\tilde{d}}_{\mathcal {B}}^n)-(1-\theta )({\tilde{d}}_{\mathcal {I}}^{n-1}-{\tilde{A}}_P{\tilde{d}}_{\mathcal {B}}^{n-1})\biggr ),\\ {\tilde{A}}_P = \ {}&{\tilde{A}}_{\mathcal {I}\mathcal {B}}{\tilde{A}}_{\mathcal {B}\mathcal {B}}^{-1}. \end{aligned}$$

The system given in (7) is unstable and a stabilization method is required (Hanert et al. 2003). To address this issue, we adopted the technique of numerical smoothing (Brebbia and Partridge 1976), which we applied at every time step by the following process:

For each interior node $i_0\in \mathcal {I}$:

• 1. Find every node sharing an edge (neighbor) with the $i_0-$node and let $\{i_0,i_1,\ldots ,i_{n_w}\}$ be the set of indices corresponding to the $i_0-$node neighbors including $i_0$.

• 2. Define arbitrary weights $\sigma _0,\ldots ,\sigma _{n_w}\in [0,1]$, where $\sum _{j=0}^{n_w} \sigma _j = 1.$

• 3. Define the smoothed solution $\mathtt s_{i_0} = \sum _{j=0}^{n_w}\sigma _j\texttt{w}_{i_j}$.

Then utilize $\mathtt s_{\mathcal {I}}$ instead of $\texttt{w}_{\mathcal {I}}^{n-1}$ to solve (7).

4 Oscillating planar flow in a frictionless elliptical paraboloid

The model performance was tested with the analytical solution of (1)-(3) with $c_d=0$ and $c_\omega =0$, provided by Thacker (1981) in the case of the elliptical paraboloid with planar surface oscillations:

$$\begin{aligned} \eta (x,y,t)&=2 \alpha \frac{h_0}{L}\left( \frac{x}{L} \cos (\kappa t)-\frac{y}{L} \sin (\kappa t)-\frac{\alpha }{2 L}\right) ,\\ u(x,y,t)&=-\alpha \kappa \sin (\kappa t),\\ v(x,y,t)&=-\alpha \kappa \cos (\kappa t), \end{aligned}$$

where $\kappa =\frac{f}{2}+\left[ \frac{f^2}{4}+\frac{2\,g h_0}{L^2}\right] ^{\frac{1}{2}}$, $\alpha$ is a constant that determines the amplitude of the motion, $h_0$ determines the depth of the paraboloid and L the radius (the ellipse is a circle for this solution).

The paraboloid basin is given by:

$$\begin{aligned} h = h_0\left( 1-\frac{x_1^2}{L^2}-\frac{x_2^2}{L^2} \right) . \end{aligned}$$

Boundary and initial conditions were extracted from the provided analytical solution. The generateMesh function from MATLAB (2019 was used for the triangulation of the basin and the corresponding system (7) was solved for different quantities of time steps and varying the L and $h_0$ value in the range of 1 to 10000 and 1 to 100, respectively (similar results were obtained for all the values tested).

We define the vectorial norm:

$$\begin{aligned} \text {vecnorm}_2(u,v)=\left( \sqrt{u_1^2+v_1^2},\ldots ,\sqrt{u_n^2+v_n^2}\right) , \end{aligned}$$

where u and v are n-dimensional vectors. The error formula used to confront velocities resulting from the model with the analytical solutions was:

$$\begin{aligned} E_\text {rel}^{\text {vel}} =\max _k\max \left( \frac{\text {vecnorm}_2(u_m^k - u_s^k, v_m^k - v_s^k)}{\text {vecnorm}_2(u_s^k, v_s^k)}\right) , \end{aligned}$$

(8)

where the vectors $u_m,v_m$ and $u_s,v_s$ are the model resulting velocities and analytical solutions, respectively, the superscript k indicates the time step and the division is elementwise. Similarly, the elevation error used was

$$\begin{aligned} E_\text {rel}^{\text {el}} = \max _k\frac{|\eta _m^k-\eta _s^k|}{|\eta _s^k|}. \end{aligned}$$

(9)

The convex combination time parameter $\theta$ and the numerical smoothing procedure weights were optimized for this experiment, minimizing the error function defined by $E_\text {rel}^{\text {vel}}+ E_\text {rel}^{\text {el}}.$ We obtained $\theta = 0.6534$ (usually this value is taken in the range of [0.5, 1] (Casulli 1990)), and the weights acting as a neighbor mean. To evaluate the target function $E_\text {rel}^{\text {vel}}+ E_\text {rel}^{\text {el}},$ it is necessary to solve the complete problem to then compare the errors; therefore, the function evaluation is computationally expensive. To avoid complicated derivatives and excessive function evaluations, we utilized a Nelder–Mead algorithm (fminsearch function from MATLAB (2019).

The numerical smoothing behaves similar to adding artificial viscosity to the SWE, creating a smother representation of the flow, but also of the elevation, which has no physical justification (Hanert et al. 2003), then we expect the errors to be close to zero, but not necessarily convergent to zero.

It can be observed in Fig. 1, that the maximum relative error diminishes its value as the number of time steps increases. The rate is linear for the velocity, but it is asymptotic for the elevation; though the relative error in the elevation is small (0.0319 or $0.3\%$ at 50000 time steps). In Fig. 2 we display the $L^2$ errors, where we utilized $L=100,$ $h_0=1$ and $\alpha =0.1,$ highlighting its convergence in space, where, analogous to the temporal error of Fig. 1, we took the maximum $L^2$ error over time.

Fig. 1

Error for the elliptical parabolid flow

Fig. 2

$L^2$ error for the elliptical parabolid flow

As expected, the errors are not strictly convergent to zero, but in both the temporal and $L^2$ errors, we observed good behavior with small relative errors.

5 Gulf of San Jorge implementation

We consider the region in between the coordinates $(-45.2049^{\circ },-44.9312^{\circ }$) latitude and $(-66.6029^{\circ },-65.5193^{\circ })$ longitude. Utilizing a .tif bathymetry file (Rodriguez-Perez and Sanchez-Carnero 2022), we determined the boundaries from the points with zero depth, and created a polygon that is an approximation of the boundary ($\partial \Omega$). Then we utilized the Gmsh package (Geuzaine and Remacle 2009) and MeshAdapt routine to create the triangulation $\mathcal {K}$ (see Fig. 3).

The depth h is defined by interpolating the data from the .tif with the scatteredInterpolant function from MATLAB (2019). For simplicity, the physical geometry (latitude-longitude) is approximated to a flat earth geometry (Stevens et al. 2015) measured in meters.

We utilized 3316 nodes (the amount of boundary nodes was reduced by selecting the most determinant ones to the geometry from the coastline obtained in the .tif file) with a maximum triangle diameter of 1000m and minimum of 200m. A 44700s $M_2$ period (Palma et al. 2020) was used ($T = 44700$), initialized by a cold start $(w_{\mathcal {I}}^0=0)$ and run through five tidal cycles to eliminate the influence of $w_{\mathcal {I}}^0$. The resolution can be easily improved by refining the mesh and adding more boundary nodes from the bathymetry file, although it should be considered that a refined spatial mesh increases the computational effort.

To address the wind terms, we used the model provided by [32]. As the model has a low resolution for our geometry size, we used six points in the vicinity of $\Omega$ and utilized the value of the mean of these points for all the region at each time step, interpolating in time. The wind drag coefficient $c_\omega$ was estimated with the formula $c_\omega =\rho (0.63+0.66\omega )\cdot 10^{-3}$ (Tubbs 2010).

We distinguish two types of boundary conditions, the closed, referring to land boundaries, and an artificial open boundary which is usually used in applications of the SWE to limit $\Omega$. Following Brebbia and Partridge (1976), we apply a no-slip condition at the closed boundaries. Physical conditions are unknown at the open boundary, and available data or a larger model is usually utilized to find these conditions. In this work, we take the $M_2$ tide (provided by a larger model), that was proved to mainly shape the circulation of the region (Palma et al. 2020), to specify the open boundary conditions. We utilized bilinear interpolation to obtain the values on the boundary nodes.

Fig. 3

Gulf of San Jorge in a depth colormap, with the region $\Omega$ considered for this work (left) and the triangulation approximating the desired region scaled to meters (right)

There are still undergoing works about suitable open boundary conditions for the SWE, which guarantees a unique, smooth, and stable solution (Nordström and Winters 2022; Blayo and Debreu 2005). In Nordström and Winters (2022), an analysis of the SWE boundary conditions when constant zero depth is set ($h\equiv 0$), the work of Palma and Matano (1998) made several numerical experiments for different boundary conditions utilizing the Princeton Ocean Model (Blumberg and Mellor 1987), whereas Praagman (1979) derives boundary conditions from the characteristic variables approach, and Blayo and Debreu (2005) revisits boundary conditions from the point of view of characteristic variables.

The approach of utilizing conditions specified by a larger model at the open boundaries grants practicality and simplicity, although the outflowing information is totally determined by these external data, and does not depend at all on the internal solution. Therefore, part of the outgoing information will be reflected into the domain as soon as the external data is not perfectly consistent with the internal dynamics (Blayo and Debreu 2005).

5.1 Parameter optimization and results

The data available for comparison at the moment of this work were collected by an ADCP (acoustic Doppler current profiler) at two spatial points $p_1=(-45.0561^{\circ },-65.8238^{\circ })$ and $p_2=(-45.047^{\circ },-65.8366^{\circ })$ for two indepenent periods of approximately 1 day (the sample campaign was executed in March 2020 and funded by the project P-UE 22920160100045CO Centro Para el Estudio de Sistemas Marinos, CCT CONICET-CENPAT). The ADCP provides the value of the current velocity at different depths every 300 seconds; therefore, at each time, we averaged the values to obtain velocity vectors $u_{p_1}$, $v_{p_1}$ and $u_{p_2}$, $v_{p_2}.$

Fig. 4

Comparison between the model results and data at $p_1$

Usually in the shallow water problems, comparisons are made with elevation data in real applications (Grotkop 1973; García-Navarro et al. 2019; Flather and Heaps 1975; Westerink et al. 1985), among others. Comparisons with current velocities are rarer as mentioned in Howarth and Proctor (1992) and Timko et al. (2013), but they provide some circulation assurance that an only elevation contrast might miss. Thus, as current circulation is the main objective in this work, ADCP data are ideal.

The ADCP data were smoothed by a fast Fourier transform (FFT) procedure (Golub and Van Loan 2013) to facilitate the convergence of the optimization algorithm. A few tests were carried out to analyze the sinusoidal behavior of the output relating to $H_{\max }$, obtaining good results with a value of 0.6.

For the parameter optimization, we utilized the Nelder–Mead algorithm mentioned in Sect. 4. Numerical smoothing weights and the $\theta$ parameter values were taken from the previous elliptical paraboloid optimization. Then we adjusted the bottom friction coefficient $c_d$ and the starting tidal phase, to minimize the error of the model output interpolated to $p_1$, compared with the available data in one $M_2$ period (because the period is 44700s, we have $\frac{44700}{300}=149$ time steps for comparison). The error function utilized was:

$$\begin{aligned} E_{p_1} = \Vert \text {vecnorm}_2(u_m^{p_1} - u_{p_1}, v_m^{p_1}-v_{p_1}) \Vert _1, \end{aligned}$$

where $u_m^{p_1}$ and $v_m^{p_1}\in \mathbb {R}^{149}$ are the model results interpolated in $p_1$. Better results were obtained with this absolute error formula rather than a relative error one (8).

The optimization was run for $\Delta t = \{ 100s,50s,20s \}$, with better quality results at $\Delta t= 20s$, as expected becuase of the CFL condition. The optimum bottom friction coefficient ($c_d$) obtained was 0.0228 with a minimum mean error $\bar{E}_{p_1} = \frac{E_{p_1}}{149} = 0.119 m/s.$ Although $c_d$ values in the range of [0.005, 0.0228] had similar mean errors. In Fig. 4, we can see the comparison between the model output and the data in $p_1,$ whereas in Fig. 5, we display the model velocity field results at a fixed time step. To further validate the model, we utilized the bottom friction coefficient value obtained from the optimization in $p_1$ to run the model and compare the output with $p_2$ data (see Fig. 6).

Fig. 5

Model velocity field in blue and data observed at $p_1$ in red at time step 50 (left), zoomed vicinity of $p_1$ data (red), and model results (blue) at time step 50 (right) (colour figure online)

Fig. 6

Comparison between the model results and data at $p_2$

The model output is in reasonable agreement with the data, with values of $\bar{E}_{p_1} = 0.119m/s$ and $\bar{E}_{p_2} = 0.143m/s$. As remarked before, velocity current comparisons are not abundant in shallow water models; works like (Fornerino and Le Provost 1985; Howarth and Proctor 1992; Proctor 1987) obtained error values of the same order and in several cases higher. Some good results are showed in Dowd and Thompson (1996) where tidal amplitudes and phases at the boundary are estimated from interior ADCP velocities using an inverse method and linearized SWE.

Error sources are likely related with the simplified coarse wind model (instead of observed wind data) and the treatment of the open boundary conditions as mentioned in the discussion previous to Sect. 5.1.

6 Conclusion

A $P_1-P_1$ finite element model utilizing numerical smoothing as stabilization technique (Brebbia and Partridge 1976) was developed, tested in a parabolic basin, and applied in the northern region of the Gulf of San Jorge. Taking into account, this is one of the simplest finite element methods to apply, with the only parameter from the equations adjusted being $c_d$, no-slip boundary conditions and prescribed (nested from a larger model) open boundary conditions; satisfactory results were obtained. This suggests that simple models as the one described in this paper are still an option to be considered in ocean modeling. Although this is possibly a first step to apply a more sophisticated model, which would utilize a wetting and drying algorithm (Horritt 2002) in a nested interface of a larger model already applied to the region (Palma et al. 2020), it is notable that a basic method can produce good results in a very complex real case application. The model described in this work stands out for its simplicity and natural construction, which makes a real case scenario implementation and code programming straight forward.