On the multiplicities of distance Laplacian eigenvalues

Abstract

In this work, connected graphs of order n and largest eigenvalue of the distance Laplacian matrix with multiplicity equal to $n-4$ are investigated. A complete characterization is presented if n is one of its distance Laplacian eigenvalues with multiplicity one. We also present a conjecture about forbidden subgraphs of G when the multiplicity of its largest eigenvalue is $n-4,$ and we analyze the case where G has diameter four.

1 Introduction

Let $G=(V,E)$ be a connected graph of order n and let $d_{i,j}$ be the distance (the length of the shortest path) between vertices $v_i$ and $v_j$ of G. The diameter of a connected graph G is $\max _{v_i,v_j\in V}d_{i,j}$. The distance matrix of G, denoted by ${\mathcal {D}}(G)$, is the $n\times n$ matrix whose (i, j)-entry is equal to $d_{i,j},$ for $i, j = 1, 2,\ldots , n$. For $1\le i\le n$, the sum of the distances from $v_i$ to all other vertices in G is known as the transmission of the vertex $v_i$ and is denoted by $Tr(v_i).$ Let Tr(G) be the transmission matrix of G,  the diagonal matrix of order n whose (i, i)-entry is equal to $Tr(v_i)$. The distance Laplacian matrix of G, ${\mathcal {D}}^L(G),$ is the difference between the transmission matrix and the distance matrix, that is, ${\mathcal {D}}^L(G) = Tr(G)-{\mathcal {D}}(G)$ (Aouchiche and Hansen 2013). Let $Spec_{D^L}(G)=(\partial _1^L(G), \partial _2^L(G), \ldots , \partial _n^L(G)=0)$ be the distance Laplacian spectrum of the connected graph G,  denoted by ${\mathcal {D}}^L(G)$-spectrum, where $\partial _1^L(G) \ge \partial _2^L(G) \ge \ldots \ge \partial _n^L(G)=0$. The multiplicity of the eigenvalue $\partial _i^L(G)$, $i=1, \ldots , n,$ is denoted by $m(\partial _i^L(G)).$ We often use exponents to exhibit the multiplicity of the distance Laplacian eigenvalues, when we write the ${\mathcal {D}}^L$-spectrum. We recall that $\partial ^L_{n-1}(G)=n$ if and only if ${\overline{G}},$ the complement of G, is disconnected (Aouchiche and Hansen 2013). Moreover, $\partial _{n-1}^L(G)\ge n$ and the multiplicity of n as an eigenvalue of ${\mathcal {D}}^L(G)$ is one less than the number of components of ${\overline{G}}$ (Aouchiche and Hansen 2013).

In recent years, several works investigated the connected graphs on n vertices in which one of its distance Laplacian eigenvalues has a high multiplicity, $n-r.$ The characterization of such graphs is completely made for r equal to one (Aouchiche and Hansen 2014), two (Fernandes et al. 2018; Lin et al. 2016; da Silva et al. 2016), or three (Fernandes et al. 2018; Lu et al. 2017; Ma et al. 2018; da Silva et al. 2016). In a recent paper (Khan et al. 2023), the case $r=4,$ under the condition that n is a distance Laplacian eigenvalue with multiplicity two or three, was studied. In this work, we consider the remaining cases where the largest distance Laplacian eigenvalue has multiplicity equal to $n-4.$ In Sect. 3, we describe all possible graphs with such multiplicity that also has n in its distance Laplacian spectrum, with multiplicity one, i.e., $\partial _{n-1}^L(G) = n$ and $m(\partial _{n-1}^L(G))=1.$ For the case $\partial ^L_{n-1}(G)\ne n,$ we first recall the following central result for $r=2$ or $r=3$, where $P_{r+2}$ denotes the path on $r+2$ vertices.

Proposition 1

(da Silva et al. 2016) If G is a connected graph on n vertices such that $m(\partial ^L_1(G))=n-r,$ $1\le r \le 3,$ then G has no $P_{r+2}$ as an induced subgraph.

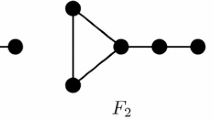
Thus, based on Proposition 1, a natural way of trying to characterize the connected graphs such that $m(\partial ^L_1(G))=n-4$ is investigating its relation with the existence of $P_6$ as an induced subgraph. Computationally, using the software nauty and Traces (McKay and Piperno 2014), and Graph6Java (Mohammad et al. 2019), we looked for graphs G on n vertices, $6\le n \le 11,$ $m(\partial ^L_1(G))=n-4$ and $\partial ^L_{n-1}(G)\ne n.$ In addition to $C_6,$ all other obtained graphs, for $6\le n \le 8,$ are presented in Fig. 1. No graphs were found if $9\le n \le 11.$ Note that, besides $C_6$, we have two graphs and their complements, with the following spectra: $Spec_{D^L}(C_6)= (13^{(2)}, \ 10, \ 9^{(2)}, \ 0),$ $Spec_{D^L}(G_1)= (14.16^{(2)}, \ 10, \ 7.84^{(2)}, \ 0),$ $Spec_{D^L}(\overline{G_1})= (10.3^{(2)}, \ 8, \ 6.7^{(2)}, \ 0),$ $Spec_{D^L}(G_2)= (12.41^{(3)}, \ 9.59^{(3)}, \ 0),$ $Spec_{D^L}(\overline{G_2})= (11.41^{(3)}, \ 8.59^{(3)}, \ 0).$ In any case, $P_6$ is a forbidden subgraph. Considering these facts, in Sect. 4 we focus our attention to investigate if there could be a connected graph G with at least six vertices, $P_6$ as a forbidden subgraph and $m(\partial ^L_1(G))=n-4.$ Such graph has diameter at most four. We conclude that this condition is not feasible if diameter of G is equal to four.

Fig. 1

Graphs with $m(\partial ^L_1(G))=n-4$ and $\partial ^L_{n-1}(G)\ne n$

2 Preliminaries

In what follows, $G=(V,E),$ or just G,  denotes a connected graph with n vertices and ${\overline{G}}$ denotes its complement. The diameter of a connected graph G is denoted by diam(G). As usual, we write, respectively, $P_n,$ $C_n,$ $S_n$, $W_n$ and $K_n,$ for the path, the cycle, the star, the wheel and the complete graph, all with n vertices. We denote by $K_{l_1,l_2,\ldots ,l_k}$ the complete k-partite graph. If $e\in E$, the graph obtained from G by deleting the edge e is denoted $G-e$. If $e\not \in E$, the graph obtained from G by adding the edge e is denoted $G+e$. Sometimes, we write $G+2e$ meaning that we have added two edges in G.

Now, we recall the definitions of some operations with graphs that will be used. For this, let $G_{1}= (V_{1},E_{1})$ and $G_{2}= (V_{2},E_{2})$ be vertex disjoint graphs. The union of $G_{1}$ and $G_{2}$ is the graph $G_{1}\cup G_{2},$ whose vertex set is $V_{1}\cup V_{2}$ and whose edge set is $E_{1}\cup E_{2}$. The union of r copies of $G_1$ will be denoted by $rG_1.$ The join of $G_{1}$ and $G_{2}$ is the graph $G_{1}\vee G_{2}$ obtained from $G_{1}\cup G_{2}$ by joining each vertex of $G_{1}$ with every vertex of $G_{2}$.

The Laplacian matrix of G is the $n\times n$ matrix $L(G)=Deg(G)-A(G)$, where Deg(G) is the diagonal matrix of vertex degrees of G and A(G) is its adjacency matrix. We denote by $(\mu _1(G), \mu _2(G), \ldots , \mu _n(G))$ the L-spectrum of G, i.e., the spectrum of the Laplacian matrix of G, and we assume that the eigenvalues are labelled such that $\mu _1(G) \ge \mu _2(G) \ge \cdots \ge \mu _n(G)=0.$ It is well known that the multiplicity of the Laplacian eigenvalue 0 is equal to the number of components of G and that $\mu _{n-i}({\overline{G}}) = n - \mu _i (G),$ $i=1, \ldots , n-1$ (see Merris 1994 for more details).

The following result relates the spectra of the matrices L and $D^L.$

Theorem 2

(Aouchiche and Hansen 2013) Let G be a connected graph on n vertices with $diam(G) \le 2$. Let $\mu _1(G) \ge \mu _2(G) \ge \cdots \ge \mu _{n-1}(G) > \mu _n(G)=0$ be the Laplacian spectrum of G. Then, the distance Laplacian spectrum of G is $2n - \mu _{n-1}(G) \ge 2n - \mu _{n-2}(G) \ge \cdots \ge 2n - \mu _{1}(G) > \partial ^L_n(G)=0$. Moreover, for every $i \in \left\{ 1, 2, \ldots , n - 1\right\}$ the eigenspaces corresponding to $\mu _i(G)$ and to $2n - \mu _i(G)$ are the same.

Propositions 3, 4, 5 provide the L-spectrum of some graphs that will be analyzed later. Proposition 5 can be easily checked.

Proposition 3

(Fernandes et al. 2018) Let G be a connected graph of order $n \ge 4$. Then, $G \cong K_{n-2} \vee \overline{K_2}$ if and only if the L-spectrum of G is $(\mu _1^{(n-2)}(G), \mu _2(G), 0),$ with $\mu _1(G)> \mu _2(G) > 0.$

Proposition 4

(Mohammadian and Tayfeh-Rezaie 2011) Let G be a connected graph on $n\ge 5$ vertices whose distinct Laplacian eigenvalues are $0<\alpha<\beta <\gamma$. Then, the multiplicity of $\gamma$ is $n-3$ if and only if $G \cong K_{n-3}\vee \overline{K_{1, 2}}$.

Proposition 5

Let G be a connected graph on $n=4$ vertices whose distinct Laplacian eigenvalues are $0<\alpha<\beta <\gamma$. Then, $G \cong P_4$ or $G\cong K_{3,1}+e.$

For proving the next result, we recall that a connected graph G has at least $diam(G)+1$ distinct Laplacian eigenvalues (Brouwer and Haemers 2011, Proposition 1.3.3).

Proposition 6

Let G be a connected graph on $n\ge 4$ vertices whose distinct Laplacian eigenvalues are $\gamma> \alpha >0$. Then, the multiplicity of $\gamma$ is $n-3$ if and only if $G \cong K_{n-4}\vee K_{2, 2},$ or $G \cong K_{n-3} \vee 3K_1,$ or $G \cong C_5,$ for $n\ge 5,$ or $G\cong K_{2,2,}$ or $G\cong K_{3,1},$ for $n=4.$

Proof

As G has three distinct Laplacian eigenvalues, so $diam(G)=2$ and its $D^L$-spectrum is $((2n-\alpha )^{(2)}, (2n-\gamma )^{(n-3)}, 0).$ For $n\ge 5,$ these graphs are precisely determined in Theorems 4.4 and 4.5 of Fernandes et al. (2018) and in Theorem 1.2 of Ma et al. (2018). For $n=4$, by Theorem 3.5 in da Silva et al. (2016), we get the result. $\square$

In Table 1 are presented the L-spectra of some connected graphs that are well known and will be useful in this work. Also, in Proposition 7 we provide the $D^L$-spectra of the complete k-partite graph and of graphs obtained from it by adding edges. As these graphs have diameter two, each $D^L$-spectrum can be easily determined by considering the relation between the Laplacian spectrum of a graph and its complement, the spectra contained in Table 1 and Theorem 2.

Table 1 L-spectrum of some graphs

Proposition 7

Let $l_1\ge l_2\ge \ldots \ge l_k\ge 1, k\ge 2,$ and n be integers such that $l_1+l_2+\cdots +l_k=n.$ If $G=K_{l_1,l_2,\ldots ,l_k}$ and $p =\vert \{ i:\ l_i\ge 2\}\vert ,$ then:

• The ${\mathcal {D}}^L$-spectrum of G is $((n+l_1)^{(l_1-1)},(n+l_2)^{(l_2-1)},\ldots ,(n+l_p)^{(l_p-1)},n^{(k-1)},0).$

• The ${\mathcal {D}}^L$-spectrum of the graph G plus one extra edge in the class with $l_j$ vertices, if possible, is obtained from $Spec_{{\mathcal {D}}^L}(G),$ by replacing one eigenvalue $n+l_j$ by $n+l_j-2$.

• The ${\mathcal {D}}^L$-spectrum of the graph G plus two extra edges, one in the class with $l_j$ vertices and other in the class with $l_f$ vertices, if possible, is obtained from $Spec_{{\mathcal {D}}^L}(G),$ by replacing one eigenvalue $n+l_j$ and one $n+l_f$ by $n+l_j-2$ and $n+l_f-2$.

• The ${\mathcal {D}}^L$-spectrum of the graph G plus two extra edges sharing a common vertex in the class with $l_j,$ if possible, is obtained from $Spec_{{\mathcal {D}}^L}(G),$ by replacing two eigenvalues $n+l_j$ by $n+l_j-3$ and $n+l_j-1$.

• The ${\mathcal {D}}^L$-spectrum of the graph G plus two extra independent edges in the class with $l_j$ vertices, if possible, is obtained from $Spec_{{\mathcal {D}}^L}(G),$ by replacing two eigenvalues $n+l_j$ by $n+l_j-2$.

• The ${\mathcal {D}}^L$-spectrum of the graph G plus three extra edges determining a $K_3$ in the class with $l_j$ vertices, if possible, is obtained from $Spec_{{\mathcal {D}}^L}(G),$ by replacing two eigenvalues $n+l_j$ by $n+l_j-3$.

3 On graphs with n as a distance Laplacian eigenvalue

In this section, we completely characterize the graphs for which $m(\partial ^L_1(G))=n-4$, $\partial ^L_{n-1}(G)=n$ and $m(n)=1$. In this case, G has diameter of two and its distance Laplacian spectrum is related with the Laplacian spectrum (Theorem 2).

Theorem 8

Let G be a connected graph with $n\ge 6$ vertices such that $m(\partial ^L_1(G))=n-4$ and $\partial ^L_{n-1}(G)=n$. Then, $m(\partial _{n-1}^L(G) )= 1$ if and only if $G\cong W_6,$ or G is isomorphic to one of the following graphs:

• for $n\ge 6$, $S_n+2e$ (where the extra edges can share a vertex or they are independent), $S_n+3e$ (where the extra edges induce a $K_3$), $K_{2,n-2}+e$ (where the extra edge is incident to vertices of the largest class) and $K_{p,p}+2e$ (where the extra edges are in different classes);

• in addition to the previous graphs, for $n\ge 7,$ $K_{3,n-3}$ and $K_{3,n-3}+e$ (where the extra edge is incident to vertices of the smallest class);

• in addition to the previous graphs, for $n\ge 8,$ $K_{p,p}+2e$ (where the extra edges are in the same class and they can share a vertex or they are independent) and $G\cong K_{p,p}+3e$ (where the extra edges induce a $K_3$).

Proof

Since $m(\partial _{n-1}^L(G) )= 1$, the graph ${\overline{G}}$ has two components, say ${\overline{G}}\cong F_1 \cup F_2.$ So, $diam(G) = 2$ and the L-spectrum of ${\overline{G}}$ is written as

$$\begin{aligned} (\partial _1^L(G)-n, \ldots , \partial _{1}^L(G)-n, \partial _{n-3}^L(G)-n, \partial _{n-2}^L(G)-n,0,0), \end{aligned}$$

that is, the largest Laplacian eigenvalue of ${\overline{G}}$ has multiplicity $n-4.$ Suppose that $\vert V(F_1)\vert \le \vert V(F_2)\vert .$ We have the following possibilities:

• $\vert V(F_1)\vert =1,$ then $F_1=K_1$ and $(\partial _1^L(G)-n, \ldots ,\partial _1^L(G)-n, \partial _{n-3}^L(G)-n, \partial _{n-2}^L(G)-n,0)$ is the L-spectrum of $F_2$. If $\partial _{n-3}^L(G)> \partial _{n-2}^L(G),$ from Proposition 4, $G\cong S_n+2e, n\ge 6,$ where the extra edges share a vertex. If $\partial _{n-3}^L(G)= \partial _{n-2}^L(G)$, from Proposition 6, $G\cong W_6$ or, for $n\ge 6$, $G\cong S_n+2e,$ where the extra edges are independent, or $G\cong S_n+3e,$ where the extra edges induce a $K_3.$

• $\vert V(F_1)\vert =2,$ then $F_1=K_2$ and its L-spectrum is (2, 0). From Propositions 4, 5, 6, $\partial _1^L(G)-n > 2.$ So, the L-spectrum of $F_2$ is $(\partial _{1}^L(G)-n,\ldots ,\partial _{1}^L(G)-n, \alpha ,0).$ Then, from Proposition 3, for $n\ge 6,$ $G\cong K_{2,n-2}+e,$ where the extra edge is incident to vertices of the largest class.

• $\vert V(F_1)\vert =3,$ then $F_1=K_3$ or $F_1=P_3$ with L-spectrum, respectively, equal to (3, 3, 0) and (3, 1, 0). If $n=6,$ then $G\cong K_{3,3}+2e,$ where the extra edges are in different classes. For $n\ge 7,$ from Propositions 3, 4, 5, 6, as $\vert V(F_2)\vert \ge 4,$ it follows that $\partial _{1}^L(G)-n > 3.$ So, the L-spectrum of $F_2$ is $(\partial _{1}^L(G)-n,\ldots ,\partial _{1}^L(G)-n,0).$ Thus, if $F_1=K_3,$ then $G \cong K_{3,n-3}, n\ge 7.$ If $F_1=P_3,$ then $G=K_{3,n-3}+e,$ $n\ge 7$, where the extra edge is incident to vertices of the smallest class.

• $\vert V(F_1)\vert =p>3,$ Case I. the L-spectrum of $F_1$ is $(\partial _{1}^L(G)-n,\ldots ,\partial _{1}^L(G)-n,\partial _{n-2}^L(G)-n,\partial _{n-3}^L(G)-n,0)$ and of $F_2$ is $(\partial _{1}^L(G)-n,\ldots ,\partial _{1}^L(G)-n,0).$ If $\partial _{n-2}^L(G)>\partial _{n-3}^L(G),$ and $\vert V(F_1)\vert =4,$ it follows, from Proposition 5, that $G\cong K_{4,4}+2e,$ where the extra edges share a vertex. If $\partial _{n-2}^L(G)>\partial _{n-3}^L(G),$ and $\vert V(F_1)\vert >4,$ then, from Proposition 4, $G\cong K_{p,p}+2e,$ $p\ge 5,$ where the extra edges share a vertex. If $\partial _{n-2}^L(G)=\partial _{n-3}^L(G),$ from Proposition 6, $G\cong K_{p,p}+2e,$ $p\ge 5,$ where the extra edges are in the same class and they are independent, $G\cong K_{p,p}+3e,$ $p\ge 5,$ where the extra edges induce a $K_3,$ $G \cong K_{4,4}+2e,$ where the extra edges are in the same class and they are independent, or $G \cong K_{4,4}+3e,$ where the extra edges induce a $K_3.$ Case II. the L-spectrum of $F_1$ is $(\partial _{1}^L(G)-n,\ldots ,\partial _{1}^L(G)-n,\partial _{n-3}^L(G)-n,0)$ and the L-spectrum of $F_2$ is $(\partial _{1}^L(G)-n,\ldots ,\partial _{1}^L(G)-n,\partial _{n-2}^L(G)-n,0).$ From Proposition 3, it follows that $G \cong K_{p,p}+2e,$ $p\ge 4,$ where the extra edges are in different classes.

By Proposition 7 we can explicit the $D^L$-spectra presented in Table 2. $\square$

Table 2 ${\mathcal {D}}^L$-spectrum of some graphs

4 Diameter four graphs with forbidden $P_6$

In this section, we focus on connected graphs with at least six vertices, having $P_6$ as a forbidden subgraph. In particular, this condition implies investigating graphs with a maximum diameter equal to four and we will consider, specifically, graphs with a diameter four. So, from now on, we denote by $v_1,v_2,v_3,v_4,v_5$ the vertices inducing a $P_5,$ with $d(v_1,v_5)=4$ and $P=v_1v_2v_3v_4v_5$ been a shortest path between $v_1$ and $v_5$. In Fig. 2 are presented all possible graphs on six vertices having $P_5$ as an induced subgraph with $d(v_1,v_5)=4.$

Besides, let G be a connected graph on n vertices, $n\ge 8,$ $m(\partial _1^L(G))=n-4$ and let M be a principal submatrix of ${\mathcal {D}}^L(G),$ of order $k\in \{6,7\},$ with largest eigenvalue $\lambda .$ By Cauchy Interlacing, we get $\lambda =\partial _1^L(G)$ and $m(\lambda )\ge k-4.$ So, as 1, the all ones vector with appropriate order, is an eigenvector for ${\mathcal {D}}^L(G),$ it is possible to get a vector z of M corresponding to $\lambda$ with at least $k-5$ entries equal to zero, which can be arbitrarily chosen (Proposition 3.1, Fernandes et al. 2018), such that $z \perp {\textbf {1}}$. This fact will be fundamental for what follows in this work.

Theorem 9

(da Silva et al. 2016) If G is a connected graph then $\partial _1^L(G) \ge \max \limits _{v_i \in V} Tr(v_i) + 1.$ Equality is attained if and only if $G \cong K_n.$

The next propositions are similar to the results that appeared in Lu et al. (2017). Since they have analogous proofs we omit them.

Proposition 10

Let G be a connected graph with $n\ge 8$ vertices. If $m(\partial _1^L)=n-4$ then $\partial _1^L$ is an integer number.

Proposition 11

Let G be a connected graph with n vertices such that $G\not \cong K_n$ and $\partial _1^L$ is an integer number. Then, $\partial _1^L\ge \max _{v\in V}Tr(v)+2$. Moreover, if there exists $v_0\in V$ such that $\partial _1^L=Tr(v_0)+2,$ then $Tr(v_0) = \max _{v\in V} Tr(v)$.

We will now state two results from matrix theory that will be useful in what follows. We denote by ${\textbf{0}}$ and ${\textbf{1}}$ vectors with a given size and all entries equal to zero and all entries equal to one, respectively.

Fig. 2

Graphs on six vertices and $P_5$ as an induced subgraph

Lemma 12

Let

$$\begin{aligned} M=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-a\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-b\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-c\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-d\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-e\\ -a&{}-b&{}-c&{}-d&{}-e&{}t_6\end{array}\right] \end{aligned}$$

and $a,b,c,d,e,t_1,t_2,t_3,t_4,t_5,t_6 \in {\mathbb {N}}.$ Let $\lambda _1$ be an eigenvalue of M and $z=(z_1,z_2,z_3,z_4,0,z_6)$ be an eigenvector of M associated to $\lambda _1$ such that $z \perp {\textbf{1}}.$

• 1. If $e=d+1$ and $t_4\ne \lambda _1,$ then $z=(z_1,z_2,z_3,0,0,z_6)$ and $-2z_1-z_2-(d-1)z_6=0$.

• 2. If $e=d+1=c+2$, $t_4\ne \lambda _1$ and $t_3\ne \lambda _1,$ then $z=(z_1,z_2,0,0,0,z_6)$ and $-z_1-(c-1)z_6=0$.

• 3. If $e=d+1=c+2=3$, $t_4\ne \lambda _1$ and $t_3\ne \lambda _1,$ then $z=(0,z_2,0,0,0,z_6).$ Moreover, $a=1$.

• 4. If $e=d+1=c+2=b+3=4$, $t_4\ne \lambda _1$, $t_2\ne \lambda _1$ and $t_3\ne \lambda _1,$ then $z=(z_1,0,0,0,0,z_6).$

Proof

• 1. Using the fifth entry of both sides of $Mz=\lambda _1z$ we get $-4z_1-3z_2-2z_3-z_4-ez_6=0$. Since $z \perp {\textbf{1}},$ we obtain $-3z_1-2z_2-z_3-(e-1)z_6=0$. Using the fourth entry of $Mz=\lambda _1z$ we get $-3z_1-2z_2-z_3+t_4z_4-dz_6=\lambda _1z_4$. As $d=e-1,$ we conclude that $t_4z_4=\lambda _1z_4$. So, $z_4=0,$ because $t_4\ne \lambda _1$, $z=(z_1,z_2,z_3,0,0,z_6)$ and $-3z_1-2z_2-z_3-dz_6=0$. This implies that $-2z_1-z_2-(d-1)z_6=0$.

• 2. From Item 1 and the third entry of $Mz=\lambda _1z,$ we get $-2z_1-z_2+t_3z_3-cz_6=\lambda _1z_3$. As $c=d-1,$ we conclude that $t_3z_3=\lambda _1z_3$. So, $z_3=0,$ because $t_3\ne \lambda _1,$ $z=(z_1,z_2,0,0,0,z_6)$ and $-2z_1-z_2-cz_6=0$. This implies that $-z_1-(c-1)z_6=0$.

• 3. From Item 2, since $c=1,$ then $z_1=0$ and $z=(0,z_2,0,0,0,z_6).$ If $a\ne 1$, using the first entry of $Mz=\lambda _1z$ we get $-z_2-az_6=0$. Consequently, $z_2=z_6=0$ and $z={\textbf{0}},$ which is impossible.

• 4. The result is immediate from Item 2.$\square$

Using a similar arguments as before, we get the next proposition.

Lemma 13

Let

$$\begin{aligned} M={\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-a\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-b\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-c\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-d\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-e\\ -a&{}-b&{}-c&{}-d&{}-e&{}t_6\end{array}\right] } \end{aligned}$$

and $a,b,c,d,e,t_1,t_2,t_3,t_4,t_5,t_6 \in {\mathbb {N}}$. Let $\lambda _1$ be an eigenvalue of M and $z=(0,z_2,z_3,z_4,z_5,z_6)$ be an eigenvector of M associated to $\lambda _1$ such that $z \perp {\textbf{1}}$.

• 1. If $a=b+1$, and $t_2\ne \lambda _1,$ then $z=(0,0,z_3,z_4,z_5,z_6)$ and $-z_4-2z_5-(b-1)z_6=0$.

• 2. If $a=b+1=c+2$, $t_2\ne \lambda _1$ and $t_3\ne \lambda _1,$ then $z=(0,0,0,z_4,z_5,z_6)$ and $-z_5-(c-1)z_6=0$.

• 3. If $a=b+1=c+2=3$, $t_2\ne \lambda _1$ and $t_3\ne \lambda _1,$ then $z=(0,0,0,z_4,0,z_6).$ Moreover, $e=1$.

Proposition 14

Let G be a connected graph with $n\ge 6$ vertices, $diam(G)=4$ and $m(\partial ^L_1)=n-4$. Then, $H_7$ and $H_8$ are not induced subgraphs of G.

Proof

The principal submatrices of $\mathcal{D}^L(G)$ with respect to $H_7$ and $H_8$ are, respectively,

$$\begin{aligned} M_1=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-1\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-3\\ -1&{}-1&{}-1&{}-2&{}-3&{}t_6\end{array}\right] , M_2=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-1\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-2\\ -2&{}-1&{}-1&{}-1&{}-2&{}t_6\end{array}\right] . \end{aligned}$$

For each of the principal submatrices, there exists an eigenvector associated with $\partial ^L_1,$ $z= (z_1, z_2, z_3, z_4, 0,z_6),$ $z \perp {\textbf{1}}.$

Case 1: If $H_7$ is an induced subgraph of G,  by Lemma 12, $z=(0,z_2,0,0,0,z_6).$ Considering the second entry of $M_1z = \partial ^L_1z$, it follows that $(t_2+1-\partial _1^L)z_2=0$. Since $t_2+1<\partial _1^L,$ then $z_2=0$. Consequently, $z={\textbf{0}}$, which is impossible.

Case 2: If $H_8$ is an induced subgraph of G,  by Lemma 12, $z=(z_1,z_2,z_3,0,0,z_6)$ and $-2z_1-z_2=0$. From this, considering the third and sixth entries of $M_2z = \partial ^L_1z$, as $t_3\ne \partial _1^L,$ it follows, respectively, that $z_3=\frac{1}{t_3-\partial _1^L}z_6, \hspace{3pt} \text{ and } \hspace{3pt} z_3=(t_6-\partial _1^L)z_6.$ Consequently, $\frac{1}{t_3-\partial _1^L}z_6=(t_6-\partial _1^L)z_6.$

If $z_6=0,$ then $z_3=0,$ implying $z_1+z_2=0$ and $-2z_1-z_2=0$. In this case, $z={\textbf{0}}$, which is impossible. So, $z_6\ne 0$ and $\frac{1}{t_3-\partial _1^L}=(t_6-\partial _1^L)$. Therefore, $1=(t_6-\partial _1^L)(t_3-\partial _1^L)$. This is impossible because $t_3+1<\partial _1^L$ and $t_6+1<\partial _1^L$. $\square$

Proposition 15

Let G be a connected graph with $n\ge 8$ vertices, $diam(G)=4$ and $m(\partial ^L_1)=n-4$. Then, $H_3$ is not an induced subgraph of G.

Proof

Suppose that $H_3$ is an induced subgraph of G. Then, the principal submatrix of $\mathcal{D}^L(G)$ with respect to $H_3$ is

$$\begin{aligned} M_1= & {} \left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-1\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-2\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-3\\ -1&{}-1&{}-2&{}-2&{}-3&{}t_6\end{array}\right] \quad \text{ or } \quad M_2=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-1\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-2\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-3\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-4\\ -1&{}-1&{}-2&{}-3&{}-4&{}t_6\end{array}\right] \\ \text{ or } M_3= & {} \left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-1\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-2\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-3\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-3\\ -1&{}-1&{}-2&{}-3&{}-3&{}t_6\end{array}\right] . \end{aligned}$$

• Suppose it is $M_1$. Let $z= (z_1, z_2, z_3, z_4, 0,z_6)$ be a vector satisfying $z \perp {\textbf{1}}$ and $M_1z = \partial ^L_1z$. By Lemma 12, $z=(z_1,z_2,z_3,0,0,z_6)$ and $-2z_1-z_2-z_6=0$. Considering the second entry of $M_1z = \partial ^L_1z$, since $t_2+1\ne \partial _1^L,$ it follows that $z_2=0$ and, then, $z_1=z_3$. Considering the first entry of both sides of $M_1z = \partial ^L_1z$, it follows that $z_1=0$. Consequently, $z_6=0$ and $z={\textbf{0}}$, which is impossible.

• In case it is $M_2,$ the proof is analogous to the case $M_1,$ by taking $z=(z_1,0,0,0,0,z_6)$ and considering the first entry of $M_2z = \partial ^L_1z.$

• Suppose it is $M_3$. Let $z= (z_1, z_2, z_3, z_4, z_5,0)$ be a vector satisfying $z \perp {\textbf{1}}$ and $M_3z = \partial ^L_1z$. Considering, respectively, the sixth and fifth entries of $M_3z = \partial ^L_1z$ and, then, looking at the first four lines of this eigenequation, we get:

  $$\begin{aligned} z_1= & {} \frac{1}{t_1+1-\partial ^L_1}z_5,\hspace{2ex}z_2=\frac{t_5+2-\partial ^L_1}{t_2-\partial ^L_1}z_5,\\ z_3= & {} \frac{t_5+2-\partial ^L_1}{t_3+1-\partial ^L_1}z_5,\hspace{2ex}z_4=\frac{t_5+2-\partial ^L_1}{t_4-\partial ^L_1}z_5. \end{aligned}$$

  Since $z_1+z_2+z_3+z_4=-z_5,$ then

  $$\begin{aligned} \left[ \frac{1}{t_1+1-\partial ^L_1}+\frac{t_5+2-\partial ^L_1}{t_2-\partial ^L_1}+\frac{t_5+2-\partial ^L_1}{t_3+1-\partial ^L_1}+\frac{t_5+2-\partial ^L_1}{t_4-\partial ^L_1}\right] z_5=-z_5 \end{aligned}$$

  and, as z is an eigenvector, then $z_5\ne 0$ and

  $$\begin{aligned} \left[ \frac{1}{t_1+1-\partial ^L_1}+\frac{t_5+2-\partial ^L_1}{t_2-\partial ^L_1}+\frac{t_5+2-\partial ^L_1}{t_3+1-\partial ^L_1}+\frac{t_5+2-\partial ^L_1}{t_4-\partial ^L_1}\right] =-1. \end{aligned}$$

  This is impossible because

  $$\begin{aligned}{} & {} (t_1+1-\partial ^L_1)(t_4-\partial ^L_1)(t_2-\partial ^L_1)(t_3+1-\partial ^L_1)>0,\\{} & {} \quad \left[ (t_2-\partial ^L_1)(t_3+1-\partial ^L_1)+(t_2-\partial ^L_1)(t_4-\partial ^L_1)+(t_3+1-\partial ^L_1)(t_4-\partial ^L_1)\right] > 0,\\ {}{} & {} \quad (t_1+1-\partial ^L_1)(t_5+2-\partial ^L_1)\ge 0 \end{aligned}$$

  and

  $$\begin{aligned} 0>\frac{(t_2-\partial ^L_1)(t_3+1-\partial ^L_1)(t_4-\partial ^L_1)}{(t_1+1-\partial ^L_1)(t_4-\partial ^L_1)(t_2-\partial ^L_1)(t_3+1-\partial ^L_1)}>-1. \end{aligned}$$

  $\square$

Proposition 16

Let G be a connected graph with $n\ge 8$ vertices, $diam(G)=4$ and $m(\partial ^L_1)=n-4$. Then, $H_5$ is not an induced subgraph of G.

Proof

Suppose that $H_5$ is an induced subgraph of G. Then, the principal submatrix of $\mathcal{D}^L(G)$ with respect to $H_5$ is

$$\begin{aligned} N_1=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-3\\ -2&{}-1&{}-1&{}-2&{}-3&{}t_6\end{array}\right] \quad \text{ or } \quad N_2=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-2\\ -2&{}-1&{}-1&{}-2&{}-2&{}t_6\end{array}\right] . \end{aligned}$$

• Suppose it is $N_1$ and let $z= (z_1, z_2, z_3, z_4, 0,z_6)$ be a vector satisfying $z \perp {\textbf{1}}$ and $N_1z = \partial ^L_1z$. By Lemma 12, we get a contradiction.

• Suppose it is $N_2$. Since $d(v_6,v_5)=2$ and $v_1v_2v_3v_4v_5$ is a path between $v_1$ and $v_5,$ then there is a vertex $v_7$ adjacent to $v_5$ and $v_6$ such that there is neither adjacent to $v_2$ nor $v_1$. If $v_7$ is adjacent to $v_4$ and it is not adjacent to $v_3,$ then the subgraph of G induced by vertices $v_1,v_2,v_3,v_4,v_5,v_7$ is isomorphic to $H_3.$ In case $v_7$ is adjacent to both, $v_4$ and $v_3,$ the subgraph of G induced by vertices $v_1,v_2,v_3,v_4,v_5,v_7$ is isomorphic to $H_8.$ In any of these cases we have a contradiction. If $v_7$ is adjacent to $v_3$ and it is not adjacent to $v_4,$ then the principal submatrix of $\mathcal{D}^L(G)$ with respect to the subgraph of G induced by vertices $v_1,v_2,v_3,v_4,v_5,v_6,v_7$ is

  $$\begin{aligned} F_1=\left[ \begin{array}{ccccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2&{}-3\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1&{}-2\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1&{}-1\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-2&{}-1\\ -2&{}-1&{}-1&{}-2&{}-2&{}t_6&{}-1\\ -3&{}-2&{}-1&{}-2&{}-1&{}-1&{}t_7\end{array}\right] . \end{aligned}$$

  Let $z= (0, z_2, z_3,0, z_5, z_6,z_7)$ be a vector satisfying $z \perp {\textbf{1}}$ and $F_1z = \partial ^L_1z$. Considering, respectively, the equations from first, second, fourth and seventh entries of $F_1z = \partial ^L_1z$, we get $z={\textbf{0}}$, a contradiction. If $v_7$ is neither adjacent to $v_3$ nor to $v_4,$ then the principal submatrix of $\mathcal{D}^L(G)$ associated with vertices $v_1,v_2,v_3,v_4,v_5,v_6,v_7$ is

  $$\begin{aligned} F_2=\left[ \begin{array}{ccccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2&{}-3\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1&{}-2\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1&{}-2\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-2&{}-1\\ -2&{}-1&{}-1&{}-2&{}-2&{}t_6&{}-1\\ -3&{}-2&{}-2&{}-2&{}-1&{}-1&{}t_7\end{array}\right] . \end{aligned}$$

  Analogously to the case of $F_1,$ we have a contradiction.$\square$

Proposition 17

Let G be a connected graph with $n\ge 8$ vertices, $diam(G)=4$ and $m(\partial ^L_1)=n-4$. Then, $H_2$ is not an induced subgraph of G.

Proof

Suppose that $H_2$ is an induced subgraph of G. Then, the principal submatrix of $\mathcal{D}^L(G)$ with respect to $H_2$ is

$$\begin{aligned} U_1=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-3\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-2\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-3\\ -3&{}-2&{}-1&{}-2&{}-3&{}t_6\end{array}\right] \hspace{0.5ex} \text{ or } \hspace{0.5ex}U_2=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-2\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-3\\ -2&{}-2&{}-1&{}-2&{}-3&{}t_6\end{array}\right] ,\\ U_3=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-3\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-2\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-2\\ -3&{}-2&{}-1&{}-2&{}-2&{}t_6\end{array}\right] \hspace{0.5ex} \text{ or } \hspace{0.5ex}U_4=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-2\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-2\\ -2&{}-2&{}-1&{}-2&{}-2&{}t_6\end{array}\right] . \end{aligned}$$

• Suppose it is $U_1$ (or $U_2$). Let $z= (z_1, z_2, z_3, z_4, 0,z_6)$ be a vector satisfying $z \perp {\textbf{1}}$ and $U_1z = \partial ^L_1z$ (or $U_1z = \partial ^L_1z$). By Lemma 12, we get a contradiction.

• Suppose it is $U_3$. Let $z= (0, z_2, z_3, z_4, z_5,z_6)$ be a vector satisfying $z \perp {\textbf{1}}$ and $U_3z = \partial ^L_1z$. By Lemma 13, we get a contradiction.

• Suppose it is $U_4$. Since $d(v_6,v_5)=2=d(v_1,v_6)$ and $v_1v_2v_3v_4v_5$ is a path between $v_1$ and $v_5,$ then there are vertices $v_7$ and $v_8$ such that $v_8$ is adjacent to $v_1$ and $v_6$ and $v_7$ is adjacent to $v_5$ and $v_6$. Moreover, $v_8$ is neither adjacent to $v_4$ nor $v_5,$ and $v_7$ is neither adjacent to $v_1$ nor $v_2$. So, $v_7$ can be adjacent to $v_3$ or $v_4$ and $v_8$ can be adjacent to $v_3$ or $v_2$. If $v_3$ is adjacent to $v_7$ and to $v_8,$ then the subgraph of G induced by vertices $v_1,v_3,v_5,v_6,v_7,v_8$ is isomorphic to $H_8.$ If $v_3$ is adjacent to $v_7$ or to $v_8,$ but not both, then the subgraph of G induced by vertices $v_1,v_3,v_5,v_6,v_7,v_8$ is isomorphic to $H_5.$ If $v_3$ is neither adjacent to $v_7$ nor to $v_8,$ but $v_4$ is adjacent to $v_7,$ then the subgraph of G induced by vertices $v_1,v_2,v_3,v_4,v_5,v_7$ is isomorphic to $H_3.$ In any of these cases we have a contradiction. If $v_3$ is neither adjacent to $v_7$ nor to $v_8$ and $v_4$ is not adjacent to $v_7,$ then the principal submatrix of $\mathcal{D}^L(G)$ with respect to the subgraph of G,  induced by vertices $v_1,v_2,v_3,v_4,v_5,v_6,v_7,$ is given by $W_1$ or $W_2,$ respectively defined as:

  $$\begin{aligned} \left[ \begin{array}{ccccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2&{}-3\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-2&{}-2\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1&{}-2\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-2&{}-1\\ -2&{}-2&{}-1&{}-2&{}-2&{}t_6&{}-1\\ -3&{}-2&{}-2&{}-2&{}-1&{}-1&{}t_7\end{array}\right] , \left[ \begin{array}{ccccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2&{}-3\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-2&{}-3\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1&{}-2\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-2&{}-1\\ -2&{}-2&{}-1&{}-2&{}-2&{}t_6&{}-1\\ -3&{}-3&{}-2&{}-2&{}-1&{}-1&{}t_7\end{array}\right] . \end{aligned}$$

  Suppose it is $W_1$. Let $z= (0, 0, z_3,z_4, z_5, z_6,z_7)$ be a vector satisfying $z \perp {\textbf{1}}$ and $W_1z = \partial ^L_1z$. Considering, respectively, the first, second, sixth and fifth entries of $W_1z = \partial ^L_1z$, we obtain that $z={\textbf{0}}$, contradiction. In case it is $W_2$, we get also get a contradiction from considering $z= (0, 0, z_3,z_4, z_5, z_6,z_7)$ be a vector satisfying $z \perp {\textbf{1}}$ and $W_2z = \partial ^L_1z$ and, respectively, first, second, fourth and fifth entries of this eigenequation.$\square$

Proposition 18

Let G be a connected graph with $n\ge 8$ vertices, $diam(G)=4$ and $m(\partial ^L_1)=n-4$. If $P_6$ is not an induced subgraph of G,  then $H_6$ is not an induced subgraph of G.

Proof

Suppose that $H_6$ is an induced subgraph of G. Then, the principal submatrix of $\mathcal{D}^L(G)$ with respect to $H_6$ is

$$\begin{aligned} Y=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-2\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-1\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-2\\ -2&{}-1&{}-2&{}-1&{}-2&{}t_6\end{array}\right] . \end{aligned}$$

Let $z= (z_1, z_2, z_3, z_4, 0,z_6)$ be a vector satisfying $z \perp {\textbf{1}}$ and $Yz = \partial ^L_1z$. By Lemma 12, we get $z=(z_1,z_2,z_3,0,0,z_6)$ and $-2z_1-z_2=0$. Considering the third entry of $Yz = \partial ^L_1z$, it follows that $z_3=\frac{2}{t_1-\partial ^L_1}z_6$. If $z_6=0,$ then $z_3=0$ and $z={\textbf{0}}$, which is impossible. So, $z_6\ne 0$. Considering the sixth entry of $Yz = \partial ^L_1z$, it follows that $z_3=\frac{t_6-\partial ^L_1}{2}z_6$ and, then, $\frac{2}{t_1-\partial ^L_1}=\frac{t_6-\partial ^L_1}{2}.$

Since $n\ge 8$, we get $\partial ^L_1\ge t_6+2$ and $\partial ^L_1\ge t_3+2$. Consequently, $\partial ^L_1= t_6+2=t_3+2$ and $v_3$ is a vertex of G with maximum transmission. Because $\sum _{i=1,i\ne 3}^6Y_{3i}=8<\sum _{i=1,i\ne 5}^6Y_{5i}=12,$ there is a vertex $v_7$ such that $d(v_7,v_5)=1<d(v_7,v_3)$.

Concluding, as $P_6$ is not an induced subgraph of G and $v_7$ is not adjacent to $v_3$, $v_1$, $v_2,$ then $v_7$ is adjacent to $v_4$ and the subgraph of G induced by vertices $v_1,v_2,v_3,v_4,v_5,v_7$ is isomorphic to $H_3$. So, we get an impossible situation. $\square$

Proposition 19

Let G be a connected graph with $n\ge 8$ vertices, $diam(G)=4$ and $m(\partial ^L_1)=n-4$. If $P_6$ is not an induced subgraph of G,  then $H_1$ is not an induced subgraph of G.

Proof

Suppose that $H_1$ is an induced subgraph of G.

• If $d(v_6,v_5)=2,$ then there is a vertex $v_7$ adjacent to $v_6$ and $v_5$. Since $d(v_1,v_5)=4,$ then $v_7$ is neither adjacent to $v_1$ nor $v_2$. Since $P_6$ is not an induced subgraph of G,  then $v_7$ is adjacent to $v_3$ or $v_4$. If $v_7$ is adjacent to $v_3$ and $v_4,$ then the subgraph of G induced by vertices $v_1,v_2,v_3,v_4,v_5,v_7$ is isomorphic to $H_7.$ If $v_7$ is adjacent to $v_3$ and it is not adjacent to $v_4,$ then the subgraph of G induced by vertices $v_1,v_2,v_6,v_7,v_5,v_4$ is isomorphic to $P_6.$ If $v_7$ is adjacent to $v_4$ and it is not adjacent to $v_3,$ then the subgraph of G induced by vertices $v_1,v_2,v_3,v_4,v_5,v_7$ is isomorphic to $H_3.$ In any of these cases we get a contradiction.

• If $d(v_6,v_5)=3,$ then there are vertices $v_7$ and $v_8$ such that $v_7$ is adjacent to $v_6$ and $v_8$ and the vertex $v_8$ is adjacent to $v_7$ and $v_5$. Since $d(v_1,v_5)=4,$ then $v_8$ is neither adjacent to $v_1$ nor $v_2$. Using similar argument, as used when $d(v_6,v_5)=2,$ with $v_8$ instead of $v_7,$ we get a contradiction.

• If $d(v_6,v_5)=4,$ then the principal submatrix of $\mathcal{D}^L(G)$ with respect to $H_1$ is

  $$\begin{aligned} M=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-2\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-3\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-4\\ -2&{}-1&{}-2&{}-3&{}-4&{}t_6\end{array}\right] . \end{aligned}$$

  Let $z= (z_1, z_2, z_3, z_4, 0,z_6)$ be a vector satisfying $z_1 + z_2 + z_3 + z_4+z_6 = 0$ and $Mz = \partial ^L_1z$. By Lemma 12, $z=(z_1,0,0,0,0,z_6).$ Considering the first entry of both sides of $Mz = \partial ^L_1z$, we have $t_1z_1-2z_6 = \partial _1^Lz_1$. Since $n\ge 8,$ then $t_1+2= \partial _1^L$ and $v_1$ is a vertex with maximum transmission in G. Because $\sum _{i=1,i\ne 1}^6M_{3i}=12<\sum _{i=1,i\ne 5}^6M_{5i}=14$ there is a vertex $v_7$ such that $d(v_7,v_5)<d(v_7,v_1)$. Considering all cases we have just seen, the subgraph of G induced by vertices $v_1,v_2,v_3,v_4,v_5,v_6,v_7$ is isomorphic to graphs $R_1$ or $R_2$ (Fig. 3). Since $d(v_6,v_5)=4,$ then, in both cases, we have $v_6$ is not adjacent to $v_7$. Let E be the principal submatrix of $\mathcal{D}^L(G)$ with respect to $R_1:$

  $$\begin{aligned} E=\left[ \begin{array}{ccccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2&{}-3\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1&{}-2\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-2&{}-1\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-3&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-4&{}-1\\ -2&{}-1&{}-2&{}-3&{}-4&{}t_6&{}-3\\ -3&{}-2&{}-1&{}-2&{}-1&{}-3&{}t_7\end{array}\right] . \end{aligned}$$

  and $z= (0, z_2, z_3, 0, z_5,z_6,z_7)$ be a vector satisfying $z \perp {\textbf{1}}$ and $Ez = \partial ^L_1z$. Considering, respectively, the first, second, fourth and fifth entries of this eigenequation, we conclude that $z={\textbf{0}}$. If $R_2$ (Fig. 3) is an induced subgraph of G,  then $d(v_6,v_7)=2$ or $d(v_6,v_7)=3$ or $d(v_6,v_7)=4$. If $d(v_6,v_7)=2$ and $d(v_6,v_5)=4,$ then there is a vertex $v_8$ adjacent to $v_6$ and $v_7,$ and $v_8$ is neither adjacent to $v_4$ nor $v_5$. So, $v_8$ can be adjacent to $v_1$ or $v_2$ or $v_3$. If $v_8$ is adjacent to $v_3,$ then $P_6$ or $H_2$ or $H_5$ or $H_7$ is an induced subgraph of G. If $v_8$ is not adjacent to $v_3,$ then $P_6$ or $H_3$ is an induced subgraph of G. In any case of these cases we get a contradiction. If $d(v_6,v_7)=3$ and $d(v_6,v_5)=4,$ then there are vertices $v_8$ and $v_9$ such that $v_9$ is adjacent to $v_6$ and $v_8,$ and $v_8$ is adjacent to $v_7$. Moreover, $v_8$ is not adjacent to $v_5,$ and $v_9$ is neither adjacent to $v_4$ nor $v_5$. If $v_8$ is not adjacent to $v_4,$ then the subgraph of G induced by vertices $v_6,v_9,v_8,v_7,v_4,v_5$ is isomorphic to $P_6.$ If $v_8$ is adjacent to $v_4,$ then $P_6$ or $H_5$ or $H_6$ or $H_8$ is an induced subgraph of G. All cases are not possible. If $d(v_6,v_7)=3,$ then $d(v_1,v_7)=4$, $d(v_2,v_7)=3$ and the principal submatrix of $\mathcal{D}^L(G)$ with respect to $R_2$ is

  $$\begin{aligned} J=\left[ \begin{array}{ccccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-2&{}-4\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-1&{}-3\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-2&{}-2\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-3&{}-1\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-4&{}-2\\ -2&{}-1&{}-2&{}-3&{}-4&{}t_6&{}-4\\ -4&{}-3&{}-2&{}-1&{}-2&{}-4&{}t_7\end{array}\right] . \end{aligned}$$

  Let $z= (0, z_2, z_3, z_4, 0,z_6,z_7)$ be a vector satisfying $z \perp {\textbf{1}}$ and $Jz = \partial ^L_1z$. Considering, respectively, the first, second, fifth and fourth entries of $Jz = \partial ^L_1z$, we conclude that $z={\textbf{0}}$.$\square$

Fig. 3

Graphs $R_1$ and $R_2$

For the last results, we need to introduce a definition and a lemma.

Definition 1

Let a, b be two positive integers. We denote by S(a, b) the graph obtained from $K_{a,1}\cup K_1\cup K_{b,1}$ by joining each pendant vertex of $K_{a,1}$ and $K_{b,1}$ with the vertex of $K_1$.

Proposition 20

Let a, b be two positive integers such that $a\le b$. Let v be a pendant vertex of $K_{a,1}$ and u be its central vertex. Let w be a pendant vertex of $K_{b,1}$. Then, in S(a, b) it follows that $Tr(v)=Tr(w)<Tr(u).$

Proof

It is easy to check that $Tr(v)=3+2(a+b)=Tr(w)$ and $Tr(u)=6+a+3b.$ Also, $Tr(v)<Tr(u)$ since $a\le b.$$\square$

Proposition 21

Let G be a connected graph with $n\ge 8$ vertices, $diam(G)=4$ and $m(\partial ^L_1)=n-4$. If $P_6$ is not an induced subgraph of G,  then $H_4$ is not an induced subgraph of G.

Proof

Suppose that $H_4$ is an induced subgraph of G. Then, the principal submatrix of $\mathcal{D}^L(G)$ with respect to $H_4$ is

$$\begin{aligned} M=\left[ \begin{array}{cccccc}t_1&{}-1&{}-2&{}-3&{}-4&{}-1\\ -1&{}t_2&{}-1&{}-2&{}-3&{}-2\\ -2&{}-1&{}t_3&{}-1&{}-2&{}-1\\ -3&{}-2&{}-1&{}t_4&{}-1&{}-2\\ -4&{}-3&{}-2&{}-1&{}t_5&{}-3\\ -1&{}-2&{}-1&{}-2&{}-3&{}t_6\end{array}\right] . \end{aligned}$$

Let $z= (z_1, z_2, z_3, z_4, 0,z_6)$ be a vector satisfying $z \perp {\textbf{1}}$ and $Mz = \partial ^L_1z$. By Lemma 12, $z=(0,z_2,0,0,0,z_6).$ Consider the second entry of $Mz = \partial ^L_1z$ and, since $n\ge 8,$ then $t_2+2= \partial _1^L$ and $v_2$ is a vertex with maximum transmission in G. Because $\sum _{i=1,i\ne 2}^6M_{3i}=9<\sum _{i=1,i\ne 5}^6M_{5i}=15,$ there is a vertex $v_7$ such that $d(v_7,v_5)<d(v_7,v_2)$. Considering all cases we have just seen we conclude $v_7$ is adjacent to $v_4$ and $v_5$. Using a similar argument, as we used before, we get $v_4$ is a vertex of G with a maximum transmission. Consequently, G has an induced subgraph isomorphic to S(a, b),  with $a,b\ge 1$, $v_1,$ $v_5$ as the central vertices of the stars in S(a, b), $v_3$ as the vertex of $K_1,$ $v_4$ as a pendent vertex of the star with central vertex $v_5$ and $a+1$ vertices, and $v_2$ as a pendent vertex of the star with central vertex $v_1$ and $b+1$ vertices. By Proposition 20, if $a\le b,$ then $Tr(v_5)>Tr(v_2)$ and if $a\ge b,$ then $Tr(v_1)>Tr(v_2)$. So, we get a contradiction. $\square$

As any diameter four graph with $P_6$ as a forbidden subgraph must have an induced subgraph isomorphic to some of the graphs $H_i, 1\le i \le 8,$ from Propositions 14, 15, 16, 17, 18, 19, 21, we can state:

Theorem 22

Let G be a connected graph with $n\ge 8$ vertices such that $m(\partial ^L_1)=n-4$. If $P_6$ is not an induced subgraph of G,  then $diam(G)\le 3$.

Concluding, based on results presented in Sect. 3 and a computational search for graphs on n vertices, $6\le n \le 11,$ we could not find a graph with $m(\partial ^L_1(G))=n-4$ and $P_6$ as an induced subgraph. So, we propose the following conjecture:

Conjecture 23

Let G be a connected graph with $n\ge 6$ vertices. If $m(\partial ^L_1(G))=n-4,$ then $P_6$ is a forbidden subgraph.

In case that $P_6$ is a forbidden subgraph, Theorem 22 presents some advances in an effort to determine all graphs such that $m(\partial ^L_1)=n-4.$