A new effective coherent numerical technique based on shifted Vieta–Fibonacci polynomials for solving stochastic fractional integro-differential equation

Abstract

In this article, an operational matrix method based on shifted Vieta–Fibonacci polynomials is utilised to find the numerical solution of fractional order stochastic integro-differential equations. In this method, the operational matrices are developed by using the shifted Vieta–Fibonacci polynomials for the fractional order Caputo differential operator in order to solve the present concerned problem. Using Newton cotes nodes as collocation points, operational matrices are employed to convert the above-mentioned equation into a system of linear algebraic equations. The coherent procedure for the appropriate numerical technique is described in this article. Additionally, the convergence analysis and error bound of the suggested method are well established. In order to illustrate the effectiveness, consistency, plausibility, and reliability of the proposed technique, three numerical examples are given. Moreover, the results obtained by the proposed method have been compared with those obtained by the Chelyshkov operational matrix method.

1 Introduction

It is generally known that fractional derivatives may characterise the memory and heredity properties of certain materials and processes in ways that integer order derivatives can not. Recently, many applications across a wide range of fields, including viscoelastic materials (Meral et al. 2010), signal processing (Machado and Lopes 2015), meteorology, earthquake (El-Misiery and Ahmed 2006), optimal control (Sahu and Saha Ray 2018), fluid-dynamic (Momani and Odibat 2006), quantum mechanics (Atman and Şirin 2020), finance (Scalas et al. 2000) and in other fields of science and engineering (Sun et al. 2018) have been remodeled using fractional calculus. Integro-differential equations have a strong physical foundation and are widely used in fields of study including polymer rheology (Lodge et al. 1978) and population model (Yzbaı et al. 2013). Deterministic fractional equations such as fractional order pantograph Volterra delay-integro-differential equations (Behera and Saha Ray 2022), Riemann–Liouville fractional integro-differential equations (Ahmad and Nieto 2011), fractional integro-differential equations (Arikoglu and Ozkol 2009) are used to represent real physical problems, which often rely on a noise source that is disregarded owing to the absence of sophisticated computational tools. As computational power has increased recently, real world phenomena can now be more effectively modeled using stochastic fractional equations such as stochastic fractional differential equations, stochastic fractional integral equations, stochastic fractional integro-differential equations (SFIDE).

This article investigates the numerical solution of the following SFIDE:

$$\begin{aligned} ^CD^{\alpha }_{\eta }z(\eta )= & {} g(\eta ) + \lambda _1 \int _0^\eta \kappa _1 (\eta , \zeta ) z(\zeta )d\zeta + \lambda _2 \int _0^\eta \kappa _2 (\eta , \zeta ) z(\zeta )dB(\zeta ),\nonumber \\ {}{} & {} \eta \in [0,1], \quad z(0)=z_0, \end{aligned}$$

(1.1)

where $\lambda _{1}$ and $\lambda _{2}$ are constant numbers and $^CD^{\alpha }_{\eta }$ is the Caputo fractional differential operator of order $0<\alpha <1$. In Eq. (1.1), $g(\eta )$ and $\kappa _i (\eta , \zeta )$ for $i=1,2$ are known smooth functions, and $z(\eta )$ is an unknown function. Brownian motion process is defined as $B=\{B(t);t\ge 0\}$ and $z(\eta )$ is a stochastic process defined on the probability space $(\Omega , {\mathcal {F}}, {\mathbb {P}})$. This is referred to as the solution of SFIDE.

There are several numerical methods to solve SFIDE, such as block pulse approximation (Mirzaee et al. 2019), cubic B spline approximation (Mirzaee and Alipour 2020), meshless discrete collocation method based on radial basis functions (Mirzaee and Samadyar 2019), shifted Legendre spectral collocation method (Taheri et al. 2017), Bernstein polynomials approximation (Mirzaee and Samadyar 2017), Galerkin method (Kamrani 2016), explicit finite difference method (Saha Ray and Patra 2013) and different other methods that have been implemented to solve SFIDE.

The main motivation of this study is to solve the SFIDE (Eq. (1.1)) using shifted Vieta–Fibonacci polynomials. These kinds of equations may be found in many different fields, including physics, biology, physiology, optics, and climatology. Explicitly solving SFIDE can be difficult and time-consuming. So, here, the operational matrix method is implemented to solve these equations. Using shifted Vieta–Fibonacci polynomials, a new stochastic operational matrix has been derived for the first time in this paper. The proposed method is effective, applicable, and consistent.

In this study, the numerical results of Eq. (1.1) obtained by the shifted Vieta–Fibonacci operational matrix (SVFOM) method are further compared with the orthonormal Chelyshkov operational matrix (OCOM) method and actual solutions. Equation (1.1) can be transformed into a system of algebraic equations by using operational matrices along with suitable collocation points. The resultant equations can be easily solved to get the desired approximate solution.

This article is organised as follows:

A few fundamental concepts about shifted Vieta–Fibonacci polynomials (SVFPs), stochastic calculus, and fractional calculus have been introduced in Sect. 2. In Sect. 3, operational matrices (OMs) for product, integral, fractional, and stochastic integrals have been constructed using shifted Vieta–Fibonacci polynomial. The SFIDE problem is handled using the suggested operational matrix approach in Sect. 4, which also provides a review of the collocation technique. In Sect. 5, theorems relating to error estimation and convergence analysis are covered. Section 6 represents the reliability and efficiency of the suggested numerical method using a few illustrative examples, and a brief overview is provided in Sect. 7.

2 Preliminaries

This section covers the properties of SVFPs as well as some fundamental stochastic calculus concepts.

2.1 Stochastic calculus

Definition 1

(Itô Integral (Øksendal 2003)) Let ${\mathcal {V}} = {\mathcal {V}}(U,V)$ be the class functions $g(\gamma ,\delta ): [0,\infty ) \times \Omega \rightarrow {\mathbb {R}}$ and $g \in {\mathcal {V}}(U,V)$. Thus, the definition of the Itô integral of g is given by

$$\begin{aligned} \int _U^V g(\gamma ,\delta )dB_{\gamma }(\delta ) = \lim _{m \rightarrow \infty }\int _U^V \psi _{m}(\gamma ,\delta )dB_{\gamma }(\delta ) \quad (\lim in\, L^2({\mathbb {P}})), \end{aligned}$$

(2.1)

where $\psi _{m}$ is a sequence of elementary functions such that

$$\begin{aligned} E\left[ \int _U^V (g(\gamma ,\delta ) - \psi _{m}(\gamma ,\delta ))^2 d\gamma \right] \rightarrow 0\, \text { as }\, m \rightarrow \infty . \end{aligned}$$

(2.2)

Theorem 2.1.1

(The Itô isometry (Øksendal 2003)). Let $g \in {\mathcal {V}}(U,V)$, be elementary and bounded functions. Then

$$\begin{aligned} E\left[ \left( \int _U^V g(\gamma ,\delta )dB_{\gamma }(\delta )\right) ^2 \right] = E\left[ \int _U^V g^2(\gamma ,\delta )d\gamma \right] . \end{aligned}$$

(2.3)

2.2 Fractional calculus

Definition 2

Consider $p-1<\alpha <p, \alpha>0, \eta >0, \alpha , \eta \in {\mathbb {R}}$, then the Caputo fractional differential operator $^CD^{\alpha }_{\eta } z(\eta )$ of order $\alpha$ is defined as (Saha Ray 2015)

$$\begin{aligned} ^CD^{\alpha }_{\eta } z(\eta ) = \dfrac{1}{\Gamma (p- \alpha )}\int _0^{\eta } (\eta -\zeta )^{p-\alpha -1} z^{(p)}(\zeta ) d\zeta . \end{aligned}$$

(2.4)

Also, the Riemann–Liouville (RL) fractional integral operator $J^{\alpha }_{\eta }$ of order $\alpha$ is defined as

$$\begin{aligned} J^{\alpha }_{\eta } z(\eta )=\dfrac{1}{\Gamma ( \alpha )}\int _0^{\eta } (\eta -\zeta )^{\alpha -1} z(\zeta ) d\zeta , \quad J^0_{\eta } z(\eta )=z(\eta ). \end{aligned}$$

(2.5)

The operators $^CD^{\alpha }_{\eta }$ and $J^{\alpha }_{\eta }$ has the following characteristics:

• 1. $J^{\alpha }_{\eta }(\delta _1 z(\eta )+\delta _2 z(\eta ))=\delta _1 J^{\alpha }_{\eta }(z(\eta ))+\delta _2 J^{\alpha }_{\eta }(z(\eta )), \quad \alpha \ge 0$.

• 2. $J^{\beta _1}_{\eta }J^{\beta _2}_{\eta }z(\eta )=J^{\beta _1 + \beta _2 }_{\eta }z(\eta ), \quad \beta _1, \beta _2 \ge 0.$

• 3. $^CD^{\alpha }_{\eta }J^{\alpha }_{\eta }z(\eta )=z(\eta ),\quad \alpha \ge 0$.

• 4. $J^{\alpha }_{\eta } ({^C}D^{\alpha }_{\eta }) z(\eta )=z(\eta )-\sum _{i=0}^{p-1} z^i(0)\frac{\eta ^i}{i!}, \quad p-1<\alpha <p, \quad p\in {\mathbb {N}}.$

2.3 Shifted Vieta–Fibonacci polynomials and its characteristics

Many problems in mathematical physics have been solved using SVFPs, such as the Lane–Emden equation, reaction-advection–diffusion, Emden–Fowler equation, etc.

Vieta–Fibonacci polynomials

According to the following relation, the Vieta–Fibonacci polynomials ${{\mathcal {V}}}{{\mathcal {F}}}_{m}(\eta )$ of degree m in $\eta$ are defined on the interval [− 2, 2].

$$\begin{aligned} {{\mathcal {V}}}{{\mathcal {F}}}_{m}(\eta ) = \dfrac{\sin (m\theta )}{\sin \theta }, \end{aligned}$$

where $\eta = 2 \cos \theta$ and $\theta \in [0, \pi ]$.

These polynomials can also be generated by the following recurrence relation:

$$\begin{aligned} {{\mathcal {V}}}{{\mathcal {F}}}_{m}(\eta )=\eta {{\mathcal {V}}}{{\mathcal {F}}}_{m-1}(\eta )-{{\mathcal {V}}}{{\mathcal {F}}}_{m-2}(\eta ),\quad m=2,3,\ldots , \end{aligned}$$

with the initial values ${{\mathcal {V}}}{{\mathcal {F}}}_{0}(\eta )=0, {{\mathcal {V}}}{{\mathcal {F}}}_{1}(\eta )=1$.

Shifted Vieta–Fibonacci polynomials

Definition 5

The shifted Vieta–Fibonacci polynomials ${{\mathcal {V}}}{{\mathcal {F}}}_{m}^*(\eta )$, of degree m in $\eta$ on [0, 1] are defined as follows (Sadri et al. 2022)

$$\begin{aligned} {{\mathcal {V}}}{{\mathcal {F}}}_{m}^*(\eta )={{\mathcal {V}}}{{\mathcal {F}}}_{m}(4\eta -2). \end{aligned}$$

Also, these polynomials, can be generated via the following recurrence relation:

$$\begin{aligned} {{\mathcal {V}}}{{\mathcal {F}}} _{m}^*(\eta )=(4\eta -2){{\mathcal {V}}}{{\mathcal {F}}} _{m-1}^*(\eta )-{{\mathcal {V}}}{{\mathcal {F}}} _{m-2}^*(\eta ),\quad m=2,3,\ldots , \end{aligned}$$

(2.6)

using the initial values ${{\mathcal {V}}}{{\mathcal {F}}}_{0}^*(\eta )=0, {{\mathcal {V}}}{{\mathcal {F}}}_{1}^*(\eta )=1$.

The SVFPs are also defined by using the following series:

$$\begin{aligned} {{\mathcal {V}}}{{\mathcal {F}}} _{m}^*(\eta ) = \sum _{l=0}^{m-1}\dfrac{(-1)^{m-l-1}2^{2l}\Gamma (m+l+1)}{\Gamma (m-l) \Gamma (2l+2)}{\eta }^l,\quad m=2,3,\ldots ,. \end{aligned}$$

(2.7)

These polynomials are orthogonal with respect to the weight function $w(\eta ) = \sqrt{\eta -{\eta }^2}$, i.e.

$$\begin{aligned} \int _{0}^{1} {{\mathcal {V}}}{{\mathcal {F}}} _{m}^*(\eta ) {{\mathcal {V}}}{{\mathcal {F}}} _{n}^*(\eta ) w(\eta ) d\eta = {\left\{ \begin{array}{ll} \frac{\pi }{8} &{}\quad m = n\ne 0\\ 0 &{}\quad m\ne n \\ \end{array}\right. }. \end{aligned}$$

(2.8)

2.4 Function approximation by SVFPs

Let $H = L^{2}_{\omega }(I)$, $I = [0,1]$, and S = span$\{{{\mathcal {V}}}{{\mathcal {F}}} _{1}^*(\eta ), {{\mathcal {V}}}{{\mathcal {F}}} _{2}^*(\eta ),\ldots , {{\mathcal {V}}}{{\mathcal {F}}} _{m+1}^*(\eta )\}$. Then for any $y(\eta ) \in H$, $y_{m}(\eta ) \in S$ is a best approximation; that is

$$\begin{aligned} y(\eta ) \simeq y_{m}(\eta ) = \sum _{i=1}^{m+1} {a_{i}}{{{\mathcal {V}}}{{\mathcal {F}}} _{i}^*(\eta )} = A^{T} V_F^*(\eta ), \end{aligned}$$

(2.9)

where $A = [a_{1}, a_{2},\ldots ,a_{m+1}]^{T}$ and $V_F^*(\eta ) = [{{\mathcal {V}}}{{\mathcal {F}}} _{1}^*(\eta ), {{\mathcal {V}}}{{\mathcal {F}}} _{2}^*(\eta ),\ldots , {{\mathcal {V}}}{{\mathcal {F}}} _{m+1}^*(\eta )]^T$. Furthermore,

$$\begin{aligned} a_{i} =\left( \dfrac{8}{\pi }\right) \int _{0}^{1}y(\eta ){{\mathcal {V}}}{{\mathcal {F}}} _{i}^*(\eta )w(\eta )d\eta , \quad i=1,2,\ldots ,m+1. \end{aligned}$$

(2.10)

In order to approximate the two-dimensional kernel function $\kappa (\eta , \zeta )$, following approximation is used.

$$\begin{aligned} \kappa (\eta , \zeta ) \simeq \kappa _{m,m} (\eta , \zeta ) = \sum _{i=1}^{m+1} \sum _{j=1}^{m+1} \kappa _{ij}{{\mathcal {V}}}{{\mathcal {F}}} _{i}^*(\eta ) {{\mathcal {V}}}{{\mathcal {F}}} _{j}^*(\zeta ) = V_F^*{T}(\eta ){\mathbb {K}} V_F^*(\zeta ), \end{aligned}$$

(2.11)

where ${\mathbb {K}}$ is a $(m+1)\times (m+1)$ order kernal matrix.

Here, the orthogonality property of the SVFPs, together with the weight function $w(\eta )$ in Eq. (2.8), is used to generate the kernel matrix.

It follows

$$\begin{aligned} {\mathbb {K}} = Q^{-1} \left( \int _0^1 w(\eta ) V_F^*(\eta ) \left( \int _0^1 \kappa (\eta ,\zeta )V_F^{*T}(\zeta ) w(\zeta )d\zeta \right) d\eta \right) Q^{-1}, \end{aligned}$$

(2.12)

where

$Q = \left\langle V_F^*(.),V_F^{*T}(.)\right\rangle _{w}$ .

The matrix form for these SVFPs is as follows:

$$\begin{aligned} V_F^*(\eta ) = {\tilde{A}}L_{m}(\eta ), \end{aligned}$$

(2.13)

where

$$\begin{aligned} V_F^*(\eta ) = [{{\mathcal {V}}}{{\mathcal {F}}} _{1}^*(\eta ), {{\mathcal {V}}}{{\mathcal {F}}} _{2}^*(\eta ),\ldots , {{\mathcal {V}}}{{\mathcal {F}}} _{m+1}^*(\eta )]^T, \quad L_{m}(\eta ) = [1, \eta ,\ldots , \eta ^m]^T. \end{aligned}$$

(2.14)

2.4.1 ${\tilde{A}}$ matrix

Using Eq. (2.7)

${\tilde{A}} = \begin{pmatrix} 1 &{}\quad 0 &{}\quad \dots &{}\quad 0 \\ \dfrac{(-1)^{1}\Gamma (2+1)}{\Gamma (2) \Gamma (2)} &{}\quad \dfrac{(-1)^{2-2}2^{2}\Gamma (2+2)}{\Gamma (2-1) \Gamma (2+2)} &{}\quad \dots &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \dfrac{(-1)^{m}\Gamma (m+2)}{\Gamma (m+1) \Gamma (2)} &{}\quad \dfrac{(-1)^{m-1}2^{2}\Gamma (m+3)}{\Gamma (m) \Gamma (2+2)} &{}\quad \dots &{}\quad \dfrac{(-1)^{0}2^{2m}}{\Gamma (1) }\\ \end{pmatrix}_{(m+1)\times (m+1)}$,

where ${\tilde{A}}$ is lower triangular non singular matrix, hence ${\tilde{A}}^{-1}$ exists.

Therefore,

$$\begin{aligned} L_{m}(\eta ) = {\tilde{A}}^{-1}V_F^*(\eta ). \end{aligned}$$

(2.15)

3 Operational matrix for SVFPs

To solve the SFIDE by operational matrix method, it is necessary to evaluate the following OMs:

3.1 Product operational matrix

The OM for the product is determined in this section.

$$\begin{aligned} V_F^*(\eta )V_F^{*T}(\eta )P \simeq {\hat{P}} V_F^*(\eta ), \end{aligned}$$

(3.1)

where ${\hat{P}}$ is an OM of $(m+1)\times (m+1)$ order that is found by applying the orthogonality property of SVFPs with the weight function $w(\eta )$.

$$\begin{aligned} {\hat{P}} = \left\langle V_F^*(\eta )V_F^{*T}(\eta )P, V_F^{*T}(\eta ) \right\rangle _{w(\eta )} Q^{-1}. \end{aligned}$$

(3.2)

3.2 Integral operational matrix

In terms of OM, the integration of vector $V_F^*(\eta )$ can be described as follows:

$$\begin{aligned} \int _0^{\eta } V_F^*(\zeta ) d\zeta \simeq {\tilde{P}} V_F^*(\eta ), \end{aligned}$$

(3.3)

where ${\tilde{P}}$ is an integral OM with a $(m+1)\times (m+1)$ dimension that can be found by utilising the orthogonality property of SVFPs with the weight function $w(\eta )$.

Using Eq. (3.3), we obtain

$$\begin{aligned} {\tilde{P}} = \left\langle \left( \int _0^\eta V_F^*(\zeta ) d\zeta \right) , V_F^{*T}(\eta ) \right\rangle _ {w(\eta )}Q^{-1}. \end{aligned}$$

(3.4)

3.3 Stochastic operational matrix

Here, the stochastic OM can be used to approximate the Itô integral of the vector $V_F^*(\eta )$ as follows:

$$\begin{aligned} \int _0^\eta V_F^*(\zeta )dB(\zeta ) \simeq H_{s} V_F^*(\eta ), \end{aligned}$$

(3.5)

where $H_s$ is a stochastic OM with a $(m+1)\times (m+1)$ dimension that can be found by utilising the orthogonality property of SVFPs with the weight function $w(\eta )$.

From Eq. (3.5), we have

$$\begin{aligned} H_{s} = \left\langle \left( \int _0^\eta V_F^*(\zeta ) dB(\zeta ) \right) , V_F^{*T}(\eta ) \right\rangle _ {w(\eta )}Q^{-1}. \end{aligned}$$

(3.6)

3.3.1 Calculation for $H_{s}$ matrix

From Eq. (2.13)

$$\begin{aligned} V_F^*(\eta ) = {\tilde{A}}L_{m}(\eta ). \end{aligned}$$

Now,

$$\begin{aligned} \int _0^\eta V_F^*(\zeta )dB(\zeta )= & {} \int _0^\eta {\tilde{A}}L_{m}(\eta ) dB(t) = {\tilde{A}}\int _0^\eta L_{m}(\zeta ) dB(\zeta ), \end{aligned}$$

(3.7)

$$\begin{aligned} \int _0^\eta L_{m}(\zeta ) dB(\zeta )= & {} \left[ \int _0^\eta dB(\zeta ), \int _0^\eta \zeta dB(\zeta ),\ldots , \int _0^\eta \zeta ^m dB(\zeta ) \right] ^T. \end{aligned}$$

(3.8)

Thus,

$$\begin{aligned} \begin{bmatrix} \int _0^\eta dB(\zeta )\\ \int _0^\eta \zeta dB(\zeta )\\ \int _0^\eta \zeta ^2 dB(\zeta )\\ \vdots \\ \int _0^\eta \zeta ^m dB(\zeta ) \end{bmatrix} = \begin{bmatrix} \ B(\eta )\\ \ \eta B(\eta ) - \int _0^\eta B(\zeta ) d\zeta \\ \ \eta ^2B(\eta ) - 2\int _0^\eta \zeta B(\zeta ) d\zeta \\ \vdots \\ \ \eta ^mB(\eta ) - m \int _0^\eta \zeta ^{(m-1)} B(\zeta ) d\zeta \end{bmatrix}= Y_{m}(\eta ) = [y_{j}]_{(m+1) \times 1}, \end{aligned}$$

(3.9)

where,

$$\begin{aligned} y_{j} = \eta ^j B(\eta ) - j\int _0^\eta \zeta ^{j-1} B(\zeta ) d\zeta \quad \hbox {and}\quad j = 0, 1, 2, \ldots , m. \end{aligned}$$

The Simpson’s $\dfrac{1}{3}$ rule is used to evaluate the integrals in Eq. (3.9), resulting in

$$\begin{aligned} y_{j} = \left( 1 - \dfrac{j}{6} \right) \eta ^{j} B(\eta ) - \dfrac{j}{3 \times 2^{j-2}} \eta ^j B\left( \dfrac{\eta }{2}\right) , \quad j = 0, 1, 2,\ldots , m. \end{aligned}$$

(3.10)

Now, $B\left( \dfrac{\eta }{2}\right) , B(\eta )$ in Eq. (3.10) are approximated by B(0.25) and B(0.5), respectively.

Thus,

$$\begin{aligned} \int _0^\eta L_{m}(\zeta ) dB(\zeta ) \simeq \Lambda L_{m}(\eta ), \end{aligned}$$

(3.11)

where

$$\begin{aligned} \small \Lambda = \begin{bmatrix} B(0.5) &{}\quad 0 &{}\quad \dots &{}\quad 0 \\ 0 &{}\quad - \frac{2}{3}B(0.25) +\frac{5}{6}B(0.5) &{}\quad \dots &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad \dots &{}\quad - \dfrac{m}{3 \times 2^{m-2}} B(0.25)+\left( 1 - \frac{m}{6} \right) B(0.5) \end{bmatrix} _{(m+1)\times (m+1)}, \end{aligned}$$

and $L_{m}(\eta ) = [1, \eta ,\ldots , \eta ^m]_{(m+1)\times 1}^T$.

Using Eqs. (2.15) and (3.11), we get

$$\begin{aligned} \int _0^\eta V_F^*(\zeta ) dB(\zeta ) = {\tilde{A}} \Lambda L_{m }(\eta ) = {\tilde{A}} \Lambda {\tilde{A}}^{-1} V_F^*(\eta ) = H_{s} V_F^*(\eta ). \end{aligned}$$

(3.12)

Hence,

$$\begin{aligned} H_{s} = {\tilde{A}} \Lambda {\tilde{A}}^{-1}. \end{aligned}$$

(3.13)

3.4 Fractional integral operational matrix

The OM for fractional integrals is discussed in this section.

$$\begin{aligned} J^{\alpha }_{\eta }V_F^*(\eta ) \simeq F^{\alpha }V_F^*(\eta ), \end{aligned}$$

(3.14)

where $F^{\alpha }$ is a fractional OM with a $(m+1)\times (m+1)$ dimension that can be found by utilising the orthogonality property of SVFPs with the weight function $w(\eta )$.

From Eq. (3.14), we obtain

$$\begin{aligned} F^{\alpha } = \left\langle J^{\alpha }_{\eta }V_F^*(\eta ), V_F^{*T}(\eta ) \right\rangle _ {w(\eta )}Q^{-1}, \end{aligned}$$

(3.15)

where $J^{\alpha }_{\eta }$ is defined in Eq. (2.5).

4 Numerical method

In the operational matrix technique, SVFPs are used to approximate each term in Eq. (1.1).

Let,

$$\begin{aligned}{} & {} ^CD^{\alpha }_{\eta } \simeq V_F^{*T}(\eta )A_1= A_1^{T} V_F^*(\eta ), \end{aligned}$$

(4.1)

$$\begin{aligned}{} & {} z(0)=z_0 \simeq A_2^{T} V_F^*(\eta ), \end{aligned}$$

(4.2)

$$\begin{aligned}{} & {} g(\eta ) \simeq A_3^{T} V_F^*(\eta ), \end{aligned}$$

(4.3)

where $A_1, A_2$, and $A_3$ are vectors of order $(m+1)\times 1$, which can be defined in the following manner as in Eqs. (2.9) and (2.10).

By using the RL operator properties

$$\begin{aligned} J^{\alpha }_{\eta }(^CD^{\alpha }_{\eta }) \simeq A_1^{T} J^{\alpha }_{\eta } V_F^*(\eta ), \end{aligned}$$

(4.4)

then, applying Eq. (3.14) into Eq. (4.4),

$$\begin{aligned} z(\eta )-z_0 \simeq A_1^{T} F^{\alpha }V_F^*(\eta ), \end{aligned}$$

(4.5)

by using Eq. (4.2) in Eq. (4.5)

$$\begin{aligned} z(\eta ) \simeq z_m(\eta )= (A_2^T + A_1^{T} F^{\alpha })V_F^*(\eta ) = \Delta ^T V_F^*(\eta )= V_F^{*T}(\eta )\Delta , \end{aligned}$$

(4.6)

where $\Delta = A_2 + (F^{\alpha })^T A_1$ and $F^{\alpha }$ is defined in Eq. (3.15).

Now, by substituting Eqs. (2.11), (4.1), (4.3), and (4.6) into Eq. (1.1), the following is obtained:

$$\begin{aligned} A_1^{T} V_F^*(\eta )&= A_3^{T} V_F^*(\eta ) + \lambda _{1}\int _0^{\eta }(V_F^{*T}(\eta ){\mathbb {K}}_1 V_F^*(\zeta )V_F^{*T}(\zeta )\Delta )d\zeta \nonumber \\&\quad +\lambda _{2}\int _0^{\eta }(V_F^{*T}(\eta ){\mathbb {K}}_2 V_F^*(\zeta )V_F^{*T}(\zeta )\Delta )dB(\zeta )\nonumber \\&= A_3^{T} V_F^*(\eta )+\lambda _{1}V_F^{*T}(\eta ){\mathbb {K}}_1 \int _0^{\eta }(V_F^*(\zeta )V_F^{*T}(\zeta )\Delta )d\zeta \nonumber \\&\quad +\lambda _{2}V_F^{*T}(\eta ){\mathbb {K}}_2 \int _0^{\eta }(V_F^*(\zeta )V_F^{*T}(\zeta )\Delta )dB(\zeta ). \end{aligned}$$

(4.7)

By using Eq. (3.1) in Eq. (4.7),

$$\begin{aligned} A_1^{T} V_F^*(\eta )\!=\! A_3^{T} V_F^*(\eta )+\lambda _{1}V_F^{*T}(\eta ){\mathbb {K}}_1 {\hat{\Delta }} \int _0^{\eta }V_F^*(\zeta )d\zeta +\lambda _{2}V_F^{*T}(\eta ){\mathbb {K}}_2 {\hat{\Delta }}\int _0^{\eta }V_F^*(\zeta )dB(\zeta ),\nonumber \\ \end{aligned}$$

(4.8)

where ${\hat{\Delta }} = \left\langle V_F^*(\eta )V_F^{*T}(\eta )\Delta , V_F^{*T}(\eta ) \right\rangle _{w(\eta )} Q^{-1}.$

By substituting Eqs. (3.3) and (3.5) in Eq. (4.8),

$$\begin{aligned} A_1^{T} V_F^*(\eta )= A_3^{T} V_F^*(\eta )+\lambda _{1}V_F^{*T}(\eta ){\mathbb {K}}_1 {\hat{\Delta }}{\tilde{P}} V_F^*(\eta ) +\lambda _{2}V_F^{*T}(\eta ){\mathbb {K}}_2 {\hat{\Delta }}H_s V_F^*(\eta ). \end{aligned}$$

(4.9)

An algebraic system of equations is created by collocating Eq. (4.9) at the Newton cotes nodes provided by $\eta _{r} = \dfrac{2r-1}{2(m+1)}, r = 1,2,\ldots ,m+1$. After solving this system of algebraic equations, the coefficient vector $A_1$ is generated. Now, calculate $\Delta ^T = A_2 ^T + A_1 ^TF^{\alpha }$. After that the final approximate solution by the SVFPs method is obtained by the equation $z(\eta ) \simeq z_m(\eta )=\Delta ^T V_F^*(\eta )$.

5 Error bound and convergence analysis

5.1 Error bound

Theorem 5.1.1

(Agarwal et al. 2021) Suppose that $z(\eta ) \in C^{m+1}[0,1]$ and $z_m(\eta )$ be the approximate solution of $z(\eta )$ defined in Eq. (4.6), then

$$\begin{aligned} ||z(\eta )-z_m(\eta )|| \le \dfrac{{\hat{E}}\lambda ^{m+1}}{2(m+1)!}\sqrt{\frac{\pi }{2}}, \end{aligned}$$

(5.1)

where

$$\begin{aligned} {\hat{E}}= \max \limits _{ \eta \in [0,1]} z^{m+1}(\eta ) \quad \hbox {and} \quad \lambda = \max \{\eta _0, 1- \eta _0\}. \end{aligned}$$

Theorem 5.1.2

Let $k(\eta ,\zeta )$ be the sufficiently smooth function in $\Omega$ such that $k(\eta ,\zeta ) \in L^{2}(\Omega )\cap C^{\infty }(\Omega )$, where $\Omega$ = $([0,L] \times [0,T])$. Suppose that $k_{m,n}(\eta ,\zeta )$ is the best approximation to $k(\eta ,\zeta )$ out of the linear span $\Pi _{m,n }(\Omega )$. Now assume

$$\begin{aligned}&\sup _{(\eta , \zeta ) \in \Omega }\left| \frac{\partial ^{m+1}k(\eta ,\zeta )}{\partial \eta ^{m+1}}\right| \le b_1,\nonumber \\ {}&\sup _{(\eta , \zeta ) \in \Omega }\left| \frac{\partial ^{n+1}k(\eta ,\zeta )}{\partial \zeta ^{n+1}}\right| \le b_2,\nonumber \\ {}&\sup _{(\eta , \zeta ) \in \Omega }\left| \frac{\partial ^{m+n+2}k(\eta ,\zeta )}{{\partial \eta ^{m+1}}{\partial \zeta ^{n+1}}}\right| \le b_3, \end{aligned}$$

then there exists ${\mathcal {R}} > 0$ such that

$$\begin{aligned} ||k(\eta ,\zeta ) -k_{m,n}(\eta ,\zeta ) ||_{2} \le {\mathcal {R}} \left[ \frac{1}{2^m(m+1)!} + \frac{1}{2^n(n+1)!} + \frac{1}{2^{m+n}(m+1)!(n+1)!}\right] \sqrt{{\mathcal {C}}},\nonumber \\ \end{aligned}$$

(5.2)

where ${\mathcal {R}} = \max \{b_1,b_2, b_3\}$ and ${\mathcal {C}}= \int _0^L \int _0^T w(\eta )w(\zeta )d\eta d\zeta$.

According the concept of interpolation, which is similar as Saha Ray and Singh (2021), we obtain the following desired results.

Theorem 5.1.2

Let $z_{m}(\eta ) = \Delta ^T V_F^*(\eta )$ be the approximate solution and $z(\eta )$ be the exact solution of Eq. (1.1). Furthermore, suppose that if

• 1. $|z(\eta )| \le {\mathcal {M}}, \forall \eta \in [0,1]$,

• 2. $|\kappa _i (\eta ,\zeta )| \le {\mathcal {K}}_i, i=1,2, \forall (\eta ,\zeta ) \in [0,1] \times [0,1]$,

• 3. $\frac{4}{\Gamma ( \alpha ))^2}[\lambda ^2_1(2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m))+\lambda ^2_2(2{\mathcal {K}}_2^2+4 {\mathcal {S}}_2^2(m))] < 1$.

Then,

$$\begin{aligned} ||e(\eta )|| \le \sqrt{\dfrac{\frac{4}{(\Gamma ( \alpha ))^2}{\mathcal {P}}^2(m)+8{\mathcal {M}}^2\frac{(\lambda ^2_1{\mathcal {S}}_1^2(m)+\lambda ^2_2{\mathcal {S}}_2^2(m))}{\Gamma ( \alpha ))^2}}{1-\frac{4}{\Gamma ( \alpha ))^2}[\lambda ^2_1(2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m))+\lambda ^2_2(2{\mathcal {K}}_2^2+4 {\mathcal {S}}_2^2(m))]}}, \end{aligned}$$

and by the Theorems 5.1.1 and  5.1.2

$$\begin{aligned}{} & {} ||g(\eta )-g_m(\eta )|| \le {\mathcal {P}}(m), \end{aligned}$$

(5.3)

$$\begin{aligned}{} & {} ||\kappa _i(\eta ,\zeta ) - P_{(m,m)}[\kappa _i](\eta ,\zeta )|| \le {\mathcal {S}}_i(m), i=1,2. \end{aligned}$$

(5.4)

where, $g_m(\eta )$ and $P_{(m,m)}[\kappa _i](\eta ,\zeta )$ are the approximate polynomials using SVFPs and

$$\begin{aligned} {\mathcal {P}}(m)=\dfrac{{\hat{E}}\lambda ^{m+1}}{2(m+1)!}\sqrt{\frac{\pi }{2}}\quad \text {and} \quad {\mathcal {S}}_i(m)= {\mathcal {R}} \left[ \frac{1}{2^{m-1}(m+1)!} + \frac{1}{2^{2m}(m+1)!^2}\right] \sqrt{{\mathcal {C}}}. \end{aligned}$$

Proof

Let $z_m(\eta )$ be the approximate solution of Eq. (1.1).

$$\begin{aligned}{} & {} ^cD^{\alpha }_{\eta }z_m(\eta ) = g_m(\eta ) + \lambda _1 \int _0^\eta P_{(m,m)}[\kappa _1](\eta ,\zeta ) z_m(\zeta )d\zeta \nonumber \\{} & {} \quad + \lambda _2 \int _0^\eta P_{(m,m)}[\kappa _2](\eta ,\zeta ) z_m(\zeta )dB(\zeta ), \quad \eta \in [0,1], \end{aligned}$$

(5.5)

Let $|z(\eta )-z_m(\eta )|$ be an error function, then by Eq. (1.1) and (5.5),

$$\begin{aligned} ^CD^{\alpha }_{\eta }(z(\eta )-z_m(\eta ))&= g(\eta )-g_m(\eta )+ \lambda _1 \int _0^\eta (\kappa _1 (\eta , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _1](\eta ,\zeta ) z_m(\zeta ))d\zeta \nonumber \\&+ \lambda _2 \int _0^\eta (\kappa _2 (\eta , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _2](\eta ,\zeta ) z_m(\zeta ))dB(\zeta ). \end{aligned}$$

(5.6)

Now, applying the RL operator $(J^{\alpha }_{\eta })$ on both sides of the Eq. (5.6),

$$\begin{aligned} J^{\alpha }_{\eta }({^C}D^{\alpha }_{\eta })(z(\eta )- z_m(\eta ))&= J^{\alpha }_{\eta } (g(\eta )-g_m(\eta ))\nonumber \\&\quad + J^{\alpha }_{\eta }\left( \lambda _1 \int _0^\eta (\kappa _1 (\eta , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _1](\eta ,\zeta ) z_m(\zeta ))d\zeta \right) \nonumber \\&\quad + J^{\alpha }_{\eta } \left( \lambda _2 \int _0^\eta (\kappa _2 (\eta , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _2](\eta ,\zeta ) z_m(\zeta ))dB\zeta \right) , \end{aligned}$$

(5.7)

where $J^{\alpha }_{\eta }$ is defined in Eq. (2.5).

By using the properties of $J^{\alpha }_{\eta }$ which are given in Sect. 2.2, Eq. (5.7) can be written as

$$\begin{aligned} z(\eta )-z_m(\eta )&= \dfrac{1}{\Gamma ( \alpha )}\int _0^{\eta } (\eta -\zeta )^{\alpha -1} (g(\zeta )-g_m(\zeta )) d\zeta \nonumber \\ {}&\quad +\dfrac{\lambda _1}{\Gamma ( \alpha )}\int _0^{\eta } (\eta -\zeta )^{\alpha -1} \left( \int _0^\gamma (\kappa _1 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _1](\eta ,\zeta ) z_m(\zeta ))d\zeta \right) d\gamma \nonumber \\ {}&\quad +\dfrac{\lambda _2}{\Gamma ( \alpha )}\int _0^{\eta } (\eta -\zeta )^{\alpha -1} \left( \int _0^\gamma (\kappa _2 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _2](\eta ,\zeta ) z_m(\zeta ))dB(\zeta ) \right) d\gamma . \end{aligned}$$

(5.8)

Using inequality $(c_1+c_2+c_3)^2\le 4(c_1^2+c_2^2+c_3^2)$, we obtain

$$\begin{aligned} ||e(\eta )||^2&=||z(\eta )-z_m(\eta )||^2 \nonumber \\ {}&\le 4\left| \left| \dfrac{1}{\Gamma ( \alpha )}\int _0^{\eta } (\eta -\zeta )^{\alpha -1} (g(\zeta )-g_m(\zeta )) d\zeta \right| \right| ^2 \nonumber \\ {}&\quad +4\left| \left| \dfrac{\lambda _1}{\Gamma ( \alpha )}\int _0^{\eta } (\eta -\gamma )^{\alpha -1} \left( \int _0^\gamma (\kappa _1 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _1](\eta ,\zeta ) z_m(\zeta ))d\zeta \right) d\gamma \right| \right| ^2 \nonumber \\ {}&\quad +4\left| \left| \dfrac{\lambda _2}{\Gamma ( \alpha )}\int _0^{\eta } (\eta -\gamma )^{\alpha -1} \left( \int _0^\gamma (\kappa _2 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _2](\eta ,\zeta ) z_m(\zeta ))dB(\zeta ) \right) d\gamma \right| \right| ^2. \end{aligned}$$

(5.9)

Let Eq. (5.9) be written as

$$\begin{aligned} ||e(\eta )||^2 \le {\mathcal {T}}_2+{\mathcal {T}}_3+{\mathcal {T}}_4. \end{aligned}$$

(5.10)

Now,

$$\begin{aligned} {\mathcal {T}}_2= & {} 4\left| \left| \dfrac{1}{\Gamma ( \alpha )}\int _0^{\eta } (\eta -\zeta )^{\alpha -1} (g(\zeta )-g_m(\zeta )) d\zeta \right| \right| ^2 \nonumber \\= & {} 4E\left[ \left| \dfrac{1}{\Gamma ( \alpha )}\int _0^{\eta } (\eta -\zeta )^{\alpha -1} (g(\zeta )-g_m(\zeta )) d\zeta \right| ^2 \right] . \end{aligned}$$

(5.11)

Since, $0<\zeta <1$ and $0< \alpha<1, 0<\zeta< \eta <1$. It implies $0< \eta - \zeta< 1- \zeta <1$. Now, using the Cauchy–Schwarz inequality in Eq. (5.11), the following is obtained:

$$\begin{aligned} {\mathcal {T}}_2&\le \dfrac{4\eta }{(\Gamma ( \alpha ))^2}E\left[ \int _0^{\eta } |g(\zeta )-g_m(\zeta )|^2 d\zeta \right] \nonumber \\ {}&= \dfrac{4\eta }{(\Gamma ( \alpha ))^2}\left| \left| g(\zeta )-g_m(\zeta )\right| \right| ^2 \nonumber \\&\le \dfrac{4\eta }{(\Gamma ( \alpha ))^2}{\mathcal {P}}^2(m). \end{aligned}$$

(5.12)

Again,

$$\begin{aligned} {\mathcal {T}}_3&=4\left| \left| \dfrac{\lambda _1}{\Gamma ( \alpha )}\int _0^{\eta } (\eta -\gamma )^{\alpha -1} \left( \int _0^\gamma (\kappa _1 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _1](\eta ,\zeta ) z_m(\zeta ))d\zeta \right) d\gamma \right| \right| ^2\nonumber \\ {}&=4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| E\left[ \left| \int _0^{\eta } (\eta -\gamma )^{\alpha -1} \left( \int _0^\gamma (\kappa _1 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _1](\eta ,\zeta ) z_m(\zeta ))d\zeta \right) d\gamma \right| ^2 \right] . \end{aligned}$$

(5.13)

Since, $\left| \eta -\gamma \right| \le 1$, then by using the Cauchy–Schwarz inequality

$$\begin{aligned} {\mathcal {T}}_3&\le 4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| E\left[ \eta \int _0^{\eta } \left( \int _0^\gamma (\kappa _1 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _1](\eta ,\zeta ) z_m(\zeta ))d\zeta \right) ^2 d\gamma \right] \nonumber \\ {}&\le 4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| E\left[ \eta \int _0^{\eta }\left( \gamma \int _0^\gamma \left( \kappa _1 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _1](\eta ,\zeta ) z_m(\zeta ))\right) ^2 d\zeta \right) d\gamma \right] \nonumber \\ {}&= 4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| E[ \eta \int _0^{\eta }( \gamma \int _0^\gamma |\kappa _1 (\gamma , \zeta )(z(\zeta )-z_m(\zeta ))\nonumber \\&\quad +(\kappa _1 (\gamma , \zeta )-P_{(m,m)}[\kappa _1](\eta ,\zeta )) \times (z_m(\zeta ))-z(\zeta )+z(\zeta )) |^2 d\zeta )d\gamma ]\nonumber \\ {}&\le 4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| E[ \eta \int _0^{\eta }( \gamma \int _0^\gamma (2|\kappa _1 (\gamma , \zeta )(z(\zeta )-z_m(\zeta ))|^2\nonumber \\ {}&\quad +2|(\kappa _1 (\gamma , \zeta )-P_{(m,m)}[\kappa _1](\eta ,\zeta ))(z_m(\zeta ))-z(\zeta )+z(\zeta )) |^2 )d\zeta )d\gamma ]\nonumber \\ {}&\le 4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| E\left[ \eta ^2 \int _0^{\eta }\left( \int _0^\gamma (2{\mathcal {K}}_1^2|e(\zeta )|^2+ 4{\mathcal {S}}_1^2(m)|e(\zeta )|^2+4 {\mathcal {M}}^2{\mathcal {S}}_1^2(m))d\zeta \right) d\gamma \right] \nonumber \\ {}&=4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| E\left[ \eta ^2 (2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m))\int _0^{\eta }\int _0^\gamma |e(\zeta )|^2 d\zeta d\gamma + 4\eta ^2 {\mathcal {M}}^2{\mathcal {S}}_1^2(m))\int _0^{\eta }\int _0^\gamma d\zeta d\gamma \right] . \end{aligned}$$

(5.14)

By changing the order of integration, the following is obtained:

$$\begin{aligned} {\mathcal {T}}_3&\le 4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| E\left[ \eta ^2 (2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m))\int _0^{\eta } |e(\zeta )|^2\left( \int _\zeta ^\eta d\gamma \right) d\zeta + 4\eta ^2 {\mathcal {M}}^2{\mathcal {S}}_1^2(m)\int _0^{\eta }\int _0^\gamma d\zeta d\gamma \right] \nonumber \\&\le 4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| E\left[ \eta ^2 (2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m))\int _0^{\eta } |e(\zeta )|^2 d\zeta + 2\eta ^4 {\mathcal {M}}^2{\mathcal {S}}_1^2(m) \right] \nonumber \\ {}&=4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| \left[ \eta ^2 (2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m)) ||e(\zeta )||^2 + 2\eta ^4 {\mathcal {M}}^2{\mathcal {S}}_1^2(m) \right] \nonumber \\ {}&= 4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| \eta ^2 (2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m)) ||e(\zeta )||^2 + 8\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| \eta ^4 {\mathcal {M}}^2{\mathcal {S}}_1^2(m) . \end{aligned}$$

(5.15)

Now,

$$\begin{aligned} {\mathcal {T}}_4&=4\left| \left| \dfrac{\lambda _2}{\Gamma ( \alpha )}\int _0^{\eta } (\eta -\gamma )^{\alpha -1} \left( \int _0^\gamma (\kappa _2 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _2](\eta ,\zeta ) z_m(\zeta ))dB\zeta \right) d\gamma \right| \right| ^2\nonumber \\ {}&= 4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| E\left[ \left| \int _0^{\eta } (\eta -\gamma )^{\alpha -1} \left( \int _0^\gamma (\kappa _2 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _2](\eta ,\zeta ) z_m(\zeta ))dB(\zeta ) \right) d\gamma \right| ^2 \right] . \end{aligned}$$

(5.16)

Since, $\left| \eta -\gamma \right| \le 1$, then by using the Cauchy–Schwarz inequality

$$\begin{aligned} {\mathcal {T}}_4&\le 4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| E\left[ \left| \eta \int _0^{\eta } \left( \int _0^\gamma (\kappa _2 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _2](\eta ,\zeta ) z_m(\zeta ))dB(\zeta ) \right) ^2 d\gamma \right| \right] \nonumber \\ {}&=4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| \eta \int _0^{\eta } E \left[ \left( \int _0^\gamma (\kappa _2 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _2](\eta ,\zeta ) z_m(\zeta ))dB(\zeta ) \right) ^2 \right] d\gamma . \end{aligned}$$

(5.17)

Now, by using the Itô isometry property, following is obtained:

$$\begin{aligned} {\mathcal {T}}_4&\le 4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| \eta \int _0^{\eta } E \left[ \int _0^\gamma (\kappa _2 (\gamma , \zeta ) z(\zeta )-P_{(m,m)}[\kappa _2](\eta ,\zeta ) z_m(\zeta ))^2 d\zeta \right] d\gamma&\nonumber \\ {}&\le 4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| \eta \int _0^{\eta } E [\int _0^\gamma (2|\kappa _2 (\gamma , \zeta )(z(\zeta )-z_m(\zeta ))|^2 \nonumber \\ {}&\quad +2|(\kappa _2 (\gamma , \zeta )-P_{(m,m)}[\kappa _2](\eta ,\zeta ))(z_m(\zeta ))-z(\zeta )+z(\zeta )) |^2 ) d\zeta ] d\gamma \nonumber \\ {}&\le 4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| \eta \int _0^{\eta } E\left[ \int _0^{\gamma } (2{\mathcal {K}}_2^2|e(\zeta )|^2+ 4{\mathcal {S}}_2^2(m)|e(\zeta )|^2+4 {\mathcal {M}}^2{\mathcal {S}}_2^2(m))d\zeta \right] d\gamma \nonumber \\ {}&=4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| \eta \left[ \left( 2{\mathcal {K}}_2^2+ 4{\mathcal {S}}_2^2(m)\right) E \left[ \int _0^\eta \int _0^\gamma |e(\zeta )|^2 d\zeta d\gamma \right] + 4 {\mathcal {M}}^2{\mathcal {S}}_2^2(m))\dfrac{\eta ^2}{2} \right] . \end{aligned}$$

(5.18)

By changing the order of integration

$$\begin{aligned} {\mathcal {T}}_4 \le 4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| \eta (2{\mathcal {K}}_2^2+4{\mathcal {S}}_2^2(m)) ||e(\zeta )||^2 + 8\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| \eta ^3 {\mathcal {M}}^2{\mathcal {S}}_2^2(m). \end{aligned}$$

(5.19)

Now, by substituting Eqs. (5.12), (5.15), (5.19) into Eq. (5.10)

$$\begin{aligned} ||e(\eta )||^2&\le \dfrac{4}{(\Gamma ( \alpha ))^2}{\mathcal {P}}^2(m)\nonumber \\ {}&\quad +4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| (2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m)) ||e(\zeta )||^2 + 8\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| {\mathcal {M}}^2{\mathcal {S}}_1^2(m)\nonumber \\ {}&\quad + 4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| (2{\mathcal {K}}_2^2+4 {\mathcal {S}}_2^2(m)) ||e(\zeta )||^2 + 8\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| {\mathcal {M}}^2{\mathcal {S}}_2^2(m). \end{aligned}$$

(5.20)

Then,

$$\begin{aligned} ||e(\eta )|| \le \sqrt{\dfrac{\frac{4}{(\Gamma ( \alpha ))^2}{\mathcal {P}}^2(m)+8{\mathcal {M}}^2\frac{(\lambda ^2_1{\mathcal {S}}_1^2(m)+\lambda ^2_2{\mathcal {S}}_2^2(m))}{\Gamma ( \alpha ))^2}}{1-\frac{4}{\Gamma ( \alpha ))^2}[\lambda ^2_1(2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m))+\lambda ^2_2(2{\mathcal {K}}_2^2+4 {\mathcal {S}}_2^2(m))]}}. \end{aligned}$$

(5.21)

$\square$

5.2 Convergence analysis

Theorem 5.2.1

Let $z(\eta )$ and $z_m(\eta )$ be the exact and approximate solutions of Eq. (1.1) respectively. And

• 1. $|z(\eta )| \le {\mathcal {M}}, \forall \eta \in [0,1]$,

• 2. $|\kappa _i (\eta ,\zeta )| \le {\mathcal {K}}_i, i=1,2, \forall (\eta ,\zeta ) \in [0,1] \times [0,1]$,

• 3. $\frac{4}{\Gamma ( \alpha ))^2}[\lambda ^2_1(2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m))+\lambda ^2_2(2{\mathcal {K}}_2^2+4 {\mathcal {S}}_2^2(m))] < 1$.

Then $z_m(\eta ) \rightarrow z(\eta )$ as $m \rightarrow \infty$ in $L^2$.

Proof

Consider the SFIDE as follows:

$$\begin{aligned} ^CD^{\alpha } z(\eta )= g(\eta ) + \lambda _1 \int _0^\eta \kappa _{1} (\eta , \zeta ) z(\zeta )d\zeta + \lambda _2 \int _0^\eta \kappa _{2} (\eta , \zeta ) z(\zeta )dB(\zeta ), \quad \eta \in [0,1].\nonumber \\ \end{aligned}$$

(5.22)

Using the same explanation as that used to prove the previous theorem, we can get to the following:

By using Eqs. (5.12), (5.15) and(5.18)

$$\begin{aligned} ||e(\eta )||^2&\le \dfrac{4\eta }{(\Gamma ( \alpha ))^2}{\mathcal {P}}^2(m)\nonumber \\ {}&\quad +4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| E\left[ \eta ^2 (2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m))\int _0^{\eta } |e(\zeta )|^2 d\zeta + 2\eta ^4 {\mathcal {M}}^2{\mathcal {S}}_1^2(m) \right] \nonumber \\ {}&\quad + 4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| \eta \left[ \left( 2{\mathcal {K}}_2^2+ 4{\mathcal {S}}_2^2(m)\right) E \left[ \int _0^\eta \int _0^\gamma |e(\zeta )|^2 d\zeta d\gamma \right] + 4 {\mathcal {M}}^2{\mathcal {S}}_2^2(m))\dfrac{\eta ^2}{2} \right] . \end{aligned}$$

(5.23)

Since $\eta \le 1$, then

$$\begin{aligned} ||e(\eta )||^2&\le \dfrac{4}{(\Gamma ( \alpha ))^2}{\mathcal {P}}^2(m)\nonumber \\ {}&\quad +4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| (2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m)) \int _0^\eta ||e(\zeta )||^2 d\zeta + 8\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| {\mathcal {M}}^2{\mathcal {S}}_1^2(m)\nonumber \\ {}&\quad + 4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| (2{\mathcal {K}}_2^2+4 {\mathcal {S}}_2^2(m)) \int _0^\eta ||e(\zeta )||^2 d\zeta + 8\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| {\mathcal {M}}^2{\mathcal {S}}_2^2(m). \end{aligned}$$

(5.24)

Now,

$$\begin{aligned} ||e(\eta )||^2&\le \dfrac{4}{(\Gamma ( \alpha ))^2}{\mathcal {P}}^2(m)+ 8 {\mathcal {M}}^2\left( \left| \dfrac{\lambda ^2_1{\mathcal {S}}_1^2(m)}{(\Gamma ( \alpha ))^2}\right| +\left| \dfrac{\lambda ^2_2 {\mathcal {S}}_2^2(m)}{(\Gamma ( \alpha ))^2}\right| \right) \nonumber \\ {}&\quad + \left( 4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| (2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m))+4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| (2{\mathcal {K}}_2^2+4 {\mathcal {S}}_2^2(m))\right) \int _0^\eta ||e(\zeta )||^2 d\zeta . \end{aligned}$$

(5.25)

Let,

$$\begin{aligned} \delta ( m)&=\dfrac{4}{(\Gamma ( \alpha ))^2}{\mathcal {P}}^2(m)+ 8 {\mathcal {M}}^2\left( \left| \dfrac{\lambda ^2_1{\mathcal {S}}_1^2(m)}{(\Gamma ( \alpha ))^2}\right| +\left| \dfrac{\lambda ^2_2 {\mathcal {S}}_2^2(m)}{(\Gamma ( \alpha ))^2}\right| \right) , \\ L_1&=\left( 4\left| \dfrac{\lambda ^2_1}{(\Gamma ( \alpha ))^2}\right| (2{\mathcal {K}}_1^2+4 {\mathcal {S}}_1^2(m))+4\left| \dfrac{\lambda ^2_2}{(\Gamma ( \alpha ))^2}\right| (2{\mathcal {K}}_2^2+4 {\mathcal {S}}_2^2(m))\right) . \end{aligned}$$

Therefore,

$$\begin{aligned} ||e(\eta )||_{2}^2 \le \delta ( m) + L_1\int _0^\zeta || e(\zeta ))||^2 d\zeta . \end{aligned}$$

(5.26)

Applying Grönwall inequality, we obtain

$$\begin{aligned} ||e(\eta )||_{2}^2 \le \delta (m)(1 + L_1\int _0^\zeta e^{L_1(\eta -\zeta )} d\zeta ). \end{aligned}$$

(5.27)

It implies

$$\begin{aligned} ||e(\eta )||_{2}^2 \rightarrow 0 \hbox {as} m \rightarrow \infty \hbox {in} L^2. \end{aligned}$$

So, $z_m(\eta )$ converges to $z(\eta )$ as $m \rightarrow \infty$ in $L^2$. $\square$

6 Applications of the proposed method

Three examples are solved in this section using the proposed numerical approach that was described in the previous section.

Example 1

Consider the following fractional order stochastic integro-differential equation:

$$\begin{aligned} ^CD^{\alpha }_{\eta } z(\eta ){} & {} = \dfrac{-\eta ^5 e^{\eta }}{5}+\dfrac{6\eta ^{2.25}}{\Gamma (3.25)} + \int _0^{\eta } e^{\eta } \zeta z(\zeta ) d\zeta \nonumber \\{} & {} + \lambda _2 \int _0^{\eta } e^{\eta } \zeta z(\zeta ) dB\zeta , \quad \zeta , \eta \in [0,1], \end{aligned}$$

(6.1)

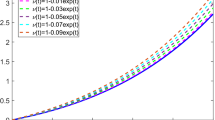
with the initial condition $z(0)=0$. The exact solution of Eq. (6.1) is not available. If $\alpha = 0.75$ and $\lambda _2 =0$, the exact solution is $z(\eta )=\eta ^3$ and the approximate solution is obtained by the proposed SVFPs method. Table 1 represents the absolute error comparison between two methods based on the orthonormal Chelyshkov polynomials (OCPs) and SVFPs. For the numerical solution of Eq. (6.1) for various values of $\alpha$ with $m = 4$ and $m = 6$, the proposed operational matrix collocation approach is employed. Newton cotes nodes have been selected from the collocation points. Tables 2 and 3 provide the comparison between numerical solutions obtained by the operational matrix method based on OCPs and SVFPs for the above problem for different values of m. The plot of SVFPs solutions for different values of $\alpha$ with $m=4$ and $m=6$ are shown in Figs. 1 and 2, respectively.

Table 1 Absolute errors for $\lambda =0$ and $\alpha =0.75$ with $m=5$ (Example 1)

Table 2 Comparison of approximate solutions by using the OCOM and SVFOM methods for $m=4$ in Example 1

Table 3 Comparison of approximate solutions by using the OCOM and SVFOM methods for $m=6$ in Example 1

Example 2

Consider the following fractional order stochastic integro-differential equation:

$$\begin{aligned} ^CD^{\alpha }_{\eta } z(\eta ){} & {} = \dfrac{7}{12}\eta ^4-\dfrac{5}{6}\eta ^3+\dfrac{2\eta ^{2-\alpha }}{\Gamma (3-\alpha )} + \dfrac{\eta ^{1-\alpha }}{\Gamma (2-\alpha )}+\int _0^{\eta } (\eta +\zeta ) z(\zeta ) d\zeta \nonumber \\{} & {} \quad + \lambda \int _0^{\eta } \zeta z(\zeta ) dB\zeta , \quad \zeta , \eta \in [0,1], \end{aligned}$$

(6.2)

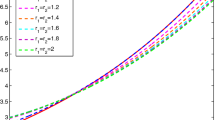
with the initial condition $z(0)=0$. The exact solution of Eq. (6.2) is not known. For the numerical solution of Eq. (6.2) for different values of $\alpha$, the proposed operational matrix collocation method is utilised. Newton cotes nodes have been selected from the collocation points. Tables 4 and 5 provide the numerical solutions comparison obtained by the operational matrix method based on OCPs and SVFPs for the above problem for different values of m. The plot of SVFPs solutions, for different values of $\alpha$ with $m=4$ and $m=6$ are shown in Figs. 3 and 4, respectively.

Example 3

Consider the following fractional order stochastic integro-differential equation:

$$\begin{aligned} ^CD^{\alpha }_{\eta } z(\eta ) = -\dfrac{\eta ^3 }{3}+\dfrac{\Gamma (2) \eta ^{1-\alpha }}{\Gamma (2-\alpha )} + \int _0^{\eta } \zeta z(\zeta ) d\zeta + \lambda \int _0^{\eta } z(\zeta ) dB\zeta , \quad \zeta , \eta \in [0,1], \end{aligned}$$

(6.3)

with the initial condition $z(0)=0$. The exact solution of Eq. (6.3) is unknown. The proposed operational matrix collocation technique is used to solve Eq. (6.3) numerically for different values of $\alpha$ with $m = 4$ and $m = 6$. From the collocation points, Newton cotes nodes have been chosen. With respect to the above-mentioned problem, Tables 6 and 7 compare the numerical solutions derived using the operational matrix technique based on OCPs and SVFPs for different values of m. The plot of SVFPs solutions for different values of $\alpha$ with $m=4$ and $m=6$ are shown in Figs. 5 and 6, respectively.

Fig. 1

The approximate solution graph by the SVFOM method for $m=4$ (Example 1)

Fig. 2

The approximate solution graph by the SVFOM method for $m=6$ (Example 1)

Table 4 Comparison of approximate solutions by using the OCOM and SVFOM methods for $m=4$ in Example 2

Table 5 Comparison of approximate solutions by using the OCOM and SVFOM methods for $m=6$ in Example 2

Fig. 3

The approximate solution graph by the SVFOM method for $m=4$ (Example 2)

Fig. 4

The approximate solution graph by the SVFOM method for $m=6$ (Example 2)

7 Conclusion

The main objective of this work is to apply the operational matrix method to solve SFIDE. In this study, a novel stochastic operational matrix has been generated for the first time using shifted Vieta–Fibonacci polynomials. The SFIDE has been transformed into a system of algebraic equations. With the use of these operational matrices, the resultant algebraic system of equations is numerically solved by applying the collocation technique. The error bound and the convergence analysis of the proposed numerical technique have also been described. The precision and effectiveness of the suggested numerical technique are demonstrated using three different examples. The numerical experiments reveal that the proposed numerical scheme based on SVFPs and OCPs based numerical method have the best agreement of results. As a consequence, it is clear from the numerical experiment results that the proposed numerical approach is extremely effective, accurate, and reliable. In future, we have a plan to work on fractional stochastic integro-differential equations with the ABC fractional derivative.

Table 6 Comparison of approximate solutions by using the OCOM and SVFOM methods for $m=4$ in Example 3

Table 7 Comparison of approximate solutions by using the OCOM and SVFOM methods for $m=6$ in Example 3

Fig. 5

The approximate solution graph by the SVFOM method for $m=4$ (Example 3)

Fig. 6

The approximate solution graph by the SVFOM method for $m=6$ (Example 3)