Abstract
This paper proposes an algorithm based on defined scaled tri-factorization (STF) for fast and accurate tensor ring (TR) decomposition. First, based on the fast tri-factorization approach, we define STF and design a corresponding algorithm that can more accurately represent various matrices while maintaining a similar level of computational time. Second, we apply sequential STFs to TR decomposition with theoretical proof and propose a stable (i.e., non-iterative) algorithm named TR-STF. It is a computationally more efficient algorithm than existing TR decomposition algorithms, which is beneficial when dealing with big data. Experiments on multiple randomly simulated data, highly oscillatory functions, and real-world data sets verify the effectiveness and high efficiency of the proposed TR-STF. For example, on the Pavia University data set, TR-STF is nearly 9240 and 39 times faster, respectively, and more accurate than algorithms based on alternating least squares and singular value decomposition. As an extension, we apply sequential STFs to tensor train (TT) decomposition and propose a non-iterative algorithm named TT-STF. Experimental results demonstrate the superiority of the proposed TT-STF compared with the state-of-the-art TT decomposition algorithm.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For an dth-order tensor \(\mathcal {X}\in \mathbb {R}^{n_{1}\times n_{2}\times \cdots \times n_{d}}\), where \(n_{1}=n_{2}=\cdots =n_{d}=n\), the storage cost (as well as the free parameters) of \(\mathcal {X}\) grows exponentially as d increases. This exponential growth is commonly referred to as the curse of dimensionality, which makes it impractical to explicitly store all the entries of the tensor except for the minimal value of d. Even for \(n=4\), storing a tensor of order \(d=25\) would require 9 petabytes. Therefore, it is crucial to approximate higher-order tensors with compression schemes that do not destroy the inherent characteristics of tensors as much as possible, for example, low-rank tensor decomposition (Sultonov et al. 2023; Wang and Yang 2022; Cichocki et al. 2016; Xue et al. 2021b; Wang et al. 2022). Tensor decomposition, which represents a high-order tensor (i.e., \(\ge 3\text {rd}\)-order tensor), as factor tensors and matrices, has been developed and applied in many fields, such as computer vision (Fu et al. 2019; Deng et al. 2019; Xiao et al. 2022; Tai et al. 2021; Xue et al. 2021a, 2022; Wang et al. 2023; Xu et al. 2022; Sun et al. 2023) and machine learning (Deng et al. 2021, 2022, 2023; Cao et al. 2020; Ran et al. 2023). The most well-known tensor decompositions include Canonical Polyadic (CP) decomposition (Bro 1997; De Lathauwer 2006; Jiang et al. 2022; Bozorgmanesh and Hajarian 2022; Xue et al. 2019) and Tucker decomposition (Tucker 1996; De Lathauwer et al. 2000; Luan et al. 2023; Che et al. 2021; Che and Wei 2020; Xue et al. 2020). Specifically, CP decomposition represents a tensor with a set of rank-1 tensors, where the smallest number of the rank-1 tensors denotes CP rank. Consequently, the storage cost of CP decomposition grows linearly with the tensor order. Assuming that the CP rank of the dth-order tensor with each dimension of n is m, then the storage cost of CP decomposition is nmd. However, there are no additional structural assumptions (De et al. 2016; Xu 2016; Qi et al. 2015; Brachat et al. 2010), (1) the estimation of the CP rank is an NP-hard problem (Hillar and Lim 2013), (2) the estimation of the rank-1 tensors is an ill-posed problem (DE Silva and Lim 2008), and (3) it is difficult to characterize different correlations among different modes flexibly (Zhao et al. 2016). These lead to (1) there is no guarantee of the existence of a low-rank approximation of a tensor through its rank-m CP decomposition, (2) a stable and efficient algorithm to estimate the rank-1 tensors may not exist, or it has poor performance when dealing with big data tensors, and (3) it performs poorly in the structure preservation of tensors. Tucker decomposition expresses a tensor by one core tensor and the factor matrices in all modes; Tucker rank is based on the Tucker decomposition, where the tensor is unfolded along each mode, which inevitably destroys the inherent structure of the tensor. In addition, the need for storing the \(m_{1}\times m_{2}\cdots \times m_{d}\) core tensor renders the Tucker decomposition increasingly unappealing as the tensor order d gets large. In particular, the storage cost of Tucker decomposition grows exponentially with its dimensions. Assume that the Tucker rank of \(\mathcal {X}\) is \([m, m, \ldots , m]^{T}\), then the storage cost of Tucker decomposition is \(dnm+m^{d}\).
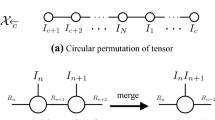
Recently, tensor network, as an extension of tensor decomposition, has emerged as a means of decomposing a high-order tensor into sparsely interconnected small-scale cores and exhibited superior properties in compressing (Orus 2014; Huckle et al. 2013; Hashemizadeh et al. 2020; Ding et al. 2019; Zniyed et al. 2020). Particularly, some TN models are introduced to practical applications due to their excellent high-order data representation capabilities. Tensor train (TT) decomposition (Oseledets 2011; Holtz et al. 2012; Oseledets and Tyrtyshnikov 2010; Dektor et al. 2021) and tensor ring (TR) decomposition (Zhao et al. 2016) are two such networks. Specifically, as shown in Fig. 1a, TT decomposition tries to represent an dth-order tensor \(\mathcal {Z}\in \mathbb {R}^{n_{1}\times n_{2}\cdots \times n_{d}}\) by a sequence of cores \(\mathcal {G}_{i}\in \mathbb {R}^{m_{i}\times n_{i}\times m_{i+1}}\), \(i=1, 2, \ldots , d\), where \(\textbf{G}_{1}\in \mathbb {R}^{n_{1}\times {m_{2}}}\) and \(\textbf{G}_{d}\in \mathbb {R}^{{m_{d}}\times n_{d}}\) are matrices (i.e., \(m_{1}=m_{d+1}=1\)) and the remaining cores are 3rd-order tensors. Vector \([m_{2}, m_{3}, \ldots , m_{d}]^{T}\) is called the TT rank. TT decomposition plays an important role in complex tensor networks and has been successfully applied in many applications, e.g., hyperspectral image super-resolution and tensor completion (Dian et al. 2019; Ding et al. 2021). However, TT decomposition has some inevitable limitations. For example, the boundary condition, i.e., \(m_{1}=m_{d+1}=1\), will limit its representation capacity and flexibility. To overcome these drawbacks, Zhao et al. (2016) propose TR decomposition, which represents \(\mathcal {Z}\) by a sequence of cores \(\mathcal {G}_{k}\in \mathbb {R}^{m_{k}\times n_{k}\times m_{k+1}}\), \(k=1, 2, \ldots , d\), where the size of the last and first cores satisfies \(m_{1}=m_{d+1}\), and vector \(\textbf{m}=[m_{1},m_{2},\ldots ,m_{d}]^{T}\) is denoted as TR rank (see Fig. 1b). Compared with TT decomposition, TR decomposition keeps the invariance when the tensor dimension makes a circular shift. Thus, TR decomposition can better represent tensors flexibly with the same parameters as in TT decomposition. Given an dth-order tensor \(\mathcal {Z}\in \mathbb {R}^{n\times n\times \cdots \times n}\), the TR rank and TT rank are \([m_{1}, m_{2} \ldots , m_{d}]^{T}\) and \([m_{2}, m_{3} \ldots , m_{d}]^{T}\), respectively, where \(m_{1}=m_{2}=\cdots =m_{d}=m\). Then, the storage cost of TR decomposition and TT decomposition is \(dnm^{2}\), which means that the storage cost of TR decomposition grows linearly with the tensor order d. Therefore, the TR decomposition helps to break the curse of dimensionality (Oseledets and Tyrtyshnikov 2009). In fact, TR decomposition degrades to TT decomposition when \(m_{1}=m_{d+1}=1\). Based on its strong representation capacity, TR decomposition has been widely used in many applications and has produced competitive outputs, e.g., hyperspectral image denoising, hyperspectral image compressive sensing, and remote sensing image reconstruction (Chen et al. 2020; He et al. 2019, 2022).
Given the size of input data, a stable and efficient algorithm for TR decomposition is critical in this era of big data. The current approaches mainly employ singular value decomposition (SVD) and alternating least squares (ALS) algorithms. Specifically, Zhao et al. (2016) utilize sequential SVDs to compute the cores (named TR-SVD), in which the TR rank can be estimated with a prescribed relative error (RE).Footnote 1 Further, Zhao et al. propose three ALS-based iterative algorithms, where each of the cores is updated by solving a least-squares problem (Xiao et al. 2021; Gnanasekaran 2022). Compared to ALS-based algorithms, TR-SVD is a non-iterative algorithm, resulting in higher computational speed. This advantage arises from the non-iterative nature of TR-SVD, which eliminates the need for repeated iterations that are inherent in ALS-based algorithms. However, for high-order data, the efficiency of TR-SVD is not satisfactory because it involves expensive SVD computation of large matrices. In this paper, we propose a non-iterative algorithm called TR-STF, based on defined scaled tri-factorization (STF), for fast and accurate TR decomposition. We are inspired by the fact that the existing fast tri-factorization (FTF) is often unfeasible when presented with some matrices without low rank due to its strict condition. We relax the condition to make it widely used, define STF, and design a corresponding algorithm to represent data more accurately in an acceptable time growth range. We then apply sequential STFs to TR decomposition with theoretical proof and propose TR-STF. Extensive experiments show that compared with the current state-of-the-art algorithms, the proposed TR-STF has advantages in accuracy and efficiency, especially the latter. As an extension, we apply the sequential STFs to TT decomposition with theoretical proof and propose the TT-STF, a non-iterative algorithm. The contributions of this paper are as follows:
-
We define STF and design a corresponding algorithm that accurately represents various matrices.
-
We propose a non-iterative TR-STF algorithm for fast and accurate TR decomposition using sequential STFs with theoretical proof.
-
Through experiments on multiple data and tasks, we demonstrate that the proposed TR-STF outperforms state-of-the-art TR decomposition algorithms in efficiency and accuracy, especially the former. Moreover, we propose TT-STF based on sequential STFs for fast and accurate TT decomposition.
We arrange the remaining part as follows: The related work is introduced in Sect. 2. We present the proposed STF and TR-STF algorithms in Sect. 3. Section 4 gives the experimental results. The application of STF in TT decomposition is shown in Sect. 5. Finally, we conclude this paper in Sect. 6.
2 Related work
In this section, we will introduce works related to this paper.
2.1 Work-related notations
We use z, \(\textbf{z}\), \(\textbf{Z}\), and \(\mathcal {Z}\) to represent scalars, vectors, matrices, and tensors, respectively. The field of real numbers is denoted as \(\mathbb {R}\). Given an dth-order tensor \(\mathcal {Z}\in \mathbb {R}^{n_1\times \cdots \times n_{d}}\), its \((j_{1}, j_{2}, \ldots , j_{d})\)th element and \((j_{1},\ldots ,j_{i-1},j_{i+1}, \ldots ,j_{d})\)th mode-i fibe are denoted by \(Z(j_{1}, j_{2}, \ldots , j_{d})\), \(\textbf{z}(j_{1},\ldots ,j_{i-1},j_{i+1}, \ldots , j_{d})\), respectively, Frobenius norm is denoted by \(\Vert \mathcal {Z}\Vert _{F}\). When the order of \(\mathcal {Z}\) is 3, i.e., d=3, we denote \(\textbf{Z}(j,:,:)\), \(\textbf{Z}(:,j,:)\), and \(\textbf{Z}(:,:,j)\) as the jth horizontal, lateral, and frontal slice, respectively, for brevity, \(\textbf{Z}(:,j,:)\) is written as \(\textbf{Z}(j)\). The inner product of two nth-order vectors \(\textbf{x}\in \mathbb {R}^{n}\) and \(\textbf{y}\in \mathbb {R}^{n}\) is defined as \(\left\langle \textbf{x},\textbf{y} \right\rangle =\sum _{i=1}^{n}x(i)y(i)\); the outer product of two vectors \(\textbf{x}\in \mathbb {R}^{m}\) and \(\textbf{y}\in \mathbb {R}^{n}\) is defined a real matrix of order \(m\times n\) obtained by multiplying each element in \(\textbf{x}\) and each element in \(\textbf{y}\), denoted as \( \textbf{x}\circ \textbf{y}\). \(\text {Tr}(\cdot )\), \(\text {vec}(\cdot )\), Rank \((\cdot )\), and \((\cdot )^{T}\) represent the trace, vectorization, rank, and transpose of the matrix, respectively. \(\textbf{Q}=\text {qr}(\textbf{A})\) means QR decomposition of \(\textbf{A}\) of size \(m\times n\), where \(\textbf{Q}\) is the orthogonal matrix of size \(m\times m\). We denote \(\text {eye}(m, n)\in \mathbb {R}^{m\times n}\) as a matrix whose elements on the main diagonal are 1 and the remaining elements are 0. We denote \(\textbf{I}\) as an identity matrix. The permuted tensors of \(\mathcal {Z}\) are denoted as “\(\text {permute}(\mathcal {Z}, [i_{1}, i_{2}, \ldots , i_{d}])\)”, therein \([i_{1}, i_{2}, \ldots , i_{d}]\) is a random permutations of \([1, 2, \ldots , d]\).
2.2 Fast tri-factorization (FTF)
In recent work, Liu et al. (2013) propose FTF to avoid the high computational complexity of SVD. Specifically, the authors decompose matrix \(\textbf{Z}\in \mathbb {R}^{n_{1}\times n_{2}}\) into three factor matrices, whose dimensions are all much smaller than \(\textbf{Z}\), as shown in Definition 1 and Fig. 2.
Definition 1
[FTF (Liu et al. 2013)] For a given matrix \(\textbf{Z}\in \mathbb {R}^{n_{1}\times n_{2}}\), FTF of \(\textbf{Z}\) is
where \(\textbf{B}\in \mathbb {R}^{m\times m}\); \(\textbf{A}\in \mathbb {R}^{n_{1}\times m}\) is column orthogonal, i.e., \(\textbf{A}^{T}\textbf{A}=\textbf{I}\), \(\textbf{C}\in \mathbb {R}^{m\times n_{2}}\) is row orthogonal, i.e., \(\textbf{C}\textbf{C}^{T}=\textbf{I}\); and m is an upper bound on the rank of \(\textbf{Z}\) and satisfies \(m\ll \min (n_{1}, n_{2})\).
The condition, \(m\ll \min (n_{1}, n_{2})\), means that FTF is only applicable to low-rank matrices. However, most data in the real world have complex structures and may not be of low rank. In that case, this condition is no longer suitable. For example, we select the first band of one image (x0043) with the size of \(321\times 481\times 3\) from the CBSD68 data setFootnote 2 to test FTF with different values of m, as shown in Fig. 3. The information of the recovered image is seriously lost when the value of m is minimal, such as 100. Less information in the recovered image is lost with the increase in the value of m, such as 200 and 250. Therefore, it is necessary to increase the value range of m. Especially, when \(m=321\), the recovered image is perfect. In addition, with the increase of m, the running time does not increase much. When m is 321, the time-consuming is only 0.004 s longer than when m is 100, but the change of RelChaFootnote 3 is obvious. Based on this observation, we define STF and design its algorithm as shown in detail in Sect. 3.1.
2.3 Tensor ring (TR) decomposition
This section introduces three forms of TR decomposition and gives several work-related definitions.
For an dth-order tensor \(\mathcal {Z}\in \mathbb {R}^{n_{1}\times n_{2}\cdots \times n_{d}}\), the TR decomposition in the element-wise form is represented by
where \(\textbf{G}_{i}(j_{i})\in \mathbb {R}^{m_{i}\times m_{i+1}}\) is the \(j_{i}\)th lateral slice of the ith core \(\mathcal {G}_{i}\in \mathbb {R}^{m_{i}\times {n_{i}\times m_{i+1}}}\). We rewrite (3) in the index form, i.e.,
where \(\beta _{d+1}=\beta _{1}\) due to the trace operation. \(\forall i\in \{1, \ldots , d\}\), \(1 \le \beta _{i}\le m_{i}\), \(1\le j_{i}\le n_{i}\), where i is the index of tensor dimensions; \(\beta _{k}\) is the index of latent dimensions; and \(j_{k}\) is the index of data dimensions. Based on Eq. (4), we express TR decomposition in the tensor form, i.e.,
where the symbol “\(\circ \)” denotes the outer product of vectors and \(\textbf{g}_{i}(\beta _{i},\beta _{i+1})\in \mathbb {R}^{n_{i}}\) is the \((\beta _{i},\beta _{i+1})\)th mode-2 fiber of \(\mathcal {G}_{i}\).
Definition 2
[k-Unfolding Matrix (Zhao et al. 2016)] Let \(\mathcal {Z}\in \mathbb {R}^{n_{1}\times n_{2}\cdots \times n_{d}}\) be an dth-order tensor. The k-unfolding of \(\mathcal {Z}\) is a matrix, denoted by \(\textbf{Z}_{\left\langle k\right\rangle }\) of size \(\prod _{i=1}^{k}n_{i}\times \prod _{j=k+1}^{d}n_{j}\), whose elements obey
where the first k indices enumerate the rows of \(\textbf{Z}_{\left\langle k\right\rangle }\), and the last \(d-k\) indices for its columns, the multi-indices \(\overline{j_{1}\ldots j_{k}}\) and \(\overline{j_{k+1}\ldots j_{d}}\) are defined by \(1+\sum _{i=1}^{k}(j_{i}-1)\prod _{l=1}^{i-1}n_{l}\) and \(1+\sum _{i=k+1}^{d}(j_{i}-1)\prod _{l=k+1}^{i-1}n_{l}\), respectively.
Definition 3
Let \(\mathcal {Z}\in \mathbb {R}^{n_{1}\times n_{2}\cdots \times n_{d}}\) be an dth-order tensor. The mode-k unfolding matrix of \(\mathcal {Z}\) is denoted by \(\textbf{Z}_{[k]}\) of size \(n_{k}\times \prod _{j\ne k}^{d}n_{j}\) with its elements defined by
where kth indices enumerate the rows of \(\textbf{Z}_{[k]}\), and the rest \(d-1\) indices for its columns.
Definition 4
Let \(\mathcal {Z}\in \mathbb {R}^{n_{1}\times n_{2}\cdots \times n_{d}}\) be an dth-order tensor. The mode-k unfolding matrix of \(\mathcal {Z}\) is denoted by \(\textbf{Z}_{(k)}\) of size \(n_{k}\times \prod _{j\ne k}^{d}n_{j}\), whose elements obey
where kth indices enumerate the rows of \(\textbf{Z}_{(k)}\), and the rest \(d-1\) indices for its columns.
Definition 5
[Tensor Subchains (Zhao et al. 2016)]
-
\(\mathcal {G}^{\le k}\in \mathbb {R}^{m_{1}\times \prod ^{k}_{j=1} n_{j}\times m_{k+1}}\) with lateral slice matrices \(\textbf{G}^{\le k}(\overline{j_{1}j_{2}\ldots j_{k}})=\prod _{i=1}^{k}\textbf{G}_{i}(j_{i})\).
-
\(\mathcal {G}^{>k}\in \mathbb {R}^{m_{k+1}\times \prod ^{d}_{j=k+1}n_{j}\times m_{1}}\) with lateral slice matrices \(\textbf{G}^{>k}(\overline{j_{k+1}j_{k+2}\ldots j_{d}})=\prod _{i=k+1}^{d}\textbf{G}_{i}(j_{i})\).
-
\(\mathcal {G}^{\ne k}\in \mathbb {R}^{m_{k+1}\times \prod ^{d}_{j=1,j\ne k}n_{j}\times m_{k}}\) with slice matrices \(\textbf{G}^{\ne k}(\overline{j_{k+1}\ldots j_{d}j_{1}\ldots j_{k-1}})=\prod _{i=k+1}^{d}\textbf{G}_{i}(j_{i})\prod _{i=1}^{k-1}\textbf{G}_{i}(j_{i})\).
3 Proposed STF and TR-STF algorithms
In this section, we define STF, design its algorithm, and then apply it to TR decomposition, thus proposing the TR-STF algorithm.
3.1 Scaled tri-factorization (STF) algorithm
As illustrated in Sect. 2.2, the condition of FTF \(m\ll \min (n_{1}, n_{2})\) is not suitable for matrices without low-rankness. Based on this fact, we define the following factorization.
Definition 6
(STF) For a matrix \(\textbf{Z}\in \mathbb {R}^{n_{1}\times n_{2}}\), STF of \(\textbf{Z}\) is
where \(\textbf{N}\) denotes the error; \(\textbf{B}\in \mathbb {R}^{R\times R}\); \(\textbf{A}\in \mathbb {R}^{n_{1}\times R}\) is column orthogonal, i.e., \(\textbf{A}^{T}\textbf{A}=\textbf{I}\), \(\textbf{C}\in \mathbb {R}^{R\times n_{2}}\) is row orthogonal, i.e., \(\textbf{C}\textbf{C}^{T}=\textbf{I}\); and R denotes an upper bound on the rank of \(\textbf{Z}\) satisfying \(\text {Rank}(Z)\le R\le \min \{n_{1}, n_{2}\}\).
With STF defined, we need to solve the following problem to find three matrices in Eq. (9) that satisfy \({\Vert \textbf{Z}-\textbf{A}\textbf{B}\textbf{C}\Vert _{F}^{2}\le \delta }\), where \(\delta \) is a positive tolerance.
Problem (10) is convex for each variable when the other two variables are fixed; therefore, we update \(\textbf{A}\), \(\textbf{B}\), and \(\textbf{C}\) alternately. We initialize the three variables as \(\textbf{A}^{0}=\text {eye}(n_{1}, R)\), \(\textbf{B}^{0}=\text {eye}(R, R)\), and \(\textbf{C}^{0}=\text {eye}(R, n_{2})\), then the three variables are updated alternately.
-
1)
\(\textbf{A}\)-subproblem: With \(\textbf{B}\) and \(\textbf{C}\) are fixed, we update \(\textbf{A}\) by
$$\begin{aligned}&\textbf{A}^{t+1}={\mathop {\mathrm{arg\,min}}\limits _{\textbf{A}^{T}\textbf{A}=\textbf{I}}}\,{\Vert \textbf{Z}-\textbf{A}\textbf{B}^{t}\textbf{C}^{t}\Vert _{F}^{2}}, \end{aligned}$$(11)which has a closed-form solution (Shen et al. 2014; Wen et al. 2012):
$$\begin{aligned}&\textbf{A}^{t+1}=\hat{\textbf{A}}(:,1:R), \end{aligned}$$(12)where \(\hat{\textbf{A}}=\text {qr}(\textbf{Z}(\textbf{C}^{t})^{T})\).
-
2)
\(\textbf{C}\)-subproblem: With \(\textbf{A}\) and \(\textbf{B}\) are fixed, we update \(\textbf{C}\) by
$$\begin{aligned}&\textbf{C}^{t+1}={\mathop {\mathrm{arg\,min}}\limits _{\textbf{C}\textbf{C}^{T}=\textbf{I}}}\,{\Vert \textbf{Z}-\textbf{A}^{t+1}\textbf{B}^{t}\textbf{C}\Vert _{F}^{2}}, \end{aligned}$$(13)which has a closed-form solution (Shen et al. 2014; Wen et al. 2012):
$$\begin{aligned}&\textbf{C}^{t+1}=\hat{\textbf{C}}^{T}, \end{aligned}$$(14)where \(\hat{\textbf{C}}=\bar{\textbf{C}}(:, 1:R)\), \(\bar{\textbf{C}}=\text {qr}(\textbf{Z}^{T}\textbf{A}^{t+1})\).
-
3)
\(\textbf{B}\)-subproblem: With \(\textbf{A}\) and \(\textbf{C}\) are fixed, we update \(\textbf{B}\) by
$$\begin{aligned}&\textbf{B}^{t+1}={\mathop {\mathrm{arg\,min}}\limits _{\textbf{B}}}\,{\Vert \textbf{Z}-\textbf{A}^{t+1}\textbf{B}\textbf{C}^{t+1}\Vert _{F}^{2}}, \end{aligned}$$(15)which has a closed-form solution:
$$\begin{aligned}&\textbf{B}^{t+1}=(\textbf{A}^{t+1})^{T}\textbf{Z}(\textbf{C}^{t+1})^{T}. \end{aligned}$$(16)
We summarize the solving procedure of problem (10) in Algorithm 1, named STF, therein \(k_{mit}\) and \(\delta \) are the maximum iteration (maxit) and stopping tolerance. In this paper, we empirically set \(k_{mit}\) and \(\delta \) to 1 and \(10^{-6}\), respectively.

Scaled Tri-Factorization (STF) Algorithm
To illustrate the advantages of STF in data representation, we compare it with the well-known SVD algorithm. Specifically, we randomly generate three matrices with the size of \(10{,}000\times 2000\), \(10{,}000\times 6000\), and \(10{,}000\times 10{,}000\) from the normal distribution, and then represent them by SVD and STF, respectively. For STF, we set R as the minimum of two dimensions of the matrix. Table 1 shows the comparison of running time and accuracy for these two approaches; the best values are shown in bold font. Both algorithms perform well in accuracy, but the time consumption of STF is always less than that of SVD, and the time advantage of STF becomes more obvious as the size increases. The reason for the shorter running time of STF compared to SVD is primarily attributed to the computational efficiency of the QR decomposition employed in STF. The QR decomposition is known to be computationally much cheaper than the SVD (The Singular Value Decomposition (SVD) 2002; Wen et al. 2012).
Motivation 2 Inspired by the powerful data representation ability and high efficiency of STF, we apply it to complex tensor networks.
3.2 TR-STF algorithm
In this section, we propose an algorithm, TR-STF, for fast and accurate TR decomposition.
Theorem 1
Suppose tensor \(\mathcal {Z}\) can be expressed by a TR decomposition. If the size of and the rank of k-unfolding matrix \(\textbf{Z}_{\left\langle k\right\rangle }\) are \(\prod _{j=1}^{k}n_{j}\times \prod _{j=k+1}^{d}n_{j}\) and \(M_{k+1}\), respectively, then there exists a TR decomposition with TR rank \(\textbf{m}=[m_{1}, m_{2}, \ldots , m_{d}]^{T}\) which has that \(\exists \) k, \(M_{k+1}\le m_{1}m_{k+1}\le \min \{\prod _{j=1}^{k}n_{j}, \prod _{j=k+1}^{d}n_{j}\}\), the equal sign holds if \(\textbf{Z}_{\left\langle k\right\rangle }\) is a full rank matrix.
Proof
Based on Eqs. (3) and (6), we obtain the following equation:
Because equation \( \text {Tr}\{\prod _{i=1}^{d}\textbf{G}_{i}(j_{i})\} = \langle {\text {vec}(\prod _{i=1}^{k}\textbf{G}_{i}(j_{i})), \text {vec}(\prod _{i=k+1}^{d}\textbf{G}_{i}^{T}(j_{i}))} \rangle \) holds (Zhao et al. 2016), we obtain the following equation:
According to the definition of tensor subchains, we rewrite the Eq. (18) as
That is,
where the classical mode-2 unfolding matrix \(\textbf{G}_{(2)}^{\le k}\in \mathbb {R}^{\prod _{j=1}^{k}n_{j}\times m_{1}m_{k+1}}\) and mode-2 unfolding matrix \(\textbf{G}_{[2]}^{> k}\in \mathbb {R}^{\prod _{j=k+1}^{d}n_{j}\times m_{1}m_{k+1}}\). Since the rank of matrix \(\textbf{Z}{\left\langle k\right\rangle }\) is \(M_{k+1}\), we can establish the following inequalities: \(M_{k+1} \le m_{1}m_{k+1}\) and \(M_{k+1} \le \min \{\prod _{j=1}^{k}n_{j}, \prod _{j=k+1}^{d}n_{j}\}\). We can always find a value for \(m_{1}m_{k+1}\) that satisfies \(m_{1}m_{k+1}\le \min \{\prod _{j=1}^{k}n_{j}, \prod _{j=k+1}^{d}n_{j}\}\). Therefore, we have \(M_{k+1}\le m_{1}m_{k+1}\le \min \{\prod _{j=1}^{k}n_{j}, \prod _{j=k+1}^{d}n_{j}\}\). If matrix \(\textbf{Z}{\left\langle k\right\rangle }\) is a full rank matrix, it means that \(M_{k+1}=\min \{\prod _{j=1}^{k}n_{j}, \prod _{j=k+1}^{d}n_{j}\}\). Hence, the equality \(M_{k+1}=m_{1}m_{k+1}=\min \{\prod _{j=1}^{k}n_{j}, \prod _{j=k+1}^{d}n_{j}\}\) holds. \(\square \)
For TR-STF algorithm, we usually choose a specific mode as the starting point (e.g., the first mode). According to Eqs. (18) and (19), TR decomposition can be easily written as
Subsequently, we represent \(\textbf{Z}_{\left\langle 1\right\rangle }\) by STF, i.e., \(\textbf{Z}_{\left\langle 1\right\rangle }=\textbf{A}_{1}\textbf{B}_{1}\textbf{C}_{1}+\textbf{N}_{1}\), where \(\textbf{N}_{1}\) denotes the error and \(R=m_{1}m_{2}\). The first core \(\mathcal {G}_{1}\in \mathbb {R}^{m_{1}\times n_{1}\times m_{2}}\) can be estimated by \(\textbf{A}_{1}\) with correct reshaping and permutation. The subchain \(\mathcal {G}^{> 1}\in \mathbb {R}^{m_{2}\times \prod ^{d}_{j=2}n_{j}\times m_{1}}\) can be generated by correct reshaping and permutation of \(\textbf{B}_{1}\textbf{C}_{1}\), which corresponds to the remaining \(d-1\) dimensions of \(\mathcal {Z}\). Then we reshape \(\mathcal {G}^{> 1}\) as a matrix \(\textbf{G}^{>1}\in \mathbb {R}^{m_{2}n_{2}\times \prod ^{d}_{j=3}n_{j}m_{1}}\) whose elements can be expressed as
Using STF, i.e., \(\textbf{G}^{>1}=\textbf{A}_{2}\textbf{B}_{2}\textbf{C}_{2}+\textbf{N}_{2}\), where \(\textbf{N}_{2}\) denotes the error and \(R=m_{3}\), we generate the second core \(\mathcal {G}_{2}\in \mathbb {R}^{m_{2}\times n_{2}\times m_{3}}\) by reshaping \(\textbf{A}_{2}\) and obtain \(\mathcal {G}^{>2}\in \mathbb {R}^{m_{3}\times \prod ^{d}_{j=3}n_{j}\times m_{1}}\) by reshaping \(\textbf{B}_{2}\textbf{C}_{2}\). We perform this procedure sequentially to obtain all d cores \(\mathcal {G}_{j}\in \mathbb {R}^{m_{j}\times n_{j}\times m_{j+1}}\), \(j=1, 2, \ldots , d\). We summarize the proposed TR-STF in Algorithm 2, where “reshape” and “permute” are Matlab commands and \(\text {Rank}(\textbf{G}^{>k-1})\le m_{k+1}\le \min \{m_{k}n_{k}, \prod _{j=k+1}^{d}n_{j}m_{1}\}\), \(k=2, 3, \ldots , d-1\) are the conditions in STF. It is worth noting that the decomposition will be different if we choose a different mode as the start point. Especially, we draw a schematic diagram of TR-STF for 4th-order tensor \(\mathcal {Z}\in \mathbb {R}^{n_{1}\times n_{2}\times n_{3}\times n_{4}}\), as shown in Fig. 4, in which we choose the first mode as the start point.

TR-STF Algorithm for TR Decomposition
TR-STF applied to a 4th-order tensor \(\mathcal {Z}\in \mathbb {R}^{n_{1}\times n_{2}\times n_{3}\times n_{4}}\). Step 1: Unfold the target tensor \(\mathcal {Z}\) along the first mode to generate \(\textbf{Z}_{\left\langle 1\right\rangle }\); Step 2: Represent \(\textbf{Z}_{\left\langle 1\right\rangle }\) by STF (i.e., \(\textbf{Z}_{\left\langle 1\right\rangle }=\textbf{A}_{1}\textbf{B}_{1}\textbf{C}_{1}\)) with \(R=m_{1}m_{2}\), then obtain the first core \(\mathcal {G}_{1}\) by \(\textbf{A}_{1}\) with correct reshaping and permutation and generate \(\textbf{G}^{>1}\) by \(\textbf{B}_{1}\textbf{C}_{1}\) with correct reshaping and permutation; Step 3: Represent \(\textbf{G}^{>1}\) by STF (i.e., \(\textbf{G}^{>1}=\textbf{A}_{2}\textbf{B}_{2}\textbf{C}_{2}\)) with \(R=m_{3}\), then obtain the second core \(\mathcal {G}_{2}\) by reshaping \(\textbf{A}_{2}\) and generate \(\textbf{G}^{>2}\) by reshaping \(\textbf{B}_{2}\textbf{C}_{2}\); Step 4: Represent \(\textbf{G}^{>2}\) by STF (i.e., \(\textbf{G}^{>2}=\textbf{A}_{3}\textbf{B}_{3}\textbf{C}_{3}\)) with \(R=m_{4}\), then obtain the third core \(\mathcal {G}_{3}\) by reshaping \(\textbf{A}_{3}\) and the fourth core \(\mathcal {G}_{4}\) by reshaping \(\textbf{B}_{3}\textbf{C}_{3}\)
3.3 Complexity analysis
Complexity analysis of STF algorithm According to Algorithm 1, the complexity of update \(\textbf{A}\), \(\textbf{C}\), and \(\textbf{B}\) in each iteration is \(\mathcal {O}(n_{1}R^{2}+n_{1}n_{2}R)\), \(\mathcal {O}(n_{2}R^{2}+n_{1}n_{2}R)\), and \(\mathcal {O}(n_{1}n_{2}R+n_{2}R^{2})\). Thus, the total complexity of STF is \(\mathcal {O}(n_{1}R^{2}+2n_{2}R^{2}+3n_{1}n_{2}R)\).
Complexity analysis of TR-STF algorithm As shown in Algorithm 2, steps 2 and 7 have high complexity. Specifically, the complexity of step 2 and step 7 is \(\mathcal {O}(P_{1}R_{1}^{2}+2Q_{1}R_{1}^{2}+3P_{1}Q_{1}R_{1})\) and \(\mathcal {O}(P_{2}R_{2}^{2}+2Q_{2}R_{2}^{2}+3P_{2}Q_{2}R_{2})\), respectively, where \(P_{1}=n_{1}\), \(Q_{1}=\prod _{j=2}^{d}n_{j}\), \(R_{1}=m_{1}m_{2}\), \(P_{2}=m_{k}n_{k}\), \(Q_{2}=\prod _{j=k+1}^{d}n_{j}m_{1}\), and \(R_{2}=m_{k+1}\). Thus, the total complexity of TR-STF is \(\mathcal {O}(P_{1}R_{1}^{2}+2Q_{1}R_{1}^{2}+3P_{1}Q_{1}R_{1}+\sum _{k=2}^{d-1}(P_{2}R_{2}^{2}+2Q_{2}R_{2}^{2}+3P_{2}Q_{2}R_{2}))\).
3.4 Convergence analysis
In this section, we propose two algorithms, i.e., Algorithms 1 and 2, where Algorithm 2 is a non-iterative algorithm that achieves convergence without the need for iterative processes (Zhao et al. 2016). Therefore, we only analyze the convergence of Algorithm 1. Specifically, we conduct an empirical analysis to evaluate the convergence of Algorithm 1. Figure 5 illustrates the convergence behavior of Algorithm 1 applied to the first band of the image (x0023) with a size of \(321\times 481\times 3\) from the CBSD68 dataset. The figure clearly demonstrates that Algorithm 1 exhibits rapid and substantial decrease in the relative error, indicating efficient convergence.
4 Experiments
Because there is little work that focuses on TR decomposition, we compare the proposed TR-STF with four classical algorithms proposed by Zhao et al. (2016): TR-ALS, TR-ALSAR, TR-BALS, and TR-SVD, where the first approach needs to be predefined rank and the last three methods can estimate rank adaptively. In all the experiments, we perform all algorithms on MATLAB R2020a on an Intel(R) Core(TM) i9-10900KF CPU @ 3.70GHz 64.00GB RAM platform.
4.1 Highly oscillatory function
In this section, we test the performance of all five algorithms on three highly oscillatory functions, i.e., \(f_{1}(x)=(x+1)sin(100(x+1)^{2})\), \(f_{2}(x)=x^{-\frac{1}{4}}sin(\frac{2}{3}x^{\frac{3}{2}})\), and \(f_{3}(x)=\sin (x)\cos (x)\), as shown in Fig. 6. We evaluate the first two functions at \(n^{d}\) point, where n and d are considered to be the dimension and order of the tensor, respectively. We set \(n^{d}\) as \(200^{3}\), \(100^{4}\), \(50^{5}\), and \(30^{6}\), respectively, then reshape them into tensors with the size of \(200\times 200\times 200\), \(100\times 100\times 100\times 100\), \(50\times 50\times 50\times 50\times 50\), and \(30\times 30\times 30\times 30\times 30\times 30\), respectively. We set the RE and the maximum iteration steps as \(10^{-4}\) and 20d, respectively, and use the rank obtained from TR-SVD as the setting of TR-ALS. Table 2 shows the running time and RelCha comparison with different orders and dimensions; the best and secondary values are bold and underlined, respectively. We find that all the algorithms leaving out TR-ALSAR can achieve good accuracy. The three ALS-based algorithms exhibit slower performance primarily because of their iterative nature, which involves repeated iterations during the computation. In contrast, the non-iterative algorithms, TR-STF and TR-SVD, demonstrate faster execution times. Among them, TR-STF achieves the best computational speed due to the utilization of the computationally more efficient QR decomposition. For example, when we decompose \(f_{2}(x)\) at \(d=6\) and \(n=30\), the speed of the proposed TR-STF is improved as much as \(448\times \) higher than TR-ALS, \(1429\times \) higher than TR-ALSAR, \(240\times \) higher than TR-BALS, \(38\times \) higher than TR-SVD. Moreover, to more intuitively highlight the high efficiency of the proposed TR-STF, we evaluate \(f_{3}(x)\) at \(n^{d}\), \(n=30\), \(d=4, 5, 6\), points (when \(d>6\), the computer used for this work does not have enough memory to run these algorithms). Specifically, we reshape these values into 4th-order, 5th-order, and 6th-order tensors, respectively, then decompose each of them using five algorithms. We record the time required for five algorithms to achieve similar accuracy. The results are shown in Fig. 7. It can be seen that the proposed TR-STF achieves an absolute advantage in time cost.
4.2 Randomly simulated tensor data
In this experiment, we consider randomly generated tensors with fixed rank and variable dimension. Specifically, we randomly generate four cores \(\mathcal {G}_{i}\in \mathbb {R}^{5\times n \times 5}\), \(i=1, 2, 3, 4\), where dimension n ranges from 20 to 100. Then, we use \(\mathcal {G}_{i}\) to produce 4th-order tensor \(\mathcal {Z}\) whose rank is \([5, 5, 5, 5]^{T}\). Subsequently, we apply the five algorithms to \(\mathcal {Z}\); the RE for TR-ALS, TR-ALSAR, and TR-SVD is set as \(10^{-4}\), and the maxit for three ALS-based algorithms is set as 10d (where d is the order of the tensor). Table 3 and Fig. 8 report the accuracy and time results, respectively; the best and secondary values of RelCha in Table 3 are bold and underlined, respectively. We observe that TR-ALSAR exhibits poor accuracy performance, which can be attributed to the fact that its estimated TR rank is too small to capture the full complexity of the input data, resulting in reduced accuracy compared to other algorithms. In addition, the running time of TR-ALSAR increases rapidly with the increase of n. TR-ALS and TR-BALS have similar running times and accuracy performance, and TR-BALS can accurately estimate rank. The rank estimated by TR-SVD is large, but its performance is excellent. In general, for randomly simulated data, the proposed TR-STF yields secondary results in accuracy and more advantages in efficiency.
4.3 Real-world image data sets
In this section, we consider the performance of all algorithms on two real-world image data sets, the Pavia University (PU) Xu et al. (2020) and the CBSD68 data set. The maxit is set as 10d (where d is the order of the tensor) for three ALS-based algorithms in these two data sets.
PU data set The PU data set is a low-rank hyperspectral image with the size of \(610\times 340\times 103\); we retain 93 bands by removing the low signal-to-noise ratio (SNR) bands, and then choose the up-left \(64\times 64 \times 93\) cube as the reference. We set the RE as \(10^{-4}\) and use the rank obtained from TR-SVD as the setting of TR-ALS. The results are shown in Table 4; the best and secondary values of RelCha and running time are bold and underlined, respectively. We find that the performance of TR-ALSAR is unsatisfactory in terms of accuracy due to the small automatically estimated TR ranks. In contrast, TR-ALS, TR-BALS, TR-SVD and the proposed TR-STF can achieve the satisfactory accuracy. Moreover, the proposed algorithm also has more advantages in running time. For example, TR-STF is nearly 39 times faster than TR-SVD and 9240 times faster than TR-ALS.
CBSD68 data set: The CBSD68 data set contains 68 color images with size of \(481\times 321\times 3\) and \(321\times 481\times 3\). We first downsample them to \(256\times 256\times 3\), then stack these images into a tensor \(\mathcal {Z}\in \mathbb {R}^{256\times 256\times 3\times 68}\). Here, \(\mathcal {Z}\) is not low-rank since this data set describes 68 different scenarios. We perform four algorithms on tensor \(\mathcal {Z}\) leaving out TR-ALS because its memory requirements outstrip the equipment used in these experiments. The RE is set as \(10^{-5}\), and the results are presented in Table 4; the best and secondary values of RelCha and running time are bold and underlined, respectively. We find that images recovered by TR-ALSAR and TR-BALS are not good, while TR-SVD and the proposed TR-STF can represent the tensor \(\mathcal {Z}\) well; with respect to efficiency, TR-STF is more than five times faster than TR-SVD.
Moreover, we show the visual comparison of the results of the PU and the CBSD68 data sets, respectively. Figure 9 shows the images consisting of 10th, 20th, and 30th bands of results generated by all algorithms and of the reference image. We find that all algorithms except TR-ALSAR can represent the PU data set well. For the CBSD68 data set, the performance of TR-ALSAR and TR-BALS is unsatisfactory, while TR-SVD and TR-STF can perfectly express this data, as shown in detail in Fig. 10. In general, the performance of TR-ALSAR is unsatisfactory for these two real data sets. The reason may be that the estimation of rank is not accurate. The performance of TR-BALS is satisfactory for the PU data set, and the accuracy of TR-ALS is good, but it is not dominant in efficiency. The rank estimated by TR-SVD is usually large, but its efficiency and accuracy are the best of the classical algorithms. The proposed TR-STF has more advantages than TR-SVD.
4.4 Feature extraction for classification
Motivated by experiments in Zhao et al. (2016), we use all five algorithms for feature extraction for classification. For this experiment, we select the COIL-100 data setFootnote 4 using 7200 images with the size of \(12 8 \times 128 \times 3\), which describe 100 different objects from 72 different directions. TR-SVD, TR-ALSAR, and TR-BALS also adopt a unified input rank. The RE and the maxit are set as \(10^{-5}\) and 10d (where d is the order of the tensor), respectively. We first downsample each of the images to the size of \(32\times 32\times 3\), then stack them into a tensor \(\mathcal {Z}\in \mathbb {R}^{32\times 32\times 3\times 7200}\). Next, we use all the algorithms on \(\mathcal {Z}\) to estimate cores \(\mathcal {G}_{i}\in \mathbb {R}^{m\times n_{i}\times {m}}\), \(i=1, 2, 3, 4,\) with predefined rank ranging from 2 to 4, where the fourth core \(\mathcal {G}_{4}\) can be used as the latent TR features while the subchain \(\mathcal {G}^{\ne 4}\) can be regarded as the basis of latent subspace. By making a permutation and reshaping, we generate a feature matrix \(\textbf{G}_{4}\in \mathbb {R}^{7200\times m^{2}}\), then use the k-nearest neighbor algorithmFootnote 5 with \(k=1\) to classification. Table 5 presents the results; the best and secondary values of classification accuracy (Acc) and running time are bold and underlined, respectively. We find that the classification accuracy of each algorithm is higher with the increase in rank. In addition, the advantage of the proposed TR-STF in efficiency is still readily apparent.
5 Proposed TT-STF algorithm
In this section, we apply the sequential STFs to TT decomposition, thus proposing the TT-STF algorithm. Specifically, we briefly introduce the TT decomposition and then present the TT-STF algorithm.
5.1 Tensor train (TT) decomposition
This section introduces three forms of TT decomposition (Oseledets 2011).
For an dth-order tensor \(\mathcal {Z}\in \mathbb {R}^{n_{1}\times n_{2}\cdots \times n_{d}}\), the TT decomposition in the element-wise form is represented by
where \(\textbf{G}_{i}(j_{i})\in \mathbb {R}^{m_{i}\times m_{i+1}}\) are the \(j_{i}\)th lateral slice of the ith core \(\mathcal {G}_{i}\in \mathbb {R}^{m_{i}\times {n_{i}\times m_{i+1}}}\). The product of these parameter-dependent matrices is a matrix of size \(m_{1}\times m_{d+1}\), so "boundary conditions" \(m_{1}=m_{d+1}=1\) have been imposed. Therefore, Eq. (23) can be rewritten as
\(\textbf{g}_{1}(j_{1})\) is the \(j_{1}\)th row vector of the first core \(\textbf{G}_{1}\in \mathbb {R}^{n_{1}\times m_{2}}\), \(\textbf{g}_{d}(j_{d})\) is the \(j_{d}\)th column vector of the last core \(\textbf{G}_{d}\in \mathbb {R}^{m_{d}\times n_{d}}\). We rewrite (23) in the index form, i.e.,
where \(\beta _{d+1}=\beta _{1}=1\), \(1 \le \beta _{k}\le m_{k}\), \( k\in \{2, \ldots , d\}\); \(1\le j_{i}\le n_{i}\), \(i\in \{1, \ldots , d\}\); \(\beta _{k}\) is the index of latent dimensions; and \(j_{i}\) is the index of data dimensions. Based on Eq. (25), we can express TT decomposition in the tensor form, given by
where the symbol “\(\circ \)” denotes the outer product of vectors, \(\textbf{g}_{1}(\beta _{2})\) and \(\textbf{g}_{d}(\beta _{d})\) are \(\beta _{2}\)th row and \(\beta _{d}\)th column of \(\textbf{G}_{1}\) and \(\textbf{G}_{d}\), respectively, \(\textbf{g}_{i}(\beta _{i},\beta _{i+1})\in \mathbb {R}^{n_{i}}\) is the \((\beta _{i},\beta _{i+1})\)th mode-2 fiber of \(\mathcal {G}_{i}\), therein \(i\in \{2,3,\ldots ,d-1\}\).
5.2 TT-STF algorithm
In this section, we define the matrix subchain similar to tensor subchain for subsequent description, and then propose TT-STF algorithm.
Definition 7
(Matrix Subchains)
-
\(\textbf{G}^{\le k}\in \mathbb {R}^{\prod ^{k}_{j=1} n_{j}\times m_{k+1}}\) with row vector \(\textbf{g}^{\le k}(\overline{j_{1}j_{2}\ldots j_{k}})=\textbf{g}_{1}(j_{1})\textbf{G}_{2}(j_{2})\ldots \textbf{G}_{k}(j_{k})\).
-
\(\textbf{G}^{>k}\in \mathbb {R}^{m_{k+1}\times \prod ^{d}_{j=k+1}n_{j}}\) with column vector \(\textbf{g}^{>k}(\overline{j_{k+1}j_{k+2}\ldots j_{d}})=\textbf{G}_{k+1} (j_{k+1}) \textbf{G}_{k+2}(j_{k+2})\ldots \textbf{g}_{d}(j_{d})\).
Next, we propose a fast and accurate algorithm, TT-STF, for TT decomposition using sequential STFs with theoretical proof.
Theorem 2
Suppose tensor \(\mathcal {Z}\) can be expressed by a TT decomposition. If the size of and the rank of k-unfolding matrix \(\textbf{Z}_{\left\langle k\right\rangle }\) are \(\prod _{j=1}^{k}n_{j}\times \prod _{j=k+1}^{d}n_{j}\) and \(M_{k+1}\), respectively, then there exists a TT decomposition with TT rank \(\textbf{m}=[m_{2}, m_{3}, \ldots , m_{d}]^{T}\) which has that \(\exists \) k, \(M_{k+1}\le m_{k+1}\le \min \{\prod _{j=1}^{k}n_{j}, \prod _{j=k+1}^{d}n_{j}\}\), the equal sign holds if \(\textbf{Z}_{\left\langle k\right\rangle }\) is a full rank matrix.
Proof
Based on Eqs. (6) and (24), we obtain the following equation:
According to the definition of matrix subchains, we rewrite Eq. (27) as
That is,
where the matrix \(\textbf{G}^{\le k}\in \mathbb {R}^{\prod _{j=1}^{k}n_{j}\times m_{k+1}}\) and matrix \(\textbf{G}^{> k}\in \mathbb {R}^{m_{k+1}\times \prod _{j=k+1}^{d}n_{j}}\). Since the rank of matrix \(\textbf{Z}{\left\langle k\right\rangle }\) is \(M_{k+1}\), we can establish the following inequalities: \(M_{k+1} \le m_{k+1}\) and \(M_{k+1} \le \min \{\prod _{j=1}^{k}n_{j}, \prod _{j=k+1}^{d}n_{j}\}\). We can always find a value for \(m_{k+1}\) that satisfies \(m_{k+1}\le \min \{\prod _{j=1}^{k}n_{j}, \prod _{j=k+1}^{d}n_{j}\}\). Therefore, we have \(M_{k+1}\le m_{k+1}\le \min \{\prod _{j=1}^{k}n_{j}, \prod _{j=k+1}^{d}n_{j}\}\). If matrix \(\textbf{Z}{\left\langle k\right\rangle }\) is a full rank matrix, it means that \(M_{k+1}=\min \{\prod _{j=1}^{k}n_{j}, \prod _{j=k+1}^{d}n_{j}\}\). Hence, the equality \(M_{k+1}=m_{k+1}=\min \{\prod _{j=1}^{k}n_{j}, \prod _{j=k+1}^{d}n_{j}\}\) holds. \(\square \)
For the TT-STF algorithm, we usually choose a specific mode as the starting point (e.g., the first mode). According to Eqs. (27)–(28), TT decomposition can be easily written as
Subsequently, we represent \(\textbf{Z}_{\left\langle 1\right\rangle }\) by STF, i.e., \(\textbf{Z}_{\left\langle 1\right\rangle }=\textbf{A}_{1}\textbf{B}_{1}\textbf{C}_{1}+\textbf{N}_{1}\), where \(\textbf{N}_{1}\) denotes the error and \(R=m_{2}\). The first core \(\textbf{G}_{1}\in \mathbb {R}^{n_{1}\times m_{2}}\) can be estimated by \(\textbf{A}_{1}\). The subchain \(\textbf{G}^{>1}\in \mathbb {R}^{m_{2}\times \prod ^{d}_{j=2}n_{j}}\) can be generated by \(\textbf{B}_{1}\textbf{C}_{1}\), which corresponds to the remaining \(d-1\) dimensions of \(\mathcal {Z}\). Then we reshape \(\textbf{G}^{>1}\) as matrix \(\widehat{\textbf{Z}_{2}}\in \mathbb {R}^{m_{2}n_{2}\times \prod _{j=3}^{d}n_{j}}\) whose elements can be expressed as
Using STF, i.e., \(\widehat{\textbf{Z}_{2}}=\textbf{A}_{2}\textbf{B}_{2}\textbf{C}_{2}+\textbf{N}_{2}\), where \(\textbf{N}_{2}\) denotes the error and \(R=m_{3}\), we generate the second core \(\mathcal {G}_{2}\in \mathbb {R}^{m_{2}\times n_{2}\times m_{3}}\) by reshaping \(\textbf{A}_{2}\) and obtain \(\textbf{G}^{>2}\in \mathbb {R}^{m_{3}\times \prod ^{d}_{j=3}n_{j}}\) by \(\textbf{B}_{2}\textbf{C}_{2}\), which corresponds to the remaining \(d-2\) dimensions of \(\mathcal {Z}\). We perform this procedure sequentially to obtain all d cores. Finally, the proposed TT-STF is summarized in Algorithm 3, where “reshape” is Matlab commands and \(\text {Rank}(\widehat{\textbf{Z}_{k}})\le m_{k+1}\le \min \{m_{k}n_{k}, \prod _{j=k+1}^{d}n_{j}\}\), \(k=2, 3, \ldots , d-1\) are the conditions in STF. It is worth noting that the decomposition will be different if we choose a different mode as the start point. Especially, we draw a schematic diagram of TT-STF for 4th-order tensor \(\mathcal {Z}\in \mathbb {R}^{n_{1}\times n_{2}\times n_{3}\times n_{4}}\), as shown in Fig. 11, in which we choose the first mode as the start point.

TT-STF Algorithm for TT Decomposition
TT-STF applied to a 4th-order tensor \(\mathcal {Z}\in \mathbb {R}^{n_{1}\times n_{2}\times n_{3}\times n_{4}}\). Step 1: Unfold the target tensor \(\mathcal {Z}\) along the first mode to generate \(\textbf{Z}_{\left\langle 1\right\rangle }\); Step 2: Represent \(\textbf{Z}_{\left\langle 1\right\rangle }\) by STF (i.e., \(\textbf{Z}_{\left\langle 1\right\rangle }=\textbf{A}_{1}\textbf{B}_{1}\textbf{C}_{1}\)) with \(R=m_{2}\), then obtain the first core \(\textbf{G}_{1}\) by reshaping \(\textbf{A}_{1}\) and generate \(\widehat{\textbf{Z}_{2}}\) by reshaping \(\textbf{B}_{1}\textbf{C}_{1}\); Step 3: Represent \(\widehat{\textbf{Z}_{2}}\) by STF (i.e., \(\widehat{\textbf{Z}_{2}}=\textbf{A}_{2}\textbf{B}_{2}\textbf{C}_{2}\)) with \(R=m_{3}\), then obtain the second core \(\mathcal {G}_{2}\) by reshaping \(\textbf{A}_{2}\) and generate \(\widehat{\textbf{Z}_{3}}\) by reshaping \(\textbf{B}_{2}\textbf{C}_{2}\); Step 4: Represent \(\widehat{\textbf{Z}_{3}}\) by STF (i.e., \(\widehat{\textbf{Z}_{3}}=\textbf{A}_{3}\textbf{B}_{3}\textbf{C}_{3}\)) with \(R=m_{4}\), then obtain the third core \(\mathcal {G}_{3}\) by reshaping \(\textbf{A}_{3}\) and the fourth core \(\textbf{G}_{4}\) by reshaping \(\textbf{B}_{3}\textbf{C}_{3}\)
5.3 Compare TT-STF with TT-HSVD
To evaluate the effectiveness of the proposed TT-STF, we compare TT-STF with the state-of-the-art TT-HSVD (Zniyed et al. 2020) on highly oscillatory function, \(f_{4}(x)=\sin (\frac{x}{4})\cos (x^{2})\) (see Fig. 6), to verify its effectiveness and efficiency. Specifically, we evaluate this function at \(n^{d}\) point, where n and d are considered to be the dimension and order of tensor, respectively. We set \(n^{d}\) as \(200^{3}\), \(100^{4}\), \(50^{5}\), and \(30^{6}\), then reshape them into tensors with the size of \(200\times 200\times 200\), \(100\times 100\times 100\times 100\), \(50\times 50\times 50\times 50\times 50\), and \(30\times 30\times 30\times 30\times 30\times 30\). The RE for TT-SVD is set as \(10^{-4}\), and the indices for TT-HSVD are set as 1, 2, 2, and 3, respectively. Table 6 shows the running time and RelCha comparison with different n and d; the best and secondary values of RelCha and running time are bold and underlined, respectively. We find that the proposed TT-STF has more advantages than TT-HSVD in efficiency under similar accuracy. For example, when \(d=6\) and \(n=30\), the running time of TT-STF is about one-twelfth that of TT-HSVD.
6 Conclusion
In this paper, we propose a stable TR-STF algorithm with theoretical proof based on sequential STFs to achieve fast and accurate TR decomposition. Specifically, to take advantage of the high efficiency of the existing FTF and overcome its limitation of only being efficient to low-rank matrices due to its strict condition, we define STF and design a corresponding algorithm. Compared with FTF, STF has a broader range of applications, can better preserve the latent information of data, and does not increase processing time appreciably. Equipped with this tool, we propose TR-STF for efficient TR decomposition. Extensive experimental results on multiple randomly simulated data, highly oscillatory functions, and real-world image data sets illustrate the high efficiency and effectiveness of the proposed TR-STF. As an extension, we use sequential STFs for fast and accurate TT decomposition with theoretical proof and propose TT-STF. Experimental results on highly oscillatory functions verify its effectiveness. The proposed TR-STF and TT-STF can generate excellent performance, but they cannot estimate rank adaptively, a topic for future research.
Data Availability
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Notes
This denotes the relative error between the given tensor and the approximated tensor.
The details of this data set can be found at https://www.github.com/clausmichele/CBSD68-dataset.
RelCha is defined by
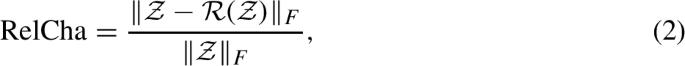
where \(\mathcal {Z}\) denotes the original image and \(\mathcal {R}(\mathcal {Z})\) is the reconstructed image. The smaller the RelCha, the better the result.
The details of this data set can be found at https://www.kaggle.com/jessicali9530/coil100.
References
Bozorgmanesh H, Hajarian M (2022) Triangular decomposition of CP factors of a third-order tensor with application to solving nonlinear systems of equations. J Sci Comput 90:74
Brachat J, Comon P, Mourrain B, Tsigaridas E (2010) Symmetric tensor decomposition. Linear Algebra Appl 433:1851–1872
Bro R (1997) PARAFAC. Tutorial and applications. Chem Intell Lab Syst 38(2):149–171
Cao X, Yao J, Xu Z, Meng D (2020) Hyperspectral image classification with convolutional neural network and active learning. IEEE Trans Geosci Remote Sens 58(7):4604–4616
Che M, Wei Y (2020) Multiplicative algorithms for symmetric nonnegative tensor factorizations and its applications. J Sci Comput 83:53
Che M, Wei Y, Yan H (2021) An efficient randomized algorithm for computing the approximate Tucker decomposition. J Sci Comput 88:32
Chen Y, Huang T-Z, He W, Yokoya N, Zhao X-L (2020) Hyperspectral image compressive sensing reconstruction using subspace-based nonlocal tensor ring decomposition. IEEE Trans Image Process 29:6813–6828
Cichocki A, Lee N, Oseledets A-H, Phan I, Zhao Q, Mandic DP (2016) Tensor networks for dimensionality reduction and large-scale optimization: part 1 low-rank tensor decompositions. Found Trends® Mach Learn 9:249–429
De Lathauwer L (2006) A link between the canonical decomposition in multilinear algebra and simultaneous matrix diagonalization. SIAM J Matrix Anal Appl 28(3):642–666
De Lathauwer L, De Moor B, Vandewalle J (2000) On the best rank-1 and rank-(R1,R2,. . .,RN) approximation of higher-order tensors. SIAM J Matrix Anal Appl 21(4):1324–1342
DE Silva V, Lim L-H (2008) Tensor rank and the ill-posedness of the best low-rank approximation problem. SIAM J Matrix Anal Appl 30:1084–1127
Dektor A, Rodgers A, Venturi D (2021) Rank-adaptive tensor methods for high-dimensional nonlinear PDEs. J Sci Comput 36:88
Deng L-J, Feng M, Tai X-C (2019) The fusion of panchromatic and multispectral remote sensing images via tensor-based sparse modeling and hyper-Laplacian prior. Inf Fusion 52:76–89
Deng L-J, Vivone G, Jin C, Chanussot J (2021) Detail injection-based deep convolutional neural networks for pansharpening. IEEE Trans Geosci Remote Sens 59(8):6995–7010
Deng L-J, Vivone G, Paoletti ME, Scarpa G, He J, Zhang Y, Chanussot J, Plaza A (2022) Machine learning in pansharpening: a benchmark, from shallow to deep networks. IEEE Geosci Remote Sens Mag 10(3):279–315
Deng S-Q, Deng L-J, Wu X, Ran R, Hong D, Vivone G (2023) PSRT: pyramid shuffle-and-reshuffle transformer for multispectral and hyperspectral image fusion. IEEE Trans Geosci Remote Sens 61:1–15. https://doi.org/10.1109/TGRS.2023.3244750
Dian R, Li S, Fang L (2019) Learning a low tensor-train rank representation for hyperspectral image super-resolution. IEEE Trans Neurral Netw Learn Syst 30(9):2672–2683
Ding M, Huang T-Z, Ji T-Y, Zhao X-L, Yang J-H (2019) Low-rank tensor completion using matrix factorization based on tensor train rank and total variation. J Sci Comput 81:941–964
Ding M, Huang T-Z, Zhao X-L, Ng MK, Ma T-H (2021) Tensor train rank minimization with nonlocal self-similarity for tensor completion. Inverse Probl Imaging 15(3):475–498
Fu X, Lin Z, Huang Y, Ding, X (2019) A variational pan-sharpening with local gradient constraints. In: Proceedings of IEEE conference on computer vision pattern recognition (CVPR), pp 10257–10266
Gnanasekaran DEA (2022) Hierarchical orthogonal factorization: sparse least squares problems. J Sci Comput 91:50
Goulart JHDM, Boizard M, Boyer R, Favier G, Comon P (2016) Tensor CP decomposition with structured factor matrices: algorithms and performance. IEEE J Sel Top Signal Process 10:757–769
Hashemizadeh M, Liu M, Miller J, Rabusseau G (2020) Adaptive tensor learning with tensor networks. In: Proceedings of NeurIPS 1st workshop on quantum tensor networks in machine learning
He W, Yokoya N, Yuan L-H, Zhao Q-B (2019) Remote sensing image reconstruction using tensor ring completion and total variation. IEEE Trans Geosci Remote Sens 57(11):8998–9009
He W, Yao Q, Chao L, Yokoya N, Zhao Q, Zhang H, Zhang L (2022) Non-Local Meets Global: an iterative paradigm for hyperspectral image restoration. IEEE Trans Pattern Anal Mach Intell 44(04):2089–2107
Hillar CJ, Lim L-H (2013) Most tensor problems are NP-hard. J ACM 60:1–39
Holtz S, Rohwedder T, Schneider R (2012) The alternating linear scheme for tensor optimization in the tensor train format. SIAM J Sci Comput 34(2):A683–A713
Huckle T, Waldherr K, Schulte-Herbriggen T (2013) Computations in quantum tensor networks. Linear Algebra Appl 438(2):750–781
Jiang J, Sanogo F, Navasca C (2022) Low-CP-rank tensor completion via practical regularization. J Sci Comput 91:18
Kolda TG, Bader BW (2009) Tensor decompositions and applications. SIAM Rev 51(3):455–500
Liu Y, Jiao LC, Shang F (2013) A fast tri-factorization method for low-rank matrix recovery and completion. Pattern Recogn 46(1):163–173
Luan Z, Ming Z, Wu Y (2023) Hankel tensor-based model and l1-tucker decomposition-based frequency recovery method for harmonic retrieval problem. Comput Appl Math 42:14
Orus R (2014) A practical introduction to tensor networks: matrix product states and projected entangled pair states. Ann Phys 349:117–158
Oseledets IV (2011) Tensor-train decomposition. SIAM J Sci Comput 33(5):2295–2317
Oseledets IV, Tyrtyshnikov EE (2009) Breaking the curse of dimensionality, or how to use SVD in many dimensions. SIAM J Sci Comput 31:3744–3759
Oseledets I, Tyrtyshnikov E (2010) TT-cross approximation for multidimensional arrays. Linear Algebra Appl 432(1):70–88
Qi L, Wang Q, Chen Y (2015) Three dimensional strongly symmetric circulant tensors. Linear Algebra Appl 482:207–220
Ran R, Deng L-J, Jiang T-X, Hu J-F, Chanussot J, Vivone G (2023) GuidedNet: a general CNN fusion framework via high-resolution guidance for hyperspectral image super-resolution. IEEE Trans Cybern. https://doi.org/10.1109/TCYB.2023.3238200
Shen Y, Wen Z, Zhang Y (2014) Augmented Lagrangian alternating direction method for matrix separation based on low-rank factorization. Optim Methods Softw 29(2):239–263
Sultonov A, Matveev S, Budzinskiy S (2023) Low-rank nonnegative tensor approximation via alternating projections and sketching. Comput Appl Math 42:68
Sun C-W, Huang T-Z, Xu T, Deng L-J (2023) NF-3DLogTNN: an effective hyperspectral and multispectral image fusion method based on nonlocal low-fibered-rank regularization. Appl Math Model 118:780–797
Tai X-C, Deng L-J, Yin K (2021) A multigrid algorithm for maxflow and Min-Cut problems with applications to multiphase image segmentation. J Sci Comput 101:87
The Singular Value Decomposition (SVD), chap. 4. Wiley, pp 261–288 (2002). https://doi.org/10.1002/0471249718.ch4. https://onlinelibrary.wiley.com/doi/abs/10.1002/0471249718.ch4
Tucker LR (1996) Some mathematical notes on three-mode factor analysis. Psychometrika 31(3):279–311
Wang Y, Yang Y (2022) Hot-svd: higher order t-singular value decomposition for tensors based on tensor-tensor product. Comput Appl Math 41:394
Wang H, Zhang F, Wang J, Huang T, Huang J, Liu X (2022) Generalized nonconvex approach for low-tubal-rank tensor recovery. IEEE Trans Neural Netw Learn Syst 33(8):3305–3319
Wang H, Peng J, Qin W, Wang J, Meng D (2023) Guaranteed tensor recovery fused low-rankness and smoothness. IEEE Trans Pattern Anal Mach Intell 1:1–17. https://doi.org/10.1109/TPAMI.2023.3259640
Wen Z, Yin W, Zhang Y (2012) Solving a low-rank factorization model for matrix completion by a non-linear successive over-relaxation algorithm. Math Program Comput 4:333–361
Xiao C, Yang C, Li M (2021) Efficient alternating least squares algorithms for low multilinear rank approximation of tensors. J Sci Comput 87:67
Xiao J-L, Huang T-Z, Deng L-J, Wu Z-C, Vivone G (2022) A new context-aware details injection fidelity with adaptive coefficients estimation for variational pansharpening. IEEE Trans Geosci Remote Sens 60:1–15
Xu C (2016) Hankel tensors, Vandermonde tensors and their positivities. Linear Algebra Appl 491:56–72
Xu T, Huang T-Z, Deng L-J, Zhao X-L, Huang J (2020) Hyperspectral image super-resolution using unidirectional total variation with Tucker decomposition. IEEE J Sel Top Appl Earth Obs Remote Sens 13:4381–4398
Xu T, Huang T-Z, Deng L-J, Yokoya N (2022) An iterative regularization method based on tensor subspace representation for hyperspectral image super-resolution. IEEE Trans Geosci Remote Sens 60:1–16. https://doi.org/10.1109/TGRS.2022.3176266
Xue J, Zhao Y, Liao W, Chan JC-W (2019) Nonlocal low-rank regularized tensor decomposition for hyperspectral image denoising. IEEE Trans Geosci Remote Sens 57(7):5174–5189
Xue J, Zhao Y, Liao W, Chan JC-W, Kong SG (2020) Enhanced sparsity prior model for low-rank tensor completion. IEEE Trans Neural Netw Learn Syst 31(11):4567–4581
Xue J, Zhao Y-Q, Bu Y, Liao W, Chan JC-W, Philips W (2021a) Spatial-spectral structured sparse low-rank representation for hyperspectral image super-resolution. IEEE Trans Image Process 30:3084–3097
Xue J, Zhao Y-Q, Huang S, Liao W, Chan JC-W, Kong SG (2021b) Multilayer sparsity-based tensor decomposition for low-rank tensor completion. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2021.3083931
Xue J, Zhao Y, Bu Y, Chan JC-W, Kong SG (2022) When Laplacian scale mixture meets three-layer transform: a parametric tensor sparsity for tensor completion. IEEE Trans Cybern 52(12):13887–13901. https://doi.org/10.1109/TCYB.2021.3140148
Zhao Q, Zhou G, Xie S, Zhang L, Cichocki A (2016) Tensor ring decomposition. arXiv:1606:05535
Zniyed Y, Boyer R, de Almeida ALF, Favier G (2020) A TT-based hierarchical framework for decomposing high-order tensors. SIAM J Sci Comput 42(2):822–848
Acknowledgements
The authors would like to thank the anonymous referees and editor for their valuable remarks, questions, and comments that enabled the authors to improve this paper. This research is supported by NSFC (12171072, 12271083), Natural Science Foundation of Sichuan Province (2022NSFSC0501), Key Projects of Applied Basic Research in Sichuan Province (Grant No. 2020YJ0216), and National Key Research and Development Program of China (Grant No. 2020YFA0714001).
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
There is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Xu, T., Huang, TZ., Deng, LJ. et al. TR-STF: a fast and accurate tensor ring decomposition algorithm via defined scaled tri-factorization. Comp. Appl. Math. 42, 234 (2023). https://doi.org/10.1007/s40314-023-02368-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-023-02368-w