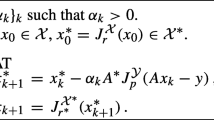RETRACTED ARTICLE: A fast adaptive algorithm for nonlinear inverse problems with convex penalty

Abstract

In this paper, we propose a fast adaptive algorithm for solving nonlinear inverse problems in Hilbert spaces. The iterative process of the proposed method combines classical two point gradient method and adaptive accelerate strategy. In practice, it is often encountered that the reconstruction solution has special feature, such as sparsity and slicing smoothness. To capture the special feature of solution, convex functions are utilized to be penalty terms in iterative format. Meanwhile, a complete convergence analysis is given to show the theoretical rationality of the algorithm. The numerical simulations are provided to demonstrate the effectiveness and acceleration effect of the proposed method.

1 Introduction

In this paper, we are interested in nonlinear inverse problem that can be formulated as

$$\begin{aligned} F(x)=y. \end{aligned}$$

(1)

Here $F:\mathcal {D}(F)\subset \mathcal {X}\rightarrow \mathcal {Y}$ is a nonlinear operator with its definition domain $\mathcal {D}(F)$. The core of the inverse problem is to try to get an approximate solution to problem (1) by knowing the composition of the data y and the forward operator F (Engl and Ramlau 1996; Kaltenbacher et al. 2008; Ito and Jin 2014; Schtster et al. 2012; Leonardo et al. 2015). Algorithmically, using gradient descent method applied to the functional

$$\begin{aligned} J_1(x):=\Vert F(x)-y\Vert ^2, \end{aligned}$$

we obtain the classical Landweber iteration (Hanke et al. 1995; Scherzer 1998) of the form

$$\begin{aligned} x_{n+1}=x_n-F'(x_n)^*(F(x_n)-y). \end{aligned}$$

(2)

Theoretically, the complete convergence analysis of this method has been widely studied. It is well known that, under the general assumptions of the next section, the rate of convergence of $x_n\rightarrow x^*$ ($x^*$ is the true solution to Eq. (1).) as $n\rightarrow \infty$ will, in general, be arbitrarily slow (Kaltenbacher et al. 2008). Therefore, it is necessary to study acceleration strategies, to apply it to practice satisfactorily.

Recently, an accelerated gradient method which applied on the convex problem

$$\begin{aligned} \min \{\varPhi (x)\mid x\in \mathcal {X}\} \end{aligned}$$

was proposed in Hubmer and Ramlau (2018) with the form

$$\begin{aligned} z_{n}= & {} x_{n}+\frac{n-1}{n+\alpha -1}(x_{n}-x_{n-1}), \nonumber \\ x_{n+1}= & {} z_{n}-\omega (\nabla \varPhi (z_{n})). \end{aligned}$$

(3)

Here, $\omega >0$ is the step size, and $\alpha \ge 3$. This is called the Nesterov acceleration strategy. It has proved that the convergence rate for Nesterov method is $\mathcal {O}(n^{-2})$. By applying this method to problem (1) and replacing $(n-1)/(n+\alpha -1)$ with the combination parameter $\lambda _n$, we obtain the so-called two point gradient method (Hubmer and Ramlau 2017) of the form

$$\begin{aligned} z_{n}= & {} x_{n}+\lambda _n(x_{n}-x_{n-1}), \nonumber \\ x_{n+1}= & {} z_{n}-\omega F'(z_n)^*(F(z_n)-y). \end{aligned}$$

(4)

In addition, the adaptive strategy uses a novel idea to solve nonlinear inverse problems (Kaltenbacher et al. 2008; Beck and Teboulle 2003). The key point of this method is to make the item after each iteration closer to the true solution by projecting the initial iteration point onto the strip containing the true solution set. We apply this method to replace the step size used in the iteration with the adaptive step size, the details of which will be discussed later.

In the case that the true solution of (1) has a priori features such as sparsity and slicing smoothness and so on, we consider $\varTheta :\mathcal {X}\rightarrow (-\infty ,\infty ]$. Meanwhile, we introduce the Bregman distance by $\varTheta$

$$\begin{aligned} D_{\xi }\varTheta (\tilde{x},x):=\varTheta (\tilde{x})-\varTheta (x)-\langle \xi ,\tilde{x}-x\rangle ,~~~\tilde{x}\in \mathcal {X}, \end{aligned}$$

where $x\in \mathcal {X}$ and $\xi \in \partial \varTheta (x)$. Inspired by the above approaches, the sought solution of (1) with desired feature can be obtained by minimizing the following functional

$$\begin{aligned} J_2(x):=\Vert F(x)-y\Vert ^2+\beta D_{\xi _0}\varTheta (x,x_0) \end{aligned}$$

with Tikhonov parameter $\beta >0$ and initial choice $x_0\in \mathcal {X}$, $\xi _0\in \partial \varTheta (x_0)$ (Jin and Lu 2014; Wald 2018; Jin 1999). By splitting the terms of F and $\varTheta$, we obtain the adaptive two point gradient iteration with convex penalty term (ATPG-$\varTheta$)

$$\begin{aligned} \zeta _{n}= & {} \xi _{n}+\lambda _{n}(\xi _{n}-\xi _{n-1}), \nonumber \\ z_{n}= & {} \arg \min \limits _{z\in \mathcal {X}}\{\varTheta (z)-\langle \zeta _{n},z\rangle \}, \nonumber \\ \xi _{n+1}= & {} \zeta _{n}-t_{n} F'(z_{n})^*(F(z_{n})-y), \nonumber \\ x_{n+1}= & {} \arg \min \limits _{x\in \mathcal {X}}\{\varTheta (x)-\langle \xi _{n+1},x\rangle \}. \end{aligned}$$

(5)

This method inherits the acceleration advantage of the two point gradient method (Nesterov), and uses the adaptive step size to improve the search direction. In addition, when we encounter true solutions with special features, we use convex penalty terms for reconstruction. In this paper, we verify the complete convergence analysis of the proposed method and obtain satisfactory results in several numerical simulations.

The subsequent paper is structured as follows: some hypotheses and follow-up useful results are introduced in Sect. 2. In Sect. 3, we give the iteration scheme in detail and show the convergence analysis of ATPG-$\varTheta$. Several numerical simulations are present to show the effectiveness and acceleration of the method in Sect. 4. Finally, we summarize our conclusions in Sect. 5.

2 Preliminaries

In the following, we discuss some of the necessary tools and assumptions for subsequent analysis.

2.1 Basic tools

Define a convex function $\varTheta :\mathcal {X}\rightarrow (-\infty ,\infty ]$ with its effective domain $\mathcal {D}(\varTheta ):=\{x\in \mathcal {X}:\varTheta (x)<\infty \}$. If $\mathcal {D}(\varTheta )\ne \emptyset$, we call it proper. Moreover, it is strongly convex of the proper lower semi-continuous function $\varTheta$ if there has $c_0>0$ such that

$$\begin{aligned} \varTheta (s\tilde{x}+(1-s)x)+c_0s(1-s)\Vert \tilde{x}-x\Vert ^2\le s\varTheta (\tilde{x})+(1-s)\varTheta (x) \end{aligned}$$

(6)

for all $0\le s\le 1$ and $\tilde{x},x\in \mathcal {X}$. The subdifferential is defined by

$$\begin{aligned} \partial \varTheta (x):=\{\xi \in \mathcal {X}:\varTheta (\tilde{x})-\varTheta (x)-\langle \xi ,\tilde{x}-x\rangle \ge 0~\mathrm{for~all}~ \tilde{x}\in \mathcal {X}\}. \end{aligned}$$

For $\xi \in \partial \varTheta (x)$ is the subgradient of x. Meanwhile, there holds

$$\begin{aligned} D_{\xi }\varTheta (\tilde{x},x)\ge c_0\Vert \tilde{x}-x\Vert ^2,~~~\forall \tilde{x},x\in \mathcal {X}~\textrm{and}~\xi \in \partial \varTheta (x), \end{aligned}$$

(7)

if $\varTheta$ is a strongly convex function.

For a proper, lower semi-continuous, convex function $\varTheta :\mathcal {X}\rightarrow (-\infty ,\infty ]$, we define its Legendre–Fenchel conjugate with the form

$$\begin{aligned} \varTheta ^*(\xi ):=\sup \limits _{x\in \mathcal {X}}\{\langle \xi ,x\rangle -\varTheta (x)\},~~~\forall \xi \in \mathcal {X}. \end{aligned}$$

Consequently,

$$\begin{aligned} \xi \in \partial \varTheta (x)\Longleftrightarrow x\in \partial \varTheta ^*(\xi )\Longleftrightarrow \varTheta (x)+\varTheta ^*(\xi )=\langle \xi ,x\rangle . \end{aligned}$$

(8)

Then the Bregman distance can be redefined as

$$\begin{aligned} D_{\xi }\varTheta (\tilde{x},x):=\varTheta (\tilde{x})-\varTheta ^*(\xi )-\langle \xi ,\tilde{x}\rangle . \end{aligned}$$

(9)

According to the reference (Zalinescu 2002; Schirotzek 2007), we know that $\varTheta ^*$ is Fréchet differentiable and its gradient $\nabla \varTheta ^*$ is Lipschitz continuous with the form

$$\begin{aligned} \Vert \nabla \varTheta ^*(\xi )-\nabla \varTheta ^*(\zeta )\Vert \le \frac{\Vert \xi -\zeta \Vert }{2c_0},~~~\forall \xi ,\zeta \in \mathcal {X}, \end{aligned}$$

(10)

where $c_0$ is shown in (7).

In this paper, we choose an initial guess $\xi _0\in \mathcal {X}$ and

$$\begin{aligned} x_{0}=\arg \min \limits _{x\in \mathcal {X}}\{\varTheta (x)-\langle \xi _{0},x\rangle \}. \end{aligned}$$

2.2 Assumption

To ensure the convergence property of the proposed method, we give the following assumptions, which are mild in iterative methods (Kaltenbacher et al. 2008).

Assumption 2.1

Let the function $\varTheta :\mathcal {X}\rightarrow (-\infty ,\infty ]$ be proper, lower semi-continuous, and strongly convex in the sense of (6).

Assumption 2.2

Define $B_\rho (x_0):=\{x\in \mathcal {X}:\Vert x-x_0\Vert {\le }\rho \}$ be the closed ball around $x_0$.

A1:

(1) has a solution $x^*\in \mathcal {D}(\varTheta )$ satisfying

$$\begin{aligned} D_{\xi _0}\varTheta (x^*,x_0)\le c_0\rho ^2. \end{aligned}$$

A2:

The G${\hat{a}}$teaux derivative $F'(\cdot )$ is bounded, i.e.,

$$\begin{aligned} \left\| F'(x)\right\| \le C_F,~~~ \forall x\in B_{3\rho }(x_0) \end{aligned}$$

with the constant $C_F>0$.

A3:

For some $0<\eta <1$, the $tangential\; cone\; condition$ (TCC) of F holds, namely

$$\begin{aligned} \left\| F(x)-F(\tilde{x})-F'(x)(x-\tilde{x})\right\| \le \eta \left\| F(x)-F(\tilde{x})\right\| ,~ \forall x, \tilde{x}\in B_{3\rho }(x_0). \end{aligned}$$

(11)

Corollary 2.1

Under (11) in Assumption 2.2, the following statement holds

$$\begin{aligned} \Vert F'(x)(x^*-\tilde{x})\Vert \le 2(1+\eta )\Vert F(x)-y\Vert +(1+\eta )\Vert F(\tilde{x})-y\Vert \end{aligned}$$

(12)

with $x^*$, $\forall x,\tilde{x}\in B_{3\rho }(x_0)$ and y is the data of (1).

Proof

For a rigorous proof of this corollary the reader is referred to Kaltenbacher et al. (2008). $\square$

3 Convergence analysis

In the setting of nth iteration, the parameters $r_n,u_n,t_n$ are decided by

$$\begin{aligned} r_{n}&:=F(z_{n})-y,\\ u_n&:=F'(z_{n})^*(F(z_{n})-y), \end{aligned}$$

and

$$\begin{aligned} t_n:=\min \left\{ \frac{c_1\Vert r_n\Vert ^2}{\Vert u_n\Vert ^2},c_2\right\} , \end{aligned}$$

where $c_1,c_2$ are given positive numbers. As for the selection of combination parameter $\lambda _n$, it will be given in detail in Algorithm 2. To understand the principle of the adaptive two point gradient iteration with convex penalty term (ATPG-$\varTheta$) more clearly, we give the following flowchart.

Without loss of generality, we stop the iteration using the residual limit, i.e., defining the stopping index $n_*$ and constant $C_*$ by

$$\begin{aligned} \Vert F(z_{n_*})-y\Vert \le C_*<\Vert F(z_{n})-y\Vert ,~~~0\le n<n_*. \end{aligned}$$

(13)

Lemma 3.1

For any $x,\tilde{x}\in \mathcal {D}(\varTheta ),\xi \in \partial \varTheta (x),{\tilde{\xi }}\in \partial \varTheta (\tilde{x})$, there holds

$$\begin{aligned} D_{\xi }\varTheta (\tilde{x},x)\le \frac{1}{4c_0}\Vert \xi -{\tilde{\xi }}\Vert ^2. \end{aligned}$$

(14)

Proof

According to (8), (9) and (10) that

$$\begin{aligned} D_{\xi }\varTheta (\tilde{x},x)&=\varTheta ^*(\xi )-\varTheta ^*({\tilde{\xi }})-\langle \xi -{\tilde{\xi }},\nabla \varTheta ^*({\tilde{\xi }}) \rangle \\&=\int _0^1\langle \xi -{\tilde{\xi }},\nabla \varTheta ^*({\tilde{\xi }}+t(\xi -{\tilde{\xi }}))-\nabla \varTheta ^*({\tilde{\xi }}) \rangle \text {d}t\\&\le \Vert \xi -{\tilde{\xi }}\Vert \int _0^1\Vert \nabla \varTheta ^*({\tilde{\xi }}+t(\xi -{\tilde{\xi }}))-\nabla \varTheta ^*({\tilde{\xi }})\Vert \text {d}t \\&\le \frac{1}{2c_0}\Vert \xi -{\tilde{\xi }}\Vert \int _0^1t\Vert \xi -{\tilde{\xi }}\Vert \text {d}t \\&=\frac{1}{4c_0}\Vert \xi -{\tilde{\xi }}\Vert ^2. \end{aligned}$$

$\square$

Define

$$\begin{aligned} \varDelta _n:=D_{\xi _n}\varTheta (x^*,x_n)-D_{\xi _{n-1}}\varTheta (x^*,x_{n-1}). \end{aligned}$$

Lemma 3.2

Let Assumptions 2.1 and 2.2 hold. For any solution $x^*$ of (1) in $B_{2\rho }(x_0)\cap \mathcal {D}(\varTheta )$, we have

$$\begin{aligned} D_{\zeta _n}\varTheta (x^*,z_n)-D_{\xi _{n}}\varTheta (x^*,x_{n})\le \lambda _n\varDelta _n+\frac{1}{4c_0}(\lambda _n+\lambda _n^2)\Vert \xi _n-\xi _{n-1}\Vert ^2. \end{aligned}$$

(15)

Define the adaptive step size $t_n$ in each iteration with the form

$$\begin{aligned} t_n:=\min \left\{ \frac{c_1\Vert r_n\Vert ^2}{\Vert u_n\Vert ^2},c_2\right\} , \end{aligned}$$

where $c_1,c_2$ are given positive numbers. Define further that

$$\begin{aligned} \varPsi :=1-\frac{c_1}{4c_0}+\eta >0. \end{aligned}$$

Then we have

$$\begin{aligned} D_{\xi _{n+1}}\varTheta (x^*,x_{n+1})-D_{\zeta _n}\varTheta (x^*,z_n)\le -t_n\varPsi \Vert r_n\Vert ^2. \end{aligned}$$

(16)

Proof

By means of the definition of Bregman distance and $\zeta _n$, and (14), there has

$$\begin{aligned}&D_{\zeta _n}\varTheta (x^*,z_n)-D_{\xi _{n}}\varTheta (x^*,x_{n})= D_{\zeta _n}\varTheta (x_{n},z_n)+\langle \zeta _n-\xi _{n},x_{n}-x^* \rangle \\&\quad \le \frac{1}{4c_0}\Vert \zeta _n-\xi _{n}\Vert ^2+\langle \zeta _n-\xi _{n},x_{n}-x^* \rangle \\&\quad =\frac{1}{4c_0}(\lambda _n^\delta )^2\Vert \xi _n^\delta -\xi _{n-1}^\delta \Vert ^2+\lambda _n^\delta \langle \xi _n^\delta -\xi _{n-1}^\delta ,x_{n}^\delta -x^* \rangle \\&\quad =\frac{1}{4c_0}(\lambda _n^\delta )^2\Vert \xi _n^\delta -\xi _{n-1}^\delta \Vert ^2\\&\quad \quad +\lambda _n^\delta \left( D_{\xi _{n}^\delta }\varTheta (x^*,x_{n}^\delta )-D_{\xi _{n-1}^\delta }\varTheta (x^*,x_{n-1}^\delta ) +D_{\xi _{n-1}^\delta }\varTheta (x_{n}^\delta ,x_{n-1}^\delta )\right) \\&\quad \le \lambda _n^\delta \varDelta _n^\delta +\frac{1}{4c_0}\left( \lambda _n^\delta +(\lambda _n^\delta )^2\right) \Vert \xi _n^\delta -\xi _{n-1}^\delta \Vert ^2. \end{aligned}$$

It follows from the definition of the proposed method, we have

$$\begin{aligned}&D_{\xi _{n+1}}\varTheta (x^*,x_{n+1})-D_{\zeta _n}\varTheta (x^*,z_n)\\&\quad = D_{\xi _{n+1}}\varTheta (z_{n},x_{n+1})+\langle \xi _{n+1}-\zeta _n,z_{n}-x^* \rangle \\&\quad \le \frac{1}{4c_0}\Vert \xi _{n+1}-\zeta _n\Vert ^2+\langle \xi _{n+1}-\zeta _n,z_{n}-x^* \rangle \\&\quad =\frac{1}{4c_0}t_n^2\Vert u_n\Vert ^2-t_n(\langle r_n,y-F(z_n)-F'(z_n)(x^*-z_{n}) \rangle +\Vert r_n\Vert ^2) \\&\quad \le -t_n(1-\frac{c_1}{4c_0}+\eta )\Vert r_n\Vert ^2 \\&\quad =-t_n\varPsi \Vert r_n\Vert ^2. \end{aligned}$$

$\square$

Corollary 3.1

Let conditions in Lemma 3.2 hold, there exists

$$\begin{aligned} \varDelta _{n+1}\le \lambda _n\varDelta _{n}+\frac{1}{4c_0}(\lambda _n+\lambda _n^2)\Vert \xi _n-\xi _{n-1}\Vert ^2-t_n\varPsi \Vert r_n\Vert ^2. \end{aligned}$$

(17)

Proof

In Eq. (17) is easily obtained by adding (15) and (16). $\square$

In the following Proposition, we need two necessary conditions for combination parameters $\{\lambda _n\}$. First, assume that

$$\begin{aligned} \lambda _0=0,~~0\le \lambda _n\le 1,~~\forall n\in \mathbb {N}^+ \end{aligned}$$

(18)

holds. Moreover, let

$$\begin{aligned} \frac{1}{4c_0}(\lambda _n+\lambda _n^2)\Vert \xi _n-\xi _{n-1}\Vert ^2\le c_0\rho ^2. \end{aligned}$$

(19)

Proposition 3.1

Let Assumptions 2.1 and 2.2 hold. Assume that the coupling condition

$$\begin{aligned} \frac{1}{4c_0}(\lambda _n+\lambda _n^2)\Vert \xi _n-\xi _{n-1}\Vert ^2-\frac{t_n\varPsi }{\gamma }\Vert r_n\Vert ^2\le 0 \end{aligned}$$

(20)

holds with $\gamma >1$. Then we have

$$\begin{aligned} D_{\xi _{n}}\varTheta (x^*,x_{n})\le D_{\xi _{n-1}}\varTheta (x^*,x_{n-1}),~~x_n\in B_{2\rho }(x_0),z_n\in B_{3\rho }(x_0),~\forall n\ge 0. \end{aligned}$$

Moreover, there holds

$$\begin{aligned} \sum \limits _{n=0}^{\infty }\Vert r_n\Vert ^2<\infty . \end{aligned}$$

(21)

Proof

We show the first assertions by induction. Due to $\xi _{-1}=\xi _0=\zeta _0$ and $x_{-1}=x_0=z_0$, the conclusion is obvious at $n=0$. Now we assume that the assertions hold for all $0\le n\le m$ for some integer $m\ge 0$. By means of (17) and (20), there holds

$$\begin{aligned} \varDelta _{n+1}\le \lambda _n\varDelta _{n}-\left( 1-\frac{1}{\gamma }\right) t_n\varPsi \Vert r_n\Vert ^2. \end{aligned}$$

(22)

Combining $\lambda _0\ge 0,\gamma >1,t_n\ge 0$ with the hypothesis $\varDelta _{m}\le 0$ that $\varDelta _{m+1}\le 0$. Then we have

$$\begin{aligned} D_{\xi _{m+1}}\varTheta (x^*,x_{m+1})\le D_{\xi _{m}}\varTheta (x^*,x_{m})\le \ldots \le D_{\xi _{0}}\varTheta (x^*,x_{0})\le c_0\rho ^2. \end{aligned}$$

It follows from (7) that $\Vert x^*-x_{m+1}\Vert ^2\le \rho ^2$. Since $x^*\in B_\rho (x_0)$ implies that $x_{m+1}\in B_{2\rho }(x_0)$. According to (15) and (19), there holds

$$\begin{aligned} D_{\zeta _{m+1}}\varTheta (x^*,z_{m+1})&\le D_{\xi _{m+1}}\varTheta (x^*,x_{m+1})+\lambda _{m+1}\varDelta _{m+1}+c_0\rho ^2\\&\le D_{\xi _{0}}\varTheta (x^*,x_{0})+c_0\rho ^2\\&\le 2c_0\rho ^2, \end{aligned}$$

which implies $z_{m+1}\in B_{3\rho }(x_0)$.

Using (22) and $\varDelta _{n}\le 0$, there holds

$$\begin{aligned} \varDelta _{n+1}\le -\left( 1-\frac{1}{\gamma }\right) t_n\varPsi \Vert r_n\Vert ^2, \end{aligned}$$

i.e.,

$$\begin{aligned} \left( 1-\frac{1}{\gamma }\right) t_n\varPsi \Vert r_n\Vert ^2\le D_{\xi _{n}}\varTheta (x^*,x_{n})-D_{\xi _{n+1}}\varTheta (x^*,x_{n+1}). \end{aligned}$$

(23)

Together with the definition of norm and the boundedness of forward operator F, we obtain that

$$\begin{aligned} \frac{\Vert F(z_{n})-y\Vert ^2}{\Vert F'(z_{n})^*(F(z_{n})-y)\Vert ^2}\ge \frac{\Vert F(z_{n})-y\Vert ^2}{C_F^2\Vert F(z_{n})-y\Vert ^2}= \frac{1}{C_F^2}. \end{aligned}$$

According to the definition of adaptive step size, we have

$$\begin{aligned} t_n=\min \left\{ \frac{c_1\Vert r_n\Vert ^2}{\Vert u_n\Vert ^2},c_2\right\} \ge \min \left\{ \frac{c_1}{C_F^2},c_2\right\} . \end{aligned}$$

Apply it to (23) and add it from $n=0$ to infinity, there has

$$\begin{aligned} \min \left\{ \frac{c_1}{C_F^2},c_2\right\} \left( 1-\frac{1}{\gamma }\right) \varPsi \sum \limits _{n=0}^{\infty }\Vert r_n\Vert ^2&\le \sum \limits _{n=0}^{\infty }(D_{\xi _{n}}\varTheta (x^*,x_{n})-D_{\xi _{n+1}}\varTheta (x^*,x_{n+1}))\\&\le D_{\xi _{0}}\varTheta (x^*,x_{0}) \le \rho ^2<\infty . \end{aligned}$$

Then the assertion (21) holds. $\square$

In the above analysis, we used several assumptions about the combination parameters $\{\lambda _n\}$. Based on this, we will discuss the selection rule of $\{\lambda _n\}$, so as to meet the necessary conditions and achieve the acceleration effect.

Algorithmically, we consider that the stopping criterion (13) has not been satisfied, then there has the sufficient coupling condition:

$$\begin{aligned} \frac{1}{4c_0}(\lambda _n+\lambda _n^2)\Vert \xi _n-\xi _{n-1}\Vert ^2\le LC_*^2, \end{aligned}$$

(24)

where $L:=\frac{4c_0\varPsi }{\gamma }\min \{\frac{c_1}{C_F^2},c_2\}$. Combining (24) with Nesterov acceleration technique, we adopt the choice of combination parameter $\lambda _{n}$ that

$$\begin{aligned} \lambda _n=\min \left\{ \sqrt{\frac{LC_*^2}{\Vert \xi _n-\xi _{n-1}\Vert ^2}+\frac{1}{4}}-\frac{1}{2},\frac{n-1}{n+\alpha -1}\right\} . \end{aligned}$$

(25)

In addition, we need a more demanding condition to satisfy the subsequent convergence analysis, i.e,

$$\begin{aligned} \sum \limits _{n=0}^{\infty }\lambda _n\Vert \xi _n-\xi _{n-1}\Vert <\infty . \end{aligned}$$

(26)

To satisfy this condition we choose a function $f:\mathbb {R}^+\rightarrow \mathbb {R}^+$ satisfying

$$\begin{aligned} f(m_1)\le f(m_2),~~\forall m_1>m_2,~~\sum \limits _{n=0}^{\infty }f(n)<\infty . \end{aligned}$$

(27)

Then, the diagram in Algorithm 2 of solving $\{\lambda _n\}$ is given.

It is easy to check that

$$\begin{aligned} \sum \limits _{n=0}^{\infty }\lambda _n\Vert \xi _n-\xi _{n-1}\Vert \le \sum \limits _{n=0}^{\infty } f(n)<\infty . \end{aligned}$$

Moreover, conditions (18)–(20), (24) and (26) can be satisfied respectively.

Proposition 3.2

Consider problem (1) for which Assumptions 2.1 and 2.2 hold. Let $\{x_n\}\subset B_{2\rho }(x_0)\cap \mathcal {D}(\varTheta )$ and $\{\xi _n\}\subset \mathcal {X}$ be such that

• 1. $\xi _n\in \partial \varTheta (x_n)$ for all n;

• 2. for any solution $x^*$ of (1) in $B_{2\rho }(x_0)\cap \mathcal {D}(\varTheta )$ the sequence $\{D_{\xi _{n}^\delta }\varTheta (x^*,x_{n})\}$ is monotonically decreasing;

• 3. $\lim \limits _{n\rightarrow \infty }\Vert F(x_n)-y\Vert =0$;

• 4. there is a subsequence $\{n_k\}$ with $n_k\rightarrow \infty$ such that for any solution $x^*$ of (1) in $B_{2\rho }(x_0)\cap \mathcal {D}(\varTheta )$ there holds

  $$\begin{aligned} \lim \limits _{l\rightarrow \infty }\sup \limits _{k\ge l}\mid \langle \xi _{n_k}-\xi _{n_l},x_{n_k}-x^*\rangle \mid =0. \end{aligned}$$

  (28)

Then there exists a solution ${\hat{x}}$ of (1) in $B_{2\rho }(x_0)\cap \mathcal {D}(\varTheta )$ such that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }D_{\xi _{n}}\varTheta ({\hat{x}},x_{n})=0. \end{aligned}$$

If, in addition, $x^\dagger \in B_{\rho }(x_0)\cap \mathcal {D}(\varTheta )$ and $\xi _{n+1}-\xi _n\in \overline{\mathcal {R}\left( F'(x^\dagger )^*\right) }$ for all n, then ${\hat{x}}=x^\dagger$.

Proof

The proof can refer to Jin and Wang (2013, Proposition 3.6). $\square$

In the following, we present the main theoretical result of this paper, namely the convergence of the proposed method.

Theorem 3.1

(Convergence) Consider problem (1) for which Assumptions 2.1 and 2.2 hold. Then there hold

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }D_{\xi _{n}}\varTheta ({\hat{x}},x_{n})=0~~\textrm{and}~~\lim \limits _{n\rightarrow \infty }\Vert x_n-{\hat{x}}\Vert =0. \end{aligned}$$

Proof

Here we only need to verify conditions (1–4) in Proposition 3.2. From the above discussion, conditions (1–3) are clearly valid.

Now we consider condition (4) in Proposition 3.2. The first case is that at some finite n, $F(z_n)=y$, then $\lambda _n(\xi _n-\xi _{n-1})=0$ according to (20). Thus, $\zeta _n=\xi _n$. It follows $\Vert r_n\Vert =0$ that $\xi _{n+1}=\zeta _n=\xi _n=\zeta _{n+1}$. Hence, $z_{n+1}=x_{n+1}=z_n$ and $F(z_{n+1})=F(z_n)=y$. Repeat the above operations to obtain $F(z_m)=y$ for all $m\ge n$. Consequently, the statement of Proposition is true in this case.

The other case is $\Vert F(z_n)\ne y\Vert$ for all $n\in \mathbb {N}^+$, and we can pick a monotonically increasing sequence $\{n_k\}$. Let $n_k$ be the first integer meeting

$$\begin{aligned} n_k\ge n_{k-1}+1,~~\textrm{and}~~\Vert F(z_{n_k})-y\Vert \le \Vert F(z_{n_{k-1}})-y\Vert . \end{aligned}$$

Then we have

$$\begin{aligned} \Vert F(z_{n_k})-y\Vert \le \Vert F(z_{n})-y\Vert ,~~0\le n<n_k. \end{aligned}$$

(29)

For $0\le l<k<\infty$, we have

$$\begin{aligned} \mid \left\langle \xi _{n_k}-\xi _{n_l},x_{n_k}-x^*\right\rangle \mid&=\mid \sum \limits _{n=n_l}^{n_k-1}\left\langle \xi _{n+1}-\xi _{n},x_{n_k}-x^*\right\rangle \mid \\&\le \sum \limits _{n=n_l}^{n_k-1}\lambda _n\mid \langle \xi _{n}-\xi _{n-1},x_{n_k}-x^*\rangle \mid \\&\quad -\sum \limits _{n=n_l}^{n_k-1}t_n\mid \langle (F'(z_n)^*r_n,x_{n_k}-x^*\rangle \mid . \end{aligned}$$

Then we have

$$\begin{aligned} \lambda _n\mid \langle \xi _{n}-\xi _{n-1},x_{n_k}-x^*\rangle \mid \le \lambda _n\Vert \xi _{n}-\xi _{n-1}\Vert \Vert x_{n_k}-x^*\Vert \le 3\rho \lambda _n\Vert \xi _{n}-\xi _{n-1}\Vert . \end{aligned}$$

Using the definition of adaptive step size, and (12), (29), we get

$$\begin{aligned} t_n\mid \langle (F'(z_n)^*r_n,x_{n_k}-x^*\rangle \mid&\le t_n\Vert r_n\Vert \Vert F'(z_n)(x_{n_k}-x^*)\Vert \\&\le t_n\Vert r_n\Vert [2(1+\eta )\Vert r_n\Vert +(1+\eta )\Vert F(x_{n_k})-y\Vert ] \\&\le 3c_2(1+\eta )\Vert r_n\Vert ^2. \end{aligned}$$

$\square$

Therefore, we obtain that

$$\begin{aligned} \mid \left\langle \xi _{n_k}-\xi _{n_l},x_{n_k}-x^*\right\rangle \mid&\le 3\rho \sum \limits _{n=n_l}^{n_k-1}\lambda _n\Vert \xi _{n}-\xi _{n-1}\Vert +3c_2(1+\eta )\sum \limits _{n=n_l}^{n_k-1}\Vert r_n\Vert ^2 \\&\le 3\rho \sum \limits _{n=n_l}^{n_k-1}\lambda _n\Vert \xi _{n}-\xi _{n-1}\Vert \\&\quad +C_s(D_{\xi _{n_l}}\varTheta (x^*,x_{n_l})-D_{\xi _{n_k}}\varTheta (x^*,x_{n_k})), \end{aligned}$$

where $C_s=\frac{3c_2\gamma }{(\gamma -1)\varPsi }(1+\eta )$. Combining the monotonicity of $\{D_{\xi _{n}}\varTheta (x^*,x_{n})\}$ and (26), we can get condition (4) in Proposition 3.2. Then $\lim _{n\rightarrow \infty }D_{\xi _{n}}\varTheta ({\hat{x}},x_{n})=0$. In view of (7), we also have $\lim _{n\rightarrow \infty }\Vert x_n-{\hat{x}}\Vert =0$, which complete the proof of Proposition.

4 Numerical simulations

In this section, we show some numerical examples to illustrate the effectiveness of the proposed method. For comparison purposes, we define the following related methods.

• 1. Landweber: The classical Landweber iteration (2).

• 2. Landweber-$\varTheta$: The classical Landweber iteration (2) with convex penalty term.

• 3. ATPG-$\varTheta$: Adaptive two point gradient method with convex penalty term, as the scheme (5).

Numerically, we need to solve

$$\begin{aligned} x=\arg \min \limits _{z\in \mathcal {X}}\{\varTheta (z)-\langle \xi ,z\rangle \} \end{aligned}$$

(30)

in each iteration (Boţ 2012). We can restrict the form of the operator $\varTheta$ for different features of the sought solution, such as when the solution is sparse, we can choose $\varTheta$ be

$$\begin{aligned} \varTheta (x):=\frac{1}{2\beta }\int _{\varOmega }\mid x(\varsigma )\mid ^2\textrm{d}\varsigma +\int _{\varOmega }\mid x(\varsigma )\mid \textrm{d}\varsigma . \end{aligned}$$

Then the explicit formula of (30) can be written as

$$\begin{aligned} x(\varsigma )=\beta \textrm{sign}(\xi (\varsigma ))\max \{\mid \xi (\varsigma )\mid -1,0\},~~~\varsigma \in \varOmega . \end{aligned}$$

(31)

In addition, when the solution has the property of piecewise continuity, we can choose

$$\begin{aligned} \varTheta (x):=\frac{1}{2\beta }\int _{\varOmega }\mid x(\varsigma )\mid ^2\textrm{d}\varsigma +\textrm{TV}(x) \end{aligned}$$

with $\beta >0$. And TV(x) denotes the total variation of x (Rudin et al. 1992; Beck and Teboulle 2009a, b). Then (30) can be written as

$$\begin{aligned} x=\arg \min \limits _{z\in L^2(\varOmega )}\left\{ \frac{1}{2\beta }\Vert z-\beta \xi \Vert _{L^2(\varOmega )}^2+\textrm{TV}(z)\right\} . \end{aligned}$$

(32)

Next, we conduct numerical simulations in two types of cases and adopt the parameter identification model with the form

$$\begin{aligned} \left\{ \begin{array}{ll} -\varDelta y+xy=f, &{} \quad \hbox {in } \varOmega , \\ y=g, &{} \quad \hbox {on }{\partial \varOmega .} \end{array} \right. \end{aligned}$$

(33)

Here, $\varOmega \subset \mathbb {R}^d,d\le 3$ is a bounded domain with Lipschitz boundary $\partial \varOmega$. And the function $f\in \mathcal {H}^{-1}(\varOmega )$, $g\in \mathcal {H}^{1/2}(\varOmega )$ are given. Assume that the sought solution $x^\dagger \in L^2(\varOmega )$. The key idea on elliptic equation shows that (33) has a unique solution for every x in the domain

$$\begin{aligned} \mathcal {D}:=\{x\in L^2(\varOmega ):\Vert x-\tilde{x}\Vert _{L^2(\varOmega )}\le \gamma _0~\mathrm{for~some}~\tilde{x}\ge 0,~\mathrm{a.e.}\} \end{aligned}$$

with some $\gamma _0>0$. Consequently, in this problem, the nonlinear operator $F:\mathcal {X}\rightarrow \mathcal {Y}$ is defined as the parameter-to-solution mapping $F(x):=y(x)$. We know that F is Fréchet differentiable (Jin and Maass 2012). And its Fréchet derivative as well as the adjoint can be found by the following principle:

$$\begin{aligned} F'(x)h=-A(x)^{-1}(hF(x)),~~~h\in L^2(\varOmega ), \\ F'(x)^*\omega =-y(x)A(x)^{-1}(\omega ),~~~\omega \in L^2(\varOmega ), \end{aligned}$$

where A(x) is defined by $A(x)y:=-\varDelta y+xy$. It is known that $F'(x)$ is locally Lipschitz continuous so as the tangential cone condition (11) holds (Real and Jin 2020).

4.1 Sparsity

Considering the sparse nature of the solution, we give the following parameter settings:

• Let $\varOmega =[0,1]$, $f_1(x)=300e^{-10(x-0.5)^2}$, and the boundary data $y(0)=1$, $y(1)=6$, the sparse solution

  $$\begin{aligned} x^\dagger (t)= \left\{ \begin{array}{ll} 0.5,&{}\quad t\in [0.292,0.300], \\ 1,&{}\quad t\in [0.500,0.508], \\ 0.7,&{}\quad t\in [0.700,0.708],\\ 0,&{}\quad \text{ otherwise }. \end{array} \right. \end{aligned}$$

• In the finite difference process of the forward problem, the grid size is set to $h=1/N$ with the grid $N=128$.

• Set $\eta =0.1$, $\tau =2$ and $C_F=0.1$. Moreover, we take $f(n)=1/n^{1.1}$ in Algorithm 2.

In Table 1, we consider several different $C_*=1\%,0.1\%,0.01\%$ of (13) for comparison. At the same time, several reference indicators are listed such as iteration steps $n_*$, CPU time T and relative error $\Vert x_{n_*}^\delta -x_*\Vert /\Vert x_*\Vert$.

Table 1 Comparisons between Landweber-$\varTheta$ and ATPG-$\varTheta$ methods for the sparsity problem

By comparison, it is found that under different $C_*$, the effect of iteration steps and computation time is obvious, which reflects the superiority of ATPG-$\varTheta$ method over Landweber-$\varTheta$ method. The resource consumption of ATPG-$\varTheta$ method (iteration and computation cost) is only about 10$\%$ that of Landweber-$\varTheta$ method. Meanwhile, under the same conditions, the relative error of ATPG-$\varTheta$ is smaller than that of Landweber-$\varTheta$ after the iteration stops, that is, it is closer to the true solution.

As can be seen more clearly from Fig. 1, the iterative acceleration advantage of ATPG-$\varTheta$ will be more obvious. At the same time, we can see that the combined parameter gradually approaches 1 as the iteration progresses to achieve a better speedup effect.

Fig. 1

Reconstructed data generated at $C_*=0.01\%$ in sparsity problem

More visually, Fig. 2 shows the refactoring results for different scenarios. The left column represents the reconstruction results after 1000 iterations for different methods, and the right column represents 5000 iterations. First of all, we find that in the iterative method without convex penalty (first row), the propagation results are more oscillating, and the sparse points cannot be caught. By comparing the results of the second and third rows, it can be seen that under the same conditions, the reconstruction results of ATPG-$\varTheta$ are more satisfactory.

Fig. 2

The reconstruction results

4.2 Piece-wise continuity property

Next, we consider the case of piecewise continuity, and simulate the two dimensions separately (Rudin et al. 1992; Zhu and Chan 2008).

4.2.1 One-dimensional case

In one-dimensional case, some related parameters are set as follows

• Let $\varOmega =[0,1]$, and the boundary data $y(0)=1$, $y(1)=6$, the sought solution

  $$\begin{aligned} x^\dagger (t)= \left\{ \begin{array}{ll} 1.5,&{}\quad t\in [0.1563,0.3120], \\ 2.5,&{}\quad t\in [0.3120,0.5469], \\ 1.3,&{}\quad t\in [0.5469,0.7813],\\ 0.5,&{}\quad t\in [0.7813,1.0],\\ 0,&{}\quad \text{ otherwise }. \end{array} \right. \end{aligned}$$

  And $f_2(x)=x^\dagger (1+5x)$.

• In the finite difference process of the forward problem, the grid size is set to $h=1/N$ with the grid $N=128$.

• Set $\eta =0.1$, $\tau =1.05$ and $C_F=0.1$. Moreover, we take $f(n)=1/n^{1.1}$ in Algorithm 2.

Table 2 Comparisons between Landweber-$\varTheta$ and ATPG-$\varTheta$ methods in the piecewise continuous case for a one-dimensional example

Table 2 shows the numerical results for different values of $C_*$. It is obvious that ATPG-$\varTheta$ has great advantages both in terms of iteration speed and computational consumption. Moreover, the relative error will be smaller after the iteration stops.

Similar to the analysis in the above example, Fig. 3 intuitively shows the wide applicability of the proposed method. On the one hand, the first line shows that the reconstruction results without convex penalties are not satisfactory. On the other hand, under the same conditions, the results of ATPG-$\varTheta$ in the third row are obviously better than those of Landweber-$\varTheta$ in the second row.

Fig. 3

The reconstruction results

Figure 4 shows parameters such as residual curve and relative error curve, which can directly see the difference between the two methods.

Fig. 4

Parametric curves in 500 iterations

4.2.2 Two-dimensional case

In two-dimensional case, some related parameters are set as follows:

• Let $\varOmega =[0,1]\times [0,1]$, and the sought solution

  $$\begin{aligned} x^\dagger (t)= \left\{ \begin{array}{ll} 0.25,&{}\quad \textrm{if}~(x-0.35)^2+(y-0.75)^2\le 0.2, \\ 0.5,&{}\quad \textrm{if}~ (x-0.65)^2+(y-0.36)^2\le 0.18,\\ 0,&{}\quad \text{ otherwise }. \end{array} \right. \end{aligned}$$

  And $f_3(x)=-5e^{x}e^{-2y}+x^\dagger e^{x}e^{-2y}$.

• In the multigrid process of the forward problem, the grid size is set to $h=1/N^2$ with the grid $N=32\times 32$.

• Set $\eta =0.1$, $\tau =1.1$ and $C_F=0.1$. Moreover, we take $f(n)=1/n^{1.1}$ in Algorithm 2.

As in the analysis of the results of the first two examples, Table 3 also shows the same conclusion in the two-dimensional case. It shows that ATPG-$\varTheta$ is still very powerful and practical in this case.

In Fig. 5, we can see the reconstruction results of the three types of methods. The first picture shows that reasonable approximate solutions can not be obtained without convex penalty terms. We can see that there is no proper feedback at the inflection point. Meanwhile, under the same conditions, the reconstruction result of ATPG-$\varTheta$ is closer to the sought solution.

5 Conclusions

In this paper, we propose an accelerated method (ATPG-$\varTheta$) for solving inverse problems. This method can be regarded as a combination of two-point gradient method and adaptive step size. In addition, the convex penalty term is proposed to solve the case that the true solution has special properties. In the theoretical analysis, we analyze the iteration mechanism of ATPG-$\varTheta$, and verify the strong convergence of the method. Numerically, we show numerical results with different properties of the true solution. ATPG-$\varTheta$ has outstanding acceleration advantage and reconstruction effect.

In the following research, we will continue to study the acceleration method of inverse problem solving and apply it to a wider range of practical applications.

Table 3 Comparisons between Landweber-$\varTheta$ and ATPG-$\varTheta$ methods in the piecewise continuous case for a two-dimensional example

Fig. 5

The reconstruction results