Iterative approaches for solving equilibrium problems, zero point problems and fixed point problems in Hadamard spaces

Abstract

In this paper, we introduce a new iterative algorithm for approximating a common element of the set of solutions of an equilibrium problem, a common zero of a finite family of monotone operators and the set of fixed points of nonexpansive mappings in Hadamard spaces. We also give numerical examples to solve a nonconvex optimization problem in a Hadamard space to support our main result.

1 Introduction

Equilibrium problems were originally studied in Blum and Oettli (1994) as a unifying class of variational problems. Let K be a nonempty closed convex subset of a Hadamard space X and $f: K\times K\rightarrow {\mathbb {R}}$ be a bifunction. An equilibrium problem is to find $x\in K$ such that

$$\begin{aligned} f(x,y)\ge 0,\,\,\text {for all }y\in K. \end{aligned}$$

(1.1)

The solution set of the equilibrium problem (1.1) is denoted by EP(f, K). Equilibrium problems and their generalizations have been important tools for solving problems arising in the fields of linear or nonlinear programming, variational inequalities, complementary problems, optimization problems, fixed point problems and have been widely applied to physics, structural analysis, management sciences and economics. An extragradient method for equilibrium problems in a Hilbert space has been studied in Quoc et al. (2008). It has the following form:

$$\begin{aligned} y_n&\in \textrm{Argmin}_{y\in K}\left\{ f(x_n,y)+\frac{1}{2\lambda _n}\Vert x_n-y\Vert ^2\right\} ,\\ x_{n+1}&\in \textrm{Argmin}_{y\in K}\left\{ f(y_n,y)+\frac{1}{2\lambda _n}\Vert x_n-y\Vert )^2\right\} . \end{aligned}$$

Under certain assumptions, the weak convergence of the sequence $\{x_n\}$ to a solution of the equilibrium problem has been established. In recent years some algorithms defined to solve equilibrium problems, variational inequalities and minimization problems, have been extended from the Hilbert space framework to the more general setting of Riemannian manifolds, especially Hadamard manifolds and the Hilbert unit ball. This popularization is due to the fact that several nonconvex problems may be viewed as a convex problem under such perspective. Equilibrium problems in Hadamard spaces were recently investigated in (Iusem and Mohebbi 2020; Khatibzadeh and Mohebbi 2019, 2021; Khatibzadeh and Ranjbar 2017; Kumam and Chaipunya 2017). In 2019, Khatibzadeh and Mohebbi (2019) studied $\Delta$-convergence and strong convergence of the sequence generated by the extragradient method for pseudo-monotone equilibrium problems in Hadamard spaces. Furthermore, in Khatibzadeh and Mohebbi (2021), the authors proved $\Delta$-convergence of the sequence generated by the proximal point algorithm to an equilibrium point of the pseudo-monotone bifunction and the strong convergence under additional assumptions on the bifunction in Hadamard spaces.

One of the most important problems in monotone operator theory is approximating a zero of a monotone operator. Martinet (1970) introduced one of the most popular methods for approximating a zero of a monotone operator in Hilbert spaces that is called the proximal point algorithm; see also (Bruck and Reich 1977; Rockafellar 1976). In 2017, Khatibzadeh and Ranjbar (2017) generalized monotone operators and their resolvents to Hadamard spaces by using the duality theory. Very recently, Moharami and Eskandani (2020) proposed the following hybrid extragradient method for approximating a common element of the set of solutions of an equilibrium problem for a single bifunction f and a common zero of a finite family of monotone operators $A_1,A_2,\ldots ,A_N$ in Hadamard spaces;

$$\begin{aligned} \left\{ \begin{aligned}&z_n=J_{\gamma _n^{N}}^{A_N}\circ J_{\gamma _n^{N-1}}^{A_{N-1}}\circ \cdots \circ J_{\gamma _n^{1}}^{A_1}x_n,\\&y_n=\textrm{argmin}_{y\in K}\left\{ f(z_n,y)+\frac{1}{2\lambda _n}d(z_n,y)^2\right\} ,\\&w_n=\textrm{argmin}_{y\in K}\left\{ f(y_n,y)+\frac{1}{2\lambda _n}d(z_n,y)^2\right\} ,\\&x_{n+1}=\alpha _n u \oplus (1-\alpha _n) w_n,\,\,\,n\in {\mathbb {N}}, \end{aligned} \right. \end{aligned}$$

(1.2)

where $\{\alpha _n\}$, $\{\lambda _n\}$ and $\{\gamma _n^i\}$ are sequences satisfying some conditions. They proved strong convergence theorem of the sequence $\{x_n\}$ generated by the above scheme.

In recent years, the problem of finding a common element of the set of solutions for equilibrium problems, zero-point problems and fixed point problems in the framework of Hilbert spaces, Banach spaces and Hadamard spaces have been intensively studied by many authors, for instance, see (Alakoya and Mewomo 2022; Alakoya et al. 2022a, b; Eskandani and Raeisi 2019; Iusem and Mohebbi 2020; Khatibzadeh and Ranjbar 2017; Kumam and Chaipunya 2017; Li et al. 2009; Moharami and Eskandani 2020; Ogwo et al. 2021; Uzor et al. 2022).

Motivated and inspired by the above results, in this paper, we propose a new iterative algorithm by using a modified hybrid extragradient method for finding a common element of the set of solutions of an equilibrium problem, a common zero of a finite family of monotone operators and the set of fixed points for nonexpansive mappings in Hadamard spaces. The $\Delta$-convergence theorem is established under suitable assumptions. We also provide a numerical example to illustrate and show the efficiency of the proposed algorithm for supporting our main results.

2 Preliminaries

In this section, we will mention basic concepts, definitions, notations, and some useful lemmas on Hadamard spaces for use in the next sections. Let (X, d) be a metric space. A geodesic from x to y is a map $\gamma$ from the closed interval $[0,d(x,y)]\subset {\mathbb {R}}$ to X such that $\gamma (0)=x,\gamma (d(x,y))=y$ and $d(\gamma (t_1),\gamma (t_2))=|t_1-t_2|$ for all $t_1,t_2\in [0,d(x,y)].$ The image of $\gamma$ is called a geodesic (or metric) segment joining x and y. When it is unique, this geodesic segment is denoted by [x, y]. The space X is said to be a geodesic metric space if every two points of X are joined by a geodesic, and X is said to be uniquely geodesic metric space if there is exactly one geodesic joining x and y for each $x,y\in X$. A subset C of X is said to be convex, if for any two points $x,y\in C$, the geodesic joining x and y is contained in C. Let X be a uniquely geodesic metric space. For each $x,y\in X$ and for each $\alpha \in [0,1]$, there exists a unique point $z\in [x,y]$ such that $d(x, z) = (1-\alpha ) d(x, y)$ and $d(y, z) = \alpha d(x, y)$. We denote the unique point z by $\alpha x \oplus (1-\alpha )y$. A geodesic metric space (X, d) is a CAT(0) space if it satisfies the $(CN^*)$ inequality (Dhompongsa and Panyanak 2008):

$$\begin{aligned} d\left( z,\alpha x\oplus (1-\alpha )y\right) ^2\le \alpha d(z,x)^2+ (1-\alpha )d(z,y)^2 - \alpha (1-\alpha )d(x,y)^2, \end{aligned}$$

for all $x,y,z\in X$ and $\alpha \in [0,1]$. In particular, if x, y, z are points in X and $\alpha \in [0,1]$, then we have

$$\begin{aligned} d\left( z,\alpha x\oplus (1-\alpha )y\right) \le \alpha d(z,x)+ (1-\alpha )d(z,y). \end{aligned}$$

It is well known that a CAT(0) space is a uniquely geodesic space. A complete CAT(0) space is called a Hadamard space. Hilbert spaces and ${\mathbb {R}}$-trees are two basic examples of Hadamard spaces, which in some sense represent the most extreme cases; curvature 0 and curvature $-\infty$. The most illuminating instances of Hadamard spaces are Hadamard manifolds. A Hadamard manifold is a complete simply connected Riemannian manifold of nonpositive sectional curvature. The class of Hadamard manifolds includes hyperbolic spaces, manifolds of positive definite matrices, the complex Hilbert ball with the hyperbolic metric and many other spaces (see Goebel and Reich 1984; Kohlenbach 2015; Tits 1977).

In the following examples, we give some Hadamard spaces.

Example 2.1

Consider ${\mathcal {H}}=\{(x,y)\in {\mathbb {R}}^2: y^2-x^2=1\,\text {and }y>0\}$. Let d be a metric defined by the function $d:{\mathcal {H}}\times {\mathcal {H}}\rightarrow {\mathbb {R}}$ that assigns to each pair of vectors $u=(u_1,u_2)$ and $v=(v_1,v_2)$ the unique nonnegative number $d(u,v)\ge 0$ such that

$$\begin{aligned} \cosh d(u,v)=u_2v_2-u_1v_1. \end{aligned}$$

It is known that, in general, the metric space $({\mathcal {H}},d)$ is a Hadamard space and also a one-dimensional hyperbolic space (see Bridson and Haefliger 1999; Kaewkhao et al. 2015). Furthermore, it is easy to see that $({\mathcal {H}},d)$ is an ${\mathbb {R}}$-tree.

Example 2.2

Let ${\mathcal {M}}=P(n,{\mathbb {R}})$ be the space of $(n\times n)$ positive symmetric definite matrices endowed with the Riemannian metric

$$\begin{aligned} \langle A,B\rangle _E:= Tr(E^{-1}AE^{-1}B), \end{aligned}$$

for all $A,B\in T_E({\mathcal {M}})$ and every $E\in {\mathcal {M}}$, where $T_E({\mathcal {M}})$ denotes the tangent plane at $E\in {\mathcal {M}}$. Therefore, $({\mathcal {M}},\langle A,B \rangle >_E)$ is a Hadamard space (see Khatibzadeh and Mohebbi 2019).

Example 2.3

Let $Y=\{(x,e^x): x\in {\mathbb {R}}\}$ and $X_n=\{(n,y): y\ge e^n\}$ for each $n\in {\mathbb {Z}}$. Set ${\mathcal {M}}=Y\cup \bigcup \limits _{n \in {{\mathbb {Z}}}} {X_n }$ equipped with a metric $d: X\times X \rightarrow [0,\infty )$, defined for all $x=(x_1,x_2),y=(y_1,y_2)\in X$ by

where ${\dot{\gamma }}$ is the derivative of the curve $\gamma : {\mathbb {R}}\rightarrow X$ given as $\gamma (t)=(t,e^t)$ for each $t\in {\mathbb {R}}$. Therefore, $({\mathcal {X}},d)$ is a Hadamard space (see Chaipunya and Kumam 2017).

Let K be a nonempty subset of a Hadamard space X and $T: K\rightarrow K$ be a mapping. The fixed point set of T is denoted by F(T), that is, $F(T) = \{x\in K: x = Tx\}$. Recall that a mapping T is called nonexpansive if

$$\begin{aligned} d(Tx,Ty)\le d(x,y) \end{aligned}$$

for all $x,y\in K$.

The fixed point theory in Hadamard spaces was first studied by Kirk (2003) in 2003. Many authors have then published papers on the existence and convergence of fixed points for nonlinear mappings in such spaces (e.g., see Bačák and Reich 2014; Nanjaras et al. 2010; Phuengrattana and Suantai 2012, 2013; Reich and Salinas 2015, 2016, 2017; Reich and Shafrir 1990; Sopha and Phuengrattana 2015).

The notion of the asymptotic center can be introduced in the general setting of a Hadamard space X as follows: Let $\{x_n\}$ be a bounded sequence in X. For $x\in X$, we define a mapping $r\left( \cdot ,\{x_{n}\} \right) :X\rightarrow [0,\infty )$ by

$$\begin{aligned} r\left( x,\{x_{n}\} \right) = \limsup _{n\rightarrow \infty } d(x, x_n). \end{aligned}$$

The asymptotic radius of $\{x_{n}\}$ is given by

$$\begin{aligned} r\left( \{x_{n}\} \right) =\inf \left\{ r\left( x,\{x_{n}\} \right) :x\in X\right\} , \end{aligned}$$

and the asymptotic center of $\{x_{n}\}$ is the set

$$\begin{aligned} A\left( \{x_{n}\} \right) =\left\{ x\in X:r\left( x,\{x_{n}\} \right) =r\left( \{x_{n}\} \right) \right\} . \end{aligned}$$

It is known that in a Hadamard space, the asymptotic center $A\left( {\left\{ {x_n } \right\} } \right)$ consists of exactly one point (Dhompongsa et al. 2006). A sequence $\{x_n\}$ in a Hadamard space X is said to be $\Delta$-converge to $x\in X$ if x is the unique asymptotic center of $\{u_n\}$ for every subsequence $\{u_n\}$ of $\{x_n\}$. It is well known that every bounded sequence in a Hadamard space has a $\Delta$-convergent subsequence (Kirk and Panyanak 2008).

Lemma 2.4

(Ranjbar and Khatibzadeh 2016) Let X be a Hadamard space and $\{x_n\}$ be a sequence in X. If there exists a nonempty subset F of X satisfying:

• (i) For every $z\in F$, $\lim _{n\rightarrow \infty }d(x_n,z)$ exists.

• (ii) If a subsequence $\{x_{x_k}\}$ of $\{x_n\}$ $\Delta$-converges to $x\in X$, then $x\in F$.

Then, there exists $p\in F$ such that $\{x_n\}$ $\Delta$-converges to $p\in X$.

Lemma 2.5

(Dhompongsa and Panyanak 2008) Let K be a nonempty closed and convex subset of a Hadamard space X, $T:K\rightarrow K$ be a nonexpansive mapping and $\{x_n\}$ be a bounded sequence in K such that $\lim _{n\rightarrow \infty } d(x_n,Tx_n)=0$ and $\{x_n\}$ $\Delta$-converges to x. Then $x=Tx$.

A function $g:K\rightarrow (-\infty ,\infty ]$ defined on a nonempty convex subset K of a Hadamard space is convex if $g(tx\oplus (1-y)y)\le tg(x) + (1-t)g(y)$ for all $x,y\in K$ and $t\in (0,1)$. We say that a function g defined on K is lower semicontinuous (or upper semicontinuous) at a point $x\in K$ if

$$\begin{aligned} g(x)\le \liminf _{n\rightarrow \infty }g(x_n)\,\,\left( \text {or } \limsup _{n\rightarrow \infty }g(x_n)\le g(x)\right) , \end{aligned}$$

for each sequence $\{x_n\}$ such that $\lim _{n\rightarrow \infty }x_n= x$. A function g is said to be lower semicontinuous (or upper semicontinuous) on K if it is lower semicontinuous (or upper semicontinuous) at any point in K.

In 2010, Kakavandi and Amini (2010) introduced the concept of quasilinearization in a Hadamard space X, see also (Berg and Nikolaev 2008), as follows:

Denote a pair $(a,b)\in X\times X$ by $\overrightarrow{ab}$ and call it a vector. The quasilinearization is a map $\langle \cdot ,\cdot \rangle : (X\times X)\times (X\times X)\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} \langle \overrightarrow{ab},\overrightarrow{cd} \rangle = \frac{1}{2}\left( d(a,d)^2 + d(b,c)^2 - d(a,c)^2 - d(b,d)^2\right) \end{aligned}$$

for any $a,b,c,d\in X$. We say that X satisfies the Cauchy-Schwarz inequality if

$$\begin{aligned} \langle \overrightarrow{ab},\overrightarrow{cd} \rangle \le d(a,b)d(c,d) \end{aligned}$$

for any $a,b,c,d\in X$. It is known that a geodesically connected metric space is a CAT(0) space if and only if it satisfies the Cauchy–Schwarz inequality; see (Berg and Nikolaev 2008). Later, Kakavandi and Amini (2010) defined a pseudometric D on ${\mathbb {R}}\times X\times X$ by

$$\begin{aligned} D((t,a,b),(s,u,v)) = L(\Theta (t,a,b)-\Theta (s,u,v)), \end{aligned}$$

where $\Theta : {\mathbb {R}}\times X\times X\rightarrow C(X;{\mathbb {R}})$ defined by $\Theta (t,a,b)(x) = t \langle \overrightarrow{ab},\overrightarrow{ax} \rangle$ for all $x\in X$ and $C(X;{\mathbb {R}})$ is the space of all continuous real-valued functions on X. For a Hadamard space X, it is obtained that $D((t,a,b),(s,u,v))=0$ if and only if $t \langle \overrightarrow{ab},\overrightarrow{xy} \rangle = s \langle \overrightarrow{uv},\overrightarrow{xy} \rangle$ for all $x,y\in X$. Then, D can impose an equivalent relation on ${\mathbb {R}}\times X\times X$, where the equivalence class of (t, a, b) is

$$\begin{aligned} \left[ t \overrightarrow{ab}\right] = \left\{ s \overrightarrow{uv}: t \langle \overrightarrow{ab},\overrightarrow{xy} \rangle = s \langle \overrightarrow{uv},\overrightarrow{xy} \rangle \right\} . \end{aligned}$$

The set $X^* = \{[t \overrightarrow{ab}]: (t,a,b)\in {\mathbb {R}}\times X\times X\}$ is a metric space with metric $D([tab],[scd]):=D((t,a,b),(s,c,d))$, which is called the dual metric space of X. It is clear that $[\overrightarrow{aa}=\overrightarrow{bb}]$ for all $a,b\in X$. Fix $o\in X$, we write $0=\overrightarrow{oo}$ as the zero of the dual space. Note that $X^*$ acts on $X\times X$ by $\langle x^*,\overrightarrow{xy} \rangle = t \langle \overrightarrow{ab},\overrightarrow{xy} \rangle$, $(x^*=[t\overrightarrow{ab}]\in X^*,\,x,y\in X)$.

Let X be a Hadamard space with dual $X^*$ and let $A: X \rightrightarrows X^*$ be a multi-valued operator with domain $D(A):=\{x\in X| Ax\ne \emptyset \}$, range $R(A):=\cup _{x\in X}Ax$, $A^{-1}(x^*):=\{x\in X| x^*\in Ax\}$ and graph $gra(A):=\{(x,x^*)\in X\times X^* | x\in D(A), x^*\in Ax\}$. A multi-valued $A: X \rightrightarrows X^*$ is said to be monotone (Khatibzadeh and Mohebbi 2019) if the inequality $\langle x^*-y^*, \overrightarrow{yx}\rangle \ge 0$ holds for every $(x,x^*),(y,y^*)\in gra(A)$. A monotone operator $A: X \rightrightarrows X^*$ is maximal if there exists no monotone operator $B: X \rightrightarrows X^*$ such that gra(B) properly contains gra(A), that is, for any $(y,y^*)\in X\times X^*$, the inequality $\langle x^*-y^*, \overrightarrow{yx}\rangle \ge 0$ for all $(x,x^*)\in gra(A)$ implies that $y^*\in Ay$. The resolvent of A of order $\gamma$, is the multi-valued mapping $J^A_{\gamma }: X \rightrightarrows X$, defined by $J^A_{\gamma }(x):=\{z\in X | [\frac{1}{\gamma } \overrightarrow{zx}]\in Az\}$. Indeed

$$\begin{aligned} J^A_{\gamma }=(\overrightarrow{oI}+\gamma A)^{-1}\circ \overrightarrow{oI}, \end{aligned}$$

where o is an arbitrary member of X and $\overrightarrow{oI}(x):=[\overrightarrow{ox}]$. It is obvious that this definition is independent of the choice of o.

Theorem 2.6

(Khatibzadeh and Ranjbar 2017) Let X be a Hadamard space with dual $X^*$. and let $A: X \rightrightarrows X^*$ be a multi-valued mapping. Then

• (i) For any $\gamma >0$, $R(J_\gamma ^A)\subset D(A)$, $F(J_\gamma ^A)=A^{-1}(0)$.

• (ii) If A is monotone, then $J_\gamma ^A$ is single-valued on its domain and

  $$\begin{aligned} d(J_\gamma ^Ax,J_\gamma ^Ay)^2\le \langle \overrightarrow{J_\gamma ^AxJ_\gamma ^Ay},\overrightarrow{xy}\rangle ,\, \forall x,y\in D(J_\gamma ^A). \end{aligned}$$

  In particular, $J_\gamma ^A$ is a nonexpansive mapping.

• (iii) If A is monotone and $0<\gamma \le \mu$, then $d(J_\gamma ^Ax,J_\mu ^Ax)^2\le \frac{\mu -\gamma }{\mu +\gamma }d(x,J_\mu ^Ax)^2$, which implies that $d(x,J_\gamma ^Ax)\le 2d(x,J_\mu ^Ax)$.

It is well known that if T is a nonexpansive mapping on a subset K of a Hadamard space X, then F(T) is closed and convex. Thus, if A is a monotone operator on a Hadamard space, then, by parts (i) and (ii) of Theorem 2.6, $A^{-1}(0)$ is closed and convex. Also by using part (ii) of Theorem 2.6 for all $u\in F(J_\gamma ^A)$ and $x\in D(J_\gamma ^A)$, we have

$$\begin{aligned} d(J_\gamma ^Ax,x)^2\le d(u,x)^2-d(u,J_\gamma ^Ax)^2. \end{aligned}$$

(2.1)

We say that $A: X \rightrightarrows X^*$ satisfies the range condition if, for every $\lambda >0$, $D(J^A_{\lambda })=X$. It is known that if A is a maximal monotone operator on a Hilbert space H, then $R(I+\lambda A)=H$ for all $\lambda >0$. Thus, every maximal monotone operator A on a Hilbert space satisfies the range condition. Also as it has been shown in Li et al. (2009) if A is a maximal monotone operator on a Hadamard manifold, then A satisfies the range condition.

For solving the equilibrium problem, we assume that the bifunction $f:K\times K \rightarrow {\mathbb {R}}$ satisfies the following assumption.

Assumption 2.7

Let K be a nonempty closed convex subset of a Hadamard space X. Let $f:K\times K \rightarrow {\mathbb {R}}$ be a bifunction satisfies the following conditions:

$(B_1)$:

$f(x,\cdot ):X\rightarrow {\mathbb {R}}$ is convex and lower semicontinuous for all $x\in X$.

$(B_2)$:

$f(\cdot ,y)$ is $\Delta$-upper semicontinuous for all $y\in X$.

$(B_3)$:

f is Lipschitz-type continuous, i.e. there exist two positive constants $c_1$ and $c_2$ such that

$$\begin{aligned} f(x,y) + f(y,z) \ge f(x,z) - c_1d(x,y)^2-c_2d(y,z)^2,\,\,\text {for all }x,y,z\in X. \end{aligned}$$

$(B_4)$:

f is pesudo-monotone, i.e. for every $x,y\in X$, $f(x,y)\ge 0$ implies $f(y,x)\le 0$.

Remark 2.8

It is known in Moharami and Eskandani (2020) that if a bifunction f satisfying conditions $(B_1)$, $(B_2)$ and $(B_4)$ of Assumption 2.7, then EP(f, K) is closed and convex.

3 Main results

In this section, we prove $\Delta$-convergence theorems for finding a common element of the set of solutions to an equilibrium problem, a common zero of a finite family of monotone operators and the set of fixed points of nonexpansive mappings in Hadamard spaces. In order to prove our main results, the following two lemmas are needed.

Lemma 3.1

Let K be a nonempty closed convex subset of a Hadamard space X and let $f:K\times K \rightarrow {\mathbb {R}}$ be a bifunction satisfying Assumption 2.7. Let $A_1,A_2,\ldots ,A_N: X \rightrightarrows X^*$ be N multi-valued monotone operators that satisfy the range condition with $D(A_N)\subset K$ and let $T:K\rightarrow K$ be a nonexpansive mapping. Assume that $\Theta = F(T) \cap EP(f,K) \cap \bigcap _{i=1}^N A_i^{-1}(0) \ne \emptyset$. Let $x_1\in K$ and $\{x_n\}$ be a sequence generated by

$$\begin{aligned} \left\{ \begin{aligned}&z_n=J_{\gamma _n^{N}}^{A_N}\circ J_{\gamma _n^{N-1}}^{A_{N-1}}\circ \cdots \circ J_{\gamma _n^{1}}^{A_1}x_n,\\&y_n=\textrm{argmin}_{y\in K}\left\{ f(z_n,y)+\frac{1}{2\lambda _n}d(z_n,y)^2\right\} ,\\&w_n=\textrm{argmin}_{y\in K}\left\{ f(y_n,y)+\frac{1}{2\lambda _n}d(z_n,y)^2\right\} ,\\&v_{n}=\beta _nx_n \oplus (1-\beta _n) Tz_n,\\&x_{n+1}=\alpha _n w_n \oplus (1-\alpha _n) Tv_n,\,\,\,n\in {\mathbb {N}}, \end{aligned} \right. \end{aligned}$$

(3.1)

where $\{\alpha _n\}, \{\beta _n\} \subset (0,1)$, $0<\alpha \le \lambda _n\le \beta < \min \{\frac{1}{2c_1},\frac{1}{2c_2}\}$ and $\{\gamma _n^i\} \subset (0,\infty )$ for all $i=1,2,\ldots ,N$. If $x^*\in \Theta$, then we have the following:

• (i) $f(y_n,w_n)\le \frac{1}{2\lambda _n}[d(z_n,x^*)^2-d(z_n,w_n)^2-d(w_n,x^*)^2]$;

• (ii) $\left( \frac{1}{2\lambda _n}-c_1\right) d(z_n,y_n)^2 +\left( \frac{1}{2\lambda _n}-c_2\right) d(y_n,w_n)^2-\frac{1}{2\lambda _n}d(z_n,w_n)^2\le f(y_n,w_n)$;

• (iii) $d(w_n,x^*)^2\le d(z_n,x^*)^2-(1-2c_1\lambda _n)d(z_n,y_n)^2-(1-2c_2\lambda _n)d(y_n,w_n)^2$.

Proof

The proof of this fact is similar to that of (Khatibzadeh and Mohebbi 2019, Lemma 2.1). For convenience of the readers, we include the details.

(i) Take $x^*\in \Theta$. By letting $y=tw_n\oplus (1-t)x^*$ such that $t\in [0,1)$, we have

$$\begin{aligned} f(y_n,w_n)+\frac{1}{2\lambda _n}d(z_n,w_n)^2&\le f(y_n,y) +\frac{1}{2\lambda _n}d(z_n,y)^2\\&=f(y_n,tw_n\oplus (1-t)x^*) +\frac{1}{2\lambda _n}d(z_n,tw_n\oplus (1-t)x^*)^2\\&\le tf(y_n,w_n) +(1-t)f(y_n,x^*)+\frac{1}{2\lambda _n}(td(z_n,w_n)^2\\&\quad +(1-t)d(z_n,x^*)^2-t(1-t)d(w_n,x^*)^2). \end{aligned}$$

Since $f(x^*,y_n)\ge 0$, pseudo-monotonicity of f implies that $f(y_n,x^*)\le 0$. Thus, we can write the above inequality as

$$\begin{aligned} f(y_n,w_n)\le \frac{1}{2\lambda _n}\left( d(z_n,x^*)^2 - d(z_n,w_n)^2 -td(w_n,x^*)^2\right) . \end{aligned}$$

Now, if $t\rightarrow 1^-$, we get

$$\begin{aligned} f(y_n,w_n)\le \frac{1}{2\lambda _n}\left( d(z_n,x^*)^2 - d(z_n,w_n)^2 -d(w_n,x^*)^2\right) . \end{aligned}$$

(ii) By letting $y=ty_n\oplus (1-t)w_n$ such that $t\in [0,1)$, we have

$$\begin{aligned} f(z_n,y_n)+\frac{1}{2\lambda _n}d(z_n,y_n)^2&\le f(z_n,y) +\frac{1}{2\lambda _n}d(z_n,y)^2\\&=f(z_n,ty_n\oplus (1-t)w_n) +\frac{1}{2\lambda _n}d(z_n,ty_n\oplus (1-t)w_n)^2\\&\le tf(z_n,y_n) +(1-t)f(z_n,w_n)+\frac{1}{2\lambda _n}(td(z_n,y_n)^2\\&\quad +(1-t)d(z_n,w_n)^2-t(1-t)d(y_n,w_n)^2), \end{aligned}$$

which implies that

$$\begin{aligned} f(z_n,y_n) - f(z_n,w_n)\le \frac{1}{2\lambda _n}\left( d(z_n,w_n)^2 - d(z_n,y_n)^2 -td(y_n,w_n)^2\right) . \end{aligned}$$

Now, if $t\rightarrow 1^-$, we get

$$\begin{aligned} f(z_n,y_n) - f(z_n,w_n)\le \frac{1}{2\lambda _n}\left( d(z_n,w_n)^2 - d(z_n,y_n)^2 -d(y_n,w_n)^2\right) . \end{aligned}$$

(3.2)

Also, by $(B_3)$, f is Lipschitz-type continuous with constants $c_1$ and $c_2$, hence we have

$$\begin{aligned} -c_1d(z_n,y_n)^2 - c_2d(y_n,w_n)^2 + f(z_n,w_n) - f(z_n,y_n)\le f(y_n,w_n). \end{aligned}$$

(3.3)

It follows by (3.2) and (3.3) that

$$\begin{aligned} \left( \frac{1}{2\lambda _n}-c_1\right) d(z_n,y_n)^2 +\left( \frac{1}{2\lambda _n}-c_2\right) d(y_n,w_n)^2-\frac{1}{2\lambda _n}d(z_n,w_n)^2\le f(y_n,w_n). \end{aligned}$$

(iii) By (i) and (ii), we can conclude that

$$\begin{aligned} d(w_n,x^*)^2\le d(z_n,x^*)^2-(1-2c_1\lambda _n)d(z_n,y_n)^2-(1-2c_2\lambda _n)d(y_n,w_n)^2 \end{aligned}$$

This completes the proof. $\square$

Lemma 3.2

Let K be a nonempty closed convex subset of a Hadamard space X and let $f:K\times K \rightarrow {\mathbb {R}}$ be a bifunction satisfying Assumption 2.7. Let $A_1,A_2,\ldots ,A_N: X \rightrightarrows X^*$ be N multi-valued monotone operators that satisfy the range condition with $D(A_N)\subset K$ and let $T:K\rightarrow K$ be a nonexpansive mapping. Assume that $\Theta = F(T) \cap EP(f,K) \cap \bigcap _{i=1}^N A_i^{-1}(0) \ne \emptyset$. Let $x_1\in K$ and $\{x_n\}$ be a sequence generated by (3.1) where $\{\alpha _n\}, \{\beta _n\} \subset (0,1)$, $0<\alpha \le \lambda _n\le \beta < \min \{\frac{1}{2c_1},\frac{1}{2c_2}\}$ and $\{\gamma _n^i\} \subset (0,\infty )$ for all $i=1,2,\ldots ,N$. If $x^*\in \Theta$, then we have $d(w_n,x^*)\le d(z_n,x^*)\le d(x_n,x^*)$ and $d(x_{n+1},x^*)\le d(x_n,x^*)$.

Proof

From the nonexpansivity of $J_{\gamma _n^{i}}^{A_i}$ for all $i=1,2,\ldots ,N$, we have

$$\begin{aligned} d(z_n,x^*)&=d(J_{\gamma _n^{N}}^{A_N}\circ J_{\gamma _n^{N-1}}^{A_{N-1}}\circ \cdots \circ J_{\gamma _n^{1}}^{A_1}x_n,x^*)\\&\le d(J_{\gamma _n^{N-1}}^{A_{N-1}}\circ \cdots \circ J_{\gamma _n^{1}}^{A_1}x_n,x^*)\\&\,\,\,\vdots \\&\le d(J_{\gamma _n^{1}}^{A_1}x_n,x^*)\\&\le d(x_n,x^*). \end{aligned}$$

Using Lemma 3.1(iii), we have

$$\begin{aligned} d(w_n,x^*)\le d(z_n,x^*)\le d(x_n,x^*). \end{aligned}$$

(3.4)

By (3.1) and (3.4), we get

$$\begin{aligned} d(x_{n+1},x^*)&\le \alpha _nd(w_n,x^*) + (1-\alpha _n)d(Tv_n,x^*)\\&\le \alpha _nd(w_n,x^*) + (1-\alpha _n)d(v_n,x^*)\\&\le \alpha _nd(w_n,x^*) + (1-\alpha _n)[\beta _nd(x_n,x^*)+(1-\beta _n)d(Tz_n,x^*)]\\&\le \alpha _nd(w_n,x^*) + (1-\alpha _n)[\beta _nd(x_n,x^*)+(1-\beta _n)d(z_n,x^*)]\\&\le \alpha _nd(w_n,x^*) + (1-\alpha _n)d(x_n,x^*)\\&\le d(x_n,x^*). \end{aligned}$$

This completes the proof. $\square$

We now state and prove our main result.

Theorem 3.3

Let K be a nonempty closed convex subset of a Hadamard space X and let $f:K\times K \rightarrow {\mathbb {R}}$ be a bifunction satisfying Assumption 2.7. Let $A_1,A_2,\ldots ,A_N: X \rightrightarrows X^*$ be N multi-valued monotone operators that satisfy the range condition with $D(A_N)\subset K$ and let $T:K\rightarrow K$ be a nonexpansive mapping. Assume that $\Theta = F(T) \cap EP(f,K) \cap \bigcap _{i=1}^N A_i^{-1}(0) \ne \emptyset$. Let $x_1\in K$ and $\{x_n\}$ be a sequence generated by (3.1) where $\{\alpha _n\}, \{\beta _n\} \subset (0,1)$ and $\{\lambda _n\}, \{\gamma _n^i\} \subset (0,\infty )$ satisfy the following conditions:

• (C1) $\liminf _{n\rightarrow \infty }\gamma _n^i >0$ for all $i=1,2,\ldots ,N$,

• (C2) $0<\alpha \le \lambda _n\le \beta < \min \{\frac{1}{2c_1},\frac{1}{2c_2}\}$,

• (C3) $\lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=1}^{\infty }\alpha _n=\infty$,

• (C4) $\liminf _{n\rightarrow \infty }\beta _n(1-\beta _n)>0$.

Then the sequence $\{x_n\}$ $\Delta$-converges to a point of $\Theta$.

Proof

Let $x^*\in \Theta$. It implies by Lemma 3.2 that $d(x_{n+1},x^*)\le d(x_n,x^*)$. Therefore $\lim _{n\rightarrow \infty }d(x_n,x^*)$ exists for all $x^*\in \Theta$. This show that $\{x_n\}$ is bounded.

Put $S_n^i=J_{\gamma _n^{i}}^{A_i}\circ J_{\gamma _n^{i-1}}^{A_{i-1}}\circ \cdots \circ J_{\gamma _n^{1}}^{A_1}$, for $i=1,2,\ldots ,N$ and $n\in {\mathbb {N}}$. Then $z_n=S_n^Nx_n$. We also assume that $S_n^0=I$, where I is the identity operator. By the nonexpansivity of $S_n^i$, we have $d(S_n^ix_n,x^*)\le d(x_n,x^*)$. This implies that

$$\begin{aligned} \limsup _{n\rightarrow \infty } \left[ d(S_n^ix_n,x^*)^2 - d(x_n,x^*)^2\right] \le 0. \end{aligned}$$

(3.5)

Using (3.1) and Lemma 3.2, we can write

$$\begin{aligned} d(x_{n+1},x^*)^2&\le \alpha _nd(w_n,x^*)^2 + (1-\alpha _n)d(Tv_n,x^*)^2\\&\le \alpha _nd(x_n,x^*)^2 + (1-\alpha _n)[\beta _nd(x_n,x^*)^2 + (1-\beta _n)d(Tz_n,x^*)^2]\\&\le \alpha _nd(x_n,x^*)^2 + (1-\alpha _n)[\beta _nd(x_n,x^*)^2 + (1-\beta _n)d(z_n,x^*)^2]\\&\le \alpha _nd(x_n,x^*)^2 + (1-\alpha _n)[\beta _nd(x_n,x^*)^2 + (1-\beta _n)d(S_n^ix_n,x^*)^2]. \end{aligned}$$

So

$$\begin{aligned} d(x_{n+1},x^*)^2 - d(x_n,x^*)^2\le (1-\alpha _n)(1-\beta _n)\left[ d(S_n^ix_n,x^*)^2 - d(x_n,x^*)^2\right] . \end{aligned}$$

By the conditions (C3) and (C4), for $i=1,2,\ldots ,N$, we have

$$\begin{aligned} 0\le \liminf _{n\rightarrow \infty } \left[ d(S_n^ix_n,x^*)^2 - d(x_n,x^*)^2\right] . \end{aligned}$$

(3.6)

Using (3.5) and (3.6), we get

$$\begin{aligned} \lim _{n\rightarrow \infty } \left[ d(S_n^ix_n,x^*)^2 - d(x_n,x^*)^2\right] =0. \end{aligned}$$

(3.7)

Applying (2.1), we obtain

$$\begin{aligned} d(J_{\gamma _n^{i}}^{A_i}(S_n^{i-1}x_n),S_n^{i-1}x_n)^2&\le d(x^*,S_n^{i-1}x_n)^2 - d(x^*,S_n^{i}x_n)^2\\&\le d(x^*,x_n)^2 - d(x^*,S_n^{i}x_n)^2. \end{aligned}$$

This implies by (3.7) that

$$\begin{aligned} \lim _{n\rightarrow \infty } d(S_n^{i}x_n,S_n^{i-1}x_n)=0, \end{aligned}$$

(3.8)

and hence for any $i=1,2,\ldots ,N$, we have

$$\begin{aligned} d(x_n,S_n^{i}x_n)\le d(x_n,S_n^{1}x_n)+d(S_n^{1}x_n,S_n^{2}x_n)+\cdots +d(S_n^{i-1}x_n,S_n^{i}x_n). \end{aligned}$$

Then

$$\begin{aligned} \lim _{n\rightarrow \infty } d(x_n,S_n^{i}x_n)=0. \end{aligned}$$

(3.9)

Since $\liminf _{n\rightarrow \infty }\gamma _n^i >0$, there exists $\gamma _0\in {\mathbb {R}}$ such that $\gamma _n^i\ge \gamma _0>0$ for all $n\in {\mathbb {N}}$ and $i=1,2,\ldots ,N$. By using Theorem 2.6, for all $i=1,2,\ldots ,N$, we have

$$\begin{aligned} d(J_{\gamma _0}^{A_i}(S_n^{i-1}x_n),S_n^{i}x_n)&\le d(J_{\gamma _0}^{A_i}(S_n^{i-1}x_n),S_n^{i-1}x_n) + d(S_n^{i-1}x_n,S_n^{i}x_n)\\&\le 2d(J_{\gamma _n^i}^{A_i}(S_n^{i-1}x_n),S_n^{i-1}x_n) + d(S_n^{i-1}x_n,S_n^{i}x_n)\\&=3d(S_n^{i}x_n,S_n^{i-1}x_n). \end{aligned}$$

By (3.8), we get

$$\begin{aligned} \lim _{n\rightarrow \infty } d(J_{\gamma _0}^{A_i}(S_n^{i-1}x_n),S_n^{i}x_n)=0. \end{aligned}$$

(3.10)

Now for every $i=1,2,\ldots ,N$, we have

$$\begin{aligned} d(J_{\gamma _0}^{A_i}x_n,x_n)&\le d(J_{\gamma _0}^{A_i}x_n,J_{\gamma _0}^{A_i}(S_n^{i-1}x_n)) +d(J_{\gamma _0}^{A_i}(S_n^{i-1}x_n),S_n^{i}x_n)+d(S_n^{i}x_n,x_n)\\&\le d(x_n,S_n^{i-1}x_n) +d(J_{\gamma _0}^{A_i}(S_n^{i-1}x_n),S_n^{i}x_n)+d(S_n^{i}x_n,x_n). \end{aligned}$$

This implies by (3.9) and (3.10) that

$$\begin{aligned} \lim _{n\rightarrow \infty } d(J_{\gamma _0}^{A_i}x_n,x_n)=0. \end{aligned}$$

(3.11)

Using (3.1) and Lemma 3.2, we have

$$\begin{aligned} d(x_{n+1},x^*)^2&\le \alpha _nd(w_n,x^*)^2 + (1-\alpha _n)d(Tv_n,x^*)^2\\&\le \alpha _nd(x_n,x^*)^2 + (1-\alpha _n)d(v_n,x^*)^2\\&\le \alpha _nd(x_n,x^*)^2 + (1-\alpha _n)[\beta _nd(x_n,x^*)^2 + (1-\beta _n)d(Tz_n,x^*)^2\\&\quad - \beta _n(1-\beta _n)d(x_n,Tz_n)^2]\\&\le \alpha _nd(x_n,x^*)^2 + (1-\alpha _n)[\beta _nd(x_n,x^*)^2 + (1-\beta _n)d(z_n,x^*)^2\\&\quad - \beta _n(1-\beta _n)d(x_n,Tz_n)^2]\\&\le \alpha _nd(x_n,x^*)^2 + (1-\alpha _n)[d(x_n,x^*)^2 - \beta _n(1-\beta _n)d(x_n,Tz_n)^2]\\&\le d(x_n,x^*)^2 - \beta _n(1-\beta _n)(1-\alpha _n)d(x_n,Tz_n)^2. \end{aligned}$$

Hence

$$\begin{aligned} d(x_n,Tz_n)^2\le \frac{1}{\beta _n(1-\beta _n)(1-\alpha _n)}\left[ d(x_{n},x^*)^2- d(x_{n+1},x^*)^2\right] . \end{aligned}$$

It implies by the conditions (C3) and (C4) that

$$\begin{aligned} \lim _{n\rightarrow \infty } d(x_n,Tz_n)=0. \end{aligned}$$

(3.12)

Consider

$$\begin{aligned} d(x_n,Tx_n)&\le d(x_n,Tz_n) + d(Tz_n,Tx_n)\\&\le d(x_n,Tz_n) + d(z_n,x_n). \end{aligned}$$

Applying (3.9) and (3.12), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty } d(x_n,Tx_n)=0. \end{aligned}$$

(3.13)

Let $\{x_{n_k}\}$ be a subsequence of $\{x_n\}$ such that $\{x_{n_k}\}$ $\Delta$-converges to $p\in K$. Using Lemma 2.5 and (3.13), we have $p\in F(T)$. By Lemma 2.5 and (3.11), we get $p\in A_i^{-1}(0)$ for any $i=1,2,\ldots ,N$. So $p\in \bigcap _{i=1}^NA_i^{-1}(0)$. To show $p\in EP(f,K)$, we assume that $z=\epsilon w_n\oplus (1-\epsilon )y$, where $0<\epsilon <1$ and $y\in K$. So we have

$$\begin{aligned} f(y_n,w_n)+\frac{1}{2\gamma _n}d(z_n,w_n)^2&\le f(y_n,z) +\frac{1}{2\gamma _n}d(z_n,z)^2\\&= f(y_n, \epsilon w_n\oplus (1-\epsilon )y) +\frac{1}{2\gamma _n}d(z_n,\epsilon w_n\oplus (1-\epsilon )y)^2\\&\le \epsilon f(y_n,w_n)+ (1-\epsilon )f(y_n,y)\\&\quad +\frac{1}{2\gamma _n}\left[ \epsilon d(z_n,w_n)^2 + (1-\epsilon )d(z_n,y)^2-\epsilon (1-\epsilon )d(w_n,y)^2\right] . \end{aligned}$$

Therefore

$$\begin{aligned} f(y_n,w_n)- f(y_n,y) \le \frac{1}{2\gamma _n}[d(z_n,y)^2-d(z_n,w_n)^2-\epsilon d(w_n,y)^2]. \end{aligned}$$

Now, if $\epsilon \rightarrow 1^-$, we obtain

$$\begin{aligned} \frac{1}{2\gamma _n}[d(z_n,w_n)^2+d(w_n,y)^2-d(z_n,y)^2]\le f(y_n,y) - f(y_n,w_n). \end{aligned}$$

(3.14)

Since

$$\begin{aligned} d(z_n,w_n)^2+d(w_n,y)^2-d(z_n,y)^2&\ge d(w_n,y)^2-d(z_n,y)^2\\&=(d(w_n,y)-d(z_n,y))(d(w_n,y)+d(z_n,y))\\&\ge -d(w_n,z_n)[d(w_n,y)+d(z_n,y)], \end{aligned}$$

it implies by (3.14) that

$$\begin{aligned} -\frac{1}{2\gamma _n}d(w_n,z_n)[d(w_n,y)+d(z_n,y)]\le f(y_n,y) - f(y_n,w_n). \end{aligned}$$

(3.15)

By $\liminf _{n\rightarrow \infty }(1-c_i\lambda _n)>0$, for $i=1,2$, using Lemma 3.1(iii), we have

$$\begin{aligned} \lim _{k\rightarrow \infty } d(z_{n_k},y_{n_k})^2 =\lim _{k\rightarrow \infty } d(y_{n_k},w_{n_k})^2=0. \end{aligned}$$

(3.16)

This implies that

$$\begin{aligned} \lim _{k\rightarrow \infty } d(w_{n_k},z_{n_k})^2=0. \end{aligned}$$

(3.17)

Using Lemma 3.1(i), Lemma 3.1(ii), (3.16) and (3.17), we have

$$\begin{aligned} f(y_{n_k},w_{n_k})=0. \end{aligned}$$

(3.18)

Since $S_n^Nx_n=z_n$, it follows by (3.9) and (3.16) that $\{y_{n_k}\}$ $\Delta$-converges to p. Now replacing n with $n_k$ in (3.15), taking $\limsup$ and using (3.17) and (3.18), we have

$$\begin{aligned} 0\le \limsup _{k\rightarrow \infty }f(y_{n_k},y)\le f(p,y),\,\,\text {for all }y\in K. \end{aligned}$$

Therefore $p\in EP(f,K)$ and so $p\in \Theta$. This implies by Lemma 2.4 that the sequence $\{x_n\}$ $\Delta$-converges to a point of $\Theta$. $\square$

We obtain the following convergence result, by replacing $T = I$, the identity mapping in Theorem 3.3.

Theorem 3.4

Let K be a nonempty closed convex subset of a Hadamard space X and let $f:K\times K \rightarrow {\mathbb {R}}$ be a bifunction satisfying Assumption 2.7. Let $A_1,A_2,\ldots ,A_N: X \rightrightarrows X^*$ be N multi-valued monotone operators that satisfy the range condition with $D(A_N)\subset K$. Assume that $\Theta = EP(f,K) \cap \bigcap _{i=1}^N A_i^{-1}(0) \ne \emptyset$. Let $x_1\in K$ and $\{x_n\}$ be a sequence generated by

$$\begin{aligned} \left\{ \begin{aligned}&z_n=J_{\gamma _n^{N}}^{A_N}\circ J_{\gamma _n^{N-1}}^{A_{N-1}}\circ \cdots \circ J_{\gamma _n^{1}}^{A_1}x_n,\\&y_n=\textrm{argmin}_{y\in K}\left\{ f(z_n,y)+\frac{1}{2\lambda _n}d(z_n,y)^2\right\} ,\\&w_n=\textrm{argmin}_{y\in K}\left\{ f(y_n,y)+\frac{1}{2\lambda _n}d(z_n,y)^2\right\} ,\\&v_{n}=\beta _nx_n \oplus (1-\beta _n) z_n,\\&x_{n+1}=\alpha _n w_n \oplus (1-\alpha _n) v_n,\,\,\,n\in {\mathbb {N}}, \end{aligned} \right. \end{aligned}$$

(3.19)

where $\{\alpha _n\}, \{\beta _n\} \subset (0,1)$ and $\{\lambda _n\}, \{\gamma _n^i\} \subset (0,\infty )$ satisfy the following conditions:

• (C1) $\liminf _{n\rightarrow \infty }\gamma _n^i >0$ for all $i=1,2,\ldots ,N$,

• (C2) $0<\alpha \le \lambda _n\le \beta < \min \{\frac{1}{2c_1},\frac{1}{2c_2}\}$,

• (C3) $\lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=1}^{\infty }\alpha _n=\infty$,

• (C4) $\liminf _{n\rightarrow \infty }\beta _n(1-\beta _n)>0$.

Then the sequence $\{x_n\}$ $\Delta$-converges to a point of $\Theta$.

Let X be a Hadamard space with dual $X^*$ and let $g: X \rightarrow (-\infty , \infty ]$ be a proper function with effective domain $D(g):= \{x: g(x) < \infty \}$. Then, the subdifferential of g is the multi-valued mapping $\partial g: X \rightrightarrows X^*$ defined by:

It has been proved in Kakavandi and Amini (2010) that $\partial g(x)$ of a convex, proper and lower semicontinuous function g satisfies the range condition. So using Theorem 3.3, we can obtain the following corollary.

Corollary 3.5

Let K be a nonempty closed convex subset of a Hadamard space X and let $f:K\times K \rightarrow {\mathbb {R}}$ be a bifunction satisfying Assumption 2.7. Let $g_1,g_2,\ldots ,g_N: K \rightarrow (-\infty , \infty ]$ be N proper convex and lower semicontinuous functions and let $T:K\rightarrow K$ be a nonexpansive mapping. Assume that $\Theta = F(T) \cap EP(f,K) \cap \bigcap _{i=1}^N \textrm{argmin}_{y\in K}g_i(y) \ne \emptyset$. Let $x_1\in K$ and $\{x_n\}$ be a sequence generated by

$$\begin{aligned} \left\{ \begin{aligned}&z_n=J_{\gamma _n^{N}}^{\partial g_N}\circ J_{\gamma _n^{N-1}}^{\partial g_{N-1}}\circ \cdots \circ J_{\gamma _n^{1}}^{\partial g_1}x_n,\\&y_n=\textrm{argmin}_{y\in K}\left\{ f(z_n,y)+\frac{1}{2\lambda _n}d(z_n,y)^2\right\} ,\\&w_n=\textrm{argmin}_{y\in K}\left\{ f(y_n,y)+\frac{1}{2\lambda _n}d(z_n,y)^2\right\} ,\\&v_{n}=\beta _nx_n \oplus (1-\beta _n) Tz_n,\\&x_{n+1}=\alpha _n w_n \oplus (1-\alpha _n) Tv_n,\,\,\,n\in {\mathbb {N}}, \end{aligned} \right. \end{aligned}$$

(3.20)

where $\{\alpha _n\}, \{\beta _n\} \subset (0,1)$ and $\{\lambda _n\}, \{\gamma _n^i\} \subset (0,\infty )$ satisfy the following conditions:

• (C1) $\liminf _{n\rightarrow \infty }\gamma _n^i >0$ for all $i=1,2,\ldots ,N$,

• (C2) $0<\alpha \le \lambda _n\le \beta < \min \{\frac{1}{2c_1},\frac{1}{2c_2}\}$,

• (C3) $\lim _{n\rightarrow \infty }\alpha _n=0$ and $\sum _{n=1}^{\infty }\alpha _n=\infty$,

• (C4) $\liminf _{n\rightarrow \infty }\beta _n(1-\beta _n)>0$.

Then the sequence $\{x_n\}$ $\Delta$-converges to a point of $\Theta$.

4 Numerical examples

In this section, we proceed to perform two numerical experiments to show the computational efficiency of our algorithms.

Example 4.1

Let $X={\mathbb {R}}^2$ be endowed with a metric $d_X: {\mathbb {R}}^2\times {\mathbb {R}}^2\rightarrow [0,\infty )$ defined by

$$\begin{aligned} d_X(x,y) = \sqrt{(x_1-y_1)^2 + (x_1^2-x_2-y_1^2+y_2)^2}, \end{aligned}$$

for all $x=(x_1,x_2),y=(y_1,y_2)\in {\mathbb {R}}^2$. Then, $({\mathbb {R}}^2,d_X)$ is a Hadamard space (see Eskandani and Raeisi 2019) with the geodesic joining x to y given by

$$\begin{aligned} tx \oplus (1-t)y= \left( tx_1+(1-t)y_1, \left( tx_1+(1-t)y_1\right) ^2-t(x_1^2-x_2)-(1-t)(y_1^2-y_2)\right) . \end{aligned}$$

Let $f_1, f_2: {\mathbb {R}}^2\rightarrow {\mathbb {R}}$ and $T:{\mathbb {R}}^2\rightarrow {\mathbb {R}}^2$ be mappings defined by

$$\begin{aligned} f_1(x_1,x_2)=200\left( (x_2+1)-(x_1+1)^2\right) ^2 + x_1^2,\,\,\, f_2(x_1,x_2)=200x_1^2,\\T(x_1,x_2)=\left( -x_1,x_2\right) .\end{aligned}$$

It follows that $f_1$ and $f_2$ are convex and lower semicontinuous in $({\mathbb {R}}^2,d_X)$ and T is nonexpansive. Let $f: {\mathbb {R}}^2\times {\mathbb {R}}^2\rightarrow {\mathbb {R}}$ be a function defined by

$$\begin{aligned} f(x,y)= d_X(y,0)^2-d_X(x,0)^2. \end{aligned}$$

It is obvious that f satisfies $(B_1)$, $(B_2)$, $(B_3)$ and $(B_4)$. Letting $N=2$, $A_1=\partial f_1$ and $A_2=\partial f_2$, the sequence $\{x_n\}$ generated by (3.1) takes the following form:

$$\begin{aligned} \left\{ \begin{aligned}&t_n=\textrm{argmin}_{y\in {\mathbb {R}}^2}\left\{ f_1(y)+\frac{1}{2\gamma ^1_n}d_X(y,x_n)^2\right\} ,\\&z_n=\textrm{argmin}_{y\in {\mathbb {R}}^2}\left\{ f_2(y)+\frac{1}{2\gamma ^2_n}d_X(y,t_n)^2\right\} ,\\&y_n=\textrm{argmin}_{y\in {\mathbb {R}}^2}\left\{ f(z_n,y)+\frac{1}{2\lambda _n}d_X(z_n,y)^2\right\} ,\\&w_n=\textrm{argmin}_{y\in {\mathbb {R}}^2}\left\{ f(y_n,y)+\frac{1}{2\lambda _n}d_X(z_n,y)^2\right\} ,\\&v_{n}=\beta _nx_n \oplus (1-\beta _n) Tz_n,\\&x_{n+1}=\alpha _n w_n \oplus (1-\alpha _n) Tv_n,\,\,\,n\in {\mathbb {N}}. \end{aligned} \right. \end{aligned}$$

(4.1)

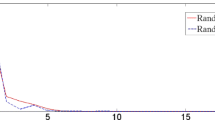
We choose $\alpha _n=\frac{1}{2n+1}, \beta _n=\frac{9}{11},\gamma ^1_n=\gamma ^2_n=4n, \lambda _n=\frac{1}{n+5}+\frac{1}{5},$ for all $n\in {\mathbb {N}}$. It can be observed that all the assumptions of Theorem 3.3 are satisfied and $\Theta = F(T) \cap EP(f,{\mathbb {R}}^2) \cap \bigcap _{i=1}^N A_i^{-1}(0) = \{(0,0)\}$. Using the algorithm (4.1) with the initial point $x_1=(5.4,2.9)$, we have the numerical results in Table 1, Figs. 1 and 2.

Table 1 Numerical results for Example 4.1

Fig. 1

Plotting of $d_X(x_n,0)$ in Table 1

Fig. 2

Plotting of $d_X(x_n,x_{n-1})$ in Table 1

Moreover, we test the effect of the different control sequence $\{\beta _n\}$ on the convergence of the algorithm (4.1). In this test, Fig. 3 presents the behaviour of $x_n$ by choosing three different control sequences (a) $\beta _n=\frac{1}{10}$, (b) $\beta _n=\frac{9}{11}$ and (c) $\beta _n=\frac{9}{11}-\frac{1}{5n}$ where the initial point $x_1=(5.4,2.9)$. We see that the sequence $\{x_n\}$ by choosing the control sequence $\beta _n=\frac{1}{10}$ converges to the solution $(0,0)\in \Theta$ faster than the others.

Fig. 3

Behaviours of $x_n$ with three different control sequences $\{\beta _n\}$

To compare the proposed algorithm (3.19) with the algorithm (1.2) in Moharami and Eskandani (2020), we consider the following example.

Example 4.2

Let X, $d_X$, $f_1$, $f_2$, f, N, $A_1$, $A_2$, $\{\alpha _n\}$, $\{\beta _n\}$, $\{\gamma ^1_n\}$, $\{\gamma ^2_n\}$, $\{\lambda _n\}$ are as in Example 4.1. We computed the iterates of (1.2) and (3.19) for the initial point $x_1=(0.7,0.5)$ and $u=(1,1)$. The numerical experiments of all iterations for approximating the point $(0,0)\in \Theta = EP(f,{\mathbb {R}}^2) \cap \bigcap _{i=1}^N A_i^{-1}(0)$ are given in Table 2 and Fig. 4.

From Table 2 and Fig. 4, we observe that the convergence rate of the proposed algorithm (3.19) is much quicker than that of the algorithm (1.2) in Moharami and Eskandani (2020).

Table 2 Numerical results for Example 4.2

Fig. 4

Comparison of Algorithm (1.2) and Algorithm (3.19) with initial point $x_1=(0.7,0.5)$