1 Introduction

A soliton or solitary wave is considered to be a localised wave that maintains its shape while it propagates at a constant speed. It has a wide number of applications, for instance, tsunami modelling in water waves, propagation of signals in neuroscience and optical fibers, the study of proteins and DNA in biology, propagation of a localised magnetisation in magnets and nuclear physics (Joseph 2016).

The Korteweg-de Vries equation (KdV)

$$\begin{aligned} u_{t}+u_x- \frac{1}{6}u_{xxx}-\frac{3}{2}uu_x=0, \end{aligned}$$
(1)

where \(u=u(x,t)\) represents the wave elevation at the position x and time t, is widely used to describe the propagation and interaction of solitons. In a remarkable work, Zabusky and Kruskal (1965) investigated numerically the interactions of two solitons during collisions for the KdV equation. They observed that after the collision the waves return to their initial forms. Later, Lax (1968) classified the two-soliton interactions geometrically and algebraically according to the number of local maxima during the collision into three categories. This classification only depends on the ratio of the initial amplitudes of the two solitons.

Conducting laboratory experiments in a tank filled with water, Weidman and Maxworthy (1978) studied soliton collisions and verified the Lax-categorization. Later, Mirie and Su (1982) used numerical methods to verify the Lax classification for a higher-order model. More recently, Craig et al. (2006) investigated experimentally and numerically two-soliton interactions and verified that the Lax-geometric categorization holds for the Euler equations, however the algebraic categorization has a different range from the one predicted by Lax.

It is well established in the literature that in the long-wave limit, the KdV equation (1) is an asymptotic approximation of the full Euler equations, however this simple model fails to capture many nonlinear phenomena such as sharp crests, wave breaking and peaking. Whitham (1967, 1974) proposed in an ad-hoc manner a nonlocal model substantially simpler than the full Euler equations that has the same nonlinearity of the KdV model and its dispersion relation reproduces the unidirectional dispersion relation of the Euler equations. This model bears his name and one of its forms is

$$\begin{aligned} u_{t}+ K* u_{x}-\frac{3}{2}uu_x=0, \end{aligned}$$
(2)

where K is the nonlocal operator whose Fourier multiplier is defined by

$$\begin{aligned} {\widehat{K}}(k)=\sqrt{\frac{\tanh k}{k}}. \end{aligned}$$

Notice that in the long-wave limit (\(k\approx 0\)) we have the approximation

$$\begin{aligned} \sqrt{\frac{\tanh k}{k}}\approx 1-\frac{k^2}{6}. \end{aligned}$$
(3)

Therefore, the KdV equation (1) is an asymptotic approximation to Eq. (2).

The Whitham equation has been extensively studied mathematically in the past few years. It is hard to give a comprehensive overview of contributions. For the interested reader, we recommend a few articles and references therein. Regarding the existence of traveling wave solutions and the proof of the Whitham conjecture we recommend the works of Ehrnström and Kalisch (2009) and Ehrnström and Wahlén (2019). For the stability of periodic solutions the articles of Hur and Pandey (2019) and Stanford et al. (2014). For a comparative study of the Whitham equation and shallow water models we recommend the works of Klein et al. (2018), Trillo et al. (2016) and Carter (2018). Comparisons between solitary waves of the Whitham equation and the full Euler equations can be found in the work of Moldabayev et al. (2015). Regarding the stability of traveling wave solutions to the Whitham equation we recommend the work of Deconinck and Trichtchenko (2015). Extensions of the Whitham equation can be found in the recent work of Carter et al. (2021).

In this work, we investigate numerically overtaking collisions of two solitary waves using the Whitham equation. We find that the three geometric categories described by Lax (1968) are hold. However, we show that an algebraic categorization similar to the one presented by Lax is not possible for the Whitham equation.

This article is organized as follows. In Sect. 2 we present the numerical methods to solve the Whitham equation. The results are presented in Sect. 3 and the conclusion in Sect. 4.

2 Numerical methods

The Whitham equation (2) is solved numerically using a Fourier pseudospectral method with an integrating factor similar to the one reported by Flamarion et al. (2019). The integrating factor solves the linear part of Eq. (2) exactly, which avoids numerical instabilities due to the dispersive term.

Equation (2) can be written in the Fourier frequency space as

$$\begin{aligned} {\hat{u}}_{t}+ ik{\hat{K}}(k) {\hat{u}}-\frac{3}{4}\widehat{\partial _{x}u^2}=0. \end{aligned}$$
(4)

Defining the integrating factor \(E(k,t)=\exp (ik{\hat{K}}(k)t)\), \({\hat{U}}(k,t)=E(k,t){\hat{u}}(k,t)\) and replacing in Eq. (4) we obtain the equation

$$\begin{aligned} {\hat{U}}_{t}-\frac{3}{4}E{\mathcal {F}}\Big [{\partial _{x}{\mathcal {F}}^{-1}\Big (E^{-1}{\hat{U}}\Big )^{2}}\Big ]=0, \end{aligned}$$
(5)

where \({\mathcal {F}}\) denotes the Fourier transform and \({\mathcal {F}}^{-1}\) its inverse. Notice that once \({\hat{U}}(k,t)\) is computed we can recover u as

$$\begin{aligned} u(x,t)={\mathcal {F}}^{-1}\Big [E^{-1}{\hat{U}}(k,t)\Big ]. \end{aligned}$$

We solve Eq. (5) in a periodic computational domain \([-L,L]\) with a uniform grid with even points N. The spatial points are discretised as

$$\begin{aligned} x_j = -L + (j-1)\varDelta x, j=1,2,\dots \text{, } \text{ N, } \text{ where } \varDelta x = 2L/N\text{, } \end{aligned}$$
(6)

and the frequencies as

$$\begin{aligned} (k_1,k_2,\ldots ,k_N) = \frac{\pi }{L}(0,1,\ldots ,N/2-1,0,-N/2+1,\ldots ,-1). \end{aligned}$$
(7)

Fourier transforms are computed through the Fast Fourier Transform (FFT) and spatial derivatives spectrally (Trefethen 2001). The time advance is computed using the Runge–Kutta fourth-order method (RK4) with time step \(\varDelta t\).

Whitham solitary waves with speed c, amplitude A and crest located at \(x=0\) are computed through a Newton method’s type by solving the equations

$$\begin{aligned} \begin{aligned}&-cu_x+ K* u_{x}-\frac{3}{2}uu_x=0, \\&u(0)-A=0. \end{aligned} \end{aligned}$$
(8)

On the grid points defined in Eq. (6), we denote by \(u_j=u(x_j)\) and \(u_{x,j}=u_x(x_j)\). The discretised version of Eq. (8) gives rise to a system of (\(N+1\)) equations with (\(N+1\)) unknowns

$$\begin{aligned} \begin{aligned} G_{j}(x_1,x_2,\ldots ,x_{N},c)&:=-cu_{x,j}+ K* u_{x,j}-\frac{3}{2}u_{j}u_{x,j}=0, \text{ for } j=1,2,\dots , \text{ N. } \\ G_{N+1}(x_1,x_2,\ldots ,x_{N},c)&:=u_{N/2+1}-A=0. \end{aligned} \end{aligned}$$
(9)

The discretisation chosen allow us to compute all spatial derivatives and the nonlocal operator K in equations (8) with spectral accuracy in Fourier space through the FFT (Trefethen 2001). The system’s Jacobian for the Newton iteration is found by finite variations in the unknowns and the stopping criterion is

$$\begin{aligned} \begin{aligned} \frac{\sum _{j=1}^{N+1}|G_{n}(x_1,x_2,\ldots ,x_{N},c)|}{N+1}< \delta , \end{aligned} \end{aligned}$$

where \(\delta \) is a given tolerance. In all simulations, the initial guess \((u_0,c_0)\) is taken as the soliton solutions of the KdV equation (1)

$$\begin{aligned} u_{0} = A{{\,\textrm{sech}\,}}^{2}\Bigg (\sqrt{\frac{3}{4}A}x\Bigg ) \text{ and } c_0 = -\frac{A}{2}. \end{aligned}$$
(10)

In what follows we use the set of parameters: \(\varDelta x =0.01\), \(N=2^{12}\), \(L=N\varDelta x/2\), \(\varDelta t = 0.001\) and for the stopping criteria in the Newton’s method we choose \(\delta =10^{-12}\). In addition, all simulations are repeated considering \(\varDelta x =0.01\), \(\varDelta x =0.02\), \(\varDelta x =0.04\) and \(\varDelta x =0.08\), which assures the accuracy of the results.

To verify the accuracy of the Newton’s method, the computed solitary waves are set as initial data of the Whitham equation (2). For \(\varDelta x =0.01\), \(\varDelta x =0.02\), \(\varDelta x =0.04\) and \(\varDelta x =0.08\), the solitary waves remain steady (in the moving wave frame) without presenting any type of numerical instability. In addition, the error

$$\begin{aligned} \mathrm{{Error}} = \frac{\max _{(x,t)\in [-L,L]\times [0,300]}||u(x,t)-u(x,0)||_{\infty }}{\max _{x\in [-L,L]}||u(x,0)||_{\infty }} \end{aligned}$$

is at least order \({\mathcal {O}}(10^{-10})\) for solitary waves with amplitudes in the interval \(A\in [0,0.6]\).

3 Results

We investigate overtaking collisions of two solitary waves for the Whitham equation in the same fashion as Flamarion and Ribeiro-Jr (2021). For this purpose, we compute two solitons \(S_1\) and \(S_2\) of amplitudes \(A_1\) and \(A_2\) respectively with \(A_1<A_2\) for the Whitham equation (2) using the Newton’s method (8). We set them far apart so that initially we have two well separated crests. To this end, the initial data is taken as

$$\begin{aligned} u(x,0) = S_{1}(x+5)+S_{2}(x-10). \end{aligned}$$
(11)

We recall that Lax classified the details of two-soliton interactions for the KdV equation according to the ratio of the initial amplitudes \(A_1<A_2\) of two solitons as follows:

(A):

For \(A_{2}/A_{1}<(3+\sqrt{5})/2\approx 2.62\), at any time t, the solution of the KdV has two well-defined and separate crests, in other words, the solution has two local maxima at any given time.

(C):

When \(A_{2}/A_{1}>3\), the number of local maxima changes as \(2\rightarrow 1\rightarrow 2\) during the interaction. It means that in a period of time the solitons join together to form a wave with a single local maximum.

(B):

This case has features of cases (A) and (C). More precisely, the two-soliton interaction can be described into the following steps: (i) initially, the solitons are well separated which defines two distinct crests; (ii) as time elapses, the solitons fuse to form a wave with a single local maximum; (iii) the wave splits into two again, and two local maxima arise; (iv) then, these two waves fuse to form one single maximum again; (v) lastly, the crest separates and the two waves with two crests reappear at large times. Mathematically, we observe that during the collision the number of local maxima varies according to the law \(2\rightarrow 1\rightarrow 2\rightarrow 1\rightarrow 2\). This case happens when \((3+\sqrt{5})/2<A_{2}/A_{1}<3\).

After the collision the solitary waves are phase shifted, i.e., their crest are slightly shifted from the trajectories of the incoming centers.

The following graphs are displayed in the moving frame of \(S_1\). Thus, \(S_2\) propagates from right to left and collides with the stationary solitary wave \(S_1\). It is worth to mention that the Whitham equation is not integrable, however the two solitary waves have almost the same shape after their collision. We point out though, that this is not an exact two-soliton solution because there is a small dispersive radiation which propagates to the right. The small dispersive tail developed is similar to the one reported by Kalisch et al. (2022) for the cubic Whitham equation.

Fig. 1
figure 1

Top: collision of two solitons for the Whitham equation—category (A). Bottom (left): crest trajectories of \(S_2\) (thicker line) and \(S_1\) (thinner line) before and after collision. Bottom (right): the local maxima of the solution as a function of time. Parameters \(A_{1}=0.10\), \(A_{2}=0.30\)

Full size image
Fig. 2
figure 2

Top: collision of two solitons for the Whitham equation—category (C). Bottom (left): crest trajectories of \(S_2\) (thicker line) and \(S_1\) (thinner line) before and after collision. Bottom (right): the local maxima of the solution as a function of time. Parameters \(A_{1}=0.10\), \(A_{2}=0.42\)

Full size image
Fig. 3
figure 3

Top: collision of two solitons for the Whitham equation—category (B). Bottom (left): crest trajectories of \(S_2\) (thicker line) and \(S_1\) (thinner line) before and after collision. Bottom (right): the local maxima of the solution as a function of time. Parameters \(A_{1}=0.1\), \(A_{2}=0.35\)

Full size image
Fig. 4
figure 4

A series of snapshots of the interaction of the solitary waves of Fig. 3 during the collision-category (B)

Full size image

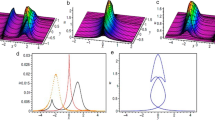
Figure 1 (top) displays the collision of two solitons. Initially, they are set apart and as time elapses, \(S_2\) propagates towards \(S_1\) and a collision takes place. During the collision, \(S_2\) begins to shrink while \(S_1\) begins to grow until the two waves interchange their roles (see Fig. 1 (bottom-right)). We point out that at any time, there are two local maxima, which means that the two wave crests never meet, see Fig. 1 (bottom-left). This case fits into case (A) of Lax categorization.

Figure 2 (top) displays the collision of two solitons with \(S_2\) much larger than \(S_1\) (\(A_2=0.42\) and \(A_1=0.10\)). In this case there is a period of time that the two solitons join together to form only one local maximum. Throughout the collision \(S_2\) absorbs \(S_1\), then \(S_2\) is reemitted later along with a phase lag in the trajectories of the crest, see Fig. 2 (bottom).

Table 1 Classification of the collision for different values of \(A_1\) and \(A_2\)
Full size table
Table 2 Classification of the collision for different values of \(A_1\) and \(A_2\)
Full size table

Now, we present the more complex interaction between two solitary waves, see Fig. 3. The initial solitons \(S_1\) and \(S_2\) have amplitudes \(A_1=0.10\) and \(A_2=0.35\) respectively. During the interaction \(S_2\) swallows \(S_1\) to form a single local maximum, then it splits into two waves, and right after that only a single local maximum is observed again. As time goes on, the waves are farther apart and the two waves with well defined crests emerge again. This case is displayed in great detail in a series of snapshots in Fig. 4. Although we do not show in this article, other simulations were carried out and their categorization is listed in Table 1.

Although it is possible to classify the interaction of two solitary waves according to the ratio of the amplitude of the two initial solitary waves for the KdV (Lax 1968) and for the full Euler equations (Craig et al. 2006), such classification is not possible for the Whitham equation. Table 2 displays three particular cases that show that a Lax-algebraic categorization based on the ratio of the initial amplitudes of two solitary waves is not possible for the Whitham equation.

4 Conclusion

In this article, we have investigated numerically two-soliton interactions during collisions for the Whitham equation. We showed that the Lax-geometric categorization for the KdV two-soliton interaction still holds for the Whitham equation. However, an algebraic categorization based on the ratio of the amplitude of the initial solitary waves is not possible.