Improved results on stability and $H_{\infty }$ performance analysis for discrete-time neural networks with time-varying delay

Abstract

In this paper, to develop less conservative delay-dependent stability criterion and the method for $H_{\infty }$ performance analysis, the problem of stability and $H_{\infty }$ performance for discrete-time neural networks with time-varying delay is investigated. Inequality is an important tool for stability and $H_{\infty }$ performance analysis. To reduce the conservatism of some existing inequalities, an improved reciprocally convex inequality is proved. This inequality is related to the quadratic of delay and encompasses some existing inequalities as its special cases. Based on the proposed reciprocally convex approach, a novel free-matrix-based summation inequality is derived. A delay-product-type Lyapunov–Krasovskii functional (LKF) term is introduced. By utilizing the constructed LKF, information of time delay, and the proposed reciprocally convex approach, two improved sufficient conditions for stability and $H_{\infty }$ performance of discrete-time neural networks with time-varying delay are derived in terms of linear matrix inequalities (LMIs), respectively. Finally, several numerical examples are provided to illustrate the effectiveness and benefits of our proposed approach.

1 Introduction

Neural networks have aroused considerable interest of many researchers owing to their extensive and successful applications such as signal and image processing, control, system identification, and telecommunications (Haykin 1998; Gabrijel and Dobnikar 2003; Liu 2002; Zeng et al. 2015; Shi et al. 2021). Since signal transduction and response between neurons in most practical systems cannot be instantaneously carried out, time-delay is unavoidably encountered in neural networks (Zhang et al. 2008), which is a non-negligible factor that will result in degradation of performance and instability of the systems (Gu et al. 2003). In view of the fact that discrete-time systems have a strong background in engineering applications (Zhang et al. 2016), the stability of discrete-time systems with time-varying delay has become the subject extensively studied in the last several decades (Mathiyalagan et al. 2012; Meng et al. 2010; Qiu et al. 2019). To derive sufficient conditions for stability of delayed systems, the Lyapunov–Krasovskii functional (LKF) approach is an efficient way, but it leads to conservatism to some extent. With the purpose of finding the maximal admissible delay upper bound, there are a great deal of efforts made on these two aspects: constructing appropriate LKFs and seeking some sharper summation inequalities to obtain a tighter upper bound of the forward difference of the constructed LKFs.

From the previous studies (Banu and Balasubramaniam 2016; Banu et al. 2015; Chen et al. 2020), we know that more available system information benefits to reduce the conservatism of stability criteria. A class of discrete recurrent neural networks with time-varying delays was investigated in Wu et al. (2010); an improved global exponential stability criterion was obtained through constructing augmented LKF terms containing the activation functions $g_i(x_i(k))$. By adding triple summation terms into the LKF and fully utilizing the information of time-delay, some novel sufficient conditions with less conservatism were established to guarantee a class of discrete-time delayed dynamical networks to be asymptotically stable (Wang et al. 2013). By employing a newly augmented LKF and a newly augmented vector including summation terms of states, a new delay-dependent stability criterion for the discrete-time neural networks with time-varying delays was proposed in Kwon et al. (2013). How to construct an appropriate LKF to reduce conservatism effectively is a difficulty in dynamic analysis for delayed discrete-time systems. By taking the advantage of the changing information of delay, the delay-variation-dependent stability of discrete-time systems with a time-varying delay is concerned in Zhang et al. (2016). By constructing the delay-product-dependent term in LKF, some significantly improved stability criteria have been derived (Zhang et al. 2016, 2017a; Nam and Luu 2020). Inspired by these works, we will introduce the delay-product-type term in the construction of the LKF to enlarge the delay bounds.

In the dynamic analysis of delayed discrete-time systems, summation terms such as $\sum ^{-1}_{s=-h}\varDelta x^{\mathrm{T}}(s)R\varDelta x(s)$ often arise in the forward difference of the constructed LKFs. To derive less conservative criteria, it is another difficulty how to bound these summation terms. Many summation inequalities have been proposed to fill the bounding gap. The discrete Jensen inequality (Gu et al. 2003) and the Wirtinger-based summation inequality (Seuret et al. 2015) were widely used to estimate the single summation term in the forward difference of the LKF. Nam et al. (2015) presented an auxiliary function-based summation inequality, which extended the Wirtinger-based summation inequality. The free-matrix-based summation inequality was developed in Chen et al. (2016), which contained the discrete Wirtinger-based inequality as a special case. The general summation inequalities including the Jensen inequality, the Wirtinger-based inequality, and the auxiliary function-based summation inequalities as special cases were obtained in Chen et al. (2016). Based on orthogonal group of sequences and the idea of approximation of a vector, a refined auxiliary function-based summation inequality was obtained in Liu et al. (2017). Although we can obtain more general summation inequality via orthogonal polynomials of high order, the computation burden may result from the orthogonal polynomials with high degree. Later, a general free-matrix-based summation inequality was proposed in Chen et al. (2019), which generalized the free-matrix-based ones proposed in Zhang et al. (2017b). Inspired by the aforementioned literatures, this paper will further investigate the summation inequality. Noting that the forward difference of an LKF may be dominated by a quadratic function of time-delay, we hope to derive a delay-quadratic-dependent inequality. To avoid the complexity of polynomials of high order, by following the main idea (Liu et al. 2017; Zhang et al. 2017a), a novel free-matrix-based summation inequality will be established.

It is well known that there often exist various external disturbances. The $H_{\infty }$ control aims to minimize the effects of the external disturbances. The objective of $H_{\infty }$ performance analysis is to find the saddle point of objective functional calculus depending on the disturbance (Kwon et al. 2013). As an important dynamic performance for neural networks, $H_{\infty }$ performance of the systems with time-varying delay has also drawn many researchers’ attention (Lee et al. 2014; Huang et al. 2015; He et al. 2020; Tian and Wang 2021). The guaranteed $H_{\infty }$ performance state estimation problem of static neural networks with time-varying delay was considered in Huang et al. (2013), in which some better performance was achieved by the proposed double-integral inequality and the reciprocally convex combination technique. Using the augmented LKF and the Writinger-based integral inequality, Kwon et al. (2016) investigated $H_{\infty }$ performance for systems of linear model with interval time-varying delays and obtained smaller disturbance attenuation $\gamma$. For delayed Markovian jump neural networks, $H_{\infty }$ performance analysis was conducted by proposing the third-order Bessel–Legendre integral inequality and the LKF with delay-product-type terms (Tan and Wang 2021). The non-integral quadratic terms and the integral terms were connected by employing the third-order Bessel–Legendre integral inequality rather than the Wirtinger-based integral inequality. Several less conservative sufficient conditions that guaranteed the $H_{\infty }$ performance for delayed Markovian jump neural networks were obtained. Zhang et al. (2021) investigated the $H_{\infty }$ performance of discrete-time networked systems subject to network-induced delays and malicious packet dropouts. A novel approach related to quartic polynomial inequalities was presented to deal with the $H_{\infty }$ performance of discrete-time networked systems. Although various methods have been proposed to tackle the $H_{\infty }$ performance analysis problem, $H_{\infty }$ performance analysis for delayed discrete-time neural networks has not yet been fully studied and there remains some space for improvement.

Motivated by the above consideration, this paper aims to improve the reciprocally convex inequality and establish a novel free-matrix-based summation inequality. By employing an LKF with delay-product-term and the new free-matrix-based summation inequality, less conservative sufficient conditions of stability and $H_{\infty }$ performance for delayed discrete-time neural networks are obtained. The major contributions and improvement of this paper are summarized as follows:

• 1. An improved reciprocally convex inequality with six free matrices is proved. To make the most of the newly proved reciprocally convex inequality, a novel free-matrix-based summation inequality is derived.

• 2. Two new zero equalities are introduced. These zero equalities are merged into the estimation of the forward difference of the constructed LKF to increase the freedom of criteria.

• 3. By combining the LKF containing delay-product-term with the improved reciprocally convex combination inequality and the newly proposed summation inequalities, a new stability condition for delayed discrete-time neural networks is developed and corresponding $H_{\infty }$ performance condition for the disturbance-affected delayed neural networks is established. Compared with the existing literatures, the stability criterion and the $H_{\infty }$ performance criterion for the considered system in this paper are with less conservatism. Their effectiveness are demonstrated by some numerical examples.

Notations Throughout this paper, ${\mathfrak {R}}^n$ is the n-dimensional Euclidean vector space, and ${\mathfrak {R}}^{m\times n}$ denotes the set of all $m\times n$ real matrices. The superscript $^{\mathrm{T}}$ stands for the transpose of a matrix. $P>0(\ge 0)$ implies that P is a positive definite (semi-positive-definite) matrix, $I_n$ and $0_{m\times n}$ represent the $n\times n$ identity matrix and $m\times n$ zero matrix, respectively. The symmetric term in a symmetric matrix is denoted by the symbol ‘$*$’ and $\text {sym}\{A\}=A+A^{\mathrm{T}}.$

2 Preliminaries

Consider the following discrete-time neural network with time-varying delay:

$$\begin{aligned} {\left\{ \begin{array}{ll} x(k+1)=Bx(k)+W_0f(x(k))+W_1f(x(k-d(k))),\\ x(k)=\varphi (k),\quad k \in [-d_M,0], \end{array}\right. } \end{aligned}$$

(1)

where $x(k)=[x_1(k),x_2(k),\ldots ,x_n(k)]^{\mathrm{T}}\in {\mathfrak {R}}^n$ denotes the neuron state vector, n is the number of neurons, $f(x(k))=[f_1(x_1(k)),f_2(x_2(k)),\ldots ,f_n(x_n(k))]^{\mathrm{T}}\in {\mathfrak {R}}^n$ is the activation function, $B,W_0,W_1$ are the state feedback matrix, the interconnection weight matrix, and the delayed interconnection weight matrix, respectively, d(k) denotes the state time-varying delay, $d_m \le d(k) \le d_M$, $\mu _m \le \varDelta d(k)=d(k+1)-d(k) \le \mu _M$, $d_m$, $d_M$, $\mu _m$ and $\mu _M$ are known integers.

The activation function $f(\cdot )$ in system (1) is assumed to be continuous and bounded with $f_j(0)=0$, and there exist constants $l_{j}^-,l_{j}^+$, such that

$$\begin{aligned} l_{j}^-\le \frac{f_j(s)-f_j(t)}{s-t}\le l_{j}^+,\quad \forall s,t\in {\mathfrak {R}},\quad s\ne t,j=1,2,\ldots , n. \end{aligned}$$

(2)

Corresponding to neural network (1), the discrete-time system subject to external disturbance u(k) can be described as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} x(k+1)=Bx(k)+W_0f(x(k))+W_1f(x(k-d(k)))+ Du(k),\\ v(k)=Cx(k),\\ x(k)=\varphi (k),k \in [-d_M,0], \end{array}\right. } \end{aligned}$$

(3)

where $u(k)\in {\mathfrak {R}}^n$ represents the exogenous disturbance, $v(k)\in {\mathfrak {R}}^m$ is the output vector, and C, D are real matrices with compatible dimensions.

The problem of $H_{\infty }$ performance analysis for delayed discrete-time neural networks is stated as follows. For a given scalar $\gamma >0$, the neural network (3) is said to have $H_{\infty }$ performance level $\gamma$ if the following conditions are satisfied:

• 1. System (3) with $u(t)=0$ is asymptotically stable;

• 2. For any positive integer h, under the zero-initial condition

  $$\begin{aligned} \langle v,v\rangle _h\le \gamma ^2 \langle u,u\rangle _h \end{aligned}$$

  holds for $\forall u(k)\in l_2$ and $u(k)\ne 0$, where $\langle u,u\rangle _h= \sum ^{h}_{k=0}u^{\mathrm{T}}(k)u(k).$

To facilitate the subsequent research, we introduce the following lemmas.

Lemma 1

For positive definite matrices $R_1,R_2 \in {\mathfrak {R}}^{n\times n},$ if there exist symmetric matrices $X_i\in {\mathfrak {R}}^{n\times n},i=1,2,3,4$ and any matrices $Y_1,Y_2\in {\mathfrak {R}}^{n\times n},$ such that

$$\begin{aligned}&\begin{bmatrix} R_1-X_1 &{} \quad -Y_1\\ * &{} \quad R_2\\ \end{bmatrix} \ge 0,\quad \begin{bmatrix} R_1&{} \quad -Y_2\\ * &{} \quad R_2-X_2\\ \end{bmatrix} \ge 0,\nonumber \\&\begin{bmatrix} R_1-X_1-X_4&{}\quad -Y_1\\ * &{}\quad R_2-X_3\\ \end{bmatrix} \ge 0, \end{aligned}$$

(4)

then the following inequality holds for any $\alpha \in (0,1){:}$

$$\begin{aligned} \begin{bmatrix} \frac{1}{\alpha }R_1&{}\quad 0\\ * &{}\quad \frac{1}{1-\alpha }R_2\\ \end{bmatrix} \ge \begin{bmatrix} R_1+(1-\alpha )X_1+(1-\alpha )^2X_4&{}\quad \alpha Y_1+(1-\alpha ) Y_2\\ * &{}\quad R_2+\alpha X_2+\alpha ^2 X_3\\ \end{bmatrix}. \end{aligned}$$

(5)

Proof

It is easy for us to get the following identical equation after simple calculation:

$$\begin{aligned}&\begin{bmatrix} R_1&{}\quad 0\\ * &{}\quad R_2\\ \end{bmatrix} -\alpha \begin{bmatrix} X_1&{}\quad Y_1\\ * &{}\quad 0\\ \end{bmatrix} -(1-\alpha ) \begin{bmatrix} 0&{}\quad Y_2\\ * &{}\quad X_2\\ \end{bmatrix} -\alpha (1-\alpha ) \begin{bmatrix} X_4&{}\quad 0\\ * &{}\quad X_3\\ \end{bmatrix}\\&\quad = \alpha ^2 \begin{bmatrix} X_4&{}\quad 0\\ * &{}\quad X_3\\ \end{bmatrix} +\alpha ^2 \begin{bmatrix} -X_1-X_4&{}\quad -Y_1+Y_2\\ * &{}\quad X_2-X_3\\ \end{bmatrix}\\&\qquad +\alpha ^2 \begin{bmatrix} R_1&{}\quad -Y_2\\ * &{}\quad R_2-X_2\\ \end{bmatrix} -\alpha ^2 \begin{bmatrix} -X_1-X_4&{}\quad -Y_1+Y_2\\ * &{}\quad X_2-X_3\\ \end{bmatrix}\\&\qquad -\alpha ^2 \begin{bmatrix} R_1&{}\quad -Y_2\\ * &{}\quad R_2-X_2\\ \end{bmatrix} +\alpha \begin{bmatrix} -X_1-X_4&{}\quad -Y_1+Y_2\\ * &{}\quad X_2-X_3\\ \end{bmatrix}\\&\qquad +\alpha \begin{bmatrix} R_1&{}\quad -Y_2\\ * &{}\quad R_2-X_2\\ \end{bmatrix} -\alpha \begin{bmatrix} R_1&{}\quad -Y_2\\ * &{}\quad R_2-X_2\\ \end{bmatrix} + \begin{bmatrix} R_1&{}\quad -Y_2\\ * &{}\quad R_2-X_2\\ \end{bmatrix}\\&\quad =\alpha ^2 \begin{bmatrix} R_1-X_1&{}\quad -Y_1\\ * &{}\quad R_2\\ \end{bmatrix} +(1-\alpha ) \begin{bmatrix} R_1&{} \quad -Y_2\\ * &{}\quad R_2-X_2\\ \end{bmatrix}\\&\qquad +\alpha (1-\alpha ) \begin{bmatrix} R_1-X_1-X_4&{}\quad -Y_1\\ * &{}\quad R_2-X_3\\ \end{bmatrix}. \end{aligned}$$

For any $\alpha \in (0,1)$, if $\begin{bmatrix} R_1-X_1&{}\quad -Y_1\\ * &{}\quad R_2\\ \end{bmatrix}\ge 0,$ $\begin{bmatrix} R_1&{}\quad -Y_2\\ * &{}\quad R_2-X_2\\ \end{bmatrix}\ge 0$, and $\begin{bmatrix} R_1-X_1-X_4&{}\quad -Y_1\\ * &{}\quad R_2-X_3\\ \end{bmatrix}\ge 0,$ then

$$\begin{aligned} \begin{bmatrix} R_1&{}\quad 0\\ * &{}\quad R_2\\ \end{bmatrix} -\alpha \begin{bmatrix} X_1&{}\quad Y_1\\ * &{}\quad 0\\ \end{bmatrix} -(1-\alpha ) \begin{bmatrix} 0&{}\quad Y_2\\ * &{}\quad X_2\\ \end{bmatrix} -\alpha (1-\alpha ) \begin{bmatrix} X_4&{}\quad 0\\ * &{}\quad X_3\\ \end{bmatrix} \ge 0. \end{aligned}$$

(6)

For any $\alpha \in (0,1)$, pre- and post-multiplying (6) by $\begin{bmatrix} \sqrt{\frac{1-\alpha }{\alpha }}I&{}\quad 0\\ * &{}\quad \sqrt{\frac{\alpha }{1-\alpha }}I\\ \end{bmatrix}$ yields

$$\begin{aligned} \begin{bmatrix} \frac{1}{\alpha }R_1&{}\quad 0\\ * &{}\quad \frac{1}{1-\alpha }R_2\\ \end{bmatrix}\ge & {} \begin{bmatrix} R_1&{}\quad 0\\ * &{}\quad R_2\\ \end{bmatrix} +\begin{bmatrix} (1-\alpha )X_1&{}\quad \alpha Y_1\\ * &{}\quad 0\\ \end{bmatrix}\\&+ \begin{bmatrix} 0&{}\quad (1-\alpha )Y_2\\ * &{}\quad \alpha X_2\\ \end{bmatrix} + \begin{bmatrix} (1-\alpha )^2X_4&{}\quad 0\\ * &{}\quad \alpha ^2 X_3\\ \end{bmatrix}. \end{aligned}$$

This completes the proof. $\square$

Remark 1

The classical reciprocally convex inequality $\begin{bmatrix} \frac{1}{\alpha }R&{}\quad 0\\ * &{}\quad \frac{1}{(1-\alpha )}R\\ \end{bmatrix} \ge \begin{bmatrix} R&{}\quad S\\ * &{}\quad R\\ \end{bmatrix}$ was proved (Park et al. 2011). It played an important role in dealing with non-convex terms occurring in the forward difference of an LKF. Seuret and Gouaisbaut (2016) extended the classical reciprocally convex inequality into the form $\begin{bmatrix} \frac{1}{\alpha }R&{}\quad 0\\ * &{}\quad \frac{1}{(1-\alpha )}R\\ \end{bmatrix} \ge \begin{bmatrix} R+(1-\alpha )X_{1}&{}\quad \alpha Y_{1}+ (1-\alpha )Y_{2}\\ * &{}\quad R+\alpha X_{2} \\ \end{bmatrix}.$ By weakening the constraints (Park et al. 2011), an improved reciprocally convex inequality comprising three slack matrices was presented (Zhang and Han 2018). In stability and $H_{\infty }$ performance analysis, a main difficulty is how to estimate the forward difference of the LKF V(k) and prove $\triangle V(k)<0$. The forward difference of an LKF may be dominated by a quadratic function of time-delay. However, the right-hand sides of both reciprocally convex inequalities (Seuret and Gouaisbaut 2016; Zhang and Han 2018) are the linear functions of $\alpha$. These reciprocally convex inequalities (Seuret and Gouaisbaut 2016; Zhang and Han 2018) cannot be directly used to estimate $\triangle V(k)$ with the square of the time-delay. A generalized reciprocally convex inequality is proved in Lemma 1. This novel reciprocally convex inequality involves the square of $\alpha$ and more slack matrices. Kim (2016) proved the quadratic function negative determination lemma, which could be used to handle the quadratic function of time-delay. Using the generalized reciprocally convex inequality derived in this paper, non-convex terms in the forward difference of the LKF can be merged into one expression of $\alpha ^{2}$, whose sign can be determined via the quadratic function negative determination lemma.

Remark 2

Let $X_3=X_4=0$, the generalized reciprocally convex inequality in Lemma 1 degenerates into the reciprocally convex inequality (Seuret and Gouaisbaut 2016). Let $X_3=X_4=0$, $Y_1=Y_2=Y$, the generalized reciprocally convex inequality in Lemma 1 degenerates into the improved reciprocally convex inequality in Zhang and Han (2018). Set $X_i=0,i=1,2,3,4$, $Y_1=Y_2=Y$, the generalized reciprocally convex inequality in Lemma 1 becomes to the classical reciprocally convex inequality (Park et al. 2011). If $X_3>0, X_4>0$, the generalized reciprocally convex inequality in Lemma 1 is less conservative than the reciprocally convex inequality (Seuret and Gouaisbaut 2016).

Lemma 2

For a vector function $y(s) : [-h,0]\rightarrow {\mathfrak {R}}^{n},$ a positive definite matrix $R\in {\mathfrak {R}}^{n\times n},$ positive integer $h\ge 1,$ any real matrix M and any vector $\chi _0$ with appropriate dimensions,  the following inequality holds : 

$$\begin{aligned} \sum \limits ^{-1}_{s=-h}y^{\mathrm{T}}(s)R y(s) \ge \frac{1}{h}\chi _1^{\mathrm{T}}R\chi _1 -\frac{h}{3}\chi _0^{\mathrm{T}}MR^{-1}M^{\mathrm{T}}\chi _0 -2\chi _0^{\mathrm{T}}M\chi _2, \end{aligned}$$

(7)

where $\chi _1:=\sum ^{-1}_{s=-h}y(s),$ $\chi _2:=\frac{2}{h+1}\sum ^{-1}_{s=-h}\sum ^{-1}_{j=s}y(j)-\sum ^{-1}_{s=-h}y(s).$

Proof

Let $f(s)=\frac{2s+h+1}{h+1}$. Carrying out simple algebraic calculation yields: $\sum ^{-1}_{s=-h}f(s)=0,$ $\sum ^{-1}_{s=-h}f^{2}(s)=\frac{h(h-1)}{3(h+1)},$ $\sum ^{-1}_{s=-h}f(s)y(s)=\chi _2.$

For any vector $\chi _0$ with appropriate dimension, let $\delta (s)=\hbox {col}[\chi _0,f(s)\chi _0,y(s)]$ $\varPhi =\begin{bmatrix} LR^{-1}L^{\mathrm{T}}&{}\quad LR^{-1}M^{\mathrm{T}}&{}\quad L\\ * &{}\quad MR^{-1}M^{\mathrm{T}}&{}\quad M\\ *&{}\quad *&{}\quad R \end{bmatrix}$. Using Schur complement, it is obvious that $\varPhi \ge 0$. Using the Jensen inequality gives

$$\begin{aligned}&\sum \limits ^{-1}_{s=-h}\delta ^{\mathrm{T}}(s)\varPhi \delta (s)\nonumber \\&\quad \ge \frac{1}{h}(\sum \limits ^{-1}_{s=-h}\delta (s))^{\mathrm{T}}\varPhi \left( \sum \limits ^{-1}_{s=-h}\delta (s)\right) \nonumber \\&\quad = h\chi _0^{\mathrm{T}} LR^{-1}L^{\mathrm{T}}\chi _0+2 \chi _0^{\mathrm{T}} L\chi _1+\frac{1}{h}\chi _1^{\mathrm{T}}R\chi _1. \end{aligned}$$

(8)

Direct computation yields

$$\begin{aligned}&\sum \limits ^{-1}_{s=-h}\delta (s)^{\mathrm{T}}\varPhi \delta (s)\nonumber \\&\quad = h\chi _0^{\mathrm{T}} LR^{-1}L^{\mathrm{T}}\chi _0+2\chi _0^{\mathrm{T}} L\chi _1 +\frac{h(h-1)}{3(h+1)}\chi _0^{\mathrm{T}}MR^{-1}M^{\mathrm{T}}\chi _0\nonumber \\&\qquad +2\chi _0^{\mathrm{T}} M\chi _2+\sum \limits ^{-1}_{s=-h}y^{\mathrm{T}}(s)Ry(s). \end{aligned}$$

(9)

Combining (8) with (9), we can get

$$\begin{aligned} \sum \limits ^{-1}_{s=-h}y^{\mathrm{T}}(s)Ry(s)\ge \frac{1}{h}\chi _1^{\mathrm{T}}R\chi _1 -\frac{h(h-1)}{3(h+1)}\chi _0^{\mathrm{T}}MR^{-1}M^{\mathrm{T}}\chi _0 -2\chi _0^{\mathrm{T}}M\chi _2. \end{aligned}$$

(10)

Since $\frac{h(h-1)}{3(h+1)}\le \frac{h}{3}$, inequality (7) can be derived from inequality (10). This completes the proof. $\square$

Corollary 1

Let vector function $x(s) : [-h,0]\rightarrow {\mathfrak {R}}^{n}$ and $\varDelta x(s)=x(s+1)-x(s).$ For any positive definite matrix R,  integer $h\ge 1,$ the following inequality holds : 

$$\begin{aligned} \sum \limits ^{-1}_{s=-h}\varDelta x(s)^{\mathrm{T}}R\varDelta x(s) \ge \frac{1}{h}{\bar{\chi }}_1^{\mathrm{T}}R{\bar{\chi }}_1 +\frac{3}{h}{\bar{\chi }}_2^{\mathrm{T}}R{\bar{\chi }}_2, \end{aligned}$$

(11)

where ${\bar{\chi }}_1=x(0)-x(-h),$ ${\bar{\chi }}_2=x(0)+x(-h)-\frac{2}{h+1}\sum ^{0}_{s=-h}x(s).$

Remark 3

If $M=0$ in Lemma 2, then inequality (7) will degrade into the Jensen summation inequality (Gu et al. 2003). By setting $y(s)=\varDelta x(s)=x(s+1)-x(s)$, $M= -\frac{3}{h}R$, $\chi _0=\chi _2$ in (7), inequality (7) becomes the Wirtinger-based summation inequality (Seuret et al. 2015), which is presented in Corollary 1. Using inequality $\sum ^{-1}_{s=-h}\delta ^{\mathrm{T}}(s)\varPhi \delta (s)>0$, the free-matrix-based summation inequality (Chen et al. 2016) was derived. Different from the method in Chen et al. (2016), based on the Jensen summation inequality, inequality (7) is proved by utilizing $\sum ^{-1}_{s=-h}\delta ^{\mathrm{T}}(s)\varPhi \delta (s)\ge \frac{1}{h}(\sum ^{-1}_{s=-h}\delta (s))^{\mathrm{T}}\varPhi (\sum ^{-1}_{s=-h}\delta (s))$. Since $\frac{1}{h}(\sum ^{-1}_{s=-h}\delta (s))^{\mathrm{T}}\varPhi (\sum ^{-1}_{s=-h}\delta (s))\ge 0$, inequality (7) may be with less conservatism than the free-matrix-based summation inequality.

Based on Lemmas 1 and 2, it is easy for us to obtain the following lemma.

Lemma 3

For a positive definite matrix $R\in {\mathfrak {R}}^{n\times n},$ $\tau _1\le \tau _{k}\le \tau _2,$ any real matrices $F_1,F_2$ with appropriate dimensions,  and any vectors $\eta _1,\eta _2,$ if there exist symmetric matrices $X_i\in {\mathfrak {R}}^{n\times n},i=1,2,3,4$ and any matrices $Y_1,Y_2\in {\mathfrak {R}}^{n\times n},$ such that

$\begin{bmatrix} R-X_1&{}\quad -Y_1\\ * &{}\quad R\\ \end{bmatrix} \ge 0,$ $\begin{bmatrix} R&{}\quad -Y_2\\ * &{}\quad R-X_2\\ \end{bmatrix} \ge 0,$ $\begin{bmatrix} R-X_1-X_4&{}\quad -Y_1\\ * &{}\quad R-X_3\\ \end{bmatrix} \ge 0,$

then the following inequality holds : 

$$\begin{aligned}&\sum \limits ^{k-\tau _1-1}_{s=k-\tau _2}\varDelta x^{\mathrm{T}}(s)R\varDelta x(s)\\&\quad \ge \frac{1}{\tau _2-\tau _1}\{\alpha _1^{\mathrm{T}}(k) (R+(1-\alpha )X_1+(1-\alpha )^2X_4)\alpha _1(k)\\&\qquad +2\alpha _1^{\mathrm{T}}(k) (\alpha Y_1+(1-\alpha )Y_2)\alpha _2(k)\\&\qquad +\alpha _2^{\mathrm{T}}(k)(R+\alpha X_2+\alpha ^2X_3)\alpha _2(k)\}\\&\qquad -2\eta _1^{\mathrm{T}}F_1\alpha _3(k)-2\eta _2^{\mathrm{T}}F_2\alpha _4(k)\\&\qquad -\frac{(\tau _k-\tau _1)}{3}\eta _1^{\mathrm{T}}F_1R^{-1}F_1^{\mathrm{T}}\eta _1 -\frac{(\tau _2-\tau _k)}{3}\eta _2^{\mathrm{T}}F_2R^{-1}F_2^{\mathrm{T}}\eta _2, \end{aligned}$$

where $\alpha _1(k)=x(k-\tau _1)-x(k-\tau _k),$ $\alpha _2(k)=x(k-\tau _k)-x(k-\tau _2),$ $\alpha _3(k)=x(k-\tau _1)+x(k-\tau _k)-2\omega _1(k),$ $\alpha _4(k)=x(k-\tau _k)+x(k-\tau _2)-2\omega _2(k),$ $\omega _1(k)=\sum _{s=k-\tau _k}^{k-\tau _1}\frac{x(s)}{\tau _k-\tau _1+1},$ $\omega _2(k)=\sum _{s=k-\tau _2}^{k-\tau _k}\frac{x(s)}{\tau _2-\tau _k+1},$ $\alpha =\frac{\tau _k-\tau _1}{\tau _2-\tau _1}.$

Remark 4

Different from the existing summation inequality, the free-matrix-based summation inequality given in Lemma 3 is related to the square of the delay. Vectors $\eta _1$ and $\eta _2$ can be freely and independently chosen. Since more free matrices are introduced in Lemma 3, the free-matrix-based summation inequality in Lemma 3 can provide more freedom.

Lemma 4

(Kim 2016) For a quadratic function $f(x)=a_2x^2+a_1x+a_0,$ where $a_0,a_1,a_2 \in {\mathfrak {R}},$ if $({\mathrm{i}})\ f(h_1)<0,\quad ({\mathrm{ii}})\ f(h_2)<0, \quad ({\mathrm{iii}})\ -(h_2-h_1)^2a_2+f(h_1)<0,$ then $f(x)<0, \forall x \in [h_1,h_2].$

3 Main results

In this section, by resorting to the above new summation inequalities and improved reciprocally convex inequality, improved sufficient conditions for stability and $H_{\infty }$ performance of delayed discrete-time neural networks are proposed. For simplifying the representation of subsequent parts, the related notations are given as follows:

$$\begin{aligned} d_k= & {} d(k), \quad d_1= d_M-d_m,\\ \alpha= & {} (d_k-d_m)/d_1, \quad \varDelta x(s)=x(s+1)-x(s),\\ e_i= & {} [0_{n\times (i-1)n},I_n,0_{n\times (13-i)n}]^{\mathrm{T}},\quad i=1,2,\ldots ,13,\\ e_s^{\mathrm{T}}= & {} (B-I_n)e_1^{\mathrm{T}}+W_0e_8^{\mathrm{T}}+W_1e_9^{\mathrm{T}},\\ \eta _1(k)= & {} \text {col}[x(k), \sum \limits _{s=k-d_m}^{k-1}x(s), \sum \limits _{s=k-d_M}^{k-d_m-1}x(s)], \\ \eta _2(k)= & {} \text {col}[x(k), \sum \limits _{s=k-d_m}^{k-1}x(s)],\quad \eta _3(k)= \text {col}[x(k),\varDelta x(k)],\\ \zeta (k)= & {} \text {col}[\varpi _1, \varpi _2, \varpi _3, \varpi _4, \varpi _5],\\ \varpi _1= & {} \text {col}[x(k), x(k-d_m), x(k-d_k), x(k-d_M)],\\ \varpi _2= & {} \text {col}[\sum \limits _{s=k-d_m}^{k}x(s), \sum \limits _{s=k-d_k}^{k-d_m}x(s), \sum \limits _{s=k-d_M}^{k-d_k}x(s)],\\ \varpi _3= & {} \text {col}[f(x(k)), f(x(k-d_k))],\\ \varpi _4= & {} \text {col}\left[ \sum \limits _{s=k-d_k}^{k-d_m}\frac{x(s)}{d_k-d_m+1}, \sum \limits _{s=k-d_M}^{k-d_k}\frac{x(s)}{d_M-d_k+1}\right] ,\\ \varpi _5= & {} \text {col}\left[ \sum \limits _{s=k-d_k}^{k-d_m-1}\sum \limits _{j=s}^{k-d_m-1}\frac{x(j)}{d_k-d_m+1}, \sum \limits _{s=k-d_M}^{k-d_k-1}\sum \limits _{j=s}^{k-d_k-1}\frac{x(j)}{d_M-d_k+1}\right] ,\\ \varPi _1= & {} \varXi _{11}P_1\varXi _{11}^{{\mathrm{T}}}-\varXi _{12}P_1\varXi _{12}^{{\mathrm{T}}} +d(k)(\varXi _{13}P_2\varXi _{13}^{{\mathrm{T}}}-\varXi _{14}P_2\varXi _{14}^{{\mathrm{T}}})\\&+\varDelta d(k)\varXi _{13}P_2\varXi _{13}^{{\mathrm{T}}},\\ \varXi _{11}= & {} [e_s+e_1,e_5-e_2,e_6+e_7-e_3-e_4],\\ \varXi _{12}= & {} [e_1,e_5-e_1,e_6+e_7-e_2-e_3],\\ \varXi _{13}= & {} [e_s+e_1,e_5-e_2],\quad \varXi _{14}= [e_1,e_5-e_1],\\ \varPi _2= & {} e_1Q_1e_1^{\mathrm{T}}+e_2(Q_2-Q_1)e_2^{\mathrm{T}}-e_4Q_2e_4^{\mathrm{T}},\\ \varPi _{3}= & {} \varGamma _1+\varGamma _2+\varGamma _3+\varGamma _4,\quad \varGamma _1=e_s(d_m^2R_1+d_1^2R_2)e_s^{\mathrm{T}},\\ \varGamma _2= & {} -\varXi _{36}R_1\varXi _{36}^{\mathrm{T}}-3\varXi _{37}R_1\varXi _{37}^{\mathrm{T}},\\ \varGamma _3= & {} d_1\text {sym}\{\varXi _{35}M_1\varXi _{32}^{\mathrm{T}}+{\tilde{\varXi }}_{35} N_1\varXi _{34}^{\mathrm{T}}\},\\ \varGamma _4= & {} -\varXi _{31} (R_2+(1-\alpha )X_1+(1-\alpha )^2X_4)\varXi _{31}^{\mathrm{T}}\\&-2\varXi _{31} (\alpha Y_1+(1-\alpha )Y_2)\varXi _{33}^{\mathrm{T}}\\&-\varXi _{33} (R_2+\alpha X_2+\alpha ^2X_3)\varXi _{33}^{\mathrm{T}},\\ {\tilde{\varPi }}_3= & {} \frac{d_1(d_{k}-d_m)}{3}\varXi _{35}M_1R_2^{-1}M_1^{\mathrm{T}}\varXi _{35}^{\mathrm{T}}\\&+\frac{d_1(d_{M}-d_k)}{3}{\tilde{\varXi }}_{35}N_1R_2^{-1} N_1^{\mathrm{T}}{\tilde{\varXi }}_{35}^{\mathrm{T}},\\ \varXi _{31}= & {} e_2-e_3,\quad \varXi _{32}=e_2+e_3-2e_{10},\\ \varXi _{33}= & {} e_3-e_4,\quad \varXi _{34}=e_3+e_4-2e_{11},\\ \varXi _{35}= & {} [e_2,e_3,e_{10}],\quad {\tilde{\varXi }}_{35}=[e_3,e_4,e_{11}], \end{aligned}$$

$$\begin{aligned} \varXi _{36}= & {} e_1-e_2,\quad \varXi _{37}= e_1+e_2-\frac{2}{d_m+1}e_5,\\ \varOmega _{1}= & {} [e_6-e_2,e_2-e_3],\quad \varOmega _{2}= [e_7-e_3,e_3-e_4],\\ \varOmega _{3}= & {} [e_2-e_6+2e_{12},e_2+e_3-2e_{10}],\\ \varOmega _{4}= & {} [e_3-e_7+2e_{13},e_3+e_4-2e_{11}],\\ \varOmega _{5}= & {} [e_2,e_{3},e_{6},e_{10},e_{12}],\quad \varOmega _{6}= [e_3,e_{4},e_{7},e_{11},e_{13}],\\ \varPi _{4}= & {} d_1[e_2U_1e_2^{\mathrm{T}}+e_3(U_2-U_1)e_3^{\mathrm{T}}-e_4U_2e_4^{\mathrm{T}}] +d_1^2[e_1,e_s]S[e_1,e_s]^{\mathrm{T}}\\&+d_1\text {sym}\{\varOmega _{5}M_2\varOmega _{3}^{\mathrm{T}}+\varOmega _{6}N_2\varOmega _{4}^{\mathrm{T}}\}\\&-[\varOmega _1 S_1 \varOmega _1^{\mathrm{T}} +(1-\alpha )\varOmega _1 {\bar{X}}_1 \varOmega _1^{\mathrm{T}}\\&+(1-\alpha )^2\varOmega _1 {\bar{X}}_4 \varOmega _1^{\mathrm{T}} +2\alpha \varOmega _1 {\bar{Y}}_1 \varOmega _2^{\mathrm{T}}\\&+2(1-\alpha )\varOmega _1 {\bar{Y}}_2 \varOmega _2^{\mathrm{T}}+\varOmega _2 S_2 \varOmega _2^{\mathrm{T}}\\&+\alpha \varOmega _2 {\bar{X}}_2 \varOmega _2^{\mathrm{T}} +\alpha ^2\varOmega _2 {\bar{X}}_3 \varOmega _2^{\mathrm{T}}],\\ {\tilde{\varPi }}_4= & {} \frac{d_1(d_{k}-d_m)}{3}\varOmega _{5} M_2S_1^{-1}M_2^{\mathrm{T}}\varOmega _{5}^{\mathrm{T}}\\&+\frac{d_1(d_{M}-d_k)}{3}\varOmega _{6}N_2S_2^{-1}N_2^{\mathrm{T}}\varOmega _{6}^{\mathrm{T}},\\ \varPi _5= & {} \text {sym}\{[e_1L_2-e_8]J_1[e_8-e_1L_1]^{\mathrm{T}} +[e_3L_2-e_9]J_2\\&\times [e_9-e_3L_1]^{\mathrm{T}} +[(e_1-e_3)L_2-(e_8-e_9)]J_3\\&\times [(e_8-e_9)-(e_1-e_3)L_1]^{\mathrm{T}}\},\\ \varPi _6= & {} \text {sym}\{H_1((d_k-d_m+1)e_{10}-e_{6})^{\mathrm{T}}\\&+H_2(d_M-d_k+1)e_{11}-e_{7})^{\mathrm{T}}\},\\ \varDelta= & {} -\frac{1}{d_1^2}[\varXi _{31}X_4\varXi _{31}^{\mathrm{T}} +\varXi _{33}X_3\varXi _{33}^{\mathrm{T}} +\varOmega _1{\bar{X}}_4\varOmega _1^{\mathrm{T}} +\varOmega _2{\bar{X}}_3\varOmega _2^{\mathrm{T}}],\\ S_1= & {} S+ \begin{bmatrix} 0&{}\quad U_1\\ * &{}\quad U_1\\ \end{bmatrix}, \quad S_2=S+\begin{bmatrix} 0&{}\quad U_2\\ * &{}\quad U_2\\ \end{bmatrix},\\ \varUpsilon _1= & {} [d_1{\tilde{\varXi }}_{35}N_1,d_1\varOmega _{6}N_2],\quad \varUpsilon _2=[d_1\varXi _{35}M_1,d_1\varOmega _{5}M_2],\\ \varGamma _1= & {} -3\hbox {diag}\{R_2,S_2\},\quad \varGamma _2=-3\hbox {diag}\{R_2,S_1\}. \end{aligned}$$

Theorem 1

For given integers $d_{m},$ $d_{M},$ $\mu _{m},$ $\mu _{M},$ system (1) is asymptotically stable if there exist positive definite matrices $Q_i\in {\mathfrak {R}}^{n\times n}, R_i\in {\mathfrak {R}}^{n\times n}, i=1,2,$ $S\in {\mathfrak {R}}^{2n\times 2n},$ positive definite diagonal matrices $J_j\in {\mathfrak {R}}^{n\times n},j=1,2,3,$ symmetric matrices $P_1\in {\mathfrak {R}}^{3n\times 3n},$ $P_2\in {\mathfrak {R}}^{2n\times 2n},$ $U_1,U_2\in {\mathfrak {R}}^{n\times n},$ $X_k\in {\mathfrak {R}}^{n\times n},$ ${\bar{X}}_k\in {\mathfrak {R}}^{2n\times 2n},k=1,2,3,4,$ matrices $M_l,$ $N_l,$ $H_l,Y_l,{\bar{Y}}_l,l=1,2$ with appropriate dimensions, such that the following LMIs hold:

$$\begin{aligned}&P(d_m)>0,\quad P(d_M)> 0,\end{aligned}$$

(12)

$$\begin{aligned}&\begin{bmatrix} R_2-X_1&{}\quad -Y_1\\ * &{}\quad R_2\\ \end{bmatrix} \ge 0,\quad \begin{bmatrix} R_2&{}\quad -Y_2\\ * &{}\quad R_2-X_2\\ \end{bmatrix} \ge 0,\nonumber \\&\begin{bmatrix} R_2-X_1-X_4&{}\quad -Y_1\\ * &{}\quad R_2-X_3\\ \end{bmatrix} \ge 0, \end{aligned}$$

(13)

$$\begin{aligned}&\begin{bmatrix} S_1-{\bar{X}}_1&{}\quad -{\bar{Y}}_1\\ * &{}\quad S_2\\ \end{bmatrix}\ge 0,\quad \begin{bmatrix} S_1&{}\quad -{\bar{Y}}_2\\ * &{}\quad S_2-{\bar{X}}_2\\ \end{bmatrix}\ge 0,\nonumber \\&\begin{bmatrix} S_1-{\bar{X}}_1-{\bar{X}}_4&{}\quad -{\bar{Y}}_1\\ * &{}\quad S_2-{\bar{X}}_3\\ \end{bmatrix}\ge 0,\end{aligned}$$

(14)

$$\begin{aligned}&\begin{bmatrix} \sum \limits _{i=1}^{6}\varPi _i|_{(d_m,\mu _m)}&{}\quad \varUpsilon _1\\ *&{}\quad \varGamma _1\\ \end{bmatrix}<0, \quad \begin{bmatrix} \sum \limits _{i=1}^{6}\varPi _i|_{(d_m,\mu _M)}&{}\quad \varUpsilon _1\\ *&{}\quad \varGamma _1\\ \end{bmatrix}<0,\nonumber \\&\begin{bmatrix} \sum \limits _{i=1}^{6}\varPi _i|_{(d_M,\mu _m)}&{}\quad \varUpsilon _2\\ *&{}\quad \varGamma _2\\ \end{bmatrix}<0,\quad \begin{bmatrix} \sum \limits _{i=1}^{6}\varPi _i|_{(d_M,\mu _M)}&{}\quad \varUpsilon _2\\ *&{}\quad \varGamma _2\\ \end{bmatrix}<0,\nonumber \\&\begin{bmatrix} \sum \limits _{i=1}^{6}\varPi _i|_{(d_m,\mu _m)}-d_1^2\varDelta &{}\quad \varUpsilon _1\\ *&{}\quad \varGamma _1\\ \end{bmatrix}<0,\quad \begin{bmatrix} \sum \limits _{i=1}^{6}\varPi _i|_{(d_m,\mu _M)}-d_1^2\varDelta &{} \quad \varUpsilon _1\\ *&{}\quad \varGamma _1\\ \end{bmatrix}<0. \end{aligned}$$

(15)

Proof

Consider the following LKF:

$$\begin{aligned} V(k)=\sum \limits _{i=1}^{4}V_{i}(k) \end{aligned}$$

(16)

with

$$\begin{aligned} V_{1}(k)= & {} \eta _1^{{\mathrm{T}}}(k) P_1 \eta _1(k)+d(k)\eta _2^{{\mathrm{T}}}(k) P_2 \eta _2(k),\\ V_{2}(k)= & {} \sum \limits _{s=k-d_{m}}^{k-1}x^{{\mathrm{T}}}(s)Q_{1}x(s) +\sum \limits _{s=k-d_{M}}^{k-d_{m}-1}x^{{\mathrm{T}}}(s)Q_{2}x(s),\\ V_{3}(k)= & {} d_m\sum \limits _{s=-d_m}^{-1}\sum \limits _{i=k+s}^{k-1} \varDelta x^{{\mathrm{T}}}(i)R_1\varDelta x(i)\\&+d_1\sum \limits _{s=-d_M}^{-d_m-1}\sum \limits _{i=k+s}^{k-1} \varDelta x^{{\mathrm{T}}}(i)R_2\varDelta x(i),\\ V_{4}(k)= & {} d_1\sum \limits _{s=-d_M}^{-d_m-1} \sum \limits _{i=k+s}^{k-1}\eta _3^{{\mathrm{T}}}(i)S\eta _3(i) . \end{aligned}$$

First, we verify the positive definiteness of the LKF candidate in (16). $V_{1}(k)$ can be equivalently written in the following form:

$$\begin{aligned} V_{1}(k)=\eta _1^{{\mathrm{T}}}(k) P(d(k)) \eta _1(k), \end{aligned}$$

where $P(d(k))=P_1+d(k) \begin{bmatrix} P_2&{}\quad 0\\ *&{}\quad 0\\ \end{bmatrix}$.

Since $S>0$, $Q_i>0$, and $R_i>0, i=1,2$, the positive definiteness of V(k) can be guaranteed by condition (12).

Now, we calculate the forward differences $\varDelta V(k)$ along the trajectory of system (1) and estimate the upper bound of $\varDelta V(k)$.

$$\begin{aligned} \varDelta V_{1}(k)= & {} \eta _1^{{\mathrm{T}}}(k+1)P_1\eta _1(k+1)-\eta _1^{{\mathrm{T}}}(k)P_1\eta _1(k)\nonumber \\&+d(k+1)\eta _2^{{\mathrm{T}}}(k+1)P_2\eta _2(k+1)-d(k)\eta _2^{{\mathrm{T}}}(k)P_2\eta _2(k)\nonumber \\= & {} \zeta ^{\mathrm{T}}(k)\varPi _1\zeta (k), \end{aligned}$$

(17)

$$\begin{aligned} \varDelta V_{2}(k)= & {} x^{\mathrm{T}}(k)Q_1x(k)+x^{\mathrm{T}}(k-d_m)(Q_2-Q_1)x(k-d_m)\nonumber \\&-x^{\mathrm{T}}(k-d_M)Q_2x(k-d_M)\nonumber \\= & {} \zeta ^{\mathrm{T}}(k)\varPi _2\zeta (k), \end{aligned}$$

(18)

$$\begin{aligned} \varDelta V_{3}(k)= & {} d_m^2\varDelta x^{\mathrm{T}}(k)R_1\varDelta x(k)+ d_1^2\varDelta x^{\mathrm{T}}(k)R_2\varDelta x(k)\nonumber \\&-d_m\sum \limits _{s=k-d_m}^{k-1}\varDelta x^{\mathrm{T}}(s)R_1\varDelta x(s)\nonumber \\&-d_1\sum \limits _{s=k-d_M}^{k-d_m-1}\varDelta x^{\mathrm{T}}(s)R_2\varDelta x(s). \end{aligned}$$

(19)

Using Corollary 1, we obtain

$$\begin{aligned}&-d_m\sum \limits _{s=k-d_m}^{k-1}\varDelta x^{\mathrm{T}}(s)R_1\varDelta x(s)\nonumber \\&\quad \le -\zeta ^{\mathrm{T}}(k)(\varXi _{36}R_1\varXi _{36}^{\mathrm{T}} +3\varXi _{37}R_1\varXi _{37}^{\mathrm{T}})\zeta (k). \end{aligned}$$

(20)

For any matrices $M_1,N_1$ with appropriate dimensions, applying Lemma 3 yields

$$\begin{aligned}&-d_1\sum \limits ^{k-d_m-1}_{s=k-d_M}\varDelta x^{\mathrm{T}}(s)R_2\varDelta x(s)\nonumber \\&\quad \le -\{{\tilde{\chi }}_1^{\mathrm{T}} (R_2+(1-\alpha )X_1+(1-\alpha )^2X_4){\tilde{\chi }}_1 +2{\tilde{\chi }}_1^{\mathrm{T}} (\alpha Y_1+(1-\alpha )Y_2){\bar{\chi }}_1\nonumber \\&\qquad +{\bar{\chi }}_1 ^{\mathrm{T}} (R_2+\alpha X_2+\alpha ^2X_3){\bar{\chi }}_1\} +2d_1{\tilde{\chi }}_0^{\mathrm{T}}M_1{\tilde{\chi }}_2+2d_1{\bar{\chi }}_0^{\mathrm{T}} N_1{\bar{\chi }}_2\nonumber \\&\qquad +\frac{d_1(d_k-d_m)}{3}{\tilde{\chi }}_0^{\mathrm{T}}M_1R_2^{-1} M_1^{\mathrm{T}}{\tilde{\chi }}_0 +\frac{d_1(d_M-d_k)}{3}{\bar{\chi }}_0^{\mathrm{T}}N_1R_2^{-1}N_1^{\mathrm{T}}{\bar{\chi }}_0, \end{aligned}$$

(21)

where ${\tilde{\chi }}_1=\varXi _{31}^{\mathrm{T}}\zeta (k),{\tilde{\chi }}_2=\varXi _{32}^{\mathrm{T}}\zeta (k),$ ${\bar{\chi }}_1=\varXi _{33}^{\mathrm{T}}\zeta (k),{\bar{\chi }}_2=\varXi _{34}^{\mathrm{T}}\zeta (k),$ ${\tilde{\chi }}_0=\varXi _{35}^{\mathrm{T}}\zeta (k),$ ${\bar{\chi }}_0={\tilde{\varXi }}_{35}^{\mathrm{T}}\zeta (k),$ $\alpha =(d_k-d_m)/d_1.$

It follows from (19)–(21) that:

$$\begin{aligned} \varDelta V_3(k) \le \zeta ^{\mathrm{T}}(k)(\varPi _3+{\tilde{\varPi }}_3) \zeta (k). \end{aligned}$$

(22)

The calculation of $\varDelta V_{4}(k)$ leads to

$$\begin{aligned} \varDelta V_{4}(k)= & {} d_1^2\eta _3^{\mathrm{T}}(k)S\eta _3(k) -d_1\sum \limits _{s=k-d_k}^{k-d_m-1}\eta _3^{\mathrm{T}}(s)S\eta _3(s)\nonumber \\&-d_1\sum \limits _{s=k-d_M}^{k-d_k-1}\eta _3^{\mathrm{T}}(s)S\eta _3(s). \end{aligned}$$

(23)

Similar to the method in Park et al. (2015), we introduce the following zero equations:

$$\begin{aligned}&d_1[x^{\mathrm{T}}(k-d_m)U_1x(k-d_m)-x^{\mathrm{T}}(k-d_k)U_1x(k-d_k)]\nonumber \\&\qquad -d_1\sum \limits _{s=k-d_k}^{k-d_m-1}\eta _3^{{\mathrm{T}}}(s) \begin{bmatrix} 0&{}\quad U_1\\ * &{}\quad U_1 \end{bmatrix}\eta _3(s)=0,\nonumber \\&d_1[x^{\mathrm{T}}(k-d_k)U_2x(k-d_k)-x^{\mathrm{T}}(k-d_M)U_2x(k-d_M)]\nonumber \\&\qquad -d_1\sum \limits _{s=k-d_M}^{k-d_k-1}\eta _3^{{\mathrm{T}}}(s) \begin{bmatrix}0&{}\quad U_2\\ * &{}\quad U_2 \end{bmatrix}\eta _3(s)=0, \end{aligned}$$

(24)

where $U_1$ and $U_2$ are any symmetric matrices with appropriate dimensions.

Let $S_1=S+\begin{bmatrix} 0&{}\quad U_1\\ * &{}\quad U_1\\ \end{bmatrix}, S_2=S+\begin{bmatrix} 0&{}\quad U_2\\ * &{}\quad U_2\\ \end{bmatrix}.$ Combining (23) with (24) yields

$$\begin{aligned} \varDelta V_{4}(k)= & {} d_1^2\eta _3^{\mathrm{T}}(k)S\eta _3(k) -d_1\sum \limits _{s=k-d_k}^{k-d_m-1}\eta _3^{\mathrm{T}}(s)S_1\eta _3(s)\nonumber \\&-d_1\sum \limits _{s=k-d_M}^{k-d_k-1}\eta _3^{\mathrm{T}}(s)S_2\eta _3(s) +d_1[x^{\mathrm{T}}(k-d_m)U_1x(k-d_m)\nonumber \\&+x^{\mathrm{T}}(k-d_k)(U_2-U_1)x(k-d_k)-x^{\mathrm{T}}(k-d_M)U_2x(k-d_M)]. \end{aligned}$$

(25)

For any matrix $M_2$ with appropriate dimension, applying Lemma 2 yields

$$\begin{aligned}&-d_1\sum \limits ^{k-d_m-1}_{s=k-d_k}\eta _3^{\mathrm{T}}(s)S_1\eta _3(s)\nonumber \\&\quad \le -\frac{1}{\alpha }{\tilde{\kappa }}_1^{\mathrm{T}}S_1 {\tilde{\kappa }}_1+2d_1{\tilde{\kappa }}_0^{\mathrm{T}}M_2{\tilde{\kappa }}_2 +\frac{d_1(d_k-d_m)}{3}{\tilde{\kappa }}_0^{\mathrm{T}}M_2S_1^{-1}M_2^{\mathrm{T}}{\tilde{\kappa }}_0, \end{aligned}$$

(26)

where ${\tilde{\kappa }}_1=\varOmega _{1}^{\mathrm{T}}\zeta (k),$ ${\tilde{\kappa }}_2=\varOmega _{3}^{\mathrm{T}}\zeta (k),$ ${\tilde{\kappa }}_0=\varOmega _{5}^{\mathrm{T}}\zeta (k),$ $\alpha =(d_k-d_m)/d_1.$

Similarly, for any matrix $N_2$ with appropriate dimension, we have

$$\begin{aligned}&-d_1\sum \limits ^{k-d_k-1}_{s=k-d_M}\eta _3^{\mathrm{T}}(s)S_2\eta _3(s)\nonumber \\&\quad \le -\frac{1}{1-\alpha }{\bar{\kappa }}_1^{\mathrm{T}}S_2{\bar{\kappa }}_1 +2d_1{\bar{\kappa }}_0^{\mathrm{T}}N_2{\bar{\kappa }}_2 +\frac{d_1(d_M-d_k)}{3}{\bar{\kappa }}_0^{\mathrm{T}}N_2S_2^{-1}N_2^{\mathrm{T}}{\bar{\kappa }}_0, \end{aligned}$$

(27)

where ${\bar{\kappa }}_1=\varOmega _{2}^{\mathrm{T}}\zeta (k),$ ${\bar{\kappa }}_2=\varOmega _{4}^{\mathrm{T}}\zeta (k),$ ${\bar{\kappa }}_0=\varOmega _{6}^{\mathrm{T}}\zeta (k).$

Using Lemma 1 to deal with $\alpha$-dependent terms gives

$$\begin{aligned}&-\frac{1}{\alpha }{\tilde{\kappa }}_1^{\mathrm{T}}S_1{\tilde{\kappa }}_1 -\frac{1}{1-\alpha }{\bar{\kappa }}_1^{\mathrm{T}}S_2{\bar{\kappa }}_1\nonumber \\&\quad =-\zeta ^{\mathrm{T}}(k)[\frac{1}{\alpha }\varOmega _1S_1\varOmega _1^{\mathrm{T}} +\frac{1}{(1-\alpha )}\varOmega _2S_2\varOmega _2^{\mathrm{T}}]\zeta (k)\nonumber \\&\quad \le -\zeta ^{\mathrm{T}}(k)\{\varOmega _1 (S_1+(1-\alpha ){\bar{X}}_1 +(1-\alpha )^2{\bar{X}}_4)\varOmega _1^{\mathrm{T}}\nonumber \\&\qquad +2\varOmega _1 (\alpha {\bar{Y}}_1+(1-\alpha ){\bar{Y}}_2)\varOmega _2^{\mathrm{T}} +\varOmega _2 (S_2+\alpha {\bar{X}}_2+\alpha ^2{\bar{X}}_3)\varOmega _2^{\mathrm{T}}\}\zeta (k). \end{aligned}$$

(28)

From (23)–(28), we obtain

$$\begin{aligned} \varDelta V_4(k) \le \zeta ^{\mathrm{T}}(k)(\varPi _4+{\tilde{\varPi }}_4) \zeta (k). \end{aligned}$$

(29)

Since the activation function $f(\cdot )$ satisfies (2), then

$$\begin{aligned}&2[f(x(k))-L_1x(k)]^{\mathrm{T}}J_1[L_2x(k)-f(x(k))]\ge 0,\nonumber \\&2[f(x(k-d_k))-L_1x(k-d_k)]^{\mathrm{T}}J_2[L_2x(k-d_k)-f(x(k-d_k))]\ge 0,\nonumber \\&2[f(x(k))-f(x(k-d_k))-L_1(x(k)-x(k-d_k))]^{\mathrm{T}} \nonumber \\&\quad \times J_{3}[L_{2} (x(k)-x(k-d_k))-(f(x(k))-f(x(k-d_k))] \ge 0, \end{aligned}$$

(30)

where $L_1=\text {diag}\{l_1^-,l_2^-,\ldots ,l_n^-\}, L_2=\text {diag}\{l_1^+,l_2^+,\ldots ,l_n^+\},$ $l_i^-,l_i^+(i=1,2,\ldots ,n)$ are constants given in (2), and $J_i (i=1,2,3)$ are any positive definite diagonal matrices with appropriate dimensions.

In addition, we have the following two zero equalities with any matrices $H_1$, $H_2$:

$$\begin{aligned} 0= & {} 2\zeta ^{\mathrm{T}}(k)H_1\left[ \sum \limits _{s=k-d_k}^{k-d_m}x(s) -(d_k-d_m+1)\sum \limits _{s=k-d_k}^{k-d_m}\frac{x(s)}{d_k-d_m+1}\right] ,\nonumber \\ 0= & {} 2\zeta ^{\mathrm{T}}(k)H_2\left[ \sum \limits _{s=k-d_M}^{k-d_k}x(s)-(d_M-d_k+1) \sum \limits _{s=k-d_M}^{k-d_k}\frac{x(s)}{d_M-d_k+1}\right] . \end{aligned}$$

(31)

From (17) to (31), the upper bound of $\varDelta V(k)$ can be described by

$$\begin{aligned} \varDelta V(k) \le \zeta ^{\mathrm{T}}(k) \varPhi (d_k,\varDelta d_k) \zeta (k), \end{aligned}$$

(32)

where $\varPhi (d_k,\varDelta d_k)=\sum ^{6}_{i=1}\varPi _i+{\tilde{\varPi }}_3+{\tilde{\varPi }}_4.$

Since $\varPhi (d_k,\varDelta d_k )$ is quadratic with respect to $d_k$ and linear with respect to $\varDelta d_k$, by applying Lemma 4, $\varPhi (d_k,\varDelta d_k )< 0$ is guaranteed by conditions (13)–(15), which means that system (1) is asymptotically stable. This complete the proof. $\square$

Remark 5

To reduce the conservatism of stability criteria, one of the possible approaches is to introduce some new zero equations. The introduction of two zero equations in (31) will enhance the feasible region of stability criteria. However, two slack matrices $H_{1}$ and $H_{2}$ are introduced with these two zero equations. The number of decision variables in Theorem 1 increases by $26n^2$, which is relatively time-consuming to find the feasible solutions of the LMIs. Computational complexity will also increase moderately. When the sizes of LMIs are not too large, the computational burden problem does not occur.

In what follows, the $H_{\infty }$ performance for the neural network (3) will be discussed.

Theorem 2

For given integers $d_{m},$ $d_{M},$ $\mu _{m},$ $\mu _{M}$ and $\gamma >0,$ the $H_{\infty }$ performance analysis problem for system (3) is solvable,  if there exist positive definite matrices $Q_i\in {\mathfrak {R}}^{n\times n}, R_i\in {\mathfrak {R}}^{n\times n}, i=1,2,$ $S\in {\mathfrak {R}}^{2n\times 2n},$ positive definite diagonal matrices $J_j\in {\mathfrak {R}}^{n\times n},j=1,2,3,$ symmetric matrices $P_1\in {\mathfrak {R}}^{3n\times 3n},$ $P_2\in {\mathfrak {R}}^{2n\times 2n},$ $U_1,U_2\in {\mathfrak {R}}^{n\times n},$ $X_k\in {\mathfrak {R}}^{n\times n},$ ${\bar{X}}_k\in {\mathfrak {R}}^{2n\times 2n},k=1,2,3,4,$ matrices $M_l,$ $N_l,$ $H_l,Y_l,{\bar{Y}}_l,l=1,2$ with appropriate dimensions,  such that the following LMIs hold : 

$$\begin{aligned}&P(d_m)>0,\quad P(d_M)> 0, \end{aligned}$$

(33)

$$\begin{aligned}&\begin{bmatrix} R_2-X_1&{}\quad -Y_1\\ * &{}\quad R_2\\ \end{bmatrix}\ge 0,\quad \begin{bmatrix} R_2&{}\quad -Y_2\\ * &{}\quad R_2-X_2\\ \end{bmatrix}\ge 0,\nonumber \\&\begin{bmatrix} R_2-X_1-X_4&{}\quad -Y_1\\ * &{}\quad R_2-X_3\\ \end{bmatrix}\ge 0, \end{aligned}$$

(34)

$$\begin{aligned}&\begin{bmatrix} S_1-{\bar{X}}_1&{}\quad -{\bar{Y}}_1\\ * &{}\quad S_2\\ \end{bmatrix}\ge 0,\quad \begin{bmatrix} S_1&{}\quad -{\bar{Y}}_2\\ * &{}\quad S_2-{\bar{X}}_2\\ \end{bmatrix}\ge 0,\nonumber \\&\begin{bmatrix} S_1-{\bar{X}}_1-{\bar{X}}_4&{}\quad -{\bar{Y}}_1\\ * &{}\quad S_2-{\bar{X}}_3\\ \end{bmatrix}\ge 0, \end{aligned}$$

(35)

$$\begin{aligned}&\begin{bmatrix} \sum \limits _{i=1}^{6}\varPi _i|_{(d_m,\mu _m)}-\digamma &{}\quad \varUpsilon _1\\ *&{}\quad \varGamma _1\\ \end{bmatrix}<0, \quad \begin{bmatrix} \sum \limits _{i=1}^{6}\varPi _i|_{(d_m,\mu _M)}-\digamma &{}\quad \varUpsilon _1\\ *&{}\quad \varGamma _1\\ \end{bmatrix}<0,\nonumber \\&\begin{bmatrix} \sum \limits _{i=1}^{6}\varPi _i|_{(d_M,\mu _m)}-\digamma &{}\quad \varUpsilon _2\\ *&{}\quad \varGamma _2\\ \end{bmatrix}<0,\quad \begin{bmatrix} \sum \limits _{i=1}^{6}\varPi _i|_{(d_M,\mu _M)}-\digamma &{}\quad \varUpsilon _2\\ *&{}\quad \varGamma _2\\ \end{bmatrix}<0,\nonumber \\&\begin{bmatrix} \sum \limits _{i=1}^{6}\varPi _i|_{(d_m,\mu _m)}-d_1^2\varDelta -\digamma &{}\quad \varUpsilon _1\\ *&{}\quad \varGamma _1\\ \end{bmatrix}<0,\quad \begin{bmatrix} \sum \limits _{i=1}^{6}\varPi _i|_{(d_m,\mu _M)}-d_1^2\varDelta -\digamma &{}\quad \varUpsilon _1\\ *&{}\quad \varGamma _1\\ \end{bmatrix}<0,\nonumber \\ \end{aligned}$$

(36)

where

$$\begin{aligned} e_i= & {} [0_{n\times (i-1)n},I_n,0_{n\times (14-i)n}]^{\mathrm{T}},\quad i=1,2,\ldots ,14,\\ e_s^{\mathrm{T}}= & {} (B-I_n)e_1^{\mathrm{T}}+W_0e_8^{\mathrm{T}}+W_1e_9^{\mathrm{T}}+De_{14}^{\mathrm{T}},\\ \zeta (k)= & {} {\mathrm{col}}[\varpi _1, \varpi _2, \varpi _3, \varpi _4, \varpi _5, u(k)],\\ \digamma= & {} -e_1C^{\mathrm{T}}Ce_1^{\mathrm{T}}+\gamma ^2e_{14}e_{14}^{\mathrm{T}}. \end{aligned}$$

The other notations are the same as those in Theorem 1.

Proof

Consider the same LKF V(k) as in Theorem 1. Denote

$$\begin{aligned} J(k)=-v^{\mathrm{T}}(k)v(k)+\gamma ^2u^{\mathrm{T}}(k)u(k) =\zeta ^{\mathrm{T}}(k)\digamma \zeta (k). \end{aligned}$$

It is easy to deduce that

$$\begin{aligned} \varDelta V(k)-J(k)\le \zeta ^{\mathrm{T}}(k)\left( \sum \limits ^{6}_{i=1}\varPi _i+{\tilde{\varPi }}_3+{\tilde{\varPi }}_4-\digamma \right) \zeta (k). \end{aligned}$$

$\varDelta V(k)-J(k)< 0$ is guaranteed by Conditions (34)–(36). Summing k from 0 to h gives $\sum ^{h}_{k=0}\varDelta V(k)-\sum ^{h}_{k=0}J(k) <0.$ Under zero-initial conditions, it is straightforward that $\sum ^{h}_{k=0}v^{\mathrm{T}}(k)v(k) \le \sum ^{h}_{k=0}\gamma ^2 u^{\mathrm{T}}(k)u(k)$. This complete the proof. $\square$

Remark 6

To reduce the conservatism of the stability criterion and $H_{\infty }$ performance analysis, more information among the system states, time-delay, and the activation functions should be considered. Therefore, many matrix variables are introduced to reflect the relationships between these factors, which results in many complex notations. In practical engineering application, the engineers only pay attention to the notations relating to the LMIs in these criteria. Basing on symmetry, we can simplify programming of MATLAB. The LMIs in these criteria can be easily solved by employing LMI toolbox in MATLAB.

Remark 7

Given a scalar $\gamma >0$, the neural network (3) is said to have $H_{\infty }$ performance level $\gamma$ if (i) when the exogenous disturbance input $u(k)=0$, system (3) is asymptotically stable; (ii) under the zero-initial condition, for all nonzero $u(k)\in l_2$ and all integer $h>0$, $\sum ^{h}_{k=0}v^{\mathrm{T}}(k)v(k) \le \gamma ^2 \sum ^{h}_{k=0}u^{\mathrm{T}}(k)u(k)$ holds. The neural network (3) is said to be passive if there exists a constant $\gamma >0$, such that, for all nonzero input $u(k)\in l_2$ and all integer $h>0$, $2\sum _{k=0}^{h}v^{\mathrm{T}}(k)u(k)\ge -\gamma \sum _{k=0}^{h}u^{\mathrm{T}}(k)u(k)$ under the zero-initial condition. $H_{\infty }$ performance and the passivity both are relevant to input, output and index $\gamma$. They both consider the relationships between input and output under the zero-initial condition. Different from passivity, $H_{\infty }$ performance requires that system (3) with the exogenous disturbance $u(k)=0$ should be asymptotically stable. $H_{\infty }$ performance index $\gamma$ is used to prescribe the level of noise attenuation. As a special case of dissipativity, passivity relates the input and output to the storage function.

Remark 8

How to construct an appropriate LKF is a main difficulty in reducing effectively the conservatism of stability criteria. To overcome this difficulty, a delay-product-type LKF term is introduced and three multiple summation LKF terms are constructed in this paper.

4 Numerical examples

Example 1

Consider the discrete-time system (1) with

$$\begin{aligned} B= & {} \begin{bmatrix} 0.8&{}\quad 0\\ 0&{}\quad 0.9\\ \end{bmatrix},\quad W_0= \begin{bmatrix} 0.001&{}\quad 0\\ 0&{}\quad 0.005\\ \end{bmatrix},\\ W_1= & {} \begin{bmatrix} -0.1&{}\quad 0.01 \\ -0.2&{}\quad -0.1 \\ \end{bmatrix},\\ L_1= & {} \text {diag}\{0,0\},\quad L_2=\text {diag}\{1,1\}. \end{aligned}$$

The maximum admissible delay upper bounds (MADUBs) $d_M$ for different $d_m$, such that the neural network (1) is asymptotically stable, are listed in Tables 1 and 2, where $\mu =-\mu _m=\mu _M$. From Tables 1 and 2, the MADUBs $d_M$ obtained in this paper are greater than or equal to those in the existing literatures, which shows that our approach is less conservative.

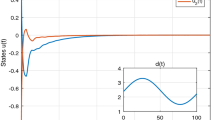
When $d(k)=17.5+5.5\cos k\pi$, the initial values $x(k)=\varphi (k)=[0.3,-0.4]^{{\mathrm{T}}}$, $k\in [-23,0]$, the trajectories of the neural network in Example 1 are depicted in Fig. 1, which shows that the discrete-time system in this example is asymptotically stable. It verifies the effectiveness of the proposed criterion.

Table 1 The MADUBs $d_M$ for different $d_m$ in Example 1

Table 2 The MADUBs $d_M$ for different $d_m$ in Example 1

Fig. 1

The trajectories of the system in Example 1 with $d(k)=17.5+5.5\cos k\pi$ and $x(0)=[0.3,-0.4]^{{\mathrm{T}}}$

Example 2

Consider the discrete-time system (1) with

$$\begin{aligned} B= & {} \begin{bmatrix} 0.1&{}\quad 0\\ 0&{}\quad 0.3\\ \end{bmatrix},\quad W_0= \begin{bmatrix} 0.02&{}\quad 0\\ 0&{}\quad 0.004\\ \end{bmatrix},\\ W_1= & {} \begin{bmatrix} -0.01&{}\quad 0.01 \\ -0.02&{}\quad -0.01 \\ \end{bmatrix},\\ L_1= & {} \text {diag}\{0,0\},\quad L_2=\text {diag}\{1,1\}. \end{aligned}$$

Table 3 The MADUBs $d_M$ for different $d_m$ in Example 2

The MADUBs $d_M$ for different $d_m$, such that the system in this example is asymptotically stable , are listed in Table 3, where $\mu =-\mu _m=\mu _M$. It can be discerned from Table 3 that the MADUBs $d_M$ calculated by our method are larger than those in the existing literatures, which shows that our approach is with less conservatism.

Example 3

Consider the discrete-time system (3) with

$$\begin{aligned} B= & {} \begin{bmatrix} 0.2&{}\quad 0\\ 0&{}\quad 0.3\\ \end{bmatrix},\quad W_0= \begin{bmatrix} 0.001&{}\quad 0\\ 0&{}\quad 0.005\\ \end{bmatrix},\\ W_1= & {} \begin{bmatrix} -0.1&{}\quad 0.01 \\ -0.2&{}\quad -0.1 \\ \end{bmatrix}, \\ C= & {} \text {diag}\{1,1\},\quad D=\text {diag}\{1,1\},\\ L_1= & {} \text {diag}\{0,0\},\quad L_2=\text {diag}\{1,1\}.\\ \end{aligned}$$

Let $d_m=3$ and $\mu =-\mu _m=\mu _M$. The optimal $H_{\infty }$ performance levels $\gamma$ for different $d_M$ computed by Theorem 2 and the methods (Feng and Zheng 2015; Jin et al. 2018) are listed in Table 4. When $(d_m,d_M)=(3,9)$ and $(d_m,d_M)=(3,11)$, Tables 5 and 6 list the optimal $H_{\infty }$ performance levels $\gamma$ for different $\mu$, respectively. From Tables 4, 5 and 6, we can see that $H_{\infty }$ performance level is improved. This means that our results are of less conservatism.

Set the initial state $x(k)=[2,-2]^{{\mathrm{T}}},k\in [-13,0]$, $d(k)=\hbox {int}[8+5*\sin (\frac{k\pi }{4})]$ and $J(k)=-v^{\mathrm{T}}(k)v(k)+\gamma ^2u^{\mathrm{T}}(k)u(k)$. Figure 2 displays the state response of the system in Example 3 with the exogenous disturbance $u(k)=\text {col}[2{\mathrm{e}}^{-0.01k}$,$3{\mathrm{e}}^{-0.02k}]$. The trajectory of $\sum _{k=0}^{h}J(k)$ is depicted in Fig. 3, which testifies the validity of the results of Theorem 2.

Table 4 The minimum $H_{\infty }$ performance $\gamma$ for $d_m=3$ and different $d_M$

Table 5 The minimum $H_{\infty }$ performance $\gamma$ for $(d_m,d_M)=(3,9)$ and different $\mu$

Table 6 The minimum $H_{\infty }$ performance $\gamma$ for $(d_m,d_M)=(3,11)$) and different $\mu$

Fig. 2

The state trajectories of the system in Example 3 with $d(k)=\hbox {int}[8+5*\sin (\frac{k\pi }{4})]$, $x(0)=\hbox {col}[2,-2]$ and $u(k)=\hbox {col}[2{\mathrm{e}}^{-0.01k}$, $3{\mathrm{e}}^{-0.02k}]$

Fig. 3

The trajectory of $\sum _{k=0}^{h}J(k)$ in Example 3 with $d_m=3$, $d_M=13$, $u(k)=[2{\mathrm{e}}^{-0.01k}$, $3{\mathrm{e}}^{-0.02k}]^{{\mathrm{T}}}$ and $\gamma =2.8633$

Example 4

The repressilator model for Escherichia coli with three repressor protein concentrations and their corresponding mRNA concentrations was considered in Elowitz and Leibler (2000). The discrete repressilator model with the stochastic jumping was investigated in Xia et al. (2020). Removing the stochastic jumping factor in Xia et al. (2020), we can obtain the following deterministic discrete repressilator model:

$$\begin{aligned} {\left\{ \begin{array}{ll} m(k+1)=B_1m(k)+D_0g(p(k))+D_1g(p(k-d(k)))+u_{1}(k),\\ p(k+1)=B_2p(k)+B_3m(k)+u_{2}(k), \end{array}\right. } \end{aligned}$$

(37)

where $p(k)=[p_{1}(k), p_{2}(k), p_{3}(k)]^{{\mathrm{T}}}$ and $m(k)=[m_{1}(k), m_{2}(k), m_{3}(k)]^{{\mathrm{T}}}$, $p_{i}(k)$ and $m_{i}(k)$ denote concentrations of protein and mRNA at time k, respectively; g(p(k)) is the feedback regulation of the protein on the transcription; the diagonal matrices $B_1, B_2, B_3$ represent the decay rates of mRNA, the decay rates of protein, and the translation rates of mRNA, respectively; $D_0,D_1$ are the coupling matrices; $u_{1}(k)$ and $u_{2}(k)$ are the external disturbances.

Let $x(k)=\text {col}[m(k),p(k)]$, $g(x(k))=\text {col}[g(m(k)),g(p(k))]$, $B=\begin{bmatrix} B_1&{}\quad 0\\ B_3&{}\quad B_2\\ \end{bmatrix}$, $W_0=\begin{bmatrix} 0&{}\quad D_0\\ 0&{}\quad 0\\ \end{bmatrix},$ $W_1=\begin{bmatrix} 0&{}\quad D_1\\ 0&{}\quad 0\\ \end{bmatrix}$, $u(k)=\begin{bmatrix} u_{1}(k)\\ u_{2}(k)\\ \end{bmatrix}$, $u_{i}(k)=\begin{bmatrix} u_{i1}(k)\\ u_{i2}(k)\\ u_{i3}(k)\\ \end{bmatrix}$, $i=1,2$.

Then, (37) can be rewritten as follows:

$$\begin{aligned} x(k+1)=Bx(k)+W_0g(x(k))+W_1g(x(k-d(k)))+u(k). \end{aligned}$$

Set $B_1=\begin{bmatrix} 0.2&{}\quad 0&{}\quad 0\\ 0&{}\quad 0.2&{}\quad 0\\ 0&{}\quad 0&{}\quad 0.2 \end{bmatrix}$, $B_2=\begin{bmatrix} 0.1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0.1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0.1 \end{bmatrix}$, $B_3=\begin{bmatrix} 0.09&{}\quad 0&{}\quad 0\\ 0&{}\quad 0.09&{}\quad 0\\ 0&{}\quad 0&{}\quad 0.09 \end{bmatrix}$, $D_0=-0.5V$, $D_1=-0.1V$, $V=\begin{bmatrix} 0&{}\quad 0&{}\quad 1\\ 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0\\ \end{bmatrix}$, the regulation function $g(x)=\frac{x^2}{1+x^2}$. It is obvious that the activation function $g(\cdot )$ satisfies (2) with $l_i^-=0,l_i^+=0.65, i=1,2,\ldots ,6.$

Fig. 4

The state trajectories of the system in Example 4 with $d(k)=\hbox {int}[49.5+0.5*\cos (\frac{k\pi }{4})]$, $x(0)=[2,1,-0.8,0.7,-0.9,-1.5]^{{\mathrm{T}}}$ and $u_{ij}(k)=0.015\sin (0.02k),i=1,2,j=1,2,3$

If $d_m=1$, the MADUB $d_M$ calculated by Theorem 1 (Zhang et al. 2017a) is 316. This discrete repressilator system is asymptotically stable for $1\le d(k)\le 316$. However, the range of d(k) derived by Theorem 1 in this paper is $1\le d(k)\le 1101$. Compared with Theorem 1 (Zhang et al. 2017a), our stability criterion can provide less conservative result.

Set $d_m=4,d_M=50$. For $\mu \ge 1$, by applying Theorem 2 in this paper, the allowable minimum $H_{\infty }$ performance level $\gamma =1.8100$.

Let $d(k)=\hbox {int}[49.5+0.5*\cos (\frac{k\pi }{4})]$, the disturbance $u_{ij}(k)=0.015\sin (0.02k)$, $i=1,2, j=1,2,3$, and the initial value $x(0)=[2,1,-0.8,0.7,-0.9,-1.5]^{{\mathrm{T}}}$. The state trajectories of the considered system are showed in Fig. 4, which indicates that the synthetic genetic regulatory network is asymptotically stable.

5 Conclusions

In this paper, the stability and $H_{\infty }$ performance for the discrete-time neural networks with a time-varying delay has been investigated. A new free-matrix-based summation inequality is proposed and applied to estimate the single summation terms. By constructing a suitable LKF with a delay-product-term and bounding its forward difference by the proposed new inequality and the improved reciprocally convex inequality, we derive less conservative conditions for stability and $H_{\infty }$ performance respectively. Four numerical examples are given to further verify the validity of the proposed criteria.