Strong stability preserving implicit and implicit–explicit second derivative general linear methods with RK stability

Abstract

In this work, we use a formulation based on forward Euler and backward derivative condition to obtain A-stable SSP implicit SGLMs up to order five and stage order $q=p$ and SSP implicit–explicit (IMEX) SGLMs where the implicit part of the method is A-stable and the time-step is apart from the explicit part. These kind of methods compared to explicit ones of the same order and number of stages have quite larger SSP time-step. Moreover, the construction of SSP IMEX schemes of order $p=q=s$ and $r=2$ up to order $p=3$ is presented where the implicit part of the method has Runge–Kutta stability together with A-stability property. Numerical results to show the expected order of convergence of the proposed methods are presented on a variety of linear and nonlinear problems.

1 Introduction

To approximate the solution of hyperbolic partial differential equations (PDEs)

$$\begin{aligned} U_t+f(U)_x=0, \end{aligned}$$

(1.1)

the use of high-order time integrations as part of the method of lines technique is required to solve the resulting system of ordinary differential equations (ODEs)

$$\begin{aligned} y_t=F(y). \end{aligned}$$

(1.2)

Here, y is a vector of approximation to U. The simplest method is the explicit forward Euler method

$$\begin{aligned}y_{n+1}=y_n+\varDelta tF(y_n),\end{aligned}$$

which is a one-step, one-stage, and one-derivative method which preserves various properties of the PDE and the fully discrete scheme is strong stable, that is

$$\begin{aligned} \Vert y_n+\varDelta tF(y_n)\Vert \le \Vert y_n\Vert , \end{aligned}$$

(1.3)

under a suitable restricted time-step $0\le \varDelta t\le \varDelta t_{FE}$. The condition (1.3) is known as forward Euler condition and $\Vert \cdot \Vert$ is some convex functional. Due to the small absolute stability region and first order of accuracy of forward Euler method, we do not wish to use this method as time discretization. Instead, we consider this method as a basis for a higher other method that satisfies the forward Euler condition (1.3), perhaps under a different time-step restriction $\varDelta t\le \mathcal {C}\varDelta t_{FE}$. Such higher order methods are called strong stability preserving (SSP) methods and the value $\mathcal {C}$ is referred as SSP coefficient. These methods can be one of three types: one-stage multistep, one-step multistage, or multistep-multistage methods.

A wide variety of successful studies on SSP schemes and their capability to preserve essential solution properties have been published by Shu (1988), Shu and Osher (1988), and Spijker Ferracina and Spijker (2004, 2005, 2008), Gottlieb et al. (2009, 2011), Higueras (2004) and Gottlieb et al. (2001). SSP general linear methods (GLMs) as multistep-multistage methods were studied by Spijker (2007) and investigated more by Izzo et al., for instance in Califano et al. (2018) and Izzo and Jackiewicz (2015a, 2015b, 2019). Recently, SSP explicit multistage two-derivative methods with one-step [(e.g., two-derivative Runge–Kutta (TDRK) methods] or multistep [e.g., second derivative general linear methods (SGLMs)] have been introduced and applied to the numerical solution of hyperbolic PDEs (Christlieb et al. 2016; Moradi et al. 2019). To study the stability properties of the two derivative time-stepping methods, considering some conditions that include the second derivative $G=\frac{\mathrm{{d}}F}{\mathrm{{d}}t}=F{\prime }F$, in addition to the forward Euler condition (1.3), are necessary. Christlieb et al. (2016) demonstrated that TDRK methods preserve the strong stability property of the forward Euler condition (1.3) when coupled with the second derivative condition

$$\begin{aligned} \Vert y_n+\varDelta t^2G(y_n)\Vert \le \Vert y_n\Vert ,\quad \text {for} \quad \varDelta t\le \widetilde{K}\varDelta t_{FE}, \end{aligned}$$

(1.4)

where $\widetilde{K}$ has a positive value that relates to the stability condition of second derivative term and forward Euler term. Using the general order conditions for SGLMs provided in Moradi et al. (2021), Moradi et al. (2019) extended the SSP approach of the TDRK methods to the SGLMs as a class of second derivative multistep-multistage time discretization and studied more in Moradi et al. (2020a, 2020b, 2020c); Moradi and Abdi (2021); Moradi et al. (2021). Another possible condition on second derivative is Taylor series condition Ditkowski et al. (2020), Grant et al. (2019) and Moradi and Abdi (2021)

$$\begin{aligned}\Vert y_n+\varDelta tF(y_n)+\dfrac{\varDelta t^2}{2}G(y_n)\Vert \le \Vert y_n\Vert ,\quad \varDelta t\le \widehat{K}\varDelta t_{FE},\end{aligned}$$

where $\widehat{K}>0$. Explicit SSP time integrations are frequently desired due to their favorable stability regions, low computational costs, and absence of difficulty in implementation. For such methods, the time-step size $\varDelta t$ is related to the mesh size and the speed of propagation of the physical problems. In the case of the problems with diffusion, very small local mesh sizes are often needed because of infinite speed of propagation of information and so that, undesirably, the maximal acceptable time-step possibly be small. To overcome these intense limitations, SSP implicit time integrations can be used to allow for larger time-steps at the cost of increasing the computational cost per time-step. Most of the research has been evoked to find SSP implicit methods which are optimal in terms of their time-step restriction (Ferracina and Spijker 2008; Ketcheson et al. 2009; Ketcheson 2004, 2011; Macdonald et al. 2008). For such methods, the SSP coefficient is bounded by $\mathcal {C}\le 2s$ (Ketcheson 2011). Unconditionally SSP implicit methods of order $p=2$ were first studied by Ketcheson (2011) which use a second operator $\widetilde{F}$ that approximates F and satisfies a downwind condition

$$\begin{aligned}\Vert y_n-\varDelta t\widetilde{F}(y_n)\Vert \le \Vert y_n\Vert ,\quad \varDelta t\le \varDelta t_{FE}.\end{aligned}$$

In the case of implicit multiderivative Runge–Kutta (RK) methods, neither the second derivative condition nor the Taylor series condition leads to unconditional SSP methods for order $p>1$. This follows from the fact that both the second derivative and Taylor series conditions require positive coefficients on the derivative of the operator, while the unconditional SSP property needs negative coefficients. Due to this restriction on the coefficients of the methods, to find unconditional SSP multiderivative RK methods, Gottlieb et al. (2021) introduced a new condition on the second derivative

$$\begin{aligned} \Vert y_n-\varDelta t^2G(y_n)\Vert \le \Vert y_n\Vert ,\quad \varDelta t^2\le K\varDelta t^2_{FE}. \end{aligned}$$

This new second derivative condition is called backward derivative condition. In Gottlieb et al. (2021) , unconditional SSP two-derivative RK methods are obtained up to order $p=4$ in the sense of preserving the forward Euler and backward second derivative conditions. In this paper, we extend this new second derivative conditions for SGLMs and obtain SSP implicit SGLMs up to order $p=5$ and stage order $q=p$. Although derived methods in this paper are not unconditional SSP, their SSP coefficients are significant large and also not bounded by twice the number of stages.

Many multiphysics and biological problems associated with the diffusion term are modeled by differential equations of the form

$$\begin{aligned} \varvec{y}_t=\epsilon \varvec{y}_{xx}+\varvec{F}(\varvec{y}), \end{aligned}$$

with $\epsilon \ge 0$. Here, $\varvec{F}(\varvec{y})$ characterizes the chemical or biological reactions. For such systems, discretizing the diffusion term by suitable spatial discretizations leads to a system of ODEs of the form

$$\begin{aligned} y_t=f_1(y)+f_2(y),\quad t\in [t_0,T], \end{aligned}$$

(1.5)

where $f_1(y)$ and $f_2(y)$, respectively, correspond to the diffusion process and the chemical or biological reactions. To integrate these systems of ODEs, we employ implicit–explicit (IMEX) methods, where the diffusion process is handled by the SSP implicit and the reaction term by explicit schemes. Such methods are useful for diffusion-dominated systems not for the case of the systems with highly stiff reactions. In Sect. 2, we determine sufficient conditions for class of implicit SGLMs to preserve the strong stability properties of spatial discretizations when coupled with forward Euler and backward derivative conditions and present SSP implicit SGLMs up to order $p=5$. In Sect. 3, we extend the theory developed in Sect. 2 to IMEX SGLMs for which the implicit method has Runge–Kutta stability (RKS) property and it is A-stable. We conclude each section by presenting numerical results to show the theoretical results on a variety of problems with diffusion part. Finally, in Sect. 4, some concluding remarks are given.

2 SSP conditions for implicit SGLMs

In this section, we are going to consider SSP implicit SGLMs for the system of ODEs (1.2) on the interval $[t_0,T]$ raised from the spatial discretization of the original PDE (1.1). We first recall the structure of SGLMs introduced by Butcher and Hojjati (2005). The general form of these methods is given by

$$\begin{aligned} \left\{ \begin{array}{c} Y_i^{[n]}=\displaystyle h\sum _{j=1}^{s}a_{ij}f(Y_j^{[n]})+h^2\sum _{j=1}^{s}\overline{a}_{ij} g(Y_j^{[n]})+\sum _{j=1}^{r}u_{ij}y_j^{[n-1]},\quad i=1,2,\dots ,s, \\ \\ [-3mm] y_i^{[n]}=\displaystyle h\sum _{j=1}^{s}b_{ij}f(Y_j^{[n]})+h^2\sum _{j=1}^{s}\overline{b}_{ij}g(Y_j^{[n]})+ \sum _{j=1}^{r}v_{ij}y_j^{[n-1]},\quad i=1,2,\dots ,r, \end{array}\right. \end{aligned}$$

(2.1)

where $n=1,2,\dots ,N$ and $Nh =T-t_0$. Here, $Y_{i}^{[n]}$, $i=1,2,\ldots ,s$, is an approximation to $y(t_{n-1}+c_ih)$ of stage order q, $f(Y^{[n]}_i)$ and $g(Y^{[n]}_i)$, respectively, denote the first and second derivative stage values, and $y_i^{[n]}$, $i=1,2,\ldots ,r$, is an approximation of order p to the linear combinations of the solution u and its derivatives at the point $t_n$, that is

$$\begin{aligned} y_i^{[n]}=\displaystyle \sum _{k=0}^{p}\alpha _{ik}y^{(k)}(t_{n})h^k+O(h^{p+1}),\quad i=1,2,\dots ,r, \end{aligned}$$

(2.2)

for some real parameters $\alpha _{ik}$, $i=1,2,\dots ,r$. The SGLM (2.1) to be of order p and stage order $q=p$ must satisfies the following conditions (Abdi and Hojjati 2011):

$$\begin{aligned} \begin{aligned} UW&=C-AC\varvec{K}-\overline{A}C\varvec{K}^2, \\ VW&=WE-BC\varvec{K}-\overline{B}C\varvec{K}^2, \end{aligned} \end{aligned}$$

(2.3)

where the matrices $C\in \mathbb {R}^{s\times (p+1)}$, $\varvec{K}\in \mathbb {R}^{(p+1)\times (p+1)}$ and $E\in \mathbb {R}^{(p+1)\times (p+1)}$ are determined by

$$\begin{aligned}C:=\left[ e\quad \frac{c}{1!} \frac{c^2}{2!} \dots \frac{c^p}{p!}\right] , \quad \varvec{K}:=[0 e_1 e_2 \dots e_p],\quad E:=\exp (\varvec{K}),\end{aligned}$$

with $c^j$ as the component-wise powers of abscissa vector c, $e=[1 1 \cdots 1]^T\in \mathbb {R}^s$, and $e_j$ as the jth unit vector in $\mathbb {R}^{p+1}$. To reduce the implementation costs when applied to stiff problems, it is important that the coefficient matrices $A\in \mathbb {R}^{s\times s}$ and $\overline{A}\in \mathbb {R}^{s\times s}$ have the form

$$\begin{aligned} A=\left[ \begin{array}{ccccc} \lambda &{} &{} &{} &{} \\ a_{21} &{} \lambda &{} &{} &{} \\ \vdots &{} \ddots &{} \ddots &{} &{} \\ a_{s-1,1} &{} \ddots &{} \ddots &{} \lambda &{} \\ a_{s,1} &{} a_{s,2} &{} \ldots &{} a_{s,s-1} &{} \lambda \end{array} \right] ,\quad \overline{A}=\left[ \begin{array}{ccccc} \mu &{} &{} &{} &{} \\ \overline{a}_{21} &{} \mu &{} &{} &{} \\ \vdots &{} \ddots &{} \ddots &{} &{} \\ \overline{a}_{s-1,1} &{} \ddots &{} \ddots &{} \mu &{} \\ \overline{a}_{s,1} &{} \overline{a}_{s,2} &{} \ldots &{} \overline{a}_{s,s-1} &{} \mu \end{array} \right] , \end{aligned}$$

where $\lambda >0$ and $\mu <0$. Moreover, to ensure the zero stability of SGLM (2.1), we suppose that the matrix V is a rank-one matrix, i.e., $V=ev^T$ with $e=[11\ldots 1]$, $v=[v_1v_2\ldots v_r]^T$, and $v^Te=1$. Applying SGLM (2.1) to the standard linear test equation $y'=\xi y$ Dahlquist (1963), $t\ge 0$, $\xi \in \mathbb {C}$, leads to the stability matrix M(z) defined by

$$\begin{aligned} M(z) = V+(zB+z^2\overline{B})(I-zA-z^2\overline{A})^{-1}U, \end{aligned}$$

and the stability function defined by $p(w,z)=\det (wI-M(z))$, where $z=\xi h$. If the stability function has the special form $p(w,z)=w^{r-1}(w-R(z))$, then the method is said to possesses Runge–Kutta stability (RKS) property.

2.1 Strong stability preserving conditions

With the aim of studying the SSP properties of implicit SGLMs, as discussed in Moradi et al. (2021), the SGLM (2.1) can be written in the following form:

$$\begin{aligned} \begin{array}{l} Y_i^{[n]} =\displaystyle { \sum _{j=1}^{l}s_{ij}y_j^{[n-1]}+h \sum _{j=1}^{m}t_{ij} F(t_{n-1}+c_jh,Y_j^{[n]})+h^2\sum _{j=1}^{m}\overline{t}_{ij}G(t_{n-1}+c_jh,Y_j^{[n]}),}\\ \quad \quad \quad i=1,2,\ldots ,m,\\ y_i^{[n]} = Y_{m-l+i}^{[n]},\quad i=1,2,\ldots ,l, \end{array} \end{aligned}$$

where $n=1,2,\ldots ,N$ and $1\le l\le m$. Introducing the vectors $F(Y^{[n]})$ and $G(Y^{[n]})$, the matrices ${\mathbf {T}}$, $\overline{\mathbf {T}}$ and ${\mathbf {S}}$ as

$$\begin{aligned}&F(Y^{[n]}):=\left[ F(Y_i^{[n]}),\ldots ,F(Y_m^{[n]})\right] ^T,\quad G(Y^{[n]}):=\left[ G(Y_i^{[n]}),\ldots ,G(Y_m^{[n]})\right] ^T, \\&\mathbf {T}=\left( \begin{array}{cc} {A} &{} \mathbf {0} \\ {B} &{} 0 \end{array}\right) ,\quad \overline{\mathbf {T}}=\left( \begin{array}{cc} \overline{{A}} &{} \mathbf {0} \\ \overline{{B}} &{} 0 \\ \end{array}\right) ,\quad \mathbf {S}=\left( \begin{array}{c} {U} \\ \hline {V} \\ \end{array}\right) , \end{aligned}$$

the matrix form of this representation is characterized by

$$\begin{aligned} Y^{[n]}= \mathbf {S}y^{[n-1]}+\varDelta t \mathbf {T}F(Y^{[n]})+\varDelta t^2 \overline{\mathbf {T}}G(Y^{[n]}). \end{aligned}$$

(2.4)

Because of the negative diagonal components of $\overline{A}$, $\mu <0$, using both the forward Euler condition and second derivative or Taylor series conditions leads to methods with $\mathcal {C}=0$. So that in the case of implicit SGLMs to be SSP, we require a new condition on the second derivative. Considering new second derivative condition discussed in Gottlieb et al. (2021)

$$\begin{aligned} \mathbf{Backward} derivative condition: \quad \Vert u_n-\varDelta t^2G(u_n)\Vert \le \Vert u_n\Vert ,\quad \varDelta t^2\le K\varDelta t^2_{FE} \end{aligned}$$

(2.5)

seems to be a useful condition to obtain SSP implicit SGLMs as well. Under this condition, coefficients on the second derivative must be negative. Due to this reason, in this paper, we consider methods with $\overline{\mathbf {T}}\le 0$ which will be SSP under the following conditions:

Theorem 1

Let the first and second derivative operators F and G satisfy (1.3) and (2.5). If the SGLM given by (2.4) satisfies the conditions

$$\begin{aligned} \left( I+\gamma \mathbf {T}+\frac{\gamma ^2}{K^2}|\overline{\mathbf {T}}|\right) ^{-1} \mathbf {S} \ge&0, \end{aligned}$$

(2.6)

$$\begin{aligned} \gamma \left( I+\gamma \mathbf {T}+\frac{\gamma ^2}{K^2}|\overline{\mathbf {T}}|\right) ^{-1}\mathbf {T} \ge&0, \end{aligned}$$

(2.7)

$$\begin{aligned} \frac{\gamma ^2}{K^2}\left( I+\gamma \mathbf {T}+\frac{\gamma ^2}{K^2}|\overline{\mathbf {T}}|\right) ^{-1}|\overline{\mathbf {T}}| \ge&0, \end{aligned}$$

(2.8)

with $|\overline{\mathbf {T}}|$ as the component-wise absolute values of the elements of $\overline{\mathbf {T}}$, then it will preserve the strong stability preserving property $\Vert Y^{[n+1]}\Vert \le \Vert Y^{[n]}\Vert$ under the time-step restriction $\varDelta t\le \gamma \varDelta t_{FE}$.

Proof

Considering method (2.4) as

$$\begin{aligned}Y^{[n]}= \mathbf {S}y^{[n-1]}+\varDelta t \mathbf {T}F(Y^{[n]})-\varDelta t^2 |\overline{\mathbf {T}}|G(Y^{[n]}),\end{aligned}$$

and adding $\gamma \mathbf {T}Y^{[n]}$ and $\widehat{\gamma }|\overline{\mathbf {T}}|Y^{[n]}$ on both sides of the above relation lead to

$$\begin{aligned}(I+\gamma \mathbf {T}+\widehat{\gamma }|\overline{\mathbf {T}}|)Y^{[n]}=\mathbf {S}y^{[n-1]}\!+\!\gamma \mathbf {T}\left( Y^{[n]}\!+\!\frac{\varDelta t}{\gamma }F(Y^{[n]})\right) \!+\!\widehat{\gamma }|\mathbf {T}|\left( Y^{[n]}\!-\!\frac{\varDelta t^2}{\widehat{\gamma }}G(Y^{[n]})\right) .\end{aligned}$$

Now, introducing

$$\begin{aligned}\mathbf {R}=(I+\gamma \mathbf {T}+\widehat{\gamma }|\overline{\mathbf {T}}|)^{-1}\mathbf {S},\quad \mathbf {P}=\gamma (I+\gamma \mathbf {T}+\widehat{\gamma }|\overline{\mathbf {T}}|)^{-1}\mathbf {T},\quad \mathbf {Q}=\widehat{\gamma }(I+\gamma \mathbf {T}+\widehat{\gamma }|\overline{\mathbf {T}}|)^{-1}\overline{\mathbf {T}},\end{aligned}$$

we obtain

$$\begin{aligned} Y^{[n]} =&\mathbf {R}y^{[n-1]}+\mathbf {P}\left( Y^{[n]}+\frac{\varDelta t}{\gamma }F(Y^{[n]})\right) +\mathbf {Q} \left( Y^{[n]}-\frac{\varDelta t^2}{\hat{\gamma }^2}G(Y^{[n]})\right) . \end{aligned}$$

(2.9)

Assuming $\mathbf {R}+\mathbf {P}+\mathbf {Q}=I$ and using the forward Euler and backward derivative conditions, we have

$$\begin{aligned}\big \Vert Y^{[n]}\big \Vert \le \mathbf {R}\big \Vert y^{[n-1]}\big \Vert +\mathbf {P}\big \Vert Y^{[n]}+\frac{\varDelta t}{\gamma } F\big \Vert +\mathbf {Q}\big \Vert Y^{[n]}-\frac{\varDelta t^2}{\hat{\gamma }}G\big \Vert , \end{aligned}$$

which is SSP whenever $\mathbf {R}\ge 0$, $\mathbf {P}\ge 0$ and $\mathbf {Q}\ge 0$, and under the time-step restrictions $\varDelta t\le \gamma \varDelta t_{FE}$ and $\varDelta t\le K\sqrt{\widehat{\gamma }}\varDelta t_{FE}$. To obtain the optimal time-step, these two time-step restrictions must be set equal, and so we require $\gamma =K\sqrt{\hat{\gamma }}$.

$\square$

This theorem allows us to formulate the search for optimal implicit SGLMs of order $p=q=s$ and $r=2$ with SSP coefficient at least $\gamma >0$ as follows:

For a given method of order p, find all the coefficients matrices of the method with $\mathbf {T}\ge 0$, and $\overline{\mathbf {T}}\le 0$, and abscissa vector with elements $-1\le c_i\le 1$, $i=1,2,\ldots ,s$ that maximize the value of $\mathcal {C}=\max \gamma$, such that the related order conditions (2.3) together with the SSP conditions $\mathbf {R}\ge 0$, $\mathbf {P}\ge 0$, and $\mathbf {Q}\ge 0$ are satisfied.

In the following subsection, we use this optimization problem to find SSP implicit SGLMs up to order five and the SSP coefficients of such methods are presented. For the sake of comparison, we have also presented the SSP coefficients of SSP implicit RK methods investigated in Ketcheson et al. (2009).

2.2 Construction of SSP implicit SGLMs

In this subsection, we are interested in finding SSP implicit methods for solving stiff problems obtained by spatial discretization of PDEs which involve diffusion. For such methods, A- or L-stability is essential. Considering these properties, we will construct L-stable SSP implicit SGLMs with RKS property, abscissa vector with elements $-1\le c_i\le 1$, $i=1,2,\ldots ,s$, $r=2$ and $p=q=s$ up to order five. Assuming A-stability, to L-stability, it is required the coefficient of $z^{2s}$ in the numerator of tr(M(z)) to be zero. Denoting $C_{p+1}$ as the error constant of a method of order p with RKS stability, we have

$$\begin{aligned}{} \mathbf{C}-condition: \quad \exp (z)-\text {tr}(M(z))=\sum _{i=1}^{s-1}C_{s+i}z^{s+i}+O(z^{2s}).\end{aligned}$$

Algorithm for construction of SSP implicit SGLMs of order $p=q=s$ and $r=2$ is described as follows:

• To ensure L-stability of a given method, choose $\lambda >0$ and $\mu <0$, such that the stability function takes the form $p(w,z)=w^{r-1}(w-R(z))$ with

  $$\begin{aligned} R(z)=\frac{N(z)}{D(z)}=\frac{\displaystyle 1+\sum _{i=1}^{2s-1}n_iz^i}{(1-\lambda z-\mu z^2)^s},\end{aligned}$$

  where as a consequence of order conditions

  $$\begin{aligned}1+\sum _{i=1}^{2s-1}n_iz^i=\exp (z)(1-\lambda z-\mu z^2)^s-C_{s+1}z^{s+1}-C_{s+2}z^{s+2}-\cdots -C_{2s-1}z^{2s-1}\\ +O(z^{2s}),\end{aligned}$$

  and E-polynomial, $E(y)=|N(\mathbf {i}y)|^{2s}-|D(\mathbf {i}y)|^s$, with $\mathbf {i}$ as the imaginary unit, is non-negative for all real value of y.

• Choose arbitrary, but small, constants $C_{s+i}$, $i=1,2,\ldots ,s-1$, and determine the pairs of $(\lambda ,\mu )$ in domain $[0,2]\times [-2,0]$ which give A-stable methods.

• In addition to order conditions, consider RKS conditions, L-stability conditions, and C-condition as equality constraints together with the nonlinear inequality SSP conditions to the optimization problem with objective function

  $$\begin{aligned} \min \quad -\gamma , \end{aligned}$$

  with $\gamma$ appearing in (2.6)–(2.8).

• Solve the optimization problem using fmincon command with the sequential quadratic programming (SQP) algorithm from the MATLAB and with many random starting points.

In the rest of the paper, we consider methods of order $p=q=s$ and $r=2$. For all the methods, since $r=2$, the RKS property is equivalent to have $\det (M(z))=0$ and the stability function of the method takes the form $p(w,z)=w(w-R(z))$.

2.2.1 Methods of order 2

In this part, we search for L-stable SSP implicit SGLMs of order $p=q=s=r=2$ with $\lambda >0$, $\mu <0$, abscissa vector $c=[c_1c_2]^T$ and RKS property. Based on the above algorithm, to ensure the L-stability, it is important to choose $\lambda$ and $\mu$, such that the stability function of the method has the form

$$\begin{aligned}R(z)=\frac{1+n_1z+n_2z^2+n_3z^3}{(1-\lambda z-\mu z^2)^2},\end{aligned}$$

and as a consequence of order conditions

$$\begin{aligned}1+n_1z+n_2z^2+n_3z^3=\exp (z)(1-\lambda z-\mu z^2)^2-C_3z^3+O(z^4).\end{aligned}$$

For such methods, A-stability requirement implies that $\lambda >0$ and $\mu <0$, so that the E-polynomial $E(y)=y^4(E_0+E_1y^2+E_2y^4)$ is non-negative for all real value of y where $E_0$, $E_1$ and $E_2$ are expressions in $\lambda$, $\mu$ and $C_3$. Choosing $C_3=-10^{-3}$ and $\lambda >0$ and $\mu <0$ in such a way that $E_0+E_1x+E_2x^2$ is non-negative for all positive real numbers x lead to the range of $(\lambda ,\mu )$ which provide L-stable methods. These pairs of $(\lambda ,\mu )$ are plotted in Fig. 1.

Fig. 1

L-stable choices of $(\lambda ,\mu )$ for $p=q=s=r=2$

Now, considering the order conditions (2.3), RKS and L-stability conditions together with C-condition as equality constraints and SSP conditions as inequality constraints to the minimization problem leads to the SSP implicit methods. For $K=1$, the SSP coefficient of derived method is $\mathcal {C}=5.33$, while for the optimal implicit RK method of the same order and stage $p=s=2$, it is 4. The coefficients matrices of the derived method are given by

$$\begin{aligned} A&=\left[ \begin{array}{c@{}c} 0.437508016495166 &{} 0\\ 0.481922545952264 &{} 0.437508016495166 \end{array}\right] ,\\ \overline{A}&=\left[ \begin{array}{c@{}c} -0.095099529112491 &{} 0\\ -0.094720307035320 &{} -0.095099529112491 \end{array}\right] ,\\ \\ B&=\left[ \begin{array}{c@{}c} 0.486156602801407 &{} 0.513390888590178\\ 0.487744233794554 &{} 0.513800602965683 \end{array}\right] ,\\ \overline{B}&=\left[ \begin{array}{c@{}c} -0.097209917437713 &{} -0.087158520960135\\ -0.096932706945793 &{} -0.090079484978238 \end{array} \right] ,\\ U&=\left[ \begin{array}{c@{}c} 0.773444985770947 &{} 0.226555014229053\\ 0.773444985770931 &{} 0.226555014229069 \end{array} \right] ,\\ V&=\left[ \begin{array}{c@{}c} 0.773444985770929 &{} 0.226555014229071\\ 0.773444985770929 &{} 0.226555014229071 \end{array} \right] ,\\ c&= \left[ \begin{array}{c} 0.518077454047736 \\ 1 \end{array}\right] , \quad \alpha _0 = \left[ \begin{array}{c} 1 \\ 1 \end{array}\right] ,\\ \alpha _1&=\left[ \begin{array}{c} 0.080116928944154 \\ 0.082114274312806 \end{array}\right] , \quad \alpha _2=\left[ \begin{array}{c} 0.003410910293517 \\ 0.000002041597084 \end{array}\right] . \end{aligned}$$

2.2.2 Methods of order 3

In this part, we are going to construct L-stable SSP implicit SGLMs of order $p=q=s=3$ and $r=2$ with $\lambda >0$, $\mu <0$, abscissa vector $c=[c_1c_2c_3]^T$ and RKS property. To do this, we first consider process for selecting $\lambda$ and $\mu$, such that the stability function has the form

$$\begin{aligned}R(z)=\frac{1+n_1z+n_2z^2+n_3z^3+n_4z^4+n_5z^5}{(1-\lambda z-\mu z^2)^3},\end{aligned}$$

and as a consequence of order conditions

$$\begin{aligned}1+n_1z+n_2z^2+n_3z^3+n_4z^4+n_5z^5=\exp (z)(1-\lambda z-\mu z^2)^3-C_4z^4-C_5z^5+O(z^6),\end{aligned}$$

where $C_4$ and $C_5$ are constant numbers. For these methods, the related E-polynomial takes the form

$$\begin{aligned}E(y)=y^4(E_0+E_1y^2+E_2y^4+E_3y^6+E_4y^8),\end{aligned}$$

where the coefficients $E_0$, $E_1$, $E_2$, $E_3$, and $E_4$ are complicated expressions in $\lambda$, $\mu$, $C_4$, and $C_5$. Choosing $C_4=10^{-3}$ and $C_5=3\times 10^{-4}$ and $\lambda >0$ and $\mu <0$ in such a way as to ensure that $E_0+E_1x^2+E_2x^4+E_3x^6+E_4x^8$ for all positive real numbers x is non-negative, lead to the pairs of $(\lambda ,\mu )$ which give L-stable schemes. Such pairs of $(\lambda ,\mu )$ are shown in Fig. 2.

Fig. 2

L-stable choices of $(\lambda ,\mu )$ for $p=q=s=3$ and $r=2$

To obtain SSP implicit SGLMs, we solve optimization problem with largest allowable time-step as objective function and subject to the order conditions (2.3), RKS and L-stability conditions along with C-conditions as equality constraints and SSP conditions as inequality constraints. Note that, in search for such methods, $\lambda$ and $\mu$ must be selected from the L-stable choices of $(\lambda ,\mu )$ plotted in Fig. 2. We select single value of K, given by $K=1$, and search for SSP implicit SGLM of order $p=q=s=3$ and $r=2$ which satisfies the above conditions. For this method, the SSP coefficient is $\mathcal {C}=6.05$, while for the implicit RK method of the same order and stage $p=s=3$, it is 4.83. The coefficients matrices of the derived method are given by

$$\begin{aligned} A&=\left[ \begin{array}{c@{}c@{}c} 0.267603000892177 &{} 0 &{} 0\\ 0.341953350263364 &{} 0.267603000892177 &{} 0\\ 0.335702875305309 &{} 0.342847250249487 &{} 0.267603000892177 \end{array}\right] , \\ \overline{A}&=\left[ \begin{array}{c@{}c@{}c} -0.026123057956006 &{} 0 &{} 0\\ -0.033405914492044 &{} -0.026123057956006 &{} 0\\ -0.034477399219702 &{} -0.034526686814204 &{}-0.026123057956006 \end{array}\right] ,\\ {B}&=\left[ \begin{array}{c@{}c@{}c} 0.336331551893402 &{} 0.339883216735631 &{} 0.300285484825070\\ 0.336935379056885 &{} 0.334580595998755 &{} 0.329427239736687 \end{array}\right] ,\\ {\overline{B}}&=\left[ \begin{array}{c@{}c@{}c} -0.034398297797059 &{} -0.035589703970484 &{} -0.033672528176838\\ -0.034332122074900 &{} -0.035648146579086 &{} -0.035263083663109 \end{array} \right] ,\\ {U}&=\left[ \begin{array}{c@{}c} 0 &{} 1.0\\ 0.036810987781440 &{} 0.963189012218560\\ 0.039064548546729 &{} 0.960935451453271 \end{array} \right] ,\\ {V}&=\left[ \begin{array}{c@{}c} 0.038588400941909 &{} 0.961411599058091\\ 0.038588400941909 &{}0.961411599058091 \end{array} \right] ,\\ c&=\left[ \begin{array}{c} 0.322404727695027\\ 0.663458308407227\\ 1.0 \end{array}\right] ,\quad {\alpha }_0=\left[ \begin{array}{c} 1\\ 1 \end{array}\right] ,\\ {\alpha }_1&=\left[ \begin{array}{c} 0.030358765464626\\ 0.054801726802850 \end{array}\right] ,\\ {\alpha }_2&=\left[ \begin{array}{c} -0.007973590605640\\ -0.008181010456956 \end{array}\right] ,\\ {\alpha }_3&=\left[ \begin{array}{c} 0.000286450015294\\ 0.000099608997408 \end{array}\right] . \end{aligned}$$

2.2.3 Methods of order 4

As the previous subsections, to construct L-stable implicit SGLMs of order $p=q=s=4$ with $r=2$, we first consider the process for choosing $\lambda$ and $\mu$ in a manner that the stability function has the form

$$\begin{aligned}R(z)=\frac{1+n_1z+n_2z^2+n_3z^3+n_4z^4+n_5z^5+n_6z^6+n_7z^7}{(1-\lambda z-\mu z^2)^4},\end{aligned}$$

with

$$\begin{aligned}&1+n_1z+n_2z^2+n_3z^3+n_4z^4+n_5z^5+n_6z^6+n_7z^7\\&=\exp (z)(1-\lambda z-\mu z^2)^4-C_5z^5-C_6z^6-C_7z^7+O(z^8),\end{aligned}$$

where $C_5$, $C_6$, and $C_7$ are constant numbers. We select $C_5=2\times 10^{-4}$, $C_6=-2\times 10^{-5}$ and $C_7 = -3\times 10^{-6}$. To ensure L-stability, we determine for which pairs of $(\lambda ,\mu )$, the related E-polynomial defined by

$$\begin{aligned}E(y) = y^6 ( E_0 + E_1 y^2 + E_2 y^4 + E_3 y^6 + E_4 y^8 + E_5 y^{10}),\end{aligned}$$

is non-negative for all positive real value of y, so that $\lambda >0$ and $\mu <0$. These pairs of $(\lambda ,\mu )$ providing L-stability are plotted in Fig. 3.

Fig. 3

L-stable choices of $(\lambda ,\mu )$ for $p=q=s=4$ and $r=2$

Considering the RKS and L-stability conditions along with C-conditions in addition to the order conditions as equality constraints to the optimization problem allows us to search for SSP implicit SGLMs in which $\lambda$ and $\mu$ are chosen from the L-stable choices of $(\lambda ,\mu )$ shown in Fig. 3. For one selected value of K, given by $K=1$, the SSP coefficient of derived method is $\mathcal {C}=4.93$, while for the optimal implicit RK method of the same order and stage $p=s=4$, it is 4.42. The coefficients matrices of this method are characterized by

$$\begin{aligned}&\begin{array}{l} A=\left[ \begin{array}{c@{}c@{}c@{}c} 0.254176341984116 &{} 0 &{} 0 &{} 0\\ 0.261582621254152 &{} 0.254176341984116 &{} 0 &{} 0\\ 0.339390711604040 &{} 0.029861425647354 &{} 0.254176341984116 &{} 0\\ 0.331676441093089 &{} 0.029142345541208 &{} 0.347123997405635 &{} 0.254176341984116 \end{array}\right] , \\ \\ \overline{A}=\left[ \begin{array}{c@{}c@{}c@{}c} -0.020938442042814&{} 0 &{} 0 &{} 0\\ -0.031521072388081 &{} -0.020938442042814 &{} 0 &{} 0\\ -0.024788471132196 &{} -0.007067900027874 &{} -0.020938442042814 &{} 0\\ -0.023784317743168 &{} -0.006911223412509&{} -0.033444226057938 &{} -0.020938442042814 \end{array}\right] ,\\ \\ {B}=\left[ \begin{array}{c@{}c@{}c@{}c} 0.323965463961283 &{} 0.028015482596813 &{} 0.333701564772902 &{} 0.348274873064158\\ 0.330670550287511 &{} 0.029289756044977 &{} 0.351865052580348 &{} 0.270751486096503 \end{array}\right] ,\\ \\ {\overline{B}}=\left[ \begin{array}{c@{}c@{}c@{}c} -0.023759085240579 &{} -0.006643983373337 &{} -0.032151019957030 &{} -0.038561682229809\\ -0.023822609235787 &{} -0.006897405040536 &{} -0.033811615960564 &{} -0.031540463372965 \end{array} \right] , \\ \\ {U}=\left[ \begin{array}{c@{}c} 0.226197082870204 &{} 0.773802917129796\\ 0.312126402799657 &{} 0.687873597200343\\ 0.349341360031528 &{} 0.650658639968472\\ 0.331291225574177 &{} 0.668708774425823 \end{array} \right] , \quad {V}=\left[ \begin{array}{c@{}c} 0.339100274129694 &{} 0.660899725870306\\ 0.339100274129694 &{} 0.660899725870306 \end{array} \right] , \\ \\ \quad c=\left[ \begin{array}{c} 0.286657422221648\\ 0.552655138282832\\ 0.662236778855867\\ 1.0 \end{array}\right] ,\quad {\alpha }_0=\left[ \begin{array}{c} 1\\ 1 \end{array}\right] , \quad {\alpha }_1=\left[ \begin{array}{c} 0.072239491497979\\ 0.020858952112161 \end{array}\right] , \end{array} \\&\begin{array}{l} {\alpha }_2=\left[ \begin{array}{c} -0.005850201740369\\ -0.012294545942157 \end{array}\right] ,\quad {\alpha }_3=\left[ \begin{array}{c} -0.003292370185643\\ 0.000296750273909 \end{array}\right] ,\quad {\alpha }_4=\left[ \begin{array}{c} 0.000668051239820\\ -0.000009500761051 \end{array}\right] . \end{array} \end{aligned}$$

2.2.4 Methods of order 5

In this part, we will look for L-stable SSP implicit SGLMs of order $p=q=s=5$ and $r=2$ with RKS property in which their stability function takes the form

$$\begin{aligned}R(z)=\frac{ 1+\sum _{j=1}^{9}n_jz^j}{(1-\lambda z-\mu z^2)^5},\end{aligned}$$

with

$$\begin{aligned}\displaystyle 1+\sum _{j=1}^{9}n_jz^j=\exp (z)(1-\lambda z-\mu z^2)^5-C_6z^6-C_7z^7-C_8z^8-C_9z^9+O(z^{10}),\end{aligned}$$

where $C_6$, $C_7$, $C_8$, and $C_9$ are constant numbers. In search for SSP implicit SGLMs of order $p=q=s=5$, we observed that C-conditions with arbitrary selected constant numbers $C_6$, $C_7$, $C_8$, and $C_9$ do not result in SSP methods and provide most restriction to the optimization problem. However, considering these constant numbers as free parameters to the optimization problem provides a practical way to dominate this disadvantage. Taken together, for one selected value of K, chosen by $K=1$, limiting $\lambda$ and $\mu$ to $0\le \lambda \le 1$ and $-1\le \mu \le 0$ and solving the optimization problem with unknown entries of coefficients matrices of the method together with constant numbers $C_6$, $C_7$, $C_8$, and $C_9$ as free parameters, subject to the order conditions (2.3), the RKS and L-stability conditions along with C-conditions correspond to the equality constraints and SSP conditions correspond to the inequality constraints lead to the SSP implicit SGLM with $\mathcal {C}=1.58$. Considering the obtained constant numbers $C_6 = -1.791\times 10^{-4}$, $C_7 = 1.681\times 10^{-4}$, $C_8 = -5.126\times 10^{-5}$, and $C_9 = 6.522\times 10^{-6}$, L-stable choices of $(\lambda ,\mu )$ are shown in Fig. 4. Note that the SSP coefficient for proposed method in this part is smaller than that for SSP implicit RK method of the same order and stage $p=s=5$ obtained in Ketcheson (2011).

Fig. 4

L-stable choices of $(\lambda ,\mu )$ for $p=q=s=5$ and $r=2$

The coefficients matrices of the derived method are given by

$$\begin{aligned}&{\begin{array}{l} A=\left[ \begin{array}{c@{}c@{}c@{}c@{}c} 0.387643780986819 &{} 0 &{} 0 &{} 0 &{} 0\\ 0.637727168252425 &{} 0.387643780986819 &{} 0 &{} 0 &{} 0\\ 0.611159777449862 &{} 0.741766315721221 &{} 0.387643780986819 &{} 0 &{} 0\\ 0.520242656261881 &{} 0.421920886114798 &{} 0.236581114595714 &{} 0.387643780986819 &{} 0\\ 0.586674660944235 &{} 0.722670449888464 &{} 0.170921769330670 &{} 0.130086060748346 &{} 0.387643780986819 \end{array}\right] , \\ \\ \overline{A}=\left[ \begin{array}{c@{}c@{}c@{}c@{}c} -0.049561787393363 &{} 0 &{} 0&{} 0 &{} 0\\ -0.042621446052528 &{} -0.049561787393363 &{} 0 &{} 0 &{} 0\\ -0.045746185534674 &{} -0.036083052428533 &{} -0.049561787393363 &{} 0 &{} 0\\ -0.052172656158891 &{} -0.233540265356757 &{} -0.064974933988016&{} -0.049561787393363&{} 0\\ -0.048662224553958 &{} -0.065726996285724 &{} -0.040949385111455 &{} -0.017303063024367 &{} -0.049561787393363 \end{array}\right] , \\ \\ {B}=\left[ \begin{array}{c@{}c@{}c@{}c@{}c} 0.540812948434475 &{} 0.247074745148801 &{} 0.053325659996030 &{} 0.075410913921221 &{} 0.081281076462137\\ 0.543208809191779 &{} 0.260917804212698 &{} 0.064866888255913 &{} 0.062806443761092 &{} 0.073308956951426 \end{array}\right] ,\\ \\ {\overline{B}}=\left[ \begin{array}{c@{}c@{}c@{}c@{}c} -0.061534523519883 &{} -0.181529377484374 &{} -0.014167338763988 &{} -0.076536493310707 &{} -0.003953899336315\\ -0.058526265069824 &{} -0.168881377810191 &{} -0.034960256366596 &{} -0.063010928351178 &{} -0.003566097409785 \end{array} \right] , \end{array}} \\&{\begin{array}{l} {U}=\left[ \begin{array}{c@{}c} 1.0&{} 0\\ 0.642756835465249 &{} 0.357243164534751\\ 0.724870718130109 &{} 0.275129281869891\\ 0.697805587968451 &{} 0.302194412031549\\ 0.721904371786921 &{} 0.278095628213079 \end{array} \right] , \quad {V}=\left[ \begin{array}{c@{}c} 0.709219261086733 &{} 0.290780738913267\\ 0.709219261086733 &{} 0.290780738913267 \end{array} \right] , \\ \\ c=\left[ \begin{array}{c} -0.612356219013181\\ 0.027944371241631\\ 0.742551784010220\\ 0.568565313057531\\ 1.0 \end{array}\right] ,\quad {\alpha }_0=\left[ \begin{array}{c} 1\\ 1 \end{array}\right] , \quad {\alpha }_1=\left[ \begin{array}{c} -1.0\\ -0.992796441589756 \end{array}\right] ,\quad {\alpha }_2=\left[ \begin{array}{c} 0.474427936924484\\ 0.468352176869725 \end{array}\right] ,\\ \\ {\alpha }_3=\left[ \begin{array}{c} -0.141299064850759\\ -0.150062555313376 \end{array}\right] ,\quad {\alpha }_4=\left[ \begin{array}{c} 0.029986316568360\\ 0.036784816602692 \end{array}\right] ,\quad {\alpha }_5=\left[ \begin{array}{c} 0.777139167068760\\ 0.774153079544181 \end{array}\right] . \end{array}} \end{aligned}$$

2.3 Numerical results

In this subsection, we are going to examine our methods to some one-dimensional linear and nonlinear problems. Moreover, we compare the proposed methods with the explicit methods investigated in Moradi et al. (2019). Such methods will be referred to as SSP im-SGLM$_{pq}$ and SSP ex-SGLM$_{pq}$, corresponding to the SSP implicit SGLMs and SSP explicit SGLMs of order $p=q=s$.

In what follows, temporal derivatives are replaced by spatial derivatives using the Lax–Wendroff type of approach. We begin with the pure heat equation

$$\begin{aligned}y_t=\epsilon y_{xx},\quad 0\le t\le 5\end{aligned}$$

with periodic boundary conditions on the unit interval [0, 1] and initial conditions $y_0(x)=\sin (2\pi x)$, and $\epsilon =0.1$. To discrete spatial derivative, we use the fourth-order 5-point spatial discretization

$$\begin{aligned}y_{xx}(x_j)\approx \frac{-y_{j+1}+16y_{j+1}-30y_j+16y_{j-1}-y_{j-2}}{(\varDelta x)^2},\end{aligned}$$

and the second temporal derivatives are approximated by

$$\begin{aligned}y_{tt}=(\epsilon y_{xx})_t=\epsilon (y_t)_{xx}=\epsilon ^2 y_{xxxx}.\end{aligned}$$

Numerical results for all the methods obtained in this section are presented in Fig. 5. By this figure, one can see that the expected order of accuracy for each method is achieved. The norm of global error at the final time $T_f=5.0$ and the expected order of convergence for SSP implicit SGLMs with $p=q=s=3,4$ 5 and for SSP explicit SGLMs with the same order, stage order, and internal stages are reported in Tables 1, 2, and 3. The results in these tables indicate that SSP explicit methods for a large time-step are not desire, while SSP implicit methods behave as expected.

Fig. 5

Convergence study for SSP im-SGLMs$_{pq}$ with $p=q=s=2,3,4,5$, and $K=1$ and grid refinement in time

Table 1 Convergence study for SSP im-SGLM$_{pq}$ and SSP ex-SGLM$_{pq}$ with $p=q=s=3$; using of time-steps, $\varDelta t=T_f/N_t$ with $T_f=5.0$ and spatial grid $\varDelta x=1/N$ with $N=8$

Table 2 Convergence study for SSP im-SGLM$_{pq}$ and SSP ex-SGLM$_{pq}$ with $p=q=s=4$; using of time-steps, $\varDelta t=T_f/N_t$ with $T_f=5.0$ and spatial grid $\varDelta x=1/N$ with $N=8$

Table 3 Convergence study for SSP im-SGLM$_{pq}$ and SSP ex-SGLM$_{pq}$ with $p=q=s=5$; using of time-steps, $\varDelta t=T_f/N_t$ with $T_f=5.0$ and spatial grid $\varDelta x=1/N$ with $N=8$

To show capability of our methods to preserve positivity, we consider a sample problem Gottlieb et al. (2021)

$$\begin{aligned} y_t=-10y^2,\quad y(0) = 10, \end{aligned}$$

(2.10)

with final time $T_f=2$. For positivity, this problem with $F=-10y^2$ and $G=200y^3$ satisfies the forward Euler and backward derivative conditions, respectively

$$\begin{aligned} \begin{array}{l} y^{n+1}=y^n+\varDelta tF(y^n)= y^n(1-10\varDelta ty^n)>0,\quad \text {for}\quad \varDelta t\le \frac{0.1}{y^n},\\[2mm] y^{n+1}=y^n-\varDelta t^2G(y^n)= y^n(1-200\varDelta t^2(y^n)^2)>0,\quad \text {for}\quad \varDelta t^2\le \frac{0.005}{(y^n)^2}. \end{array} \end{aligned}$$

Numerical results for second-order SSP implicit SGLM compared to the second-order non-SSP implicit SGLM studied in Behzad et al. (2018) for $\varDelta t=\frac{1}{N_t}$ where $N_t=4,8,16,32,64$ are presented in Fig. 6. Note that because of small $y^n$, explicit methods loss positivity even for very small time-step, $\varDelta t> 4\text {e}-05$. The norm of global error at the final time $T_f=2.0$ for SSP im-SGLMs with $p=q=s=3,4$, and 5 together with that for non-SSP implicit SGLMs of the same order investigated in Behzad et al. (2018) are reported in Table 4. From this table, we can conclude that the second-, third-, and fourth-order methods proposed in this paper preserve positivity up till a large time-step, while in the case of non-SSP implicit methods, positivity is lost for $\varDelta t>\frac{1}{256}$.

Fig. 6

The numerical solution of problem (2.10) obtained by SSP im-SGLM$_{22}$ and Non-SSP im-SGLM$_{22}$ compared to the correct solution

Table 4 Numerical results for problem (2.10) obtained by SSP im-SGLMs$_{pq}$ and Non-SSP im-SGLMs$_{pq}$

3 SSP implicit–explicit SGLMs

In this section, we consider equations associated with diffusion terms modeled by

$$\begin{aligned} {y}_t=\epsilon {y}_{xx}+\varvec{F}({y}),\quad \epsilon \ge 0, \end{aligned}$$

where $\varvec{F}({y})$ represents the chemical or biological reactions. Discretizing the diffusion term by suitable spatial discretizations gives an ODE of the form

$$\begin{aligned} y_t=f_1(y)+f_2(y),\quad t\in [t_0,T], \end{aligned}$$

(3.1)

where $f_1(y)$ and $f_2(y)$, respectively, correspond to the diffusion process and the chemical or biological reactions. In previous section, we observed that the SSP coefficients of implicit SGLMs are considerably larger than their explicit peers which at the cost of increasing the computational cost per time-step provide a remarkable benefit over the explicit ones. In the case of problems where in addition to the diffusion term there is a nonlinear part that is expensive to solve implicitly, we turn to implicit–explicit methods which the implicit part has SSP property. In this section, we are going to search for IMEX methods in which use SSP implicit SGLMs for integrate the stiff part, corresponds to the diffusion process, and explicit GLMs for the non-stiff part, corresponds to the reaction processes. To do this, we use an s-stage implicit SGLM, defined by six matrices $A\in \mathbb {R}^{s\times s}$, $\overline{A}\in \mathbb {R}^{s\times s}$, $U\in \mathbb {R}^{s\times r}$, $B\in \mathbb {R}^{r\times s}$, $\overline{B}\in \mathbb {R}^{r\times s}$ and $V\in \mathbb {R}^{r\times r}$ and the abscissa vector c, and s-stage explicit GLM, defined by four matrices $A^*\in \mathbb {R}^{s\times s}$, $U\in \mathbb {R}^{s\times r}$, $B^*\in \mathbb {R}^{r\times s}$, and $V\in \mathbb {R}^{r\times r}$ and the abscissa vector c, such that

$$\begin{aligned} Y_i^{[n]}=&h\sum _{j=1}^{i}a_{ij}f_1\left( Y_{j}^{[n]}\right) + h\sum _{j=1}^{i-1}a^*_{ij}f_2\left( Y_{j}^{[n]}\right) + h^2\sum _{j=1}^{i}\overline{a}_{ij}g\left( Y_{j}^{[n]}\right) +\sum _{j=1}^{r} u_{ij}y_j^{[n-1]},\quad i=1,2,\dots ,s,\nonumber \\ y_i^{[n]}=&h\sum _{j=1}^{s}b_{ij}f_1\left( Y_{j}^{[n]}\right) + h\sum _{j=1}^{s}b^*_{ij}f_2\left( Y_{j}^{[n]}\right) + h^2\sum _{j=1}^{s}\overline{b}_{ij}g\left( Y_{j}^{[n]}\right) +\sum _{j=1}^{r} v_{ij}y_j^{[n-1]},\quad i=1,2,\dots ,r, \end{aligned}$$

(3.2)

for $n=1,2,\dots ,N$. Here, $Y_i^{[n]}$ are approximations of the stage order q to the $y(t_{n-1}+c_ih)$, that is

$$\begin{aligned} Y_i^{[n]}=y(t_{n-1}+c_ih)+O(h^{q+1}),\quad i=1,2,\dots ,s, \end{aligned}$$

(3.3)

and the values $y_i^{[n]}$, $i=1,2,\ldots ,r$, stand for approximations of order p to the linear combinations of the solution $y:=x+z$ to (3.1) and its derivatives at the point $t_n$ as

$$\begin{aligned} y_i^{[n]}=\sum _{k=0}^{p}\alpha _{ik}h^kx^{(k)}(t_n)+ \sum _{k=0}^{p}\alpha _{ik}^*h^kz^{(k)}(t_n)+O(h^{p+1}),\quad i=1,2,\dots ,r, \end{aligned}$$

(3.4)

where x is the solution obtained by the implicit SGLM and z obtained by the explicit GLM. Note that the both implicit SGLM and explicit GLM use the same coefficients matrices U and V and the same abscissa vector $c=[c_1,\ldots ,c_s]^T$. In this section, we develop the theory explained in the previous section to IMEX methods of order $p=q=s$ with $r=2$ up to order $p=4$. In fact, to construct implicit methods, we will use the same algorithm mentioned in Sect. 2. The IMEX SGLMs-GLMs with SSP implicit part are interesting from the computational perspective, because such methods allow for solve the nonlinear diffusion-dominated systems. We are going to construct SSP IMEX SGLMs with large region of absolute stability together with large SSP coefficients. To discuss the stability properties of the IMEX methods, the scalar test problem

$$\begin{aligned} y'(t)=\lambda _1y(t)+\lambda _2y(t),\quad t\ge 0,\end{aligned}$$

where $\lambda _1$ and $\lambda _2$ are complex parameters, is considered. Applying the IMEX method (3.2) to this problem leads to

$$\begin{aligned} y^{[n]}=M(z_1,z_2)y^{[n-1]},\end{aligned}$$

where $M(z_1,z_2)$ is defined as the stability matrix and given by

$$\begin{aligned} M(z_1,z_2)=V+(z_1B+z_1^2\overline{B}+z_2B^*)(I-z_1A-z_1^2\overline{A}-z_2B^*)^{-1}U,\end{aligned}$$

with $z_1=h\lambda _1$ and $z_2=h\lambda _2$. The stability function $p(w,z_1,z_2)$ corresponds to this stability matrix is defined by

$$\begin{aligned} \frac{p(w,z_1,z_2)}{(1-\lambda z_1-\mu z_1^2)^s}=\det (wI_r-M(z_1,z_2)).\end{aligned}$$

The aim of this section is to search for IMEX SGLMs-GLMs that their stability region $S_\alpha$ defined by

$$\begin{aligned} S_{\alpha }=\bigcap _{y\in \mathbb {R}}S_{\alpha ,y}=\left\{ \begin{array}{ll} z_2\in \mathbb {C}:\text { the IMEX SGLM-GLM is stable for any }\\ \qquad \quad z_1\in \mathbb {C}:\quad \text { Re }(z_1)<0 \;\text { and }\; |\text {Im}(z_1)|\le \tan (\alpha )|\text {Re}(z_1)| \end{array}\right\} ,\end{aligned}$$

not only is not insignificant but also includes a part of the stability region of the explicit scheme, i.e., $S_\alpha \subset S_E=S_{\alpha ,0}$ for $\alpha \in (0,\pi /2]$. Here, for fixed values $y\in \mathbb {R}$, $S_{\alpha ,y}$ is defined as

$$\begin{aligned} S_{\alpha ,y}=\left\{ \begin{array}{ll} z_2\in \mathbb {C}:\text { the IMEX SGLM-GLM is stable for fixed }\\ \qquad \quad z_1=-|y|/\tan (\alpha )+iy \end{array}\right\} . \end{aligned}$$

(3.5)

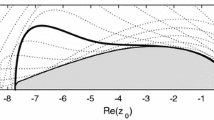
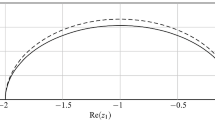
In search for SSP IMEX SGLMs-GLMs, we will use the same optimization problem mentioned in the previous section with the additional equality constraints corresponding to the order conditions of explicit part and obtain SSP IMEX SGLMs-GLMs up to order $p=3$. In this section, the constructed methods will be referred to as IMEX SGLMs$_{pq}$, where p is the order and q is the stage order. The SSP coefficients of the obtained IMEX methods of order $p=q=s=2,3,4$ with $r=2$ are listed in Table 5, for single value of $K=1$, together with the area(S$_{\pi /2}$), area(S$_E$) and intervals of absolute stability int($S_{\pi /2}$), and int($S_E$). For the sake of comparison, in this table, the SSP coefficients for IMEX TDRK methods studied in Gottlieb et al. (2021) are also reported. The stability regions $S_E$ and $S_{\pi /2}$ of the proposed IMEX methods are plotted in Figs. 7 and 8 together with the boundaries of the regions $S_{\pi /2,y}$ for $y = -5,-4.8,\dots ,5$. We will continue this section by listing the coefficients matrices of the constructed methods and presenting numerical results obtained by applying such methods on linear and nonlinear problems.

Table 5 The SSP coefficients, $\mathcal {C}$, together with area($S_{\pi /2}$), area($S_E$), int($S_{\pi /2}$ ), and int($S_E$) for the SSP IMEX SGLM$_{pq}$ of order $p=q=s=2$ and $p=q=s=3$ and SSP coefficients for IMEX TDRK of order $p=2$ and $p=3$

Fig. 7

Left: the boundaries of the stability regions $S_{\pi /2,y}$, $y = -5,-4.8,\dots ,5$ (thin lines), $S_E$ (thick line), and the stability region $S_{\pi /2}$ (shaded region); right: the boundaries of the stability regions $S_{\pi /2}$ (thin line) and $S_E$ (thick line) for SSP IMEX SGLM$_{pq}$ with $p=q=2$

Fig. 8

Left: the boundaries of the stability regions $S_{\pi /2,y}$, $y = -5,-4.8,\dots ,5$ (thin lines), $S_E$ (thick line), and the stability region $S_{\pi /2}$ (shaded region); right: the boundaries of the stability regions $S_{\pi /2}$ (thin line) and $S_E$ (thick line) for SSP IMEX SGLM$_{pq}$ with $p=q=3$

• Coefficients matrices of the IMEX SGLM$_{22}$

  $$\begin{aligned}&A=\left[ \begin{array}{c@{}c} 0.420359985237433 &{} 0\\ 0.462116390077325 &{} 0.420359985237433 \end{array}\right] , \\ \\&\overline{A}=\left[ \begin{array}{c@{}c} -0.087297406242430&{} 0\\ -0.087479459921831 &{} -0.087297406242430 \end{array}\right] , \\ \\&B=\left[ \begin{array}{c@{}c} 0.455152368103553 &{} 0.544847631896447\\ 0.455152368103553 &{} 0.544847631896446 \end{array}\right] , \\ \\&\overline{B}=\left[ \begin{array}{c@{}c} -0.086161158095212&{} -0.085981847936385\\ -0.086161158095212 &{} -0.085981847936385\\ \end{array} \right] , \\ \\&A^*=\left[ \begin{array}{c@{}c} 0 &{} 0\\ 0.576079291733572 &{} 0 \end{array}\right] ,\quad \!\!\! {B}^*=\left[ \begin{array}{c@{}c} 0.716798824251877 &{} 0.868858072696912\\ -1.0 &{} 0.597537554877228 \end{array} \right] ,\\ \\&U=\left[ \begin{array}{c@{}c} 0.773536868425739 &{} 0.226463131574261\\ 0.716214906285628 &{} 0.283785093714372 \end{array} \right] ,\\ \\&V=\left[ \begin{array}{c@{}c} 0.705421659275971 &{} 0.294578340724029\\ 0.705421659275971 &{} 0.294578340724029 \end{array} \right] ,\quad c = \left[ \begin{array}{c} 0.537883609922676 \\ 1 \end{array}\right] , \\ \\&\alpha _0 =\alpha _0^*= \left[ \begin{array}{c} 1 \\ 1 \end{array}\right] ,\quad \alpha _1=\left[ \begin{array}{c} 0.117523624685243 \\ 0.117523624685242 \end{array}\right] ,\quad \alpha _2=\left[ \begin{array}{c} 0.005852048827601\\ 0.005852048827601 \end{array}\right] ,\\ \\&\alpha _1^*=\left[ \begin{array}{c} 0.988119342071560 \\ -1.0 \end{array}\right] , \quad \alpha _2^*=\left[ \begin{array}{c} -0.035007599343755 \\ 0.758353275808517 \end{array}\right] . \end{aligned}$$

• Coefficients matrices of the IMEX SGLM$_{33}$

  $$\begin{aligned} { \begin{array}{l} A=\left[ \begin{array}{c@{}c@{}c} 0.301498061353180 &{} 0 &{} 0\\ 0.360536778027282 &{} 0.301498061353180 &{} 0\\ 0.447174124166318 &{} 0.070296353336502 &{} 0.301498061353180 \end{array}\right] ,\\ \\ \overline{A}=\left[ \begin{array}{c@{}c@{}c} -0.032438555835085 &{} 0 &{} 0\\ -0.044744365772315 &{} -0.032438555835085 &{} 0\\ -0.033709196624029 &{} -0.013918564673132 &{} -0.032438555835085 \end{array}\right] ,\\ \\ B=\left[ \begin{array}{c@{}c@{}c} 0.442251850536822 &{} 0.069179450030712 &{} 0.489179953866666\\ 0.446343288291238 &{} 0.070391123434179 &{} 0.460409040728055 \end{array}\right] ,\\ \\ \overline{B}=\left[ \begin{array}{c@{}c@{}c} -0.033685357820056 &{} -0.013697419618554 &{} -0.031923155981072\\ -0.033655282336012 &{} -0.013901892411796 &{} -0.032800247678669 \end{array}\right] , \end{array}} \end{aligned}$$
  $$\begin{aligned} { \begin{array}{l} A^*=\left[ \begin{array}{c@{}c@{}c} 0 &{} 0 &{} 0\\ 0.580937016698536 &{} 0 &{} 0\\ 0.237510052522150 &{} 0.331407133015593 &{} 0 \end{array}\right] , \\ \\ B^*=\left[ \begin{array}{c@{}c@{}c} 0.541467328039897 &{} -1.390182660140339&{} 1.901019355283103\\ 1.426576559773577 &{} -1.793525795556836&{} -0.588847443735250 \end{array}\right] ,\\ \\ U = \left[ \begin{array}{c@{}c} 1.0 &{} 0\\ 0.888946596324566&{} 0.111053403675434\\ 0.974077468928260 &{} 0.025922531071740 \end{array}\right] ,\\ V=\left[ \begin{array}{c@{}c} 0.973953485942062 &{} 0.026046514057938\\ 0.973953485942062 &{} 0.026046514057938 \end{array}\right] ,\quad c = \left[ \begin{array}{c} 0.483137867323211\\ 0.841068466063751\\ 1.0 \end{array}\right] , \\ \\ \alpha _0 =\alpha _0^*= \left[ \begin{array}{c} 1 \\ 1 \end{array}\right] , \quad \alpha _1=\left[ \begin{array}{c} 0.181639805970031 \\ 0.158172003989303 \end{array}\right] , \quad \alpha _2=\left[ \begin{array}{c} 0.003484524891637\\ 0.000125753528738 \end{array}\right] , \\ \\ \alpha _3=\left[ \begin{array}{c} -0.000720024972859\\ -0.000141263142128 \end{array}\right] \quad \alpha _1^*=\left[ \begin{array}{c} 0.483137867323211 \\ -1.524962835377959 \end{array}\right] ,\\ \\ \alpha _2^*=\left[ \begin{array}{c} 0.116711099420810 \\ -0.276664402530574 \end{array}\right] \quad \alpha _3^*=\left[ \begin{array}{c} 0.018795850555706 \\ 0.131928682384583 \end{array}\right] . \end{array}} \end{aligned}$$

3.1 Numerical results

In this subsection, to show the order of accuracy of the constructed methods, first, we consider the convection–diffusion equation

$$\begin{aligned} y_t+cy_x=\epsilon y_{xx},\quad 0\le t\le T_f,\end{aligned}$$

with values $c=1$, $\epsilon =0.1$, final time $T_f=5.0$, periodic boundary condition on the domain $x\in [0,2\pi ]$, and a smooth initial condition $y_0(x) = \sin (x)$. In this case, to discrete the first and second derivatives, we use the fourth-order 5-point spatial discretization and the second temporal derivatives can be approximated by

$$\begin{aligned} y_{tt}=c^2y_{xx}-2\epsilon cy_{xxx}+\epsilon ^2y_{xxxx}.\end{aligned}$$

Numerical results for the all methods obtained in this section are presented in Fig. 9. By this figure, we can conclude that the expected order of accuracy for the proposed methods is achieved.

Fig. 9

Convergence study for SSP IMEX SGLMs$_{pq}$ with $p=q=s=2,3$ and $K=1$

As a second test, we consider Fisher’s equation with linear diffusion and reaction terms (Al-Khaled 2001)

$$\begin{aligned} y_t=y_{xx}+(1-y),\quad -1<x<1,\quad 0<t\le T_f,\end{aligned}$$

with Dirichlet boundary conditions $y(-1,t)=y(1,t)=0$, the initial condition $y(x,0)=0$, final time $T_f=5$, and initial time $T_0=0.05$. We use the second-order centered differences to discrete the diffusion term and then integrate this stiff diffusion term in time implicitly and the other terms explicitly. The norm of global error at the final time for SSP IMEX SGLMs of order $p=q=s=2$ and $p=q=s=3$ is reported in Table 6.

Table 6 Convergence study for SSP IMEX SGLM$_{pq}$ with $p=q=s=2$ and $p=q=s=3$; using of time-steps, $\varDelta t=T_f/N_t$ with $T_f=5.0$ and spatial grid $\varDelta x=2/N$ with $N=8$

As a final test, we consider Fisher’s equation with linear diffusion and nonlinear reaction terms (Al-Khaled 2001)

$$\begin{aligned} y_t=ay_{xx}+by(1-y),\quad -5<x<5,\quad 0<t\le T_f,\end{aligned}$$

with values $a=0.1$ and $b=1$, Dirichlet boundary conditions $y(-5,t)=y(5,t)=0,$ and the initial condition $y(x,0)=\mathop {\mathrm {sech}}^2(7x)$, final time $T_f=5$, and initial time $T_0=0.05$. As the previous problem, we solve this problem using the second-order centered differences as spatial discretization and our IMEX schemes as time integrators. Numerical results for this nonlinear problem are listed in Table 7. Tables 6 and 7 indicate that the expected order of convergence of all constructed methods in this section is confirmed.

It should be noted that for the problems in this subsection, the reference solutions are obtained using MATLAB functions ode45 and ode15s, to linear and nonlinear problems, respectively, with absolute and relative tolerance equal to $10^{-14}$. Moreover, to fulfill the need of suitable starting procedure, we use several steps of an IMEX RK method of the same order.

Table 7 Convergence study for SSP IMEX SGLM$_{pq}$ with $p=q=s=2$ and $p=q=s=3$; using time-steps, $\varDelta t=T_f/N_t$ with $T_f=5.0$ and spatial grid $\varDelta x=10/N$ with $N=24$

4 Conclusions

Obtaining SSP implicit second derivative methods using the forward Euler condition and both second derivative and Taylor series conditions given in Moradi et al. (2019); Moradi and Abdi (2021) is not possible. To overcome this drawback, we used an alternative to the second derivative condition, the so-called backward derivative conditions, investigated in Gottlieb et al. (2021). Using this approach enabled us to find SSP implicit SGLMs up to order $p=5$. To show efficiency of the proposed methods, we compared our methods with the SSP explicit ones studied in Moradi et al. (2019) and Non-SSP implicit ones investigated in Behzad et al. (2018). Moreover, we formulated SSP IMEX SGLMs-GLMs up to order $p=3$ which are highly relevant to a range of diffusion-dominated problems. The diffusion part of these problems is handled by SSP implicit SGLMs and the other parts by explicit GLMs.