Error estimates of fictitious domain method with an $H^1$ penalty approach for elliptic problems

Abstract

This work is devoted to finding the error estimates of the fictitious domain method for elliptic problems defined on the simply connected domain. We embed the given domain into a larger rectangular domain to use the uniform mesh and extend the variational form of the original problem onto a rectangular domain with a modified $H^1$ penalty approach. We address the convergence of the new penalized problem for both continuous and discrete cases, and find the error estimates in $H^1$ and $L^2$ norms with the order of 1/2 and 1, respectively. In addition, numerical experiments are performed to guarantee the theoretical outcomes, and numerically, we obtain the optimal order of convergence for the proposed method.

1 Introduction

In recent years, fictitious domain methods have shown an enormous potential to solve partial differential equations defined on complex domains due to the advantage of using a uniform mesh on a larger rectangular domain. The ultimate goal of these methods is to obtain a numerical solution by solving a problem on a rectangle by fast solvers using preconditioned iterations; Del Pino et al. have given such solver in Del Pino and Pironneau (2003).

First, MA Hyman in Hyman (1952) proposed the idea of embedding a domain into a rectangle to solve a problem by finite difference scheme. Later, many advances and practical applications of these methods came into the picture. Particularly, Peskin used the idea of immersed boundary method to simulate flow pattern around heart valves, and these methods came into the limelight (Peskin 2002). Recently, many applications of these methods are found to solve complicated problems from science and engineering, such as in analyzing biomedical devices, simulating blood flow through arteries, simulation of the flow due to suspended particles in a fluid, swimming pattern of bacteria, eels, sperms, etc. (Mittal and Iaccarino 2005; Peskin 2002). For time-dependent moving boundary value problems, these methods are most suitable, since there is no need to meshing the given domain and imposing the boundary conditions at each time step, which would be a very time-consuming and laborious job. Only the uniform meshing of the larger rectangular domain at the initial time step is adequate. In Liu (2002), Liu has introduced mesh-free methods, but these methods have very high computational costs due to the complicated structure of basis functions, and these methods still do not have mathematical support of error analysis.

Let $\omega$ be a bounded and simply connected domain in $\mathbb {R}^{2}$ (or $\mathbb {R}^{3}$) having a smooth boundary $\varGamma .$ Let $\sigma , c \in L^{\infty }(\omega )$ and $\alpha \in L^{\infty }(\partial \omega )$ be smooth functions, such that $\sigma _1\ge \sigma (x)\ge \sigma _0 > 0, c_1\ge c(x)\ge c_0\ge 0$ a.e. in $\omega$, and $\alpha _1\ge \alpha (x)\ge \alpha _0\ge 0$ a.e. on $\varGamma$. Consider the general second-order elliptic boundary value problem, find u, such that

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} -\nabla \cdot (\sigma \nabla u)+cu=f \text { in } \omega \\ u=0 \text { on } \varGamma _d,\\ \frac{\partial u}{\partial n}=0 \text { on } \varGamma _n,\\ \sigma \frac{\partial u}{\partial n}+\alpha u=0 \text { on } \varGamma _r, \end{array}\right. } \end{aligned} \end{aligned}$$

(1.1)

where n is the outward pointing normal vector to $\varGamma$. Boundary $\varGamma$ is partitioned into $\varGamma _d, \varGamma _n$ and $\varGamma _r$ relating to the Dirichlet, Neumann, and Robin boundary condition applied to the particular parts of the boundary $\varGamma$.

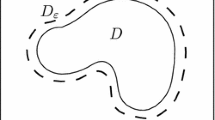
To use the idea of the fictitious domain method, Eq. 1.1 is extended to the rectangular domain $\mathrm {R}$, such that $\omega \subset \subset \mathrm {R}$, using suitable parameters depending on the boundary conditions. Here, the fascinating fact is that one can implement any periodic boundary condition on rectangle boundary $\partial \mathrm {R}$ (Glowinski et al. 1994). However, we use a homogeneous Dirichlet boundary condition, since it reduces the degrees of freedom and its mathematical simplicity for the error analysis. The domain $\varOmega :=\mathrm {R}\backslash \overline{\omega }$ is coined as a fictitious domain, and it is partitioned as $\varOmega =\varOmega _d\cup \varOmega _n\cup \varOmega _r$, as shown in Fig. 1. In the fictitious domain formulation for the Dirichlet part ($\varOmega _d$), the penalty parameter ($\epsilon ^{-1}$), and for the Neumann and Robin parts ($\varOmega _n$ and $\varOmega _r$), regularization parameter ($\epsilon$) is used to take care of the boundary conditions (Angot 2005; Glowinski et al. 1994; Zhang 2006, 2008; Zhou 2018; Zhou and Saito 2014). To impose the Dirichlet boundary condition, Girault et al. Girault and Glowinski (1995), Glowinski et al. Glowinski et al. (1994), Glowinski et al. (1997), Glowinski et al. (1999), Glowinski et al. (2001), and Yin et al. Yin and Liandrat (2016) used a Lagrange multiplier (saddle point method), but in this approach, the difficulty is to prove the inf-sup condition. Moreover, we refer readers to Suito and Kawarada (2004), Zhou and Saito (2015) for an $L^2$ penalty approach and to Burman and Hansbo (2014), Massing et al. (2014) for a Nitsche-based approach. In Angot (2005), Angot has given the idea of a unified domain embedding method to take care of all the boundary conditions together; we are modifying his approach to achieve more precise computational results and theoretical simplicity to do the error analysis. We write new unified fictitious domain formulation for Eq. 1.1 as

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {find } u^{\epsilon }\in H^{1}_{0}(\mathrm {R}) \text {such that}\\ (\nabla u^{\epsilon }, \nabla v)_{\omega }+\epsilon ^{-1}(\nabla u^{\epsilon }, \nabla v)_{\varOmega _d}+\epsilon (\nabla u^{\epsilon }, \nabla v)_{\mathrm {R}}+\alpha (u,v)_{\varGamma _r} =(\tilde{f},v)_{\mathrm {R}},\\ \ \ \forall v\in H^{1}_{0}(\mathrm {R}). \end{array}\right. } \end{aligned}$$

(1.2)

In the modified formulation (1.2), we use both the penalty parameter ($\epsilon ^{-1}$) and regularization parameter ($\epsilon$) for the Dirichlet problems. Also, for the Neumann problems, there is no need to take extra care, since it is already considered by the third term in the formulation (1.2). For completely Neumann and Robin problems, these methods are simple and convenient to implement. Glowinski and Pan Glowinski et al. (1994) have given optimal error estimates for Neumann problems. In Zhang (2008), Zhang has also given optimal error estimates for Neumann and Robin problems. However, fictitious domain methods with an $H^1$ penalty do not have any mathematical evidence of the optimal order convergence for the Dirichlet problems besides the one-dimensional problems (Adjerid and Lin 2009; Lin et al. 2015). There is a scope of future research to improve the accuracy of these methods for the Dirichlet problems; Zhang (2008) Zhang and Zhou and Saito (2014) Zhou et al. have obtained error estimates of order 1/2 and 1 in $H^1$ and $L^2$ norms, respectively, depending on the choice of parameter $\epsilon$. Also, Zhang in Zhang (2008) suggests that adjusting the mesh near the boundary significantly improves the convergence rate, but it is still not optimal. Also, X. He et al. He et al. (2012) accomplished a sub-optimal error estimate of order 1/2 in the $H^1$ norm for the interface problems. Therefore, to enhance the convergence rate of the method, Tao Lin and co-authors in Adjerid and Lin (2009), Li et al. (2003), Lin et al. (2015) address the various penalty methods by considering the different types of basis functions over the simplices near the interface boundary $\varGamma$.

Fig. 1

Unified domain embedding method

The new modified fictitious domain formulation given in Eq. 1.2 and the idea of constructive proof of $H^1$ seminorm estimate make the analysis simpler than that of the existing analysis in Zhang (2008), Zhou and Saito (2014), with the improvement in the accuracy of the method in the numerical experiments whenever the penalty parameter $\epsilon$ is compatible with the mesh size h . Additionally, we prove the convergence of the new penalized problem to the original problem in the $H^2$ norm. Moreover, in the case of mesh matching precisely to the boundary, our analysis suggests an optimal convergence rate in the $H^1$ seminorm, which is a recent achievement.

The outline of the paper is as per the following. In Sect. 2, we provide notations and some preliminary results. Proposed method with variational formulation is discussed in Sect. 3. Section 4 contains the convergence of the penalized problem to the original problem at the sharp rate of $\epsilon$. Section 5 depict the error estimates in $H^1$ and $L^2$ norms. Numerical experiments are performed in Sect. 6, and in Sect. 7, we conclude our discussion.

2 Notations and preliminary results

For a domain $\hat{\varOmega }$, we denote $(\cdot ,\cdot )_{\hat{\varOmega }}$ as the standard inner product on $L^{2}({\hat{\varOmega }})$. Let $m\in \mathbb {N},$ and $\alpha$ a multi-index notation, there is a general class of Sobolev spaces $W^{m,p}(\hat{\varOmega }):=\{v\in L^{p}(\hat{\varOmega }):D^{\alpha } v \in L^{p}(\hat{\varOmega }), |\alpha |\le m\}$, $\displaystyle W^{m,p}_{0}(\hat{\varOmega }):=\text {closure of } C_{0}^{\infty }(\hat{\varOmega }) \text { in } W^{m,p}(\hat{\varOmega })$. In particular, for $p=2$, the above spaces are Hilbert spaces and we denote them by $H^{m}(\hat{\varOmega })$, and $H^{m}_{0}(\hat{\varOmega }),$ respectively (Adams 1975). For $v\in H^{m}(\hat{\varOmega })$, we define the seminorm as $|v|_{m,\hat{\varOmega }}:=\big ( \sum _{\alpha =m} ||D^{\alpha }v||_{0,\hat{\varOmega }}^{2}\big )^{1/2}$, and norm as $||v||_{m,\hat{\varOmega }}:=\big (||v||_{m-1,\hat{\varOmega }}^2+|v|_{m,\hat{\varOmega }}^2\big )^{1/2}$. Also, the space $H^{-m}({\hat{\varOmega }})$ will be considered as a dual space of $H^{m}_{0}({\hat{\varOmega }})$, with the respective norm defined by a duality (Adams 1975). Furthermore, note that C will denote a generic constant throughout the discussion, with different values at different locations.

Now, let $\hat{\varOmega }$ be a polygonal domain, denote $\mathscr {T}_h$ as a regular and uniform triangulation of $\hat{\varOmega }$, such that $\hat{\varOmega }=\cup _{{T\in \mathscr {T}_h}}\{T\}$, where regular triangulation means $h_T\rightarrow 0$ and $\frac{h_T}{\rho _T} \le c$, for some constant c, $h_T=\text {diam}(T)$ and $\rho _T=\text {sup} \ \{\text {diam}(B) : \text { B is ball contained in } T\}$ (Ciarlet 1977). The finite-element space $V_h$ is given by

$$\begin{aligned} V_h=\{v_h\in H^{1}_{0}(\hat{\varOmega })\cap C^{0}(\hat{\varOmega }) : {{v_h}_{|}}_{T}\in P_1\ \ \forall \ T \in \mathscr {T}_h\}, \end{aligned}$$

where $P_1$ denotes the polynomial space of degrees $\le$ 1. For the space $V_h,$ $\{\varphi _i\}_{i=1}^{N}$ be the basis, where N is the dimension of the finite-element space $V_h$. Let $\{a_i\}_{i=1}^{N}$ be the node points of the grid of the domain $\hat{\varOmega }$, and then

$$\begin{aligned} \varphi _i(a_j)=\delta _{ij}={\left\{ \begin{array}{ll} 1 \ \ \text { if } i=j,\\ 0 \ \ \text { if } i \ne j, \end{array}\right. } 1\le i,j\le N. \end{aligned}$$

For $v\in C^{0}(\hat{\varOmega })$, define the interpolation operator $\mathscr {I}_h:C^{0}(\hat{\varOmega })\rightarrow V_h$, as

$$\begin{aligned} \mathscr {I}_h(v)=\sum _{i=1}^{N}v(a_i)\varphi _i. \end{aligned}$$

For $k>0$, Sobolev embedding theorem implies $H^{k+1}(\hat{\varOmega })\subset \subset H^{1}({\hat{\varOmega }})$, with the interpolation estimate (Adams 1975; Ciarlet 1977; Brenner and Scott 2008)

$$\begin{aligned} \left\| v-\mathscr {I}_hv\right\| _{1,\hat{\varOmega }} \le Ch^{k}|v|_{k+1,\hat{\varOmega }}\ \ , \ \ \forall v\in H^{k+1}(\hat{\varOmega })\cap H^{1}_{0}(\hat{\varOmega }). \end{aligned}$$

(2.1)

For a Lipschitz domain $\hat{\varOmega }$ in $\mathbb {R}^2$, we have the following Sobolev and Morrey’s inequalities, which will be used to give the discrete error estimates in the $H^{1}$ seminorm

$$\begin{aligned}&\left\| v\right\| _{\infty , \hat{\varOmega }}\le C\left\| v\right\| _{2,\hat{\varOmega }}\ \ \text { for } v \in H^{2}(\hat{\varOmega }). \end{aligned}$$

(2.2)

$$\begin{aligned}&\left\| v\right\| _{W^{1,p}(\hat{\varOmega })}\le C \left\| v\right\| _{2,\hat{\varOmega }} \text { for } 1\le p<\infty , \text { and } v\in H^{2}(\hat{\varOmega }). \end{aligned}$$

(2.3)

$$\begin{aligned}&|v(x)-v(y)|\le C \left\| v\right\| _{W^{1,p}(\hat{\varOmega })}|x-y|^\beta , \nonumber \\&\quad \text { for } x,y\in \hat{\varOmega },\ p>2, \; \beta =1-\frac{2}{p}, \text { and } v\in W^{1,p}(\hat{\varOmega }). \end{aligned}$$

(2.4)

Since we will need to extend the data from domain $\omega$ to rectangle $\mathrm {R}$, we provide the following existence and stability estimate.

Lemma 1

(Lions and Magenes 1972; Küfner et al. 1977) For a smooth bounded domain $\hat{\varOmega }$ in $\mathbb {R}^2,$ there exists an extension operator $E^{k}(\hat{\varOmega }):H^k(\hat{\varOmega })\rightarrow H^{k}(\mathbb {R}^{2})$, such that

$$\begin{aligned}&E^k(\hat{\varOmega })v=v \text { a.e. in } \hat{\varOmega }, \text { and } \\&\left\| E^{k}(\hat{\varOmega })v\right\| _{1,\mathbb {R}^2} \le C_k(\hat{\varOmega }) \left\| v\right\| _{1,\hat{\varOmega }} , \text { for } v\in H^{k}(\hat{\varOmega }), \text { where } k \text { is a positive integer.} \end{aligned}$$

Lemma 2

Let D be a domain in $\mathbb {R}^2$, and then, for a tube $\gamma _{\delta }=\{x\in D\,|\,dist(x,\gamma )\le \delta \}$ and $v\in H^{1}(D)$, we have

$$\begin{aligned} \left\| v\right\| _{0,\gamma _\delta }\le C\sqrt{\delta }\left\| v\right\| _{1,D}. \end{aligned}$$

(2.5)

Further, if $v\in H^{2}(D)$, we have

$$\begin{aligned} \left\| v\right\| _{1,\gamma _{\delta }}\le C\sqrt{\delta }\left\| v\right\| _{2,D}. \end{aligned}$$

(2.6)

Proof

The proof follows by the trace theorem. See (Zhang 2008). $\square$

Lemma 3

(Ciarlet 1977) Let $\mathscr {I}_T$ be the linear interpolation of v on the vertices of a triangle $T\in \mathscr {T}_h$, where $\mathscr {T}_h$ is the triangulation of a domain D. Then, for $v\in H^{2}(D)$, we have

$$\begin{aligned} C_1\sum _{i,j=1;i\ne j}^{3}|v(\nu _i) -v(\nu _j)|\le |\mathscr {I}_Tv|_{1,T}\le C_2 \sum _{i,j=1;i\ne j}^{3}|v(\nu _i)-v(\nu _j)|, \end{aligned}$$

(2.7)

where $C_1$ and $C_2$ are constants that depend on the regularity of the triangulation $\mathscr {T}_h$ and $\nu _i$; $i=1,2,3$ are the vertices of a triangle T.

Lemma 4

(Lions and Magenes 1972) Let $\hat{\varOmega }$ be a bounded domain in $\mathbb {R}^{2}$, and $\partial \hat{\varOmega }=(\partial \hat{\varOmega })_{1}\cup (\partial \hat{\varOmega })_{2}$, with $(\partial \hat{\varOmega })_{1}\cap (\partial \hat{\varOmega })_{2}=\phi$. Let $v\in H^{1}(\hat{\varOmega })$ be the unique solution of the problem

$$\begin{aligned} \varDelta v=f_1 \text { in } \hat{\varOmega }, \;v=g_{1} \text { on } (\partial \hat{\varOmega })_{1}, \; \frac{\partial v}{\partial n}=g_{2} \text { on } (\partial \hat{\varOmega })_{2}, \end{aligned}$$

for $f_{1}\in L^{2}(\hat{\varOmega }),\; g_{1} \in H^{\frac{1}{2}}((\partial \hat{\varOmega })_{1})$ and $g_{2}\in L^{2}((\partial \hat{\varOmega })_{2}).$ Then if $g_{1} \in H^{\frac{3}{2}}((\partial \hat{\varOmega })_{1})$ and $g_{2}\in H^{\frac{1}{2}}((\partial \hat{\varOmega })_{2}),$ we have $v\in H^{2}(\hat{\varOmega })$ and

$$\begin{aligned} \left\| v\right\| _{2,\hat{\varOmega }} \le C \Big ( \left\| f_{1}\right\| _{0,\hat{\varOmega }} + \left\| g_{1}\right\| _{H^{\frac{3}{2}}((\partial \hat{\varOmega })_{1})}+\left\| g_{2}\right\| _{H^{\frac{1}{2}}((\partial \hat{\varOmega })_{2})}\Big ). \end{aligned}$$

3 Problem formulation

To simplify our analysis, we consider Poisson’s problem with the Dirichlet boundary condition on a smooth curved domain $\omega$ in $\mathbb {R}^{2}$. For a given $f\in L^2(\omega )$, find u, such that

$$\begin{aligned} {\left\{ \begin{array}{ll} -\varDelta u=f \;\;\text {in} \;\;\omega , \\ u=0 \;\;\text {on}\;\;\partial \omega . \end{array}\right. } \end{aligned}$$

(3.1)

The variational formulation for Eq. 3.1 is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {find}\;\; u \in H^{1}_{0}(\omega ) \;\;\text {such that}\\ (\nabla u, \nabla v)_{\omega }=(f,v)_\omega , \;\; \forall v\in H^{1}_{0}(\omega ). \end{array}\right. } \end{aligned}$$

(3.2)

To impose the idea of the domain embedding method, we embed $\omega$ into a rectangular domain $\mathrm {R}$, such that $\omega \subset \subset \mathrm {R}$ (Hyman 1952; Glowinski and Pan 1991). Define the $H^{1}$ penalized problem of Eq. 3.2 as

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {find } u^{\epsilon }\in H^{1}_{0}(\mathrm {R}) \; \text {such that}\\ (\nabla u^{\epsilon }, \nabla v)_{\omega }+\epsilon ^{-1}(\nabla u^{\epsilon }, \nabla v)_{\varOmega }+\epsilon (\nabla u^{\epsilon }, \nabla v)_{\mathrm {R}} =(\tilde{f},v)_{\mathrm {R}},\; \; \forall v\in H^{1}_{0}(\mathrm {R}), \end{array}\right. } \end{aligned}$$

(3.3)

where $\tilde{f}$ is the zero extension of f in the fictitious domain $\varOmega$, and $\epsilon ^{-1}$ is a penalty parameter, with $0<\epsilon \rightarrow 0$. Note that we can take any extension $\tilde{f}$ of f in $\varOmega$, such that $||\tilde{f}||\le C ||f||$, but the zero extension is more suitable to implement. We see that Eq. 3.3 has a unique solution by applying the Lax–Milgram lemma.

We solve Eq. 3.3 instead of Eq. 3.2 by a finite-element method using linear simplices. Let $\mathscr {T}_h$ be the uniform triangulation of the domain $\mathrm {R}$, $V_h(\mathrm {R})$ be the finite-dimensional subspace of $H^{1}_{0}(\mathrm {R})$ consisting of linear polynomials corresponding to the meshing $\mathscr {T}_h$. Therefore, the finite-element formulation of Eq. 3.3 is

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {find } u^{\epsilon }_h \in V_h(\mathrm {R}) \text { such that}\\ (\nabla u^{\epsilon }_h, \nabla v_h)_{\omega }+\epsilon ^{-1}(\nabla u^{\epsilon }_{h}, \nabla v_h)_{\varOmega }+\epsilon (\nabla u^{\epsilon }_{h}, \nabla v_h)_{\mathrm {R}}=(\tilde{f}, v_h)_{\mathrm {R}}, \;\; \forall v_h \in V_h(\mathrm {R}). \end{array}\right. } \end{aligned}$$

(3.4)

In the next section, we prove the convergence of $u^{\epsilon }$ a solution of the modified penalized Eq. 3.3 to the solution u of the original Eq. 3.2, as $\epsilon \rightarrow 0$, in the $H^1$ norm as a sharp error estimate of $O(\epsilon )$. In Sect. 5, we give an error estimate between $u^\epsilon _{h}$, a solution of the discrete Eq. 3.4 and $u^{\epsilon }$, a solution of the continuous Eq. 3.3, in both the $H^1$ and $L^2$ norms as $O(\sqrt{\epsilon }+\sqrt{h})$ and $O(\epsilon +h+\sqrt{\epsilon h}),$ respectively. Therefore, finally, we have $\left\| u-u^{\epsilon }_{h}\right\| _{1,\omega } =O(\sqrt{h})$ and $\left\| u-u^{\epsilon }_{h}\right\| _{0,\omega } =O(h)$ when the parameter $\epsilon$ is chosen as O(h).

Remark 1

Note that if we have the non-homogeneous boundary condition in Eq. 3.1, we employ the splitting method to transform the non-homogeneous admissible space into $H^{1}_{0}(\omega )$, or approximate the Dirichlet boundary condition by the Robin boundary condition.

4 convergence of a continuous problem

In this section, we prove $u^{\epsilon }$ converges to the original solution u at the sharp rate of $\epsilon$. In Lemma 1, let $\varphi \in C_{0}^{\infty }(\mathrm {R}), 0\le \varphi \le 1$ and $\varphi \equiv 1$ in $\varOmega _1$, with $\varOmega \subset \varOmega _1 \subset \mathrm {R}$; define the operator $E_{0}^{1}(\varOmega )v=(\varphi E^{1}(\varOmega ))v$ for $v \in H^{1}(\varOmega )$; so that

$$\begin{aligned}&E^{1}_{0}(\varOmega ) v=v \text { a.e. in } \varOmega , \\&\left\| E^{1}_{0}(\varOmega )v\right\| _{1,\mathrm {R}} \le C (\varOmega )\left\| v\right\| _{1,\varOmega }, \text { for } v \in H^{1}(\varOmega ). \end{aligned}$$

Lemma 5

Let $u^{\epsilon }\in H^{1}_{0}(\mathrm {R})$ be a solution of Eq. 3.3 and $f\in L^{2}(\omega )$; then

$$\begin{aligned} \left\| u^{\epsilon }\right\| _{1,\mathrm {R}}\le \left\| f\right\| _{0,\omega } , \end{aligned}$$

(4.1)

and

$$\begin{aligned} \left\| u^{\epsilon }\right\| _{1,\varOmega }\le C \epsilon \left\| f\right\| _{0,\omega }. \end{aligned}$$

(4.2)

Proof

Using Poincare’s inequality and Eq. 3.3, we obtain

$$\begin{aligned} \begin{aligned} \left\| u^{\epsilon }\right\| ^{2}_{1,\mathrm {R}}&\le |u^{\epsilon }|^{2}_{1,\mathrm {R}}\\&=(\nabla u^{\epsilon },\nabla u^{\epsilon })_{\omega }+(\nabla u^{\epsilon },\nabla u^{\epsilon })_{\varOmega }\\&\le (\nabla u^{\epsilon },\nabla u^{\epsilon })_{\omega }+\epsilon ^{-1}(\nabla u^{\epsilon },\nabla u^{\epsilon })_{\varOmega }+\epsilon (\nabla u^{\epsilon },\nabla u^{\epsilon })_{\mathrm {R}}\\&\le \left\| \tilde{f}\right\| _{0,\mathrm {R}}\left\| u^{\epsilon }\right\| _{1,\mathrm {R}}.\\ \therefore \left\| u^{\epsilon }\right\| _{1,\mathrm {R}}&\le \left\| f\right\| _{0,\omega }. \end{aligned} \end{aligned}$$

Substituting $v=E^{1}_{0}(\varOmega )$ in Eq. 3.3, and using Poincare’s inequality, we get

$$\begin{aligned} \begin{aligned} \epsilon ^{-1}\left\| u^{\epsilon }\right\| ^{2}_{1,\varOmega }\le \epsilon ^{-1}|u^{\epsilon }|^{2}_{1,\varOmega }&\le \left\| \tilde{f}\right\| _{0,\mathrm {R}}\left\| E^{1}_{0}(\varOmega )u^{\epsilon }\right\| _{0,\mathrm {R}}+ \epsilon \left\| u^{\epsilon }\right\| _{1,\mathrm {R}}\left\| E^{1}_{0}(\varOmega )u^{\epsilon }\right\| _{1,\mathrm {R}}\\&\le C\big ( \left\| f\right\| _{0,\omega }\left\| u^{\epsilon }\right\| _{1,\varOmega }+\epsilon \left\| f\right\| _{0,\omega }\left\| u^{\epsilon }\right\| _{1,\varOmega }\big )\\&\le C \left\| f\right\| _{0,\omega }\left\| u^{\epsilon }\right\| _{1,\varOmega }.\\ \therefore \left\| u^{\epsilon }\right\| _{1,\varOmega }&\le C \epsilon \left\| f\right\| _{0,\omega }. \end{aligned} \end{aligned}$$

Proposition 1

Let $f\in L^{2}(\omega )$, and $u^{\epsilon }\in H^{1}_{0}(\mathrm {R})$ be the solution of Eq. 3.3; then, $u^{\epsilon }|_{\omega } \in H^{2}(\omega )$ and $u^{\epsilon }|_{\varOmega } \in H^{2}(\varOmega ),$ with the following estimates:

$$\begin{aligned} \left\| u^{\epsilon }\right\| _{2,\omega }\le C\left\| f\right\| _{0,\omega } \text { and } \left\| u^{\epsilon }\right\| _{2,\varOmega } \le C \epsilon \left\| f\right\| _{0,\omega }. \end{aligned}$$

Proof

Applying Green’s theorem to Eq. 3.3, we have

$$\begin{aligned}&(-\varDelta u^{\epsilon },v)_{\omega } +\Big (\frac{\partial u^{\epsilon }}{\partial n_1},v\Big )_{\varGamma }+\epsilon ^{-1}(-\varDelta u^{\epsilon },v)_{\varOmega }+\epsilon ^{-1}\Big (\frac{\partial u^{\epsilon }}{\partial n_2},v\Big )_{\varGamma } \nonumber \\&\quad +\epsilon (-\varDelta u^{\epsilon },v)_{\mathrm {R}} +\epsilon \Big (\frac{\partial u^{\epsilon }}{\partial n},v\Big )_{\partial \mathrm {R}}=(\tilde{f},v)_{\mathrm {R}}~ \text { for } u^{\epsilon },v \in H^{1}_{0}(\mathrm {R}), \end{aligned}$$

(4.3)

where $n_1$ and $n_2$ are unit normal vectors to $\varGamma$, as a boundary of $\omega$ and $\varOmega$, respectively, and also, n is outer pointing unit normal to $\partial \mathrm {R}$. Comparing both sides of Eq. 4.3, we arrive at

$$\begin{aligned} -\varDelta u^{\epsilon }= & {} \frac{1}{1+\epsilon }f \text { in } \omega , \end{aligned}$$

(4.4)

$$\begin{aligned} \varDelta u^{\epsilon }= & {} 0 \text { in } \varOmega \end{aligned}$$

(4.5)

and

$$\begin{aligned} \frac{\partial u^{\epsilon }}{\partial n_1}= & {} -\epsilon ^{-1}\frac{\partial u^{\epsilon }}{\partial n_2} \text { on } \varGamma . \end{aligned}$$

(4.6)

$\therefore$ By the elliptic regularity (Grisvard 1985; Lions and Magenes 1972), we have $\left\| u^{\epsilon }\right\| _{2,\omega }\le C\left\| \frac{1}{1+\epsilon }f\right\| _{0,\omega }\le C\left\| f\right\| _{0,\omega }$. Using Lemma 4, Eq. 4.5, Eq. 4.6, and trace theorem (Adams 1975), we obtain

$$\begin{aligned} \left\| u^{\epsilon }\right\| _{2,\varOmega }\le C\left\| \frac{\partial u^{\epsilon }}{\partial n_2}\right\| _{\frac{1}{2},\varGamma } = C\left\| -\epsilon \frac{\partial u^{\epsilon }}{\partial n_1}\right\| _{\frac{1}{2},\varGamma } \le C \epsilon \left\| u^{\epsilon }\right\| _{2,\omega } \le C \epsilon \left\| f\right\| _{0,\omega }. \end{aligned}$$

$\square$

From Proposition 1, we also deduce $\left\| u^{\epsilon }\right\| _{2,\mathrm {R}}\le C \left\| f\right\| _{0,\omega }$.

Theorem 1

Let u and $u^{\epsilon }$ be the solutions of Eq. 3.2 and Eq. 3.3, respectively, and then, $u^{\epsilon }$ converges to u as $\epsilon \rightarrow 0$ with the estimate

$$\begin{aligned} \left\| u^{\epsilon }-u\right\| _{1,\omega } \le C \epsilon \left\| f\right\| _{0,\omega }. \end{aligned}$$

Proof

Let us define the trace mappings of the domains $\omega$ and $\varOmega$, on common boundary $\varGamma$ as, $\gamma (\omega ,\varGamma ):H^{1}(\omega )\rightarrow H^{1/2}(\varGamma )$ and $\gamma (\varOmega ,\varGamma ):H^{1}(\varOmega )\rightarrow H^{1/2}(\varGamma ).$ Here, $u^{\epsilon } \in H^{1}(\mathrm {R})$, so that $\gamma (\omega ,\varGamma )u^{\epsilon }=\gamma (\varOmega ,\varGamma )u^{\epsilon } \in H^{1/2}(\varGamma )$. Since $u=0$ on boundary $\varGamma$, we find $\gamma (\omega ,\varGamma )(u-u^{\epsilon })=-\gamma (\omega ,\varGamma )u^{\epsilon }=-\gamma (\varOmega ,\varGamma )u^{\epsilon }.$ Letting $w=u-u^{\epsilon }|_{\omega }$ and using trace theorem, we obtain

$$\begin{aligned} \left\| \gamma (\omega ,\varGamma )w\right\| _{\frac{1}{2},\varGamma } =\left\| \gamma (\varOmega ,\varGamma )u^{\epsilon }\right\| _{\frac{1}{2},\varGamma } \le C\left\| u^{\epsilon }\right\| _{1,\varOmega } \le C\epsilon \left\| f\right\| _{0,\omega }. \end{aligned}$$

We define the operator $\mathscr {A} :H^{1}(\omega )\rightarrow H^{-1}(\omega )$ as

$$\begin{aligned} \langle \mathscr {A}u,v\rangle =\langle \nabla u, \nabla v \rangle _{\omega }, \; \forall v \in H^{1}_{0}(\omega ). \end{aligned}$$

Using Eqs. 3.2 and 3.3, we have

$$\begin{aligned} \begin{aligned} \langle \mathscr {A}w, v\rangle&=(\nabla u, \nabla v)_{\omega }-(\nabla u^{\epsilon }, \nabla \tilde{v})_{\omega } \\&=(f,v)_{\omega }+\epsilon ^{-1}(\nabla u^{\epsilon },\nabla \tilde{v})_{\varOmega }+\epsilon (\nabla u^{\epsilon },\nabla \tilde{v})_{\mathrm {R}}-(\tilde{f},\tilde{v})_{\mathrm {R}}\\&=\epsilon (\nabla u^{\epsilon },\nabla v)_{\omega }. \end{aligned} \end{aligned}$$

Therefore, $\displaystyle \frac{|\langle \mathscr {A}w,v\rangle |}{\left\| v\right\| _{1,\omega }}\le \epsilon \left\| u^{\epsilon }\right\| _{1,\omega }, \; \forall v\in H^{1}_{0}(\omega ).$ Hence, we arrive at

$$\begin{aligned} \displaystyle \sup _{v\in H^{1}_{0}(\omega )}\frac{|\langle \mathscr {A}w,v\rangle |}{\left\| v\right\| _{1,\omega }}\le \epsilon \left\| u^{\epsilon }\right\| _{1,\omega }. \end{aligned}$$

Since the mapping $w\rightarrow \{\mathscr {A}w, \gamma (\omega ,\varGamma )w\}$ is an isomorphic map of $H^{1}(\omega )\rightarrow H^{-1}(\omega )\times H^{1/2}(\varGamma )$, so that

$$\begin{aligned} \begin{aligned} \left\| w\right\| _{1,\omega }&\le C\big (\left\| \mathscr {A}w\right\| _{-1,\omega }+\left\| \gamma (\omega ,\varGamma )w\right\| _{\frac{1}{2},\varGamma }\big )\\&= C\Big (\sup _{v\in H^{1}_{0}(\omega )}\frac{|\langle \mathscr {A}w,v\rangle |}{\left\| v\right\| _{1,\omega }}+\left\| \gamma (\omega ,\varGamma )w\right\| _{\frac{1}{2},\varGamma }\Big )\\&\le C\epsilon \left\| f\right\| _{0,\omega }. \end{aligned} \end{aligned}$$

It gives us the desired convergence estimate. $\square$

Corollary 1

Let u and $u^{\epsilon }$ be the solutions of Eq. 3.2 and Eq. 3.3, respectively, then $u^{\epsilon }$ converges to u as $\epsilon \rightarrow 0$ with the estimate

$$\begin{aligned} \left\| u^{\epsilon }-u\right\| _{2,\omega } \le C \epsilon \left\| f\right\| _{0,\omega }. \end{aligned}$$

Proof

Subtracting Eq. 4.4 from Eq. 3.1, we obtain $-\varDelta (u-u^{\epsilon })=\frac{\epsilon }{1+\epsilon }f \;\; \text { in }\omega .$ So that, $|u-u^{\epsilon }|_{2,\omega }\le C \epsilon \left\| f\right\| _{0,\omega }$. Together with Theorem 1, we complete the proof. $\square$

5 Error analysis

In this section, we derive error estimates between the solution $u^{\epsilon }$ of Eq. 3.3 and solution $u^{\epsilon }_{h}$ of Eq. 3.4 in the $H^1$ seminorm, $L^2$ norm, and $H^1$ norm. Here, $V_h(\mathrm {R})\subset H^{1}_{0}(\mathrm {R})$; subtracting Eq.3.4 from Eq. 3.3, we arrive at the orthogonality relation

$$\begin{aligned} (\nabla (u^{\epsilon }-u^{\epsilon }_{h}),\nabla v_h)_{\omega }+ & {} \epsilon ^{-1}(\nabla (u^{\epsilon }-u^{\epsilon }_{h}),\nabla v_{h})_{\varOmega }\nonumber \\ {}+ & {} \epsilon (\nabla (u^{\epsilon }-u^{\epsilon }_{h}),\nabla v_{h})_{\mathrm {R}}=0, \; \forall v_h \in V_{h}(\mathrm {R}). \end{aligned}$$

(5.1)

Lemma 6

Let $u^\epsilon$ and $u^\epsilon _h$ be solutions of Eq. 3.3 and Eq. 3.4, respectively, then

$$\begin{aligned} \begin{aligned}&|u^{\epsilon }-u^{\epsilon }_{h}|_{1,\omega }+\frac{1}{\sqrt{\epsilon }}|u^{\epsilon }-u^{\epsilon }_{h}|_{1,\varOmega }+\sqrt{\epsilon }|u^{\epsilon }-u^{\epsilon }_{h}|_{1,\mathrm {R}}\\&\le C \inf _{v_h \in V_h(\mathrm {R})}\Big (\left\| u^{\epsilon }-v_h\right\| _{1,\omega }+\frac{1}{\sqrt{\epsilon }}\left\| u^{\epsilon }-v_h\right\| _{1,\varOmega }+\sqrt{\epsilon }\left\| u^{\epsilon }-v_h\right\| _{1,\mathrm {R}}\Big ). \end{aligned} \end{aligned}$$

(5.2)

Proof

Using Eq. 5.1 twice, we get

$$\begin{aligned} \begin{aligned}&|u^{\epsilon }-u^{\epsilon }_{h}|^{2}_{1,\omega }+\epsilon ^{-1}|u^{\epsilon }-u^{\epsilon }_{h}|^{2}_{1,\varOmega }+\epsilon |u^{\epsilon }-u^{\epsilon }_{h}|^{2}_{1,\mathrm {R}}\\&= (\nabla (u^{\epsilon }-u^{\epsilon }_{h}), \nabla (u^{\epsilon }-v_{h}))_{\omega } +\epsilon ^{-1}(\nabla (u^{\epsilon }-u^{\epsilon }_{h}), \nabla (u^{\epsilon }-v_h))_{\varOmega }\\ {}&\;\;\;\;\;+\epsilon (\nabla (u^{\epsilon }-u^{\epsilon }_{h}),\nabla (u^{\epsilon }-v_h))_{\mathrm {R}} \\&\le |u^{\epsilon }-u^{\epsilon }_{h}|_{1,\omega }|u^{\epsilon }-v_h|_{1,\omega }+\epsilon ^{-1}|u^{\epsilon }-u^{\epsilon }_{h}|_{1,\varOmega }|u^{\epsilon }-v_h|_{1,\varOmega }\\&\;\;\;\;\;+\epsilon |u^{\epsilon }-u^{\epsilon }_{h}|_{1,\mathrm {R}}|u^{\epsilon }-v_{h}|_{1,\mathrm {R}}\\&\le C\{\left\| u^{\epsilon }-v_h\right\| _{1,\omega }^{2}+\epsilon ^{-1} \left\| u^{\epsilon }-v_h\right\| _{1,\varOmega }^{2}+\epsilon \left\| u^{\epsilon }-v_h\right\| _{1,\mathrm {R}}^{2}\}.\\ \end{aligned} \end{aligned}$$

Therefore, in particular

$$\begin{aligned}&|u^{\epsilon }-u^{\epsilon }_h|_{1,\omega }\le C\{ \left\| u^{\epsilon }-v_h\right\| _{1,\omega }+\frac{1}{\sqrt{\epsilon }}\left\| u^{\epsilon }-v_h\right\| _{1,\varOmega }+\sqrt{\epsilon }\left\| u^{\epsilon }-v_h\right\| _{1,\mathrm {R}}\}, \end{aligned}$$

(5.3)

$$\begin{aligned}&\frac{1}{\sqrt{\epsilon }}|u^{\epsilon }-u^{\epsilon }_h|_{1,\varOmega }\le C\{ \left\| u^{\epsilon }-v_h\right\| _{1,\omega }+\frac{1}{\sqrt{\epsilon }}\left\| u^{\epsilon }-v_h\right\| _{1,\varOmega }+\sqrt{\epsilon }\left\| u^{\epsilon }-v_h\right\| _{1,\mathrm {R}}\}, \end{aligned}$$

(5.4)

$$\begin{aligned}&|u^{\epsilon }-u^{\epsilon }_h|_{1,\mathrm {R}}\le C\{ \left\| u^{\epsilon }-v_h\right\| _{1,\omega }+\frac{1}{\sqrt{\epsilon }}\left\| u^{\epsilon }-v_h\right\| _{1,\varOmega }+\sqrt{\epsilon }\left\| u^{\epsilon }-v_h\right\| _{1,\mathrm {R}}\}. \end{aligned}$$

(5.5)

Adding Eq. 5.3, Eq. 5.4, and Eq. 5.5, and taking infimum over all $v_h$ in $V_h(\mathrm {R})$ on the RHS, we get the desired result. $\square$

To find $H^1$ seminorm estimate, we define $\mathscr {T}_\omega =\{T\in \mathscr {T}_{h} : T \subset \omega \}$ set of the simplices T which lie completely inside the domain $\omega$. $\mathscr {T}_{\varGamma }=\{T\in \mathscr {T}_h : T\cap \varGamma \ne \phi \}$ set of the simplices T through which the boundary $\varGamma$ passes. $\mathscr {V}(T)=\{\vartheta _i\}_{i=1}^{3}$ set of the vertices of a simplex T. $\mathscr {V}_\omega =\{\vartheta _i : \vartheta _i\in \mathscr {V}(T), T\in \mathscr {T}_\omega \}$, set of the vertices of the simplices which lie completely inside the domain $\omega$, and $\mathscr {V}_\varGamma =\{\vartheta _i : \vartheta _i\in \mathscr {V}(T), T\in \mathscr {T}_\varGamma \}$, set of the vertices of the simplices through which the boundary $\varGamma$ passes. Observe that $\mathscr {V}_{\omega }\cap \mathscr {V}_{\varGamma }\ne \phi$. We choose suitable $v_h$ which will give us the desired estimate in a simple way, as

$$\begin{aligned} v_h(\vartheta )={\left\{ \begin{array}{ll} u^{\epsilon }(\vartheta )\;\; \text { for } \vartheta \in \mathscr {V}_\omega ,\\ 0 \;\;\;\;\;\;\;\;\;\text { otherwise}. \end{array}\right. } \end{aligned}$$

(5.6)

Theorem 2

Let $u^\epsilon$ and $u^\epsilon _h$ be solutions of Eqs. 3.3 and 3.4, respectively, and then

$$\begin{aligned} |u^{\epsilon }-u^{\epsilon }_{h}|_{1,\omega } \le C(\sqrt{h}+\sqrt{\epsilon })\left\| f\right\| _{0,\omega }. \end{aligned}$$

(5.7)

Proof

The proof is based on individual bounds of all the three terms in RHS of Eq. 5.3

$$\begin{aligned} \left\| u^{\epsilon }-v_h\right\| _{1,\omega }\le \left\| u^{\epsilon }-v_h\right\| _{1,\mathscr {T}_{\omega }}+\left\| u^{\epsilon }-v_h\right\| _{1,\mathscr {T}_{\varGamma }}. \end{aligned}$$

(5.8)

Since $\mathscr {T}_\omega$ is a polygonal domain

$$\begin{aligned}&\left\| u^{\epsilon }-v_h\right\| _{1,\mathscr {T}_\omega }\le h \left\| u^{\epsilon }\right\| _{2,\mathscr {T}_\omega } \le h \left\| u^{\epsilon }\right\| _{2,\mathrm {R}} \nonumber \\&\therefore \left\| u^{\epsilon }-v_h\right\| _{1,\mathscr {T}_\omega } \le Ch\left\| f\right\| _{0,\omega }. \end{aligned}$$

(5.9)

Also

$$\begin{aligned} \left\| u^{\epsilon }-v_h\right\| _{1,\mathscr {T}_{\varGamma }} \le \left\| u^{\epsilon }-\mathscr {I} u^{\epsilon }\right\| _{1,\mathscr {T}_{\varGamma }}+\left\| \mathscr {I}u^{\epsilon }-v_h\right\| _{1,\mathscr {T}_{\varGamma }}. \end{aligned}$$

(5.10)

Now

$$\begin{aligned} \begin{aligned} \left\| u^{\epsilon }-\mathscr {I}u^{\epsilon }\right\| _{1,\mathscr {T}_{\varGamma }}^{2}&=\sum _{T\in \mathscr {T}_{\varGamma }}\left\| u^{\epsilon }-\mathscr {I}u^{\epsilon }\right\| _{1,T}^2\\&\le \sum _{T\in \mathscr {T}_{\varGamma }}h^2\left\| u^{\epsilon }\right\| _{2,T}^2\\&\le h^2 \left\| u^{\epsilon }\right\| _{2,\mathrm {R}}^2. \end{aligned} \end{aligned}$$

Therefore, we have

$$\begin{aligned} \left\| u^{\epsilon }-\mathscr {I}u^{\epsilon }\right\| _{1,\mathscr {T}_{\varGamma }} \le C h \left\| f\right\| _{0,\omega }. \end{aligned}$$

(5.11)

For $T\in \mathscr {T}_\varGamma$, we have

$$\begin{aligned} \left\| \mathscr {I}u^{\epsilon }-v_h\right\| _{1,T}=\left\| \mathscr {I}u^{\epsilon }-v_h\right\| _{0,T}+|\mathscr {I}u^{\epsilon }-v_h|_{1,T}. \end{aligned}$$

To estimate $\left\| \mathscr {I}u^{\epsilon }-v_h\right\| _{0,T}$

$$\begin{aligned} \begin{aligned} \left\| \mathscr {I}u^{\epsilon }-v_h\right\| _{0,T}&\le \left\| \mathscr {I}u^{\epsilon }-u^{\epsilon }\right\| _{0,T}+\left\| u^{\epsilon }-v_h\right\| _{0,T}\\&\le h\left\| u^{\epsilon }\right\| _{1,T}+\left\| u^{\epsilon }\right\| _{0,T}+\left\| v_h\right\| _{0,T}. \end{aligned} \end{aligned}$$

(5.12)

Now, for all the vertices $\vartheta _i\in \mathscr {V}(T)$, we have the following two cases.

Case-I: $\forall$ $\vartheta _i\in \mathscr {V}(T)$, $u^{\epsilon }(\vartheta _i)$ have the same sign, and then

$$\begin{aligned}&|v_h(x)|^2\le |\mathscr {I}u^{\epsilon }|^2 \\&\mathbf \therefore \left\| v_h\right\| _{0,T}\le \left\| \mathscr {I}u^{\epsilon }\right\| _{0,T}. \end{aligned}$$

Case-II: For one of the $\vartheta _i$, $u^{\epsilon }(\vartheta _i)$ do not have the same sign as at the remaining two vertices. We can assume that $\left\| u^{\epsilon }\right\| _{\infty ,T}=|u^{\epsilon }(\vartheta _3)|, \; u^{\epsilon }(\vartheta _2)u^{\epsilon }(\vartheta _3)\ge 0$ and $u^{\epsilon }(\vartheta _1)\le 0$. Furthermore, the directional derivative $\nabla (\mathscr {I}u^{\epsilon }).\overline{\vartheta _1\vartheta _3}=u^{\epsilon }(\vartheta _3)-u^{\epsilon }(\vartheta _1)$. Also, since $u^{\epsilon }(\vartheta _1)\le 0$, we have $|u^{\epsilon }(\vartheta _3)|\le |u^{\epsilon }(\vartheta _3)-u^{\epsilon }(\vartheta _1)|\le |\nabla \mathscr {I}u^{\epsilon }||\overline{\vartheta _1\vartheta _3}|$. As, $|\overline{\vartheta _1\vartheta _3}|$ is the length of the side of the triangle T, which is $\le h.$ Therefore, we have

$$\begin{aligned} |u^{\epsilon }(\vartheta _3)| \le h |\nabla (\mathscr {I}u^{\epsilon })|. \end{aligned}$$

(5.13)

Therefore, by Cauchy–Schwartz’s inequality and definition of $v_h$ given in Eq. 5.6, we have

$$\begin{aligned} \begin{aligned} \left\| v_h\right\| _{0,T}&\le (\text {diam} (T))^{\frac{1}{2}}\left\| u^{\epsilon }\right\| _{\infty ,T}\\&\le (\text {diam} (T))^{\frac{1}{2}} h|\nabla (\mathscr {I} u^{\epsilon })|\\&\le h\left\| \nabla (\mathscr {I}u^{\epsilon })\right\| _{0,T}\\&\le h \left\| \mathscr {I}u^{\epsilon }\right\| _{1,T}. \end{aligned} \end{aligned}$$

From Case-I and Case-II, we obtain

$$\begin{aligned} \left\| v_h\right\| _{0,T}\le \left\| \mathscr {I} u^{\epsilon }\right\| _{1,T}\le \left\| \mathscr {I}u^{\epsilon }-u^{\epsilon }\right\| _{1,T}+\left\| u^{\epsilon }\right\| _{1,T}. \end{aligned}$$

Thus

$$\begin{aligned} \left\| v_h\right\| _{0,T}\le h \left\| u^{\epsilon }\right\| _{2,T}+\left\| u^{\epsilon }\right\| _{1,T}. \end{aligned}$$

(5.14)

Using Eq. 5.14 in Eq. 5.12, we arrive at

$$\begin{aligned} \begin{aligned} \left\| \mathscr {I}u^{\epsilon }-v_h\right\| _{0,T}&\le h\left\| u^{\epsilon }\right\| _{1,T}+\left\| u^{\epsilon }\right\| _{0,T}+h\left\| u^{\epsilon }\right\| _{2,T}+\left\| u^{\epsilon }\right\| _{1,T}\\&\le C\Big (h\left\| u^{\epsilon }\right\| _{2,T}+\left\| u^{\epsilon }\right\| _{1,T}\Big ) \end{aligned} \\ \begin{aligned} \therefore \left\| \mathscr {I}u^{\epsilon }-v_h\right\| _{0,\mathscr {T}_\varGamma }^2&=\sum _{T\in \mathscr {T}_\varGamma }\left\| \mathscr {I}u^{\epsilon }-v_h\right\| _{0,T}^2\\&\le C \sum _{T\in \mathscr {T}_{\varGamma }}\Big (h\left\| u^{\epsilon }\right\| _{2,T}+\left\| u^{\epsilon }\right\| _{1,T}\Big )^2\\&\le C \Big ( h\left\| u^{\epsilon }\right\| ^2_{2,\mathrm {R}}+\left\| u^{\epsilon }\right\| _{1,\mathscr {T}_{\varGamma }}^2\Big )\\&\le C h\left\| u^{\epsilon }\right\| _{2,\mathrm {R}}^2. \end{aligned} \end{aligned}$$

The last step follows due to Lemma 2, with tube size $\delta =h.$ Thus

$$\begin{aligned} \left\| \mathscr {I}u^{\epsilon }-v_h\right\| _{0,\mathscr {T}_{\varGamma }} \le C\sqrt{h}\left\| f\right\| _{0,\omega }. \end{aligned}$$

(5.15)

Fig. 2

Partition of the simplices $T\in T_{\varGamma }$, as type-1 and type-2

To estimate $|\mathscr {I}u^{\epsilon }-v_h|_{1,\mathscr {T}_{\varGamma }}$, we refer Fig. 2. For $T\in \mathscr {T}_\varGamma$, there are two types depending on the number of vertices of T lying outside the domain $\omega$. If only one vertex (say $\vartheta _1$) of the simplex T lies outside the domain $\omega$, consider such simplices of type-1. If two vertices of the simplex T lie outside the domain $\omega$ (say $\vartheta _1$, $\vartheta _2$), then consider such simplices of type-2.

Case-A: In this case, we have $(\mathscr {I}u^{\epsilon }-v_h)(\vartheta _1)=u^{\epsilon }(\vartheta _1)$, and $(\mathscr {I}u^{\epsilon }-v_h)(\vartheta _i)=0,\; \text { for } i=2,3$. Using Lemma 3, we get

$$\begin{aligned} |\mathscr {I}u^{\epsilon }-v_h|_{1,T}&\le C|u^{\epsilon }(\vartheta _1)|&\le C\big (|u^{\epsilon }(\vartheta _1)-u^{\epsilon }(\gamma _p)|+|u^{\epsilon }(\gamma _p)|\big ), \end{aligned}$$

where $\gamma _p\in \varGamma \cap T$. Using Eq. 2.4 with $p=4$, and Eqs. 2.3 and 2.2, we obtain

$$\begin{aligned} \begin{aligned} |\mathscr {I}u^{\epsilon }-v_h|_{1,T}&\le C\big (\left\| u^{\epsilon }\right\| _{W^{1,4}(\varOmega \cap T)} |\vartheta _1-\gamma _p|^{\frac{1}{2}}+\left\| u^{\epsilon }\right\| _{\infty , (\varOmega \cap T)}\big )\\&\le C\big (\left\| u^{\epsilon }\right\| _{2,(\varOmega \cap T)}|\vartheta _1-\gamma _p|^{\frac{1}{2}}+\left\| u^{\epsilon }\right\| _{2,(\varOmega \cap T)}\big )\\&\le C\big (\sqrt{h}\left\| u^{\epsilon }\right\| _{2,(\varOmega \cap T)}+\left\| u^{\epsilon }\right\| _{2,(\varOmega \cap T)}\big ). \end{aligned} \end{aligned}$$

Case-B: Similar to the Case-A, we have $(\mathscr {I}u^{\epsilon }-v_h)(\vartheta _i)=u^{\epsilon }(\vartheta _i)$, for $i=1,2$ and $(\mathscr {I}u^{\epsilon }-v_h)(\vartheta _3)=0$. Using the same results used in the Case-A, we have

$$\begin{aligned} \begin{aligned} |\mathscr {I}u^{\epsilon }-v_h|_{1,T}&\le \sum _{i=1,2}|u^{\epsilon }(\vartheta _i)-u^{\epsilon }(\gamma _p)|+2|u^{\epsilon }(\gamma _p)|\\&\le C\Big (\sum _{i=1,2}\left\| u^{\epsilon }\right\| _{W^{1,4}(\varOmega \cap T)} |\vartheta _i-\gamma _p|^{\frac{1}{2}}+\left\| u^{\epsilon }\right\| _{2,(\varOmega \cap T)}\Big )\\&\le C\big (\sqrt{h}\left\| u^{\epsilon }\right\| _{2,(\varOmega \cap T)}+\left\| u^{\epsilon }\right\| _{2,(\varOmega \cap T)}\big ). \end{aligned} \end{aligned}$$

From Case-A and Case-B, we derive

$$\begin{aligned}&|\mathscr {I}u^{\epsilon }-v_h|_{1,T}\le C\big (\sqrt{h}\left\| u^{\epsilon }\right\| _{2,(\varOmega \cap T)}+\left\| u^{\epsilon }\right\| _{2,(\varOmega \cap T)}\big ), \; \forall T\in T_{\varGamma }. \\&\begin{aligned} \therefore |\mathscr {I}u^{\epsilon }-v_h|_{1,\mathscr {T}_{\varGamma }}^{2}=&\sum _{T\in \mathscr {T}_{\varGamma }}|\mathscr {I}u^{\epsilon }-v_h|_{1,T}^{2}\\ \le&C\sum _{T\in \mathscr {T}_{\varGamma }}\Big (h\left\| u^{\epsilon }\right\| _{2,(\varOmega \cap T)}^2+\left\| u^{\epsilon }\right\| _{2,(\varOmega \cap T)}^2\Big )\\ \le&C\Big (h\left\| u^{\epsilon }\right\| _{2,\varOmega }^{2}+\left\| u^{\epsilon }\right\| _{2,\varOmega }^2\Big )\\ \therefore |\mathscr {I}u^{\epsilon }-v_h|_{1,\mathscr {T}_{\varGamma }}\le&C(\sqrt{h}\left\| u^{\epsilon }\right\| _{2,\varOmega }+\left\| u^{\epsilon }\right\| _{2,\varOmega }) \end{aligned} \end{aligned}$$

Thus

$$\begin{aligned} |\mathscr {I}u^{\epsilon }-v_h|_{1,\mathscr {T}_{\varGamma }}\le C\{(\epsilon \sqrt{h}+\epsilon )\left\| f\right\| _{0,\omega }\}. \end{aligned}$$

(5.16)

From Eqs. 5.15 and 5.16, we obtain

$$\begin{aligned} \left\| \mathscr {I}u^{\epsilon }-v_h\right\| _{1,\mathscr {T}_\varGamma }\le C (\sqrt{h}+\epsilon )\left\| f\right\| _{0,\omega }. \end{aligned}$$

(5.17)

Thus, from Eqs. 5.10, 5.11, and 5.17, we get

$$\begin{aligned} \left\| u^{\epsilon }-v_h\right\| _{1,\mathscr {T}_{\varGamma }}\le C(\sqrt{h}+\epsilon )\left\| f\right\| _{0,\omega }, \end{aligned}$$

(5.18)

which was very challenging to obtain due to the non-uniform intersection of the boundary $\varGamma$ through the simplices T. Using Eqs. 5.8, 5.9, and 5.18, we find the estimate

$$\begin{aligned} \left\| u^{\epsilon }-v_h\right\| _{1,\omega }\le C(\sqrt{h}+\epsilon )\left\| f\right\| _{0,\omega }. \end{aligned}$$

(5.19)

Now

$$\begin{aligned}&\begin{aligned} \left\| u^{\epsilon }-v_h\right\| _{1,\varOmega }&\le \left\| u^{\epsilon }\right\| _{1,\varOmega }+\left\| v_h\right\| _{1,\varOmega } \le \left\| u^{\epsilon }\right\| _{2,\varOmega }+0 \end{aligned} \nonumber \\&\quad \therefore \left\| u^{\epsilon }-v_h\right\| _{1,\varOmega }\le C\epsilon \left\| f\right\| _{0,\omega }. \end{aligned}$$

(5.20)

Since $\mathrm {R}$ is a polygonal domain, we obtain

$$\begin{aligned} \left\| u^{\epsilon }-v_h\right\| _{1,\mathrm {R}}\le C h\left\| u^{\epsilon }\right\| _{2,\mathrm {R}} \le C h \left\| f\right\| _{0,\omega }. \end{aligned}$$

(5.21)

Thus, Eqs. 5.3, 5.19, 5.20, 5.21 complete the proof. $\square$

Remark 2

Note that whenever the grid $\mathscr {T}$ matches precisely with the boundary $\varGamma$, $\mathscr {T}_{\varGamma }$ becomes an empty set. Then, in the estimation of the $H^1$ seminorm error, there is no contribution in error by the term $\left\| u^{\epsilon }-v_h\right\| _{1,\mathscr {T}_{\varGamma }}$, which used to reduce the order of convergence of the method. Consequently, Eq. 5.8 implies $\left\| u^{\epsilon }-v_h\right\| _{1,\omega }=\left\| u^{\epsilon }-v_h\right\| _{1,\mathscr {T}_{\omega }}$. Thus, we will get the order of convergence as 1 in the $H^1$ seminorm, which is optimal.

Proposition 2

Let $u^\epsilon$ and $u^\epsilon _h$ be solutions of Eqs. 3.3 and 3.4, respectively, and then

$$\begin{aligned} |u^{\epsilon }-u^{\epsilon }_{h}|_{1,\varOmega }\le C(\sqrt{\epsilon h}+\epsilon )\left\| f\right\| _{0,\omega }. \end{aligned}$$

(5.22)

Proof

Proof follows from Eqs. 5.4, 5.19, 5.20, 5.21. $\square$

Proposition 3

Let $u^\epsilon$ and $u^\epsilon _h$ be solutions of Eqs. 3.3 and 3.4, respectively, and then

$$\begin{aligned} \left\| u^{\epsilon }-u^{\epsilon }_h\right\| _{0,\omega }\le C (h+\epsilon +\sqrt{\epsilon h})\left\| f\right\| _{0,\omega }. \end{aligned}$$

Proof

To find an $L^2$ estimate, we define the adjoint problem of Eq. 3.3 as

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {for given } f\in L^2(\omega ), \text { find } u^{\epsilon }_{f}\in H^{1}_{0}(\mathrm {R}),\text { such that }\\ (\nabla v, \nabla u^{\epsilon }_{f})_{\omega }+\epsilon ^{-1}(\nabla v, \nabla u^{\epsilon }_{f})_{\varOmega }+\epsilon (\nabla v, \nabla u^{\epsilon }_{f})_{\mathrm {R}}=(\tilde{f},v)_{\mathrm {R}},\;\;\forall v\in H^{1}_{0}(\mathrm {R}). \end{array}\right. } \end{aligned}$$

(5.23)

The regularity estimates and $H^1$ seminorm estimates can be derived to Eq. 5.23 as same as that of Eq. 3.3. Here

$$\begin{aligned} \left\| u^{\epsilon }-u^{\epsilon }_{h}\right\| _{0,\omega }=\sup _{f\in L^2(\omega )}\frac{\big |(f,u^{\epsilon }-u^{\epsilon }_{h})_{\omega }\big |}{\left\| f\right\| _{0,\omega }}=\sup _{f\in L^2(\omega )}\frac{\big |(\tilde{f},u^{\epsilon }-u^{\epsilon }_{h})_{\mathrm {R}}\big |}{\left\| f\right\| _{0,\omega }}. \end{aligned}$$

Since $u^{\epsilon }-u^{\epsilon }_h\in H^{1}_{0}(\mathrm {R})$, we substitute $v=u^{\epsilon }-u^{\epsilon }_h$ in Eq. 5.23. Therefore

$$\begin{aligned} \left\| u^{\epsilon }-u^{\epsilon }_{h}\right\| _{0,\omega }= \sup _{f\in L^2(\omega )}\Big \{\big |\big (\nabla (u^{\epsilon }-u^{\epsilon }_h),\nabla u^{\epsilon }_{f}\big )_{\omega }+\epsilon ^{-1} \big (\nabla (u^{\epsilon }-u^{\epsilon }_h),\nabla u^{\epsilon }_{f}\big )_{\varOmega }\\+\epsilon \big (\nabla (u^{\epsilon }-u^{\epsilon }_h),\nabla u^{\epsilon }_{f}\big )_{\mathrm {R}}\big |\Big /\left\| f\right\| _{0,\omega }\Big \}. \end{aligned}$$

Using orthogonality relation and RHS of the above equation becomes

$$\begin{aligned}&\begin{aligned} \sup _{f\in L^2(\omega )}\Big \{\Big (\big |\big (\nabla (u^{\epsilon }-u^{\epsilon }_h),\nabla (u^{\epsilon }_f-v_h)\big )_{\omega }+\epsilon ^{-1}\big (\nabla (u^{\epsilon }-u^{\epsilon }_h),\nabla (u^{\epsilon }_{f}-v_h)\big )_{\varOmega }\\+ \epsilon \big (\nabla (u^{\epsilon }-u^{\epsilon }_h),\nabla (u^{\epsilon }_f-v_h)\big )_{\mathrm {R}}\big | \Big )\Big / \left\| f\right\| _{0,\omega }\Big \}\\ \end{aligned} \\&\begin{aligned} \le \sup _{f\in L^2(\omega )}\Big \{\Big (|u^{\epsilon }-u^{\epsilon }_{h}|_{1,\omega }|u^{\epsilon }_{f}-v_h|_{1,\omega }+\epsilon ^{-1}|u^{\epsilon }-u^{\epsilon }_{h}|_{1,\varOmega }|u^{\epsilon }_{f}-v_h|_{1,\varOmega }\\ + \epsilon |u^{\epsilon }-u^{\epsilon }_h|_{1,\mathrm {R}}|u^{\epsilon }_{f}-v_h|_{1,\mathrm {R}}\Big )\Big /\left\| f\right\| _{0,\omega }\Big \} \end{aligned} \\&\begin{aligned} \le C \sup _{f\in L^2(\omega )} \frac{\Big ((\sqrt{h}+\sqrt{\epsilon })(\sqrt{h}+\epsilon )+\epsilon ^{-1}(\sqrt{h\epsilon }+\epsilon )(\epsilon )+\epsilon (h)(h)\Big )\left\| f\right\| _{0,\omega }^{2}}{\left\| f\right\| _{0,\omega }}. \end{aligned} \end{aligned}$$

Thus, we obtain

$$\begin{aligned} \left\| u^{\epsilon }-u^{\epsilon }_h\right\| _{0,\omega }\le C (h+\epsilon +\sqrt{\epsilon h})\left\| f\right\| _{0,\omega }. \end{aligned}$$

(5.24)

$\square$

If the parameter $\epsilon =O(h),$ order of convergence is 1 in the $L^2$ norm. Next, we propose an $H^1$ norm error estimate.

Corollary 2

Let $u^\epsilon$ and $u^\epsilon _h$ be solutions of Eqs. 3.3 and 3.4, respectively, and then

$$\begin{aligned} \left\| u^{\epsilon }-u^{\epsilon }_{h}\right\| _{1,\omega } \le C(\sqrt{\epsilon }+\sqrt{h})\left\| f\right\| _{0,\omega }. \end{aligned}$$

(5.25)

Proof

Result follows from Eqs. 5.24 and 5.7. $\square$

If the parameter $\epsilon =O(h),$ order of convergence is 1/2 in the $H^1$ norm.

6 Numerical experiments

We consider Poisson’s problem with homogeneous Dirichlet boundary conditions on two domains types (i.e., circle/ellipse, and L-shape). In the first type, we consider the non-matching case of the boundary with the mesh. In the second type, we consider boundary matching precisely with the mesh. To estimate the integrals over the domain $\omega$, we need to approximate $\omega$ as the union of some of the simplices $T \in \mathscr {T}_{h}$. Rather than just considering simplices T which lie completely inside $\omega$, we consider all those simplices whose center of gravity lies inside the domain $\omega$. No ambiguity regarding the simplices that lie completely inside or outside the domain $\omega$, but it is there for the simplices $T\in T_{\varGamma }$. For reference, in Fig.2, the green-colored simplices are considered as a part of $\omega$, while the red colored simplices are considered in the outer part of the domain $\omega$.

Fig. 3

Plot for the computed solution $u^{\epsilon }_h$ $(h=0.01,\epsilon =h^2)$ of Example 1

Example: 1

Let $\omega =\big \{ (x,y)\in \mathbb {R}^{2}\big |(x-0.5)^2+(y-0.5)^2<\frac{1}{16}\big \}$, and $u=0.0625-(x-0.5)^2-(y-0.5)^2$ be the exact solution of Eq. 3.1. We embed the circle $\omega$ into a unit rectangle $(0,1)\times (0,1)$ and solve the finite-element penalized Eq. 3.4 for $f=4$. For different values of $\epsilon$ and mesh sizes h, we compute the approximate solution $u^{\epsilon }_{h}$ at each node point. We also determine the error between the exact solution u and the computed solution $u^{\epsilon }_h$, and the convergence rate in the $H^{1}(\omega )$ and $L^{2}(\omega )$ norms. The computed solution $u^{\epsilon }_h$ is depicted in Fig. 3. Also, the error plots and convergence rate of the proposed method are displayed in Fig. 4 and Table 1, respectively.

Example: 2

Let $\omega =\big \{(x,y)\in \mathbb {R}^2 \big | (x-0.5)^2+2(y-0.5)^2<\frac{1}{8}\big \}$, and $u=0.0625-0.5(x-0.5)^2-(y-0.5)^2$ be the exact solution of Eq. 3.1. We embed the ellipse $\omega$ into a unit rectangle $(0,1)\times (0,1)$ and solve the finite-element penalized Eq. 3.4 for $f=3$. For different values of $\epsilon$ and mesh sizes h, we compute the approximate solution $u^{\epsilon }_{h}$ at each node point. We also determine the error between the exact solution u and the computed solution $u^{\epsilon }_h$ and the convergence rate in the $H^{1}(\omega )$ and $L^{2}(\omega )$ norms. The computed solution $u^{\epsilon }_h$ is depicted in Fig. 5. Also, the error plots and convergence rate of the proposed method are displayed in Fig. 6 and Table 2, respectively.

Example: 3

For an L shape domain $\omega =(0.2,0.8)^2\backslash (0.5, 0.8)^2 \subset \mathbb {R}^{2}$, $u=(x-0.2)(x-0.8)(x-0.5)(y-0.2)(y-0.8)(y-0.5)$ be the exact solution of Eq. 3.1. We embed $\omega$ into a unit rectangle $(0,1)\times (0,1)$ and solve the finite-element penalized Eq. 3.4 for $f=(3-6x)(y^3-1.5y^2+0.66y-0.08)+(3-6y)(x^3-1.5x^2+0.66x-0.08)$. For different values of $\epsilon$ and boundary fitting mesh sizes h, we compute the approximate solution $u^{\epsilon }_{h}$ at each node point. We also determine the error between the exact solution u and the computed solution $u^{\epsilon }_h$ and the convergence rate in the $H^1$ and $L^{2}$ norms. By Remark 2, we expect an optimal convergence rate, 1 in the $H^1$ norm if we choose $\epsilon$ at least of O(h), and 2 in the $L^2$ norm if we choose $\epsilon$ as at least of $O(h^2)$. We can observe this from Table 3 and Fig. 8. Also, computed solution $u^{\epsilon }_h$ is depicted in Fig. 7.

Fig. 4

Error vs mesh size plots of Example 1, for different values of $\epsilon$

Table 1 Error analysis of Example 1 $(\epsilon =h^2)$

Fig. 5

Plot for the computed solution $u^{\epsilon }_h$ $(h=0.01,\epsilon =h^2)$ of Example 2

Fig. 6

Error vs mesh size plots of Example 2, for different values of $\epsilon$

Table 2 Error analysis of Example 2 $(\epsilon =h^2)$

Table 3 Error analysis of Example 3 ($\epsilon =h^2$)

Fig. 7

Plot for the computed solution $u^{\epsilon }_h$ $(h=0.01,\epsilon =h^2)$ of Example 3

Fig. 8

Error vs mesh size plots of Example 3, for different values of $\epsilon$

7 Conclusion

The fictitious domain method with the modified $H^1$ penalty approach for the homogeneous Dirichlet problems is proposed. The $H^1$ and $L^2$ estimates are derived, and the sub-optimal order of convergences are achieved, i.e., 1/2 and 1 in the $H^1$ and $L^2$ norms, respectively, with the parameter $\epsilon =O(h)$. If we choose the mesh that exactly fits the domain’s boundary, we attain the optimal order of convergence. However, we get the optimal order of convergence, i.e., 1 in the $H^1$ norm, and 2 in the $L^2$ norm, during the numerical experiments. In addition, we find the rate of convergence as 2 in the $\sup$ norm during the numerical experiments which can be seen from Fig.12. Also, Figs.4, 6, and 8 depict the dependency of the accuracy over the penalty parameter $\epsilon$, and we observe that whenever $\epsilon$ is compatible with the mesh size h, we get the least error. Also, from Table 4, Table 5, and Table 6, with Figs.9, 10, and 11, we see that the proposed method is more accurate with the obvious implementation of the Neumann and Robin boundary conditions.

Table 4 Comparison of the errors in different norms of the proposed method with the $H^1$ penalty method (Zhou and Saito 2014) for Example 1 with $\epsilon =h$

Table 5 Comparison of the error in different norms of the proposed method with the $H^1$ penalty method (Zhou and Saito 2014) for Example 2, with $\epsilon =h$

Table 6 Comparison of the error in different norms of the proposed method with the $H^1$ penalty method (Zhou and Saito 2014) for Example 3, with $\epsilon =h$

Fig. 9

Modified $H^1$ penalty method vs $H^1$ penalty method for Example 1, with $\epsilon =h$

Fig. 10

Modified $H^1$ penalty method vs $H^1$ penalty method for Example 2, with $\epsilon =h$

Fig. 11

Modified $H^1$ penalty method vs $H^1$ penalty method for Example 3, with $\epsilon =h$

Fig. 12

Rate of convergence in the $L^\infty$ norm, with $\epsilon =h^2$