The first integral method and some nonlinear models

Abstract

In this article, first integral method [Ref. : Feng. Z., Journal of Physics A: Mathematical and General, 35(2002), 343–349] is used to find exact solutions of some nonlinear partial differential equations. It is applied to find exact solutions to a variant Boussinesq equation, the extended modifed Korteweg-de Vries equation and the Kudryashov–Sinel’shchikov equation. The properties of solutions are then discussed and plotted by using suitable values of the parameters involved. Shock wave-like solutions for variant Boussinesq and extended mKdv equations are found. For the Kudryashov–Sinel’shchikov equation one singular and two exponential solutions are obtained.

1 Introduction:

Recently, study of nonlinear partial differential equations (NPDE) has got paramount importance to get physical and mathematical insights for problems related to diverse disciplines, such as, fluid and plasma dynamics, astrophysics, mathematical biology, nonlinear optics, chemistry etc. Many analytical techniques have been developed and the use of suitable numerical methods significantly enriches the solution procedure for them. Obtaining exact solutions gives an advantage in studying these equations. But till now there is no general method to solve NPDEs as well as for a higher order linear PDEs. Numerous methods such as tanh method (Malfliet and Hereman 1996), homogeneous balance method (Wang et al. 1996, Maitra et al. 2019), $G'/G$ expansion method (Manafian and Lakestani 2017), Lie symmetry analysis method (Hydon 2000), sine-cosine method (Wazwaz 2004), Kudryashov method (Kudryashov 2000), new version of Kudryashov and exponential methods (Hosseini et al. 2020), $\hbox {exp}_\alpha$ and Jacobi elliptic function method (Hosseini et al. 2020), extended mapping method (Ma et al. 2012) etc are used to obtain exact solutions of NPDEs. The first integral method is one of the effective methods which was first proposed by Zhaosheng Feng in the article (Feng 2002), based on the theory of commutative algebra. This method is widely used to find analytic solutions of NPDEs. Raslan used this method in (Raslan 2008) to find exact solutions of Fisher equation and modified equal width equation. Taghizadeh et al. consturcted exact solutions of the modified KdV-KP equation and Burgers-KP equation by using this first integral method in (Taghizadeh et al. 2011). Exact solutions of the Eckhaus equation (Taghizadeh et al. 2012) and nonlinear Schrödinger equation (Taghizadeh et al. 2011) are also obtained by Taghizadeh et al. by using this method. Hosseini et al. applied this method to obtain exact solutions of KdV system, Kaup-Boussinesq system and Wu-Zhang system in (Hosseini et al. 2012).

In this article, we use the first integral method to obtain exact solutions of some remarkable NPDEs- a variant Boussinesq equation, the extended modifed Korteweg-de Vries(K-dV) equation and the Kudryashov–Sinel’shchikov equation.

A variant Boussinesq equation is given by

$$\begin{aligned}&H_t+(Hu)_x+u_{xxx}=0,\\&u_t+H_x+uu_x=0. \end{aligned}$$

In his article, (Sachs 1988) Robert L. Sachs showed the integrability of this system; he expressed it in bilinear form and constructed infinite number of rational solutions. Solitary wave solutions for this system were found by Wang in (Wang 1995). Hirota showed that this integrable system is related to first modified KP equation (Hirota 1985). Jabbari et al. obtained approximate solution of the Variant Boussinesq equation by the HAM and Homotopy Padé technique (Jabbari et al. 2014).

The extended modified K-dV equation is given by

$$\begin{aligned} u_t+a_1u_{xxx}+a_2u_x+a_3uu_x+a_4u^2u_x=0. \end{aligned}$$

For different values of the parameters $a_1,a_2,a_3,a_4$ this equation gives different types of K-dV equations which are so important to describe many physical models in different branches of science, e.g. to describe dust acoustic solitary waves in plasmas, dust ion-acoustic waves in Saturn’s F-ring and in the supernova shells etc (Drazin and Johnson 1989).

This equation is now called as Gardener equation. It is integrable by inverse scattering transform and has infinitely many conservation laws. Gardener equation models deep ocean waves and is an extension of KdV equation which models shallow water waves (Daoui et al. 2014). Hanze Liu and Jibin Li obtained some exact solutions using Lie symmetry analysis and dynamical systems approach (Liu and Li 2010). Generalised Gardener equation

$$\begin{aligned} u_t+(p+qu^n+ru^{2n})u_x+u_{xxx}=0. \end{aligned}$$

has been considered by Lu et al. (Lu and Liu 2010).

In 2009 Kudryashov and Sinel’shchikov derived the following equation (Kudryashov and Sinel’shchikov 2010), known as Kudryashov-Sinel’shchikov equation:

$$\begin{aligned} u_t+\alpha u u_x+u_{xxx}-(uu_{xx})_x-\beta u_xu_{xx}=0. \end{aligned}$$

It describes nonlinear pressure waves in a mixture of liquid and gas bubbles and can be considered as a generalization of the KdV and BKdV equations. In He et al. (2013) Y. He et al. found exact solutions of this equation by $G'{/}G$ expansion method. This equation is also studied in the articles (Randruut 2011, Ryabov 2010).

The rest of this article is arranged as follows: in Sect. 2, the method of finding exact solutions using first integral of differential equations is discussed. Using this method some exact solutions of the variant Boussinesq system given in (8), (9) and of the extended modified K-dV equation are obtained in Sects. 3, 4 respectively. And that for the Kudryashov–Sinel’shchikov equation is given in Sect. 5. Ultimately in Sect. 6 we draw the conclusion of this work.

2 The first integral method

Definition

(Goriely 2001) Consider a system of differential equations that are of class $C^k$ with $k>0$ on an open set U of ${\mathbb {K}}^n$

$$\begin{aligned} \frac{\mathrm{d}X_i}{\mathrm{d}\xi }=f_i(X_1(\xi ),X_2(\xi ),...,X_n(\xi )), i=1,2,...,n. \end{aligned}$$

(1)

Then a $C^1$ function $Q:U\rightarrow {\mathbb {K}}$ is said to be a time independent first integral of (1) if

$$\begin{aligned} \frac{\mathrm{d}Q}{\mathrm{d}\xi }=\frac{\partial Q}{\partial X_1}.\frac{\mathrm{d}X_1}{\mathrm{d}\xi }+...+\frac{dQ}{dX_n}.\frac{dX_n}{\mathrm{d}\xi }=0 \end{aligned}$$

on the solutions $X_i=X_i(\xi )$ of (1).

In the first integral method at first we reduce a given PDE

$$\begin{aligned} F(u,u_x,u_{t},u_{xx},...)=0 \end{aligned}$$

(2)

to an ordinary differential equation(ODE)

$$\begin{aligned} G\left( f(\xi ),\frac{df}{\mathrm{d}\xi },\frac{d^2f}{\mathrm{d}\xi ^2},...\right) =0 \end{aligned}$$

(3)

by using the transformation $u(x,t)\rightarrow f(\xi )$ where $\xi =kx-\omega t$. Then we introduce new dependent variables $X(\xi )=f(\xi )$ and $Y(\xi )=\frac{df}{\mathrm{d}\xi }$. Thus (3) reduces to a system of ODEs

$$\begin{aligned}&\frac{dX}{\mathrm{d}\xi }=Y, \end{aligned}$$

(4)

$$\begin{aligned}&\frac{dY}{\mathrm{d}\xi }=P(X,Y). \end{aligned}$$

(5)

From the theory of integrability of ordinary differential equations (ODE) we know that if one can found two first integrals of the system of ODEs (4), (5) under the same conditions then the general solution of (4), (5) can be obtained explicitly Goriely (2001). But unfortunately there is no systematic theory for finding a first integral of a plane autonomous system. Using Hilbert-Nullstellensatz theorem of commutative algebra Zhaosheng Feng obtained the following division theorem (Feng 2002), applying which a polynomial first integral (if exists) can be obtained systematically.

Division Theorem: If p(w, z), q(w, z) are polynomials in ${\mathbb {C}}[w,z]$ and p(w, z) is irreducible in ${\mathbb {C}}[w,z]$ and q(w, z) vanishes at all zero points of p(w, z), then there exists a polynomial g(w, z) in ${\mathbb {C}}[w,z]$ such that $q(w,z)=g(w,z)p(w,z).$

Now let us try to find a first integral of (4), (5) in the form $Q(X,Y)=\Sigma _{i=0}^m a_i(X).Y^i$, an irreducible polynomial in ${\mathbb {C}}[X,Y]$ such that

$$\begin{aligned} Q(X(\xi ),Y(\xi ))=\Sigma _{i=0}^m a_i(X(\xi )).Y(\xi )^i=0 \end{aligned}$$

(6)

where $X=X(\xi ), Y=Y(\xi )$ are nontrivial solutions of (4), (5). The polynomials $a_i(X)$ of X are relatively prime in ${\mathbb {C}}[X,Y]$ and $a_m(X)$ is not identically zero.

$\frac{dQ}{\mathrm{d}\xi }$ is also a polynomial in X, Y and $Q[X(\xi ),Y(\xi )]=0$ give $\left[ \frac{dQ}{\mathrm{d}\xi }\right] _{4,5}=0$, which shows that (6) is a first integral of (4), (5).

By division theorem there exists polynomial $g(X)+h(X)Y$ such that

$$\begin{aligned} \frac{dQ}{\mathrm{d}\xi }=(g(X)+h(X)Y)Q(X,Y)=(g(X)+h(X)Y)\Sigma _{i=0}^m a_i(X).Y^i. \end{aligned}$$

(7)

Now comparing the coefficients of different powers of Y from both sides of (7) we get a system of algebraic equations, solving which we find $a_i(X)$s and then Y from (6). Putting this value of Y in (4) and integrating we obtain exact solution of (2) as

$$\begin{aligned} u(x,t)=f(\xi )=X(\xi )=X(kx-\omega t). \end{aligned}$$

3 Variant Boussinesq equation

A variant Boussinesq equation is given by

$$\begin{aligned}&H_t+(Hu)_x+u_{xxx}=0, \end{aligned}$$

(8)

$$\begin{aligned}&u_t+H_x+uu_x=0. \end{aligned}$$

(9)

where $u=u(x,t), H=H(x,t);$ the suffixes indicate the partial derivatives with respect to the corresponding independent variables.

Physically this is a model for water waves where H(x, t) describes the total depth and u(x, t) is velocity. By using the transformation $\xi =kx-\omega t$, Eqs. (8), (9) respectively become

$$\begin{aligned}&-\omega H'+k(Hu)'+k^3u'''=0, \end{aligned}$$

(10)

$$\begin{aligned}&-\omega u'+kH'+kuu'=0\nonumber \\ {}&\Rightarrow H=\frac{\omega }{k}u-\frac{1}{2}u^2. \end{aligned}$$

(11)

Using (11) in (10) and integrating once (taking integration constant 0) we get,

$$\begin{aligned} -\frac{\omega ^2}{k}u+\frac{3\omega }{2}u^2-\frac{k}{2}u^3+k^3u''=0. \end{aligned}$$

(12)

Now we reduce (12) to the following system by the new dependent variables $X(\xi ), Y(\xi )$, defined by $X(\xi )=u(\xi ), Y(\xi )=u'(\xi )$,

$$\begin{aligned}&\frac{dX}{\mathrm{d}\xi }=Y, \end{aligned}$$

(13)

$$\begin{aligned}&\frac{dY}{\mathrm{d}\xi }=\frac{1}{k^3}\left( \frac{\omega ^2}{k}X-\frac{3\omega }{2}X^2+\frac{k}{2}X^3\right) . \end{aligned}$$

(14)

Here, we want to find a polynomial first integral of (13), (14) in the form of an irreducible polynomial $Q(X,Y)=\Sigma _{i=0}^ma_i(X)Y^i=0$, where $X(\xi ), Y(\xi )$ are nontrivial solutions of (13), (14). Q(X, Y) is a first integral of (13), (14). We consider the following two cases:

Case 1: m=1

In this case

$$\begin{aligned} Q(X,Y)=a_0(X)+a_1(X)Y=0, \quad a_1(X)\ne 0. \end{aligned}$$

(15)

By division theorem there exist polynomials g(X), h(X) such that

$$\begin{aligned} \frac{dQ}{\mathrm{d}\xi }= & {} (g(X)+h(X)Y)(a_0(X)+a_1(X)Y)\nonumber \\\Rightarrow & {} \dot{a_0}(X)Y+\dot{a_1}(X)Y^2+\frac{1}{k^3}a_1(X)\left( \frac{ \omega ^2}{k}X-\frac{3\omega }{2}X^2+\frac{k}{2}X^3\right) \nonumber \\= & {} \left( g(X)+h(X)Y\right) \left( a_0(X)+a_1(X)Y\right) . \end{aligned}$$

(16)

Equating the coefficients of different powers of Y from (16) we obtain a system of equations. The coefficient of $Y^2$ gives

$$\begin{aligned} \dot{a_1}(X)=h(X)a_1(X). \end{aligned}$$

(17)

Since $a_1(X)$ is a polynomial in X then (17) shows that

$$\begin{aligned} h(X)=0, a_1(X)=constant=1(say). \end{aligned}$$

(18)

Then the coefficients of Y and Y free terms in (17) are respectively:

$$\begin{aligned}&\dot{a_0}(X)=g(X), \end{aligned}$$

(19)

$$\begin{aligned}&\frac{1}{k^3}a_1(X)\left( \frac{\omega ^2}{k}X-\frac{3\omega }{2}X^2+\frac{k}{2}X^3\right) =g(X)a_0(X). \end{aligned}$$

(20)

Comparing the degrees of $g(X), a_0(X)$ from (19) and (20), we get deg $g(x)=1$ only and deg $a_0(X)=2.$

So, we choose $g(X)=c_0+c_1X$ and $a_0(X)=d_0+d_1X+d_2X^2$, where $c_i,d_i$ are constants to be determined. Using these forms of $g(X), a_0(X)$ in (19) and (20) we get a system of algebraic equations, solving which we obtain

$$\begin{aligned} a_0(X)=\mp \left( \frac{1}{2k}X^2-\frac{\omega }{k^2}X\right) . \end{aligned}$$

(21)

Thus we obtain a first integral of (13) and (14) in the form

$$\begin{aligned}&\mp \left( \frac{1}{2k}X^2-\frac{\omega }{k^2}X\right) +Y=0\nonumber \\ {}&\Rightarrow Y=\pm \left( \frac{1}{2k}X^2-\frac{\omega }{k^2}X\right) . \end{aligned}$$

(22)

Then from (13) we obtain exact solutions of (8) and (9) as follows:

$$\begin{aligned} u(x,t)=u(\xi )=X(\xi )=\frac{2\omega }{e^{\omega (kx-\omega t)/k^2}+k}, \quad H(x,t)=\frac{\omega }{k}u-\frac{1}{2}u^2=\frac{2\omega ^2e^{\omega (kx-\omega t)/k^2}}{k(e^{\omega (kx-\omega t)/k^2}+k)^2};\nonumber \\ \end{aligned}$$

(23)

and

$$\begin{aligned} u(x,t)=\frac{2\omega e^{\omega (kx-\omega t)/k^2}}{1+ke^{\omega (kx-\omega t)/k^2}},\quad H(x,t)=\frac{2\omega ^2 e^{\omega (kx-\omega t)/k^2}}{k(1+ke^{\omega (kx-\omega t)/k^2})^2}. \end{aligned}$$

(24)

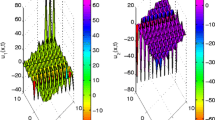
The solution u(x, t) in (24) represents shock wave in Fig. 1, whereas H(x, t) gives a periodic like wave in Fig. 2. Shock pattern for u(x, t) indicates the sudden changes in the velocity. Fig. 2. shows that the water depth changes almost periodically.

Fig. 1

Plot of u(x, t) given in (24) with $\omega =k=1$

Fig. 2

Plot of H(x, t) given in (24) with $\omega =k=1$

Now we consider the case for m=2

Case 2: m=2

Here

$$\begin{aligned} Q(X,Y)=a_0(X)+a_1(X)Y+a_2(X)Y^2=0,\quad a_2(X)\ne 0. \end{aligned}$$

(25)

By division theorem there exist polynomials g(X), h(X) such that

$$\begin{aligned} \frac{dQ}{\mathrm{d}\xi }= & {} (g(X)+h(X)Y)(a_0(X)+a_1(X)Y+a_2(X)Y^2)\nonumber \\\Rightarrow & {} \dot{a_0}(X)Y+\dot{a_1}(X)Y^2+\frac{1}{k^3}a_1(X)\left( \frac{\omega ^2}{k}X-\frac{3\omega }{2}X^2+\frac{k}{2}X^3\right) +\dot{a_2}(X)Y^3\nonumber \\&+\frac{2}{k^3}a_2(X)Y\left( \frac{\omega ^2}{k}X-\frac{3\omega }{2}X^2+\frac{k}{2}X^3\right) \nonumber \\= & {} (g(X)+h(X)Y)(a_0(X)+a_1(X)Y+a_2(X)Y^2).\nonumber \\ \end{aligned}$$

(26)

Equating the coefficients of different powers of Y from both sides of (26) we obtain the following system of equations:

$$\begin{aligned}&\dot{a_2}(X)=h(X)a_2(X), \end{aligned}$$

(27)

$$\begin{aligned}&\dot{a_1}(X)=g(X)a_2(X)+h(X)a_1(X), \end{aligned}$$

(28)

$$\begin{aligned}&\dot{a_0}(X)+\frac{2}{k^3}a_2(X)\left( \frac{\omega ^2}{k}X-\frac{3\omega }{2}X^2+\frac{k}{2}X^3\right) =g(X)a_1(X)+h(X)a_0(X), \end{aligned}$$

(29)

$$\begin{aligned}&\frac{1}{k^3}a_1(X)\left( \frac{\omega ^2}{k}X-\frac{3\omega }{2}X^2+\frac{k}{2}X^3\right) =g(X)a_0(X). \end{aligned}$$

(30)

Since $a_2(X)$ is a polynomial in X then from (27) we get

$$\begin{aligned} h(X)=0,\quad a_2(X)=constant=1(say). \end{aligned}$$

(31)

Then from (28), (29), (30) we find that deg $g(X)=1$, deg $a_1(X)=2$, deg $a_0(X)=4$. Let us take

$$\begin{aligned}&g(X)=b_0+b_1X,\quad a_1(X)=c_0+c_1X+c_2X^2,\nonumber \\ {}&a_0(X)=d_0+d_1X+d_2X^2+d_3X^3+d_4X^4, \end{aligned}$$

(32)

where $b_i,c_i,d_i$ are constants to be determined. Using (32) in (28)–(30) and solving we obtain the following two cases:

$$\begin{aligned} c_0=0, c_1=\pm \frac{2\omega }{k^2},c_2=\mp \frac{1}{k} \end{aligned}$$

(33)

and in both of these cases

$$\begin{aligned} d_0=0,d_1=0,d_2=\frac{\omega ^2}{k^4},d_3=-\frac{\omega }{k^3},d_4=\frac{1}{4k^2}. \end{aligned}$$

(34)

Thus we get the values of $a_0(X),a_1(X),a_2(X)$, using which from (25) we obtain two values of Y. We put these values of Y in (13) and after integration get two exact solutions of (8) and (9) which are same as (23) and (24).

4 Extended modified KdV equation

The extended modified K-dV equation is given by

$$\begin{aligned} u_t+a_1u_{xxx}+a_2u_x+a_3uu_x+a_4u^2u_x=0, \end{aligned}$$

(35)

where $u=u(x,t)$ and $a_1,a_2,a_3,a_4$ are real parameters. For $a_1=a_3=1$, $a_2=a_4=0$ the Eq. (35) represents the K-dV equation $u_t+uu_x+u_{xxx}=0$ and when $a_1=-1,a_3=-6,a_2=a_4=0$ (35) reduces to the classical K-dV equation $u_t-6uu_x-u_{xxx}=0$. When $a_1=1,a_4=6,a_2=a_3=0$ then (35) gives the celebrated mK-dV equation $u_t+6u^2u_x+u_{xxx}=0$.

We reduce the PDE (35) to the following ODE by using the transformation $u(x,t)=f(\xi ),\quad \xi =kx-\omega t$ and integrating once (taking integration constant 0):

$$\begin{aligned} a_1k^3f''(\xi )-\omega f(\xi ) +a_2kf(\xi )+a_3\frac{k}{2} \{f(\xi )\}^2+a_4\frac{k}{3} \{f(\xi )\}^3=0. \end{aligned}$$

(36)

We obtain a system of ODEs from (36) by introducing two new dependent variables $X(\xi )=f(\xi ),\quad Y(\xi )=f'(\xi )$:

$$\begin{aligned}&\frac{\mathrm{d}X}{\mathrm{d}\xi }=Y, \end{aligned}$$

(37)

$$\begin{aligned}&\frac{\mathrm{d}Y}{\mathrm{d}\xi }=\frac{1}{a_1k^3}\left\{ (\omega -a_2k)X-\frac{a_3k}{2}X^2-\frac{a_4k}{3}X^3\right\} . \end{aligned}$$

(38)

Let $X(\xi ), Y(\xi )$ be nontrivial solutions of (37), (38). We wish to find a first integral of the above system in the form $Q(X,Y)=\Sigma _{i=0}^m b_i(X)Y^i=0$, an irreducible polynomial in X, Y. Here we consider the following two cases for m:

Case 1: m=1

Here $Q(X,Y)=b_0(X)+b_1(X)Y$.

By division theorem there exists a polynomial $g(X)+h(X)Y$ such that

$$\begin{aligned}&\frac{dQ}{\mathrm{d}\xi }=(g(X)+h(X)Y)(b_0(X)+b_1(X)Y)\nonumber \\&\quad \Rightarrow \dot{b_0}(X)Y+\dot{b_1}(X)Y^2+\frac{1}{a_1k^3}b_1(X)\left\{ (\omega -a_2k)X-\frac{a_3k}{2}X^2-\frac{a_4k}{3}X^3\right\} \nonumber \\&\quad =(g(X)+h(X)Y)(b_0(X)+b_1(X)Y). \end{aligned}$$

(39)

Equating the coefficients of different powers of Y from both sides of (39) we get the following system of equations:

$$\begin{aligned}&\dot{b_1}(X)=h(X)b_1(X), \end{aligned}$$

(40)

$$\begin{aligned}&\dot{b_0}(X)=h(X)b_0(X)+g(X)b_1(X), \end{aligned}$$

(41)

$$\begin{aligned}&\frac{1}{a_1k^3}b_1(X)\left\{ (\omega -a_2k)X-\frac{a_3k}{2}X^2-\frac{a_4k}{3}X^3\right\} =g(X)b_0 (X). \end{aligned}$$

(42)

As $b_1(X)$ is a polynomial in X, from (40) we get $h(X)=0,\quad b_1(X)=constant=0$(say). Then from (41), (42) we get deg $g(X)=1$ only and deg $b_0(X)=2$. Let us suppose

$$\begin{aligned} g(X)=c_0+c_1X,\quad b_0(X)=d_0+d_1X+d_2X^2. \end{aligned}$$

(43)

We use these values of g(X), $b_0(X)$ in (41), (42). We equate the coefficients of different powers of X from both sides of the resulting equations. We thus obtain a system of algebraic equations, solving which we find the values of the constants $c_i,\quad d_i$.

We obtain $b_0(X)=\pm \left( a_3\sqrt{ -\frac{1}{6a_1a_4k^2}}X-\sqrt{-\frac{a_4}{6a_1k^2}}X^2\right)$.

From the first integral $b_0(X)+b_1(X)Y=0$, we get

$$\begin{aligned} Y=-b_0(X)=\pm \left( a_3\sqrt{ -\frac{1}{6a_1a_4k^2}}X-\sqrt{-\frac{a_4}{6a_1k^2}}X^2\right) . \end{aligned}$$

(44)

Then from (37), after integration we obtain exact solutions of (35) as:

$$\begin{aligned} u(x,t)=f(\xi )=X(\xi )=\frac{a_3\sqrt{ -\frac{1}{a_1a_4k^2}}}{\sqrt{-\frac{a_4}{a_1k^2}}-exp\left( \mp a_3\sqrt{ -\frac{1}{6a_1a_4}}\left( x-(a_2-\frac{a_3^2}{6a_4})t \right) \right) }. \end{aligned}$$

(45)

Case 2: m=2

Here we wish to find a first integral of (37), (38) in the form

$$\begin{aligned} Q(X,Y)=b_0(X)+b_1(X)Y+b_2(X)Y^2=0 \end{aligned}$$

(46)

where $X(\xi ), Y(\xi )$ are solutions of (37), (38). By division theorem there exists polynomial $g(X)+h(X)Y$ satisfying

$$\begin{aligned} \frac{\mathrm{d}Q}{\mathrm{d}\xi }= & {} (g(X)+h(X)Y)(b_0(X)+b_1(X)Y+b_2(X)Y^2)\nonumber \\\Rightarrow & {} \dot{b_0}(X)Y+\dot{b_1}(X)Y^2+\frac{1}{a_1k^3}b_1(X)\left\{ (\omega -a_2k)X-\frac{a_3k}{2}X^2-\frac{a_4k}{3}X^3\right\} +\dot{b_2}(X)Y^3 \nonumber \\ {}&+\frac{2}{a_1k^3}b_2(X)Y\left\{ (\omega -a_2k)X-\frac{a_3k}{2}X^2-\frac{a_4k}{3}X^3\right\} \nonumber \\ {}= & {} (g(X)+h(X)Y)(b_0(X)+b_1(X)Y+b_2(X)Y^2). \end{aligned}$$

(47)

Calculating the coefficients of Y from both sides of (47), in a similar fashion as in the previous cases, we obtain that

$$\begin{aligned}&b_0(X)=\frac{a_3^3k-6a_2a_3a_4k+6a_3a_4\omega }{3a_1a_4^2k^3}X +\frac{\omega -a_2k}{a_1k^3}X^2-\frac{a_3}{3a_1k^2}X^3-\frac{a_4}{6a_1k^2}X^4, \end{aligned}$$

(48)

$$\begin{aligned}&b_1(X)=\frac{a_3^2k+6a_4(\omega -a_2k)}{\sqrt{6a_1}(-a_4)^{\frac{3}{2}}k^2}+\frac{\sqrt{\frac{2}{3}}a_3}{\sqrt{-a_4a_1}k}X-\frac{\sqrt{-\frac{2a_4}{3}}}{\sqrt{a_1}k}X^2, \end{aligned}$$

(49)

$$\begin{aligned}&b_2(X)=1. \end{aligned}$$

(50)

Now using (48)-(50) in (46) with the particular values $a_1=a_2=a_3=1,a_4=-1$ and $\omega =\frac{7k}{6}$ we get

$$\begin{aligned} Y=\pm \frac{(X-1)X}{\sqrt{6}k}, \end{aligned}$$

(51)

Accordingly from (37) we obtain exact solutions of (35) as

$$\begin{aligned} u(x,t)=f(\xi )=X(\xi )=\frac{1}{1+exp\left( \pm (x-\frac{7}{6}t)/\sqrt{6}\right) }, \end{aligned}$$

(52)

which show shock like waves in the Figs. 3 and 4.

Fig. 3

Plot of u(x, t) given in (52) with − sign

Fig. 4

Plot of u(x, t) given in (52) with $+$ sign

In general for arbitrary values of $a_1,a_2,a_3$ and $a_4=-1$ we find the exact solution

$$\begin{aligned} u(x,t)=\frac{a_3}{1+exp\left( a_3(x-\frac{1}{6}(6a_2+a_3^2)t)/\sqrt{6a_1}\right) }. \end{aligned}$$

(53)

5 Kudryashov–Sinel’shchikov equation

$$\begin{aligned} u_t+\alpha u u_x+u_{xxx}-(uu_{xx})_x-\beta u_xu_{xx}=0, \end{aligned}$$

(54)

where $u=u(x,t)$ and $\alpha , \beta$ are real parameters. Under the transformation $u(x,t)=f(\xi ), \xi =kx-ct$ equation (54) reduces to (integrating once and taking integration constant 0)

$$\begin{aligned} -cf(\xi )+\frac{\alpha k}{2}\left( f(\xi )\right) ^2+k^3f''(\xi )-k^3f(\xi )f''(\xi )-\frac{\beta k^3}{2}\left( f'(\xi )\right) ^2=0. \end{aligned}$$

(55)

By introducing new dependent variables $X(\xi )=f(\xi ), Y(\xi )=f'(\xi )$ (55) reduces to the following system:

$$\begin{aligned}&\frac{\mathrm{d}X}{\mathrm{d}\xi }=Y, \end{aligned}$$

(56)

$$\begin{aligned}&\frac{\mathrm{d}Y}{\mathrm{d}\xi }=\frac{\frac{\beta k^3}{2}Y^2+cX-\frac{\alpha k}{2}X^2}{k^3(1-X)}. \end{aligned}$$

(57)

To reduce the right hand side of (57) to a polynomial form we use the substitution

$$\begin{aligned} \mathrm{d}\xi =k^3(1-X)\mathrm{d}z. \end{aligned}$$

(58)

Then (56), (57) become

$$\begin{aligned}&\frac{\mathrm{d}X}{\mathrm{d}z}=\frac{\mathrm{d}X}{\mathrm{d}\xi }\frac{\mathrm{d}\xi }{\mathrm{d}z}=k^3(1-X)Y, \end{aligned}$$

(59)

$$\begin{aligned}&\frac{\mathrm{d}Y}{\mathrm{d}z}=\frac{\mathrm{d}Y}{\mathrm{d}\xi }\frac{\mathrm{d}\xi }{\mathrm{d}z}=\frac{\beta k^3}{2}Y^2+cX-\frac{\alpha k}{2}X^2. \end{aligned}$$

(60)

Then we proceed in a similar fashion as in the earlier cases and obtain the following exact solutions of (54):

$$\begin{aligned}&u(x,t)=\frac{2}{1-exp\left\{ \pm \sqrt{\alpha }(x-\alpha t)\right\} },\quad (with\quad \beta =-4) \end{aligned}$$

(61)

$$\begin{aligned}&u(x,t)=-\frac{2}{\beta }+exp\left\{ \pm \sqrt{\frac{\alpha }{2+\beta }}\left( x+\frac{\alpha }{\beta }t\right) \right\} , \quad (with\quad \beta \ne -2,0) \end{aligned}$$

(62)

$$\begin{aligned}&u(x,t)=exp\left\{ \pm \sqrt{\frac{\alpha }{2+\beta }}\left( x-\frac{\alpha }{2+\beta }t\right) \right\} , \quad (with\quad \beta \ne -2). \end{aligned}$$

(63)

(61), (62), (63) represent solution of (54) with some particular values of the parameter $\beta$ indicated in the parenthesis. The solutions (61) show that the pressure wave governed by (54) does not change much but has a singularity along $x=\alpha t$, where $\alpha$ is constant. However solutions (62), (63) show exponential blow up or decay for u(x, t) at $\infty$ or $-\infty$.

Fig. 5

Plot of u(x, t) given in (61) with $+$ sign and $\alpha =1$

Fig. 6

Plot of u(x, t) given in (61) with − sign and $\alpha =1$

Fig. 7

Plot of u(x, t) given in (62) with $+$ sign and $\alpha =1, \beta =1$

Fig. 8

Plot of u(x, t) given in (62) with − sign and $\alpha =1,\beta =1$

Fig. 9

Plot of u(x, t) given in (63) with $+$ sign and $\alpha =1,\beta =1$

Fig. 10

Plot of u(x, t) given in (63) with − sign and $\alpha =1,\beta =1$

6 Conclusion

Because of its simple computational procedure the first integral method is widely applicable to solve PDEs with polynomial first integral. Moreover, this method is less complicated compared to some other methods (e.g. homogeneous balance method, Lie symmetry method etc) for finding exact solutions of nonlinear PDEs. In this work, the first integral method has been applied successfully to obtain the exact solutions of the above equations. The obtained solutions are checked by using the Mathematica software and then plotted using some particular values of the parameters used in the corresponding equation. For variant Boussinesq system shock wave-like soutions for u(x, t) are obtained here, whereas solitary wave solutions were found by Wang in (Wang 1995). Shock wave-like solutions are also found for the extended mK-dV equation. For the Kudryashov–Sinel’shchikov equation, the solution (61) has singularity along $x=\alpha t$, where $\alpha$ is constant. The other solutions for this system exponentially blow up or decay at $\infty$ or $-\infty$.