An effective approximation to the dispersive soliton solutions of the coupled KdV equation via combination of two efficient methods

Abstract

The numerical solutions of the coupled Korteweg-de Vries equation is investigated via combination of two efficient methods that includes Crank–Nicolson scheme for time integration and quintic B-spline based differential quadrature method for space integration. The differential quadrature method has the advantage of using less number of grid points. And the advantage of the Crank–Nicolson scheme is the prevention of long and tedious algebraic computations for time integration. Those advantages come together and produce better results. To display the accuracy and efficiency of the present hybrid method three well-known test problems, namely single soliton, interaction of two soliton and birth of solitons are solved and the error norms $L_{2}$ and $L _{\infty }$ are computed and compared with earlier works. Present hybrid method obtained superior results than earlier works by using the same parameters and less number of grid points. This situation is shown by comparison of the earlier works. At the same time, two lowest invariants and numerical and analytical values of the amplitudes of the solitons during the simulations are computed and tabulated. Besides those, relative changes of invariants are computed. Properties of solitons observed clearly at the all of the test problems and figures of the all of the simulations are given.

1 Introduction

The Korteweg-de Vries equation (KdV)

$$\begin{aligned} u_{t}+\rho uu_{x}+\sigma u_{xxx}=0, \end{aligned}$$

(1)

is a nonlinear partial differential equation arising in the study of a number of different physical systems, e.g., water waves, plasma physics, anharmonic lattices, and elastic rods. It describes the long time evolution of small-but-finite amplitude dispersive waves (Miura 1976). Many researchers have investigated solutions of KdV type equations (Başhan 2018; Hepson et al. 2018; Başhan et al. 2015, 2016, 2018c).

In this study, we will research the set of equations known as coupled KdV which describes interactions of two long waves with different dispersion relations given by Hirota and Satsuma (1981) in 1981 as follows:

$$\begin{aligned} u_{t}= & {} \varepsilon \left( 6uu_{x}+u_{xxx}\right) +2\mu vv_{x}\text {,} \end{aligned}$$

(2)

$$\begin{aligned} v_{t}= & {} -3uv_{x}-v_{xxx}\text {, }\quad x\in \left[ x_{L},x_{R}\right] , \text { }t\in \left[ 0,T\right] \end{aligned}$$

(3)

where $\varepsilon$ and $\mu$ are arbitrary constants. For the value of $\mu =0,$ the effect of v vanishes and the Eq. (2) turns into the ordinary KdV equation. Because of the importance of the coupled KdV equation many scientists obtained analytical and numerical solutions such as (Wazwaz 2010a, b; Fan and Zhang 1998; Assas 2008; Tam et al. 2000; Abazari and Abazari 2012; Chen et al. 2012; Adem and Khalique 2012; Cao et al. 2012; Inan 2007; Rady et al. 2009; Roy 1998; Zhou et al. 2003; Halim et al. 2003; Kaya and Inan 2004; Oruç et al. 2017; Ismail and Ashi 2014; Ismail 2009; Al-Khaled et al. 2008; Biswas and Ismail 2010; Islam et al. 2009; Kutluay and Uçar 2013) .

Differential quadrature method (DQM) was first introduced by Bellman et al. (1972) to obtain numerical solution of partial differential equations. Many researchers have developed different types of DQMs utilizing various base functions such as Legendre polynomials and spline functions (Bellman et al. 1972), Hermite polynomials (Cheng et al. 2005), radial basis functions (Shu and Wu 2007), harmonic functions (Striz et al. 1995), Sinc functions (Korkmaz and Dağ 2011), B-spline functions (Başhan et al. 2018a; Karakoç et al. 2014), and modified B-spline functions (Mittal and Jain 2012; Başhan et al. 2017, 2018b; Başhan 2019).

In this work, a hybrid method which includes powerful type of finite difference method, namely Crank–Nicolson method and quintic B-spline based differential quadrature method is applied to obtain numerical solutions of coupled KdV equation. There are some advantages of the quintic B-splines such as the first-, the second- and the third-order weighting coefficients obtained directly without any recurrence formulae or matrix multiplication approach.

2 Space discretization via DQM

DQM can be defined as a numerical approximation to the partial differential equations via fewer nodal points than common methods that gets high accurate solutions. Let us take the grid distribution $a=x_{1}<x_{2}<\cdots <x_{N}=b$ of a finite interval $\left[ a,b\right]$ into consideration. Provided that any given function $U\left( x\right)$ is smooth enough over the solution domain, its derivatives with respect to x at a nodal point $x_{i}$ can be approximated by a linear summation of all the functional values in the solution domain, namely

$$\begin{aligned} \frac{d^{\left( r\right) }U}{dx^{\left( r\right) }}\left( x_{i}\right) =\sum _{j=1}^{N}w_{ij}^{\left( r\right) }U\left( x_{j}\right) ,\quad i=1,2, \ldots ,N,\quad r=1,2, \ldots ,N-1 \end{aligned}$$

(4)

where r denotes the order of the derivative, $w_{ij}^{\left( r\right) }$ represent the weighting coefficients of the rth order derivative approximation, and N denotes the number of nodal points in the solution domain. Here, the index j represents the fact that $w_{ij}^{\left( r\right) }$ is the corresponding weighting coefficient of the functional value $U\left( x_{j}\right)$. In this study, we need first-, second-, and third-order derivative of the function U(x). So, we will find value of the Eq. (4) for $r=1,2,3$.

Let $Q_{m}(x)$ be the quintic B-splines with knots at the points $x_{i}$ where the uniformly distributed N nodal points are taken as $a=x_{1}<x_{2}<\cdots <x_{N}=b$ on the ordinary real axis. The B-splines $\{Q_{-1},Q_{0},\ldots ,Q_{N+2}\}$ form a basis for functions defined over [a, b]. The quintic B-splines $Q_{m}(x)$ are defined by the following relationships (Prenter 1975):

$$\begin{aligned} Q_{m}\left( x\right) =\frac{1}{h^{5}}\left\{ \begin{array}{ll} q_{1}, &{} x\in [x_{m-3},x_{m-2}], \\ q_{1}-6q_{2}, &{} x\in [x_{m-2},x_{m-1}], \\ q_{1}-6q_{2}+15q_{3}, &{} x\in [x_{m-1},x_{m}], \\ q_{1}-6q_{2}+15q_{3}-20q_{4}, &{} x\in [x_{m},x_{m+1}], \\ q_{1}-6q_{2}+15q_{3}-20q_{4}+15q_{5}, &{} x\in [x_{m+1},x_{m+2}], \\ q_{1}-6q_{2}+15q_{3}-20q_{4}+15q_{5}-6q_{6}, &{} x\in [x_{m+2},x_{m+3}], \\ 0, &{} {\text {otherwise}}. \end{array} \right. \end{aligned}$$

where $q_{1}=(x-x_{m-3})^{5},$$q_{2}=(x-x_{m-2})^{5},\ q_{3}=(x-x_{m-1})^{5},\ q_{4}=(x-x_{m})^{5},\ q_{5}=(x-x_{m+1})^{5},\ q_{6}=(x-x_{m+2})^{5}\$and $h=x_{m}-x_{m-1}$ for all m.

2.1 First-order derivative approximation

Using the quintic B-splines as test functions in the fundamental DQM equation (4) leads to the following equation:

$$\begin{aligned} \frac{\partial ^{\left( r\right) }Q_{m}\left( x_{i}\right) }{\partial x^{\left( r\right) }}=\sum _{j=m-2}^{m+2}w_{i,j}^{\left( r\right) }Q_{m}\left( x_{j}\right) ,\quad m=-1,0,\ldots ,N+2,\text { }i=1,2,\ldots ,N. \end{aligned}$$

(5)

When DQM methodology is applied, the fundamental equality for determining the corresponding weighting coefficients of the first- order derivative approximation is obtained as follows:

$$\begin{aligned} \frac{\partial Q_{m}}{\partial x}\left( x_{i}\right) =\sum _{j=m-2}^{m+2}w_{i,j}^{\left( 1\right) }Q_{m}\left( x_{j}\right) ,\quad i=1,2,\ldots ,N,\quad m=-1,0,\ldots ,N+2, \end{aligned}$$

(6)

In the process, after all of the test functions are applied, we get the following system of algebraic equations:

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1 &{} 26 &{} 66 &{} 26 &{} 1 &{} &{} &{} &{} &{} &{} \\ &{} 1 &{} 26 &{} 66 &{} 26 &{} 1 &{} &{} &{} &{} &{} \\ &{} &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} &{} 1 &{} 26 &{} 66 &{} 26 &{} 1 &{} \\ &{} &{} &{} &{} &{} &{} 1 &{} 26 &{} 66 &{} 26 &{} 1 \end{array} \right] \left[ \begin{array}{l} w_{1,-3}^{\left( 1\right) } \\ w_{1,-2}^{\left( 1\right) } \\ w_{1,-1}^{\left( 1\right) } \\ w_{1,0}^{\left( 1\right) } \\ w_{1,1}^{\left( 1\right) } \\ w_{1,2}^{\left( 1\right) } \\ \vdots \\ w_{1,N+3}^{\left( 1\right) } \\ w_{1,N+4}^{\left( 1\right) } \end{array} \right] =\left[ \begin{array}{c} -\frac{5}{h} \\ -\frac{50}{h} \\ 0 \\ \frac{50}{h} \\ \frac{5}{h} \\ 0 \\ \vdots \\ 0 \\ 0 \end{array} \right] \end{aligned}$$

(7)

This system consists of $N+8$ unknowns and $N+4$ equations. For this system to have a unique solution, it is required to add four additional equations to the system. If we take the derivative of the equations, then we obtain the following:

$$\begin{aligned} \frac{\partial ^{2}Q_{-1}}{\partial x^{2}}\left( x_{1}\right)= & {} \sum _{j=-3}^{1}w_{1,j}^{\left( 1\right) }Q_{-1}^{^{\prime }}\left( x_{j}\right) \end{aligned}$$

(8)

$$\begin{aligned} \frac{\partial ^{2}Q_{0}}{\partial x^{2}}\left( x_{1}\right)= & {} \sum _{j=-2}^{2}w_{1,j}^{\left( 1\right) }Q_{0}^{^{\prime }}\left( x_{j}\right) \end{aligned}$$

(9)

$$\begin{aligned} \frac{\partial ^{2}Q_{N+1}}{\partial x^{2}}\left( x_{1}\right)= & {} \sum _{j=N-1}^{N+3}w_{1,j}^{\left( 1\right) }Q_{N+1}^{^{\prime }}\left( x_{j}\right) \end{aligned}$$

(10)

$$\begin{aligned} \frac{\partial ^{2}Q_{N+2}}{\partial x^{2}}\left( x_{1}\right)= & {} \sum _{j=N}^{N+4}w_{1,j}^{\left( 1\right) }Q_{N+2}^{^{\prime }}\left( x_{j}\right) \end{aligned}$$

(11)

By using the Eqs. (8), (9), (10) and (11) which we obtained by derivations, four unknown terms will be eliminated from equation system and solvable new algebraic equation system is obtained:

$$\begin{aligned} \left[ M\right] \left[ W_{1}^{1}\right] =\left[ \Phi _{1}^{1}\right] \end{aligned}$$

(12)

where

$$\begin{aligned} \left[ M\right] =\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 37 &{} 82 &{} 21 &{} &{} &{} &{} &{} &{} &{} \\ 8 &{} 33 &{} 18 &{} 1 &{} &{} &{} &{} &{} &{} \\ 1 &{} 26 &{} 66 &{} 26 &{} 1 &{} &{} &{} &{} &{} \\ &{} 1 &{} 26 &{} 66 &{} 26 &{} 1 &{} &{} &{} &{} \\ &{} &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} &{} &{} \\ &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ &{} &{} &{} &{} 1 &{} 26 &{} 66 &{} 26 &{} 1 &{} \\ &{} &{} &{} &{} &{} 1 &{} 26 &{} 66 &{} 26 &{} 1 \\ &{} &{} &{} &{} &{} &{} 1 &{} 18 &{} 33 &{} 8 \\ &{} &{} &{} &{} &{} &{} &{} 21 &{} 82 &{} 37 \end{array} \right] , \end{aligned}$$

and

$$\begin{aligned} \left[ W_{1}^{1}\right] =\left[ w_{1,-1}^{\left( 1\right) }\quad w_{1,0}^{\left( 1\right) }\quad w_{1,1}^{\left( 1\right) }\quad w_{1,2}^{\left( 1\right) }\quad w_{1,3}^{\left( 1\right) }\quad w_{1,4}^{\left( 1\right) }\quad \cdots \quad w_{1,N+1}^{\left( 1\right) }\quad w_{1,N+2}^{\left( 1\right) }\right] ^\mathrm{{T}} \end{aligned}$$

and

$$\begin{aligned} \left[ \Phi _{1}^{1}\right] =\left[ -\frac{109}{2h}\quad -\frac{29}{h}\quad 0\quad \frac{50}{h}\quad \frac{5}{h}\quad 0\quad \cdots \quad 0\quad 0\right] ^\mathrm{{T}}. \end{aligned}$$

So, the number of algebraic equations and the unknowns will be equal and the equation system will be solvable with 5-band Thomas algorithm. The new matrix system contains $N+4$ equations and $N+4$ unknowns.

By the same idea, for the determination of weighting coefficients $w_{k,j}^{\left( 1\right) },\,j=-1,0,\ldots ,N+2$ at grid points $x_{k}$, $2\le k\le N-1$ we got the following algebraic equation system:

$$\begin{aligned} \left[ M\right] \left[ W_{k}^{1}\right] =\left[ \Phi _{k}^{1}\right] , \end{aligned}$$

(13)

where

$$\begin{aligned} \left[ W_{k}^{1}\right] =\left[ w_{k,-1}^{\left( 1\right) }\text { }\cdots \text { }w_{k,k-3}^{\left( 1\right) }\text { }w_{k,k-2}^{\left( 1\right) } \text { }w_{k,k-1}^{\left( 1\right) }\text { }w_{k,k}^{\left( 1\right) }\text { }w_{k,k+1}^{\left( 1\right) }\text { }w_{k,k+2}^{\left( 1\right) }\text { } w_{k,k+3}^{\left( 1\right) }\text { }\cdots \text { }w_{k,N+2}^{\left( 1\right) }\right] ^\mathrm{{T}} \end{aligned}$$

and

$$\begin{aligned} \left[ \Phi _{k}^{1}\right] =\left[ 0\quad \cdots \quad 0\quad -\frac{5}{h} \quad -\frac{50}{h}\quad 0\quad \frac{50}{h}\quad \frac{5}{h}\quad 0\quad \cdots \quad 0\right] ^\mathrm{{T}}. \end{aligned}$$

For the last grid point of the domain $x_{N}$ with the same idea, by determining weighting coefficients $w_{N,j}^{\left( 1\right) },\quad j=-1,0,\ldots ,N+2$ we got the following algebraic equation system:

$$\begin{aligned} \left[ M\right] \left[ W_{N}^{1}\right] =\left[ \Phi _{N}^{1}\right] , \end{aligned}$$

(14)

where

$$\begin{aligned} \left[ W_{N}^{1}\right] =\left[ w_{N,-1}^{\left( 1\right) }\quad w_{N,0}^{\left( 1\right) }\quad \cdots \quad w_{N,N-3}^{\left( 1\right) }\quad w_{N,N-2}^{\left( 1\right) }\quad w_{N,N-1}^{\left( 1\right) }\quad w_{N,N}^{\left( 1\right) }\quad w_{N,N+1}^{\left( 1\right) }\quad w_{N,N+2}^{\left( 1\right) }\right] ^\mathrm{{T}} \end{aligned}$$

and

$$\begin{aligned} \left[ \Phi _{N}^{1}\right] =\left[ 0\quad 0\quad \cdots \quad 0\quad -\frac{ 5}{h}\quad -\frac{50}{h}\quad 0\quad \frac{29}{h}\quad \frac{109}{2h}\right] ^\mathrm{{T}}. \end{aligned}$$

2.2 Second-order derivative approximation

If we use quintic B-splines and its second derivatives, then all the corresponding weighting coefficients can be found out. If we use all test functions for the first grid point and follow in a similar manner the first-order derivative approximations, then the weighting coefficients $w_{1,j}^{\left( 2\right) }$,$\quad j=-1,0,\ldots ,N+2$ can be found out by solving the following system of algebraic equations:

$$\begin{aligned} \left[ M\right] \left[ W_{1}^{2}\right] =\left[ \Phi _{1}^{2}\right] , \end{aligned}$$

(15)

where

$$\begin{aligned} \left[ W_{1}^{2}\right] =\left[ w_{1,-1}^{\left( 2\right) }\quad w_{1,0}^{\left( 2\right) }\quad w_{1,1}^{\left( 2\right) }\quad \cdots \quad w_{1,N+1}^{\left( 2\right) }\quad w_{1,N+2}^{\left( 2\right) }\right] ^\mathrm{{T}} \end{aligned}$$

and

$$\begin{aligned} \left[ \Phi _{1}^{2}\right] =\left[ \frac{80}{h^{2}}\quad \frac{8}{h^{2}} \quad -\frac{120}{h^{2}}\quad \frac{40}{h^{2}}\quad \frac{20}{h^{2}}\quad 0\quad \cdots \quad 0\right] ^\mathrm{{T}}. \end{aligned}$$

So, the number of algebraic equations and the unknowns will be equal and the equation system will be solvable with 5-band Thomas algorithm. The new matrix system contains $N+4$ equations and $N+4$ unknowns.

By the same idea, for the determination of weighting coefficients $w_{k,j}^{\left( 2\right) },\,j=-1,0,\ldots ,N+2$ at grid points $x_{k}$, $2\le k\le N-1$ we got the following algebraic equation system:

$$\begin{aligned} \left[ M\right] \left[ W_{k}^{2}\right] =\left[ \Phi _{k}^{2}\right] , \end{aligned}$$

(16)

where

$$\begin{aligned} \left[ W_{k}^{2}\right] =\left[ w_{k,-1}^{\left( 2\right) }\text { }\cdots \text { }w_{k,k-3}^{\left( 2\right) }\text { }w_{k,k-2}^{\left( 2\right) } \text { }w_{k,k-1}^{\left( 2\right) }\text { }w_{k,k}^{\left( 2\right) }\text { }w_{k,k+1}^{\left( 2\right) }\text { }w_{k,k+2}^{\left( 2\right) }\text { } w_{k,k+3}^{\left( 2\right) }\text { }\cdots \text { }w_{k,N+2}^{\left( 2\right) }\right] ^\mathrm{{T}} \end{aligned}$$

and

$$\begin{aligned} \left[ \Phi _{k}^{2}\right] =\left[ 0\quad \cdots \quad 0\quad \frac{20}{ h^{2}}\quad \frac{40}{h^{2}}\quad -\frac{120}{h^{2}}\quad \frac{40}{h^{2}} \quad \frac{20}{h^{2}}\quad 0\quad \cdots \quad 0\right] ^\mathrm{{T}}. \end{aligned}$$

For the last grid point of the domain $x_{N}$ with the same idea, by determining weighting coefficients $w_{N,j}^{\left( 2\right) },\quad j=-1,0,\ldots ,N+2$ we got the following algebraic equation system:

$$\begin{aligned} \left[ M\right] \left[ W_{N}^{2}\right] =\left[ \Phi _{N}^{2}\right] , \end{aligned}$$

(17)

where

$$\begin{aligned} \left[ W_{N}^{2}\right] =\left[ w_{N,-1}^{\left( 2\right) }\quad w_{N,0}^{\left( 2\right) }\quad \cdots \quad w_{N,N-3}^{\left( 2\right) }\quad w_{N,N-2}^{\left( 2\right) }\quad w_{N,N-1}^{\left( 2\right) }\quad w_{N,N}^{\left( 2\right) }\quad w_{N,N+1}^{\left( 2\right) }\quad w_{N,N+2}^{\left( 2\right) }\right] ^\mathrm{{T}} \end{aligned}$$

and

$$\begin{aligned} \left[ \Phi _{N}^{2}\right] =\left[ 0\quad 0\quad \cdots \quad 0\quad \frac{ 20}{h^{2}}\quad \frac{40}{h^{2}}\quad -\frac{120}{h^{2}}\quad \frac{8}{h^{2}} \quad \frac{80}{h^{2}}\right] ^\mathrm{{T}}. \end{aligned}$$

2.3 Third-order derivative approximation

Now, if we use quintic B-splines and its third derivatives, then all the corresponding weighting coefficients are found out. If we use all test functions for the first grid point and follow in a similar manner the first- and second-order derivative approximations, then the weighting coefficients $w_{1,j}^{\left( 3\right) }$, $j=-1,0,\ldots ,N+2$ can be found out by solving the following system of algebraic equations:

$$\begin{aligned} \left[ M\right] \left[ W_{1}^{3}\right] =\left[ \Phi _{1}^{3}\right] , \end{aligned}$$

(18)

where

$$\begin{aligned} \left[ W_{1}^{3}\right] =\left[ w_{1,-1}^{\left( 3\right) }\quad w_{1,0}^{\left( 3\right) }\quad w_{1,1}^{\left( 3\right) }\quad \cdots \quad w_{1,N+1}^{\left( 3\right) }\quad w_{1,N+2}^{\left( 3\right) }\right] ^\mathrm{{T}} \end{aligned}$$

and

$$\begin{aligned} \left[ \Phi _{1}^{3}\right] =\left[ \frac{46}{h^{3}}\quad \frac{108}{h^{3}} \quad 0\quad -\frac{120}{h^{3}}\quad \frac{60}{h^{3}}\quad 0\quad \cdots \quad 0\right] ^\mathrm{{T}}. \end{aligned}$$

So, the number of algebraic equations and the unknowns will be equal and the equation system will be solvable with 5-band Thomas algorithm. The new matrix system contains $N+4$ equations and $N+4$ unknowns.

By the same idea, for the determination of weighting coefficients $w_{k,j}^{\left( 3\right) },\,j=-1,0,\ldots ,N+2$ at grid points $x_{k}$, $2\le k\le N-1$, we got the following algebraic equation system:

$$\begin{aligned} \left[ M\right] \left[ W_{ k}^{3}\right] =\left[ \Phi _{k}^{3}\right] , \end{aligned}$$

(19)

where

$$\begin{aligned} \left[ W_{k}^{3}\right] =\left[ w_{k,-1}^{\left( 3\right) }\text { }\cdots \text { }w_{k,k-3}^{\left( 3\right) }\text { }w_{k,k-2}^{\left( 3\right) } \text { }w_{k,k-1}^{\left( 3\right) }\text { }w_{k,k}^{\left( 3\right) }\text { }w_{k,k+1}^{\left( 3\right) }\text { }w_{k,k+2}^{\left( 3\right) }\text { } w_{k,k+3}^{\left( 3\right) }\text { }\cdots \text { }w_{k,N+2}^{\left( 3\right) }\right] ^\mathrm{{T}} \end{aligned}$$

and

$$\begin{aligned} \left[ \Phi _{k}^{3}\right] =\left[ 0\quad \cdots \quad 0\quad -\frac{60}{ h^{3}}\quad \frac{120}{h^{3}}\quad 0\quad -\frac{120}{h^{3}}\quad \frac{60}{ h^{3}}\quad 0\quad \cdots \quad 0\right] ^\mathrm{{T}}. \end{aligned}$$

For the last grid point of the domain $x_{N}$ with same idea, by determining weighting coefficients $w_{N,j}^{\left( 3\right) },\quad j=-1,0,\ldots ,N+2$ we got the following algebraic equation system:

$$\begin{aligned} \left[ M\right] \left[ W_{N}^{3}\right] =\left[ \Phi _{N}^{3}\right] , \end{aligned}$$

(20)

where

$$\begin{aligned} \left[ W_{N}^{3}\right] =\left[ w_{N,-1}^{\left( 3\right) }\quad w_{N,0}^{\left( 3\right) }\quad \cdots \quad w_{N,N-3}^{\left( 3\right) }\quad w_{N,N-2}^{\left( 3\right) }\quad w_{N,N-1}^{\left( 3\right) }\quad w_{N,N}^{\left( 3\right) }\quad w_{N,N+1}^{\left( 3\right) }\quad w_{N,N+2}^{\left( 3\right) }\right] ^\mathrm{{T}} \end{aligned}$$

and

$$\begin{aligned} \left[ \Phi _{N}^{3}\right] =\left[ 0\quad 0\quad \cdots \quad 0\quad -\frac{ 60}{h^{3}}\quad \frac{120}{h^{3}}\quad 0\quad -\frac{108}{h^{3}}\quad -\frac{ 46}{h^{3}}\right] ^\mathrm{{T}}. \end{aligned}$$

So the systems (12)–(20) can be solved by 5-banded Thomas algorithm.

3 Discretization in time and solution process

We have discretized Eq. (2) using effective type of finite difference method, namely Crank–Nicolson type scheme. First Eq. ( 2) is discretized as

$$\begin{aligned} \frac{U^{n+1}-U^{n}}{\Delta t}-6\varepsilon \frac{\left( UU_{x}\right) ^{n+1}+\left( UU_{x}\right) ^{n}}{2}-2\mu \frac{\left( VV_{x}\right) ^{n+1}+\left( VV_{x}\right) ^{n}}{2}-\varepsilon \frac{ U_{3x}^{n+1}+U_{3x}^{n}}{2}=0 \nonumber \\ \end{aligned}$$

(21)

Equation (21) is rewritten as follows:

$$\begin{aligned}&2U^{n+1}-\Delta t\left[ 6\varepsilon \left( UU_{x}\right) ^{n+1}+2\mu \left( VV_{x}\right) ^{n+1}+\varepsilon U_{3x}^{n+1}\right] \nonumber \\= & {} 2U^{n}+\Delta t\left[ 6\varepsilon \left( UU_{x}\right) ^{n}+2\mu \left( VV_{x}\right) ^{n}+\varepsilon U_{3x}^{n}\right] . \end{aligned}$$

(22)

Then, Rubin and Graves type linearization technique (Rubin and Graves 1975) is used at the left-hand side of the Eq. (22) to linearize the nonlinear terms as given below:

$$\begin{aligned} \left( UU_{x}\right) ^{n+1}= & {} \left( U^{n+1}U_{x}^{n}+U^{n}U_{x}^{n+1}-U^{n}U_{x}^{n}\right) \\ \left( UU_{x}\right) ^{n}= & {} U^{n}U_{x}^{n}\text { .} \end{aligned}$$

Accordingly, we have obtained after the vanishes the same terms at both the sides:

$$\begin{aligned}&2U^{n+1}-\Delta t\left[ 6\varepsilon \left( U^{n+1}U_{x}^{n}+U^{n}U_{x}^{n+1}\right) +2\mu \left( V^{n+1}V_{x}^{n}+V^{n}V_{x}^{n+1}\right) +\varepsilon U_{3x}^{n+1}\right] \nonumber \\&\quad =2U^{n}+\Delta t\left( \varepsilon U_{3x}^{n}\right) . \end{aligned}$$

(23)

By the same process applied to the Eq. (3)

$$\begin{aligned} 2V^{n+1}+\Delta t\left[ 3\left( U^{n+1}V_{x}^{n}+U^{n}V_{x}^{n+1}\right) +V_{3x}^{n+1}\right] =2V^{n}-\Delta tV_{3x}^{n}. \end{aligned}$$

(24)

is obtained. Now, let us define some terms to use in Eqs. (23) and (24) as

$$\begin{aligned} A_{i}^{n}= & {} \sum _{j=1}^{N}w_{ij}^{\left( 1\right) }U_{j}^{n}=U_{x_{i}}^{n},\quad B_{i}^{n}=\sum _{j=1}^{N}w_{ij}^{\left( 3\right) }U_{j}^{n}=U_{3x_{i}}^{n}, \nonumber \\ C_{i}^{n}= & {} \sum _{j=1}^{N}w_{ij}^{\left( 1\right) }V_{j}^{n}=V_{x_{i}}^{n},\quad D_{i}^{n}=\sum _{j=1}^{N}w_{ij}^{\left( 3\right) }V_{j}^{n}=V_{3x_{i}}^{n}, \nonumber \\ U_{x_{i}}^{n+1}= & {} \sum _{j=1}^{N}w_{ij}^{\left( 1\right) }U_{j}^{n+1},\quad U_{3x_{i}}^{n+1}=\sum _{j=1}^{N}w_{ij}^{\left( 3\right) }U_{j}^{n+1}, \nonumber \\ V_{x_{i}}^{n+1}= & {} \sum _{j=1}^{N}w_{ij}^{\left( 1\right) }V_{j}^{n+1},\quad V_{3x_{i}}^{n+1}=\sum _{j=1}^{N}w_{ij}^{\left( 3\right) }V_{j}^{n+1}, \end{aligned}$$

(25)

where $A_{i}^{n}$ and $B_{i}^{n}$ are the first-order and third-order derivative approximations of U functions at the nth time level on points $x_{i}$ and $C_{i}^{n}$ and $D_{i}^{n}$ are the first-order and third-order derivative approximations of V functions at the nth time level on points $x_{i}$ , respectively. By the substitution of definition (25) in Eq. (23) and reorganizing for each grid points as follows, we obtain

$$\begin{aligned}&\left[ 2-\varepsilon \Delta t\left( 6\left( A_{i}^{n}+U_{i}^{n}w_{ii}^{\left( 1\right) }\right) +w_{ii}^{\left( 3\right) }\right) \right] U_{i}^{n+1} \nonumber \\&\qquad +\left[ \sum _{j=1,i\ne j}^{N}-\varepsilon \Delta t\left( 6U_{i}^{n}w_{ij}^{\left( 1\right) }+w_{ij}^{\left( 3\right) }\right) U_{j}^{n+1}\right] \nonumber \\&\qquad +\left[ -2\mu \Delta t\left( C_{i}^{n}+V_{i}^{n}w_{ii}^{\left( 1\right) }\right) \right] V_{i}^{n+1} \nonumber \\&\qquad +\left[ \sum _{j=1,i\ne j}^{N}-2\mu \Delta t\left( V_{i}^{n}w_{ij}^{\left( 1\right) }\right) V_{j}^{n+1}\right] \nonumber \\&\quad =F_{i}^{n}, \end{aligned}$$

(26)

where

$$\begin{aligned} F_{i}^{n}=2U_{i}^{n}+\varepsilon \Delta tB_{i}^{n}, \quad \text {for }i=1(1)N. \end{aligned}$$

Then by using the same process used for Eq. (24), we obtain the following equations for each grid point.

$$\begin{aligned}&\left[ 3\Delta tC_{i}^{n}\right] U_{i}^{n+1}+\left[ 2+\Delta t\left( 3U_{i}^{n}w_{ii}^{\left( 1\right) }+w_{ii}^{\left( 3\right) }\right) \right] V_{i}^{n+1} \nonumber \\&\qquad +\left[ \sum _{j=1,i\ne j}^{N}\Delta t\left( 3U_{i}^{n}w_{ij}^{\left( 1\right) }+w_{ij}^{\left( 3\right) }\right) V_{j}^{n+1}\right] , \nonumber \\&\quad =G_{i}^{n}, \end{aligned}$$

(27)

where

$$\begin{aligned} G_{i}^{n}=2V_{i}^{n}-\Delta tD_{i}^{n}, \quad \text {for }i=1(1)N. \end{aligned}$$

By implementing the system of Eqs. (26) on $x_{i}$ , $i=1(1)N$ grid points, N equations consisting of N unknowns which are denoted by $U^{n+1}$ will be obtained. The equation system has been shown in matrix form below:

$$\begin{aligned} \left[ \begin{array}{ccccc} \Upsilon _{1,1} &{} \Upsilon _{1,2} &{} \cdots &{} &{} \Upsilon _{1,N} \\ \Upsilon _{2,1} &{} \Upsilon _{2,2} &{} \cdots &{} &{} \Upsilon _{2,N} \\ \vdots &{} \vdots &{} \ddots &{} &{} \vdots \\ &{} &{} &{} &{} \\ \Upsilon _{N-1,1} &{} \Upsilon _{N-1,2} &{} \cdots &{} &{} \Upsilon _{N-1,N} \\ \Upsilon _{N,1} &{} \Upsilon _{N,2} &{} \cdots &{} &{} \Upsilon _{N,N} \end{array} \right] \left[ \begin{array}{c} U_{1}^{n+1} \\ U_{2}^{n+1} \\ \vdots \\ \\ U_{N-1}^{n+1} \\ U_{N}^{n+1} \end{array} \right] =\left[ \begin{array}{c} F_{1}^{n} \\ F_{2}^{n} \\ \vdots \\ \\ F_{N-1}^{n} \\ F_{N}^{n} \end{array} \right] \end{aligned}$$

(28)

Then, the boundary conditions have been applied to the system of Eq. (28) and the first and the last equations are eliminated from the systems. So,

$$\begin{aligned} \left[ \begin{array}{ccccc} \Upsilon _{2,2} &{} \Upsilon _{2,3} &{} \cdots &{} &{} \Upsilon _{2,N-1} \\ \Upsilon _{3,2} &{} \Upsilon _{3,3} &{} \cdots &{} &{} \Upsilon _{3,N-1} \\ \vdots &{} \vdots &{} \ddots &{} &{} \vdots \\ &{} &{} &{} &{} \\ \Upsilon _{N-1,2} &{} \Upsilon _{N-1,3} &{} \cdots &{} &{} \Upsilon _{N-1,N-1} \end{array} \right] \left[ \begin{array}{c} U_{2}^{n+1} \\ U_{3}^{n+1} \\ \vdots \\ \\ U_{N-1}^{n+1} \end{array} \right] =\left[ \begin{array}{c} F_{2}^{n}-\Upsilon _{2,1}U_{1}^{n+1}-\Upsilon _{2,N}U_{N}^{n+1} \\ F_{3}^{n}-\Upsilon _{3,1}U_{1}^{n+1}-\Upsilon _{3,N}U_{N}^{n+1} \\ \vdots \\ \\ F_{N-1}^{n}-\Upsilon _{N-1,1}U_{1}^{n+1}-\Upsilon _{N-1,N}U_{N}^{n+1} \end{array} \right] \nonumber \\ \end{aligned}$$

(29)

is obtained and by the same process the boundary conditions have been applied to the system of Eq. (27) and the first and the last equations are eliminated from the systems and both of the systems are solved at the same time by Gauss elimination method easily.

4 Numerical examples

Here, three famous test problems, namely single soliton, interaction of two solitons and birth of the solitons are going to be investigated. The accuracy of the numerical method is checked by using the error norms $L_{2}$ and $L_{\infty },$ respectively:

$$\begin{aligned} L_{2}=\sqrt{h\sum _{j=1}^{N}\left| u_{j}-U_{j}\right| ^{2}}, \quad L_{\infty }=\max _{j}\left| u_{j}-U_{j}\right| \end{aligned}$$

(30)

Moreover, the following lowest two invariants (Ismail 2009) are going to be computed:

$$\begin{aligned} \begin{array}{l} I_{1}=\displaystyle \int _{-\infty }^{\infty }U\mathrm{{d}}x,\quad I_{2}=\displaystyle \int _{-\infty }^{\infty }\left( {U^{2}+}\frac{2}{3}\mu {V^{2}}\right) \mathrm{{d}}x. \end{array} \end{aligned}$$

(31)

Relative changes of invariants are defined as

$$\begin{aligned} \overset{\thicksim }{I}_{s}=\frac{I_{s}^{\text {final}}-I_{s}^{\text {initial}}}{ I_{s}^{\text {initial}}},\quad s=1,2. \end{aligned}$$

4.1 Single soliton

The coupled KdV equation has an exact solution given in the following form (Hirota and Satsuma 1981):

$$\begin{aligned} U(x,t)=2\gamma ^{2}\sec \text {h}^{2}\left( \zeta \right) ,\quad V(x,t)= \frac{1}{2\sqrt{\psi }}\sec \text {h}\left( \zeta \right) , \end{aligned}$$

(32)

where

$$\begin{aligned} \zeta =\gamma \left( x-\gamma ^{2}t+x_{0}\right) +\frac{1}{2\log \left( \psi \right) },\quad \psi =\frac{-\mu }{8\left( 4\varepsilon +1\right) \gamma ^{4}}. \end{aligned}$$

(33)

We take as initial condition Eq. (25) at $t=0$ of the following form:

$$\begin{aligned} U(x,0)=2\gamma ^{2}\sec \text {h}^{2}\left( \zeta \right) ,\quad V(x,0)= \frac{1}{2\sqrt{\psi }}\sec \text {h}\left( \zeta \right) \end{aligned}$$

(34)

and boundary condition

$$\begin{aligned} U(x_{L},t)=U(x_{R},t)=V(x_{L},t)=V(x_{R},t)=0, \end{aligned}$$

(35)

To allow comparison with earlier work (Ismail 2009), we use three different set of value of parameters as $\left( \text {a}\right)$$\varepsilon =-0.125$, $\mu =-3$, $\gamma =0.5$, $\left( \text {b}\right)$$\varepsilon =0.5$, $\mu =-3$, $\gamma =0.5,$$\left( \text {c}\right)$$\varepsilon =-0.5$, $\mu =3$ , $\gamma =0.5$ with fixed values $x_{0}=0$ and $-25\le x\le 25.$

First for the type $\left( \text {a}\right)$$\varepsilon =-0.125$, $\mu =-3$, $\gamma =0.5$ parameters are used and the solitons are going to move toward the right having the constant velocities with unchanged amplitudes, respectively. This situation is the result of properties of solitons that they protect their shape, amplitude and velocity during the simulation. The numerical and exact values of the amplitudes for the both of the solitons U and V are calculated and reported in Table 1. It is seen clearly from Table 1 that the amplitudes and velocities of both the solitons conserved during the simulation and present numerical values are in compliance with analytical values.

Table 1 Type (a) positions and amplitudes of single soliton: $\Delta t=0.01,$$N=361$

Fig. 1

Type (a) Simulations of single soliton and maximum error at ${t =20}$

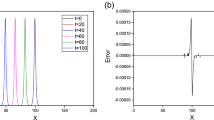
We have plotted the graphs of the numerical solution of single solitons for the type $\left( \text {a}\right)$ with $\Delta t=0.01$ and $N=361$ from $t=0$ to $t=20,$ in Fig. 1. It is clearly observed from Fig. 1 that the amplitudes and velocities of the both of the solitons of the U and V are conserved during the simulation. We have plotted maximum error values of the both of the solitons U and V at time $t=20$ at Fig. 1. To make a comparison quantitatively, the error norms $L_{2}$ and $L_{\infty }$ for +both of the solitons U and V have been computed and compared with earlier works (Oruç et al. 2017; Ismail and Ashi 2014) in Table 2 until $t=10,$ respectively. It is clearly seen from Table 2 that by using the same parameters $\Delta t=0.01$ and less number of grid points$\ N=361$, we have obtained superior results than other ones. Besides those, for the comparison with another work (Ismail 2009), simulation time is run up to $t=20$ with same parameters and again less number of grid points$\ N=361$ present results produce superior, again. The error norms $L_{2}$ and $L_{\infty }$ for the both of the solitons U and V are calculated and compared with earlier work (Ismail 2009) and given in Table 3. In addition to those results, the two lowest invariants $I_{1}$ and $I_{2}$ are computed and added to the Tables 2 and 3, respectively. It is clearly seen from the Tables 2 and 3 that invariants $I_{1}$ and $I_{2}$ are almost constant and in compliance with earlier works (Oruç et al. 2017; Ismail and Ashi 2014; Ismail 2009).

Table 2 Type (a) comparison of single soliton: $\varepsilon =-0.125$, $\mu =-3$ ,$\gamma =0.5$ ,$\Delta t=0.01$

Table 3 Type (a) comparison of single soliton: $\varepsilon =-0.125$ , $\mu =-3$, $\gamma =0.5$, $\Delta t=0.01$

Secondly for the type $\left( \text {b}\right)$$\varepsilon =0.5$, $\mu =-3$ , $\gamma =0.5$ parameters are used and the solitons are going to move toward the right having the constant velocities with unchanged amplitudes, respectively. As we expressed before, the properties of solitons are observed during the simulation. The numerical and exact value of the amplitudes for the both of the solitons U and V are calculated and reported in Table 4. As seen clearly from Table 4, the amplitudes and velocities of the both of the solitons conserved during the simulation and present numerical values are in compliance with analytical values.

Table 4 Type (b) positions and amplitudes of single soliton: $\Delta t=0.01,$$N=371$

For the type $\left( \text {b}\right)$ we have plotted the graphs of the numerical solution of single solitons with $\Delta t=0.01$ and $N=371$ from $t=0$ to $t=20,$ in Fig. 2. It is clearly observed from Fig. 2 that the amplitudes and velocities of the both of the solitons of the U and V are observed during the simulation. We have plotted maximum error values of the both of the solitons U and V at time $t=20$ in Fig. 2. To make a comparison quantitatively, the error norms $L_{2}$ and $L_{\infty }$ for the both of the solitons U and V have been computed and compared with earlier works (Ismail and Ashi 2014; Ismail 2009) in Table 5 until $t=20,$ respectively. It is clearly seen from Table 5 that by using the same parameter $\Delta t = 0.01$ and less number of grid points $N = 371$ the present results yield superior. In addition of those results, the two lowest invariants $I_{1}$ and $I_{2}$ are computed and added to the Table 5, respectively. It is clearly seen from the Table 5 that invariants $I_{1}$ and $I_{2}$ are almost constant and in compliance with earlier works (Ismail and Ashi 2014; Ismail 2009).

Fig. 2

Type (b) Simulations of single solitons and maximum error at $t =20$

Table 5 Type (b) comparison of single soliton: $\varepsilon =0.5$, $\mu =-3$, $\gamma =0.5$ for $\Delta t=0.01$

Third, for the type $\left( \text {c}\right)$$\varepsilon =-0.5$, $\mu =3$ , $\gamma =0.5$ parameters are used and the solitons are going to move toward the right having the constant velocities with unchanged amplitudes, respectively. As we expressed before, the properties of solitons are observed during the simulation. The numerical and exact value of the amplitudes for the both of the solitons U and V are calculated and reported at Table 6. As seen clearly from Table 6, the amplitudes and velocities of the both of the solitons conserved during the simulation and present numerical values are in compliance with analytical values.

Table 6 Type (c) positions and amplitudes of single soliton: $\Delta t=0.01,$$N=451$

For the type $\left( \text {c}\right)$ we have plotted the graphs of the numerical solution of single solitons with $\Delta t=0.01$ and $N=451$ from $t=0$ to $t=20,$ in Fig. 3. It is clearly observed from Fig. 3 that the amplitudes and velocities of both of the solitons of the U and V are conserved during the simulation. We have plotted maximum error values of the both of the solitons U and V at time $t=20$ at Fig. 3. To make a comparison quantitatively, the error norms $L_{2}$ and $L_{\infty }$ for the both of the solitons U and V have been computed and compared with earlier work (Ismail 2009) in Table 7 until $t=20,$ respectively. It is clearly seen from Table 7 that by the same parameter $\Delta t = 0.01$ and less number of grid points $N = 451$, we have obtained superior results. In addition of those results, the two lowest invariants $I_{1}$ and $I_{2}$ are computed and added to the Table 7, respectively. It is clearly seen from the Table 7 that invariants $I_{1}$ and $I_{2}$ are almost constant and in compliance with earlier work (Ismail 2009).

4.2 The interaction of double solitons

For the second test problem, the interaction of two solitons has the initial condition of the form (Ismail 2009)

$$\begin{aligned} U(x,0)=\sum \limits _{i=1}^{2}U_{i}\left( x,0\right) ,\quad V(x,0)=\sum \limits _{i=1}^{2}V_{i}\left( x,0\right) , \end{aligned}$$

(36)

where

$$\begin{aligned}&U_{i}\left( x,0\right) =2\gamma _{i}^{2}\sec \text {h}^{2}\left( \zeta _{i}\right) ,\quad V_{i}\left( x,0\right) =\frac{1}{2\sqrt{\psi _{i}}}\sec \text {h}\left( \zeta _{i}\right) ,\nonumber \\&\zeta _{i}=\gamma _{i}\left( x-\rho _{i}\right) +\frac{1}{2\log \left( \psi _{i}\right) },\quad \psi _{i}=\frac{-\mu }{8\left( 4\varepsilon +1\right) \gamma _{i}^{4}}\quad \left( i=1,2\right) . \end{aligned}$$

(37)

We have chosen those parameters $\gamma _{1}=1,$$\gamma _{2}=0.6,$$\rho _{1}=10,$$\rho _{2}=30,$$\varepsilon =0.5$ and $\mu =-3$ at the region $[-10, 120]$ in order to be able to compare the present results with those in the earlier work (Ismail 2009). This condition represents two solitons moving to the right. To provide interaction with increasing time, we place the greater soliton to the left side of the smaller one. Thus we place the greater soliton with amplitude $c_{1}=1.99673$ at $x_{1}=10.2$ and small soliton with amplitude $c_{2}=0.71957$ at $x_{2}=53.1$ for U at initial time $t=0$. To observe the interaction clearly at the simulation, we place the greater soliton with amplitude $c_{1}=1.41306$ at $x_{1}=10.2$ and small soliton with amplitude $c_{2}=0.50896$ at $x_{2}=53.1$ for V at initial time $t=0$. After the interaction completed and simulation finished at time $t=90$, the greater soliton with amplitude $c_{1}=1.99537$ at $x_{1}=103.0$ and small soliton with amplitude $c_{2}=0.71983$ at $x_{2}=80.8$ for U and the greater soliton with amplitude $c_{1}=1.41251$ at $x_{1}=103.0$ and small soliton with amplitude $c_{2}=0.50908$ at $x_{2}=80.8$ for V. These results show that during the interaction of solitons, they preserve their shapes, velocities and amplitudes. In fact, this is a well-known characteristic of solitons.

Fig. 3

Type (c) simulations of single solitons and maximum error at $t =20$

Table 7 Type (c) comparison of single soliton: $\varepsilon =-0.5$, $\mu =3$, $\gamma =0.5$, $\Delta t=0.01$

Fig. 4

Simulations of double solitons for U

Fig. 5

Simulations of double solitons for V

For simulation of interaction of double solitons to compare with earlier work (Ismail 2009) we used the same parameters as $h=0.1$ and $\Delta t=0.01$ for a long run from time $t=0$ to $t=90.$ As it is seen from Figs. 4 and 5 the greater soliton at the left position of the smaller soliton is located at the beginning of the run. With the increase of time, the greater soliton catches up the smaller one until time $t=50$ and the smaller soliton is being absorbed. The overlapping process continues until $t=70,$ greater soliton has overtaken the smaller soliton and start in the process of the separation. At time $t=90$, the interaction is complete and the greater soliton has separated completely from the smaller soliton. The two lowest invariants are computed and compared with earlier work (Ismail 2009) in Table 8. By using the same parameters with earlier work (Ismail 2009) two lowest invariants $I_{1},$ and $I_{2}$ changed by less than $-1.20\times 10^{-5}$ and $1.60\times 10^{-5}$, respectively, at the end of the simulation with respect to their initial values during the very long run and, therefore, they can be considered almost constant.

Table 8 The invariants for double solitons: $h=0.1$, $\Delta t=0.01$

4.3 The birth of solitons

Our last test problem is the birth of the solitons of the coupled KdV equation has been studied using the Gaussian initial condition

$$\begin{aligned} U(x,0)=e^{-0.01x^{2}}\text {,}\quad V(x,0)=e^{-0.01x^{2}}, \end{aligned}$$

(38)

and with boundary condition given at Eq. (35). First of all, in order to be able to compare the present solutions with earlier studies (Oruç et al. 2017; Ismail and Ashi 2014; Ismail 2009), we have selected the value of $\varepsilon =0.5$ and $\mu =-3$ , $\Delta t=0.01$ and $N=1301$ over the region of the $-50\le x\le 150.$ The graphs drawn for the both of the U and V at various times up to $t=50$ are given in Figs. 6 and 7. One can see from Figs. 6 and 7 clearly that at the initial time of the simulation there exist only one wave with same amplitudes values 1.0 at location $x=0$ for the each U and V, respectively. By the increasing of the time new solitons occur like trains of the waves. The locations and amplitude values of the all occurred sequent waves at time $t=50$ are given at Table 9. The two lowest invariants are computed and compared with earlier works (Oruç et al. 2017; Ismail and Ashi 2014) in Table 10. One can see clearly from the Table 10 that present hybrid method has used same parameters with earlier works (Oruç et al. 2017; Ismail and Ashi 2014) and obtained better results. For comparison with another work (Ismail 2009) invariants values for the different time steps are given at Table 11. It is clearly seen from Table 11 that using the same parameters with earlier work (Ismail 2009) two lowest invariants $I_{1},$ and $I_{2}$ changed by less than $-1.13\times 10^{-6}$ and $-2.71\times 10^{-5}$, respectively, at the end of the simulation with respect to their initial values during the very long run and, therefore, they can be considered almost constant.

Fig. 6

Simulations of the birth of the solitons for U

Fig. 7

Simulations of the birth of the solitons for V

Table 9 Positions and amplitudes of the birth of the solitons at t = 50: $\Delta t=0.01,N=1301$

Table 10 The invariants for the birth of the solitons

Table 11 The invariants for the birth of the solitons: $\Delta t=0.01$, $N=1301$

5 Conclusion

In this study, soliton solutions of the coupled KdV equation have been obtained using hybrid method including Crank–Nicolson scheme and differential quadrature method. For the time integration of coupled KdV equation we have used effective type of finite difference method, namely Crank–Nicolson scheme and then Rubin and Graves linearization technique is implemented. For the space integration of coupled KdV equation we used simple and powerful base functions, namely quintic B-splines for the differential quadrature method. For the last step, the obtained linear equation system has been solved by Gauss elimination method. Three well-known test problems have been solved. It can be seen straightforwardly from comparison of present results and given earlier works (Oruç et al. 2017; Ismail and Ashi 2014; Ismail 2009) that hybrid method can be effectively used for long runs of the coupled KdV equation. It is observed that conservation laws are reasonably satisfied for all of the test problems given in the present study. The obtained numerical results and the comparison of the error norms $L_{2}$ and $L_{\infty }$ and also the two invariants show that the hybrid method can achieve high accuracy and good conservation properties. As a conclusion, it can be said that the present hybrid method is an effective and efficient one for solving the coupled KdV equation and can also be used for numerical solutions of other partial differential equations.