Numerical Solution of Coupled Korteweg-de Vries Equation Employing Quintic Hyperbolic B-Spline Based Differential Quadrature Method

Abstract

In the present paper, the differential quadrature method is functionalized to solve coupled Korteweg-de Vries equation numerically with the usage of quintic hyperbolic B-spline basis as a test function. To judge the accuracy of this method, obtained results are compared with exact as well as with numerical solutions which are present in the literature gotten by other researchers. To obtain the weighting coefficients in the differential quadrature method, hyperbolic B-spline of quintic order is used, utilizing which system of equation will reduce to the first-order differential equation which is further solved by SSP- RK 43 scheme. The method Differential quadrature method has a great advantage over the traditional methods, especially it prevents the perturbation to find the better results for the given nonlinear equations, and quintic HBS can solve the diverse class of linear and nonlinear problems. To verify the efficiency and accurateness of this method, three types of test problems viz. single soliton, interaction of two solitons, and the birth of solitons are solved numerically, and also error norms ${L}_{2}$ and ${L}_{\infty }$ are calculated and matched with the prior work present in the literature.

Introduction

It is very well known that particular non-linear partial differential equations are used to illustrate many vital vigorous processes. This is of major physical curiosity to elucidate the closed-form of PDE’s along with a definite category of traveling wave resolutions while a nonlinear partial differential equation is used to illustrate a physical factor signifying certain types of properties like propagation or aggregation. Many attempts have been made in this direction by several researchers. During the past few years, in order to get the solutions of models with higher dimensions having soliton-like structures are also considered [39]. Solitons play a very significant part in the concept of nonlinear differential equations. Even for a variety of equations, soliton solutions are found including the Schrödinger equation [48,49,50], the coupled KdV equation [41, 50], and also the sine–Gordon equation [40]. Korteweg-de Vries (KdV) equations are nonlinear evolution equations having abundant solicitations in physics, plasma as well as in an engineering field. Also to designate the concept of tidal waves, the nonlinear Schrödinger equation describes waves occurring in deep water, whereas the KdV system of equation designates the special effects in surface water. Even the collaboration of two extended waves having unlike dispersion affairs is defined with the coupled KdV equations.

Coupled Korteweg-de Vries equation, abbreviated as (CKdV), was given by [1]. They hosted the CKdV equation as:

$$ \frac{\partial w}{{\partial t}} = a\left( {\frac{{\partial^{3} w}}{{\partial x^{3} }} + 6w\frac{\partial w}{{\partial x}}} \right) + 2bz\frac{\partial z}{{\partial x}} $$

(1)

$$ { }\frac{\partial z}{{\partial t}} = - \frac{{\partial^{3} z}}{{\partial x^{3} }} - 3w\frac{\partial z}{{\partial x}} $$

(2)

where a, b are random parameters, $w = w\left( {x,t} \right)$ defines the field of horizontal velocity, $z = z\left( {x,t} \right)$ defines the deviation of height from an ambient position of liquid and $\left( {z,z_{x} } \right)$ defines the part of force on the KdV wave scheme along with the linear dispersion relation $\left( {\omega = \frac{{k^{2} }}{2}} \right)$ respectively.

Originally Korteweg-de Vries equation was obtained through a long process and has taken near about sixty years of period [16], which was begun by the trials of Scott-Russell [6], the research of Boussinesq and Rayleigh nearby 1870 [7,8,9,10,11] then lastly concluding by the study of Korteweg and De Vries[2].

Korteweg-de Vries equation in simplified form is given by:

$$ \frac{\partial w}{{\partial t}} - 6w\frac{\partial w}{{\partial x}} + \frac{{\partial^{3} w}}{{\partial x^{3} }} = 0 $$

(3)

This is the outcome of research about extensive waves in water having little depth, where position, time is represented by x, t respectively, and $w = w\left( {x,t} \right)$ represents the wave surface.

The coupled Korteweg-de Vries equations have been solved by many researchers numerically as well as analytically. As a reference in [1, 9], the CKdV equation is solved by using the Hirota method. Kaya and Inan [10] solved coupled KdV equations numerically as well as analytically using the Adomian decomposition method. Fan [11] obtained different traveling solutions of CkdV equations by using the method. Assas [12] used the variational iteration method to solve this system of equations. Abbasbandy [13] solved the generalized form of Hirota–Satsuma CKdV by using the homotopy analysis method. Halim et al. [14], Halim and Leble [15] presented the numerical technique to resolve the general form of coupled KdV equations, which is suitable to solve a random number of equations having capricious persistent coefficients. The technique is practiced in the Hirota system and obtained solutions are paralleled with its already well-known analytical solution inspecting the effect of the initial condition and grid size to its accuracy. Zhu [16] offered a difference scheme to solve coupled KdV equations having a periodic initial-boundary problem and to solve the difference equations, the iterative method known as catch-ran is used. Zayed et al. [17] proposed an algebraic method to formalize the precise wave soliton solution for a generalized nonlinear coupled Korteweg-de Vries system. Cao et al. [18] used the trigonometric function transform method to achieve the specific solutions for coupled type equations like MKdV and KdV equations. Zhang et al. [19] derived hyperbolic and some other functions for Hirota–Satsuma combined KdV system by the F-expansion method. In [20, 21] homotopy perturbation method is used to solve the modified KdV equation. Kutluay and Ucar [47, 59] used quadratic B-splines based Galerkin method to solve modified KdV equation. Yagmurlu et al. [60] offers lumped Galerkin finite element method for the numerical solution of coupled KdV and coupled modified KdV equations. Tasbozan et al. [61] proposed homotopy analysis method to solve fractional modified KdV equation numerically. KdV equation is solved numerically through sub-domains based on similarity reduction by [22].

In this paper, we are going to use the quintic hyperbolic B-spline basis function by means of the differential quadrature method to crack coupled KdV equation numerically. The applicability of quantic Hyperbolic B-spline method employed in the present work is straight forward and very simple. Moreover, DQM has a great advantage due to its simple implementation, wide applicability and conceptual simplicity.

Initially, the Differential quadrature method (DQM) was presented by [23] to resolve the partial differential equations numerically. In DQM, a derivative of a function can be estimated as a linear summation of its value at different node points about the solution dominion of a problem. Several investigators have conceded out the diverse types of DQMs consuming various test functions to evaluate the weighting coefficients for the functional values at distinct nodal points. Bellman and his associates [23] have applied Legendre polynomial and spline functions, Quan and Chang [24, 25] introduced explicit formulation using Lagrange polynomial, [26] conceptualize the idea of linear vector space and polynomial approximation to compute weighting coefficients, [55] used cubic B-spline based DQM, [27, 56,57,58] used Quintic B-spline based DQM, [28] introduced polynomial DQM, as well as Quartic B-spline establishing DQM, [29], used quintic B-spline as per trial function in DQM, [30] define the revised form of trigonometric cubic B-spline with DQM, [31] utilize modified extended cubic B-spline by means of DQM, [32] used G-spline.

Numerical Scheme

Let’s consider the mesh division system $a = x_{1} < x_{2} < \ldots < x_{n} = b$ of a closed interval [a,b], with the deliberation that the assumed function $F\left( x \right)$ is sufficiently smooth over its solution domain. Differentiation of the function $F\left( x \right)$ with respect to $^{\prime}x^{\prime}$ for the mesh value $x_{i}$ can be estimated by a linear addition in the entire domain of all the functional values, can be written as:

$$ F_{x}^{\left( r \right)} \left( {x_{i} } \right) = \frac{{d^{r} F}}{{dx^{r} }} \left| {x_{i} } \right. = \mathop \sum \limits_{j = 1}^{N} d_{ij}^{\left( r \right)} F\left( {x_{j} } \right) $$

(4)

with $i = 1,2,3, \ldots ,N and r = 1,2,3, \ldots ,N - 1$.

where $r$ represents the derivative’s order, $d_{ij}^{\left( r \right)}$ is representing the weighting coefficients of $r^{th}$ order, $N$ tells about the number of grid points in whole domain, the index $j$ denotes that $d_{ij}^{\left( r \right)}$ is the corresponding weighting coefficients of the functional value of $F({x}_{j})$. So, for the further calculation, we need to calculate the first, second, and third-order derivative of the function $F(x)$, which can be evaluated by substituting $r=\mathrm{1,2},3$ in Eq. (4).

The approximate values of derivatives of 1st, 2nd and 3rd order can be given as:

$F_{x}^{\left( 1 \right)} \left( {x_{i} } \right) = \mathop \sum \limits_{j = 1}^{N} d_{ij}^{\left( 1 \right)} F\left( {x_{j} } \right)$,

$F_{x}^{\left( 2 \right)} \left( {x_{i} } \right) = \mathop \sum \limits_{j = 1}^{N} d_{ij}^{\left( 2 \right)} F\left( {x_{j} } \right)$,

$$ F_{x}^{\left( 3 \right)} \left( {x_{i} } \right) = \mathop \sum \limits_{j = 1}^{N} d_{ij}^{\left( 3 \right)} F\left( {x_{j} } \right) $$

(5)

Hyperbolic B-spline: Hyperbolic B-splines $H_{m}^{l}$ of order $l$ which is associated with the partition $X$ are defined as [62]

$$ H_{m}^{1} \left( x \right) = \left\{ {\begin{array}{*{20}c} {1, x_{m} \le x < x_{m + 1} } \\ {0, otherwise} \\ \end{array} } \right. $$

(6)

So, Eq. (6) represents the Hyperbolic B-spline of orfer 1, and for $l > 1$,

$$ H_{m}^{l} \left( x \right) = \frac{{p\left( {x - x_{m} } \right)}}{{p\left( {x_{l + m - 1} - x_{m} } \right)}}H_{m}^{l - 1} \left( x \right) + \frac{{p\left( {x_{m + l} - x} \right)}}{{p\left( {x_{m + l} - x_{m + 1} } \right)}}H_{m + 1}^{l - 1} \left( x \right) $$

(7)

where $p\left( x \right) = {\text{sinh}}\left( x \right)$.

Let $H_{m} \left( x \right)$ represents the quintic Hyperbolic B-splines with knots at the points ${x}_{i}$ where the evenly disseminated $N$ grid points are assumed as $a={x}_{1}<{x}_{2}<\dots <{x}_{N}=b$ on the usual real axis. The B-splines $\{{H}_{-1},{H}_{0},\dots ,{H}_{N+2}\}$ form a basis for functions defined over [a, b]. The quintic Hyperbolic B-splines ${H}_{m}(x)$ can be defined by the formula [51, 63]:

$$ H_{m} \left( x \right) = \frac{1}{\eta }*\left\{ \begin{gathered} p^{5} \left( {x_{m} } \right), {\varvec{x}} \in \left[ {{\varvec{x}}_{{\varvec{m}}} ,{\varvec{x}}_{{{\varvec{m}} + 1}} } \right) \hfill \\ p^{4} \left( {x_{m} } \right)g\left( {x_{m + 2} } \right) + p^{3} \left( {x_{m} } \right)g\left( {x_{m + 3} } \right)p\left( {x_{m + 1} } \right) + p^{2} \left( {x_{m} } \right)g\left( {x_{m + 4} } \right)p^{2} \left( {x_{m + 1} } \right) \hfill \\ + p\left( {x_{m} } \right)g\left( {x_{m + 5} } \right)p^{3} \left( {x_{m + 1} } \right) + g\left( {x_{m + 6} } \right)p^{4} \left( {x_{m + 1} } \right), {\varvec{x}} \in \left[ {{\varvec{x}}_{{{\varvec{m}} + 1}} ,{\varvec{x}}_{{{\varvec{m}} + 2}} } \right) \hfill \\ p^{3} \left( {x_{m} } \right)g^{2} \left( {x_{m + 3} } \right) + p^{2} \left( {x_{m} } \right)g\left( {x_{m + 4} } \right)p\left( {x_{m + 1} } \right)g\left( {x_{m + 3} } \right) + p^{2} \left( {x_{m} } \right)g^{2} \left( {x_{m + 4} } \right)p\left( {x_{m + 2} } \right) \hfill \\ + p\left( {x_{m} } \right)g\left( {x_{m + 5} } \right)p^{2} \left( {x_{m + 1} } \right)g\left( {x_{m + 3} } \right) + p\left( {x_{m} } \right)g\left( {x_{m + 5} } \right)p\left( {x_{m + 1} } \right)g\left( {x_{m + 4} } \right)p\left( {x_{m + 2} } \right) \hfill \\ + p\left( {x_{m} } \right)g^{2} \left( {x_{m + 5} } \right)p^{2} \left( {x_{m + 2} } \right) + g\left( {x_{m + 6} } \right)p^{3} \left( {x_{m + 1} } \right)g\left( {x_{m + 3} } \right) \hfill \\ + g\left( {x_{m + 6} } \right)p^{2} \left( {x_{m + 1} } \right)g\left( {x_{m + 4} } \right)p\left( {x_{m + 2} } \right) + g\left( {x_{m + 6} } \right)p\left( {x_{m + 1} } \right)g\left( {x_{m + 5} } \right)p^{2} \left( {x_{m + 2} } \right) \hfill \\ + g^{2} \left( {x_{m + 6} } \right)p^{3} \left( {x_{m + 2} } \right),{\varvec{x}} \in \left[ {{\varvec{x}}_{{{\varvec{m}} + 2}} ,{\varvec{x}}_{{{\varvec{m}} + 3}} } \right) \hfill \\ p^{2} \left( {x_{m} } \right)g^{3} \left( {x_{m + 4} } \right) + p\left( {x_{m} } \right)g\left( {x_{m + 5} } \right)p\left( {x_{m + 1} } \right)g^{2} \left( {x_{m + 4} } \right) \hfill \\ + p\left( {x_{m} } \right)g^{2} \left( {x_{m + 5} } \right)p\left( {x_{m + 2} } \right)g\left( {x_{m + 4} } \right) + p\left( {x_{m} } \right)g^{3} \left( {x_{m + 5} } \right)p\left( {x_{m + 3} } \right) \hfill \\ + g\left( {x_{m + 6} } \right)p^{2} \left( {x_{m + 1} } \right)g^{2} \left( {x_{m + 4} } \right) + g\left( {x_{m + 6} } \right)p\left( {x_{m + 1} } \right)g\left( {x_{m + 5} } \right)p\left( {x_{m + 2} } \right)g\left( {x_{m + 4} } \right) \hfill \\ + g\left( {x_{m + 6} } \right)p\left( {x_{m + 1} } \right)g^{2} \left( {x_{m + 5} } \right)p\left( {x_{m + 3} } \right) + g^{2} \left( {x_{m + 6} } \right)p^{2} \left( {x_{m + 2} } \right)g\left( {x_{m + 4} } \right) \hfill \\ + g^{2} \left( {x_{m + 6} } \right)p\left( {x_{m + 2} } \right)g\left( {x_{m + 5} } \right)p\left( {x_{m + 3} } \right) + g^{3} \left( {x_{m + 6} } \right)p^{2} \left( {x_{m + 3} } \right), {\varvec{x}} \in \left[ {{\varvec{x}}_{{{\varvec{m}} + 3}} ,{\varvec{x}}_{{{\varvec{m}} + 4}} } \right) \hfill \\ p\left( {x_{m} } \right)g^{4} \left( {x_{m + 5} } \right) + g\left( {x_{m + 6} } \right)p\left( {x_{m + 1} } \right)g^{3} \left( {x_{m + 5} } \right) \hfill \\ + g^{2} \left( {x_{m + 6} } \right)p\left( {x_{m + 2} } \right)g^{2} \left( {x_{m + 2} } \right) + g^{3} \left( {x_{m + 6} } \right)p\left( {x_{m + 3} } \right)g\left( {x_{m + 5} } \right) \hfill \\ g^{4} \left( {x_{m + 6} } \right)p\left( {x_{m + 4} } \right), \user2{ x} \in \left[ {{\varvec{x}}_{{{\varvec{m}} + 4}} ,{\varvec{x}}_{{{\varvec{m}} + 5}} } \right) \hfill \\ g^{5} \left( {x_{m + 6} } \right),\user2{ x} \in \left[ {{\varvec{x}}_{{{\varvec{m}} + 5}} ,{\varvec{x}}_{{{\varvec{m}} + 6}} } \right) \hfill \\ 0, otherwise \hfill \\ \end{gathered} \right. $$

(8)

where $p\left( {x_{m} } \right) = {\text{sinh}}\left( {x - x_{m} } \right)$, $g\left( {x_{m} } \right) = {\text{sinh}}\left( {x_{m} - x} \right)$, $\eta = {\text{sinh}}\left( {5h} \right){\text{sinh}}\left( {4h} \right){\text{sinh}}\left( {3h} \right){\text{sinh}}\left( {2h} \right){\text{sinh}}\left( h \right)$, $h = x_{m} - x_{m - 1}$ for all m.

with the values.

$h = x_{m} - x_{m - 1}$,

$e_{1} = \frac{{\sinh^{5} \left( h \right)}}{\eta },e_{2} = \frac{{2\sinh^{2} \left( h \right)\sinh^{3} \left( {2h} \right) + \sinh^{3} \left( h \right)\sinh \left( {2h} \right)\sinh \left( {3h} \right) + \sinh^{4} \left( h \right)\sinh \left( {4h} \right)}}{\eta }$,,

$e_{3} = \frac{{2\sinh^{3} \left( h \right)\sinh^{2} \left( {3h} \right) + 4\sinh^{2} \left( h \right)\sinh^{2} \left( {2h} \right)\sinh \left( {3h} \right)}}{\eta },e_{4} = \frac{{5\sinh^{4} \left( h \right)\cosh \left( h \right)}}{\eta }$,,

$$ e_{5} = \frac{{50\sinh^{4} \left( h \right) + 130\sinh^{6} \left( h \right) + 80\sinh^{8} \left( h \right)}}{\eta },e_{6} = 0 $$

To get better results, the hyperbolic B-spline can be reformed in such a way that the resultant matrix will turn into a diagonally dominant matrix [44]. So the modification of these functions can be done by using the formulas given below:

$$ \begin{gathered} {\rm H}_{1} \left( x \right) = H_{1} \left( x \right) + 2H_{0} \left( x \right) \hfill \\ {\rm H}_{2} \left( x \right) = H_{2} \left( x \right) - H_{0} \left( x \right) \hfill \\ {\rm H}_{j} \left( x \right) = H_{j} \left( x \right), \left( {3,4,5, \ldots ,N - 2} \right) \hfill \\ {\rm H}_{N - 1} \left( x \right) = H_{N - 1} \left( x \right) - H_{N + 1} \left( x \right) \hfill \\ {\rm H}_{N} \left( x \right) = H_{N} \left( x \right) + 2H_{N + 1} \left( x \right) \hfill \\ \end{gathered} $$

(9)

Computation of Weighting Coefficients $w_{ij}$

From Eq. (4) with $r = 1$ and the test function $H_{m} \left( x \right)$, the first-order approximation at the knot points $x_{i}$ is given by:

$$ H_{m}^{^{\prime}} \left( {x_{i} } \right) = \mathop \sum \limits_{j = 1}^{N} d_{ij}^{\left( 1 \right)} H_{m} \left( {x_{j} } \right) $$

(10)

for $i,m = 1,2,3, \ldots ,N$

That results in the following system of matrix

$$ B\vec{d}^{\left( 1 \right)} \left[ i \right] = \vec{S}\left[ i \right] $$

(11)

where B is the coefficient matrix given by:

$$ \left[ {\begin{array}{*{20}c} {e_{3} } & {e_{2} } & {e_{1} } & 0 & 0 & 0 & \cdots & 0 \\ {e_{2} } & {e_{3} } & {e_{2} } & {e_{1} } & 0 & 0 & \cdots & 0 \\ {e_{1} } & {e_{2} } & {e_{3} } & {e_{2} } & {e_{1} } & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & {e_{1} } & {e_{2} } & {e_{3} } & {e_{2} } & {e_{1} } \\ 0 & \cdots & 0 & 0 & {e_{1} } & {e_{2} } & {e_{3} } & {e_{2} } \\ 0 & \cdots & 0 & 0 & 0 & {e_{1} } & {e_{2} } & {e_{3} } \\ \end{array} } \right] $$

$\vec{d}^{\left( 1 \right)}$ [i] is the weighting coefficient vector corresponding to grid point $x_{i}$, which is given by:

$$ \vec{d}^{\left( 1 \right)} \left[ i \right] = \left[ {\begin{array}{*{20}c} {d_{i1}^{\left( 1 \right)} } \\ {d_{i2}^{\left( 1 \right)} } \\ : \\ : \\ {d_{in}^{\left( 1 \right)} } \\ \end{array} } \right] $$

and $\vec{S}\left[ i \right] = \left[ {s_{i1} , s_{i2} , s_{i3} , \ldots ,s_{iN} } \right]^{T}$ is the vector corresponding to $x_{i}$, where $i = 1,2, \ldots ,N$ which can be calculated as:

$\vec{S}\left[ 1 \right] = \left[ {\begin{array}{*{20}c} {e_{6} } \\ {e_{5} } \\ {e_{4} } \\ 0 \\ : \\ : \\ 0 \\ \end{array} } \right]$, $\vec{S}\left[ 2 \right] = \left[ {\begin{array}{*{20}c} { - e_{5} } \\ {e_{6} } \\ {e_{5} } \\ {e_{4} } \\ 0 \\ : \\ : \\ 0 \\ \end{array} } \right]$, $\vec{S}\left[ 3 \right] = \left[ {\begin{array}{*{20}c} { - e_{4} } \\ { - e_{5} } \\ {e_{6} } \\ {e_{5} } \\ {e_{4} } \\ : \\ : \\ 0 \\ \end{array} } \right]$,……, $\vec{S}\left[ {N - 2} \right] = \left[ {\begin{array}{*{20}c} 0 \\ : \\ : \\ { - e_{4} } \\ { - e_{5} } \\ {e_{6} } \\ {e_{5} } \\ {e_{4} } \\ \end{array} } \right]$,

$\vec{S}\left[ {N - 1} \right] = \left[ {\begin{array}{*{20}c} 0 \\ : \\ : \\ 0 \\ { - e_{4} } \\ { - e_{5} } \\ {e_{6} } \\ {e_{5} } \\ \end{array} } \right]$, $\vec{S}\left[ N \right] = \left[ {\begin{array}{*{20}c} 0 \\ : \\ : \\ 0 \\ { - e_{4} } \\ { - e_{5} } \\ {e_{6} } \\ \end{array} } \right]$.

The above five-band matrix system is resolved by the encoding in MATLAB, by which $\vec{d}^{\left( 1 \right)} \left[ i \right]$ will be obtained that is weighting coefficients of the first order, $d_{i1}^{\left( 1 \right)} ,d_{i2}^{\left( 1 \right)} ,d_{i3}^{\left( 1 \right)} , \ldots ,d_{{i\left( {N - 1} \right)}}^{\left( 1 \right)} ,d_{iN}^{\left( 1 \right)} .$ After evaluating the weighting coefficients of partial derivative having first order, their second and higher-order partial derivative can be premeditated by using the formula [34, 35] given below.

$$ \begin{gathered} d_{ij}^{\left( r \right)} = r\left[ {d_{ij}^{\left( 1 \right)} d_{ii}^{{\left( {r - 1} \right)}} - \frac{{d_{ij}^{{\left( {r - 1} \right)}} }}{{x_{i} - x_{j} }}} \right],\;{\text{for}}\;i \ne j\left\{ {i,j = 1,2,3, \ldots , N} \right\} \hfill \\ r = 2,3, \ldots , N - 1 \hfill \\ d_{ii}^{\left( r \right)} = - \mathop \sum \limits_{j = 1,j \ne i}^{N} d_{ij}^{\left( r \right)} ,\;{\text{for}}\;i = j \hfill \\ \end{gathered} $$

(12)

So, by applying the formulae given in Eq. (5) into the Eq. (1), (2), we will get the following system of equations:

$$ \begin{gathered} w_{t} = a\left[ {\mathop \sum \limits_{j = 1}^{N} d_{ij}^{\left( 3 \right)} w\left( {x_{j} } \right) + 6w\mathop \sum \limits_{j = 1}^{N} d_{ij}^{\left( 1 \right)} w\left( {x_{j} } \right)} \right] + 2bz\mathop \sum \limits_{j = 1}^{N} d_{ij}^{\left( 1 \right)} z\left( {x_{j} } \right) \hfill \\ z_{t} = - \mathop \sum \limits_{j = 1}^{N} d_{ij}^{\left( 3 \right)} z\left( {x_{j} } \right) - 3w\mathop \sum \limits_{j = 1}^{N} d_{ij}^{\left( 1 \right)} z\left( {x_{j} } \right) \hfill \\ \end{gathered} $$

(13)

Then further this scheme of ordinary differential equations will be elucidated using the Runge–Kutta method acknowledged as a strong stability-preserving time-stepping Runge–Kutta (SSP-RK43) regime [36].

Stability

To check the stability of the suggested system, the matrix stability analysis method is used and the idea of which is taken from the literature [30, 42, 43]. After the discretization of the system of Eqs. (1) and (2), they will be transformed into the system of ODEs Eq. (13). So, after converting the CKdV system of an equation into a system of ODEs (13) and assuming the nonlinear term as constant the system (1) and (2) can be inscribed as:

$$ \frac{\partial }{\partial t}\left[ {\begin{array}{*{20}c} w \\ z \\ \end{array} } \right] = P\left[ {\begin{array}{*{20}c} w & z \\ \end{array} } \right]^{T} + f\left( {w, z} \right) $$

(14)

where $P = \left[ {\begin{array}{*{20}c} {ad_{ij}^{\left( 3 \right)} } & O \\ O & { - d_{ij}^{\left( 3 \right)} } \\ \end{array} } \right]$ and $f\left( {w,z} \right)$ is nonlinear term of the equation, O is the null matrix. For the constancy of the proposed technique, eigen values of the matrix P will be computed for different grid points as shown in the Fig. 21, and Fig. 22. It is found that all the eigenvalues of P are complex and lie within the stability region, so it can be determined that proposed scheme is stable.

Numerical Problems and Discussion

To get to know about the accurateness of the suggested method, different numerical tests are performed like single soliton test, double soliton and also the birth of solitons and their preciseness is checked by using the $L_{2}$ and $L_{\infty }$ error norms which are given by

$$ \begin{gathered} L_{2} \left( w \right) = \sqrt {h\mathop \sum \limits_{j = 1}^{N} \left| {w_{j}^{exact} - w_{j}^{numerical} } \right|^{2} } \hfill \\ L_{\infty } \left( w \right) = \mathop {\max }\limits_{j} \left| {w_{j}^{exact} - w_{j}^{numerical} } \right| \hfill \\ \end{gathered} $$

Also, the conservation of the method is checked by evaluating the conserved values $I_{1}$, $I_{2}$, $I_{3}$ that is.

$I_{1} = \mathop \smallint \limits_{ - \infty }^{\infty } w{ }dx$ and $I_{2} = \mathop \smallint \limits_{ - \infty }^{\infty } \left( {w^{2} + \frac{2}{3}bz^{2} } \right)dx$,

$$ I_{3} = \mathop \smallint \limits_{ - \infty }^{\infty } \left[ {\left( {1 + a} \right)\left( {w^{3} - \frac{1}{2}w_{x}^{2} } \right) + b\left( {wz^{2} - z_{x}^{2} } \right)} \right]dx $$

Example 1: Single Soliton:

The exact solution of Coupled KdV equation [1] is given by

$$ w\left( {x,t} \right) = 2\alpha^{2} {\text{sech}}^{2} \left( \beta \right)\;{\text{and}}\;z\left( {x,t} \right) = \frac{1}{2\sqrt \gamma }{\text{sech}} \left( \beta \right), $$

(15)

where $\beta = \alpha \left( {x - \alpha^{2} t} \right) + \frac{1}{{2{\text{log}}\left( \gamma \right)}}$, $\gamma = \frac{ - b}{{8\left( {4a + 1} \right)\alpha^{4} }}$.

In this test, the initial condition can easily be attained from an exact solution with $t=0$ and are given as follows,

$$ w\left( {x,0} \right) = 2\alpha^{2} sech^{2} \left( \beta \right){\text{ and }}z\left( {x,0} \right) = \frac{1}{2\sqrt \gamma }{\text{sech}}\left( \beta \right), $$

(16)

where $\beta = \alpha x + \frac{1}{{2{\text{log}}\left( \gamma \right)}}$, $\gamma = \frac{ - b}{{8\left( {4a + 1} \right)\alpha^{4} }}$.

Now, for a single soliton, we are going to take the following three sets of parameters [37].

(a): $a = 0.5,{ }b = - 3,{ }\alpha = 0.5$

(b): $a = - 0.125, b = - 3, \alpha = 0.5$

(c): $a = - 0.5, b = 3, \alpha = 0.5$

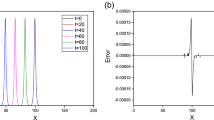
(a): Let’s take the CKdV Eq. (1) and (2) with parameters having value $a=0.5, b=-3, \alpha =0.5$ and exact solution (15), initial conditions (16). The graphical representation of analytical and numerical solutions for $N=421$ at different times are shown in Fig. 1. A soliton is a name given to the solitary wave that behaves like a “particle” satisfying the condition that when it propagates with the constant velocity it must maintain its shape and also a soliton conserves its amplitude, speed, and shape after a collision with a different soliton. For single solitons graphs are plotted for numerical as well as for exact solution with $N=421, \Delta t=0.0001, t=5\; to\; t=20.$ Also in Figs. 2 and 3 3-D graphs are plotted for exact as well as for numerical solution for both the solitons w and z. For the comparison error norms ${L}_{2}$ and ${L}_{\infty }$ are figured and matched with the previous [50] work for the solitons w and z in Tables 2 and 3 respectively till $t=20$. In Fig. 4 error plots for both the solitons w and z are represented by increasing grid points. Furthermore the conserved quantities for CKdV ${I}_{1}, {I}_{2}$ and ${I}_{3}$ are computed and given in Tables 2 and 3 which are in good agreement with previous work [37, 50] present in the literature. Also, in Tables 4 and 5 comparison of error norms is stimulated with [45, 47, 59]. Moreover from Table 2, it can be observed clearly that the invariants ${I}_{1}, {I}_{2}$ and ${I}_{3}$ are almost constant.

Fig. 1

Comparison of analytical and numerical solution for time $\mathrm{t}=\mathrm{5,10,15,20}$, $\Delta \mathrm{t}=0.0001$ and $\mathrm{N}=421$ of example 1a

Fig. 2

Comparison of exact and numerical solution at different time levels $(\mathrm{t}=5, 10, 15, 20)$ of $\mathrm{w}(\mathrm{x},\mathrm{t})$ example 1a

Fig. 3

Comparison of analytical and numerical solution of $\mathrm{z}(\mathrm{x},\mathrm{t})$ at different time levels $(\mathrm{t}=5, 10, 15, 20)$ of example 1(a)

Table 1 The values of quintic hyperbolic B-spline ${\mathrm{H}}_{\mathrm{m}}(\mathrm{x})$ basis functions and derivative functions ${{\mathrm{H}}^{\mathrm{^{\prime}}}}_{\mathrm{m}}(\mathrm{x})$ at different grid points is given by

Table 2 Evaluation of error norms and conserved quantities at different time levels of $\mathrm{w}(\mathrm{x},\mathrm{t})$ with $\mathrm{N}=421$, $\Delta \mathrm{t}=0.0001$, $\mathrm{a}=0.5,\mathrm{ b}=-3,{\alpha}=0.5$ (single soliton case (a))

Table 3 Evaluation of error norms and conserved quantities at different time levels of $\mathrm{z}(\mathrm{x},\mathrm{t})$ with $\mathrm{N}=421$, $\Delta \mathrm{t}=0.0001$, $\mathrm{a}=0.5,\mathrm{ b}=-3,{\alpha}=0.5$ (single soliton case (a))

Fig. 4

Plot of errors with respect to grid points $\mathrm{N}=\mathrm{121,221,421}$ at $\mathrm{t}=1$ (single soliton case (a))

Table 4 Comparison of error norms with $\mathrm{N}=421$, $\Delta \mathrm{t}=0.0001$, $\mathrm{a}=0.5,\mathrm{ b}=-3,{\alpha}=0.5$ (single soliton case (a))

Table 5 Comparison of error norms with $\mathrm{N}=421$, $\Delta \mathrm{t}=0.0001$, $\mathrm{a}=0.5,\mathrm{ b}=-3,{\alpha}=0.5$ (single soliton case (a))

(b) Consider the coupled KdV EqS. (1), (2) with parameters $a = - 0.125, b = - 3, \alpha = 0.5$ having exact solution (15) and initial boundary value problem (16). The comparison between exact and analytical solution for N = 421 at various values of ‘t’ is shown from Figs. 5, 6, and 7. By using the above values of $a, b \;and \;\alpha$, this can be perceived evidently from Fig. 5 that with the increasing time, solitons are moving on the way to the right consuming persistent velocities and unaffected amplitudes respectively. Also in Figs. 6 and 7 3-D graphs are plotted for exact as well as for numerical solution for both the solitons w and z. For the comparison error norms ${L}_{2}$ and ${L}_{\infty }$ are calculated and associated with the previous [50] work for the solitons w and z in Tables 6 and 7 respectively till $t=20$. In Fig. 8 error plots for both the solitons w and z are represented by increasing grid points.Furthermore the conserved quantities for CKdV ${I}_{1}, {I}_{2}$ and ${I}_{3}$ are computed and given in the Table 6 and in Table 7 hich are in worthy agreement with previous work [37, 50] present in the literature. Also, in Tables 8, 7 comparison of error norms is stimulated with [46, 47, 59]. Moreover from Table 6, it can be observed clearly that the invariants ${I}_{1}, {I}_{2}$ and ${I}_{3}$ are almost constant.

Fig. 5

Comparison of accurate and numerical solution for time $\mathrm{t}=\mathrm{5,10,15,20}$ and $\Delta \mathrm{t}=0.0001$ and $\mathrm{N}=421$ of example 1(b)

Fig. 6

Comparison of accurate and numerical solution of $\mathrm{w}(\mathrm{x},\mathrm{t})$ at different time levels $(\mathrm{t}=5, 10, 15, 20)$ example 1(b)

Fig. 7

Comparison of accurate and numerical solution of $\mathrm{z}(\mathrm{x},\mathrm{t})$ at different time levels $(\mathrm{t}=5, 10, 15, 20)$ of example 1(b)

Table 6 Comparability of error norms and conserved quantities at different time levels of $\mathrm{w}(\mathrm{x},\mathrm{t})$ with $\mathrm{N}=421$, $\Delta \mathrm{t}=0.0001$, $\mathrm{a}=-0.125,\mathrm{ b}=-3,{\alpha }=0.5$ (single soliton case (b))

Table 7 Comparability of error norms and conserved quantities at different time levels of $\mathbf{z}(\mathbf{x},\mathbf{t})$ with $\mathbf{N}=421$, $\Delta \mathbf{t}=0.0001$, $\mathbf{a}=-0.125,\mathbf{b}=-3,{\varvec{\alpha}}=0.5$ (single soliton case (b))

Fig. 8

Plot of errors with respect to grid points $N=\mathrm{101,121,221,421}$ at $t=1$(single soliton case (b))

Table 8 Comparison of error norms with $\mathrm{N}=421$, $\Delta \mathrm{t}=0.0001$, $\mathrm{a}=-0.125,\mathrm{ b}=-3,{\alpha }=0.5$ (single soliton case (b))

Table 9 Comparison of error norms with $\mathrm{N}=421$, $\Delta \mathrm{t}=0.0001$, $\mathrm{a}=-0.125,\mathrm{ b}=-3,{\alpha }=0.5$ (single soliton case (b))

(c): Let’s take the CKdV Eq. (1) and (2) with parameters having value $a=-0.5, b=3, \alpha =0.5$ and exact solution (15), initial conditions (16). The graphical representation of analytical and numerical solutions for $N=421$ at different times $(t=5, 10, 15, 20)$ are shown from Fig. 9 to Fig. 11. By using the above values of $a, b \;and \;\alpha$, this can be perceived clearly from Fig. 9 that with the increasing time, solitons are moving on the way to the right consuming persistent velocities and unaffected amplitudes respectively. Also in Figs. 10 and 11 3D graphs are plotted for exact as well as for numerical solution for both the solitons w and z. For the comparison error norms ${L}_{2}$ and ${L}_{\infty }$ are calculated and related with the previous [50] work for the solitons w and z in Tables 10 and 11 respectively till $t=20$. In Fig. 12 error plots for both the solitons w and z are represented by increasing grid points. Furthermore the conserved quantities for CKdV ${I}_{1}, {I}_{2}$ and ${I}_{3}$ are computed and given in the Tables 10 and 11 which are in good agreement with previous work [37, 50] present in the literature. Also, in Tables 12 and 13 comparison of error norms is stimulated with [45, 47, 59]. Moreover from Table 10, it can be observed clearly that the invariants ${I}_{1}, {I}_{2}$ and ${I}_{3}$ are almost constant.

Fig. 9

Comparison of accurate and numerical solution for time $\mathrm{t}=\mathrm{5,10,15,20}$ and $\Delta \mathrm{t}=0.0001$ and $\mathrm{N}=421$ of example 1(c)

Fig. 10

Comparison of accurate and numerical solution of $\mathrm{w}(\mathrm{x},\mathrm{t})$ at different time levels $(\mathrm{t}=5, 10, 15, 20)$ of example 1(c)

Fig. 11

Comparison of accurate and numerical solution at different time levels $(\mathrm{t}=5, 10, 15, 20)$ of $\mathrm{z}(\mathrm{x},\mathrm{t})$ example 1(c)

Table 10 Comparability of error norms and conserved quantities at different time levels of $\mathbf{w}(\mathbf{x},\mathbf{t})$ with $\mathbf{N}=421$, $\Delta \mathbf{t}=0.0001$, $\mathbf{a}=-0.5,\mathbf{b}=3,{\varvec{\alpha}}=0.5$ (single soliton case (c))

Table 11 Comparability of error norms and conserved quantities at different time levels of $\mathbf{z}(\mathbf{x},\mathbf{t})$ with $\mathbf{N}=421$, $\Delta \mathbf{t}=0.0001$, $\mathbf{a}=-0.5,\mathbf{b}=3,{\varvec{\alpha}}=0.5$ (single soliton case (c))

Fig. 12

Plot of errors with respect to grid points $N=\mathrm{101,121,221,421}$ at $t=1$(single soliton case (c))

Table 12 Comparison of error norms with $\mathrm{N}=421$, $\Delta \mathrm{t}=0.0001$, $\mathrm{a}=-0.5,\mathrm{ b}=3,{\alpha }=0.5$ (single soliton case (c))

Table 13 Comparison of error norms with $\mathrm{N}=421$, $\Delta \mathrm{t}=0.0001$, $\mathrm{a}=-0.5,\mathrm{ b}=3,{\alpha }=0.5$ (single soliton case (c))

Example 2: Double Solitons

Now to study the collaboration of two solitons, initial conditions are taken [37], that is representation of the sum of two single solitons is given by:

$$ w\left( {x,0} \right) = \mathop \sum \limits_{k = 1}^{2} w_{k} \left( {x,0} \right),z\left( {x,0} \right) = \mathop \sum \limits_{k = 1}^{2} z_{k} \left( {x,0} \right) $$

where,

$$ w_{k} \left( {x,0} \right) = 2\alpha_{k}^{2} {\text{sech}}^{2} \left( {\beta_{k} } \right),z_{k} \left( {x,0} \right) = \frac{1}{{2\sqrt {\gamma_{k} } }}{\text{sech}} \left( {\beta_{k} } \right) $$

with $\beta_{k} = \alpha_{k} \left( {x - y_{k} } \right) + \frac{1}{{2\log \left( {\gamma_{k} } \right)}},\gamma_{k} = \frac{ - b}{{8\left( {4a + 1} \right)\alpha_{k}^{4} }},k = 1,2$

Analytical solution for double solitons of coupled Korteweg–de Vries equation is given by

$$ w\left( {x,t} \right) = \mathop \sum \limits_{k = 1}^{2} w_{k} \left( {x,t} \right),z\left( {x,t} \right) = \mathop \sum \limits_{k = 1}^{2} z_{k} \left( {x,t} \right) $$

where,

$$ w_{k} \left( {x,t} \right) = 2\alpha_{k}^{2} {\text{sech}}^{2} \left( {\beta_{k} } \right),z_{k} \left( {x,t} \right) = \frac{1}{{2\sqrt {\gamma_{k} } }}{\text{sech}} \left( {\beta_{k} } \right) $$

with $\beta_{k} = \alpha_{k} \left( {x - y_{k} - \alpha_{k}^{2} t} \right) + \frac{1}{{2\log \left( {\gamma_{k} } \right)}},\gamma_{k} = \frac{ - b}{{8\left( {4a + 1} \right)\alpha_{k}^{4} }},k = 1,2$

To get the numerical solutions of double solitons parameters [38] are chosen as $a = 0.5, b = - 3, \alpha_{1} = 1.0, \alpha_{2} = 0.6, y_{1} = 10, y_{2} = 30, N = 421\;{\text{and}}\;\Delta t = 0.0001\;{\text{for}}\;0 \le x \le 70$. By using the above parameters and conditions for a sum of two single solitons, we will get the representation of two solitons as shown in Fig. 13. For double solitons graphs are plotted for numerical as well as for exact solution with $N = 421, \Delta t = 0.0001, t = 1\;{\text{to}}\;t = 4$. Likewise simulation for exact as well as for numerical solution for both the solitons w and z are shown in Figs. 14 and 15. Furthermore the conserved quantities for double solitons of CKdV ${I}_{1}, {I}_{2}$ and ${I}_{3}$ are computed and given in the Table 14 and also error norms in Table 15. In Fig. 16 error plots for both the solitons w and z are represented by increasing grid points.

Fig. 13

Graphical representation of numerical and analytical solution at different time values $(\mathrm{t}=\mathrm{1,2},\mathrm{3,4})$ for simulations of double solitons of coupled KdV equation

Fig. 14

Simulations of Example 2 at different time values $(\mathrm{t}=\mathrm{1,2},\mathrm{3,4})$ of $\mathrm{w}(\mathrm{x},\mathrm{t})$ for $\mathrm{N}=421,\Delta\mathrm{t}=0.0001$

Fig. 15

Simulations of Example 2 at different time values $(\mathrm{t}=\mathrm{1,2},\mathrm{3,4})$ of $\mathrm{z}(\mathrm{x},\mathrm{t})$ for $\mathrm{N}=421,\Delta\mathrm{t}=0.0001$

Table 14 The invariants for double solitons at distinct time levels with $\mathbf{N}=421,\Delta \mathrm{t}=0.0001,\mathrm{ a}=0.5,\mathrm{ b}=-3, {{\alpha }}_{1}=1.0, {{\alpha }}_{2}=0.6, {\mathrm{y}}_{1}=10, {\mathrm{y}}_{2}=30, [\mathrm{0,70}]$

Table 15 The error norms for double solitons at distinct time levels with $\mathrm{N}=421, \Delta \mathrm{t}=0.0001,\mathrm{ a}=0.5,\mathrm{ b}=-3, {{\alpha }}_{1}=1.0, {{\alpha }}_{2}=0.6, {\mathrm{y}}_{1}=10, {\mathrm{y}}_{2}=30, [\mathrm{0,70}]$

Fig. 16

Plot of errors for double solitons with respect to grid points $N=\mathrm{101,201,301,401}$ at $t=0.1$

Example 3: Birth of Solitons

In this example birth of solitons of coupled KdV equation will be studied with the initial condition taken as Gaussian initial condition [38] as:

$$ \begin{gathered} w\left( {x,0} \right) = \exp \left( { - 0.01x^{2} } \right) \hfill \\ z\left( {x,0} \right) = \exp \left( { - 0.01x^{2} } \right) \hfill \\ \end{gathered} $$

and boundary conditions

$$ \begin{gathered} w\left( {x_{L} ,t} \right) = w\left( {x_{R} ,t} \right) = 0 \hfill \\ z\left( {x_{L} ,t} \right) = z\left( {x_{R} ,t} \right) = 0 \hfill \\ \end{gathered} $$

with the parameters $a = 0.5, b = - 3, - 50 \le x \le 150, N = 421, \Delta t = 0.0001$.

By using the above-defined parameters and conditions graphical representation for the birth of solitons is symbolized in Figs. 17 and 18 for different values of time ($t = 1,2,3,4,5$) for both the solitons ‘w and z’ of CKdV system respectively. From both the figures it can be observed clearly that for the initial value of time that is for $t=1$ there exist a single wave with amplitude near about 1 at the location $x=0$ for each soliton w and z. And with the increasing time the curves in the simulation are also increasing or we can say that new solitons are occurring as we increase the time for simulations. Furthermore the conserved quantities for the birth of solitons of CKdV ${I}_{1}, {I}_{2}$ and ${I}_{3}$ are computed and given in the Table 16 from where it can be observed that the values of the invariants ${I}_{1}, {I}_{2}$ and ${I}_{3}$ are preserved during the evolution of the numerical solution. Furthermore simulation for exact as well as for numerical solution for both the solitons w and z are presented in Figs. 19, 20.

Fig. 17

Numerical solution of birth of solitons at different time values $(\mathrm{t}=\mathrm{1,2},\mathrm{3,4},5)$ of coupled KdV equations for $\mathrm{w}\left(\mathrm{x},\mathrm{t}\right)$

Fig. 18

Numerical solution of birth of solitons at different time values $(\mathrm{t}=\mathrm{1,2},\mathrm{3,4},5)$ of coupled KdV equations for $\mathrm{z}(\mathrm{x},\mathrm{t})$

Table 16 The invariants for birth of solitons at different time levels with $\mathrm{N}=421, \Delta \mathrm{t}=0.0001,\mathrm{ a}=0.5,\mathrm{ b}=-3,\mathrm{ \alpha }=0.5, \left[-\mathrm{50,150}\right].$

Fig. 19

Simulations of Example 3 at different time values $(\mathrm{t}=\mathrm{1,2},\mathrm{3,4})$ of $\mathrm{w}(\mathrm{x},\mathrm{t})$ for $\mathrm{N}=421,\Delta\mathrm{t}=0.0001$

Fig. 20

Simulations of Example 3 at different time values $(\mathrm{t}=\mathrm{1,2},\mathrm{3,4})$ of $\mathrm{z}(\mathrm{x},\mathrm{t})$ for $\mathrm{N}=421,\Delta\mathrm{t}=0.0001$

Fig. 21

Plot of eigen values for n = 101, 221

Fig. 22

Plot of eigen values for n = 321, 421

Conclusion

In recent years, solitons have been publicized to perform an important role in the study of non-linear differential equations. For the different types of equations, soliton resolutions have been found including the KdV equation. Different numerical schemes have been proposed by many authors [45, 50,51,52,53,54] to solve coupled KdV equation numerically. In this study, we have proposed the quintic hyperbolic B-spline basis function with differential quadrature method to achieve the numerical solution of coupled KdV equation. The computed arithmetical results are compared with the analytical solution and also with the results presented by other researchers in the literature. Three well-known test problems (single soliton, double solitons, and birth of solitons) have been solved to assess the effectiveness of the present method. Also, to check the accurateness of the scheme, numerical results are compared with the exact solutions by calculating the error norms ${L}_{2}$ and ${L}_{\infty }$ and even it has been noticed that it keeps the preserved quantities nearly constant during the simulation. As a deduction, it can be concluded that the method is an efficient and effective technique for elucidating the coupled KdV equation and likewise for the variety of partial differential equations.